Число 37 четное или нечетное: Таблица нечётных чисел от 0 до 100

Урок 37. Занимательные задачи — гдз по математике для 5 класса С.М. Никольский, М.К. Потапов, Н.Н. Решетников, А.В. Шевкин

Класс

• 1 класс

• 2 класс

  • Английский язык
  • Математика

• 3 класс

  • Русский язык
  • Английский язык
  • Математика

• 4 класс

  • Русский язык
  • Английский язык
  • Математика

• 5 класс

  • Русский язык
  • Английский язык
  • Математика
  • Биология

• 6 класс

  • Русский язык
  • Английский язык
  • Математика
  • Биология

• 7 класс

  • Русский язык
  • Английский язык
  • Математика
  • Биология
  • Физика
  • Химия

• 8 класс

  • Русский язык
  • Английский язык
  • Математика
  • Биология
  • Физика
  • Химия

• 9 класс

  • Русский язык
  • Английский язык
  • Математика
  • Биология
  • Физика
  • Химия

• 10 класс

  • Английский язык
  • Биология
  • Физика
  • Химия

• 11 класс

  • Английский язык
  • Биология
  • Химия

5 КЛАСС

Урок 37.

Занимательные задачи

Решение в
сумма является нечетным числом, так как складывается нечетное количество нечетных чисел.

Решение б
Пусть:
2a + 1 − первое нечетное число;
2b + 1 − второе нечетное число;
2c + 1 − третье нечетное число;
2d + 1 − четвертое нечетное число;
2e + 1 − пятое нечетное число, тогда их сумма:
2a + 1 + 2b + 1 + 2c + 1 + 2d + 1 + 2e + 1 = (2a + 2b + 2c + 2d + 2e + 4) + 1 = 2(a + b + c + d + e + 2) + 1 − получается, что к четному числу 2(a + b + c + d + e + 2) прибавляется 1, значит число 2(a + b + c + d + e + 2) + 1 − нечетное, а число 100 четное. Значит подобрать пять нечетных чисел, сумма которых равна 100 нельзя.

Решение б
Возьмем четное количество нечетных чисел, например 3 числа, тогда пусть:
2a + 1 − первое нечетное число;
2b + 1 − второе нечетное число;
2c + 1 − третье нечетное число, тогда их сумма:
2a + 1 + 2b + 1 + 2c + 1 = (2a + 2b + 2c + 2) + 1 = 2(a + b + c + 1) + 1 − получается, что к четному числу 2(a + b + c + 1) прибавляется 1, значит число 2(a + b + c + 1) + 1 − нечетное.   Получается, что если количество нечетных слагаемых нечетное, то их нельзя сгруппировать по парам, так как останется одно нечетное слагаемое без пары. А сумма четного и нечетного числе будет нечетной.

Непростое натуральное число, большее единицы, называют составным.

Решение б
Число 1 не является составным числом.

Внимательно читайте условие задания.

Соседи числа — это число, которое предшествует этому числу при счете (предыдущее число), и число, которое при счёте следует за ним.

Простые числа: 5, 7, 11, 13.
Составные числа: 6, 8, 9, 10, 12, 14, 15.

Решение д
12321 делится на 1 и на само себя;
12321 делится на 3 и на 9, так как 1 + 2 + 3 + 2 + 1 = 9, значит:
12321 − составное.

 Решение г
59 делится только на 1 и на само себя, значит, оно простое.

Решение в
Составные числа, большие 30, но меньшие 50:
32, 33, 34, 35, 36, 38, 39, 40, 42, 44, 45, 46, 48, 49. 

1000 − составное.

Увеличить число на несколько единиц - использовать действие сложение, знак"+" Уменьшить на несколько единиц- использовать действие вычитание, знак "-".

Решение в
Любое простое число, большее 2, − это нечетное число, его можно представить в виде суммы четного и нечетного чисел. Например;
5 = 4 + 1;
37 = 34 + 3, а простое число 2 нельзя записать в виде суммы четного и нечетного чисел.

Нет не верно. Например:
3 + 5 = 8 − число 8 составное.

Сумма, разность, произведение рациональных чисел является рациональным числом (без деления на нуль).

Решение г
7 + 2 + a + b + 8 = 3n
a + b = 3n − 7 − 2 − 8
a + b = 3n − 17
Пусть b = 1, тогда:
a + 1 = 3n − 17
a = 3n − 18
a = 3(n − 6)
Пусть n = 7, тогда:
a = 3(7 − 6)
a = 3 * 1
a = 3
Ответ: 72318
 
делятся на 5:
35325; 43140; 53205.
делятся на 2:
43140; 72318.  
делятся на 10:
43140.
делятся на 4:
43140.

3333 − делится на 3, но не делится на 9, так как:
3 + 3 + 3 + 3 = 12 − не делится на 9.

Решение б
Разложить данное составное число на простые множители − значит представить его в виде произведения различных его простых делителей или их степеней.

Единичным называют отрезок, длину которого принимают за единицу.

Вопросники:

Увлекательная математика — теоретический материал

Меню сайта Форма входа

Инварианты.  Инвариантом некоторого преобразования называется величина или свойство, не изменяющееся при этом преобразовании. В качестве инварианта чаще всего рассматриваются четность и остаток от деления.  Известно, что целые числа бывают четными и нечетными.  Четные числа можно записать в виде 2k, где k — целое число, а нечетные – в виде 2k +1 или 2k-1.   Cвойства четности:  0. Сумма двух четных чисел четна. Сумма двух нечетных чисел четна. Сумма четного и нечетного чисел — нечетна.  1. Сумма любого количества четных чисел четна.  Доказательство: все четные числа делятся на 2, поэтому из их суммы можно вынести 2 за скобку; а тогда сумма будет делится на 2, т.е. будет четной.  2. Сумма четного числа нечетных чисел четна, сумма нечетного числа нечетных чисел нечетна.  Доказательство: Если нечетных чисел — четное число (2n), то разобьем их на пары (всего n пар). Сложим числа в каждой паре (сумма двух нечетных чисел — четная !). Получим сумму n четных чисел, которая четна по п.1. Если же было нечетное число (2n+1) нечетных чисел, то возьмем все числа, кроме одного (2n штук) — их сумма четна. Прибавим к ней оставшееся нечетное число и получим, что сумма всех чисел нечетна по п.0.  2′ Противоположные числа имеют одинаковую четность. 3. Сумма нескольких целых чисел четна тогда и только тогда, когда среди них четное число нечетных чисел.  Доказательство: Сложим отдельно все четные и отдельно все нечетные числа. Первая сумма всегда четна (п.1), вторая четна тогда и только тогда, когда в ней четное число нечетных чисел (п.2). Если вторая сумма четна, то сумма всех четна, если она нечетна, то сумма всех нечетна (см. п.0), поэтому четность суммы всех чисел определяется указанным в условии правилом.  4. Разность двух четных чисел четна. Разность двух нечетных чисел четна. Разность четного и нечетного чисел в любом порядке — нечетна. 5. Разность двух чисел имеет ту же четность, что и их сумма. Доказательство: Заметим, что a+b=(a-b)+2b, т.е. сумма и разность двух чисел различаются на четное число, следовательно, имеют одинаковую четность ч.т.д.  6. Алгебраическая (со знаками + или -) сумма целых чисел имеет ту же четность, что и их сумма.   (напр. 2-7+(-4)-(-3)=-6 и 2+7+(-4)+(-3)=2 оба четны)  Доказательство: Возьмем сумму чисел и изменим в ней несколько знаков с + на — (перед первым числом мы тоже можем поставить знак -). Так мы сможем получить любую алгебраическую сумму. При изменении знака перед некоторым числом a значение алгебраической суммы уменьшится на 2a, т.е. четность сохраниться. Поэтому четность сохраниться после изменения любых нескольких (ноль и один — это тоже несколько !) перемен знака, и она в любом случае будет совпадать с четностью исходной суммы.  7. Алгебраическая сумма целых чисел четна тогда и только тогда, когда среди них четное число нечетных чисел. Доказательство: Очевидно следует из п.3 и п.6.  Все эти соображения можно на олимпиаде вставлять в текст решения задачи, как очевидные утверждения.

Калькулятор Статистика Онлайн всего: 1 Гостей: 1 Пользователей: 0

нечетный | Найдите факторы

2017-11-09 2017-11-10 / ivasallay / Оставить комментарий

945 = 1 × 3 × 5 × 7 × 9

Сумма собственных делителей числа определяет, является ли число обильным, недостаточным или совершенным. Если сумма больше числа, то число в изобилии. Если сумма меньше числа, число является недостаточным. Если сумма равна числу, то число совершенное.

Что такое правильный делитель? Все делители числа, кроме самого себя. Правильные делители — это ПОЧТИ то же самое, что и правильные множители. (Число 1 всегда является правильным делителем, но НИКОГДА не является правильным множителем.)

Первые 25 кратных чисел: 12, 18, 20, 24, 30, 36, 40, 42, 48, 54, 56, 60, 66, 70, 72, 78, 80, 84, 88, 90, 96, 100, 102, 104 и 108. Обратите внимание, что все эти числа четные.

OEIS сообщает нам, что 945 — это 232-е распространенное число. Все первые 231 избыточное число являются четными числами.

Ух ты, 945 — самое маленькое нечетное число. OEIS также перечисляет первые 31 нечетное обильное число. Каждый из первых 31 делится на 3 и оканчивается на 5, но если вы прокрутите страницу вниз, вы увидите некоторые, которые не делятся на 3 или не делятся на 5.

Поскольку 1 × 3 × 5 × 7 × 9 = 945 — это наименьшее число в списке, вам могут быть интересны другие числа:
1 × 3 × 5 × 7 × 9 × 11 = 10 395 попало в список.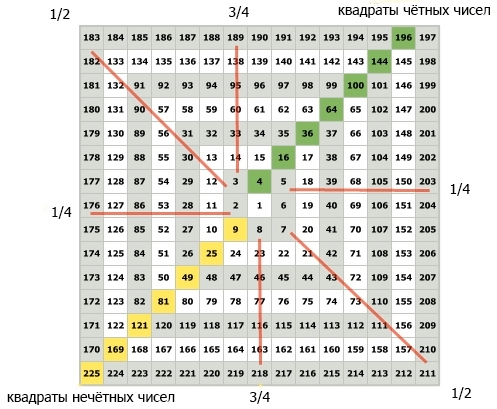
1 × 3 × 5 × 7 × 9 × 11 × 13 = 135 135, что слишком велико, чтобы быть одним из первых 31 нечетного обильного числа. Мне было любопытно, является ли это также обильным числом, поэтому я нашел его правильные делители и сложил их:

945 также является гипотенузой пифагорейской тройки:
567-756-945, что равно (3-4- 5

) умножить на 189

945 выглядит интересно в нескольких других системах счисления:
1661 в базе 8, потому что 1(8³) + 6(8²) + 6(8¹) + 1(8⁰) = 945
RR в базе 34 ( R равно 27 по основанию 10), потому что 27(34¹) + 27(34⁰) = 27(35) = 945
R0 в системе счисления по основанию 35, потому что 27(35) + 0(1) = 945

• 945 — составное число.
• Простая факторизация: 945 = 3 × 3 × 3 × 5 × 7, что можно записать как 945 = 3³ × 5 × 7
• Показатели степени в простой факторизации равны 3, 1 и 1. Прибавляя к каждому единицу и умножая, мы получаем (3 + 1)(1 + 1)(1 + 1) = 4 × 2 × 2 = 16. Следовательно, 9Число 45 имеет ровно 16 множителей.
• Факторы 945: 1, 3, 5, 7, 9, 15, 21, 27, 35, 45, 63, 105, 135, 189, 315, 945
• Пары множителей: 945 = 1 × 945, 3 × 315, 5 × 189, 7 × 135, 9 × 105, 15 × 63, 21 × 45 или 27 × 35
• Взяв пару множителей с наибольшим квадратным множителем, мы получим √945 = (√9)(√105) = 3√105 ≈ 30,74085

26.08.2017 04.02.2021 / ivasallay / Оставить комментарий

Деревья факторов для 840:

840 имеет больше множителей, чем любое предыдущее число. Эти факторы помогут нам записать 840 как сумму последовательных счетных чисел, последовательных четных чисел и последовательных нечетных чисел. Каковы факторы 840? Вот несколько возможных деревьев множителей для числа 840:

Красные листья на дереве — это простые числа. Собирая шесть красных листьев из любого приведенного выше дерева множителей, мы получаем простую факторизацию числа 840: 840 = 2³ × 3 × 5 × 7. Теперь 840 — не самое маленькое число, имеющее шесть красных листьев. На самом деле, есть меньшие числа с девятью листьями, но шесть невинно выглядящих красных листьев у 840 превратятся в колоссальные 32 фактора!

Факторы 840:

• 840 — составное число.
• Простая факторизация: 840 = 2 × 2 × 2 × 3 × 5 × 7, что можно записать как 840 = 2³ × 3 × 5 × 7.
• Показатели степени в простой факторизации равны 3, 1, 1 и 1. Прибавляя к каждому единицу и умножая, мы получаем (3 + 1)(1 + 1)(1 + 1) )(1 + 1) = 4 × 2 × 2 × 2 = 32. Следовательно, число 840 имеет ровно 32 множителя.
• Факторы 840: 1, 2, 3, 4, 5, 6, 7, 8, 10, 12, 14, 15, 20, 21, 24, 28, 30, 35, 40, 42, 56, 60, 70 , 84, 105, 120, 140, 168, 210, 280, 420, 840
• Пары множителей: 840 = 1 × 840, 2 × 420, 3 × 280, 4 × 210, 5 × 168, 6 × 140, 7 × 120, 8 × 105, 10 × 84, 12 × 70, 14 × 60, 15 × 56, 20 × 42, 21 × 40, 24 × 35 или 28 × 30
• Взяв пару множителей с наибольшим квадратным множителем, мы получим √840 = (√4)(√210) = 2√210 ≈ 28,98275.

840 также является наименьшим числом, которое можно без остатка разделить на первые восемь счетных чисел!

Головоломки «Сумма-разность»:

210 имеет восемь пар факторов. Одна из этих пар факторов дает в сумме 29., а другой вычитает до 29. Другая пара множителей дает в сумме 37, а другая вычитает до 37. Таким образом, 210 дает две разные головоломки суммы-разности, показанные на первых двух рисунках ниже!

840 кратно 210 и имеет шестнадцать пар множителей! Одна из пар множителей дает в сумме 58, а другая — 74. Другая пара множителей вычитает 58, а другая — 74. Если вы сможете идентифицировать эти пары множителей, то сможете решить две головоломки, расположенные рядом с 210 головоломок ниже!

840 имеет еще одну пару множителей, которая в сумме дает 113, и еще одну, которая вычитает 113. Если вы сможете найти эти пары множителей, то сможете решить следующую примитивную головоломку:

Если вам нужно Помогите с любой из этих головоломок 840 Sum-Difference, в приведенной ниже таблице показаны суммы и разности всех пар факторов 840. Посмотрите, какие суммы также появляются в столбце разницы.

Как найти числа последовательного счета, которые в сумме дают 840:

840 больше 40-го треугольного числа (820) и меньше 41-го треугольного числа (861). Мы также можем получить число 40, используя √(1 + 840 × 2) – 1 = 40 , округление не требуется. Число 840 имеет шесть нечетных множителей, не превышающих 40, а именно 1, 3, 5, 7, 15, 21 и 35.

Я опишу, как мы можем записать 840 в виде суммы последовательных чисел. Вы можете написать суммы? Я сделал для вас один из них:

• , используя 3 числа с 280 в качестве среднего числа,
• с использованием 5 чисел со 168 в качестве среднего числа,
• с использованием 7 чисел со 120 в качестве среднего числа; 117 + 118 + 119 + 120 + 121 + 122 + 123 = 840
• с использованием 15 чисел с 56 в качестве среднего числа,
• с использованием 21 числа с 40 в качестве среднего числа
• с использованием 35 номеров с 24 в качестве среднего числа.

Обратите внимание, что каждый из этих способов имеет в описании пару факторов 840.

Наибольшая степень двойки, которая является множителем 840, равна 8, удвоение которого дает 16. Какие из нечетных множителей числа 840, умноженные на 16, не больше 40? 1 × 16 = 16, а 3 × 16 = 48. Ой, это слишком много. Остальные его нечетные множители, умноженные на 16, тоже будут слишком большими. Тем не менее, мы можем записать 840 как сумму 16 счетных чисел. 840÷16 = 52,5, поэтому 52 и 53 будут 8-м и 9-м.числа в сумме.

• 45 + 46 + 47 + 48 + 49 + 50 + 51 + 52 + 53 + 54 + 55 + 56 + 57 + 58 + 59 + 60 = 840

Как найти последовательные ЧЕТНЫЕ числа, которые в сумме дают четное число?

Только четные числа могут быть суммой последовательных четных чисел. Давайте снова возьмем 840 в качестве примера. 840÷2 = 420.

Сначала мы найдем все способы записать 420 в виде суммы последовательных чисел. Затем мы просто удвоим среднее число и окружим его соответствующим количеством четных чисел, чтобы получить сумму четных чисел, которая в сумме составляет 840:9.0007

√(1 + 420 ×2) – 1 = 28 , округлять не нужно, поэтому составим список нечетных множителей, число которых не превышает 28. Это 1, 3, 5, 7, 15 и 21. Заметим также, что наибольшая степень двойки, являющаяся множителем 420, равна 4. Удвоив 4, получим 8. Какие из нечетных множителей числа 420, умноженных на 8, не больше 28? 1 × 8 = 8, а 3 × 8 = 24. Все остальное будет слишком много.

Я опишу, как мы можем записать 840 как сумму последовательных четных чисел. Вы можете увидеть пары факторов 420 и пары факторов 840 в описаниях. Вы можете написать суммы? Я сделал один из них для вас:

• используя 3 четных числа с 2 × 140 = 280 в качестве среднего числа
• с использованием 5 четных чисел с 2 × 84 = 168 в качестве среднего числа
• с использованием 7 четных чисел с 2 × 60 = 120 в качестве среднего числа
• с использованием 15 четных чисел с 2 × 28 = 56 в качестве среднего числа
• с использованием 21 четного числа с 2 × 20 = 40 в качестве среднего числа; 20 + 22 + 24 + 26 + 28 + 30 + 32 + 34 + 36 + 38 + 40 + 42 + 44 + 46 + 48 + 50 + 52 + 54 + 56 + 58 + 60 = 840

Мы также можем записать 840 как сумму четного количества последовательных четных чисел.

• с использованием 8 четных чисел: 2 раза (49 + 50 + 51 + 52 + 53 + 54 + 55 + 56 = 420) получается 98 + 100 + 102 + 104 + 106 + 108 + 110 + 112 = 840. Обратите внимание, что 840÷8 = 105 , нечетное число, которое находится между двумя числами точно посередине суммы.
• Аналогично, используя 24 четных числа: 12 + 14 + 16 + 18 + 20 + 22 + 24 + 26 + 28 + 30 + 32 + 34 + 36 + 38 + 40 + 42 + 44 + 46 + 48 + 50 + 52 + 54 + 56 + 58 = 840. Обратите внимание, что 840÷ 24 = 35 , нечетное число, которое находится между двумя числами точно посередине суммы.

Как найти последовательные НЕЧЕТНЫЕ числа, которые в сумме дают четное число, такое как 841: 

Прежде всего позвольте мне отметить, что каждое квадратное число n² представляет собой сумму первых n чисел.

Например: 100 = 10², а 100 также является суммой первых 10 нечетных чисел, как показано ниже:

Аналогичное утверждение верно для любого другого квадратного числа:

Да, каждое квадратное число n² является суммой первых n нечетных чисел.

Чтобы записать неквадратное четное число в виде суммы последовательных нечетных чисел, первое, что мы должны сделать, это определить, можно ли записать это число как разность двух квадратов. Если число даже имеет пару множителей, b × a, в которой b > a, и ОБА a и b равны даже , то это четное число можно выразить как разность двух квадратов, используя [(b + а)/2]² – [(б – а)/2]².

Теперь, поскольку четное число может быть выражено как разность двух квадратов, B² – A² , тогда это число может быть записано как сумма всех нечетных чисел от 2A+1 до 2B-1 .

840 — четное число с восемью парами множителей, в которых оба числа четные. Давайте используем эти четные пары множителей, чтобы найти способы записать 840 в виде суммы последовательных нечетных чисел:

• 420 × 2 = 840 означает 211² – 209² = 840, а это означает сумму 2 последовательные нечетные числа от 419 до 421 = 840
• 210 × 4 = 840 означает 107² – 103² = 840, а это означает сумму 4 последовательных нечетных чисел от 207 до 213 = 0440 8440
• 140 × 6 = 840 означает 73² – 67² = 840, а это означает сумму 6 последовательных нечетных чисел от 135 до 145 = 840 9000
• 84 × 10 = 840 означает 47² – 37² = 840, а это означает сумму 10 последовательных нечетных чисел от 75 до 93 = 840
• 70 × 12 = 840 означает 41² – 29² = 840, а это означает сумму 12 последовательных нечетных чисел от 59 до 81 = 840 9004
• 60 × 14 = 840 означает 37² – 23² = 840, а это означает сумму 14 последовательных нечетных чисел из 47 до 73 = 840
• 42 × 20 = 840 означает 31² – 11² = 840, а это означает сумму 20 последовательных нечетных чисел от 23 до 61 = 840 9004
• 30 × 28 = 840 означает 29² – 1² = 840, а это означает сумму 28 последовательных нечетных чисел от 3 до 29 = 840

Таким образом, 840 с его рекордными 32 факторами может быть записано как сумма 7 последовательных чисел, 7 последовательных четных чисел и 8 последовательных нечетных чисел!

Подробнее о числе 840:

Кстати, возможность записать 840 как разность двух квадратов восемью разными способами также дает 840 катет, по крайней мере, в восьми различных пифагорейских тройках. Эти пифагоровы тройки можно вычислить, используя числа из разности двух квадратов. Например, 682-840-1082 можно рассчитать как 2(31)(11), 31² – 11² , 31² + 11².

840 был этапом для этих восьми троек. Возможно, что просмотр 2(b)(a), где b × a = 420, даст еще несколько пифагорейских троек с 840 в качестве катета.

840 также является гипотенузой одной пифагорейской тройки, 504-672-840.

В заметке, совершенно не связанной с чем-либо, что я написал выше, 840 является повторяющейся цифрой в двух основаниях:

• SS BASE 29 (S равно 28 по основанию 10) Обратите внимание, что 28(29) + 28(1) = 28( 30) = 840
• 00 ОСНОВАНИЕ 34 (0 равно 24 по основанию 10) Обратите внимание, что 24(34) + 24(1) = 24(35) = 840

840 также является суммой простых чисел-близнецов 419 и 421.

15.11.2015 27.06.2021 / ivasallay / 2 комментария

680 — это число, состоящее только из четных цифр. (В конце поста написано гораздо больше о 680.)

Числа, оканчивающиеся на 0, 2, 4, 6 или 8, четные. Числа, оканчивающиеся на 1, 3, 5, 7 или 9, являются нечетными. Эти две простые концепции не всегда легко понять маленьким детям.

Иногда мы учим детей рифмовать, чтобы помочь им понять разницу:

• 0, 2, 4, 6, 8; быть ЧЕТЫРНЫМ просто здорово.
• 1, 3, 5, 7, 9; быть ODD — это нормально.

Учащиеся младших классов борются с понятиями четного и нечетного.

Еще одно, казалось бы, простое понятие — какие пары чисел в сумме дают десять. Эта концепция также не так проста для понимания детей, как могут подумать взрослые.

Донна Баучер — специалист по математике в начальной школе с многолетним опытом. Помимо многих других тем, она является экспертом по обучению сложению и вычитанию первоклассников и второклассников. Вот пара ее твитов со ссылками на ее сайт:

Используя свой потенциал, десять кадров — мощный инструмент! https://t. co/wEhz0LBfHs pic.twitter.com/SclL2WBv9G

— Донна Буше (@MathCoachCorner) 12 ноября 2015 г. t.co/0C6oglMkiEpic.twitter.com/1wBsGnHxvt — Донна Буше (@MathCoachCorner) 15 ноября 2015 г.

//platform.twitter.com/widgets.js

Бесплатные карточки с десятью рамками доступны на ее сайте, чтобы помочь учащимся изучить факты сложения и вычитания. Какой мощный способ для студентов учиться! У нее также есть десять рамок на Хэллоуин / День Благодарения для продажи в Teachers Pay Teachers.

Когда я читал ее сообщение о том, как использовать карточки с десятью рамками, я задавался вопросом, что произойдет, если мы ТОЧНО будем следовать ее инструкциям, но десять рамок выглядели так:

Дети все равно научатся складывать и вычитать , но поймут ли они также инстинктивно разницу между нечетными и четными числами?

Узнают ли они для себя, что сложение двух четных чисел или сложение двух нечетных чисел ВСЕГДА дает четное число? Или что сложение нечетного числа и четного числа ВСЕГДА дает нечетное число? Или замена десятикадра вообще ничего не изменит? Будет ли иметь значение десятирамка в рукавицах только в том случае, если родитель/учитель/репетитор будет говорить о четных и нечетных числах?

Я не знаю ответа на эти вопросы, но я думаю, что эту идею стоит попробовать. Я сделал варежки с десятью рамками для всех чисел от 0 до 10. На «пустых» рамках есть контуры варежек, чтобы помочь детям понять, какая варежка там левая или правая. Десять рамок варежек не имеют второго края, по которому можно было бы их вырезать, поэтому карточки могут выглядеть не так хорошо, как у Донны Буше, но они все равно должны работать как карточки. Точно следуйте инструкциям Донны Буше. Если вы используете варежки с десятью рамками, пожалуйста, добавьте комментарий, чтобы сообщить мне, имеют ли они какое-либо значение, помогая учащимся изучать свойства нечетных и четных чисел.

———————————————————

Подробнее о числе 680:

1² + 3² + 5² + 7² + 9² + 11² + 13² + 15² = 680

Поскольку 5, 17 и 85 являются некоторыми из его множителей, 680 является гипотенузой четырех пифагорейских троек. Сможете ли вы найти наибольший общий делитель каждой тройки?

• 104-672-680
• 288-616-680
• 320-600-680
• 408-544-680

680 15-е четырехгранное число. OEIS.org сообщает нам, что это также наименьшее тетраэдрическое число, которое может быть получено путем сложения двух других тетраэдрических чисел, в частности, сумма 10-го и 14-го тетраэдрических чисел равна этому 15-му тетраэдрическому числу, как показано ниже: 93) х 5 х 17

Показатели степени в простой факторизации равны 1, 3 и 1. Прибавив к каждому единицу и умножив, мы получим (3 + 1)(1 + 1)(1 + 1) = 4 x 2 x 2 = 16. Следовательно, 680 имеет ровно 16 факторов.

Факторы 680: 1, 2, 4, 5, 8, 10, 17, 20, 34, 40, 68, 85, 136, 170, 340, 680

Пары коэффициентов: 680 = 1 x 680, 2 x 340, 4 x 170, 5 x 136, 8 x 85, 10 x 68, 17 x 40 или 20 x 34

Взяв пару множителей с наибольшим квадратным множителем, мы получим √680 = (√4)(√170) = 2√170 ≈ 26,07 92) х 11

Показатели степени в простой факторизации равны 2 и 1. Прибавляя к каждому единицу и умножая, мы получаем (2 + 1)(1 + 1) = 3 x 2  = 6. Следовательно, 275 имеет 6 множителей.

Коэффициенты 275: 1, 5, 11, 25, 55, 275

Пары коэффициентов: 275 = 1 x 275, 5 x 55 или 11 x 25

Взяв пару множителей с наибольшим квадратным множителем, мы получим √275 = (√11)(√25) = 5√11 ≈ 16,583

Шестилетние дети слишком малы, чтобы узнавать о четных и нечетных числах?

Паула Берделл Криг дала мне разрешение использовать изображения этой гибкой числовой линии, которую она разработала в этом посте:

Дизайн и фотография Паулы Берделл Криг; http://bookzoompa.wordpress.com/

Недавно я прочитал сообщение на mathfour.com, в котором обсуждалась «базовая» концепция нечетных и четных чисел и способность детей понимать разницу. Статья очень заинтересовала меня, поэтому я кратко поговорил с 45 первоклассниками о четных и нечетных числах. Что я узнал?

• Почти все они были ознакомлены с этим понятием в детском саду и знали, что 1, 3, 5, 7, 9 — нечетные числа, а 2, 4, 6, 8, 10 — четные.
• Несколько студентов ускоренного обучения смогли объяснить мне, что цифра единицы в числе определяет, является ли число четным или нечетным,
• Но большинство первоклассников не поняли этого факта, потому что около трети учащихся считали 32 нечетным!
• Одна маленькая девочка объяснила мне, как чередуются нечетные и четные числа. Она сказала: «Если 99 четно, тогда 100 будет нечетно». Она помнила эту концепцию, но не понимала ее достаточно хорошо, чтобы применить ее к приведенному ею примеру!

Несмотря на то, что нечетные и четные числа могут быть сложными для изучения понятиями, обучайте этому понятию и используйте его в любом случае. На самом деле, расскажите об этом дошкольникам, пока вы надеваете им носки, обувь или варежки. Раз,_Два,_Пряжка_Мой_Ботинок.

Дети учатся называть числа по порядку, прежде чем научатся считать, и это помогает им научиться считать, а затем прибавлять или вычитать 1 из числа. Я учил сбитых с толку студентов, которые не знали, что делать с 8 + 1 =, пока я не сказал им, что 8 + 1 = означает «какое число идет сразу после 8, когда вы считаете?» Точно так же 8 – 1 = означает «какое число идет непосредственно перед 8, когда вы считаете?» Услышав эти вопросы, эти студенты сразу же знали ответ, и не рассчитывали, что найдут его.

Детям, которые могут быстро назвать нечетные числа до 11 и четные числа до 10, будет легче прибавлять или вычитать два из числа. Когда они видят 3 + 2 = , они могут вспомнить, что 3 — нечетное, а затем спросить себя, какое нечетное число идет после 3. Точно так же, когда они видят 8 — 2, они могут вспомнить, что 8 — четное, и вспомнить, что 6 — четное. номер прямо перед 8.

Насколько я помню, я был во втором классе, когда мне впервые сказали, что четное число плюс четное число четно, нечетное число плюс нечетное число четно, а четное число плюс нечетное число нечетно. Любой ученик, который учится складывать или вычитать, извлечет пользу из этого совета.

Добавление 3 к нечетному числу дает четное число, фактически это второе четное число после исходного числа. Прибавление 3 к четному числу дает нечетное число, которое является вторым нечетным числом после исходного числа. Вычитание 3 имеет то же правило, но заменяет слово «до» на слово «после».

Прибавление 4 к нечетному числу дает второе нечетное число после него, а добавление 4 к четному числу дает второе четное число после него.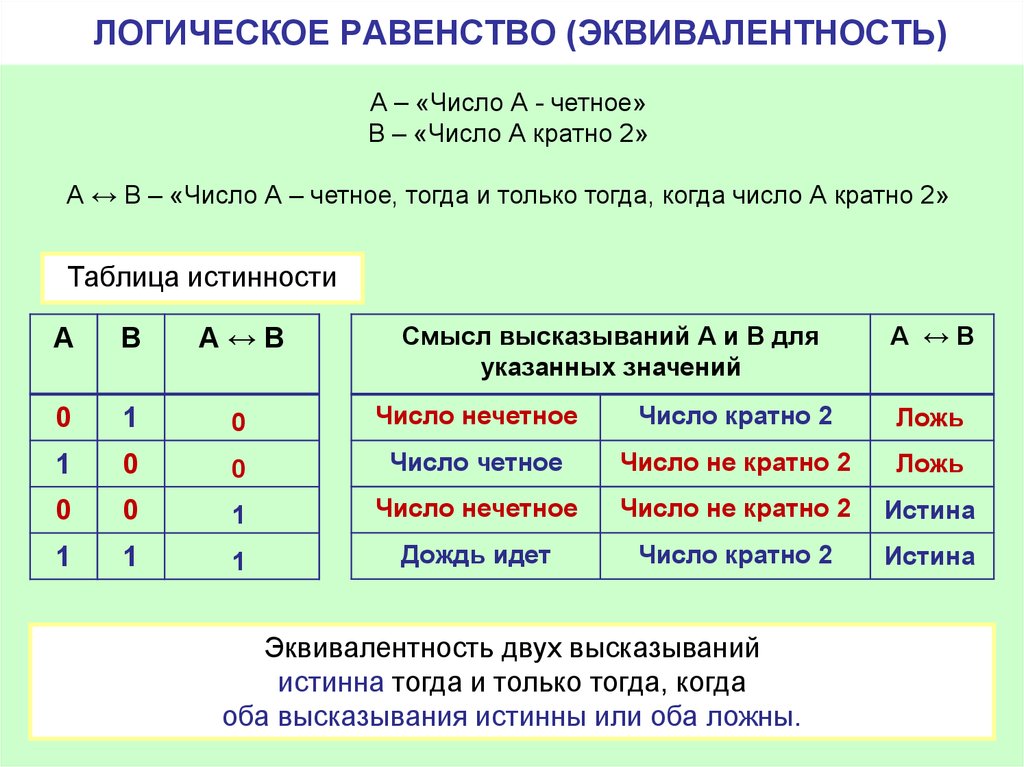 Вычитание 4 имеет аналогичное правило.

Добавление 3 или 4 означает дополнительное запоминание того, что 12 и 14 четные, а 13 нечетное, но это все, что первокласснику нужно знать о нечетных и четных числах. Позже эти две категории чисел пригодятся им на протяжении всей жизни по многим и многим причинам.

Как помочь детям запомнить нечетные и четные числа? Паула Берделл Криг разработала самую захватывающую числовую линию в мире.

Это может легко измениться:

Дизайн и фотография Paula Beardell Krieg; http://bookzoompa.wordpress.com/

на следующий вид:

Дизайн и фотограф Паула Берделл Криг; http://bookzoompa.wordpress.com/

Трансформацию может выполнить ребенок или взрослый. Эта числовая линия, состоящая из конвертов  , достаточно красива, чтобы повесить ее на стену в классе, но ее можно сложить, как книгу, или с ней можно играть и изменять ее, чтобы можно было реально учиться. Паула Берделл Криг показывает несколько применений в своем посте, способность потока искусной числовой линии, и обещает дать указания, как сделать это в ближайшее время!

Попробуйте эти рифмы: 0, 2, 4, 6, 8; Быть ЧЕТЫРНЫМ просто здорово! 1, 3, 5, 7, 9; Быть ODD просто прекрасно!

На сайте Smartfirstgraders. com есть несколько упражнений и стишков, которые помогут учащимся запомнить четные и нечетные числа.

• Наконец, если вы хлопаете, когда говорите ODD, вы хлопаете один раз. 1 — нечетное число.
• Если вы хлопнете, когда скажете ЧЕТНЫЙ, вы хлопнете два раза, 2 будет четным.
• И, как более подробно указал сайт mathfour.com, я показываю здесь: нечетное число состоит из 3 букв, а 3 – это нечетное число.
• Также четное число состоит из 4 букв, чтобы помочь нам запомнить, что 4 – это четное число.

 

Искать:

• 13 833 454 просмотров

Введите свой адрес электронной почты, чтобы следить за этим блогом и получать уведомления о новых сообщениях по электронной почте.

Адрес электронной почты

Присоединяйтесь к 1966 другим подписчикам

Что такое нечетное число?

В целых числах есть две категории чисел: нечетные числа и четные числа. Нечетные числа — это числа, которые при делении на 2 дают в остатке 1. В этой статье вы узнаете о нечетных числах, их типах, свойствах и забавных фактах о нечетных числах. Прокрутите вниз, чтобы узнать больше.

Что такое нечетные числа?

Нечетные числа — это числа, которые нельзя разделить на 2. Например, 1, 3, 5 и 7 — нечетные числа, потому что при делении их на 2 в остатке останется 1. Нечетные числа не входят в таблицу четных чисел, таких как 2, 4 и 6.

Проверка разрядности нечетных целых чисел является наиболее эффективным методом идентификации. Например, число 59031 является нечетным числом, так как в разряде единиц стоит единица.

Проще говоря, любое число, оканчивающееся цифрами 1, 3, 5, 7 и 9.является нечетным числом.

Как определить нечетные числа?

Многие из нас вообще путаются между нечетными и четными числами и допускают глупые ошибки на экзаменах. Несколько способов, с помощью которых мы можем идентифицировать нечетные числа, приведены ниже:

• Четные числа полностью и без остатка делятся на 2, тогда как нечетные числа не делятся на два полностью. Следовательно, посмотрите, делится ли данное число на 2. Если данное число делится на 2, то это четное число, иначе это нечетное число.
• При делении нечетного числа на 2 в остатке всегда будет 1. Четные числа можно разделить на две равные части. Но нечетное число оставит нечетное число в качестве напоминания и не может быть разделено на две равные части.
• Еще один простой способ определить четные и нечетные числа — по последним цифрам любого числа. Если номер места 1, 3, 5, 7, 9 и т. д., то это нечетное число. Точно так же, если последняя цифра 0, 2, 4, 6 или 8, то это четное число.

Типы нечетных чисел

Нечетные числа бывают двух типов: составные и последовательные. Ниже приводится четкое объяснение для обоих типов:

• Составные нечетные числа: Нечетные числа, которые не являются простыми числами, известны как составные нечетные числа. Например, 1 и другие простые числа, такие как 3, 5, 7 и т. д., не являются составными нечетными числами. Однако 9, 15, 21 и т. д. являются составными нечетными числами.
• Последовательные нечетные числа: Нечетные числа, которые встречаются подряд, называются последовательными нечетными числами. Когда нечетные числа идут в такой последовательности, как 1, 3, 5, 7, 9, 11, 13 или 15, это известно как последовательные нечетные числа.

Свойства нечетных чисел

Пришло время поиграть с нечетными числами и узнать некоторые свойства и то, как они взаимодействуют с другими числами. У нечетных чисел есть четыре основных свойства:

Сложение нечетных чисел

Когда мы складываем два нечетных числа, получается четное число.

Нечетное + Нечетное = Четное число

Примеры решения:

• 3 + 5 = 8
• 7 + 3 = 10,
• 3 + 9 = 12.

Попробуйте себя:

• 1 + 3 = ___
• 5 + 9 = ___
• 7 + 1 = ___

2

2

7 + 1 = ___ нечетных чисел

При вычитании двух нечетных чисел получается четное число.

ODD — ODD = даже номер

Решенные Примеры:

• 5 — 1 = 4
• 9 — 7 = 2
• 15 — 5 = 10.

15 — 5 = 10.

Попробуйте сами: 

• 3 – 1 = ___
• 5 – 3 = ___
• 9 – 5 = ___

Умножение нечетных чисел

В отличие от умножения нечетных чисел, сложение и вычитание нечетных чисел совсем другие. Когда мы умножаем два нечетных числа, их произведение будет нечетным числом.

Нечетное X Нечетное = Нечетное число

Решенные примеры:

• 1 x 5 = 5
• 3 x 7 = 21
• 9 x 7 = 63.

Попробуйте себя:

• 5 x 3 = ___
• 9 x 1 = ___
• 3 x 3 = ___

деления нечетных номеров

числа делятся, получается нечетное число.

ODD / ODD = нечетное число

Решенные Примеры:

• 15/3 = 5
• 29 x 3 = 3
• 1 /3 = 7.

Попробуйте себя:

9009

.0041 21 /7 = ___

• 25/5 = ___
• 27/3 = ___

Список нечетных чисел с 1 до 1000

Диаграмма нечетных чисел от 1 до 1000 1000 ниже:

. 073107310731. 0731

1307330 1307330 1307330 1307330.	3	5	7	9	11	13	15	17	19
21	23	25	27	29	31	33	35	37	39
41	43	45	47	49	51	53	55	57	59
61	63	65	67	69	71	73	75	77	79
81	83	85	87	89	91	93	95	97	99
101	103	105	107	109	111	113	115	117	119
121	123	125	127	129	131	133	149	151	153	155	157	159
161	163	165	167	169	171	173	175	177	179
181	183	185	187	189	191	193	195	197	199
201	203	205	207	209	211	213	215	217	219
221	223	225	227	229	231	233	235	237	239
241	243	245	247	249	251	253	255	257	259
261	263	265	267	269	271	273	275	277	279
281	283	285	287	289	291	293	295	297	299
301	303	305	307	309	311	313	315	317	319
321	323	325	327	329	331	333	335	337	339
341	343	345	347	367	369	371	373	375	377	379
381	383	385	387	389	391	393	395	397	399
401	403	405	407	409	411	413	415	417	419
421	423	425	427	429	431	433	435	437	439
441	443	445	447	449	451	453	455	457	459
461	463	465	467	469	471	473	475	477	479
481	483	485	487	489	491	493	495	497	499
501	503	505	507	509	511	513	515	517	519
521	523	525	527	529	531	533	535	537	539
541	543	545	547	549	551	553	555	557	559
561	563	565	585	587	589	591	593	595	597	599
601	603	605	607	609	611	613	615	617	619
621	623	625	627	629	631	633	635	637	639
641	643	645	647	649	651	653	655	657	659
661	663	665	667	669	671	673	675	677	679
681	683	685	687	689	691	693	695	697	699
701	703	705	707	709	711	713	715	717	719
721	723	725	727	729	731	733	735	737	739
741	743	745	747	749	751	753	755	757	759
761	763	765	767	769	771	773	775	777	779
781	783	785	787	789	791	793	795	797	799
801	803	805	807	809	811	813	815	817	819
821	823	825	827	829	831	833	835	837	839
841	843	845	847	849	851	853	855	857	859
861	863	865	867	869	871	873	875	877	879
881	883	885	887	889	891	893	895	897	899
901	903	905	907	909	911	913	915	917	919
921	923	925	927	929	931	933	935	937	939
941	943	945	947	949	951	953	955	957	955	957	959	957	959	957	955	967	969	971	973	975	977	979
981	983	985	987	989	991	993	995	997	999

Таблица нечетных чисел от 1 до 1000

Часто задаваемые вопросы о нечетных числах

Какое самое маленькое нечетное число?
Наименьшее нечетное число равно 1, а наименьшее составное нечетное число равно 9.

Сколько нечетных чисел от 1 до 100?
Есть 50 нечетных и 50 четных чисел.

0 нечетное число четного числа?
0 является четным числом, потому что оно делится на 2 и дает 0 в остатке, например, когда мы делим 0 / 2 равно 0. 

Может ли число быть и нечетным, и четным?
Нет. Нечетные и четные числа являются взаимоисключающими числами, поэтому данные числа не могут совпадать.

No related posts.