Как доказать четность функции. Исследование функции
Функция
называется четной (нечетной), если для
любогои выполняется равенство
.
График четной
функции симметричен относительно оси
.
График нечетной функции симметричен относительно начала координат.
Пример 6.2. Исследовать на четность или нечетность функции
1)
;
2)
;
3)
.
Решение .
1) Функция определена
при
.
Найдем
.
Т.е.
.
Значит, данная функция является четной.
2) Функция определена
при
Т.е.
.
Таким образом, данная функция нечетная.
3) функция определена для , т.е. для
,
.
Поэтому функция не является ни четной,
ни нечетной. Назовем ее функцией общего
вида.
3. Исследование функции на монотонность.
Функция
называется возрастающей (убывающей) на
некотором интервале, если в этом интервале
каждому большему значению аргумента
соответствует большее (меньшее) значение
функции.
Функции возрастающие (убывающие) на некотором интервале называются монотонными.
Если функция
дифференцируема на интервале
и имеет положительную (отрицательную)
производную
,
то функция
возрастает (убывает) на этом интервале.
Пример 6.3 . Найти интервалы монотонности функций
1)
;
3)
.
Решение .
1) Данная функция определена на всей числовой оси. Найдем производную .
Производная равна
нулю, если
и
.
Область определения – числовая ось,
разбивается точками
,
на интервалы. Определим знак производной
в каждом интервале.
В интервале
производная отрицательна, функция на
этом интервале убывает.
В интервале
производная положительна, следовательно,
функция на этом интервале возрастает.
2) Данная функция
определена, если
или
.
Определяем знак квадратного трехчлена в каждом интервале.
Таким образом, область определения функции
Найдем производную
,
,
если
,
т.
, но
. Определим знак производной в интервалах
.
В интервале
производная отрицательна, следовательно,
функция убывает на интервале
.
В интервале
производная положительна, функция
возрастает на интервале
.
4. Исследование функции на экстремум.
Точка
называется точкой максимума (минимума)
функции
,
если существует такая окрестность точки,
что для всех
из этой окрестности выполняется
неравенство
.
Точки максимума и минимума функции называются точками экстремума.
Если функция
в точкеимеет экстремум, то производная функции
в этой точке равна нулю или не существует
(необходимое условие существования
экстремума).
Точки, в которых производная равна нулю или не существует называются критическими.
5. Достаточные условия существования экстремума.
Правило 1 .
Если при переходе (слева направо) через
критическую точку
производная
меняет знак с «+» на «–», то в точкефункция
не меняет знак, то экстремума нет.
Правило 2 .
Пусть в точке
первая производная функции
равна нулю
,
а вторая производная существует и
отлична от нуля. Если
,
то– точка максимума, если
,
то– точка минимума функции.
Пример 6.4 . Исследовать на максимум и минимум функции:
1)
;
2)
;
3)
;
4)
.
Решение.
1) Функция определена
и непрерывна на интервале
.
Найдем производную
и решим уравнение
,
т.е.
.Отсюда
– критические точки.
Определим знак
производной в интервалах
,
.
При переходе через
точки
и
производная меняет знак с «–» на «+»,
поэтому по правилу 1
– точки минимума.
При переходе через
точку
производная меняет знак с «+» на «–»,
поэтому
– точка максимума.
,
.
2) Функция определена
и непрерывна в интервале
.
Найдем производную
.
Решив уравнение
,
найдем
и
– критические точки. Если знаменатель
,
т.
е.
,
то производная не существует. Итак,
– третья критическая точка. Определим
знак производной в интервалах.
Следовательно,
функция имеет минимум в точке
,
максимум в точках
и
.
3) Функция определена
и непрерывна, если
,
т.е. при
.
Найдем производную
.
Найдем критические
точки:
Окрестности точек
не принадлежат области определения,
поэтому они не являются т. экстремума.
Итак, исследуем критические точки
и
.
4) Функция определена
и непрерывна на интервале
.
Используем правило 2. Найдем производную
.
Найдем критические точки:
Найдем вторую
производную
и определим ее знак в точках
В точках
функция имеет минимум.
В точках
функция имеет максимум.
Которые в той или иной степени были вам знакомы. Там же было замечено, что запас свойств функций будет постепенно пополняться. О двух новых свойствах и пойдет речь в настоящем параграфе.
Определение 1.
Функцию у = f(x), х є Х, называют четной, если для любого значения х из множества X выполняется равенство f (-х) = f (х).
Определение 2.
Функцию у = f(x), х є X, называют нечетной, если для любого значения х из множества X выполняется равенство f (-х) = -f (х).
Доказать, что у = х 4 — четная функция.
Решение. Имеем: f(х) = х 4 , f(-х) = (-х) 4 . Но (-х) 4 = х 4 . Значит, для любого х выполняется равенство f(-х) = f(х), т.е. функция является четной.
Аналогично можно доказать, что функции у — х 2 ,у = х 6 ,у — х 8 являются четными.
Доказать, что у = х 3 ~ нечетная функция.
Решение. Имеем: f(х) = х 3 , f(-х) = (-х) 3 . Но (-х) 3 = -х 3 . Значит, для любого х выполняется равенство f (-х) = -f (х), т.е. функция является нечетной.
Аналогично можно доказать, что функции у = х, у = х 5 , у = х 7 являются нечетными.
Мы с вами не раз уже убеждались в том, что новые термины в математике чаще всего имеют «земное» происхождение, т.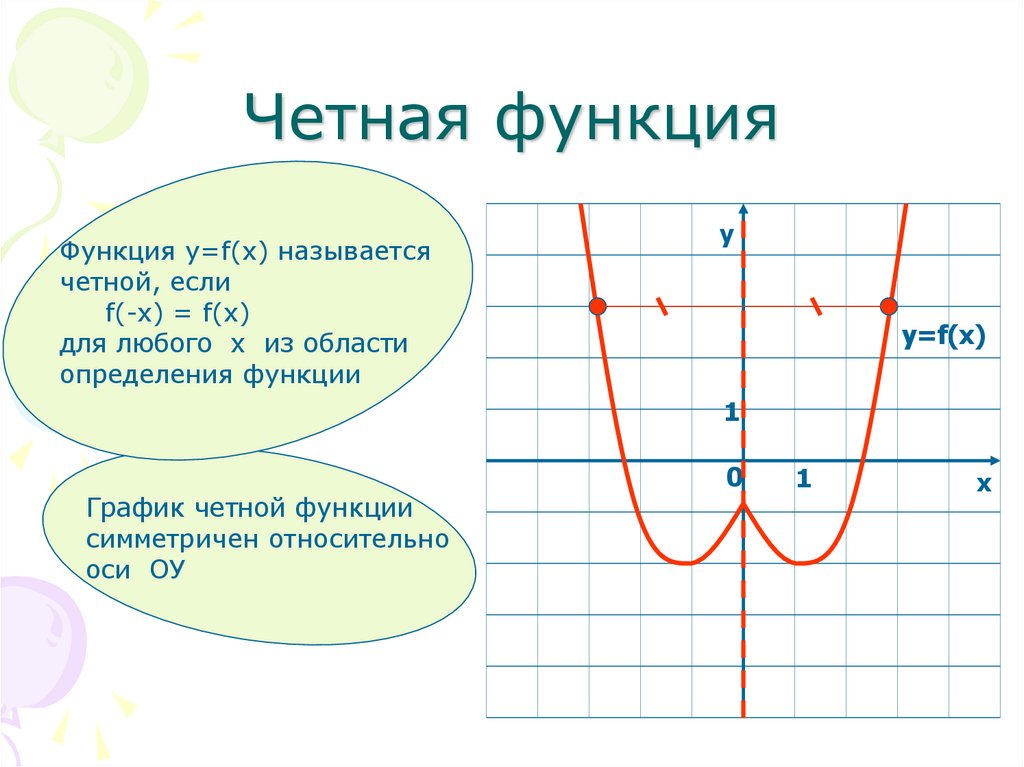
е. их можно каким-то образом объяснить. Так обстоит дело и с четными, и с нечетными функциями. Смотрите: у — х 3 , у = х 5 , у = х 7 — нечетные функции, тогда как у = х 2 , у = х 4 , у = х 6 — четные функции. И вообще для любой функции вида у = х» (ниже мы специально займемся изучением этих функций), где n — натуральное число , можно сделать вывод: если n — нечетное число, то функция у = х» — нечетная; если же n — четное число, то функция у = хn — четная.
Существуют и функции, не являющиеся ни четными, ни нечетными. Такова, например, функция у = 2х + 3. В самом деле, f(1) = 5, а f (-1) = 1. Как видите, здесь Значит, не может выполняться ни тождество f(-х) = f (х), ни тождество f(-х) = -f(х).
Итак, функция может быть четной, нечетной, а также ни той ни другой.
Изучение вопроса о том, является ли заданная функция четной или нечетной, обычно называют исследованием функции на четность.
В определениях 1 и 2 речь идет о значениях функции в точках х и -х. Тем самым предполагается, что функция определена и в точке х, и в точке -х.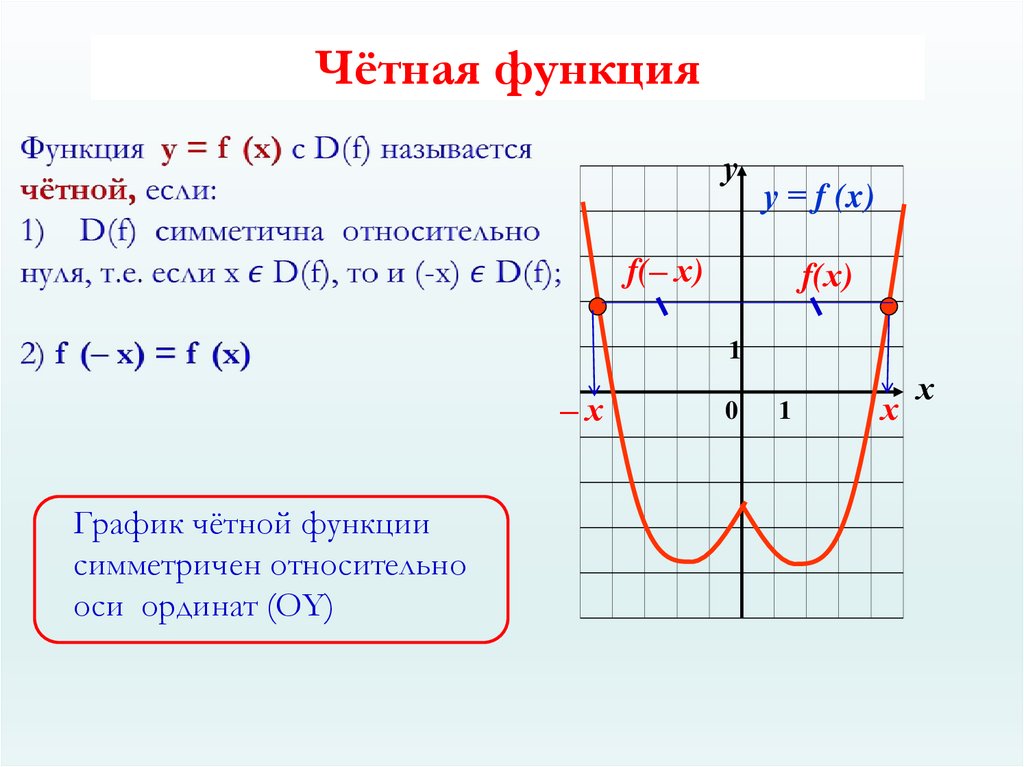
{2}-3
, можно вычислить только одно значение функции, которое ему соответствует. Функцию можно представить в виде таблицы:
| x | −2 | −1 | 0 | 1 | 2 | 3 |
| y | −4 | −3 | −2 | −1 | 0 | 1 |
Пользуясь данной таблицей, можно разобрать, что для значения аргумента −1 будет соответствовать значение функции −3 ; а значению x=2 будет соответствовать y=0 и т.д. Также важно знать, что каждому значению аргумента в таблице соответствует лишь одно значение функции.
Еще функции возможно задать, используя графики. С помощью графика устанавливается какое значение функции соотносится с определенным значением x . Наиболее часто, это будет приближенное значение функции.
Четная и нечетная функция
Функция является четной функцией , когда f(-x)=f(x)
для любого x
из области определения. Такая функция будет симметрична относительно оси Oy
.
{2}} \neq 1
для любого x \in [-1;1]
.
Ограниченной принято называть функцию y=f(x), x \in X тогда, когда существует такое число K > 0 , для которого выполняется неравенство \left | f(x) \right | \neq K для любого x \in X .
Пример ограниченной функции: y=\sin x ограничена на всей числовой оси, так как \left | \sin x \right | \neq 1 .
Возрастающая и убывающая функция
О функции, что возрастает на рассматриваемом промежутке принято говорить как о возрастающей функции тогда, когда большему значению x будет соответствовать большее значение функции y=f(x) . Отсюда выходит, что взяв из рассматриваемого промежутка два произвольных значения аргумента x_{1} и x_{2} , причем x_{1} > x_{2} , будет y(x_{1}) > y(x_{2}) .
Функция, что убывает на рассматриваемом промежутке, называется убывающей функцией тогда, когда большему значению x будет соответствовать меньшее значение функции y(x) . Отсюда выходит, что взяв из рассматриваемого промежутка два произвольных значений аргумента x_{1} и x_{2} , причем x_{1} > x_{2} , будет y(x_{1})
Корнями функции принято называть точки, в которых функция F=y(x)
пересекает ось абсцисс (они получаются в результате решения уравнения y(x)=0
).
а) Если при x > 0 четная функция возрастает, то убывает она при x
б) Когда при x > 0 четная функция убывает, то возрастает она при x
в) Когда при x > 0 нечетная функция возрастает, то возрастает она и при x
г) Когда нечетная функция будет убывать при x > 0 , то она будет убывать и при x
Экстремумы функции
Точкой минимума функции y=f(x) принято называть такую точку x=x_{0} , у которой ее окрестность будет иметь остальные точки (кроме самой точки x=x_{0} ), и для них тогда будет выполняться неравенство f(x) > f(x_{0}) . y_{min} — обозначение функции в точке min.
Точкой максимума функции y=f(x) принято называть такую точку x=x_{0} , у которой ее окрестность будет иметь остальные точки (кроме самой точки x=x_{0} ), и для них тогда будет выполняется неравенство f(x)
Необходимое условие
Согласно теореме Ферма: f»(x)=0
тогда, когда у функции f(x)
, что дифференцируема в точке x_{0}
, появится экстремум в этой точке.
Достаточное условие
- Когда у производной знак меняется с плюса на минус, то x_{0} будет точкой минимума;
- x_{0} — будет точкой максимума только тогда, когда у производной меняется знак с минуса на плюс при переходе через стационарную точку x_{0} .
Наибольшее и наименьшее значение функции на промежутке
Шаги вычислений:
- Ищется производная f»(x) ;
- Находятся стационарные и критические точки функции и выбирают принадлежащие отрезку ;
- Находятся значения функции f(x) в стационарных и критических точках и концах отрезка. Меньшее из полученных результатов будет являться наименьшим значением функции , а большее — наибольшим .
Четность или нечетность функции примеры. Исследование функции. Алгоритм исследования функции у = f(х) на четность
Определение 1. Функцияназываетсячетной (нечетной ),
если вместе с каждым значением переменной
значение –х также принадлежит
и выполняется равенство
Таким образом, функция может быть четной
или нечетной только тогда, когда ее
область определения симметрична
относительно начала координат на
числовой прямой (числа х и –х одновременно принадлежат
).
Например, функция
не является четной и нечетной, так как
ее область определения
не симметрична относительно начала
координат.
Функция
четная, так как
симметрична относительно начала
координат и.
Функция
нечетная, так как
и
.
Функция
не является четной и нечетной, так как
хотя
и симметрична относительно начала
координат, равенства (11.1) не
выполняются. Например,.
График четной функции симметричен
относительно оси Оу , так как если
точка
тоже принадлежит графику. График нечетной
функции симметричен относительно начала
координат, так как если
принадлежит графику, то и точка
тоже принадлежит графику.
При доказательстве четности или нечетности функции бывают полезны следующие утверждения.
Теорема 1. а) Сумма двух четных (нечетных) функций есть функция четная (нечетная).
б) Произведение двух четных (нечетных) функций есть функция четная.
в) Произведение четной и нечетной функций
есть функция нечетная.
г) Если f – четная
функция на множествеХ , а функцияg определена на
множестве
,
то функция
–
четная.
д) Если f – нечетная
функция на множествеХ , а функцияg определена на
множестве
и четная (нечетная), то функция
–
четная (нечетная).
Доказательство . Докажем, например, б) и г).
б) Пусть
и
–
четные функции. Тогда,
поэтому.
Аналогично рассматривается случай
нечетных функций
и
.
г) Пусть f – четная функция. Тогда.
Остальные утверждения теоремы доказываются аналогично. Теорема доказана.
Теорема 2. Любую функцию
,
заданную на множествеХ , симметричном
относительно начала координат, можно
представить в виде суммы четной и
нечетной функций.
Доказательство . Функцию
можно записать в виде
.
Функция
– четная, так как
,
а функция
– нечетная, поскольку.
Таким образом,
,
где
–
четная, а
–
нечетная функции.
Теорема доказана.
Определение 2. Функция
называетсяпериодической , если
существует число
,
такое, что при любом
числа
и
также
принадлежат области определения
и выполняются равенства
Такое число T называетсяпериодом функции
.
Из определения 1 следует, что если Т – период функции
,
то и число –Т тоже является
периодом функции
(так
как при заменеТ на –Т равенство
сохраняется). С помощью метода
математической индукции можно показать,
что еслиТ – период функцииf ,
то и
,
тоже является периодом. Отсюда следует,
что если функция имеет период, то она
имеет бесконечно много периодов.
Определение 3. Наименьший из положительных периодов функции называется ееосновным периодом.
Теорема 3. ЕслиТ – основной период функцииf , то остальные периоды кратны ему.
Доказательство . Предположим
противное, то есть что существует периодфункцииf (>0),
не кратныйТ .
Тогда, разделивнаТ с остатком, получим
,
где
.
Поэтому
то есть
– период функцииf ,
причем
,
а это противоречит тому, чтоТ –
основной период функцииf .
Из полученного противоречия следует
утверждение теоремы. Теорема доказана.
Хорошо известно, что тригонометрические
функции являются периодическими.
Основной период
и
равен
,
и
.
Найдем период функции
.
Пусть
— период этой функции. Тогда
(так как
.
илиилиили
.
Значение T , определяемое
из первого равенства, не может быть
периодом, так как зависит отх , т.е.
является функцией отх , а не постоянным
числом. Период определяется из второго
равенства:
.
Периодов бесконечно много, при
наименьший
положительный период получается при
:
.
Это – основной период функции
.
Примером более сложной периодической функции является функция Дирихле
Заметим, что если T –
рациональное число, то
и
являются рациональными числами при
рациональномх и иррациональными
при иррациональномх .
Поэтому
при любом рациональном числе T . Следовательно, любое рациональное числоT является периодом функции Дирихле. Ясно, что основного периода у этой функции нет, так как есть положительные рациональные числа, сколь угодно близкие к нулю (например, рациональное числоможно сделать выборомn сколь угодно близким к нулю).
Теорема 4. Если функцияf задана на множествеХ и имеет
периодТ , а функцияg задана на множестве
,
то сложная функция
тоже имеет периодТ .
Доказательство . Имеем, поэтому
то есть утверждение теоремы доказано.
Например, так как cos x имеет период
,
то и функции
имеют период
.
Определение 4. Функции, не являющиеся периодическими, называютсянепериодическими .
Которые в той или иной степени были вам знакомы. Там же было замечено, что запас свойств функций будет постепенно пополняться.
О двух новых свойствах и пойдет речь в настоящем параграфе.
Определение 1.
Функцию у = f(x), х є Х, называют четной, если для любого значения х из множества X выполняется равенство f (-х) = f (х).
Определение 2.
Функцию у = f(x), х є X, называют нечетной, если для любого значения х из множества X выполняется равенство f (-х) = -f (х).
Доказать, что у = х 4 — четная функция.
Решение. Имеем: f(х) = х 4 , f(-х) = (-х) 4 . Но (-х) 4 = х 4 . Значит, для любого х выполняется равенство f(-х) = f(х), т.е. функция является четной.
Аналогично можно доказать, что функции у — х 2 ,у = х 6 ,у — х 8 являются четными.
Доказать, что у = х 3 ~ нечетная функция.
Решение. Имеем: f(х) = х 3 , f(-х) = (-х) 3 . Но (-х) 3 = -х 3 . Значит, для любого х выполняется равенство f (-х) = -f (х), т.е. функция является нечетной.
Аналогично можно доказать, что функции у = х, у = х 5 , у = х 7 являются нечетными.
Мы с вами не раз уже убеждались в том, что новые термины в математике чаще всего имеют «земное» происхождение, т.
е. их можно каким-то образом объяснить. Так обстоит дело и с четными, и с нечетными функциями. Смотрите: у — х 3 , у = х 5 , у = х 7 — нечетные функции, тогда как у = х 2 , у = х 4 , у = х 6 — четные функции. И вообще для любой функции вида у = х» (ниже мы специально займемся изучением этих функций), где n — натуральное число , можно сделать вывод: если n — нечетное число, то функция у = х» — нечетная; если же n — четное число, то функция у = хn — четная.
Существуют и функции, не являющиеся ни четными, ни нечетными. Такова, например, функция у = 2х + 3. В самом деле, f(1) = 5, а f (-1) = 1. Как видите, здесь Значит, не может выполняться ни тождество f(-х) = f (х), ни тождество f(-х) = -f(х).
Итак, функция может быть четной, нечетной, а также ни той ни другой.
Изучение вопроса о том, является ли заданная функция четной или нечетной, обычно называют исследованием функции на четность.
В определениях 1 и 2 речь идет о значениях функции в точках х и -х. Тем самым предполагается, что функция определена и в точке х, и в точке -х.
Это значит, что точка -х принадлежит области определения функции одновременно с точкой х. Если числовое множество X вместе с каждым своим элементом х содержит и противоположный элемент -х, то X называют симметричным множеством. Скажем, (-2, 2), [-5, 5], (-оо, +оо) — симметричные множества, в то время как }
Я написал подробное и подробное объяснение того, как работает это доказательство, если кому-то интересно.2+4yz=p$. Это показывает, что число решений конечно.
Порядок чисел в тройке важен. Например, когда $p=17$, решение $(3,1,2)$ отличается от решения $(3,2,1)$.
Инволюция определяется как функция, обратная самой себе. Например, $f(x)=\frac{1}{x}$ является инволюцией, поскольку $f(f(x))=\frac{1}{f(x)}=\frac{1}{\frac {1}{x}}=x$. Второй пример: $g(x)=-x\quad g(g(x))=-g(x)=-(-x)=x$.
Фиксированные точки 92=1 \стрелка вправо x=\pm1$.
Мощность набора — это количество элементов в наборе. Если $A$ — множество, то мощность множества можно обозначить как $|A|$. Если $A=\left\{1,2,3,6,8\right\}$, то $|A|=5$
Теперь я хочу показать, что карта:
$$(x,y, г)\стрелка вправо
\левый\{
\begin{массив}{ll}
(x+2z,\space z,\space y-x-z) &\text{if}\space x
Поэтому $y-z\lt 2y$. Остаются только те возможности, которые показаны на отображении: $x\lt y-z\lt 2y$ или $y-z\lt x\lt 2y$ или $y-z\lt 2y\lt x$. Это означает, что неравенства справедливы.
Отображение показывает три тройки (всего девять записей). Записи только с положительными членами должны давать натуральные числа. Записи, которые могут быть отрицательными, — это записи с отрицательными терминами. Неравенство первой тройки показывает, что третья запись положительна $x\lt y-z \rightarrow 0\lt y-x-z$. Неравенство второго члена показывает, что и первая запись, и третья запись положительны. $x\lt 2y \rightarrow 0\lt 2y-x$ и $y-z\lt x \rightarrow 0\lt x-y+z$. Неравенство третьего члена показывает, что первая запись положительна $2y\lt x \rightarrow 0\lt x-2y$. Если $2y\lt x$, то $y-z\lt x\rightarrow 0 Теперь я хочу показать, что отображение является инволюцией, используя второй набор троек в качестве входных данных. $$(а,б,в)\стрелка вправо
\левый\{
\begin{массив}{ll}
(a+2b,\space c,\space b-a-c) &\text{if}\space a Теперь, если мы используем первую тройку из отображения $(x,y,z)$ в качестве входных данных для этого, тогда $a=x+2z,b=z,c=y-x-z$ в этом случае выходом будет третья тройка отображения $(a,b,c)$, поскольку $2b\lt a$. Таким образом, результат равен $(a-2b,\space a-b+c,\space b)$. Теперь мы просто применяем подстановки, чтобы получить результат в виде $x,y,$ и $z$. $((x+2z)-2(z),(x+2z)-(z)+(y-x-z),(z))=(x+2z-2z,x+2z-z+y-x-z,z)= (x,y,z)$ Если вторая тройка из отображения $(x,y,z)$ является входом для отображения $(a,b,c)$, то $a=2y-x,b =y,c=x-y+z$, в этом случае на выходе будет вторая тройка отображения $(a,b,c)$, поскольку $b-c\lt a\lt 2b$. Если третья тройка из отображения $(x,y,z)$ является входом для отображения $(a,b,c)$, то $a=x-2y,b=x-y+z,c =y$, в этом случае на выходе получается первая тройка отображения $(a,b,c)$, поскольку $a\lt b-c$. Таким образом, результат равен $(a+2c,\space c,\space b-a-c)$. Теперь мы просто применяем подстановки, чтобы получить результат в виде $x,y,$ и $z$. $((x-2y)+2(y),(y),(x-y+z)-(x-2y)-(y))=(x-2y+2y,y,x-y+z -x+2y-y)=(x,y,z)$ Это показывает, что отображение является инволюцией. Применение карты дважды вернуло исходный результат во всех трех случаях. Теперь я хочу найти все фиксированные точки отображения. Если первая тройка совпадает с входной, то $x=x+2z$ и $y=z$ и $z=y-x-z$ $x=x+2z\rightarrow 0=2z \rightarrow 0=z$ $y=z\стрелка вправо y=0$ $z=y-x-z\стрелка вправо 0=-x \стрелка вправо x=0$ Из первой тройки нет неподвижных точек. Если вторая тройка совпадает с введенной, то $x=2y-x$ и $y=y$ и $z=x-y+z$ $x=2y-x\rightarrow 2x=2y \ стрелка вправо х=у$ 92+4xz=x(x+4z)=p=4k+1$ Поскольку $x(x+4z)$ — простое число, а $x\lt x+4z$, единственный способ получить простое число, если $х=1$. Итак, $x(x+4z)=4z+1=4k+1\стрелка вправо 4z=4k\стрелка вправо z=k$. Вторая тройка имеет одну неподвижную точку $(1,1,k)$. Если третья тройка совпадает с введенной, то $x=x-2y$ и $y=x-y+z$ и $z=y$ $x=x+2y\rightarrow 0=2y \ стрелка вправо 0=y$ $y=x-y+z\стрелка вправо 0=x+z\стрелка вправо -x=z$ $z=y\стрелка вправо z=0 \стрелка вправо -x=0 \стрелка вправо x= 0$ Неподвижных точек из третьего триплета нет. Имеется только одна фиксированная точка отображения. Если все решения приходят парами, кроме неподвижной точки, это означает, что существует нечетное число решений или, другими словами, $|S|$ нечетно. С этими новыми знаниями можно использовать второе отображение $(x,y,z) \rightarrow (x,z,y)$.
В этой части поста легко запутаться. Чтобы попытаться избежать путаницы, я поставлю отдельное сопоставление с немного другими метками.
Таким образом, результат равен $(2b-a,\space b,\space a-b+c)$. Теперь мы просто применяем подстановки, чтобы получить результат в виде $x,y,$ и $z$. $(2(y)-(2y-x),(y),(2y-x)-(y)+(x-y+z))=(2y-2y+x,y,2y-x-y +x-y+z)=(x,y,z)$
