Первый признак подобия треугольников 8 класс онлайн-подготовка на Ростелеком Лицей
Тема 3: Подобные треугольники
- Видео
- Тренажер
- Теория
Заметили ошибку?
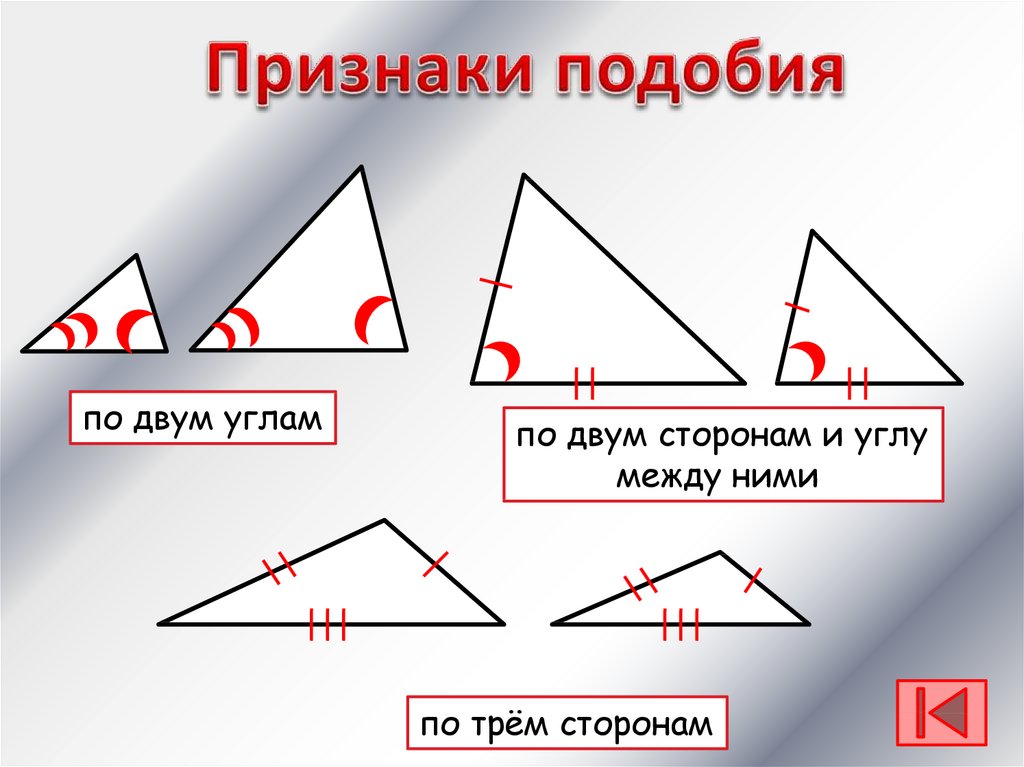
Первый признак подобия треугольников.
Докажем подобие треугольников по двум углам.
Если два угла одного треугольника соответственно равны двум углам другого треугольника, то такие треугольники подобны.
Дано: ΔABC, ΔA1B1C1,
∠A = ∠A1, ∠B = ∠B1,
Доказать: ΔABC∼ΔA1B1C1
Доказательство:
-
По теореме о сумме углов треугольника
∠C = 180°-(∠A+∠B), ∠C1 = 180°-(∠A1+∠B1).
Так как ∠A = ∠A1и ∠B = ∠B1, то и ∠C = ∠C1.

-
Пусть AB<A1B1. На луче A1B1 отложим отрезок A1B2 такой, что A1B2 = AB.
-
Через точку B2 проведем прямую B2C2, параллельную прямой B1C1.
-
∠A1B2C2 = ∠A1B1C1 (как соответственные при B2C2∥ B1C1 и секущей A1B1).
Значит, ∠A1B2C2 = ∠B.
-
В треугольниках A1B2C2и ABC:
∠A1 = ∠A,
∠A1B2C2 = ∠B,
A1B2 = AB.

Значит, ΔA1B2C2= ΔABC (по стороне и двум прилежащим к ней углам).
Из равенства треугольников следует равенство соответствующих сторон: A1C2 = AC.
-
По теореме о пропорциональных отрезках А1С2:А1С1 = А1В2:А1В1.
Так как A1B2= AB и A1C2 = AC, то АС:А1С1 = АВ:А1В1.
-
Аналогично доказывается, что АВ:А1В1 = ВС:В1С1.
-
Таким образом, в треугольниках ABC и A1B1C1:
∠A = ∠A1, ∠B = ∠B1, ∠C = ∠C
АВ:А1В1 = ВС:В1С1 = АС:А1С1.

Значит, ΔABC∼ΔA1B1C1 по определению подобных треугольников, что и требовалось доказать.
При решении задач чаще других используется именно 1-й признак подобия треугольников.
Задача 1. Доказать, что любые два равнобедренных треугольника, у которых углы между равными сторонами равны, являются подобными.
Решение. Пусть даны равнобедренные треугольники ABC и A1B1C1 с ∠A = ∠A1 (углы А и А1 лежат против оснований ВС и В1С1 соответственно). Так как треугольник ABC равнобедренный, то ∠B = ∠C = (180−∠A):2. Так как треугольник A1B1C1 равнобедренный, то ∠B 1 = ∠C1 = (180−A1):2 = (180−∠A):2 = ∠B = ∠C.
То есть ∠B = ∠B1, ∠C = ∠C1. По первому признаку подобия получаем, что треугольники ABC и A1B1C1 подобны.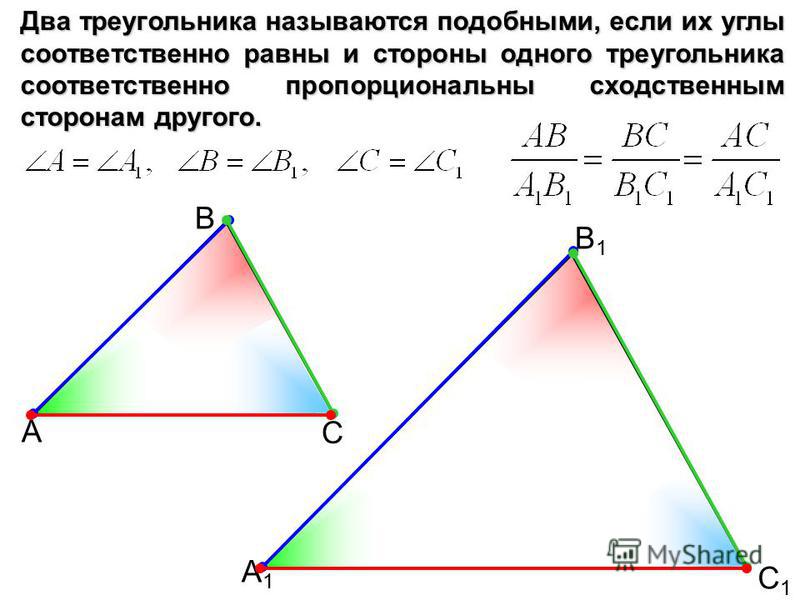
Задача 2.
Дано:
∠А = ∠В
СО:DO = 7:2
AC = 21 см
Найти: ВD
Решение: рассмотрим ∆АОС и ∆ВОD.
Так как ∠А = ∠В (по условию задачи), ∠АОС = ∠ВОD (как вертикальные углы), то по первому признаку подобия треугольников ∆АОС ~ ∆ВОD.
Следовательно, сходственные стороны треугольников пропорциональны:
АО:ВО = АС:BD = CO:DO
Подставив данные, получим 21:BD = 7:2
Ответ: BD = 6см.
Заметили ошибку?
Расскажите нам об ошибке, и мы ее исправим.Подобие треугольников — определение, признак подобия по двум углам
Login to your account
Пароль
Запомнить меня
- Регистрация
- Забыли логин?
- Забыли пароль?
Искать…
Подобие треугольников — определение, признак подобия по двум углам
Диагностический тест «Подобие треугольников — определение, признак подобия по двум углам»
Начните с диагностического теста
Обучающий тест №1 «Определение подобных треугольников»
Разбираемся, какие два треугольника называются подобными.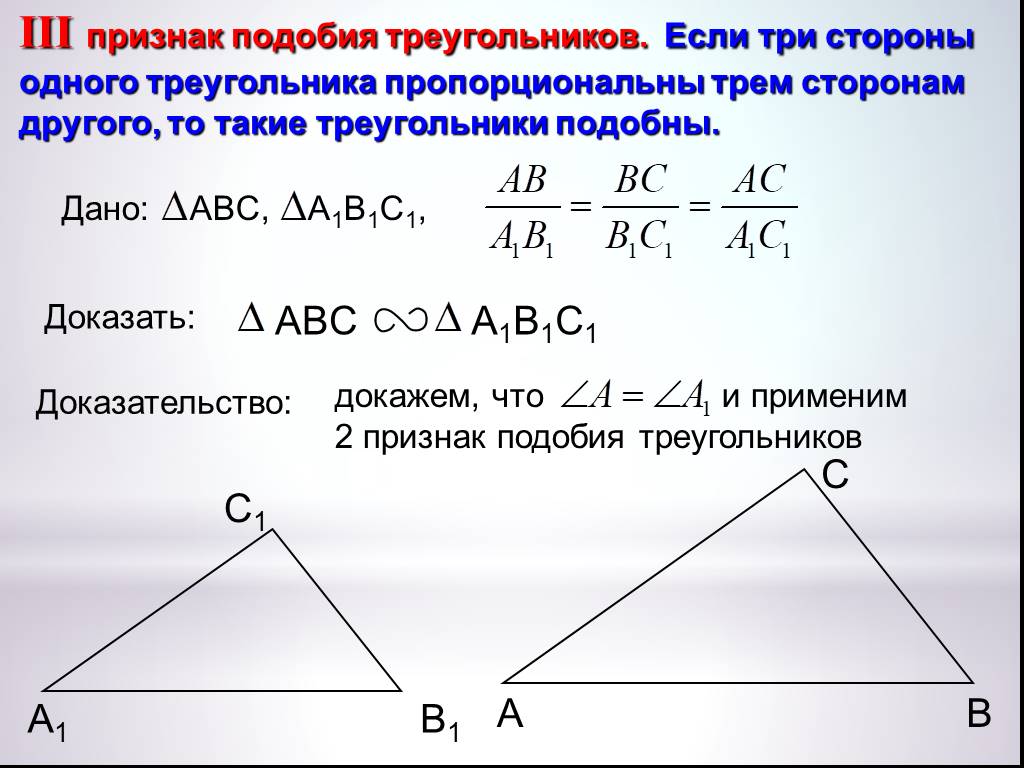
Обучающий тест №2 «Коэффициент подобия в подобных треугольниках»
Коэффициент подобия — это число, показывающее во сколько раз размеры одного подобного треугольника больше размеров другого. С помощью этого теста Вы сможете научиться использовать коэффициент подобия для решения задач, чем повысите свой уровень подготовки.
Обучающий тест №3 «Площади подобных треугольников»
Зная площадь одного треугольника, легко можно найти площадь подобного ему треугольника. Узнайте, как именно, пройдя этот тест.
Обучающий тест №4 «Признак подобия треугольников по двум углам» (часть 1)
Самый часто используемый признак подобия треугольников — по двум углам. Задачи и примеры в этом тесте помогут Вам быстро находить подобные треугольники, имеющие два равных угла. Также Вы познакомитесь с различными способами нахождения неизвестных сторон подобных треугольников.
Обучающий тест №5 «Признак подобия треугольников по двум углам» (часть 2)
Во второй части Вас ждёт ещё больше ситуаций, в которых можно встретить подобные треугольники, имеющие два равных угла.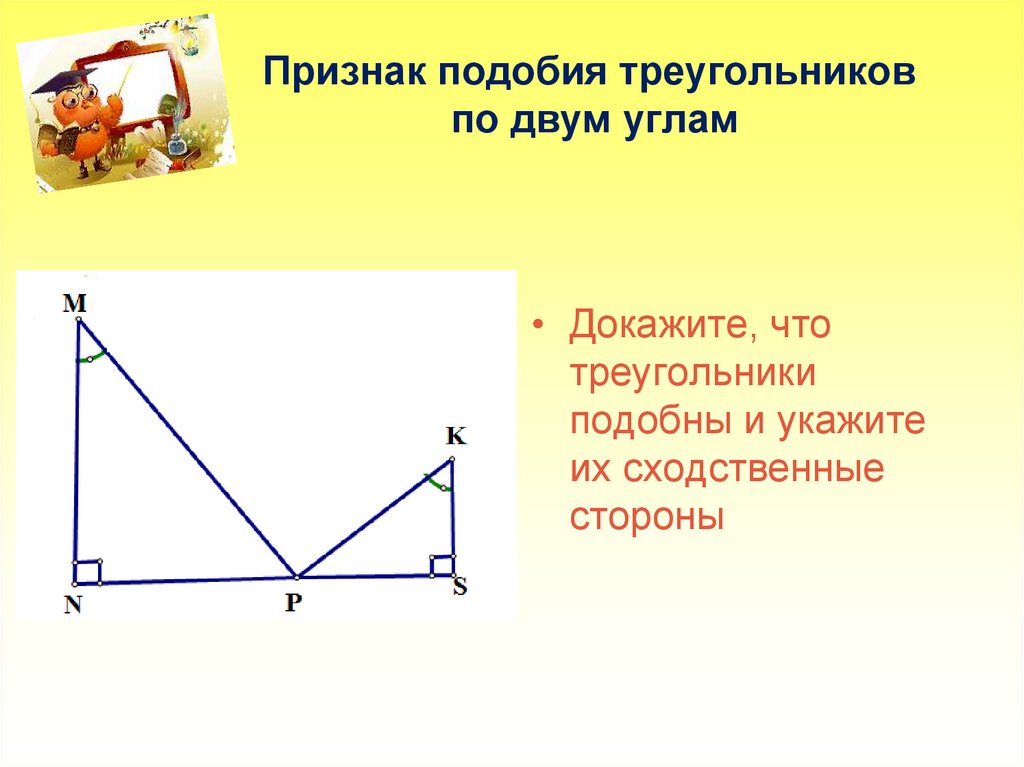
Контролирующий тест «Подобие треугольников — определение, признак подобия по двум углам»
После обучающих тестов пройдите контролирующий тест, аналогичный диагностическому: проверьте, насколько улучшились Ваши знания!
20 декабря 2022
© Math Galaxy 2018-2022. Designed by InspireTheme.
Геометрия: большая тройка
Чтобы доказать, что два треугольника подобны, вам нужно будет убедиться, что все три соответствующих угла конгруэнтны и что между всеми соответствующими сторонами выполняются требуемые отношения пропорциональности. Когда вы работали с конгруэнтными треугольниками, у вас были некоторые постулаты и теоремы, которые помогали вам доказать конгруэнтность. Я дам вам несколько постулатов и теорем, которые помогут вам с проблемами подобия. К сожалению, некоторые из ваших теорем подобия имеют те же инициалы, что и постулаты конгруэнтного треугольника.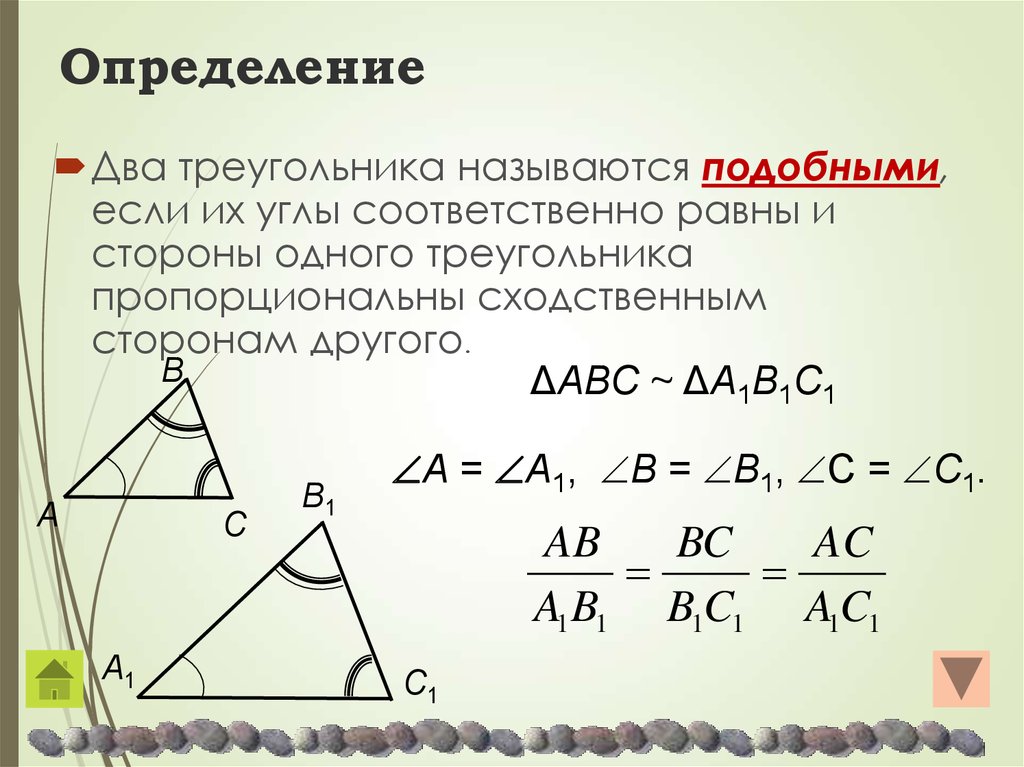 Важно обратить внимание на то, пытаетесь ли вы показать, что два треугольника подобны или конгруэнтны. Я буду использовать слово «сходство» в любых постулатах или теоремах, чтобы вы понимали, какой из них я использую.
Важно обратить внимание на то, пытаетесь ли вы показать, что два треугольника подобны или конгруэнтны. Я буду использовать слово «сходство» в любых постулатах или теоремах, чтобы вы понимали, какой из них я использую.
Постулат подобия ААА
Позвольте мне познакомить вас с вашим первым упрощением, связанным с подобием двух треугольников. Это постулат, так что это то, что вы не можете доказать. Вам останется только поверить в это и использовать в свое удовольствие.
- Постулат 13.1 : Постулат подобия ААА. Если три угла одного треугольника равны трем углам другого треугольника, то эти два треугольника подобны.
Этот постулат позволяет доказать сходство, не нарушая пропорциональности. Вам нужно только проверить соотношение углов. Но вы можете сделать даже лучше, чем это! Если два угла одного треугольника равны двум углам другого треугольника, то и третьи углы должны быть равны. Итак, если вы хотите показать, что два треугольника подобны, все, что вам нужно сделать, это показать, что два угла одного треугольника равны двум углам другого треугольника.
- Теорема 13.1 : Теорема подобия AA. Если два угла одного треугольника равны двум углам другого треугольника, то эти два треугольника подобны.
Эту теорему легче применить, чем постулат подобия ААА (поскольку вам нужно проверить только два угла вместо трех). Доказательство теоремы 13.1 не так уж много. Он основан главным образом на том факте, что сумма внутренних углов треугольника составляет 180º. Воспользуемся им, чтобы доказать подобие некоторых треугольников.
- Пример 7 : Если ¯AB ¯DE, как показано на рис. 13.4, напишите доказательство в два столбца, которое показывает ABC ~ EDC.
Рис. 13.4 Отрезки ¯AB и ¯DE параллельны.
- Решение : Чтобы написать это доказательство, вам нужен план игры. Цифры становятся немного сложнее, и вам приходится использовать все больше и больше ваших предыдущих результатов, чтобы выписывать доказательства. Поскольку ¯AB ¯DE , ¯AB и ¯DE можно рассматривать как две параллельные прямые, пересекаемые секущей ¯AE.
 В этом случае BAE и DEA являются альтернативными внутренними углами, поэтому они равны. Поскольку ACB и DCE являются вертикальными углами, они равны. Итак, по теореме подобия AA вы видите, что ABC ~ EDC.
В этом случае BAE и DEA являются альтернативными внутренними углами, поэтому они равны. Поскольку ACB и DCE являются вертикальными углами, они равны. Итак, по теореме подобия AA вы видите, что ABC ~ EDC.
| Затверждения | Причины | ||
|---|---|---|---|
| 1. | ¯ab ¯de | . | Определение поперечной |
| 3. | BAE и DEA — альтернативные внутренние углы | Определение альтернативных внутренних углов | |
| ~ 0 9005 2 BAE91 0 2A 9091 | 0051 Theorem 10.8 | ||
| 5. | ACB and DCE are vertical angles | Definition of vertical angles | |
| 6. | ACB ~= DCE | Theorem 8.1 | |
| 7. | ABC ~ EDC | AA Теорема подобия |
Один метод оценки высоты объекта (например, дерева или пирамиды) использует идеи подобных треугольников. Этот метод предполагает, что вы знаете свой рост и можете измерить длину теней. Чтобы этот метод работал, и вы, и объект, который пытаетесь измерить, должны отбрасывать тень.
Этот метод предполагает, что вы знаете свой рост и можете измерить длину теней. Чтобы этот метод работал, и вы, и объект, который пытаетесь измерить, должны отбрасывать тень.
Предположим, светит солнце, и вы хотите определить высоту соседнего дерева. Чтобы этот прием сработал, солнце не может светить прямо над головой, иначе ни вы, ни дерево не отбросите измеримую тень. На рис. 13.5 показана роль подобных треугольников в этой технике. Предположим, ваш рост 6 футов, и вы отбрасываете тень длиной 8 футов. Вы не знаете, какой высоты это дерево, но длина его тени составляет 36 футов. Если вы предполагаете, что и у вас, и у дерева хорошая осанка, и вы стоите перпендикулярно земле, то и вы, и дерево образуют два треугольника. Поскольку солнце находится очень далеко, можно предположить, что A и D конгруэнтны. Используя вашу теорему подобия AA, вы можете показать, что ABC ~ EDC.
Используя идею, что CSSTAP, мы видим, что
- AC / BC = DF / EF или 6 / 8 = H / 369999999999999999999999999999999999.

Перемножаем, и мы видим, что
- h = 6 36 / 8 = 27.
Итак, дерево примерно 27 футов в высоту. Фалес использовал этот метод для оценки высоты пирамид, и он был достаточно точен, чтобы поразить своих друзей и произвести впечатление на некоторых фараонов.
Рисунок 13.5 Фигурка и дерево отбрасывают тень. Образуются два подобных треугольника, и поскольку стороны пропорциональны, мы можем определить высоту дерева.
Теоремы подобия SAS и SSS
Существуют и другие теоремы, которые могут помочь показать, что два треугольника подобны. Я лишь сформулирую две другие теоремы, которые могут быть полезны. Я не буду тратить время на доказательство этих теорем, потому что так много нужно обсудить, а мне не хватает места.
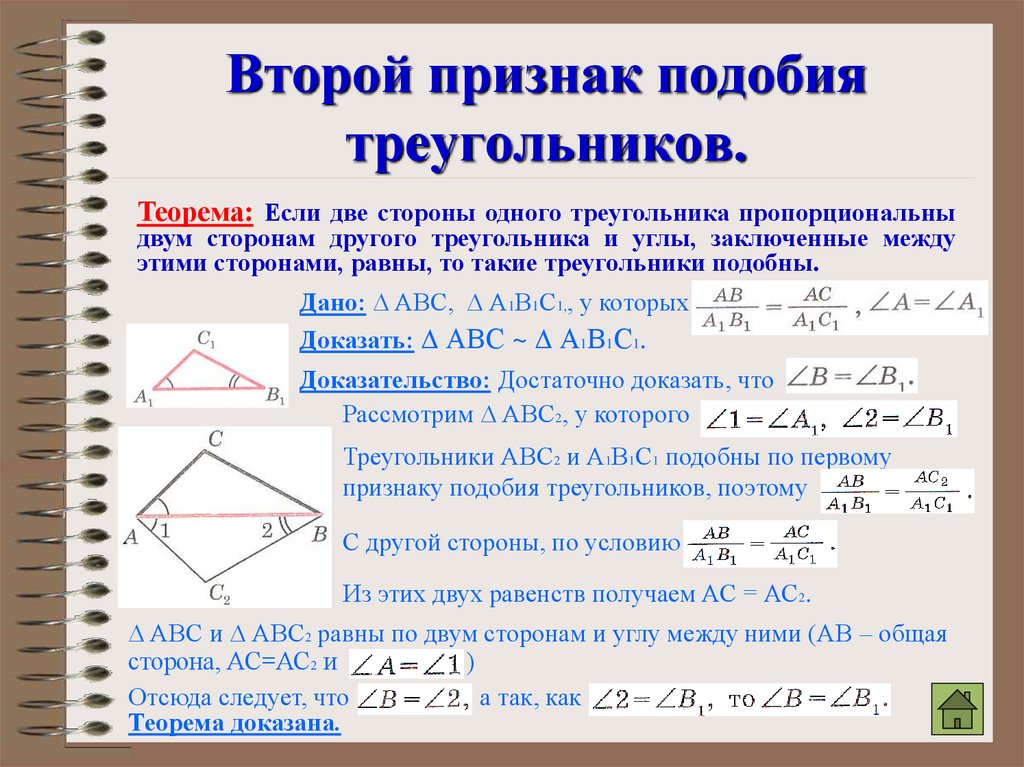
- Теорема 13.2 : Теорема подобия SAS. Если угол одного треугольника равен углу другого треугольника и стороны этого угла пропорциональны, то такие треугольники подобны.

- Теорема 13.3 : Теорема подобия SSS. Если три стороны одного треугольника пропорциональны трем соответствующим сторонам другого треугольника, то такие треугольники подобны.
- Пример 8 : Учитывая два треугольника, показанных на рисунке 13.6, найдите RS.
Рисунок 13.6 ABC и «RST.
- Решение : мы видим, что C ~ = T и что пары включающих бок пропорциональны:
- 6 / 10 = 12 / 20
- Не будьте обманываны в разграбленные в разграбленные в разграбленные в разграбленные в разграбленные в разграбленные в разграбленные в разграбленные в разграбленные в разграбленные в разграбленные в разграбленные в разграбленные в разграбленные в разграбленные в разграбленные в раздуваем думая, что две стороны не пропорциональны, потому что
- 6 / 10 20 / 12 .
- Вы должны попробовать различные комбинации, чтобы определить соответствие сторон.
 В этом случае ¯AC соответствует ¯ST, ¯BC соответствует ¯RT, ¯AB соответствует ¯RS. Таким образом, ABC ~ RST по теореме подобия SAS, и вы можете использовать тот факт, что CSSTAP для определения RS:
В этом случае ¯AC соответствует ¯ST, ¯BC соответствует ¯RT, ¯AB соответствует ¯RS. Таким образом, ABC ~ RST по теореме подобия SAS, и вы можете использовать тот факт, что CSSTAP для определения RS: - RS / ST = AB / AC
- RS / 20 = 14 / 10 9099 RS = 28 / 10
- RS = 28 / 10
- RS = 28 9011.
- 1. Используйте свойство «Средние-экстремальные значения», чтобы найти x: x — 2 / 3 = x + 1 / 4 .
- 2. Используйте свойство Means-Extremes, чтобы найти x: 6 / х = х / 24 .
- 3. Предположим, что величины двух дополнительных углов относятся как 2 к 7. Найдите величину каждого угла.
- 4. Если A ~= D, как показано на рис.
 13.7, напишите доказательство в два столбца, чтобы показать, что BC / AB = CE / DE .
13.7, напишите доказательство в два столбца, чтобы показать, что BC / AB = CE / DE .
Рисунок 13.7
A ~= D.
- 5. Расстояние через озеро, кишащее аллигаторами, следует безопасно измерять с помощью подобных треугольников, как показано на рисунке 13.8. Если XY = 160 футов, YW = 40 футов, TY = 120 футов и WZ = 50 футов, найдите XT.
Рисунок 13.8 Измерение длины озера с помощью подобных треугольников.
Выдержка из Полное руководство по геометрии для идиотов © 2004 г. Дениз Сечеи, доктор философии. Все права защищены, включая право на полное или частичное воспроизведение в любой форме. Используется по договоренности с Alpha Books , членом Penguin Group (USA) Inc.
Чтобы заказать эту книгу непосредственно у издателя, посетите веб-сайт Penguin USA или позвоните по телефону 1-800-253-6476. Вы также можете приобрести эту книгу на Amazon.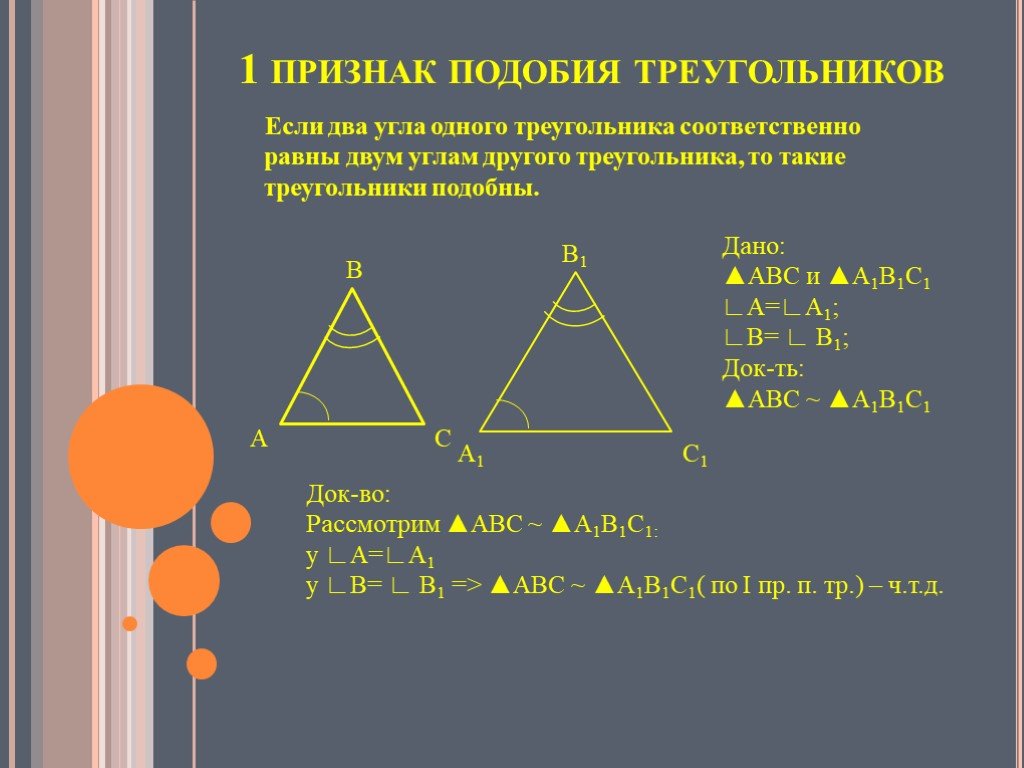 com и в Barnes & Noble.
com и в Barnes & Noble.
- Геометрия: параллельные сегменты и пропорции сегментов
Подобные треугольники, углы и стороны
Вы устали слышать, что у подобных треугольников равные углы и пропорциональные стороны? Мы продолжаем говорить это только потому, что это важно. И правда. И важно.
Если мы знаем, что два треугольника имеют равные углы и пропорциональные стороны, то мы знаем, что они подобны. На самом деле, если мы знаем, что два треугольника имеют конгруэнтные углы и/или пропорциональные стороны, то мы знаем, что они подобны. Нам не обязательно знать и то, и другое, хотя хорошо, когда у вас есть все основания.
Посмотрите на эти треугольники.
Они действительно похожи, но иногда рисунки могут поставить нас в тупик. К счастью, нам известны длины сторон треугольников, что очень удобно, потому что мы не можем сказать, равны ли углы, просто взглянув на них.
Давайте настроим коэффициенты и сравним. Они равны?
Да, действительно, длины сторон пропорциональны, поэтому мы можем быть уверены, что ∆ OAK ~ ∆ MIL .
Пример задачи
∆ PIT имеет длины сторон 4, 5 и 8, а ∆ KAN имеет длины сторон 12, 15 и 22. Похожи ли они?
Давайте настроим некоторые коэффициенты и посмотрим.
Нет. Так что они не похожи.
Совсем другое дело, когда мы имеем дело с углами. Хотя в подобных треугольниках длины сторон пропорциональны, углы должны быть равны. Если мы вырежем любые два одинаковых треугольника (что мы не рекомендуем делать на экране, но не стесняйтесь распечатать страницу, а затем продолжить работу с бумагой) и поместим их друг на друга, мы сможем выровнять каждый набор треугольников. соответствующие углы и убедитесь, что углы в точности одинаковы.
Треугольники ∆ TEX и ∆ WAS подобны, потому что их углы равны. В частности, ∠ T ≅ ∠ W , ∠ E ≅ ∠ A и ∠ X ≅ ∠ S .
Пример задачи
∆ NYM имеет углы, равные 50°, 87° и 43°. ∆ PHI имеет углы 87°, 50° и 43°. Они похожи?
∆ PHI имеет углы 87°, 50° и 43°. Они похожи?
Ага. Запишите это: тройная игра с тремя парами конгруэнтных углов. Это делает треугольники похожими.
Возникает интересный вопрос. Нужно ли нам знать меры 90 306 всех 90 307 углов, чтобы решить, подобны ли два треугольника?
Короче говоря, нет.
Длинный ответ основан на том факте, что три угла внутри каждого треугольника всегда составляют в сумме 180° (помните теорему о сумме углов для треугольников?). Это означает, что если мы знаем только меру 90 306 двух 90 307 углов, мы можем вычислить меру третьего. Однако приблизительные цифры не помогут.
А как насчет этих двух треугольников? Они похожи?
В первом треугольнике мы знаем, что ∠ P = 48° и ∠ I = 79°. Поскольку m∠ P + m∠ I + m∠ T = 180, мы можем вычислить, что m∠ T = 53°. Во втором треугольнике m∠ L = 48° и m∠ A = 79°. Опять же, поскольку m∠ L + m∠ A + m∠ D = 180, мы знаем, что ∠ D также должно быть равно 53°. Оба треугольника имеют по три равных угла, значит, они должны быть подобны.
Оба треугольника имеют по три равных угла, значит, они должны быть подобны.
Чтобы написать утверждение о сходстве, мы должны расставить буквы в правильном порядке. Конгрузки углы должны быть в одном и том же месте во имя каждого треугольника: тий P ≅ тий L , тий I ≅ тий A и ♂ T ≅ ▲ 906 D . ~ ∆ LAD .
Но нам действительно не нужно было вычислять размер этих третьих углов. Вот почему:
| Заявления | Причины | |
| 1. m∠ P + m∠ I + m∠ T = 180 | Angle Sum Theorem for Triangles | |
| 2. m∠ L + m∠ A + mT D = 180 | Угла суммирований для треугольников | |
| 3. m секретируется P = m секрети. ) | ||
| 4. m∠ T = 180 – (m∠ P + m∠ I ) | Перестановление (1) | |
5. мнение D = 180 — (MT L + MT A ) мнение D = 180 — (MT L + MT A ) | Переброса Секрет T = 180 — (MT L + MT A ) | Заместитель (3, 4) |
| 7. MT D = MRT 903 , 6) | ||
| 8. ∠ D ≅ ∠ T | Определение равных углов (7) |
Даже не требуя точных измерений углов, мы знаем, что ∠ T и ∠ D равны по размеру, а это означает, что они также конгруэнтны.
И мы только что открыли то, что называется Постулатом Угла-Угла , который гласит, что если два треугольника имеют две пары конгруэнтных углов, то эти треугольники подобны. Видите, разве не приятно делиться?
Пример задачи
Два угла в ∆ BOS измеряет 22° и 108°, а два угла в ∆ CLE измеряют 108° и 48°. Подобны ли треугольники?
Из задачи мы знаем, что у них есть хотя бы один конгруэнтный угол (108°). Но есть ли у них другой набор? Чтобы найти недостающий угол в ∆ BOS , мы решим 180° – (108° + 22°) = x или x = 50°.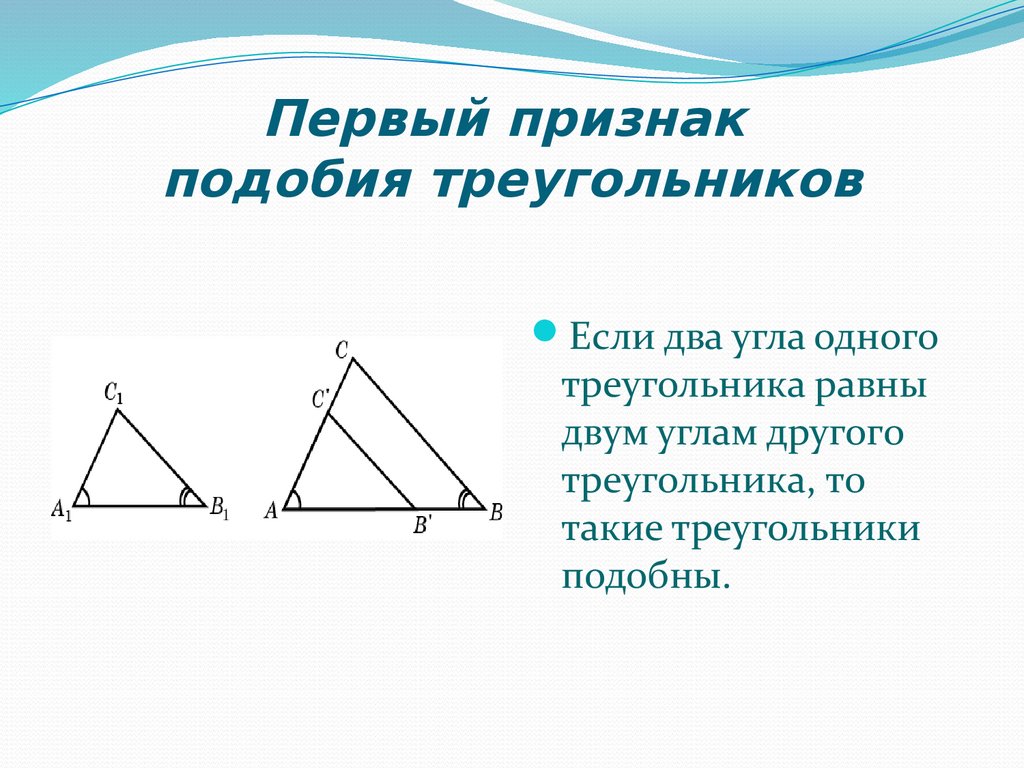


 В этом случае BAE и DEA являются альтернативными внутренними углами, поэтому они равны. Поскольку ACB и DCE являются вертикальными углами, они равны. Итак, по теореме подобия AA вы видите, что ABC ~ EDC.
В этом случае BAE и DEA являются альтернативными внутренними углами, поэтому они равны. Поскольку ACB и DCE являются вертикальными углами, они равны. Итак, по теореме подобия AA вы видите, что ABC ~ EDC.

 В этом случае ¯AC соответствует ¯ST, ¯BC соответствует ¯RT, ¯AB соответствует ¯RS. Таким образом, ABC ~ RST по теореме подобия SAS, и вы можете использовать тот факт, что CSSTAP для определения RS:
В этом случае ¯AC соответствует ¯ST, ¯BC соответствует ¯RT, ¯AB соответствует ¯RS. Таким образом, ABC ~ RST по теореме подобия SAS, и вы можете использовать тот факт, что CSSTAP для определения RS: 13.7, напишите доказательство в два столбца, чтобы показать, что BC / AB = CE / DE .
13.7, напишите доказательство в два столбца, чтобы показать, что BC / AB = CE / DE .