Онлайн калькулятор децибелы в разы, напряжения в мощность
Децибел… Что за странный пассажир? Ладно бы дебил, или, на худой конец, имбецил, так ведь нет — децибел, мать его.
Выпили по децелу, закусили, понимания не прибавило, ещё по сто, уже лучше — начали генерить мыслю.
И на кой хрен нам в батарее разводить мудрёные величины, да ещё (не при бабах будет сказано), численно равные десятичному логарифму
безразмерного отношения физической величины к одноимённой физической величине, принимаемой за исходную, умноженному на десять?
Всё равно — как отмеряли потери сигнала в линиях километрами стандартного кабеля, так и будем отмерять.
Ответ не сложен — для удобства мировосприятия.
Природа наша такова, что воздействие на органы чувств многих физических и биологических процессов пропорционально
не амплитуде входного воздействия, а логарифму входного воздействия. Поэтому и созерцать отображения больших
диапазонов изменяющихся величин удобнее всего в логарифмическом масштабе.
Итак, децибелы — это соотношение двух величин, выраженное в логарифмическом масштабе. При этом отношение токов и
напряжений имеет коэффициент 20, а отношение мощностей — коэффициент 10.
Для напряжений формула приобретает вид
,
а для мощностей —
.
Если в лесах Чухломы у нас затерялось какое-либо электронное устройство, то в качестве отношения напряжений (либо токов,
либо мощностей) принимается отношение выходной величины к входной, и это отношение называется коэффициентом передачи, или коэффициентом
преобразования данного устройства.
Пока хватит, нарисуем таблицу.
ТАБЛИЦА ПЕРЕВОДА ОТНОШЕНИЙ ВЕЛИЧИН В ДЕЦИБЕЛЛЫ
Коэффициент передачи, выраженный в децибелах, может иметь знак плюс или минус в зависимости от соотношения величин на выходе и входе (если выходная величина больше входной — плюс, если меньше — минус). А ТЕПЕРЬ НАОБОРОТ, ДЕЦИБЕЛЛЫ В ОТНОШЕНИЯ
| Логарифмическая величина Децибел (дБ) |
|
| Отношение напряжений (токов) | |
| Отношение мощностей |
В случае включения по каскадной схеме (последовательно, друг за другом) нескольких устройств — общий коэффициент передачи в децибельном выражении вычисляется простым сложением значений Кпер.
 (дБ) каждого из устройств.
(дБ) каждого из устройств.А теперь переведём логарифмическую меру мощности, измеряемую в дБм (dBm — децибел на милливатт)
в мощность устройства, измеряемую в привычных нашему организму ваттах.
На всякий пожарный — некоторые производители указывают именно этот параметр, характеризуя богатырскую мощь своих изделий.
ТАБЛИЦА ПЕРЕВОДА ДБМ В ВАТТЫ
| Мера мощности, выраженная в дБм (dBm) |
||
| Мощность, выраженная в ваттах |
Так ведь мало того, что мощность усилителей надумали измерять в дБм, посягнули и на святое — на чувствительность приёмной аппаратуры.
 Чувствительность стали определять как отношение мощности на входе приёмника к уровню мощности 1 мВт и
также выражать в логарифмическом масштабе в дБм.
Чувствительность стали определять как отношение мощности на входе приёмника к уровню мощности 1 мВт и
также выражать в логарифмическом масштабе в дБм. Куда деваться бедному крестьянину? Придётся привести таблицу и для этого бесчинства.
ТАБЛИЦА ПЕРЕВОДА ДБМ В МИКРОВОЛЬТЫ
А ещё, иногда бывает полезно знать, каким должен быть размах выходного напряжения на нагрузке, для получения заданного параметра
мощности.
Некоторые при расчёте выходной мощности пользуются простой формулой
, подставляя вместо Uд — пиковое значение (амплитудное значение,
равное максимальной амплитуде полуволны выходного сигнала).
Это не правильно, вернее правильно только для сигналов
прямоугольной формы.
Для синусоидальных, для получения точного результата надо подставлять действующее значение напряжения —
.

ЗАВИСИМОСТЬ АМПЛИТУДЫ НАПРЯЖЕНИЯ ОТ МОЩНОСТИ
| Сопротивление нагрузки (Ом) |
|
| Желаемый параметр выходной мощности (Вт) |
|
| Напряжение амплитудное (В) | |
| Напряжение peak-to-peak (В) | |
| Логарифмическая мощность (dBm) |
ЗАВИСИМОСТЬ МОЩНОСТИ ОТ ВЫХОДНОГО НАПРЯЖЕНИЯ
| Сопротивление нагрузки (Ом) |
|
| Амплитудное значение выходного сигнала (В) |
|
| Напряжение peak-to-peak (В) |   |
|
Выходная мощность (Вт) |
  |
| Логарифмическая мощность (dBm) |   |
Лог или линейный? Отличительные представления о числовой шкале в культурах коренных народов Запада и Амазонки
- Список журналов
- Рукописи авторов HAL
- PMC2610411
Наука.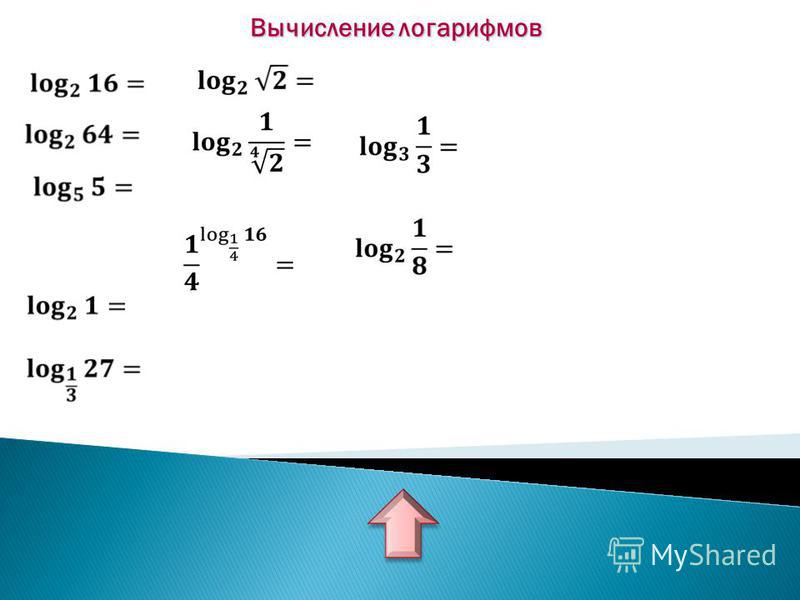 Авторская рукопись; доступно в PMC 2009 5 января.
Авторская рукопись; доступно в PMC 2009 5 января.
Опубликовано в окончательной редакции как:
Наука. 2008 май; 320 (5880): 1217–1220.
doi: 10.1126/science.1156540
PMCID: PMC2610411
HALMS: HALMS285215
PMID: 18511690
INSERM Subrepository
, 1, * , 1 , 2 and 3
Информация об авторе Информация об авторских правах и лицензиях Отказ от ответственности
- Дополнительные материалы
Отображение чисел в пространстве имеет фундаментальное значение для измерения и математики. Является ли это картографирование культурным изобретением или универсальной интуицией, разделяемой всеми людьми, независимо от культуры и образования? Мы исследовали отображения числового пространства у мундуруку, коренной амазонской группы с ограниченным числовым лексиконом и практически без формального образования. В любом возрасте мундуруку сопоставляли символические и несимволические числа с логарифмической шкалой, в то время как взрослые западные люди использовали линейное сопоставление с маленькими или символическими числами и логарифмическое сопоставление, когда числа представлялись несимволически в условиях, препятствующих счету. Таким образом, отображение чисел в пространство есть всеобщее созерцание, и это исходное созерцание числа логарифмично. Концепция линейной числовой прямой кажется культурным изобретением, которое не может развиваться без формального образования.
В любом возрасте мундуруку сопоставляли символические и несимволические числа с логарифмической шкалой, в то время как взрослые западные люди использовали линейное сопоставление с маленькими или символическими числами и логарифмическое сопоставление, когда числа представлялись несимволически в условиях, препятствующих счету. Таким образом, отображение чисел в пространство есть всеобщее созерцание, и это исходное созерцание числа логарифмично. Концепция линейной числовой прямой кажется культурным изобретением, которое не может развиваться без формального образования.
Ключевые слова: Подросток, Взрослый, Антропология, Культура, Бразилия, Ребенок, Культурная эволюция, Образовательный статус, Женщины, Люди, Индейцы, Южноамериканцы, Интуиция, Мужчины, Математика, Средний возраст
Что же такое математика, если она не является уникальной, строгой, логической структурой? Это ряд великих интуиций, тщательно просеянных и организованных с помощью логики, которую люди хотят и могут применить в любое время.
0014
Отображение чисел в пространстве играет существенную роль в математике, от измерения и геометрии до изучения иррациональных чисел, декартовых координат, линии действительных чисел и комплексной плоскости (1, 2). Как человеческий разум получает доступ к таким абстрактным математическим понятиям? Конструктивистские теории рассматривают математику как набор культурных изобретений, которые постепенно совершенствуются в истории математики и медленно усваиваются в детстве и юности (3). Однако ментальное построение математики может иметь более глубокие основания. Математические объекты могут найти свое окончательное происхождение в базовых интуитивных представлениях о пространстве, времени и числе, которые были интернализованы в течение миллионов лет эволюции в структурированной среде и которые возникают в начале онтогенеза, независимо от образования (2, 4). Здесь мы представляем доказательства, которые примиряют эти две точки зрения: наши результаты показывают, что все люди разделяют интуицию о том, что числа отображаются в пространстве, но культурно-специфический опыт изменяет форму этого отображения.
Предыдущие исследования в области психологии и нейровизуализации подтверждают мнение о том, что чувство числа присутствует у людей и многих других видов в раннем возрасте и с воспроизводимым субстратом в двусторонней внутритеменной борозде (5–8). Эта область удивительно близка или даже перекрывается с областями, участвующими в кодировании пространственных измерений, таких как размер, местоположение и направление взгляда (9–11). Следовательно, на этом уровне могут происходить взаимодействия между числовыми и пространственными кодами в теменной коре. Действительно, у взрослых людей простое представление арабской цифры автоматически вызывает пространственное смещение как в моторных реакциях, так и в ориентации внимания (11–13). У пациентов с поражением головного мозга наблюдаются соответствующие нарушения в сравнении и разделении пополам отрезков и чисел (14), а некоторые люди даже сообщают о живом опыте видения чисел в фиксированных местах на идиосинкразической пространственно непрерывной «числовой форме» (15, 16).
Недавние эксперименты зафиксировали заметный сдвиг в представлениях детей о том, как числа отображаются в пространстве (17–19). Когда детей просят указать правильное место для произносимого числового слова на отрезке линии, помеченном 0 слева и 100 справа, даже детсадовцы понимают задачу и ведут себя неслучайно, систематически помещая меньшие числа слева и большие числа справа. Однако они распределяют числа неравномерно и вместо этого отводят больше места небольшим числам, применяя сжатое логарифмическое отображение. Например, они могут поместить число 10 в середине сегмента 0–100. Эта компрессионная реакция хорошо согласуется с исследованиями на животных и младенцах, которые демонстрируют, что численное восприятие подчиняется закону Вебера, вездесущему психофизическому закону, согласно которому все большие величины представляются с пропорционально большей неточностью, совместимой с логарифмическим внутренним представлением с фиксированным шумом (7, 20, 21). . Переход от логарифмического к линейному отображению происходит позже в развитии, между 1 ст и 4 й класс в зависимости от опыта и диапазона протестированных номеров (17–19).
Однако все эти наблюдения были сделаны на западных субъектах, которые в раннем возрасте имели доступ к математическому образованию и культуре. До формального школьного обучения западные дети могут усвоить понятие числовой линии из арабских цифр, которые можно увидеть на лифтах, линейках, книгах и т. д. Таким образом, существующие исследования не раскрывают, какие аспекты отображения числового пространства составляют основную интуицию, которая будет продолжать существовать. при отсутствии структурированного математического языка и образования. В частности, мы не знаем, будет ли переход от логарифмического к линейному происходить спонтанно в процессе созревания мозга или же для этого потребуется знакомство с критически важным учебным материалом или культурно-специфическими устройствами, такими как линейки или графики.
Чтобы решить эти проблемы, мы собрали данные психологических экспериментов в мундуруку, коренной амазонской культуре с ограниченным доступом к образованию (22, 23). Предыдущие исследования установили, что, хотя их словарный запас числовых слов ограничен, и у них практически нет доступа к линейкам, измерительным приборам, графикам или картам, мундуруку используют сложные понятия как о числе, так и о пространстве, хотя и в приблизительной и невербальной манере. 22, 23). Поэтому мы спросили, считают ли они эти две области связанными систематическим отображением, и если да, то какую форму принимает это отображение числового пространства.
Предыдущие исследования установили, что, хотя их словарный запас числовых слов ограничен, и у них практически нет доступа к линейкам, измерительным приборам, графикам или картам, мундуруку используют сложные понятия как о числе, так и о пространстве, хотя и в приблизительной и невербальной манере. 22, 23). Поэтому мы спросили, считают ли они эти две области связанными систематическим отображением, и если да, то какую форму принимает это отображение числового пространства.
В общей сложности 33 взрослых и детей мундуруку были индивидуально протестированы в числово-пространственном задании ()(24). В каждом испытании на экране компьютера отображался отрезок линии с одной точкой слева и десятью точками справа (или в отдельном блоке 10 и 100 точек соответственно). Затем в случайном порядке предъявлялись другие числа в различных формах (наборы точек, последовательности тонов, произносимые слова мундуруку, произносимые португальские слова). Для каждого числа участник указывал на место на экране, и этот ответ записывался щелчком мыши без обратной связи. Было представлено только два тренировочных испытания с наборами точек, количество которых соответствовало концам шкалы (например, один и десять). Участникам сказали, что эти два стимула принадлежат их соответствующим концам, но другие стимулы могут быть размещены в любом месте. Поскольку в обучении не использовались промежуточные числа, результаты всех последующих испытаний служили для выявления того, будут ли участники спонтанно использовать систематическое картирование, и если да, то будет ли их картирование компрессионным или линейным.
Было представлено только два тренировочных испытания с наборами точек, количество которых соответствовало концам шкалы (например, один и десять). Участникам сказали, что эти два стимула принадлежат их соответствующим концам, но другие стимулы могут быть размещены в любом месте. Поскольку в обучении не использовались промежуточные числа, результаты всех последующих испытаний служили для выявления того, будут ли участники спонтанно использовать систематическое картирование, и если да, то будет ли их картирование компрессионным или линейным.
Открыть в отдельном окне
Задача сопоставления номеров с номерами 1–10. Горизонтальный сегмент, помеченный набором из одной точки слева и набором из 10 точек справа, постоянно присутствовал на экране. Числа представлялись визуально в виде набора точек или на слух в виде последовательностей тонов (см. 24), цифр мундуруку или португальских цифр. Для числительных мундуруку дан грубый перевод на арабские цифры (например, «pũg põgbi xex xep bodi» ≈ «одна горсть (и) две сбоку» ≈ 7; «xex xep põgbi» ≈ «две горсти» ≈ 10). Для каждого стимула участники указывали на место на линии, и экспериментатор щелкал по нему компьютерной мышью, в результате чего появлялась небольшая полоса.
Для каждого стимула участники указывали на место на линии, и экспериментатор щелкал по нему компьютерной мышью, в результате чего появлялась небольшая полоса.
Скупые ответы мундуруку показали, что они поняли задачу. Хотя некоторые участники, как правило, использовали только конечные точки шкалы (см. 24), большинство использовали континуум полного ответа и применяли последовательную стратегию сопоставления последовательных чисел с последовательными местоположениями (см. 24). Существовала значительная положительная корреляция между номером стимула и средним местоположением ответа, независимо от модальности, в которой были представлены числа. Задача упрощалась, когда стимулами служили наборы точек, похожие на эталонные метки, расставленные на концах (цифры 1–10, r 2 =92,6%, 8 д.ф.; числа 10–100, r 2 =91,9%, 8 д.ф.). Однако мундуруку продолжали использовать систематическое отображение числового пространства с необученными стимулами, которые разделяли с эталонными метками только абстрактное понятие числа: последовательности тонов 1–10 (r 2 = 92,5%, 8 d. f), разговорный мундуруку. числовые слова (r 2 = 91,8, 6.d.f) и числовые слова на португальском языке (r 2 = 91,1%, 8 d.f), хотя небольшая часть случайных ответов имела тенденцию слегка сглаживать кривые. Обратите внимание, что стимулы мундуруку включали сложные выражения, которые очень редко произносятся, такие как «pũg põgbi ebadipdip bodi» [примерный перевод: «одна горсть (и) четыре на боку»]. Результаты показывают, что мундуруку частично понимают количество, к которому относятся эти выражения.
f), разговорный мундуруку. числовые слова (r 2 = 91,8, 6.d.f) и числовые слова на португальском языке (r 2 = 91,1%, 8 d.f), хотя небольшая часть случайных ответов имела тенденцию слегка сглаживать кривые. Обратите внимание, что стимулы мундуруку включали сложные выражения, которые очень редко произносятся, такие как «pũg põgbi ebadipdip bodi» [примерный перевод: «одна горсть (и) четыре на боку»]. Результаты показывают, что мундуруку частично понимают количество, к которому относятся эти выражения.
Открыть в отдельном окне
Среднее расположение чисел на горизонтальном отрезке, отдельно для участников Мундуруку (левая колонка) и для американских участников (правая колонка). Данные являются средними +/- стандартная ошибка среднего. Графики успеваемости в разбивке по возрастным группам и уровню образования доступны в качестве дополнительного материала (24).
Важно отметить, что линейная регрессия не дала наилучшую модель ответов участников.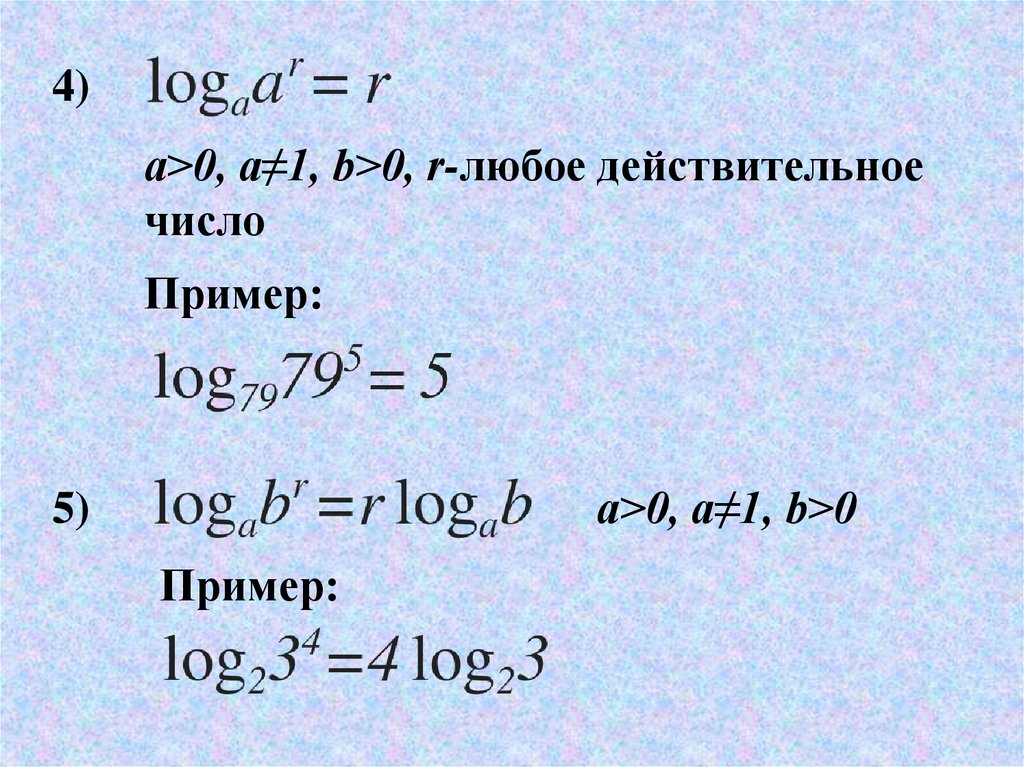 Скорее, для всех модальностей представления кривые были отрицательно ускорены. Процедура множественной регрессии оценивала вклад логарифмического регрессора сверх линейного регрессора. Эффект логарифмического сжатия был значительным для всех модальностей стимула, хотя он был незначительным только для португальских слов (односторонний p = 0,04; см. уровни значимости и веса регрессии на ). Дополнительный анализ позволил нам исключить интерпретации с точки зрения линейного ответа с разным наклоном для малых и больших чисел, ошибки параллакса, предвзятости экспериментатора или бимодального ответа (см. 24). Мундуруку, кажется, придерживаются интуитивных представлений о числах как о логарифмической шкале, где середина интервала от 1 до 10 равна 3 или 4, а не 5 или 6.
Скорее, для всех модальностей представления кривые были отрицательно ускорены. Процедура множественной регрессии оценивала вклад логарифмического регрессора сверх линейного регрессора. Эффект логарифмического сжатия был значительным для всех модальностей стимула, хотя он был незначительным только для португальских слов (односторонний p = 0,04; см. уровни значимости и веса регрессии на ). Дополнительный анализ позволил нам исключить интерпретации с точки зрения линейного ответа с разным наклоном для малых и больших чисел, ошибки параллакса, предвзятости экспериментатора или бимодального ответа (см. 24). Мундуруку, кажется, придерживаются интуитивных представлений о числах как о логарифмической шкале, где середина интервала от 1 до 10 равна 3 или 4, а не 5 или 6.
Предыдущие эксперименты по отображению числового пространства с западными субъектами включали только символические числа, тогда как настоящий эксперимент включал несимволические визуальные и слуховые числа. Таким образом, было важно проверить, линейно или логарифмически оценивались эти новые стимулы у образованных западных испытуемых. Как показано на рисунке, взрослые американцы линейно оценили все числа, представленные в английском и испанском языках, а также наборы из 1–10 точек, которые можно было легко сосчитать. Однако они показали значительный логарифмический компонент с наборами из 10–100 точек и последовательностями тонов. Когда две группы участников сравнивали напрямую, мундуруку показали большую компрессионную нелинейность, чем американские испытуемые, только с наборами из 1–10 точек (p = 0,003) и с числительными на родном языке (p = 0,033). Этот вывод согласуется с предыдущими данными, свидетельствующими о том, что западные испытуемые оценивают большое число приблизительно и сжато (25, 26). Их суждения линейны только тогда, когда числа представлены в символической форме или в виде небольших наборов, количество которых можно точно оценить.
Как показано на рисунке, взрослые американцы линейно оценили все числа, представленные в английском и испанском языках, а также наборы из 1–10 точек, которые можно было легко сосчитать. Однако они показали значительный логарифмический компонент с наборами из 10–100 точек и последовательностями тонов. Когда две группы участников сравнивали напрямую, мундуруку показали большую компрессионную нелинейность, чем американские испытуемые, только с наборами из 1–10 точек (p = 0,003) и с числительными на родном языке (p = 0,033). Этот вывод согласуется с предыдущими данными, свидетельствующими о том, что западные испытуемые оценивают большое число приблизительно и сжато (25, 26). Их суждения линейны только тогда, когда числа представлены в символической форме или в виде небольших наборов, количество которых можно точно оценить.
Население мундуруку неоднородно, и некоторые из наших участников, особенно дети, получили небольшое образование. Чтобы изучить влияние этой переменной, мы рассчитали для каждого участника индекс нелинейности в отображении числового пространства: вес логарифмического регрессора в множественной регрессии данных на линейных и логарифмических регрессорах. Для этого анализа мы объединили испытания с точками 1–10 и числовыми словами, но исключили те с точками 10–100 и тонами, для которых западные испытуемые показали некоторую нелинейность. Индекс подтвердил очень значимую нелинейность у участников Мундуруку (t=6,20, 34 d.f., p<10 -6 ). У американских участников производительность не отклонялась от линейности (p = 0,08) и заметно отличалась от таковой у мундуруку (Welch t = 4,37, 48,6 df, p <0,0001). Важно отметить, что нелинейность мундуруку оставалась значительной даже при ограничении анализа взрослыми (t = 4,34, 23 df, p = 0,0002), одноязычными носителями (t = 5,36, 29 df, p <10 −5 ) или для необразованных участников (t = 2,60, 7 d.f., p = 0,035; см. рисунки S7–S10 для графического изображения производительности подгруппы) (24). Т-тесты, линейный и ранговый регрессионный анализ не показали влияния пола, возраста, образования или двуязычия. Наблюдалась только тенденция к уменьшению нелинейности в зависимости от возраста (тау Кендалла = -0,23, р = 0,055).
Для этого анализа мы объединили испытания с точками 1–10 и числовыми словами, но исключили те с точками 10–100 и тонами, для которых западные испытуемые показали некоторую нелинейность. Индекс подтвердил очень значимую нелинейность у участников Мундуруку (t=6,20, 34 d.f., p<10 -6 ). У американских участников производительность не отклонялась от линейности (p = 0,08) и заметно отличалась от таковой у мундуруку (Welch t = 4,37, 48,6 df, p <0,0001). Важно отметить, что нелинейность мундуруку оставалась значительной даже при ограничении анализа взрослыми (t = 4,34, 23 df, p = 0,0002), одноязычными носителями (t = 5,36, 29 df, p <10 −5 ) или для необразованных участников (t = 2,60, 7 d.f., p = 0,035; см. рисунки S7–S10 для графического изображения производительности подгруппы) (24). Т-тесты, линейный и ранговый регрессионный анализ не показали влияния пола, возраста, образования или двуязычия. Наблюдалась только тенденция к уменьшению нелинейности в зависимости от возраста (тау Кендалла = -0,23, р = 0,055). Хотя это наблюдение предполагает, что пожилые мундуруку могут эволюционировать в сторону большего понимания линейной числовой линии, следует отметить, что у западных детей отображение становится линейным в диапазоне 10–100 к 19 годам.0029 st или 2 nd класс (17–19), в то время как в наших данных даже самые старые взрослые мундуруку (возраст> 40 лет) продолжали демонстрировать весьма значительную нелинейность в диапазоне 1–10 (1 = 3,36, 11 д.ф., р=0,006).
Хотя это наблюдение предполагает, что пожилые мундуруку могут эволюционировать в сторону большего понимания линейной числовой линии, следует отметить, что у западных детей отображение становится линейным в диапазоне 10–100 к 19 годам.0029 st или 2 nd класс (17–19), в то время как в наших данных даже самые старые взрослые мундуруку (возраст> 40 лет) продолжали демонстрировать весьма значительную нелинейность в диапазоне 1–10 (1 = 3,36, 11 д.ф., р=0,006).
Наконец, мы проанализировали частный случай португальских числительных. Хотя общая успеваемость была логарифмической, разделение по уровню образования показало, что логарифмический ответ имел место для участников с 1–2 годами образования (t = 3,15, 16 d.f., p = 0,006; рисунок S9), но не для тех, у кого вообще не было образования или с дополнительным образованием. У необразованных участников работа с португальскими числительными была сильно изменчива и слабо коррелировала с числом (r 2 =39,0, р=0,053; рисунок S8), предполагая, что многие из этих испытуемых просто не знали значения португальских числительных. С другой стороны, для наиболее образованной группы результаты были строго линейными (r 2 = 94,5%, p<10 -5 ; рисунок S10). Исключая участников без образования, мы обнаружили, что более высокое образование значительно изменило ответы на португальский язык с логарифмических на линейные (t = 2,48, 16,6 df, p = 0,024), но оставило ответы на цифры и узоры точек мундуруку без изменений (p> 0,5), таким образом, давая значительное взаимодействие (p = 0,008). Поразительно, но в более образованной группе результаты значительно различались в зависимости от записи чисел (t = 3,12, 9d.f., p = 0,012), так как он был линейным для португальских цифр, но логарифмическим для цифр мундуруку и точечных узоров 1–10.
С другой стороны, для наиболее образованной группы результаты были строго линейными (r 2 = 94,5%, p<10 -5 ; рисунок S10). Исключая участников без образования, мы обнаружили, что более высокое образование значительно изменило ответы на португальский язык с логарифмических на линейные (t = 2,48, 16,6 df, p = 0,024), но оставило ответы на цифры и узоры точек мундуруку без изменений (p> 0,5), таким образом, давая значительное взаимодействие (p = 0,008). Поразительно, но в более образованной группе результаты значительно различались в зависимости от записи чисел (t = 3,12, 9d.f., p = 0,012), так как он был линейным для португальских цифр, но логарифмическим для цифр мундуруку и точечных узоров 1–10.
В целом, эти результаты раскрывают как универсальные, так и зависящие от культуры грани чувства числа. После минимального периода обучения даже представители отдаленной культуры с ограниченным словарным запасом и образованием легко понимают, что число может быть отображено в пространственной шкале. Однако точная форма этого отображения резко меняется с логарифмической на линейную, в зависимости от возраста, в котором люди проходят тестирование, полученного ими образования и формата, в котором представлены числа.
Однако точная форма этого отображения резко меняется с логарифмической на линейную, в зависимости от возраста, в котором люди проходят тестирование, полученного ими образования и формата, в котором представлены числа.
В свете поведения взрослых амазонок становится ясно, что умственная революция в числовом ряду западных детей не является результатом простого процесса созревания: логарифмическое мышление сохраняется у мундуруку и во взрослом возрасте даже для очень малых чисел в диапазоне 1. –10, независимо от того, представлены ли они в виде точек, тонов или произнесенных слов мундуруку. Каковы источники этого универсального логарифмического отображения? Исследования мозговых механизмов восприятия числа выявили сжатый числовой код, при котором отдельные нейроны в теменной и префронтальной коре демонстрируют кривую настройки Гаусса на логарифмической оси числа (27). Как впервые заметил Густав Фехнер, такая постоянная неточность в логарифмическом масштабе может объяснить закон Вебера — тот факт, что большие числа требуют пропорционально большей разницы, чтобы оставаться одинаково различимыми. Действительно, недавняя модель предполагает, что свойства настройки числовых нейронов могут объяснить многие детали элементарной ментальной арифметики у людей и животных (21). Как правило, логарифмическая шкала обеспечивает компактное нейронное представление величин в несколько порядков с фиксированной относительной точностью.
Действительно, недавняя модель предполагает, что свойства настройки числовых нейронов могут объяснить многие детали элементарной ментальной арифметики у людей и животных (21). Как правило, логарифмическая шкала обеспечивает компактное нейронное представление величин в несколько порядков с фиксированной относительной точностью.
Пока неизвестно, какой критический образовательный или культурный опыт превращает это исходное представление в линейную шкалу. Когда у отдаленного населения наблюдаются культурные различия в концептуальной репрезентации, часто ссылаются на гипотезу Уорфа (28), согласно которой язык определяет организацию мышления. В данном случае, однако, объяснение Уорфа не работает, поскольку ни лингвистическая компетенция per se (присутствует у всех мундуруку), ни числовой словарный запас и словесный счет (присутствующие у большинства мундуруку, включая некоторых говорящих на одном языке и маленьких детей, см. 24) достаточно, чтобы вызвать логарифмический сдвиг (17–19). Умозрительно, двумя факторами, лежащими в основе сдвига, могут быть опыт измерения, посредством которого фиксированная числовая единица применяется к различным пространственным положениям, и опыт сложения и вычитания, в конечном итоге дающий интуитивное представление о том, что все последовательные числа разделены одним и тем же интервалом +1. Наиболее образованные мундуруку в конечном итоге понимают, что линейное масштабирование, которое позволяет измерять и сохранять неизменность по сравнению с сложением и вычитанием, является центральным элементом португальской системы числовых слов. В то же время они по-прежнему не распространяют этот принцип на числовые слова мундуруку, где перцептивное сходство между количествами по-прежнему рассматривается как наиболее важное свойство чисел. Система числовых слов мундуруку может быть культурным приемом, который не делает упор на измерение или неизменность путем сложения / вычитания как определяющую черту числа, в отличие от западных цифр.
Умозрительно, двумя факторами, лежащими в основе сдвига, могут быть опыт измерения, посредством которого фиксированная числовая единица применяется к различным пространственным положениям, и опыт сложения и вычитания, в конечном итоге дающий интуитивное представление о том, что все последовательные числа разделены одним и тем же интервалом +1. Наиболее образованные мундуруку в конечном итоге понимают, что линейное масштабирование, которое позволяет измерять и сохранять неизменность по сравнению с сложением и вычитанием, является центральным элементом португальской системы числовых слов. В то же время они по-прежнему не распространяют этот принцип на числовые слова мундуруку, где перцептивное сходство между количествами по-прежнему рассматривается как наиболее важное свойство чисел. Система числовых слов мундуруку может быть культурным приемом, который не делает упор на измерение или неизменность путем сложения / вычитания как определяющую черту числа, в отличие от западных цифр.
Одновременное присутствие линейных и сжатых мысленных представлений чисел, вероятно, не уникально для мундуруку. У американских детей логарифмическое отображение не исчезает сразу, а исчезает сначала для небольших чисел, а гораздо позже для больших чисел от 1 до 1000 (до 4-го -го или 6-го -го класса у некоторых детей) (17–19). . На самом деле логарифмическое представление может дремать у всех нас для очень больших чисел или всякий раз, когда мы аппроксимируем числа (29), включая цены (30). Таким образом, логарифмические и линейные шкалы могут быть глубоко укоренены во всей нашей умственной деятельности (31).
У американских детей логарифмическое отображение не исчезает сразу, а исчезает сначала для небольших чисел, а гораздо позже для больших чисел от 1 до 1000 (до 4-го -го или 6-го -го класса у некоторых детей) (17–19). . На самом деле логарифмическое представление может дремать у всех нас для очень больших чисел или всякий раз, когда мы аппроксимируем числа (29), включая цены (30). Таким образом, логарифмические и линейные шкалы могут быть глубоко укоренены во всей нашей умственной деятельности (31).
1
Нажмите здесь для просмотра. (251K, pdf)
1. Клайн М. Математика: потеря уверенности. Издательство Оксфордского университета; Нью-Йорк: 1980. [Google Scholar]
2. Дехан С. Чувство числа. Издательство Оксфордского университета; Нью-Йорк: 1997. [Google Scholar]
3. Пиаже Дж. Представление ребенка о числе. Нортон; Нью-Йорк: 1952. [Google Scholar]
4. Шепард Р.Н. Behav Brain Sci. 2001 авг; 24:581. [PubMed] [Google Scholar]
5. Dehaene S, Molko N, Cohen L, Wilson AJ. Курр Опин Нейробиол. 2004 апр; 14:218. [PubMed] [Академия Google]
Dehaene S, Molko N, Cohen L, Wilson AJ. Курр Опин Нейробиол. 2004 апр; 14:218. [PubMed] [Академия Google]
6. Баттерворт Б. Математический мозг. Макмиллан; London: 1999. [Google Scholar]
7. Feigenson L, Dehaene S, Spelke E. Trends Cogn Sci. 2004 июль; 8:307. [PubMed] [Google Scholar]
8. Nieder A. Nat Rev Neurosci. 2005 [PubMed] [Google Scholar]
9. Simon O, Mangin JF, Cohen L, Le Bihan D, Dehaene S. Neuron. 2002; 33:475. [PubMed] [Google Scholar]
10. Pinel P, Piazza M, Le Bihan D, Dehaene S. Neuron. 2004 25 марта; 41:983. [PubMed] [Академия Google]
11. Hubbard EM, Piazza M, Pinel P, Dehaene S. Nat Rev Neurosci. 2005 июнь; 6:435. [PubMed] [Google Scholar]
12. Дехан С., Боссини С., Жиро П. Журнал экспериментальной психологии: Общие сведения. 1993; 122:371. [Google Scholar]
13. Fischer MH, Castel AD, Dodd MD, Pratt J. Nat Neurosci. 2003 июнь; 6:555. [PubMed] [Google Scholar]
14. Зорзи М., Прифтис К., Умилта С. Природа. 2002; 417:138. [PubMed] [Google Scholar]
2002; 417:138. [PubMed] [Google Scholar]
15. Гальтон Ф. Природа. 1880;21:252. [Академия Google]
16. Пьяцца М., Пинель П., Дехане С. Когнитивная нейропсихология. 2006; 23:1162. [PubMed] [Google Scholar]
17. Бут Дж.Л., Зиглер Р.С. Дев Психология. 2006 Январь; 42:189. [PubMed] [Google Scholar]
18. Siegler RS, Booth JL. Детский Дев. 2004 март – апрель; 75:428. [PubMed] [Google Scholar]
19. Siegler RS, Opfer JE. Психологические науки. 2003 Май; 14:237. [PubMed] [Google Scholar]
20. Шепард Р.Н., Килпатрик Д.В., Каннингем Дж.П. Когнитивная психология. 1975; 7:82. [Академия Google]
21. Дехане С. Внимание и производительность XXII. В: Хаггард П., Россетти Ю., редакторы. Сенсомоторные основы высшего познания. Издательство Гарвардского университета; Кембридж, Массачусетс: 2007. стр. 527–574. [Google Scholar]
22. Пика П., Лемер С., Изард В., Дехан С. Наука. 2004 15 октября; 306: 499. [PubMed] [Google Scholar]
23. Дехане С. , Изард В., Пика П., Спелке Э. Наука. 2006; 311:381. [PubMed] [Google Scholar]
, Изард В., Пика П., Спелке Э. Наука. 2006; 311:381. [PubMed] [Google Scholar]
24. Материалы и методы доступны в качестве вспомогательного материала на сайте Science Online.
25. Изард В., Дехане С. Познание. 2008 март; 106:1221. [PubMed] [Google Scholar]
26. van Oeffelen MP, Vos PG. Восприятие и психофизика. 1982; 32:163. [PubMed] [Google Scholar]
27. Нидер А., Миллер Э.К. Proc Natl Acad Sci U S A. 2004; 101:7457. [Бесплатная статья PMC] [PubMed] [Google Scholar]
28. Гордон П. Наука. 2004; 306:496. [PubMed] [Google Scholar]
29. Banks WP, Coleman MJ. Восприятие и психофизика. 1981; 29:95. [PubMed] [Академия Google]
30. Дехане С., Маркес Ж.Ф. Ежеквартальный журнал экспериментальной психологии. 2002; 55:705. [PubMed] [Google Scholar]
31. Эта работа является частью более крупного проекта по природе количественного определения. Он основан на психологических экспериментах и лингвистических исследованиях на территории Мундуруку (Пара) под наблюдением PP, в соответствии с Consehlo de Desenvolvimento Cientifico et Tecnologicico и Fundacão do Indio (Funaï; Processo 2857/04). Мы благодарим C Tawé, A Ramos и C Romeiro за полезные обсуждения и советы, а также Ana Armo и Ya-hsin Liu за помощь в сборе данных. При поддержке INSERM, отдела SHS CNRS (PP), NIH (ES) и столетней стипендии McDonnell Foundation (SD).
Мы благодарим C Tawé, A Ramos и C Romeiro за полезные обсуждения и советы, а также Ana Armo и Ya-hsin Liu за помощь в сборе данных. При поддержке INSERM, отдела SHS CNRS (PP), NIH (ES) и столетней стипендии McDonnell Foundation (SD).
Примечания к статистике: Логарифмы | BMJ
Предназначен для медицинских работников
Переключить навигацию
Логотип БМЖ
Карта сайта
Поиск
Переключить верхнее меню
- Примечания к статистике:…
- Примечания к статистике: логарифмы
Образование и дебаты
БМЖ
1996 год;
312
Дои: https://doi. org/10.1136/bmj.312.7032.700
(опубликовано 16 марта 1996 г.)
Цитируйте это как: BMJ 1996;312:700
org/10.1136/bmj.312.7032.700
(опубликовано 16 марта 1996 г.)
Цитируйте это как: BMJ 1996;312:700
- Артикул
- Связанный контент
- Метрики
- ответов
- Экспертная оценка
- J Martin Bland, профессор медицинской статистикиa,
- Douglas G Altman, руководительb
- a Департамент наук об общественном здравоохранении, Медицинская школа госпиталя Святого Георгия, Лондон SW17 0RE
- b Группа медицинской статистики ICRF, Центр медицинской статистики, Институт медицинских наук, PO Box 777, Oxford OX3 7LF
- Адрес для переписки: профессор Блэнд.
Логарифмы (или для краткости журналы) широко используются в статистике. Мы часто анализируем журналы измерений, а не сами измерения, и некоторые широко используемые методы анализа, такие как логистическая регрессия и регрессия Кокса, дают коэффициенты в логарифмической шкале. Здесь мы дадим краткий обзор свойств логарифмов, которые делают их такими полезными.
Здесь мы дадим краткий обзор свойств логарифмов, которые делают их такими полезными.
Мы начнем с логарифмов по основанию 10. Это десятичные логарифмы, которые раньше широко использовались для вычислений, для которых мы теперь используем калькуляторы и компьютеры. Журнал по основанию 10 числа a равен b, где a=10 b . Мы пишем b=log10a. Так, например, log10(10)=1, log10(100)=2, log10(1000)=3, log10(10000)=4 и так далее. Обычно скобки опускают и пишут log10a, но мы используем их для ясности.
Если мы умножим два числа, логарифм произведения будет суммой их логов: log(ab)=log(a)+log(b). Например, 100×1000=10 2 x 10 3 =10 2 + 3 =10 5 =100000. Или в терминах журнала: log10(100×1000)=log10(100)+log10(1000)=2+3=5. Следовательно, 100×1000=10 5 = 100000. Отсюда следует, что любое мультипликативное отношение вида y=axbxcxd можно сделать аддитивным с помощью логарифмического преобразования: log(y)=log(a)+log(b)+log(c)+log(d). Точно так же разница между двумя журналами представляет собой журнал отношения: log(a)-log(b)=log(a/b). Поскольку статистические методы гораздо легче справляются с аддитивными отношениями, чем с мультипликативными, логарифмы имеют множество применений. Как мы увидим в будущих статистических заметках, работа с логарифмами данных, а не с самими данными, может иметь несколько преимуществ. Мультипликативные отношения могут стать аддитивными, асимметричные распределения могут стать симметричными, а кривые могут стать прямыми.
Точно так же разница между двумя журналами представляет собой журнал отношения: log(a)-log(b)=log(a/b). Поскольку статистические методы гораздо легче справляются с аддитивными отношениями, чем с мультипликативными, логарифмы имеют множество применений. Как мы увидим в будущих статистических заметках, работа с логарифмами данных, а не с самими данными, может иметь несколько преимуществ. Мультипликативные отношения могут стать аддитивными, асимметричные распределения могут стать симметричными, а кривые могут стать прямыми.
Большинство научных калькуляторов имеют клавишу LOG, которая выводит логарифм числа на дисплей. Обычно у них также есть ключ 10 x , который дает нам число, логарифм которого отображается на дисплее. Это называется антилогарифмом или антилогарифмом и полезно при рассогласовании с результатами вычислений в логарифмической шкале.
Многие статистические компьютерные программы используют не логарифмы по основанию 10, а логарифмы по основанию e, называемые натуральными логарифмами. Здесь e=2,7183… — математическая константа, почти такая же, как (pi)=3,1412…. Математики, а, следовательно, и статистики, почти всегда используют логарифмы по основанию e, потому что это упрощает многие формулы. На калькуляторе это обычно задается клавишей LN, а антилог — e 9.Ключ 0029 х . Числовое отношение между логарифмами по основанию e и 10 таково, что log10(e)xloge(x)=log10(x). Натуральные логарифмы также записываются как ln(x) или часто просто как log(x).
Здесь e=2,7183… — математическая константа, почти такая же, как (pi)=3,1412…. Математики, а, следовательно, и статистики, почти всегда используют логарифмы по основанию e, потому что это упрощает многие формулы. На калькуляторе это обычно задается клавишей LN, а антилог — e 9.Ключ 0029 х . Числовое отношение между логарифмами по основанию e и 10 таково, что log10(e)xloge(x)=log10(x). Натуральные логарифмы также записываются как ln(x) или часто просто как log(x).
Основание, используемое для логарифмов, является вопросом удобства и зависит только от конкретного приложения. Выбранная база влияет на значения самих журналов, но не более того. При условии, что мы используем правильный антилог для возврата к естественному масштабу, не имеет значения, какую базу мы используем.
Посмотреть реферат
Инструменты статьи
PDF 0 ответов
Электронное письмо другу
Спасибо за ваш интерес к распространению информации о BMJ.

