Окружность и круг
Урок 23. Математика 5 класс
В этом уроке мы сформируем представление об окружности и ее элементах. Научимся строить окружность с помощью циркуля. Познакомим с понятиями окружность, центр окружности, радиус, хорда, диаметр. Введем термины: точка лежит на окружности, внутри (вне) окружности. Сформируем представление о круге. Определим расположение точек по отношению к кругу. Уточним разницу между окружностью и кругом.
Конспект урока «Окружность и круг»
На этом уроке мы познакомимся с понятиями окружности и круга. Научимся чертить окружность и круг.
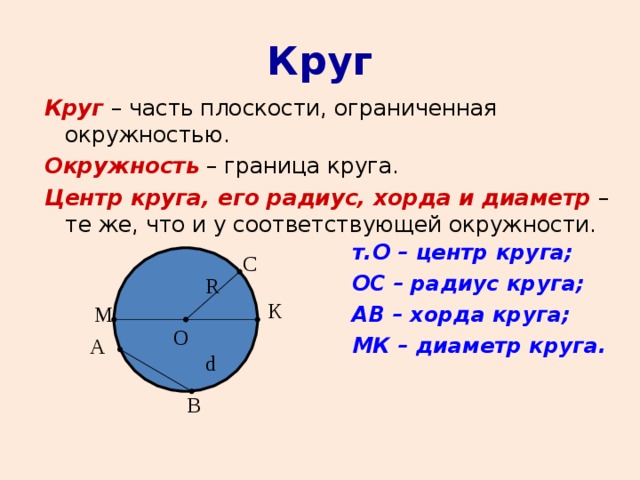
Чертить окружности вы научились ещё в младших классах. Давайте вспомним, как происходит этот процесс. Для того чтобы начертить окружность мы должны установить остриё циркуля в некоторой точке О. Далее будем вращать ножку с карандашом.
Определение
Карандаш начертит на плоскости листа линию, которая и называется окружностью
Точка, в которой устанавливалось остриё
циркуля, или точка О, называется центром
окружности.Давайте соединим центр окружности, т.е. точку О, с любой понравившейся вам точкой на окружности. Обозначим эту точку, например, буквой А. Видим, у нас получился отрезок ОА.
Определение
Отрезок, соединяющий центр окружности с любой точкой на окружности, называется радиусом. Радиус обозначают маленькой латинской буквой r.
Отметим на этой окружности ещё несколько точек, например, В, С и D. И соединим их с центром окружности. Эти отрезки ОВ, ОС и OD также называют радиусами.
Все точки окружности равноудалены от её центра, т.е. удалены от центра на расстояние, равное длине радиуса.
Часто слово «длина» не произносят, а вместо «длина радиуса» говорят просто «радиус
». Например, говорят: «Изображена окружность с радиусом, равным 3 см».
Теперь давайте соединим любые 2 точки на окружности, не проходящие через центр окружности, например, E и F. У нас получился отрезок EF.
Определение
Отрезок, концы которого лежат на окружности, называется хордой.
Хорда, проходящая через центр окружности, называется её диаметром.
Посмотрите внимательно на экран. На рисунке изображён отрезок АВ, он является диаметром окружности. По рисунку нетрудно заметить, что диаметр окружности равен двум её радиусам, т.е.
Диаметр обозначают маленькой латинской буквой d, тогда d = 2r.
Запомните, диаметр окружности в два раза длиннее радиуса.
Все диаметры окружности равны между собой.
Отметим на окружности 2 точки, например, M и N.
Определение
Эти 2 точки разделили окружность на 2 части, каждую
из которых называют дугой.
На нашем рисунке они изображены линиями разного цвета.
Точки M и N называют концами дуг.
Окружность является замкнутой линией. Она разбивает плоскость на две части – внутреннюю и внешнюю.
Часть плоскости, находящаяся внутри окружности, вместе с этой окружностью называется кругом.
Окружность – это граница круга. Центром круга называется центр этой окружности. Радиусом круга называется радиус этой окружности. Диаметром круга называется диаметр этой окружности. Хордой круга называется хорда этой окружности.
Круг состоит из точек, удалённых от данной точки (его центра) на расстояние, меньшее или равное его радиусу.
Определение
Если в круге провести два его радиуса, например, ОА и ОВ, они
выделят из круга его часть, которая называется сектором.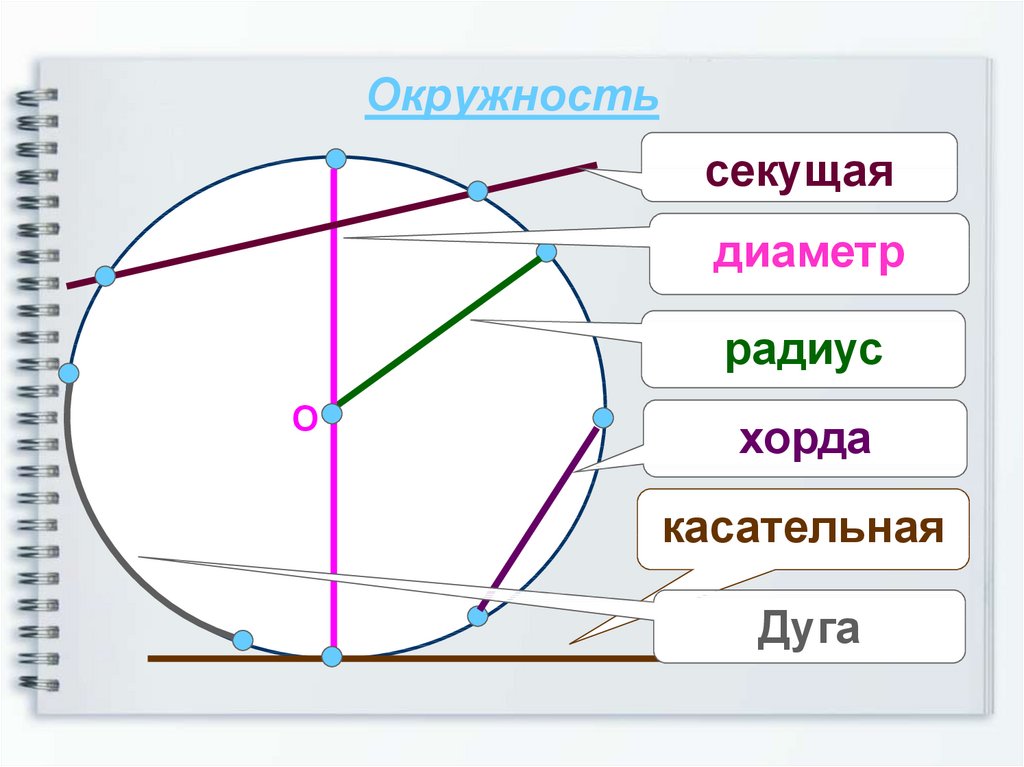
В нашем случае, получился сектор АОВ. Оставшаяся часть круга – также сектор.
Теперь давайте разберёмся с расположением точек, окружности и круга. Посмотрите внимательно на экран.
На нём изображена окружность с центром в точке О и точки А, В, С, D и E.
Точки А и Е лежат на окружности или ещё можно сказать принадлежат ей.
Точки В, С, D, O не принадлежат этой окружности.
Точки А, В, С, Е и О принадлежат кругу.
Точка D находится вне окружности или вне круга.
Итоги
Итак, сегодня на уроке мы познакомились с понятиями окружность, круг и их элементами. А также научились их чертить.
Предыдущий урок 22 Объемы. Объем прямоугольного параллелепипеда
Следующий урок 24
Доли.
Обыкновенные дроби
Получите полный комплект видеоуроков, тестов и презентаций Математика 5 класс
Чтобы добавить комментарий зарегистрируйтесь или войдите на сайт
7 класс. Геометрия. Окружность. Типовые задачи. — Окружность. Типовые задачи.
Комментарии преподавателяОкружность – это геометрическая фигура, состоящая из множества точек, которые равноудалены от заданной точки.
На рисунке 1 изображена окружность.
Рис. 1. Окружность
Сокращенная запись заданной окружности – это Окр (O, r), что читается: «Окружность с центром в точке О и радиусом r». Точка, от которой остальные точки являются равноудаленными, называется центром окружности.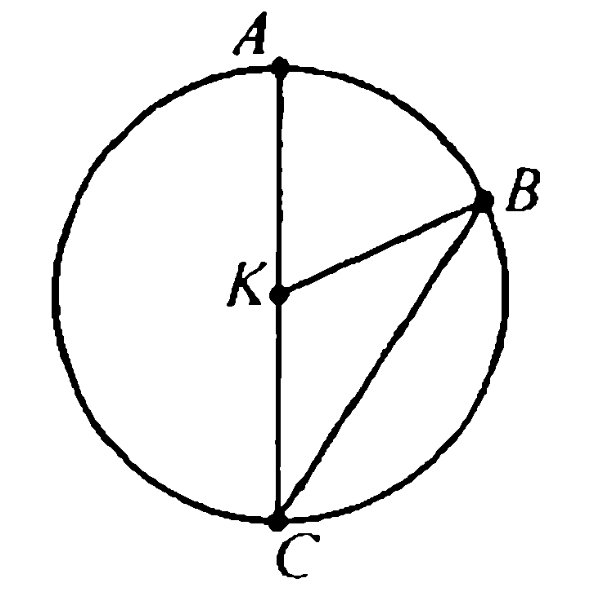
Отрезок, соединяющий центр и точку, лежащую на окружности, называется радиусом. Если соединить две точки, лежащие на окружности, можно провести отрезок, который называется хордой. Хорда, проходящая через центр окружности, называется диаметром.
Таким образом, существуют следующие обозначения:
О – центр окружности;
OM = r – радиус окружности;
OM = ON = r – радиусы окружности;
MN – хорда;
АМ – диаметр;
АM = 2r – связь между радиусом и диаметром.
Любые две точки рассекают окружность на две дуги, например: дуги NLMи NAM для заданных точек N и M.
Пример 1: На рисунке 2 изображена окружность. Определить центр, радиус, хорды, диаметр и возможные дуги.
Решение:
Рис. 2. Чертеж к примеру 1
Определим основные элементы данной окружности:
О – центр окружности;
OE = OD = OA = OC – радиусы окружности;
EF, BA – хорды;
DС – диаметр.
В данный момент вспомним определение круга. Круг – это часть плоскости, ограниченная окружностью. Совершенно понятно, что различие окружности от круга следующее: окружность – это линия, а круг – это часть плоскости, которую ограничивает данная линия. К примеру, на рисунке 3 изображен круг.
Рис. 3. Круг
Пример 2: На рисунке изображена окружность с диаметрами АВ и СD. Докажите, что хорды АС и BD равны. Докажите, что хорды ВС и АD равны. Докажите, что углы BАD и BСD равны.
Рис. 4. Чертеж к примеру 2
Решение:
Для начала выясним, что СО = ОD = ОВ = ОА, так как указанные отрезки – радиусы одной и той же окружности. Будем доказывать указанные утверждения цепочками треугольников. Например, по первому признаку, так как ОВ = ОА как радиусы, СО = ОD аналогично, как вертикальные.
Из равенства треугольников следует, что АС = ВD.
Далее докажем, что аналогично по первому признаку. ОD = ОА, СО = ОВ как радиусы, а как вертикальные. Из равенства треугольников следует, что АD = ВC.
Далее докажем, что по третьему признаку. АD – общая сторона у треугольников, АС = ВD по доказанному утверждению в п. 1, АВ = СD как диаметры окружности. Из равенства треугольников следует, что
Что и требовалось доказать.
Пример 3: отрезок МК – диаметр окружности, а РМ и РК – равные хорды. Найдите угол РОМ.
Рис. 5. Чертеж к примеру 3
Решение:
По определению, – равнобедренный, так как РК = РМ. Поскольку ОК – ОМ – радиусы окружностей, то РО – медиана, проведенная к основанию . По свойству равнобедренного треугольника медиана, проведенная к основанию, является высотой, соответственно,.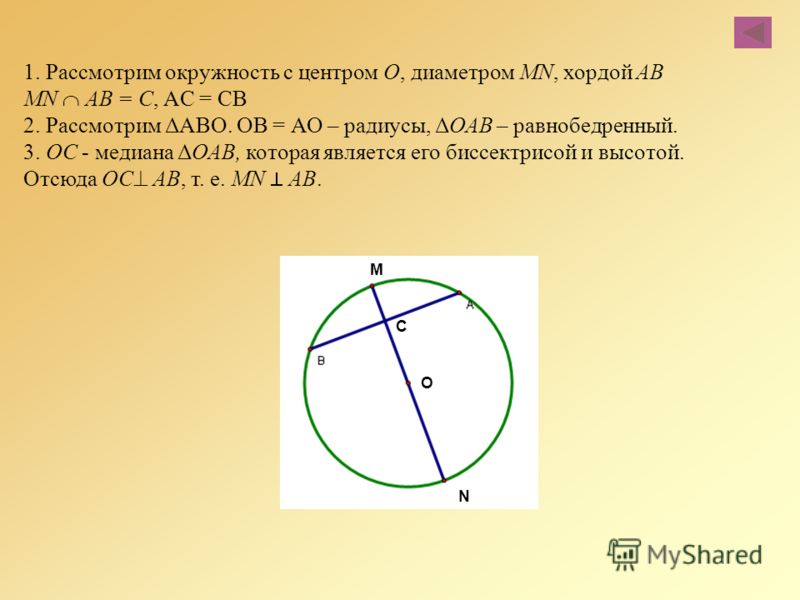
Ответ: 90°.
ИСТОЧНИК
http://interneturok.ru/ru/school/geometry/7-klass/treugolnikib/okruzhnost-4
http://nsportal.ru/sites/default/files/2012/02/26/geometriya7.ppt
http://school-assistant.ru/?predmet=matematika&theme=okruznost_i_krug
http://gaonula.com/images/55aa5aad90ae9.jpg
http://i.ytimg.com/vi/suVm1I42W1k/maxresdefault.jpg
Меры окружности (центр, диаметр, хорда, радиус) Рабочие листы
Что такое центр, диаметр, хорда и радиус окружности? Круг представляет собой двумерную форму. Круг имеет центр, диаметр, радиус и хорду. Когда дело доходит до нахождения площади, окружности или решения круговых задач, учащиеся должны иметь четкое представление о каждом из этих терминов. Начиная с первого термина, центра. Итак, что такое центр круга? Это точка, равноудаленная от точек на ребре. Круг в основном создается с помощью циркуля, где заостренный конец служит центром. Перемещение по диаметру и радиусу окружности.
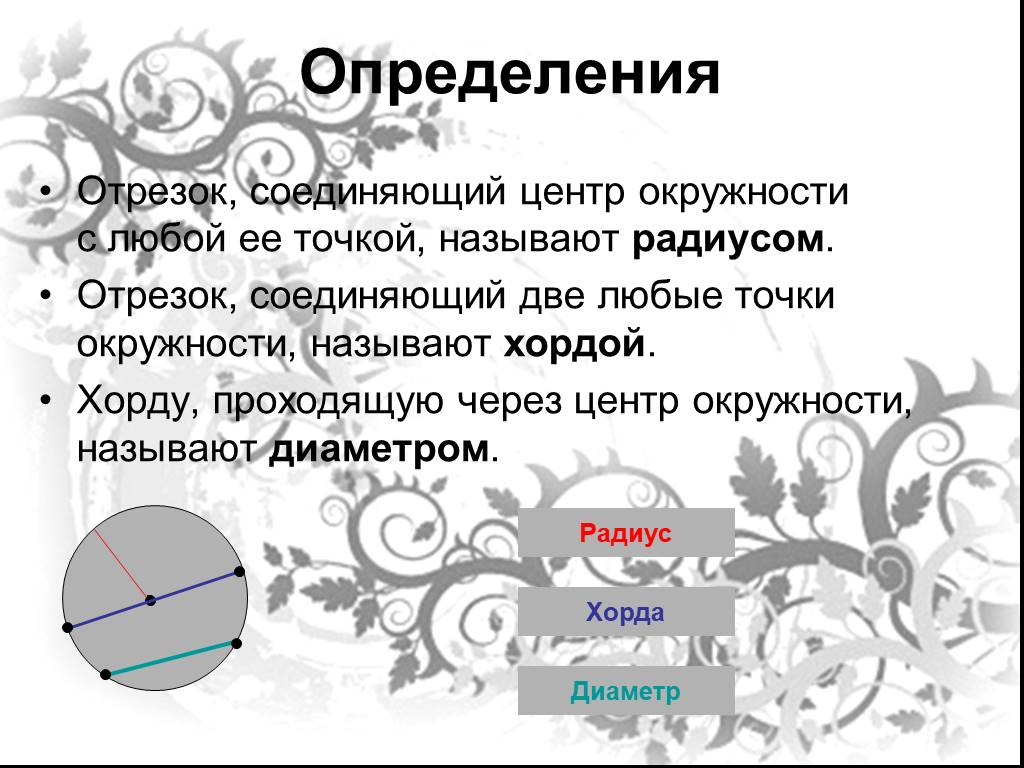Радиус — это расстояние от центра к окружности или границе круга. Диаметр проходит прямо через окружность, через центр и в два раза больше радиуса.
Хорда — еще одно измерение окружностей, которое часто сбивает с толку многих учащихся. Помните, что это не диаметр. Это прямолинейный отрезок, концы которого лежат на окружности. Бесконечное продолжение хорды — это секущая линия или просто секущая. В более общем смысле хорда — это отрезок, соединяющий две точки любой кривой, например эллипса. Эта коллекция рабочих листов похожа на изучение анатомии круга. Учащиеся будут строить круги и находить размеры уже построенных кругов. Они узнают, что радиус круга — это линия, проведенная из любой части круга к прямому центру круга. Диаметр — это длина линии, проведенной через окружность, которая проходит непосредственно через центр. Окружность — это расстояние по окружности, которое можно рассчитать, взяв произведение радиуса на два Пи. Эти рабочие листы объясняют, как найти радиус, диаметр, окружность, периметр и площадь кругов.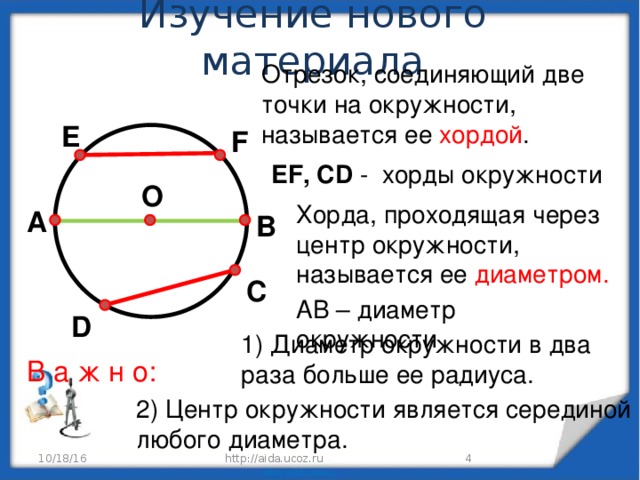
Используются различные типы единиц измерения, которые могут включать дроби или десятичные дроби.
Получите бесплатные рабочие листы в свой почтовый ящик!
Нажмите кнопки, чтобы распечатать каждый рабочий лист и связанный с ним ключ ответа.
В этом рабочем листе объясняется, как отметить диаметр, длину окружности и радиус окружности. Примерная задача решена. В этом листе рассматривается, как найти радиус окружности. Решается примерная задача и предлагаются две практические задачи.
Учащиеся заполняют таблицу, находя недостающий диаметр, длину окружности или радиус. Дано десять описаний.
Учащиеся найдут периметр каждой фигуры. Дано десять задач.
Учащиеся нарисуют указанные фигуры. Предлагается восемь задач.
Учащиеся найдут радиус каждой окружности. Предлагаются три задачи.
Учащиеся определят отмеченные части каждого круга.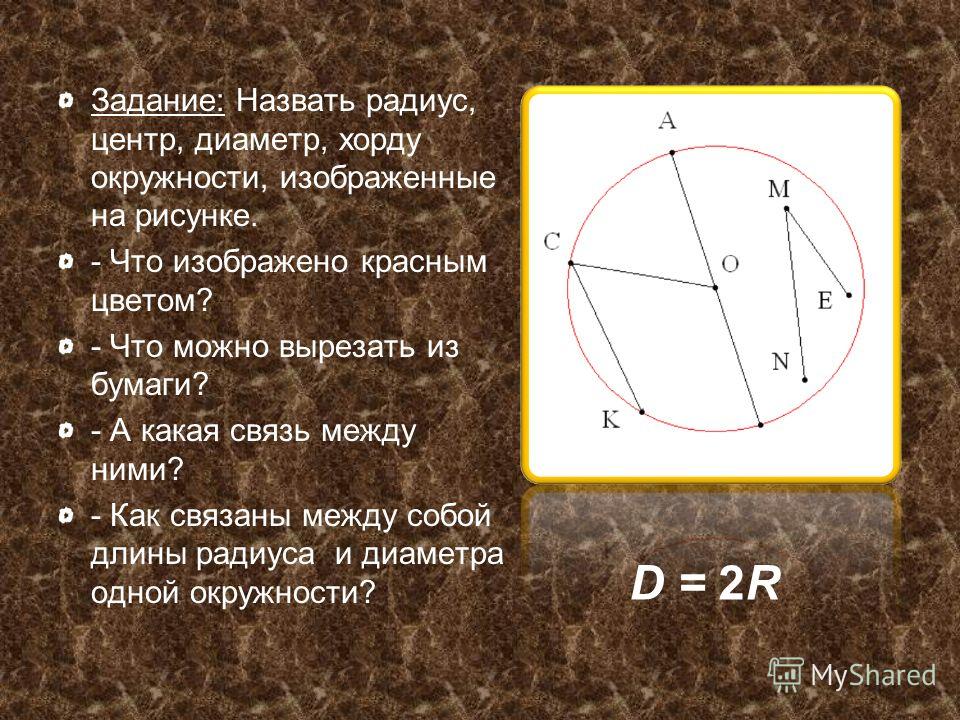
Дано десять задач.
Учащиеся определят указанную часть каждого круга. Дано десять задач.
Учащиеся должны определить, является ли отмеченный элемент центром, диаметром, хордой или радиусом окружности. Дано десять задач.
Учащиеся назовут указанную часть каждого круга. Дано десять задач.
Учащиеся анализируют отмеченную часть каждого круга и называют ее. Даны десять описаний углов.
Этот рабочий лист объясняет, как идентифицировать отмеченную часть круга. Примерная задача решена.
В этом листе рассматривается, как идентифицировать указанную часть круга. Решается примерная задача и предлагаются две практические задачи.
Учащиеся определят определенную часть каждого круга. Дано десять описаний.
Учащиеся называют указанные части каждого круга. Дано десять задач.
Учащиеся называют заданную линию, отрезок или точку. Предлагается восемь задач.
Учащиеся определят заданную линию, сегмент или точку.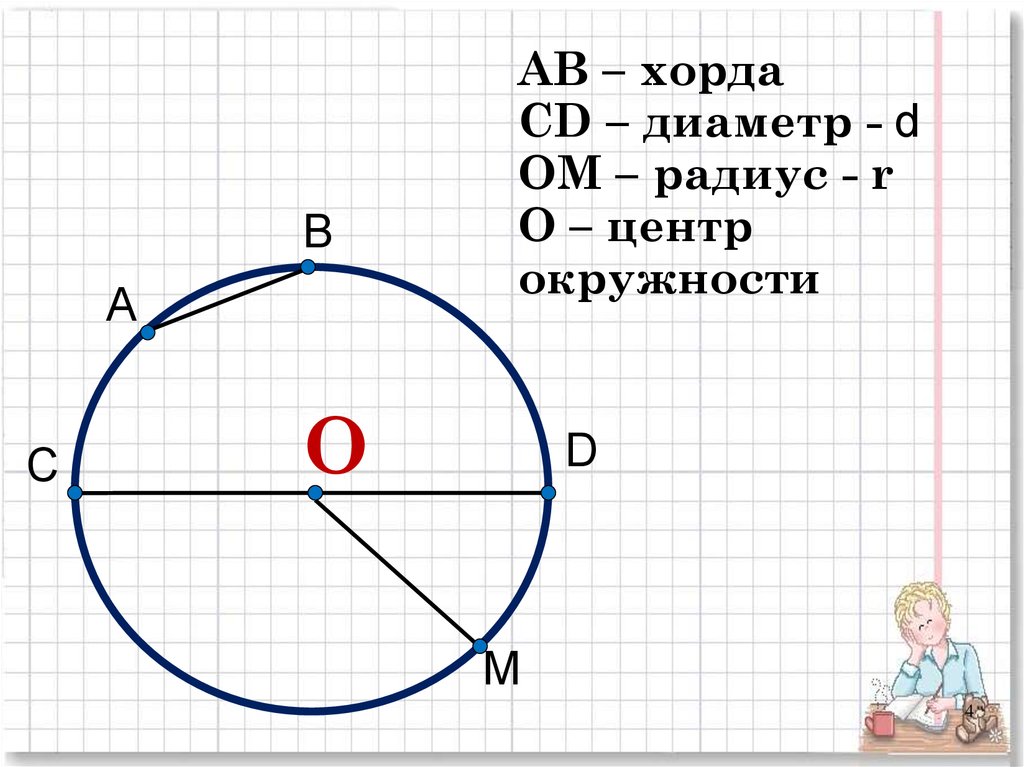
Предлагаются три задачи.
Этот рабочий лист объясняет, как идентифицировать основные части круга. Решается примерная задача и предлагаются две практические задачи.
Учащиеся будут классифицировать указанный сегмент или точку. Дано десять задач.
Предоставляется десять кругов. Учащиеся называют указанный отрезок или точку.
Пересмотрены основные части круга. Предлагаются шесть практических задач.
Учащиеся продемонстрируют свое умение называть основные части круга. Дано десять задач.
Учащиеся называют части каждого указанного круга. Предлагаются три задачи, а также место, где учащиеся могут скопировать правильный ответ, когда он будет дан.
Этот рабочий лист объясняет, как найти площадь и длину окружности. Примерная задача решена.
В этом рабочем листе рассматривается, как найти площадь и длину окружности. Решается примерная задача и предлагаются две практические задачи.
Учащиеся найдут площадь и длину окружности каждого круга.
Учащиеся найдут площадь и длину окружности предоставленных кругов. Дано десять задач.
Для каждой описанной формы учащиеся найдут площадь и длину окружности. Предлагается восемь задач.
Учащиеся найдут площадь и длину окружности. Предлагаются три задачи.
Этот рабочий лист объясняет, как найти радиус окружности. Примерная задача решена.
В этом рабочем листе рассматривается, как найти радиус окружности. Решается примерная задача и предлагаются две практические задачи.
Учащиеся найдут радиус окружности. Дано десять описаний.
Учащиеся найдут радиус каждой окружности. Дано десять задач.
Учащиеся начертят с помощью циркуля круг заданного радиуса. Предлагается восемь задач.
Учащиеся найдут радиус заданных окружностей. Предлагаются три задачи.
Радиус, диаметр и длина окружности
Автор:
Малкольм МакКинси
Факт проверен
Пол Маццола
Что такое круг?
В математике окружность – это множество всех компланарных точек, равноудаленных от данной точки. Эта заданная точка является центром круга и не лежит на круге. Окружность — это всего лишь набор точек (образующих изогнутую линию, возвращающуюся обратно на себя), которые находятся в одной плоскости и на одном и том же расстоянии от центральная точка , центр окружности.
Сам круг не является внутренним пространством, центральной точкой или пространством вне круга. Окружность — это линия, которая замыкается на себя.
Что такое кругБез определяющей центральной точки круг безымянный. Центр круга — это то, как называется круг, поэтому возьмите круг и поместите Точка I в середину, и теперь у нас есть Окружность I.
Радиус круга
Чтобы добраться от центральной точки до фактический круг, мы движемся по прямой линии, называемой радиус .
Радиус является мерой этого расстояния. Радиус круга является одним из способов измерения размера круга. Радиус всегда обозначается маленькой буквой r .
Вот отрезок IE с конечной точкой II в центре окружности и конечной точкой E на самой окружности:
Радиус окружностиФормула радиуса
Радиус равен 12\frac{1}{2} 21 диаметр. Вот формула радиуса:
Диаметр круга
Если у нас есть два радиуса вместе, они могут образовывать центральные углы или прямую линию, пересекающую окружность. Прямая линия, начинающаяся на окружности, проходящая через центр и снова достигающая окружности, имеет диаметр .
Вот диаметр для Круга 2 , построенный путем расширения радиуса IE в другом направлении до точки P :
Диаметр круга Вместо того, чтобы идентифицировать его как два отдельных радиуса (множественное число от радиуса) , мы можем просто вызвать PE диаметр круга. Это расстояние по всей окружности.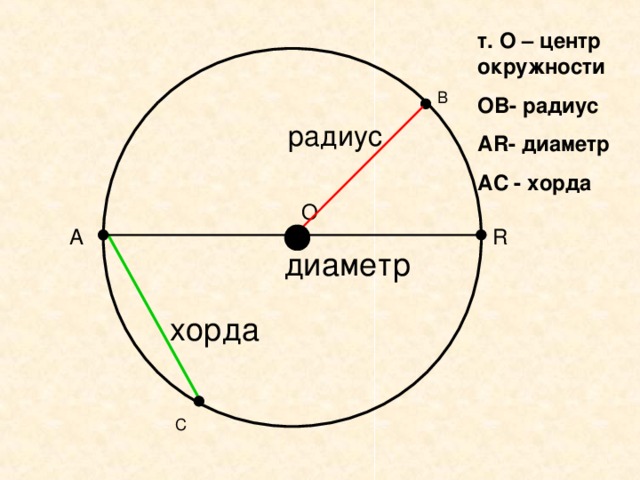
Диаметр круга всегда обозначается строчной буквой d .
Формула диаметра
Это означает, что диаметр в 2 раз больше радиуса окружности. Вот формула диаметра:
Круги появляются повсюду, как пицца за обедом!
Окружность круга
Для многоугольников периметр равен сумме длин их сторон. У кругов тоже есть периметр, но мы даем ему специальное слово: окружность (от латинского носить с собой) . Длина окружности – это расстояние по окружности.
Давайте посмотрим на отношение длины окружности к диаметру в этих кругах ниже. Вот Окружность 1 диаметром 1 метр и Окружность 2 диаметром 2 метра :
Окружность и отношение диаметраРасстояние по всей окружности Окружность 1 , это 3.1415926 метров .
Длина окружности Круга 2 составляет 6,2831852 метра .
Установите длину окружности каждого круга на его диаметр. Эти формы соотношений.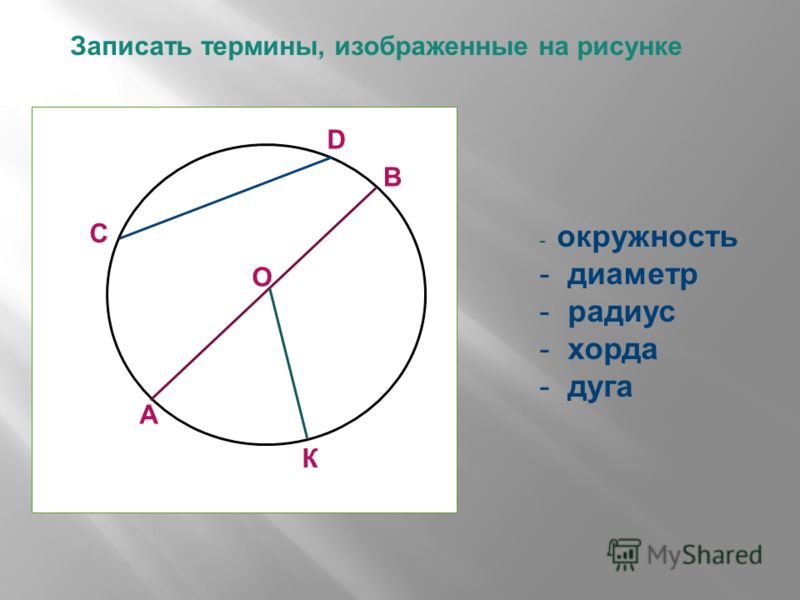
Вижу ничего?
Отношение длины окружности C к диаметру dd обоих кругов упрощают до одинакового значения, 3,1415926 !
Отношение длины окружности, C , любого круга к его диаметру dd равно всегда одному и тому же значению, 3,1415926 , названный с использованием греческой буквы pi (как в яблочном пироге), который выглядит так: π .
При использовании пи допускается округление до двух знаков после запятой.
Формула окружности
Теперь мы можем подставить π вместо этого длинного числа и вывести формулу длины окружности ( C ) и диаметра ( d ). Когда мы умножаем обе части формулы на ( d ), мы получаем:
Теперь мы можем найти длину окружности ( C) любого круга, если нам известен диаметр ( d) . Если у вас есть радиус, вы все равно можете найти длину окружности, так как радиус равен половине диаметра:
Как найти длину окружности
Давайте попробуем решить практическую задачу и найти длину окружности диаметром 20 .