Дифференциальное и интегральное исчисления для втузов, т.2
Дифференциальное и интегральное исчисления для втузов, т.2
ОглавлениеПРЕДИСЛОВИЕ К ДЕВЯТОМУ ИЗДАНИЮГЛАВА XIII.  (n) = f(x)§ 18. Некоторые типы дифференциальных уравнений второго порядка, приводимых к уравнениям первого порядка. Задача о второй космической скорости § 19. Графический метод интегрирования дифференциального уравнения второго порядка § 20. Линейные однородные уравнения. Определения и общие свойства § 21. Линейные однородные уравнения второго порядка с постоянными коэффициентами § 22. Линейные однородные уравнения n-го порядка с постоянными коэффициентами § 23. Неоднородные линейные уравнения второго порядка § 24. Неоднородные линейные уравнения второго порядка с постоянными коэффициентами § 25. Неоднородные линейные уравнения высших порядков § 26. Дифференциальное уравнение механических колебаний § 27. Свободные колебания. Векторное и комплексное изображение гармонических колебаний § 28. Вынужденные колебания § 29. Системы обыкновенных дифференциальных уравнений § 30. Системы линейных дифференциальных уравнений с постоянными коэффициентами § 31.  Понятие о теории устойчивости Ляпунова. Поведение траектории дифференциального уравнения в окрестности особой точки§ 32. Приближенное решение дифференциальных уравнений первого порядка методом Эйлера § 33. Разностный метод приближенного решения дифференциальных уравнений, основанный на применении формулы Тейлора.. Метод Адамса § 34. Приближенный метод интегрирования систем дифференциальных уравнений первого порядка Упражнения к главе XIII ГЛАВА XIV. КРАТНЫЕ ИНТЕГРАЛЫ § 2. Вычисление двойного интеграла § 3. Вычисление двойного интеграла (продолжение) § 4. Вычисление площадей и объемов с помощью двойных интегралов § 5. Двойной интеграл в полярных координатах § 6. Замена переменных в двойном интеграле (общий случай) § 9. Момент инерции площади плоской фигуры § 10. Координаты центра масс площади плоской фигуры § 11. Тройной интеграл § 12. Вычисление тройного интеграла § 13. Замена переменных в тройном интеграле § 14.  Момент инерции и координаты центра масс тела§ 15. Вычисление интегралов, зависящих от параметра Упражнения к главе XIV ГЛАВА XV. КРИВОЛИНЕЙНЫЕ ИНТЕГРАЛЫ И ИНТЕГРАЛЫ ПО ПОВЕРХНОСТИ § 2. Вычисление криволинейного интеграла § 3. Формула Грина § 4. Условия независимости криволинейного интеграла от пути интегрирования § 5. Поверхностный интеграл § 6. Вычисление поверхностного интеграла § 7. Формула Стокса § 9. Оператор Гамильтона. Некоторые его применения Упражнения к главе XV ГЛАВА XVI. РЯДЫ § 1. Ряд. Сумма ряда § 2. Необходимый признак сходимости ряда § 3. Сравнение рядов с положительными членами § 4. Признак Даламбера § 5. Признак Коши § 6. Интегральный признак сходимости ряда § 7. Знакочередующиеся ряды. Теорема Лейбница § 8. Знакопеременные ряды. Абсолютная и условная сходимость § 9. Функциональные ряды § 10. Мажорируемые ряды § 11. Непрерывность суммы ряда § 12. Интегрирование и дифференцирование рядов § 13.  Степенные ряды. Интервал сходимости§ 14. Дифференцирование степенных рядов § 15. Ряды по степеням x-a § 16. Ряды Тейлора и Маклорена § 17. Примеры разложения функций в ряды § 18. Формула Эйлера § 19. Биномиальный ряд § 20. Разложение функции ln(1+x) в степенной ряд. Вычисление логарифмов § 21. Вычисление определенных интегралов с помощью рядов § 22. Интегрирование дифференциальных уравнений с помощью рядов § 23. Уравнение Бесселя § 25. Степенные ряды с комплексной переменной § 26. Решение дифференциального уравнения первого порядка методом последовательных приближений (метод итераций) § 27. Доказательство существования решения дифференциального уравнения. Оценка погрешности при приближенном решении § 28. Теорема единственности решения дифференциального уравнения Упражнения к главе XVI ГЛАВА XVII. РЯДЫ ФУРЬЕ § 2. Примеры разложения функций в ряды Фурье § 3. Одно, замечание о разложении периодической функции в ряд Фурье § 4.  Ряды Фурье для четных и нечетных функций§ 5. Ряд Фурье для функции с периодом 2l § 6. О разложении непериодической функции в ряд Фурье § 7. Приближение в среднем заданной функции с помощью тригонометрического многочлена § 8. Интеграл Дирихле § 9. Сходимость ряда Фурье в данной точке § 10. Некоторые достаточные условия сходимости ряда Фурье § 11. Практический гармонический анализ § 12. Ряд Фурье в комплексной форме § 13. Интеграл Фурье § 14. Интеграл Фурье в комплексной форме § 15. Ряд Фурье по ортогональной системе функций § 16. Понятие о линейном функциональном пространстве. Аналогия между разложением функций в ряд Фурье и разложением векторов Упражнения к главе XVII ГЛАВА XVIII. УРАВНЕНИЯ МАТЕМАТИЧЕСКОЙ ФИЗИКИ § 1. Основные типы уравнений математической физики § 2. Вывод уравнения колебаний струны. Формулировка краевой задачи. Вывод уравнений электрических колебаний в проводах § 3. Решение уравнения колебаний струны методом разделения переменных (методом Фурье) § 4.  Уравнение распространения тепла в стержне. Формулировка краевой задачи§ 5. Распространение тепла в пространстве § 6. Решение первой краевой задачи для уравнения теплопроводности методом конечных разностей § 8. Задачи, приводящие к исследованию решений уравнения Лапласа. Формулировка краевых задач § 9. Уравнение Лапласа в цилиндрических координатах. Решение задачи Дирихле для кольца с постоянными значениями искомой функции на внутренней и внешней окружностях § 10. Решение задачи Дирихле для круга § 11. Решение задачи Дирихле методом конечных разностей Упражнения к главе XVIII ГЛАВА XIX. ОПЕРАЦИОННОЕ ИСЧИСЛЕНИЕ И НЕКОТОРЫЕ ЕГО ПРИЛОЖЕНИЯ § 1. Начальная функция и ее изображение § 2. Изображение функций … § 3. Изображение функции с измененным масштабом независимой переменной. Изображение функций sin at, cos at § 4. Свойство линейности изображения § 5. Теорема смещения § 6. Изображение функций … § 7.  Дифференцирование изображения§ 8. Изображение производных § 9. Таблица некоторых изображений § 10. Вспомогательное уравнение для данного дифференциального уравнения § 11. Теорема разложения § 12. Примеры решения дифференциальных уравнений и систем дифференциальных уравнений операционным методом § 13. Теорема свертывания § 14. Дифференциальные уравнения механических колебаний. Дифференциальные уравнения теории электрических цепей § 15. Решение дифференциального уравнения колебаний § 16. Исследование свободных колебаний § 17. Исследование механических и электрических колебаний в случае периодической внешней силы § 18. Решение уравнения колебаний в случае резонанса § 19. Теорема запаздывания § 20. Дельта-функция и ее изображение Упражнения к главе XIX ГЛАВА XX. ЭЛЕМЕНТЫ ТЕОРИИ ВЕРОЯТНОСТЕЙ И МАТЕМАТИЧЕСКОЙ СТАТИСТИКИ § 1. Случайное событие. Относительная частота случайного события. Вероятность события. Предмет теории вероятностей  Классическое определение вероятности и непосредственный подсчет вероятностей§ 3. Сложение вероятностей. Противоположные случайные события § 4. Умножение вероятностей независимых событий § 5. Зависимые события. Условная вероятность. Полная вероятность § 6. Вероятность гипотез. Формула Байеса § 7. Дискретная случайная величина. Закон распределения дискретной случайной величины § 8. Относительная частота и вероятность относительной частоты при повторных испытаниях § 9. Математическое ожидание дискретной случайной величины § 10. Дисперсия. Среднеквадратичное отклонение. Понятие о моментах § 11. Функции от случайных величин § 12. Непрерывная случайная величина. Плотность распределения непрерывной случайной величины. Вероятность попадания случайной величины в заданный интервал § 13. Функция распределения, или интегральный закон распределения. Закон равномерного распределения вероятностей § 14. Числовые характеристики непрерывной случайной величины § 15.  Нормальный закон распределения. Математическое ожидание нормального распределения§ 16. Дисперсия и среднеквадратичное отклонение случайной величины, подчиненной нормальному закону распределения § 17. Вероятность попадания значения случайной величины в заданный интервал. Функция Лапласа. Интегральная функция распределения для нормального закона § 18. Вероятное (срединное) отклонение или срединная ошибка § 19. Выражение нормального закона распределения через срединное отклонение. Приведенная функция Лапласа § 20. Правило трех сигм. Шкала вероятностей распределения ошибок § 21. Среднеарифметическая ошибка § 22. Мера точности. Соотношение между характеристиками распределения ошибок § 24. Нормальный закон распределения на плоскости § 25. Вероятность попадания двумерной случайной величины в прямоугольник со сторонами, параллельными главным осям рассеивания, при нормальном законе распределения § 26. Вероятность попадания двумерной случайной величины в эллипс рассеивания § 27.  Задачи математической статистики. Статистический материал§ 28. Статистический ряд. Гистограмма § 29. Определение подходящего значения измеряемой величины § 30. Определение параметров закона распределения. Теорема Ляпунова. Теорема Лапласа Упражнения к главе XX ГЛАВА XXI. МАТРИЦЫ. МАТРИЧНАЯ ЗАПИСЬ СИСТЕМ И РЕШЕНИЙ СИСТЕМ ЛИНЕЙНЫХ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ § 1. Линейные преобразования. Матрица § 2. Общие определения, связанные с понятием матрицы § 3. Обратное преобразование § 4. Действия над матрицами. Сложение матриц § 5. Преобразование вектора в другой вектор с помощью матрицы § 6. Обратная матрица § 7. Нахождение матрицы, обратной данной § 8. Матричная запись системы линейных уравнений § 9. Решение системы линейных уравнений матричным методом § 10. Ортогональные отображения. Ортогональные матрицы § 11. Собственный вектор линейного преобразования § 12. Матрица линейного преобразования, при котором базисные векторы являются собственными векторами § 13.  Преобразование матрицы линейного преобразования при переходе от одного базиса к другому§ 14. Квадратичные формы и их преобразования § 15. Ранг матрицы. Существование решений системы линейных уравнений § 16. Дифференцирование и интегрирование матриц § 17. Матричная запись системы дифференциальных уравнений и решений системы дифференциальных уравнений с постоянными коэффициентами § 18. Матричная запись линейного уравнения n-го порядка § 19. Решение систем линейных дифференциальных уравнений с переменными коэффициентами методом последовательных приближений с использованием матричной записи Упражнения к главе XXI ПРИЛОЖЕНИЯ |
18. Замена переменных в двойном интеграле
Пусть функции осуществляют взаимно однозначное непрерывно дифференцируемое отображение области P плоскости на область S плоскости . Тогда существует обратное непрерывно дифференцируемое отображение , области S на область P, если якобиан преобразования
=.
Величины U и V можно рассматривать как прямоугольные координаты для точек области P и в то же время как Криволинейные координаты точек области S. Точки плоскости Oxy, для которых одна из координат U и V сохраняет постоянное значение, образуют Координатную линию. Всего будет два семейства таких линий.
Теорема 14.3. Пусть есть дифференцируемое преобразование области P из плоскости на область S Из плоскости . Тогда справедливо равенство
(2.5)
Замечание. Равенство (2.5) сохраняет справедливость, когда условие взаимно однозначного соответствия между областями S и P нарушается в отдельных точках или вдоль отдельных линий.
Переход в двойном интеграле к полярным координатам
Формулы
(2.6)
Преобразуют полярные координаты точки в декартовы координаты этой точки и переводят область (или область ) на всю плоскость Oxy.
Обратное преобразование декартовых координат в полярные осуществляется по формулам:
Фиксируя в последних формулах И, получим координатные линии из разных семейств: окружность с центром в точке И луч, исходящий из точки .
Якобиан преобразования
И формула (2.5) принимает вид:
(2.7)
Рекомендация. К полярным координатам целесообразно переходить, когда в подынтегральное выражение или в уравнения границы области интегрирования входит комбинация .
В некоторых случаях при вычислении двойного интеграла удобно перейти от декартовых координат к Эллиптическим полярным Координатам по формулам
, (2.8)
— постоянные, . Тогда
, (2.9)
Пример 6. Записать в полярной системе координат область S , заданную в декартовой системе координат неравенством (круг радиуса R с центром в точке ).
Ñ Перейдем от декартовых координат X, Y к полярным по формулам , . Подставим X и Y в исходное неравенство, получим: или . На координату j дополнительных ограничений не накладывается, поэтому (или ).
В полярной системе координат круг записывается неравенствами: . #
Пример 7. Записать в полярной системе координат область S — часть круга, ограниченную линиями , , (), — постоянные, .
Ñ Изобразим область S (рис. 14.9). Запишем заданные линии в полярных координатах, которые связаны с декартовыми формулами , : 1)Þ ;
2) Þ, ;
3)Þ.
Область переходит в область
.
В полярной системе координат заданная область определяется системой неравенств: . #
|
Пример 8. Вычислить двойной интеграл , S — множество точек, удовлетворяющих неравенству .
Ñ Границей области является линия или — окружность радиуса 2 с центром в точке (Рис. 14.10).
Рис. 14.10
Наличие в уравнении границы комбинации наводит на мысль, что для вычисления двойного интеграла удобно перейти к полярным координатам по формулам , , . Уравнение границы переходит в уравнение или . Отсюда r=0 (соответствует полюсу O) и — уравнение окружности. Так как всегда (по смыслу r), то из следует , отсюда получаем (этот же результат можно усмотреть из рисунка).
Итак, в полярных координатах область интегрирования есть . Тогда по формуле (2.7)
. #
Пример 9. Вычислить , где .
Ñ Область D ограничена линиями: – эллипс с полуосями A и B, – эллипс с полуосями и , Y=0 – прямая (ось Ox), – прямая (рис. 14.11).
Рис.14.11
Анализ границы области указывает на целесообразность перехода к Эллиптическим полярным координатам по формулам (2.8), (2.9): , . Уравнения границы области в координатах будут: 1), 2) , 3) ,
4) . Итак, область интегрирования в координатах есть
. Тогда
. #
Задачи для самостоятельного решения
Перейти в двойном интеграле к полярным координатам и расставить пределы интегрирования в порядке: внешнее – по j, внутреннее — по r:
27. D – область, ограниченная окружностями , и прямыми , .
28. D — область, являющаяся общей частью двух кругов и .
29. D — меньший из двух сегментов, на которые прямая рассекает круг .
30. D — внутренняя часть правой петли лемнискаты Бернулли .
31. D:.
32. D: .Указание. Перейти к эллиптическим полярным координатам.
33. D — область, ограниченная линией . Указание. Перейти к эллиптическим полярным координатам.
34. . 35. . 36. .
С помощью перехода к полярным координатам вычислить интегралы:
37. . 38. .
39. . 40. , D — часть кольца ,
, . 41. .
Вычислить, перейдя к эллиптическим полярным координатам, интегралы:
42. .
43. — область, ограниченная линией .
| < Предыдущая | Следующая > |
|---|
Двойные интегралы в полярных координатах · Исчисление
Двойные интегралы в полярных координатах · Исчисление- Распознавание формата двойного интеграла по полярной прямоугольной области.
- Вычисление двойного интеграла в полярных координатах с помощью повторного интеграла.
- Распознать формат двойного интеграла по общей полярной области.
- Используйте двойные интегралы в полярных координатах для вычисления площадей и объемов.
Двойные интегралы иногда гораздо легче вычислить, если мы заменим прямоугольные координаты на полярные. Однако, прежде чем мы опишем, как сделать это изменение, нам нужно установить понятие двойного интеграла в полярной прямоугольной области.
Полярные прямоугольные области интегрирования
Когда мы определили двойной интеграл для непрерывной функции в прямоугольных координатах, скажем, g
по региону R
в ху
-самолет — мы разделили R
на подпрямоугольники со сторонами, параллельными осям координат. Эти стороны имеют константу x
— значения и/или константа y
-значения. В полярных координатах фигура, с которой мы работаем, представляет собой полярный прямоугольник , стороны которого имеют константу r
— значения и/или константа θ
-значения.
Это означает, что мы можем описать полярный прямоугольник, как в [link](a), с R={(r,θ)\|a≤r≤b,α≤θ≤β}.
В этом разделе мы рассматриваем интегрирование по полярным прямоугольникам. Рассмотрим функцию f(r,θ)
над полярным прямоугольником R.
Разделим интервал [a,b] на
в м
подинтервалов [ri−1,ri]
длины Δr=(b−a)/м
и разделим интервал [α,β] на
в п
подинтервалов [θi−1,θi]
ширины Δθ=(β−α)/n.
Это означает, что круги r=ri
и лучи θ=θi
для 1≤i≤m
и 1≤j≤n
разделить полярный прямоугольник R
на меньшие полярные подпрямоугольники Rij
([ссылка](б)).
Как и прежде, нам нужно найти площадь ΔA
полярного подпрямоугольника Rij
и «полярный» объем тонкого ящика над Rij.
Напомним, что в окружности радиуса r
длина с
дуги, опирающейся на центральный угол θ
радиан равно s=rθ.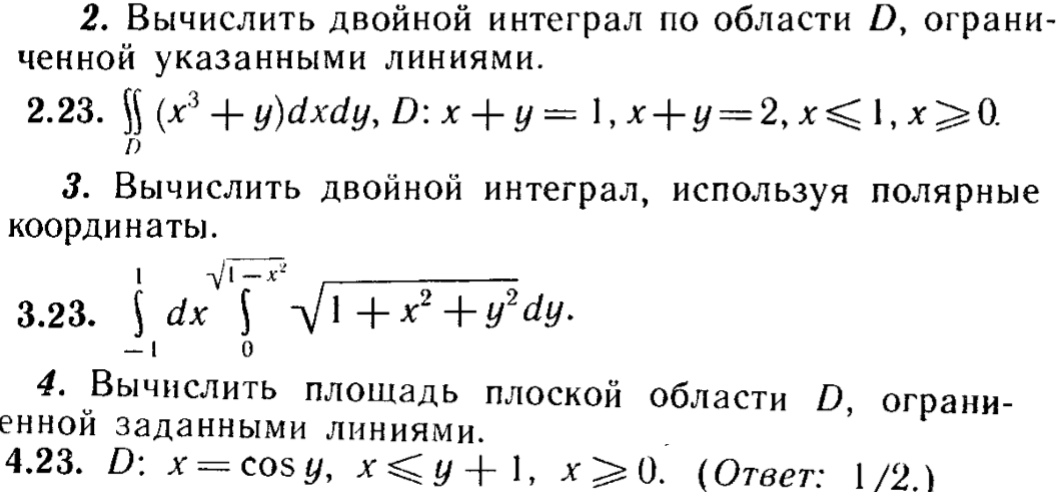
Обратите внимание, что полярный прямоугольник Rij
очень похож на трапецию с параллельными сторонами ri−1Δθ
и riΔθ
и шириной Δr.
Отсюда площадь полярного подпрямоугольника Rij
это
ΔA=12Δr(ri−1Δθ+r1Δθ).
Упрощая и допуская rij*=12(ri−1+ri),
имеем ΔA=rij*ΔrΔθ.
Следовательно, полярный объем тонкого ящика над Rij
([ссылка]) это
f(rij*,θij*)ΔA=f(rij*,θij*)rij*ΔrΔθ.
Используя ту же идею для всех подпрямоугольников и суммируя объемы прямоугольных ящиков, мы получаем двойную сумму Римана как
∑i=1m∑j=1nf(rij*,θij*)rij*ΔrΔθ.
Как мы видели ранее, мы получаем лучшее приближение к полярному объему твердого тела над областью R
когда мы позволим м
и №
становятся больше. Следовательно, мы определяем полярный объем как предел двойной суммы Римана,
V=limm,n→∞∑i=1m∑j=1nf(rij*,θij*)rij*ΔrΔθ.
Это становится выражением для двойного интеграла.
Определение
Двойной интеграл функции f(r,θ)
над полярной прямоугольной областью R
в плоскости rθ
определяется как )ΔA=limm,n→∞∑i=1m∑j=1nf(rij*,θij*)rij*ΔrΔθ.
Опять же, как и в случае с двойными интегралами по прямоугольным областям, двойной интеграл по полярной прямоугольной области может быть выражен как повторный интеграл в полярных координатах. Следовательно,
∬Rf(r,θ)dA=∬Rf(r,θ)rdrdθ=∫θ=αθ=β∫r=ar=bf(r,θ)rdrdθ.
Обратите внимание, что выражение для dA
заменен на rdrdθ
при работе в полярных координатах. Другой способ взглянуть на двойной полярный интеграл — изменить двойной интеграл в прямоугольных координатах подстановкой. Когда функция f
дается через х
и у,
с использованием x=rcosθ, y=rsinθ и dA=rdrdθ
меняет его на
∬Rf(x,y)dA=∬Rf(rcosθ,rsinθ)rdrdθ.
Обратите внимание, что все свойства, перечисленные в разделе Двойные интегралы по прямоугольным областям для двойного интеграла в прямоугольных координатах, справедливы и для двойного интеграла в полярных координатах, так что мы можем использовать их без колебаний.
Создание эскиза полярной прямоугольной области
Создание эскиза полярной прямоугольной области R={(r,θ)\|1≤r≤3,0≤θ≤π}.
Как видно из [ссылка], r=1
и r=3
— окружности радиусом 1 и 3
и 0≤θ≤π
покрывают всю верхнюю половину плоскости. Следовательно, область R
выглядит как полукруглая полоса.
Теперь, когда мы нарисовали полярную прямоугольную область, давайте продемонстрируем, как вычислить двойной интеграл по этой области, используя полярные координаты.
Вычисление двойного интеграла по полярной прямоугольной области
Вычисление интеграла ∬R3xdA
по области R={(r,θ)\|1≤r≤2,0≤θ≤π}.
Сначала нарисуем фигуру, похожую на [ссылка], но с внешним радиусом 2.
Из рисунка видно, что у нас есть правильные пределы интегрирования.=∫θ=0θ=πcosθ[r3\|r=1r=2]dθПроинтегрируем сначала по tor.=∫θ=0θ=π7cosθdθ=7sinθ\|θ=0θ=π=0.
Нарисуйте область R={(r,θ)\|1≤r≤2,−π2≤θ≤π2},
и вычислите ∬RxdA.
143
Подсказка
Следуйте инструкциям в [ссылка].
Вычисление двойного интеграла путем преобразования прямоугольных координат
Вычисление интеграла ∬R(1−x2−y2)dA
, где R
— единичная окружность на плоскости xy
.
Область R
представляет собой единичную окружность, поэтому мы можем описать ее как R={(r,θ)\|0≤r≤1,0≤θ≤2π}.
Используя преобразование x=rcosθ,y=rsinθ,
и dA=rdrdθ,
имеем
∬R(1−x2−y2)dA=∫02π∫01(1−r2)rdrdθ=∫02π∫01(r−r3)drdθ=∫02π[r22 −r44]01dθ=∫02π14dθ=π2.
Вычисление двойного интеграла путем преобразования прямоугольных координат
Вычисление интеграла ∬R(x+y)dA
, где R={(x,y)\|1≤x2+y2≤4,x≤0}.
Мы видим, что R
представляет собой кольцевую область, которая может быть преобразована в полярные координаты и описана как R={(r,θ)\|1≤r≤2,π2≤θ≤3π2}
(см. следующий график).
Отсюда, используя преобразование x=rcosθ,y=rsinθ,
и dA=rdrdθ,
, получаем
∬R(x+y)dA=∫θ=π/2θ=3π/2 ∫ r=1r=2(rcosθ+rsinθ)rdrdθ=(∫r=1r=2r2dr)(∫π/23π/2(cosθ+sinθ)dθ)=[r33]12[sinθ−cosθ]\|π/23π/ 2=-143.
Вычислить интеграл ∬R(4−x2−y2)dA
, где R
— окружность радиусом 2
на плоскости xy
.
8π
Подсказка
Выполните действия, описанные в предыдущем примере.
Общие полярные регионы интеграции
Чтобы вычислить двойной интеграл непрерывной функции с помощью повторных интегралов по общим полярным областям, мы рассмотрим два типа областей, аналогичных типам I и II, как обсуждалось для прямоугольных координат в Двойных интегралах по общим областям. Чаще всего полярные уравнения записывают как r=f(θ)
., чем θ=f(r),
поэтому мы описываем общую полярную область как R={(r,θ)\|α≤θ≤β,h2(θ)≤r≤h3(θ)}
(см. следующий рисунок).
Двойные интегралы по основным полярным областям
Если f(r,θ)
непрерывна в общей полярной области D
, как описано выше, то
∬Df(r,θ)rdrdθ=∫θ=αθ=β ∫r=h2(θ)r=h3(θ)f(r,θ)rdrdθ
Вычисление двойного интеграла по общей полярной области
Вычисление интеграла ∬Dr2sinθrdrdθ
где D
— область, ограниченная полярной осью и верхней половиной кардиоиды r=1+cosθ.
Мы можем описать область D
как {(r, θ)\|0≤θ≤π,0≤r≤1+cosθ}
, как показано на следующем рисунке.
Отсюда имеем
∬Dr2sinθrdrdθ=∫θ=0θ=π∫r=0r=1+cosθ(r2sinθ)rdrdθ=14∫θ=0θ=π[r4]r=0r=1+cosθ sinθdθ= 14∫θ=0θ=π(1+cosθ)4sinθdθ=−14[(1+cosθ)55]0π=85.
Вычислить интеграл
∬Dr2sin22θrdrdθ, где D={(r,θ)\|0≤θ≤π,0≤r≤2cos2θ}.
π/8
Подсказка
Нарисуйте график области и выполните действия, описанные в предыдущем примере.
Полярные районы и тома
Как в прямоугольных координатах, если твердое S
ограничен поверхностью z=f(r,θ),
, а также поверхностями r=a,r=b,θ=α,
и θ=β,
мы можем найти объем V
S
двойным интегрированием, как
V=∬Rf(r,θ)rdrdθ=∫θ=αθ=β∫r=ar=bf(r,θ)rdrdθ.
Если основание твердого тела можно описать как D={(r,θ)\|α≤θ≤β,h2(θ)≤r≤h3(θ)},
, то двойной интеграл объема становится равным
. V=∬Df(r,θ)rdrdθ=∫θ=αθ=β∫r=h2(θ)r=h3(θ)f(r,θ)rdrdθ.
Проиллюстрируем эту мысль несколькими примерами.
Нахождение объема с помощью двойного интеграла
Найдите объем твердого тела, лежащего под параболоидом z=1−x2−y2
и над единичной окружностью на плоскости xy
(см. следующий рисунок).
Методом двойного интегрирования видим, что объем есть повторный интеграл вида ∬R(1−x2−y2)dA
, где R={(r,θ)\|0≤r ≤1,0≤θ≤2π}.
Это интегрирование было показано ранее в [ссылка], поэтому объем равен π2
кубических единиц.
Нахождение объема с помощью двойного интегрирования
Найти объем тела, лежащего под параболоидом z=4−x2−y2
и над диском (x−1)2+y2=1
на xy
-самолет. См. параболоид в [ссылка], пересекающий цилиндр (x−1)2+y2=1
над плоскостью xy
.
Сначала замените диск (x−1)2+y2=1
в полярные координаты. Расширяя квадратный член, мы имеем x2−2x+1+y2=1.
Затем упростите, чтобы получить x2+y2=2x,
, что в полярных координатах становится r2=2rcosθ
, а затем либо r=0
, либо r=2cosθ.
Аналогично уравнение параболоида меняется на z=4−r2.
Следовательно, мы можем описать круг (x−1)2+y2=1
на плоскости xy
как область
D={(r,θ)\|0≤θ≤π,0≤ r≤2cosθ}.
Отсюда объем твердого тела, ограниченного сверху параболоидом z=4−x2−y2
и ниже на r=2cosθ
равно
V=∬Df(r,θ)rdrdθ=∫θ=0θ=π∫r=0r=2cosθ(4−r2)rdrdθ=∫θ=0θ=π[ 4r22−r44\|02cosθ]dθ=∫0π[8cos2θ−4cos2θ]dθ=[52θ+52sinθcosθ−sinθcos3θ]0π=52π.
Обратите внимание, что в следующем примере интегрирование не всегда просто с полярными координатами. Сложность интеграции зависит от функции, а также от региона, по которому нам нужно выполнить интеграцию. Если область имеет более естественное выражение в полярных координатах или если f
имеет более простую первообразную в полярных координатах, тогда уместно изменение полярных координат; в противном случае используйте прямоугольные координаты.
. Нахождение объема с помощью двойного интеграла. =2
в плоскости xy
([ссылка]).
Сначала исследуем область, по которой нам нужно установить двойной интеграл и сопутствующий ему параболоид.
Область D
есть {(x,y)\|0≤x≤1,x≤y≤2−x}.
Преобразование строк y=x,x=0,
и x+y=2
в плоскости xy
к функциям r
и θ,
имеем θ=π/4,
θ=π/2,
9001 2 и г = 2 /(cosθ+sinθ),соответственно. Нарисовав область на xy
-плоскости, мы видим, что она имеет вид D={(r,θ)\|π/4≤θ≤π/2,0≤r≤2/(cosθ+sinθ)}.
Теперь преобразование уравнения поверхности дает z=x2+y2=r2.
Следовательно, объем твердого тела определяется двойным интегралом
V=∬Df(r,θ)rdrdθ=∫θ=π/4θ=π/2∫r=0r=2/(cosθ+sinθ) r2rdrdθ=∫π/4π/2[r44]02/(cosθ+sinθ)dθ=14∫π/4π/2(2cosθ+sinθ)4dθ=164∫π/4π/2(1cosθ+sinθ)4dθ=4∫ π/4π/2(1cosθ+sinθ)4dθ.
Как видите, этот интеграл очень сложен. Таким образом, мы можем вместо этого вычислить этот двойной интеграл в прямоугольных координатах как
V=∫01∫x2−x(x2+y2)dydx.
Оценка дает
V=∫01∫x2−x(x2+y2)dydx=∫01[x2y+y33]\|x2−xdx=∫0183−4x+4×2−8x33dx=[8×3−2×2+4×33− 2×43]\|01=43.
Чтобы ответить на вопрос, как находятся формулы объемов различных стандартных тел, таких как сфера, конус или цилиндр, мы хотим продемонстрировать пример и найти объем произвольного конуса.
Нахождение объема с помощью двойного интеграла
Используйте полярные координаты, чтобы найти объем внутри конуса z=2−x2+y2
и над плоскостью xy.
Область D
для интегрирования является основанием конуса, который выглядит как окружность на плоскости xy
(см. следующий рисунок).
Находим уравнение окружности, полагая z=0:
0=2−x2+y22=x2+y2x2+y2=4.
Это означает, что радиус окружности равен 2,
, поэтому для интегрирования мы имеем 0≤θ≤2π
и 0≤r≤2.
Подставив x=rcosθ
и y=rsinθ
в уравнение z=2−x2+y2
, мы получим z=2−r.
Следовательно, объем конуса равен
∫θ=0θ=2π∫r=0r=2(2−r)rdrdθ=2π43=8π3
кубических единиц.
Анализ
Заметим, что если бы нам нужно было найти объем произвольного конуса с радиусом a
единиц и высотой h
единиц, то уравнение конуса было бы z=h−hax2+y2.
Мы все еще можем использовать [ссылка] и установить интеграл как ∫θ=0θ=2π∫r=0r=a(h−har)rdrdθ.
Вычисляя интеграл, получаем 13πa2h.
Используйте полярные координаты, чтобы найти повторный интеграл для нахождения объема твердого тела, заключенного в параболоиды z=x2+y2
и z=16−x2−y2.
V=∫02π∫022(16−2r2)rdrdθ=64π
кубических единиц
Подсказка
Наброски графиков могут помочь.
Как и в случае с прямоугольными координатами, мы также можем использовать полярные координаты для нахождения площадей определенных регионов с помощью двойного интеграла. Как и прежде, нам нужно понять область, площадь которой мы хотим вычислить. Набросок графика и определение области может помочь понять пределы интегрирования.
В общем случае формула площади при двойном интегрировании будет иметь вид 9.0013
ПлощадьA=∫αβ∫h2(θ)h3(θ)1rdrdθ.
Нахождение площади с помощью двойного интеграла в полярных координатах
Оценить площадь, ограниченную кривой r=cos4θ.
Набросав график функции r=cos4θ
, мы увидим, что это полярная роза с восемью лепестками (см. следующий рисунок).
Используя симметрию , мы видим, что нам нужно найти площадь одного лепестка, а затем умножить ее на 8.
Обратите внимание, что значения θ
, для которых график проходит через начало координат, являются нулями функции cos4θ,
и являются нечетными кратными π/8.
Таким образом, один из лепестков соответствует значениям θ
в интервале [−π/8,π/8].
Следовательно, площадь, ограниченная кривой r=cos4θ
, равна
A=8∫θ=−π/8θ=π/8∫r=0r=cos4θ1rdrdθ=8∫−π/8π/8[12r2\ |0cos4θ]dθ=8∫−π/8π/812cos24θdθ=8[14θ+116sin4θcos4θ\|−π/8π/8]=8[π16]=π2.
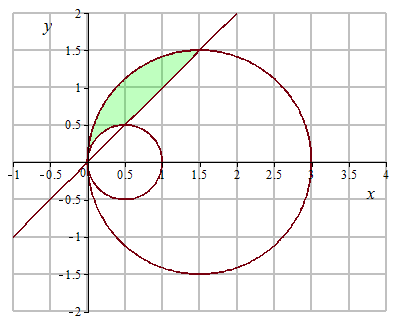
Поиск площади между двумя полярными кривыми
Найдите площадь окружности r=3cosθ
и кардиоиды r=1+cosθ.
В первую очередь нарисуйте графы региона ([ссылка]).
Из симметрии графа видно, что нам нужно найти точки пересечения. Уравнивание двух уравнений дает
3cosθ=1+cosθ.
Одна из точек пересечения θ=π/3.
Область над полярной осью состоит из двух частей, одна часть определяется кардиоидой от θ=0
до θ=π/3
, а другая часть, обозначенная окружностью, от θ=π/3
до θ=π/2.
По симметрии общая площадь в два раза больше площади над полярной осью. Таким образом, имеем
A=2[∫θ=0θ=π/3∫r=0r=1+cosθ1rdrdθ+∫θ=π/3θ=π/2∫r=0r=3cosθ1rdrdθ].
Оценивая каждую часть отдельно, получаем, что площадь равна
A=2(14π+9163+38π−9163)=2(58π)=54πквадратных единиц.
Найдите площадь, заключенную внутри кардиоиды r=3−3sinθ
и вне кардиоиды r=1+sinθ.
A=2∫−π/2π/6∫1+sinθ3−3sinθrdrdθ=8π+93
Подсказка
Нарисуйте график и найдите точки пересечения.
Вычисление неправильного двойного интеграла в полярных координатах
Вычисление интеграла ∬R2e−10(x2+y2)dxdy.
Это неправильный интеграл, потому что мы интегрируем по неограниченной области R2.
В полярных координатах всю плоскость R2
можно рассматривать как 0≤θ≤2π,
0≤r≤∞.
Используя замены переменных прямоугольных координат на полярные координаты, мы имеем
∬R2e−10(x2+y2)dxdy=∫θ=0θ=2π∫r=0r=∞e−10r2rdrdθ=∫θ=0θ=2π(lima→∞∫r=0r=ae−10r2rdr)dθ= (∫θ=0θ=2πdθ)(лима→∞∫r=0r=ae−10r2rdr)=2π(лима→∞∫r=0r=ae−10r2rdr)=2πlima→∞(−120)(e−10r2\| 0a)=2π(−120)лима→∞(e−10a2−1)=π10.
Вычислить интеграл ∬R2e−4(x2+y2)dxdy.
π4
Подсказка
Преобразование в полярную систему координат.
Ключевые понятия
- Чтобы применить двойной интеграл к ситуации с круговой симметрией, часто удобно использовать двойной интеграл в полярных координатах. Мы можем применить эти двойные интегралы к полярной прямоугольной области или общей полярной области, используя повторный интеграл, аналогичный тем, которые используются с прямоугольными двойными интегралами.
- Район
dA
в полярных координатах становится
rdrdθ. - Использование
х=rcosθ,y=rsinθ,
и
dA=rdrdθдля преобразования интеграла в прямоугольных координатах в интеграл в полярных координатах.
- Использование
г2=х2+у2
и
θ=tan-1(yx)для преобразования интеграла в полярных координатах в интеграл в прямоугольных координатах, если это необходимо.
- Чтобы найти объем в полярных координатах, ограниченный сверху поверхностью
z=f(r,θ)
над регионом на
xy— плоскость, используйте двойной интеграл в полярных координатах.
Мы можем применить эти двойные интегралы к полярной прямоугольной области или общей полярной области, используя повторный интеграл, аналогичный тем, которые используются с прямоугольными двойными интегралами.Ключевые уравнения
В следующих упражнениях выразите область D
в полярных координатах.
D
— это область диска радиусом 2
с центром в начале координат, которая находится в первом квадранте.
D
— это область между окружностями радиусом 4
и радиусом 5
с центром в начале координат, лежащим во втором квадранте.
D={(r,θ)\|4≤r≤5,π2≤θ≤π}
D
— область, ограниченная осью y
и x=1−y2.
D
— область, ограниченная осью x
и y=2−x2.
D={(r,θ)\|0≤r≤2,0≤θ≤π}
Д={(х,у)\|х2+у2≤4х}
D={(x,y)\|x2+y2≤4y}
D={(r,θ)\|0≤r≤4sinθ,0≤θ≤π}
В следующих упражнениях график полярной прямоугольной области D
дано. Экспресс Д
в полярных координатах.
jpg)
D={ (r,θ)\|3≤r≤5,π4≤θ≤π2}
D ={(r,θ)\|3≤r≤5,3π4≤θ≤5π4}
На следующем графике область D
расположена ниже y=x
и ограничена точками x=1,x=5,
и y=0.
На следующем графике область D
ограничена y=x
и y=x2.
D={(r,θ)\|0≤r≤tanθsecθ,0≤θ≤π4}
В следующих упражнениях вычислите двойной интеграл ∬Rf(x,y)dA
над полярной прямоугольной областью D.
f(x,y)=x2+y2,D={(r,θ)\|3≤r≤5,0≤θ≤2π}
f(x,y)=x+y,D={(r,θ)\|3≤r≤5,0≤θ≤2π}
0
f(x,y)=x2+xy,D={(r,θ)\|1≤r≤2,π≤θ≤2π}
f(x,y)=x4+y4,D={(r,θ)\|1≤r≤2,3π2≤θ≤2π}
63π16
f(x,y)=x2+y23,
, где D={(r,θ)\|0≤r≤1,π2≤θ≤π}.
f(x,y)=x4+2x2y2+y4,
, где D={(r,θ)\|3≤r≤4,π3≤θ≤2π3}.
3367π18
f(x,y)=sin(arctanyx),
, где D={(r,θ)\|1≤r≤2,π6≤θ≤π3}
f(x,y)=arctan(yx),
, где D={(r,θ)\|2≤r≤3,π4≤θ≤π3}
35π2576
∬Dex2+y2[1+2arctan(yx)]dA,D={(r,θ)\|1≤r≤2,π6≤θ≤π3}
∬D(ex2+y2+x4+2x2y2+y4)arctan(yx)dA,D={(r,θ)\|1≤r≤2,π4≤θ≤π3}
7576π2(21−e+ д4)
В следующих упражнениях интегралы были преобразованы в полярные координаты. Убедитесь, что тождества верны, и выберите самый простой способ вычисления интегралов в прямоугольных или полярных координатах.
∫12∫0x(x2+y2)dydx=∫0π4∫secθ2secθr3drdθ
∫23∫0xxx2+y2dydx=∫0π/4∫0tanθsecθrcosθdrdθ
54ln(3+22)
∫01∫x2x1x2+y2dydx=∫0π/4∫0tanθsecθdrdθ
∫01∫x2xyx2+y2dydx=∫0π/4∫0tanθsecθrsinθdrdθ
16(2−2)
В следующих упражнениях преобразуйте интегралы в полярные координаты и оцените их.
∫03∫09−y2(x2+y2)dxdy
∫02∫−4−y24−y2(x2+y2)2dxdy
∫0π∫02r5drdθ=32π3
∫01∫01−x2(x+y)dydx
∫04∫−16−x216−x2sin(x2+y2)dydx
∫−π/2π/2∫04rsin(r2)drdθ=πsin28
Вычислить интеграл ∬DrdA
, где D
— область, ограниченная полярной осью и верхней половиной кардиоиды r=1+cosθ.
Найти площадь области D
, ограниченной полярной осью и верхней половиной кардиоиды r=1+cosθ.
3π4
Вычислить интеграл ∬DrdA,
где D
— область, ограниченная частью четырехлепестковой розы r=sin2θ
расположен в первом квадранте (см. следующий рисунок).
Найдите общую площадь области, ограниченной четырехлепестковой розой r=sin2θ
(см. рисунок в предыдущем упражнении).
№2
Найдите площадь области D,
, которая является областью, ограниченной y=4−x2,
x=3,x=2,
и y=0.
Найдите площадь области D,
которая является областью внутри диска x2+y2≤4
и правее строки x=1.
13(4π−33)
Определить среднее значение функции f(x,y)=x2+y2
по области D
, ограниченной полярной кривой r=cos2θ,
, где −π4≤θ≤π4
(см. график).
Определить среднее значение функции f(x,y)=x2+y2
по области D
, ограниченной полярной кривой r=3sin2θ,
, где 0≤θ≤π2
(см. следующий график ).
163π
Найти объем тела, расположенного в первом октанте и ограниченного параболоидом z=1−4×2−4y2
и плоскостями x=0,y=0,
и z=0.
Найдите объем твердого тела, ограниченного параболоидом z=2−9×2−9y2
и плоскостью z=1.
№18
- Найти объем твердого тела
S1
ограничен цилиндром
x2+y2=1и плоскости
г=0и
г=1. - Найдите объем твердого тела
S2
снаружи двойного конуса
z2=x2+y2,внутри цилиндра
x2+y2=1,и выше плоскости
г=0. - Найдите объем твердого тела внутри конуса
z2=x2+y2
и ниже плоскости
z=1путем вычитания объемов твердых тел
S1и
С2.
- Найти объем твердого тела
S1
внутри единичной сферы
x2+y2+z2=1и над плоскостью
г=0. - Найдите объем твердого тела
S2
внутри двойного конуса
(z−1)2=x2+y2и над плоскостью
г=0. - Найдите объем твердого тела вне двойного конуса
(z−1)2=x2+y2
и внутри сферы
х2+у2+z2=1.
а. 2π3;
б. π2;
в. №6
В следующих двух упражнениях рассмотрим сферическое кольцо, представляющее собой сферу с цилиндрическим отверстием, прорезанным так, что ось цилиндра проходит через центр сферы (см. следующий рисунок).
Если сфера имеет радиус 4
, а цилиндр имеет радиус 2,
, найдите объем сферического кольца.
Цилиндрическое отверстие диаметром 6
см просверлено в сфере радиусом 5
см так, что ось цилиндра проходит через центр сферы. Найдите объем получившегося сферического кольца.
256π3см3
Найдите объем тела, лежащего под двойным конусом z2=4×2+4y2,
внутри цилиндра x2+y2=x,
и над плоскостью z=0.
Найдите объем тела, лежащего под параболоидом z=x2+y2,
внутри цилиндра x2+y2=x,
и над плоскостью z=0.
3π32
Найдите объем тела, лежащего под плоскостью x+y+z=10
и над диском x2+y2=4x.
Найдите объем тела, лежащего под плоскостью 2x+y+2z=8
и над единичным кругом x2+y2=1.
4π
Радиальная функция f
— функция, значение которой в каждой точке зависит только от расстояния между этой точкой и началом системы координат; то есть f(x,y)=g(r),
, где r=x2+y2.
Покажите, что если f
— непрерывная радиальная функция, то ∬Df(x,y)dA=(θ2−θ1)[G(R2)−G(R1)],
, где G′(r)= rg(r)
и (x,y)∈D={(r,θ)\|R1≤r≤R2,0≤θ≤2π},
с 0≤R1 и 0≤θ1 <θ2≤2π. Используйте информацию из предыдущего упражнения для вычисления интеграла ∬D(x2+y2)3dA, , где D — единичный круг. №4 Пусть f(x,y)=F′(r)r — непрерывная радиальная функция, определенная на кольцевой области D={(r,θ)\|R1≤r≤R2,0≤θ≤2π}, , где r=x2+y2, 0 и F — дифференцируемая функция. Покажите, что ∬Df(x,y)dA=2π[F(R2)−F(R1)]. Примените предыдущее упражнение для вычисления интеграла ∬Dex2+y2x2+y2dxdy, , где D — кольцевая область между окружностями радиусов 1 и 2 , расположенными в третьем квадранте. 12πe(e−1) Пусть f — непрерывная функция, которая выражается в полярных координатах как функция θ 9только 0013 ; то есть f(x,y)=h(θ), , где (x,y)∈D={(r,θ)\|R1≤r≤R2,θ1≤θ≤θ2}, с 0≤R1 и 0≤θ1<θ2≤2π. Покажите, что ∬Df(x,y)dA=12(R22−R12)[H(θ2)−H(θ1)], , где H — первопроизводная h. Примените предыдущее упражнение для вычисления интеграла ∬Dy2x2dA, , где D={(r,θ)\|1≤r≤2,π6≤θ≤π3}. 3−π4 Пусть f — непрерывная функция, которая выражается в полярных координатах как функция θ 9только 0013 ; то есть f(x,y)=g(r)h(θ), , где (x,y)∈D={(r,θ)\|R1≤r≤R2,θ1≤θ≤θ2} с 0≤R1 и 0≤θ1<θ2≤2π. Покажите, что ∬Df(x,y)dA=[G(R2)−G(R1)][H(θ2)−H(θ1)], , где G и H являются первообразными g и ч, соответственно. Вычислить ∬Darctan(yx)x2+y2dA, , где D={(r,θ)\|2≤r≤3,π4≤θ≤π3}. 133π3864 Сферическая шапка — это область сферы, расположенная выше или ниже заданной плоскости. показывают, что объем сферического сегмента на рисунке ниже равен В статистике — совместная плотность для двух независимых нормально распределенных событий со средним значением μ=0 и стандартное распределение σ определяется как p(x,y)=12πσ2e−x2+y22σ2. Рассмотрим (X,Y), декартовы координаты шара в положении покоя после того, как он был выпущен из положения на оси z по направлению к плоскости xy . Предположим, что координаты мяча независимо распределены нормально со средним значением μ=0 и стандартным отклонением σ (в футах). Вероятность того, что шарик остановится не более чем на футов от начала координат определяется как P[X2+Y2≤a2]=∬Dp(x,y)dydx, , где D — это диск радиуса a с центром в начале координат. Покажите, что P[X2+Y2≤a2]=1−e−a2/2σ2. Двойной несобственный интеграл ∫−∞∞∫−∞∞e(−x2+y2/2)dydx может быть определен как предельное значение двойных интегралов ∬Dae(−x2+y2/2)dA по диски Da радиусов a с центром в начале координат, поскольку a неограниченно возрастает; то есть ∫−∞∞∫−∞∞e(−x2+y2/2)dydx=lima→∞∬Dae(−x2+y2/2)dA. , используя соотношение и и углы и описывается как Вы также можете бесплатно скачать на http://cnx.org/contents/[email protected] Атрибуция: Рисунок 15.2.2. Объем по области с непостоянными ограничениями. Возможно, вы выучили формулу вычисления площадей в полярных широтах.
координаты. можно
вычисляйте области как объемы, так что вам нужно запомнить только один
техника. Рассмотрим поверхность $z=1$, горизонтальную плоскость. Громкость
под этой поверхностью и над ней находится область в плоскости $x$-$y$.
просто $1\cdot(\hbox{площадь области})$, поэтому вычисление объема
на самом деле просто вычисляет площадь региона.
92=г$.
(отвечать) Пример 15.2.7 Найдите площадь внутри $r=1+\sin\theta$ и снаружи
$r=2\sin\тета$.
(отвечать) Пример 15.2.8 Найдите площадь внутри обоих
$r=2\sin\theta$ и $r=2\cos\theta$.
(отвечать) Пример 15.2.9 Найдите площадь внутри четырехлистной розы $r=\cos(2\theta)$
и вне $r=1/2$.
(отвечать) Пример 15.2.10 Найдите площадь внутри кардиоиды $r=2(1+\cos\theta)$
и вне $r=2$.
Если расстояние между плоскостями
h,
Глоссарий
Эта работа находится под лицензией Creative Commons Attribution 4.0 International License.
\cr
}$$
$\квадрат$