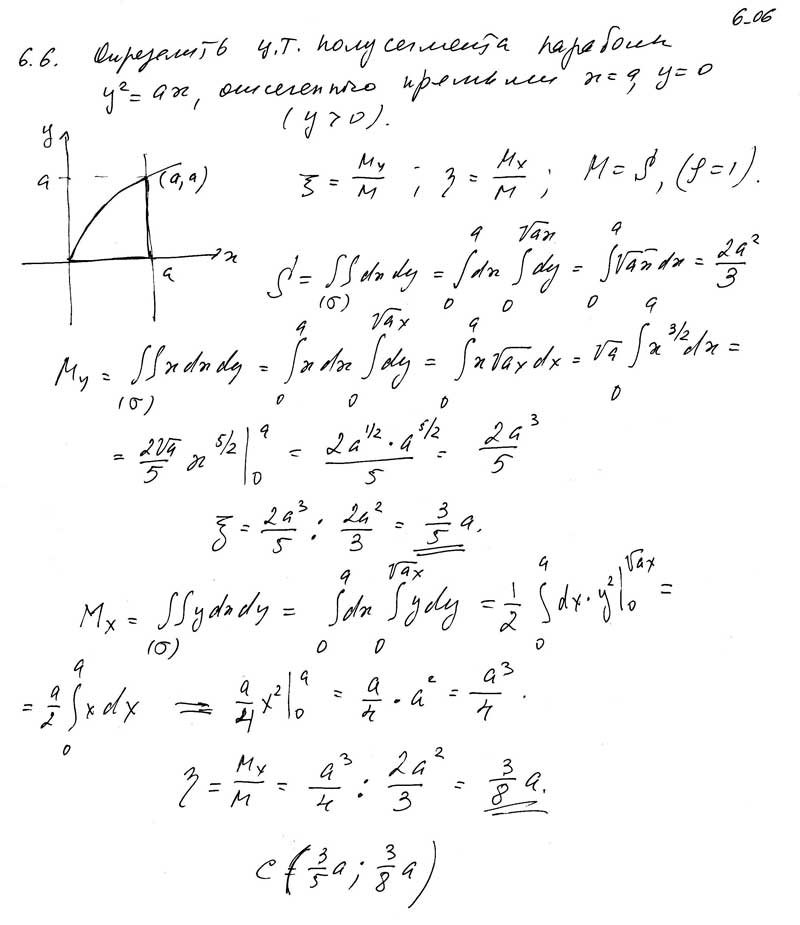17. Изменить порядок интегрирования в двойном интеграле:
18. Найти площадь поверхности параболоида вырезанной поверхностью .
19. Вычислить с помощью тройного интеграла объем тела, ограниченного указанными поверхностями: .
20. Определить массу тела, ограниченной поверхностями , если плотность в каждой точке пропорциональна аппликате этой точки.
Вариант – 19
Найти интегралы: 1. 2. 3. 4. 5. | 6. 7. 8. 9. 10. |
Вычислить несобственные интегралы или доказать их расходимость:
 | 12. |
Найти площадь фигуры, ограниченной линиями:
13. . | 14. |
Вычислить длину дуги, заданной уравнением:
15. | 16. |
17. Изменить порядок интегрирования в двойном интеграле:
18. Вычислить площадь части сферы , заключенной внутри цилиндра .
19. Вычислить с помощью тройного интеграла объем тела, ограниченного указанными поверхностями: .
20. Найти массу сферического слоя между поверхностями , если плотность в каждой точке обратно пропорциональна расстоянию точки от начала координат.
Вариант – 20
| Найти интегралы: 1. 2. 3. 4. 5. | 6. 7. 8. 9. 10. |
Вычислить несобственные интегралы или доказать их расходимость:
11. | 12. |
Найти площадь фигуры, ограниченной линиями:
13. . | 14. |
Вычислить длину дуги, заданной уравнением:
15. | 16. |
17. Изменить порядок интегрирования в двойном интеграле:
18. Вычислить площадь части поверхности конуса , расположенной внутри цилиндра .
19. Вычислить с помощью тройного интеграла объем тела, ограниченного указанными поверхностями: .
20. Найти массу сферы , если поверхностная плотность в каждой точке равна расстоянию от этой точки до оси Oz.
Вариант – 21
Найти интегралы: 1. 2. 3. . 4.5. | 6. 7. 8. 9. 10. |
Вычислить несобственные интегралы или доказать их расходимость:
11. | 12. |
Найти площадь фигуры, ограниченной линиями:
13. . | 14. |
Вычислить длину дуги, заданной уравнением:
15. | 16. . |
17. Изменить порядок интегрирования в двойном интеграле:
18. Вычислить площадь части поверхности , лежащей в I октанте.
19. Вычислить с помощью тройного интеграла объем тела, ограниченного указанными поверхностями: .
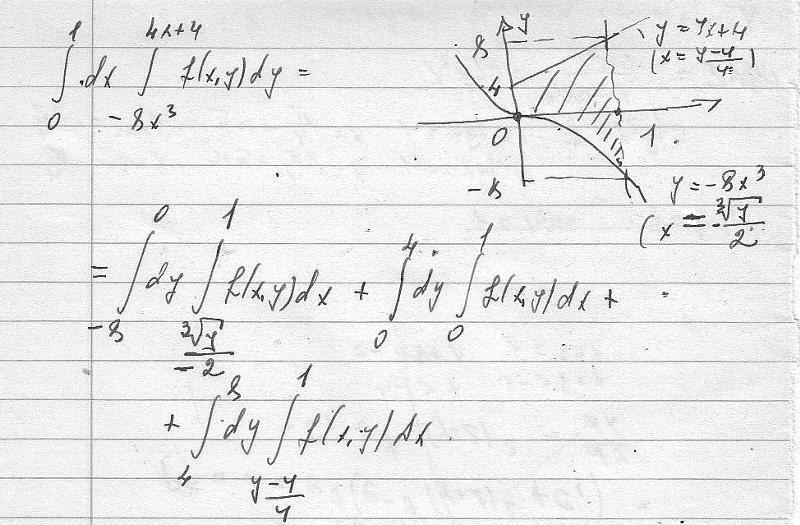
20. Вычислить массу тела, ограниченного поверхностью и имеющего в каждой точке плотность .
Вариант – 22
Найти интегралы: 1. 2. 3. . 4. 5. | 6. 7. 8. 9. 10. |
Вычислить несобственные интегралы или доказать их расходимость:
11. | 12. |
Найти площадь фигуры, ограниченной линиями:
13. | 14. |
.Вычислить длину дуги, заданной уравнением:
15. | 16. . |
17. Изменить порядок интегрирования в двойном интеграле:
18. Вычислить площадь части поверхности конуса , расположенной внутри цилиндра .
19. Вычислить с помощью тройного интеграла объем тела, ограниченного указанными поверхностями: .
20. Найти координаты центра тяжести однородного тела, ограниченного параболоидом и плоскостью .
Вариант – 23
Найти интегралы: 1. 2. 3. 4. 5. | 6. 7. 8. 9. 10. |
Вычислить несобственные интегралы или доказать их расходимость:
11. | 12. |
Найти площадь фигуры, ограниченной линиями:
13. . | 14. |
Вычислить длину дуги, заданной уравнением:
15. | 16. |
Пример 2.3. Поменять порядок интегрирования в интеграле §3.
Замена переменных в двойном интегралеРассмотрим две прямоугольные системы координат х0у и u0v.
И пусть в каждой из координатных плоскостей имеются квадрируемые компакты Р и Q соответственно. Рассмотрим отображение g : QP, которое является вектор-функцией двух переменных, т.е. . Пусть g удовлетворяет следующим условиям:
g – взаимно однозначное отображение Q на Р.
g и непрерывные функции на Р и Q
Компоненты функции g непрерывны вместе со своими частными производными , , , на Q. Матрица: называется матрицей Якоби отображения g, а определитель этой матрыцы I=I(u,v)= — называется якобианом отображения g.
Определение
3.1.
Описанное выше отображение g квадрируемого компакта Q на квадрируемый компакт Р,
которое удовлетворяет условиям
—
,
якобиан которого не равен нулю, называют регулярным
отображением Q на Р.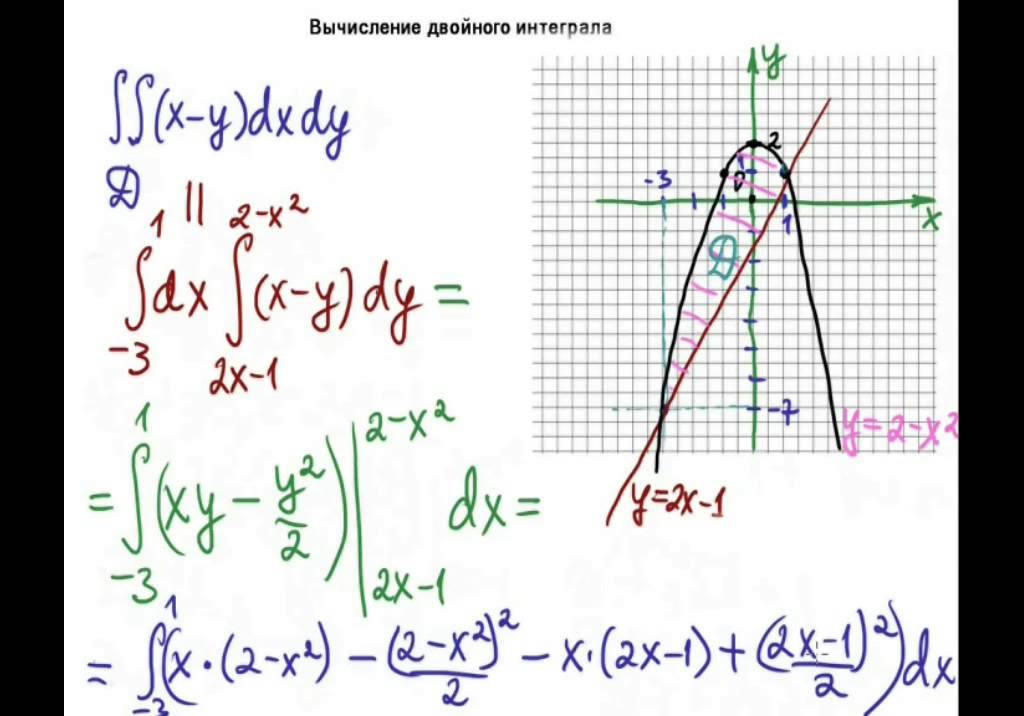
Можно доказать, что при регулярным отображении:
образом непрерывной кривой является непрерывная кривая;
образом области является область;
образом границы является граница.
Теорема 3.1.Пусть функция z=f(х,у) непрерывна на квадрируемом компакте Р плоскости х0у. Пусть g — регулярное отображение квадрируемого компакта Q плоскости u0v на квадрируемый компакт плоскости х0у. Тогда имеет место равенство:
. (3.1)
Отметим, что формула (3.1) называется формулой замены переменной в двойном интеграле.
Пример.
Замечание
3.1. Связь
между декартовой и полярной системами
координат осуществляется при помощью
равенств: x = r , y = r .
Таким образом, отображение компакта Q из полярной системы координат в компакт Р плоскости х0у осуществляется при помощью вектор-функции
g(r, .
Якобиан этого отображения:
I
(3.2)
Замечание 3.2.Очевидно, что площадь области Р в соответствии с равенством (1.11) в полярных координатах вычисляется по формуле: . (3.3)
Пример 3.1. Найти площадь лемнискаты Бернулли:
Пусть в квадрируемом компакте Р определена непрерывная функция f(x,y), имеющая непрерывные частные производные в каждой точке . График этой функции – множества точек П= называется гладкой поверхностью. Рассмотрим задачу вычисления площади гладкой поверхности П.
Разобьем область Р на квадрируемые области Рk , не имеющих общих внутренних точек, с диаметром разбиения .
В каждой
частной области Рк выберем произвольную точку .
Точке на поверхности соответствует точка .
Через точку проведем плоскость, касательную к
поверхности, уравнение которой имеет
вид:
, (4.1)
Нормальный вектор в точке Nk задается координатами .
Построим цилиндрическую поверхность с образующими, параллельными оси 0z, направляющей которого будет граница области Рк. Этот цилиндр вырежет на касательной плоскости фигуру . Эту операцию проделаем в каждой области Pk, k=1,2,…. Получим чешуйчатую поверхность, состоящую из плоских фигур Pk’, покрывающих всю поверхность П. Рассмотрим сумму
= площадей S( всех фигур . Если предел этой суммы, когда диаметр разбиения , существует, то он называется площадью поверхности , т.е.
, (4.2)
а
поверхность называется квадрируемой.
Теорема 4.1. Гладкая поверхность на квадрируемом компакте Р является квадрируемой фигурой и ее площадь может быть вычислена по формуле:
Если есть угол между касательной плоскостью и плоскостью х0у, то как известно из стереометрии
S( = . (4.3)
В то же время угол равен углу между осью 0z, т.е. вектором нормали к плоскости хОу: = (0,0,1) , и вектором нормали к плоскости Pk’. Поэтому
. (4.4)
Таким образом, с учетом равенств (4.3) и (4.4) из формулы (4.2) получим:
. (4.5)
Под знаком предела стоит интегральная сумма непрерывной на квадрируемом компакте Р функции , которая является интегрируемой. Поэтому последний предел существует и по определению: (4.6)
Это и есть формула для вычисления площади поверхности П.
Замечание
6.
1.Если
поверхность П задается уравнением: ,
где ,
или ,где ,
то соответствующие формулы для вычисления
площади поверхности прибретают вид:
, . (4.7)
Пример.
Замечание 6.2.Отметим, что при помощи формулы (4.5) можно вычислить площадь S поверхности, которая получается в результате вращения гладкой кривой Г: , вокруг оси 0х . Можно доказать , что полученная ранее формула в теме “Определенный интеграл”:
(4.8)
является частным случаем формулы (4.5)
Двойные и тройные интегралы можно использовать в вопросах физики и механики: нахождение массы плоской фигуры и тела, статистических моментов и координат центра масс плоской фигуры и тела.
Изменение порядка интеграции
Изменение порядка интеграцииРассмотрим повторный интеграл
Его можно вычислить, проинтегрировав сначала по x или с
уважение к y в первую очередь.
В некоторых случаях один заказ лучше, чем
Другой. По этой причине полезно знать, как перейти от
«плохой» порядок интегрирования в «хороший» порядок
интеграция.
Пример. Вычислить .
Поскольку интеграл дан, мне нужно сначала интегрировать по отношению к Икс. Однако я не знаю первообразной . я поменяю порядок интегрирование и сначала интегрируем по y.
Шаг 1: Преодолеть пределы интеграции, как неравенства.
Шаг 2: Нарисуйте область, заданную неравенства.
Шаг 3: Описать область неравенствами с переменными в обратном порядке.
В первом наборе неравенств y стоит первым. В этом наборе x будет приходи первым. Для x я могу взять числовые оценки в x-направление: .
Далее мне нужны неравенства для y. у вертикаль переменная, поэтому она будет ограничена выражениями для нижней части кривая и верхняя кривая региона.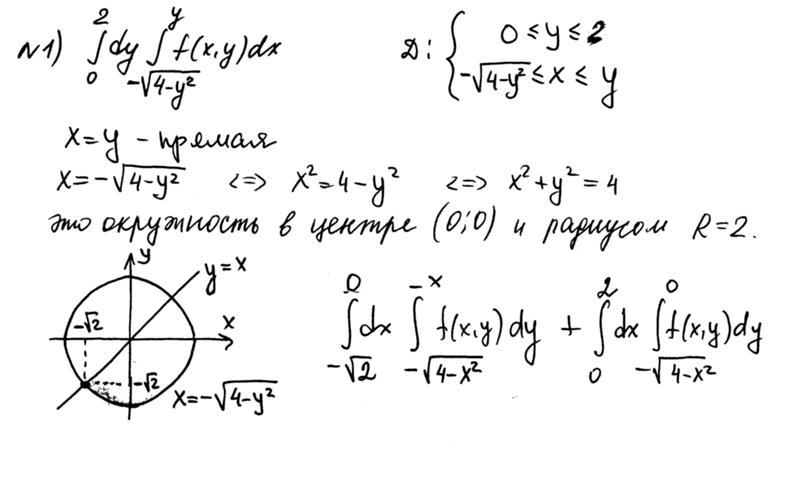
Нижняя кривая
это ось x, которая равна . Верхняя кривая
. Поскольку я ограничиваю y, мне нужно выразить y
с точки зрения х. Таким образом, .
Следовательно, неравенства для y равны . Новый набор неравенств
Шаг 4: Верните неравенства на интеграл:
Схематически вот что происходит:
Это похоже на процедуру преобразования двойного интеграла в полярные координаты.
Пример. Вычислить интеграл, поменяв местами порядок интегрирования:
Вытяните пределы как неравенства:
Далее нарисуйте область, определяемую неравенствами. неравенства означают, что область лежит в горизонтальной полосе между (внизу) и (вверху).
Неравенства дают слева и справа границы, потому что x
горизонтальная переменная. Левая кривая , или . Правая кривая .
Регион указан выше.
Далее описываем область неравенствами с переменными переключился. Сначала я сделаю x, так как первый набор неравенств имел число ограничивает y. Числовые границы x равны 0 и 1, поэтому .
Чтобы получить границы y, я смотрю на нижнюю кривую и верхняя кривая . Нижняя кривая – это линия. Верхняя кривая . Следовательно, неравенства для y равны .
Новые неравенства
Вернем неравенства к интегралу:
Пример. Выразите следующую сумму как одну повторный интеграл, поменяв местами порядок интегрирования:
Вытяните пределы как неравенства:
Нарисуйте область, определяемую неравенствами.
Описать область неравенствами с перестановкой переменных:
Вернем новые неравенства к интегралу:
Пример.
Вычислить .
Вытяните пределы как неравенства:
Нарисуйте область, определяемую неравенствами.
Описать область неравенствами с перестановкой переменных:
Вернем новые неравенства к интегралу:
Контактная информация
Домашняя страница Брюса Икенаги
Copyright 2018 Брюс Икенага
Страница не найдена | Институт науки и технологий Сатьябама (считается университетом)
Наш веб-сайт был обновлен, а пункты меню изменены. Пожалуйста, посетите нашу ДОМАШНЮЮ СТРАНИЦУ [www.sathyabama.ac.in]
К сожалению, страница, которую вы ищете, не найдена
Перейти на домашнюю страницу
Имя
Адрес электронной почты
Мобильный номер
Город
Курсы
— Выберите — Курсы бакалавриата (UG) Инженерные курсы (BE / B.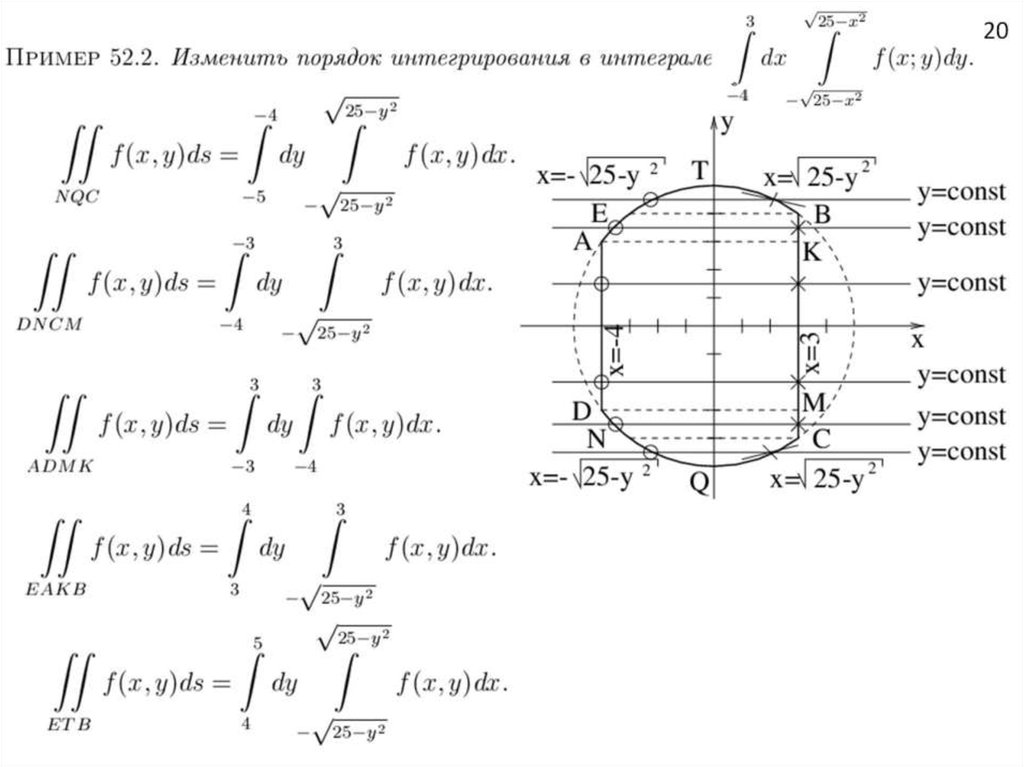
Tech / B.Arch / B.Des)BE — Информатика и инженерияB.E — Информатика и инженерия со специализацией в области искусственного интеллектаB.E — Информатика и инженерия со специализацией в Интернете вещейB.E — Информатика и инженерия со специализацией в области науки о данныхB.E — Информатика и инженерия со специализацией в области искусственного интеллекта и робототехникиB.E — Информатика и инженерия со специализацией в области искусственного интеллекта и машин ОбучениеB.E — Информатика и инженерия со специализацией в технологии блокчейнB.E — Информатика и инженерия со специализацией в области кибербезопасностиB.E — Электротехника и электроникаB.E — Электроника и инженерия связиB.E — МашиностроениеB.E — Автомобильная инженерияB .E — МехатроникаB.E — Авиационная техникаB.E — Гражданское строительствоB.Tech — Информационные технологии nologyB.Tech – химическая инженерияB.Tech – биотехнологияB.Tech – биомедицинская инженерияB.Arch – бакалавр архитектурыB.Des. — Курсы бакалавра дизайна и инженерии (BE / B.
Tech) — Неполный рабочий деньB.E — Информатика и инженерияB.E — Электротехника и электроникаB.E — Электроника и инженерия связиB.E — МашиностроениеB.E — Гражданское строительствоB.Tech — Химическая промышленность Курсы инженерного искусства и наукиB.B.A. — Бакалавр делового администрирования B.Com. — Бакалавр коммерцииB.Com. — Финансовый учетB.Sc. — Визуальная коммуникацияB.Sc — Медицинская лаборатория технологийB.Sc — Клиника и питание и диетологияB.Sc. — ФизикаB.Sc. — ХимияB.Sc. — ИнформатикаB.Sc. — МатематикаB.Sc. — БиохимияB.Sc. — Дизайн одеждыB.Sc. — Бакалавр биотехнологий. — Бакалавр микробиологии. — ПсихологияБ.А. — АнглийскийB.Sc. — Биоинформатика и наука о данных, бакалавр наук — Информатика, специализация в области искусственного интеллекта, бакалавр наук. — Бакалавр наук в области сестринского дела B.Sc. — Курсы авиационного праваB.A. бакалавр права (с отличием) BBA бакалавр права (с отличием) B.Com.LL.B. (с отличием) LL.B.Курсы фармацевтикиB.Pharm., Бакалавр фармацииD.Pharm.
, Диплом фармацевтаПоследипломное образование(PG)Инженерные курсыM.E. Информатика и инженерияМ.Е. Прикладная электроникаМ.Е. Компьютерное проектированиеМ.Е. Строительная инженерияМ.Е. Силовая электроника и промышленные приводыM.Tech. БиотехнологияM.Tech. Медицинское оборудованиеM.Tech. Встроенные системы и IoTM.Arch. Устойчивая архитектураM.Arch. Управление зданиемПрограмма управленияMBA — Магистр делового администрированияНеполный рабочий день последипломного образованияM.E. Информатика и инженерияМ.Е. Прикладная электроникаМ.Е. Компьютерное проектированиеМ.Е. Строительная инженерияM.Tech. Медицинское оборудованиеM.Tech. БиотехнологияM.B.A. Master of Business AdministrationPG Arts & Science Courses AdmissionM.A — EnglishM.Sc — Visual CommunicationM.Sc — PhysicsM.Sc — MathematicsM.Sc — ChemistryM.Sc — BioInformatics & Data ScienceResearch Programs AdsPh.D in all Disciplines Engineering / Technology, Management и наукБакалавр стоматологической хирургии(B.D.S)B.D.S — Бакалавр стоматологической хирургииМагистр стоматологической хирургии(M.