Вычислите длину окружности / Хабр
«Пожалуйста, напишите на C++ функцию, которая получает диаметр круга как float и возвращает длину окружности как float».
Звучит как задание на первой неделе курса по C++. Но это только на первый взгляд. Сложности возникают уже на первых этапах решения задачи. Предлагаю рассмотреть несколько подходов.
Студент: Как вам такой вариант?
#include <math.h>
float CalcCircumference1(float d)
{
return d * M_PI;
}Преподаватель: Да, этот код может нормально откомпилироваться. А может и нет. M_PI не определена в стандартах C или C++. С компилятором в VC++ 2005 это сработает, но для более поздних версий придется использовать #define _USE_MATH_DEFINES перед включением math.h, чтобы получить доступ к этой нестандартной константе. Причем в результате вы напишете код, с которым могут не справиться другие компиляторы.
Сцена вторая
Студент: Благодарю за мудрость, учитель.
float CalcCircumference2(float d)
{
return d * 3.14159265358979323846;
}Преподаватель: Да, так лучше. Этот код будет скомпилирован, и вы получите искомый результат. Но ваш код неэффективен. Вы умножаете число с одинарной точностью на константу с двойной точностью. Компилятору придется привести параметр функции типа float к типу double, а затем выполнить обратное преобразование для получения возвращаемого значения. Если вы компилируете код для SSE2, то это добавляет две инструкции в цепочку зависимостей и вычисления могут выполняться втрое дольше! В большинстве случаев такие задержки вполне допустимы, но во внутреннем цикле негативный эффект может быть весьма значительным.
Если вы компилируете для платформы x87, то преобразование в тип double ничего не стоит, а вот обратное преобразование затратно – настолько затратно, что некоторые оптимизирующие компиляторы выбрасывают это преобразование, а в результате можно получить КРАЙНЕ НЕОЖИДАННЫЕ результаты – например, CalcCircumference( r ) == CalcCircumference( r ) вернет false!
Сцена третья
Студент: Спасибо, учитель. Честно говоря, я не знаю, что такое SSE2 и x87, но я вижу, насколько элегантным становится код, когда типы согласованы. Это настоящая поэзия. Я буду использовать константу одинарной точности. Как вам вот это?
Честно говоря, я не знаю, что такое SSE2 и x87, но я вижу, насколько элегантным становится код, когда типы согласованы. Это настоящая поэзия. Я буду использовать константу одинарной точности. Как вам вот это?
float CalcCircumference3(float d)
{
return d * 3.14159265358979323846f;
}Преподаватель: Да, превосходно! Символ «f» в конце константы все меняет. Если бы вы посмотрели на сгенерированный машинный код, вы бы поняли, что этот вариант намного компактнее и эффективнее. Однако у меня есть замечания к стилю. Не кажется ли вам, что этой загадочной константе не место внутри функции? Даже если это число Пи, значение которого вряд ли изменится, лучше присвоить константе имя и поместить в заголовочный файл.
Сцена четвертая
Студент: Спасибо. Вы объясняете все очень доходчиво. Я помещу строку кода ниже в общий файл заголовка и буду использовать ее в своей функции. Так нормально?
const float pi = 3.14159265358979323846f;
Преподаватель: Да, отлично! С помощью ключевого слова «const» вы указали, что переменная не должна и не может быть изменена, кроме того, ее теперь можно поместить в заголовочный файл. Но, боюсь, теперь нам придется углубиться в некоторые тонкости определения областей видимости в C++.
Объявив pi с ключевым словом const, вы получите в качестве бонуса эффект ключевого слова static. Для целочисленных типов это нормально, но если вы имеете дело с другим типом данных (число с плавающей точкой, массив, класс, структура), память под вашу переменную может быть выделена отдельно в каждой единице трансляции, которая включает в себя ваш заголовочный файл. В некоторых случаях у вас в итоге будет несколько десятков или даже сотен экземпляров переменной типа float и ваш исполняемый файл будет неоправданно большим.
Сцена пятая
Студент: Вы шутите? И что делать?
Преподаватель: Да, мы пока далеки от идеала.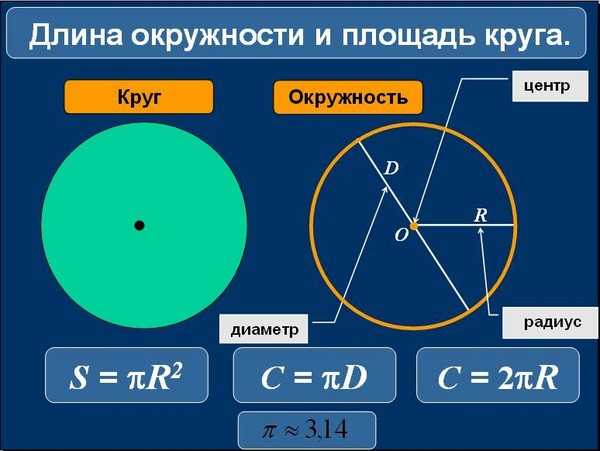 Вы можете повесить на объявление константы атрибут __declspec(selectany) или __attribute __(weak), для того чтобы VC++ и GCC, соответственно, поняли, что достаточно сохранить одну из многочисленных копий этой константы. Но поскольку мы с вами находимся в идеалистическом мире науки, я настаиваю на применении стандартных конструкций C++.
Вы можете повесить на объявление константы атрибут __declspec(selectany) или __attribute __(weak), для того чтобы VC++ и GCC, соответственно, поняли, что достаточно сохранить одну из многочисленных копий этой константы. Но поскольку мы с вами находимся в идеалистическом мире науки, я настаиваю на применении стандартных конструкций C++.
Сцена шестая
Студент: То есть примерно так? С помощью constexpr из C++11?
constexpr float pi = 3.14159265358979323846f;
Преподаватель: Да. Теперь ваш код идеален. Конечно, VS 2013 не сможет его откомпилировать, потому что не знает, что делать с constexpr. Но вы всегда можете воспользоваться набором инструментов Visual C++ Compiler Nov 2013 CTP либо последней версией GCC или Clang.
Студент: А #define можно использовать?
Преподаватель: Нет!
Студент: А, к черту все это! Лучше я стану бариста.
Сцена седьмая
Студент: Стоп, я кое-что припоминаю. Это же просто! Вот как будет выглядеть код:
Это же просто! Вот как будет выглядеть код:
mymath.h: extern const float pi; mymath.cpp: extern const float pi = 3.14159265358979323846f;
Преподаватель: Точно, в большинстве случаев это будет верное решение. Но что если вы работаете над DLL, как внешние функции будут обращаться к mymath.h в вашей DLL? В таком случае вам придется обеспечить экспорт и импорт этого символа.
Проблема в том, что правила для целочисленных типов абсолютно другие. Целесообразно и рекомендуется добавить в заголовочный файл C++ следующее:
const int pi_i = 3;
Число Пи здесь указано недостаточно точно, но дело в том, что целочисленные константы в заголовочных файлах не требуют выделения памяти в отличие от остальных констант. Чем такое отличие обусловлено, не совсем понятно, но чаще всего это и не важно.
О том, что значит «static» в «const», я узнал несколько лет назад, когда меня попросили выяснить, почему одна из наших ключевых библиотек DLL вдруг прибавила в весе 2 МБ.
И да, я по-прежнему считаю, что #define — ужасный выбор в данном случае. Может быть, это еще не самое худшее решение, но мне оно совершенно не нравится. Однажды я столкнулся с ошибками компиляции, вызванными объявлением pi с помощью #define. Приятного мало, скажу я вам! Замусоривание пространства имен — вот главная причина, почему следует избегать #define, насколько это возможно.
Заключение
Не знаю точно, какой урок мы извлекли из всего этого. Суть проблемы, которая возникает, когда мы объявляем в заголовочных файлах константу типа float или double либо структуру или массив констант, ясна далеко не всем. В большинстве серьезных программ из-за этого возникают дубликаты статических констант, и иногда они неоправданно большого размера. Полагаю, constexpr может избавить нас от этой проблемы, но у меня нет достаточного опыта его использования, чтобы знать наверняка.
Я сталкивался с программами, которые были на сотни килобайт больше своего «реального» размера — и все из-за массива констант в заголовочном файле. Я также видел программу, в которой в конечном счете оказалось 50 копий объекта класса (плюс еще по 50 вызовов конструкторов и деструкторов), потому что этот объект класса был определен как тип const в заголовочном файле. Иначе говоря, тут есть над чем подумать.
Вы можете увидеть, как это происходит с GCC, загрузив тестовую программу отсюда. Соберите её с помощью команды make, а затем выполните команду objdump -d constfloat | grep flds, чтобы найти четыре инструкции чтения со смежных адресов в сегменте данных. Если вы хотите занять больше пространства, добавьте в header.h следующее:
const float sinTable[1024] = { 0.0, 0.1, };
В случае с GCC прирост составит 4 КБ на одну запись преобразования (исходный файл), то есть исполняемый файл вырастет на 20 КиБ, даже если к таблице ни разу никто не обращается.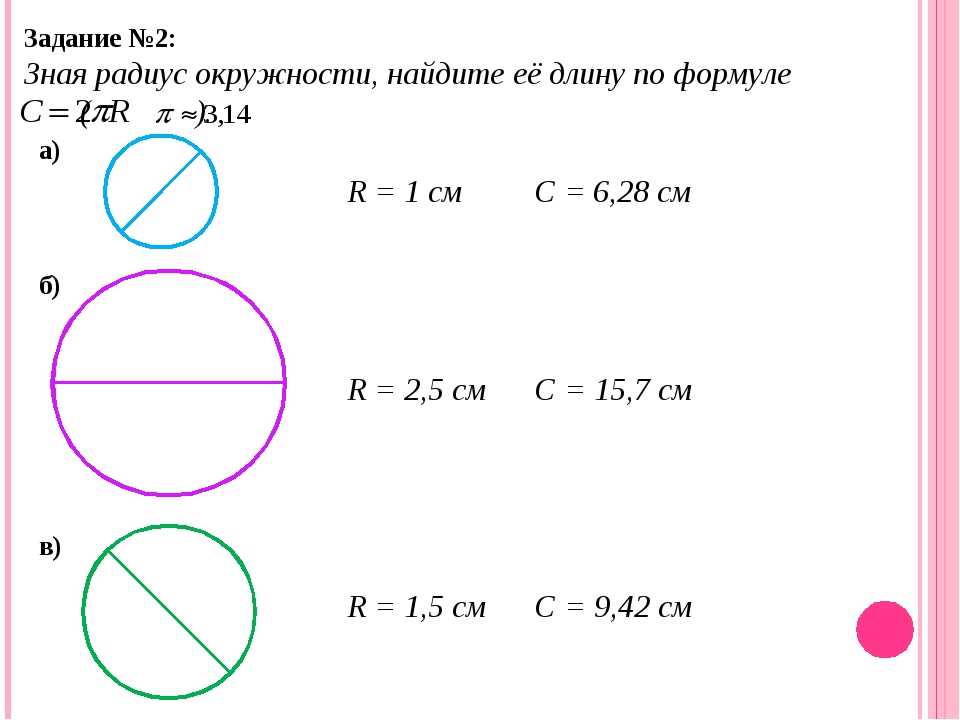
Как обычно, операции над числами с плавающей точкой связаны со значительными трудностями, но в данном случае, как мне кажется, в этом виновата слишком медленная эволюция языка С++.
Что еще почитать по теме:
VC++: как избежать дублирования и как понять, что дублирования не избежать
У компилятора в VC++ 2013 Update 2 появился параметр /Gw, который помещает каждую глобальную переменную в отдельный контейнер COMDAT, позволяя компоновщику выявлять и избавляться от дубликатов. Иногда такой подход помогает избежать негативных последствий объявления констант и статических переменных в заголовочных файлах. В Chrome такие изменения помогли сэкономить около 600 КБ (подробности). Частично такой экономии удалось добиться (сюрприз!) путем удаления тысячи экземпляров twoPiDouble и piDouble (а также twoPiFloat и piFloat).
Однако в VC++ 2013 STL есть несколько объектов, объявленных как static или const в объявлении класса, которые /Gw не может удалить.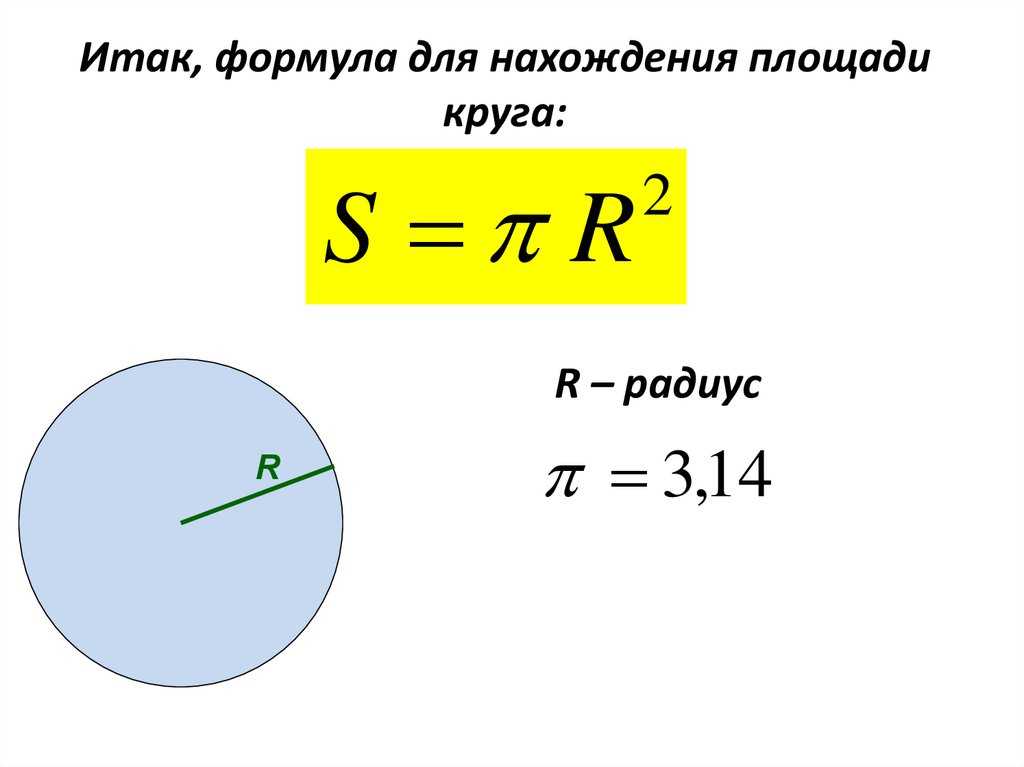 Все эти объекты занимают по одному байту, но в итоге набегает свыше 45 килобайт. Я сообщил разработчикам об этой ошибке и получил ответ, что в VC++ 2015 она была исправлена.
Все эти объекты занимают по одному байту, но в итоге набегает свыше 45 килобайт. Я сообщил разработчикам об этой ошибке и получил ответ, что в VC++ 2015 она была исправлена.
По просьбе автора делимся ссылкой на оригинал здесь
Калькулятор вычисления длины окружности. Как рассчитать длину окружности, если не указан диаметр и радиус круга
Предпринимательство
Окружность — замкнутая кривая, все точки которой находятся на одинаковом расстоянии от центра. Эта фигура является плоской. Поэтому решение задачи, вопрос которой состоит в том, как найти длину окружности, является достаточно простым. Все имеющиеся способы, мы рассмотрим в сегодняшней статье.
Описания фигуры
Кроме достаточно простого описательного определения существуют еще три математических характеристики окружности, которые уже сами по себе содержат ответ на вопрос, как найти длину окружности:
- Состоит из точек A и B и всех других, из которых AB можно увидеть под прямым углом. Диаметр данной фигуры равен длине рассматриваемого отрезка.

- Включает исключительно такие точки X, что отношение AX/BX неизменно и не равно единице. Если это условие не соблюдается, то это не окружность.
- Состоит из точек, для каждой из которых выполняется следующее равенство: сумма квадратов расстояний до двух других — это заданная величина, которая всегда больше половине длины отрезка между ними.
Терминология
Не у всех в школе был хороший учитель математики. Поэтому ответ на вопрос, как найти длину окружности, осложняется еще и тем, что не все знают основные геометрические понятия. Радиус — отрезок, который соединяет центр фигуры с точкой на кривой. Особым случаем в тригонометрии является единичная окружность. Хорда — отрезок, который соединяет две точки кривой. Например, под это определение подпадает уже рассмотренный AB. Диаметр — это хорда, проходящая через центр. Число π равно длине единичной полуокружности.
Основные формулы
Из определений непосредственно следуют геометрические формулы, которые позволяют рассчитать основные характеристики окружности:
- Длина равна произведению числа π и диаметра.
 Формулу обычно записывают следующим образом: C = π*D.
Формулу обычно записывают следующим образом: C = π*D. - Радиус равен половине диаметра. Его также можно рассчитать, вычислив частное от деления длины окружности на удвоенное число π. Формула выглядит так: R = C/(2* π) = D/2.
- Диаметр равен частному от деления длины окружности на π или удвоенному радиусу. Формула является достаточно простой и выглядит так: D = C/π = 2*R.
- Площадь круга равна произведению числа π и квадрата радиуса. Аналогично в этой формуле можно использовать диаметр. В этом случае площадь будет равна частному от деления произведения числа π и квадрата диаметра на четыре. Формулу можно записать следующим образом: S = π*R 2 = π*D 2 /4.
Как найти длину окружности по диаметру
Для простоты объяснения обозначим буквами необходимые для расчета характеристики фигуры. Пусть C — это искомая длина, D — ее диаметр, а число π приблизительно равно 3,14. Если у нас есть всего одна известная величина, то задачу можно считать решенной. Зачем это нужно в жизни? Предположим мы решили обнести круглый бассейн забором.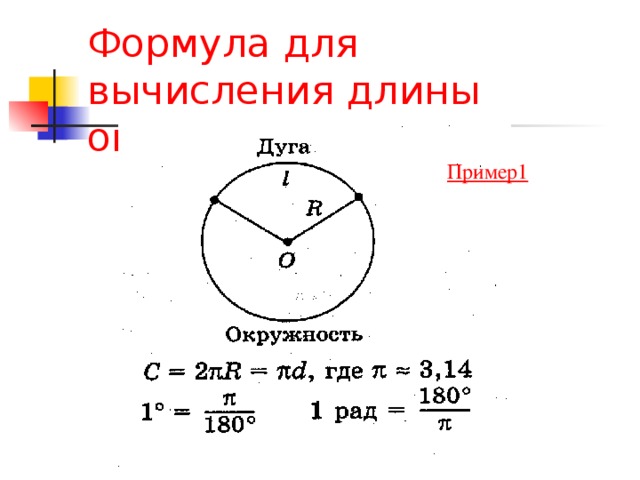 Как вычислить необходимое количество столбиков? И тут на помощь приходит умение, как вычислить длину окружности. Формула выглядит следующим образом: C = π D. В нашем примере диаметр определяется на основе радиуса бассейна и необходимого расстояния до забора. Например, предположим, что наш домашний искусственный водоем составляет 20 метров в ширину, а столбики мы собираемся ставить на десятиметровом расстоянии от него. Диаметр получившейся окружности равен 20 + 10*2 = 40 м. Длина — 3,14*40 = 125,6 метров. Нам понадобятся 25 столбиков, если промежуток между ними будет около 5 м.
Как вычислить необходимое количество столбиков? И тут на помощь приходит умение, как вычислить длину окружности. Формула выглядит следующим образом: C = π D. В нашем примере диаметр определяется на основе радиуса бассейна и необходимого расстояния до забора. Например, предположим, что наш домашний искусственный водоем составляет 20 метров в ширину, а столбики мы собираемся ставить на десятиметровом расстоянии от него. Диаметр получившейся окружности равен 20 + 10*2 = 40 м. Длина — 3,14*40 = 125,6 метров. Нам понадобятся 25 столбиков, если промежуток между ними будет около 5 м.
Длина через радиус
Как всегда, начнем с присвоения характеристикам окружности букв. На самом деле они являются универсальными, поэтому математикам из разных стран вовсе не обязательно знать язык друг друга. Предположим, что C — это длина окружности, r — ее радиус, а π приблизительно равно 3,14. Формула выглядит в этом случае следующим образом: C = 2*π*r. Очевидно, что это абсолютно правильное равенство. Как мы уже разобрались диаметр окружности равен ее удвоенному радиусу, поэтому эта формула так и выглядит. В жизни этот способ тоже может часто пригодиться. Например, мы печем торт в специальной раздвижной форме. Чтобы он не испачкался, нам нужна декоративная обертка. Но как вырезать круг нужного размера. Здесь на помощь и приходит математика. Те, кто знают, как узнать длину окружности, сразу скажут, что нужно умножить число π на удвоенный радиус формы. Если ее радиус равен 25 см, то длина будет составлять 157 сантиметров.
Как мы уже разобрались диаметр окружности равен ее удвоенному радиусу, поэтому эта формула так и выглядит. В жизни этот способ тоже может часто пригодиться. Например, мы печем торт в специальной раздвижной форме. Чтобы он не испачкался, нам нужна декоративная обертка. Но как вырезать круг нужного размера. Здесь на помощь и приходит математика. Те, кто знают, как узнать длину окружности, сразу скажут, что нужно умножить число π на удвоенный радиус формы. Если ее радиус равен 25 см, то длина будет составлять 157 сантиметров.
Примеры задач
Мы уже рассмотрели несколько практических случаев полученных знаний о том, как узнать длину окружности. Но зачастую нас заботят не они, а реальные математические задачи, которые содержатся в учебнике. Ведь за них учитель выставляет баллы! Поэтому давайте рассмотрим задачу повышенной сложности. Предположим, что длина окружности составляет 26 см. Как найти радиус такой фигуры?
Решение примера
Для начала запишем, что нам дано: C = 26 см, π = 3,14.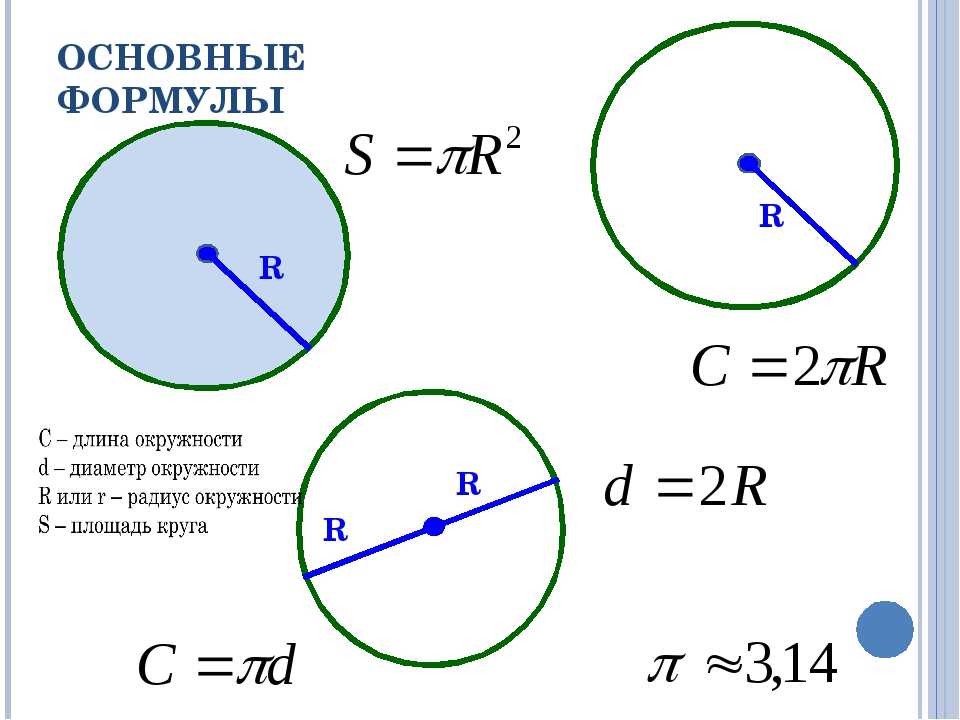 Также вспомним формулу: C = 2* π*R. Из нее можно извлечь радиус окружности. Таким образом, R= C/2/π. Теперь приступим к непосредственному расчету. Сначала делим длину на два. Получаем 13. Теперь нужно разделить на значение числа π: 13/3,14 = 4,14 см. Важно не забыть записать ответ правильно, то есть с единицами измерения, иначе теряется весь практический смысл подобных задач. К тому же за подобную невнимательность можно получить оценку на один балл ниже. И как бы досадно ни было, придется мириться с таким положением вещей.
Также вспомним формулу: C = 2* π*R. Из нее можно извлечь радиус окружности. Таким образом, R= C/2/π. Теперь приступим к непосредственному расчету. Сначала делим длину на два. Получаем 13. Теперь нужно разделить на значение числа π: 13/3,14 = 4,14 см. Важно не забыть записать ответ правильно, то есть с единицами измерения, иначе теряется весь практический смысл подобных задач. К тому же за подобную невнимательность можно получить оценку на один балл ниже. И как бы досадно ни было, придется мириться с таким положением вещей.
Не так страшен зверь, как его малюют
Вот мы и разобрались с такой непростой на первый взгляд задачей. Как оказалось, нужно просто понимать значение терминов и запомнить несколько легких формул. Математика — это не так страшно, нужно только приложить немного усилий. Так что геометрия ждет вас!
Часто звучит, как часть плоскости, которая ограничена окружностью. Окружность круга является плоской замкнутой кривой. Все точки, расположенные на кривой, удалены от центра круга на одинаковое расстояние.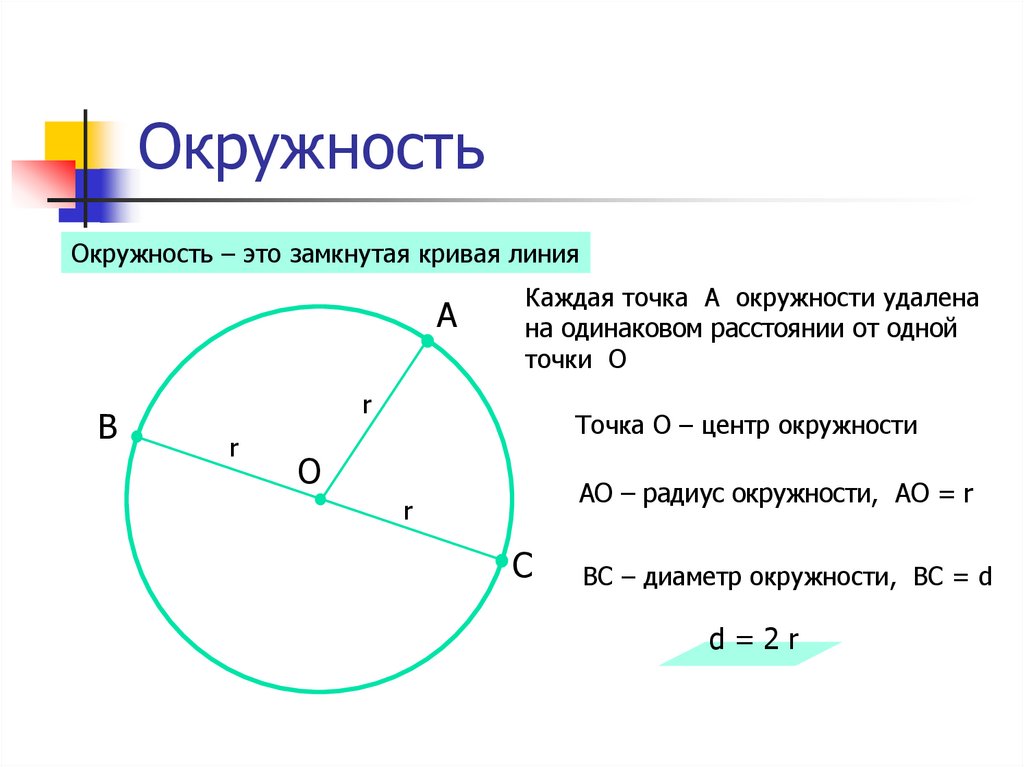 В круге его длина и периметр одинаковы. Соотношение длины любой окружности и ее диаметра постоянное и обозначается числом π = 3,1415
.
В круге его длина и периметр одинаковы. Соотношение длины любой окружности и ее диаметра постоянное и обозначается числом π = 3,1415
.
Определение периметра круга
Периметр круга радиуса r равен удвоенному произведению радиуса r на число π(~3.1415)
Формула периметра круга
Периметр круга радиуса \(r\) :
\[ \LARGE{P} = 2 \cdot \pi \cdot r \]
\[ \LARGE{P} = \pi \cdot d \]
\(P \) – периметр (длина окружности).
\(r \) – радиус.
\(d \) – диаметр.
Окружностью будем называть такую геометрическую фигуру, которая будет состоять из всех таких точек, которые находятся на одинаковом расстоянии от какой-либо заданной точки.
Центром окружности будем называть точку, которая задается в рамках определения 1.
Радиусом окружности будем называть расстояние от центра этой окружности до любой ее точки.
В декартовой системе координат \(xOy \)
мы также можем ввести уравнение любой окружности. Обозначим центр окружности точкой \(X \)
, которая будет иметь координаты \((x_0,y_0) \)
. 0}{n}}=\frac{2τ}{2τ»} \)
0}{n}}=\frac{2τ}{2τ»} \)
Получаем, что отношение \(\frac{ρ}{ρ»}=\frac{2τ}{2τ»} \) будет верным независимо от значения числа сторон вписанных правильных многоугольников. То есть
\(\lim_{n\to\infty}(\frac{ρ}{ρ»})=\frac{2τ}{2τ»} \)
С другой стороны, если бесконечно увеличивать число сторон вписанных правильных многоугольников (то есть \(n→∞ \) ), будем получать равенство:
\(lim_{n\to\infty}(\frac{ρ}{ρ»})=\frac{C}{C»} \)
Из последних двух равенств получим, что
\(\frac{C}{C»}=\frac{2τ}{2τ»} \)
\(\frac{C}{2τ}=\frac{C»}{2τ»} \)
Видим, что отношение длины окружности к его удвоенному радиусу всегда одно и тоже число, независимо от выбора окружности и ее параметров, то есть
\(\frac{C}{2τ}=const \)
Эту постоянную принять называть числом «пи» и обозначать \(π \) . Приближенно, это число будет равняться \(3,14 \) (точного значения этого числа нет, так как оно является иррациональным числом). Таким образом
\(\frac{C}{2τ}=π \)
Окончательно, получим, что длина окружности (периметр круга) определяется формулой
\(C=2πτ \)
В вашем браузере отключен Javascript.
Чтобы произвести расчеты, необходимо разрешить элементы ActiveX!
И в чем ее отличие от круга. Возьмите ручку или цвета и нарисуйте на листке бумаги обычный круг. Закрасьте всю середину полученной фигуры синим карандашом. Красный контур, обозначающий границы фигуры, — это окружность. А вот синее содержимое внутри нее — и есть круг.
Размеры круга и окружности определяются диаметром. На красной линии, обозначающей окружность, отметьте две точки таким образом, чтобы они оказались зеркальным отражением друг друга. Соедините их линией. Отрезок обязательно пройдет через точку в центре окружности. Этот отрезок, соединяющий противоположные части окружности, и называется в геометрии диаметром.
Отрезок, который тянется не через центр окружности, но смыкается с ней противоположными концами, называется хордой. Следовательно, хорда, пролегающая через точку центра окружности, и является ее диаметром.
Обозначается диаметр латинской буквой D. Находить диаметр окружности можно по таким значениям, как площадь, длина и радиус круга.
Расстояние от центральной точки до точки, отложенной на окружности, называется радиусом и обозначается буквой R. Знание величины радиуса помогает вычислить диаметр окружности одним несложным действием:
К примеру, радиус — 7 см. Умножаем 7 см на 2 и получаем величину, равную 14 см. Ответ: D заданной фигуры равен 14 см.
Иногда приходится определять диаметр окружности лишь по ее длине. Здесь необходимо применить специальную формулу, помогающую определить Формула L = 2 Пи * R, где 2 — это неизменная величина (константа), а Пи = 3,14. А так как известно, что R = D * 2, то формулу можно представить и другим способом
Данное выражение применимо и как формула диаметра окружности. Подставив известные в задаче величины, решаем уравнение с одним неизвестным. Допустим, длина равна 7 м. Следовательно:
Ответ: диаметр равен 21,98 метрам.
Если известно значение площади, то также можно определить диаметр окружности. Формула, которая применяется в данном случае, выглядит так:
D = 2 * (S / Пи) * (1 / 2)
S — в данном случае Допустим, в задаче она равна 30 кв. м. Получаем:
м. Получаем:
D = 2 * (30 / 3, 14) * (1 / 2) D = 9, 55414
При обозначенной в задаче величине, равной объему (V) шара, применяется следующая формула нахождения диаметра: D = (6 V / Пи) * 1 / 3.
Иногда приходится находить диаметр окружности, вписанной в треугольник. Для этого по формуле находим радиус представленной окружности:
R = S / p (S — площадь заданного треугольника, а p — периметр, разделенный на 2).
Полученный результат увеличиваем вдвое, учитывая, что D = 2 * R.
Нередко находить диаметр окружности приходится и в быту. К примеру, при определении что равносильно его диаметру. Для этого необходимо обмотать палец потенциального обладателя кольца ниткой. Отметить точки соприкосновения двух концов. Измерить линейкой длину от точки до точки. Полученное значение умножаем на 3,14, следуя формуле определения диаметра при известной длине. Так что, утверждение о том, что познания в геометрии и алгебре в жизни не пригодятся, не всегда соответствует действительности.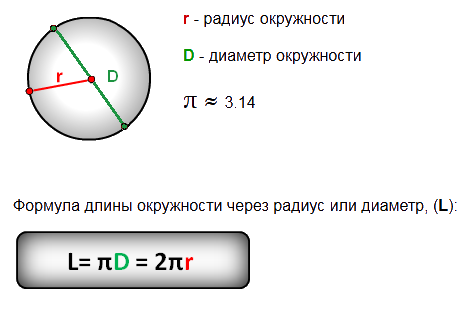 А это является серьезным поводом для того, чтобы более ответственно относиться к школьным предметам.
А это является серьезным поводом для того, чтобы более ответственно относиться к школьным предметам.
Калькулятор круга — это сервис, специально разработанный для расчета геометрических размеров фигур онлайн. Благодаря данному сервису Вы без проблем сможете определить любой параметр фигуры, в основе которой лежит круг. Например: Вы знаете объем шара, а необходимо получить его площадь. Нет ничего проще! Выберите соответствующий параметр, введите числовое значение и нажмите кнопку рассчитать. Сервис не только выдает результаты вычислений, но и предоставляет формулы, по которым они были сделаны. При помощи нашего сервиса вы без труда рассчитаете радиус, диаметр, длину окружности (периметр круга), площадь круга и шара, объем шара.
Вычислить радиус
Задача на вычисление значения радиуса – одна из самых распространенных. Причина тому достаточно проста, ведь зная этот параметр, вы без особого труда сможете определить значение любого другого параметра круга или шара. Наш сайт построен именно на такой схеме.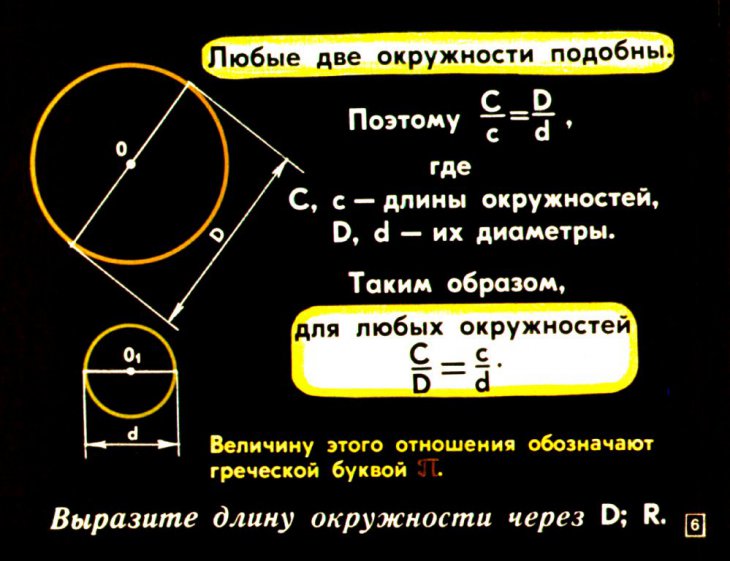 Вне зависимости от того, какой вы выбрали исходный параметр, первым делом вычисляется значение радиуса и на его основе строятся все последующие вычисления. Для большей точности вычислений, сайт использует число Пи с округлением до 10-го знака после запятой.
Вне зависимости от того, какой вы выбрали исходный параметр, первым делом вычисляется значение радиуса и на его основе строятся все последующие вычисления. Для большей точности вычислений, сайт использует число Пи с округлением до 10-го знака после запятой.
Рассчитать диаметр
Расчет диаметра – самый простой вид расчета из тех, что умеет выполнять наш калькулятор. Получить значение диаметра совсем нетрудно и вручную, для этого совсем не надо прибегать к помощи интернета. Диаметр равен значению радиуса умноженному на 2. Диаметр – важнейший параметр круга, который чрезвычайно часто используется в повседневной жизни. Уметь его правильно рассчитать и использовать должен абсолютно каждый. Воспользовавшись возможностями нашего сайта, вы вычислите диаметр с большой точностью за доли секунды.
Узнать длину окружности
Вы даже не представляете, как много вокруг нас круглых объектов и какую важную роль они играют в нашей жизни. Умение рассчитать длину окружности необходимо всем, от рядового водителя, до ведущего инженера-проектировщика.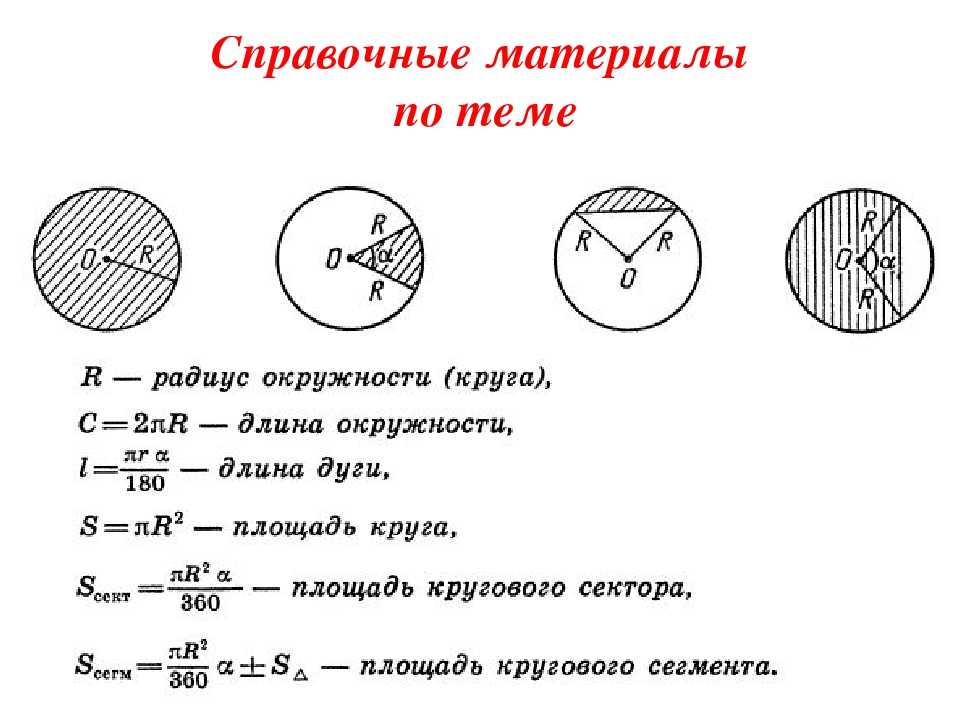 Формула для вычисления длинны окружности очень проста: D=2Pr. Расчет можно легко провести как на листке бумаги, так и при помощи данного интернет помощника. Преимущество последнего в том, что он проиллюстрирует все вычисления рисунками. И ко всему прочему, второй способ намного быстрее.
Формула для вычисления длинны окружности очень проста: D=2Pr. Расчет можно легко провести как на листке бумаги, так и при помощи данного интернет помощника. Преимущество последнего в том, что он проиллюстрирует все вычисления рисунками. И ко всему прочему, второй способ намного быстрее.
Вычислить площадь круга
Площадь круга – как и все перечисленные перечисленные в этой статье параметры является основой современной цивилизации. Уметь рассчитать и знать площадь круга полезно всем без исключения слоям населения. Трудно представить область науки и техники, в которой не надо было бы знать, площадь круга. Формула для вычисления опять же нетрудная: S=PR 2 . Эта формула и наш онлайн-калькулятор помогут Вам без лишних усилий узнать площадь любого круга. Наш сайт гарантирует высокую точность вычислений и их молниеносное выполнение.
Рассчитать площадь шара
Формула для расчета площади шара ничуть не сложнее формул, описанных в предыдущих пунктах. S=4Pr 2 . Этот нехитрый набор букв и цифр уже многие годы дает людям возможность достаточно точно вычислять площадь шара.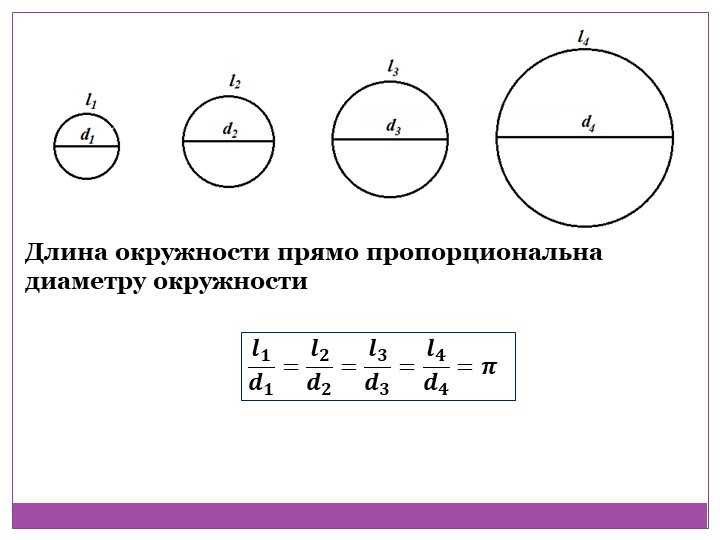 Где это может быть применено? Да везде! Например, вы знаете, что площадь земного шара равна 510 100 000 километров квадратных. Перечислять, где может быть применено знание этой формулы перечислять бесполезно. Слишком широка область применения формулы для вычисления площади шара.
Где это может быть применено? Да везде! Например, вы знаете, что площадь земного шара равна 510 100 000 километров квадратных. Перечислять, где может быть применено знание этой формулы перечислять бесполезно. Слишком широка область применения формулы для вычисления площади шара.
Вычислить объем шара
Для вычисления объема шара используют формулу V=4/3(Pr 3). Она была использована при создании нашего онлайн сервиса. Сайт сайт дает возможность рассчитать объем шара за считанные секунды, если вы Вам известен любой из следующих параметров: радиус, диаметр, длинна окружности, площадь круга или площадь шара. Так же вы можете применять его для обратного вычисления, например, чтобы зная объем шара, получить значение его радиуса или диаметра. Спасибо, что кратко ознакомились с возможностями нашего калькулятора круга. Надеемся, Вам у нас понравилось, и вы уже добавили сайт в закладки.
Окружностью называется ряд равноудалённых точек от одной точки, которая, в свою очередь, является центром этой окружности. Окружность имеет также свой радиус, равный расстоянию этих точек от центра.
Окружность имеет также свой радиус, равный расстоянию этих точек от центра.
Отношение длины, какой либо окружности к её диаметру, для всех окружностей одинаково. Это отношение есть число, являющееся математической константой, которое обозначается греческой буквой π .
Определение длины окружности
Произвести расчёт окружности можно по следующей формуле:
L = π D = 2 π r
r — радиус окружности
D — диаметр окружности
L — длина окружности
π — 3.14
Задача:
Вычислить длину окружности , имеющей радиус 10 сантиметров.
Решение:
Формула для вычисления дины окружности имеет вид:
L = π D = 2 π r
где L – длина окружности, π – 3,14 , r – радиус окружности, D – диаметр окружности.
Таким образом, длина окружности, имеющей радиус 10 сантиметров равна:
L = 2 × 3,14 × 10 = 62,8 сантиметра
Окружность представляет собой геометрическую фигуру, являющуюся совокупностью всех точек на плоскости, удаленных от заданной точки, которая называется ее центром, на некоторое расстояние, не равное нулю и именуемое радиусом. Определять ее длину с различной степенью точности ученые умели уже в глубокой древности: историки науки считают, что первая формула для вычисления длины окружности была составлена примерно в 1900 году до нашей эры в древнем Вавилоне.
Определять ее длину с различной степенью точности ученые умели уже в глубокой древности: историки науки считают, что первая формула для вычисления длины окружности была составлена примерно в 1900 году до нашей эры в древнем Вавилоне.
С такими геометрическими фигурами, как окружности, мы сталкиваемся ежедневно и повсеместно. Именно ее форму имеет внешняя поверхность колес, которыми оснащаются различные транспортные средства. Эта деталь, несмотря на свою внешнюю простоту и незатейливость, считаются одним из величайших изобретений человечества, причем интересно, что аборигены Австралии и американские индейцы вплоть до прихода европейцев совершенно не имели понятия о том, что это такое.
По всей вероятности, самые первые колеса представляли собой отрезки бревен, которые насаживались на ось. Постепенно конструкция колеса совершенствовалась, их конструкция становилась все более и более сложной, а для их изготовления требовалось использовать массу различных инструментов. Сначала появились колеса, состоящие из деревянного обода и спиц, а затем, для того, чтобы уменьшить износ их внешней поверхности, ее стали обивать металлическими полосами. Для того чтобы определить длины этих элементов, и требуется использовать формулу расчета длины окружности (хотя на практике, вероятнее всего, мастера это делали «на глаз» или просто опоясывая колесо полосой и отрезая требуемый ее участок).
Для того чтобы определить длины этих элементов, и требуется использовать формулу расчета длины окружности (хотя на практике, вероятнее всего, мастера это делали «на глаз» или просто опоясывая колесо полосой и отрезая требуемый ее участок).
Следует заметить, что колесо используется отнюдь не только в транспортных средствах. Например, его форму имеет гончарный круг, а также элементы шестеренок зубчатых передач, широко применяемых в технике. Издавна колеса использовались в конструкциях водяных мельниц (самые древние из известных ученым сооружений такого рода строились в Месопотамии), а также прялок, применявшихся для изготовления нитей из шерсти животных и растительных волокон.
Окружности нередко можно встретить и в строительстве. Их форму имеют достаточно широко распространенные круглые окна, очень характерные для романского архитектурного стиля. Изготовление этих конструкций – дело весьма непростое и требует высокого мастерства, а также наличия специального инструмента.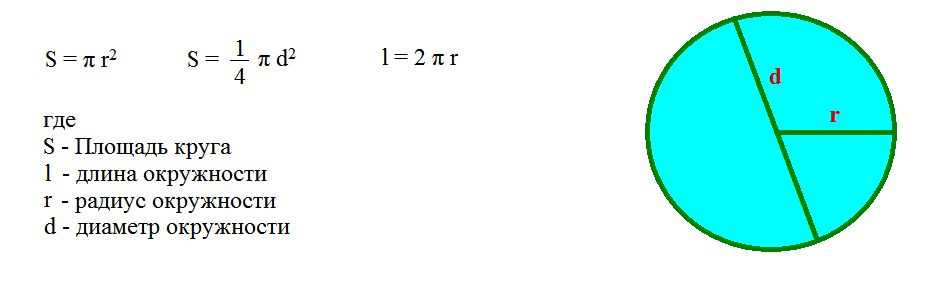 Одной из разновидностей круглых окон являются иллюминаторы, устанавливаемые в морских и воздушных судах.
Одной из разновидностей круглых окон являются иллюминаторы, устанавливаемые в морских и воздушных судах.
Таким образом, решать задачу определения длины окружности часто приходится инженерам-конструкторам, разрабатывающим различные машины, механизмы и агрегаты, а также архитекторам и проектировщикам. Поскольку число π , необходимое для этого, является бесконечным, то с абсолютной точностью определить этот параметр не представляется возможным, и поэтому при вычислениях учитывается та ее степень, которая в том или ином конкретном случае является необходимой и достаточной.
How to Calculate the Circumference of Earth (Step by Step)
Written by
Malcolm McKinsey
Fact-checked by
Paul Mazzola
Earth is an oblate spheroid
Smart and образованные люди древнего мира знали, что земля круглая. Они знали, что это сфера, а сегодня мы знаем, что это сплющенная сфера, сплющенный сфероид . Он сдавлен из-за сильного гравитационного притяжения Солнца, из-за чего он слегка выпячивается на экваторе.
Они знали, что это сфера, а сегодня мы знаем, что это сплющенная сфера, сплющенный сфероид . Он сдавлен из-за сильного гравитационного притяжения Солнца, из-за чего он слегка выпячивается на экваторе.
Эратосфен, главный библиотекарь великой Александрийской библиотеки, имел в своем распоряжении практически все знания мира того времени. Он знал, что земля круглая, но , а не , знал ее размер. Он понятия не имел, какова окружность Земли.
Представьте, что вы главный библиотекарь величайшей библиотеки на планете, и посетитель библиотеки задает вам простой вопрос:
Он не знал, но, как любой хороший математик и ученый, намеревался выяснить это, используя имеющиеся у него ресурсы.
Еще в 240 г. до н. э. грек по имени Эратосфен вычислил длину окружности Земли. Сегодня мы знаем, как измерить окружность многих вещей, в том числе земли, с помощью многих современных инструментов, но Эратосфен делал это с помощью колодца, солнца и палки.
Установка космологической стадии
Наше Солнце находится очень далеко от Земли, 149 600 000 км в среднем.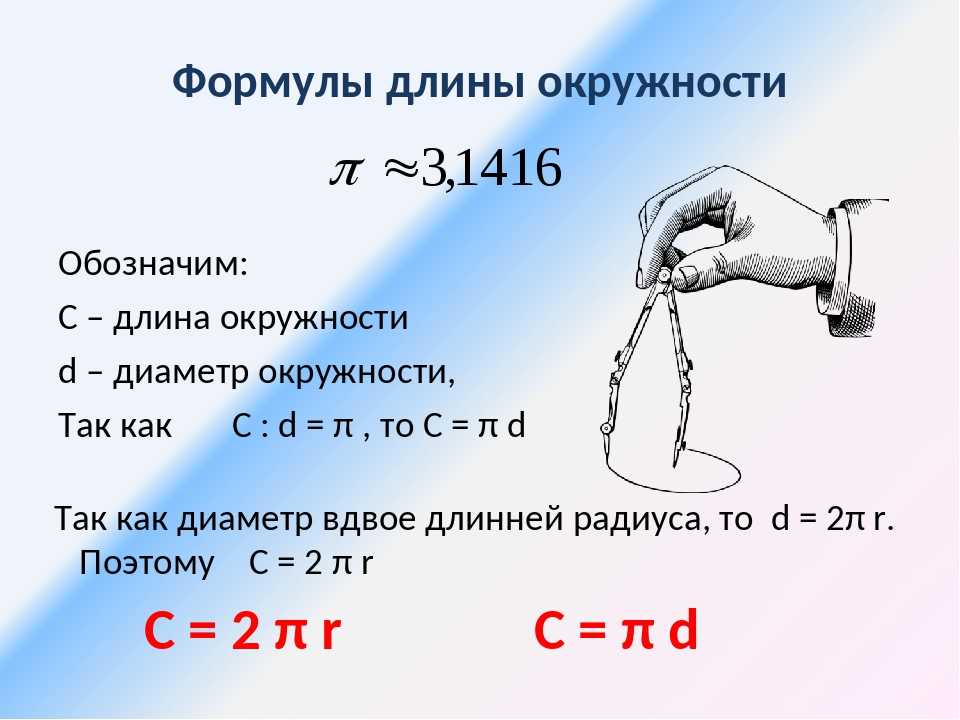 Земля настолько мала по сравнению с Солнцем (примерно 109 земных шаров могут поместиться поперек поверхности (диаметра) Солнца), что солнечные лучи падают на землю почти параллельно друг другу. Земля занимает лишь небольшую часть окружности Солнца.
Земля настолько мала по сравнению с Солнцем (примерно 109 земных шаров могут поместиться поперек поверхности (диаметра) Солнца), что солнечные лучи падают на землю почти параллельно друг другу. Земля занимает лишь небольшую часть окружности Солнца.
Это означает, что солнечные лучи, падающие на дом Эратосфена в Александрии, параллельны солнечным лучам, падающим на Сиену, город далеко на юге, который сегодня мы называем Асуаном.
Поколения внимательных египетских землемеров знали, что Сиена была 5000 стадий — древние единицы измерения, эквивалентные 804 километрам или 500 милям — к югу от Александрии. Эратосфен тоже это знал.
Параллельные линии
В Сиене был глубокий, широкий колодец. В местный полдень каждого летнего солнцестояния (самый длинный день на Земле и самая короткая ночь) солнечные лучи шли прямо в колодец, а это означало, что Сиена идеально выровнялась с этими параллельными солнечными лучами. В колодце не появилось тени.
Эратосфен хорошо знал о Сиене, и он также знал солнце в Александрии, 804 км или 500 миль . на севере был , а не , идеально выровненный с параллельными лучами солнца в местный полдень в день летнего солнцестояния.
Все, что торчит из земли в Александрии — как палка — отбрасывало тень, в то же время палка в Сиене отбрасывала нет тень.
Если бы Эратосфен мог точно измерить угол тени палки, вбитой перпендикулярно в александрийскую землю, он мог бы использовать только две части информации для вычисления окружности земли:
Угол тени палки в Александрии в день летнего солнцестояния
Расстояние от Александрии до Сиены
Дуга — это часть или часть окружности круга или сферы. Один полный оборот вокруг Земли (один оборот) равен
360° , поэтому любая дуга круга или сферы является дробным срезом 360° . Люди в 240 г. до н.э. умел измерять окружность. Они знали формулу длины окружности сферы 2πr. Они знали о центральных углах и дугах.
Они знали о центральных углах и дугах.
Расстояние от Александрии до Сиены является одной из таких дуг, измеримой и известной частью общей окружности Земли.
Соответствующие углы
Эратосфен знал, что расстояние от Александрии до Сиены на сферической земле равно дуге окружности, а это означает, что два города образуют центральный угол в центре земли, который мы будем называть 𝜃.
Это провело линию от недоступного центра Земли, C , до Александрии, A , пересекая параллельные солнечные лучи.
Секущая — это линия, которая пересекает другие прямые, а в случае параллельных прямых секущей образуется соответствующих углов . Какой угол он образует на одной параллельной линии, такой же угол он создает и на другой.
Это сделало угол тени палки в Александрии в день летнего солнцестояния соответствующим углу центрального угла 𝜃 в недоступном центре Земли.
Если бы он мог точно измерить угол тени палки в Александрии в местный полдень в день летнего солнцестояния, у Эратосфена были бы обе части информации, необходимые для вычисления окружности Земли.
[справочная диаграмма с https://ourplnt.com/how-eratosthenes-calculated-earth-circumference/eratosthenes-calculation-earth-circumference/ предоставлена для ясности и вдохновения]
Эратосфен провел измерения и обнаружил, что угол равен 7,2° , что означало центральный угол 𝜃 также был 7,2° . Этот угол, 7,2 ° , 1/50 полного круга:
7,2 °/360 ° = 1/50
SO, если 804 KM или 500 MI. (или 5000 стадий для Эратосфена) было 1/50, умножение дает вам окружность Земли:
500 миль. х 50 = 25 000 миль.
804 km x 50 = 40,200 km
And for any of you ancient Greeks out there, 5,000 stadia x 50 = 250,000
stadia
The Земля, как мы сказали, представляет собой сплюснутый сфероид, поэтому геодезисты (ученые, которые измеряют Землю и ее положение в пространстве) измерили и вычислили среднюю длину окружности Земли как 40,075 км или 24,901 миль .
Эратосфен около 2200 лет назад отклонялся всего на 125 км или 101 миль . И он сделал это, имея лишь небольшие познания в географии и математике, колодец и палку.
Расчет окружности Земли
Научные проекты
131 отзыв
Аннотация
Какой большой линейки вам понадобится, чтобы измерить окружность Земли? Знаете ли вы, что вы можете сделать это с помощью аршина? (И вам не придется путешествовать по всему миру!)
Краткий обзор
Астрономия
Краткий (2-5 дней)
Для этого проекта вам необходимо понять некоторые основные принципы геометрии. Вам понадобится друг или родственник в далеком городе, чтобы сделать для вас измерение тени в тот же день, когда вы сделаете свое. Вам обоим понадобится ясная погода.
Доступен
Очень низкий (менее 20 долларов США)
Нет проблем
Эндрю Олсон, доктор философии, Научные друзья
Источники
Этот проект основан на:
- SIT.
 (2004). Оцените окружность Земли, используя расчеты Эратосфена, Технологический институт Стивенса, Центр инноваций в инженерном и научном образовании. Проверено 1 июля 2022 г.
(2004). Оцените окружность Земли, используя расчеты Эратосфена, Технологический институт Стивенса, Центр инноваций в инженерном и научном образовании. Проверено 1 июля 2022 г.
Задача
Целью этого проекта является оценка окружности Земли путем составления математической пропорции на основе простых измерений.
Введение
В этом проекте вы оцените окружность Земли, используя метод, разработанный около 2200 лет назад Эратосфеном, греческим математиком и библиотекарем большой библиотеки в Александрии, в Египте.
Из прочитанного Эратосфен знал, что в Сиене (городе почти к югу от Александрии) солнце в полдень в определенный день года находится прямо над головой. В тот день в полдень вертикальные предметы не отбрасывали тени, а на дне колодца можно было увидеть отражение солнца. Он рассудил, что солнце находится достаточно далеко от земли, так что лучи света от солнца для всех практических целей параллельны друг другу, когда достигают земли. Если бы он измерил угол тени в Александрии в полдень того же дня, когда солнце находилось прямо над головой в Сиене, угол тени был бы таким же, как центральный угол «клина» земли между Александрией и Сиеной. .
Если бы он измерил угол тени в Александрии в полдень того же дня, когда солнце находилось прямо над головой в Сиене, угол тени был бы таким же, как центральный угол «клина» земли между Александрией и Сиеной. .
На рис. 1 ниже показаны рассуждения Эратосфена. Представьте, что земля разрезана пополам вдоль линии север-юг между Александрией и Сиеной, а затем вы смотрите на разрез лицом к лицу (синий кружок). Конечно, рисунок не является чертежом в масштабе, но он иллюстрирует принцип метода. Солнечные лучи представлены желтыми линиями. В Сиене солнечные лучи не отбрасывают теней. В Александрии вертикальная палка действительно отбрасывает тень. По мнению Эратосфена, угол тени в Александрии («солнечный угол», показанный оранжевым треугольником) также равен углу клина Земли между двумя городами («центральный угол», показанный оранжевым треугольником). другой оранжевый треугольник).
Так как в окружности 360 градусов, то, разделив центральный угол на 360, он мог вычислить, сколько подобных секторов потребуется для завершения окружности. Он нанял кого-то, чтобы измерить сухопутное расстояние между двумя городами. Умножив сухопутное расстояние на количество секторов, он получил свою оценку окружности Земли. Например, предположим, что измеренный угол наклона солнца составил 7,2℃. Это означает, что центральный угол между Александрией и Сиеной также составлял 7,2℃. Тогда количество секторов, образующих полный круг, будет 360/7,2 = 50. Окружность Земли тогда будет в 50 раз больше расстояния по суше между Александрией и Сиеной.
Он нанял кого-то, чтобы измерить сухопутное расстояние между двумя городами. Умножив сухопутное расстояние на количество секторов, он получил свою оценку окружности Земли. Например, предположим, что измеренный угол наклона солнца составил 7,2℃. Это означает, что центральный угол между Александрией и Сиеной также составлял 7,2℃. Тогда количество секторов, образующих полный круг, будет 360/7,2 = 50. Окружность Земли тогда будет в 50 раз больше расстояния по суше между Александрией и Сиеной.
Оценка окружности Земли
Вы можете использовать метод Эратосфена для самостоятельного вычисления окружности Земли. Вы даже можете сделать расчет, когда солнце отбрасывает тень в полдень в обоих местах. Справочник Технологического института Стивенса по методу Эратосфена (SIT, 2004a) покажет вам, как справиться с этой ситуацией. Вы захотите внимательно изучить эту ссылку, как часть вашего фонового исследования.
Термины и понятия
Чтобы выполнить этот проект, вы должны провести исследование, которое позволит вам понимать следующие термины и понятия:
- Метод Эратосфена
- Местный полдень
- Долгота
- Широта
Вопросы
- Как вычислить центральный угол между двумя городами, если в полдень в обоих городах есть тени? (См.
 Библиографию, SIT. (2004), Часть B)
Библиографию, SIT. (2004), Часть B) - Как рассчитать центральный угол между двумя городами, если они находятся на противоположных сторонах зенита солнца (например, города на противоположных сторонах экватора)?
Библиография
- СИТ. (2004). Оцените окружность Земли, используя расчеты Эратосфена, Технологический институт Стивенса, Центр инноваций в инженерном и научном образовании. Проверено 12 июля 2022 г.
- Бизнес-инсайдер. (2016, 10 сентября). Как Эратосфен вычислил окружность Земли. Инсайдер бизнеса. Проверено 12 июля 2022 г.
- На этой веб-странице есть онлайн-калькулятор для определения поверхностного расстояния между двумя точками на Земле с учетом их широты и долготы:
Байерс, Дж.А. (1997). Поверхностное расстояние между двумя точками широты и долготы. Министерство сельского хозяйства США, Служба сельскохозяйственных исследований. Проверено 3 ноября 2006 г. . - На этих веб-страницах есть информация об Эратосфене:
- Хейнс, М.
 и С. Черчмен. (н.д.). Эратосфен. Астрономия 201: Наш дом во Вселенной, Корнельский университет. Проверено 2 ноября 2006 г. .
и С. Черчмен. (н.д.). Эратосфен. Астрономия 201: Наш дом во Вселенной, Корнельский университет. Проверено 2 ноября 2006 г. . - участников Википедии. (2006). Эратосфен. Википедия, свободная энциклопедия. Проверено 2 ноября 2006 г.
- Хейнс, М.
Материалы и оборудование
Для проведения этого эксперимента вам потребуются следующие материалы и оборудование:
- Участок открытой ровной поверхности на солнце в полдень
- Солнечный день
- Стержень метра
- Ведро с песком
- Большой лист бумаги (например, газетная бумага для измерения длины тени)
- Карандаш
- Т-образный угольник плотника или отвес (необязательно, но полезно, чтобы убедиться, что измерительная рейка стоит вертикально)
- Рулетка (метрическая)
- Транспортир
- Напишите другу по переписке из далекого города, который может провести измерения в полдень по местному времени того же дня
- Калькулятор
Экспериментальная процедура
- Проведите предварительное исследование, чтобы ознакомиться с приведенными выше терминами, понятиями и вопросами.

- Выясните, какое время будет «полдень по местному времени» в день проведения измерения. Местный полдень — это время на полпути между восходом и заходом солнца, когда солнце находится высоко в небе. Вы должны быть настроены и готовы измерить длину тени примерно за десять минут до этого времени, чтобы не пропустить его.
- Установите измерительную рейку в ведро с песком так, чтобы она стояла вертикально. Используйте Т-образный угольник, чтобы проверить вертикальность.
- Разложите большой лист бумаги, на котором отметьте длину тени от метровой палочки. Другой конец бумаги должен проходить под измерительной линейкой (см. рис. 2).
- Вы хотите измерить длину тени метровой линейки — от основания метровой палки до кончика тени — когда солнце находится в самой высокой точке неба.
- Отметьте, где основание измерительной линейки соприкасается с бумагой.
- Отметьте конец тени.
 Это будет немного нечетко; сделать все возможное, чтобы быть точным и последовательным. Отметьте время измерения рядом с отметкой.
Это будет немного нечетко; сделать все возможное, чтобы быть точным и последовательным. Отметьте время измерения рядом с отметкой. - Отмечайте конец тени каждые две минуты, начиная как минимум за 10 минут до местного полудня. Тень должна быть самой короткой прямо в местный полдень. Когда тень начнет увеличиваться в длину, измерения можно прекратить.
- Удалите бумагу из-под измерительной линейки и с помощью рулетки измерьте длину тени в местный полдень (самую короткую длину).
- Измерьте высоту метровой палки от земли до кончика (поскольку вы держите ее вертикально в ведре с песком, она будет немного выше одного метра).
- Вот как использовать транспортир и ваши измерения, чтобы определить угол наклона солнца.
- Создайте прямоугольный треугольник с длиной основания ( BC ), равной длине тени, и высотой ( AB ), равной высоте метровой палки (см. рисунок 3).

- Расположите транспортир, как показано на рис. 3, и прочтите значение угла ( BAC ).
- Создайте прямоугольный треугольник с длиной основания ( BC ), равной длине тени, и высотой ( AB ), равной высоте метровой палки (см. рисунок 3).
- Отправьте свои измерения своему партнеру в отдаленный город по электронной почте, и пусть они отправят свои измерения вам. Следуйте процедуре шага 7, чтобы вычислить угол наклона солнца в их местоположении.
- Узнайте широту и долготу каждого местоположения.
- Вычислите расстояние с севера на юг между двумя точками.
- Чтобы найти расстояние, вы можете использовать масштаб карты. Измерьте, как далеко каждый город от экватора (по прямой линии). Если города находятся по одну сторону от экватора, из большего расстояния вычтите меньшее расстояние. Если два города находятся на противоположных сторонах экватора, сложите два расстояния вместе.
- Альтернативой использованию масштаба карты является использование информации о широте и долготе для каждого города и онлайн-калькулятора расстояния (например, Byers, 1997).
 Как и в случае с масштабом карты, вы хотите рассчитать расстояние каждого города от экватора (введите 0℃ для широты и ту же долготу, что и для интересующего города), а затем используйте эту информацию, чтобы определить расстояние с севера на юг между два города.
Как и в случае с масштабом карты, вы хотите рассчитать расстояние каждого города от экватора (введите 0℃ для широты и ту же долготу, что и для интересующего города), а затем используйте эту информацию, чтобы определить расстояние с севера на юг между два города.
- Используя расстояние с севера на юг между двумя точками и угол наклона солнца в каждой точке, вы сможете вычислить окружность Земли.
- Насколько близка ваша оценка к фактическому значению?
Задать вопрос эксперту
У вас есть конкретные вопросы о вашем научном проекте? Наша команда ученых-добровольцев может помочь. Наши эксперты не сделают всю работу за вас, но они сделают предложения, дадут рекомендации и помогут устранить неполадки.
Опубликовать вопрос
Варианты
- Проведите сравнительное исследование, используя солнце в разное время суток. Какое время суток дает наиболее точный результат?
- Каковы возможные источники ошибок в ваших измерениях? Можете ли вы использовать оценки погрешности, чтобы установить верхнюю и нижнюю границы ваших вычислений для окружности Земли? Например, предположим, что вы определили, что ваши измерения угла наклона солнца точны с точностью до 0,5 градуса, каковы будут верхняя и нижняя границы для вашей оценки окружности?
- Используйте архивные данные проекта The Noon Day для оценки окружности Земли с использованием нескольких различных пар измерений (SIT, 2004b).
 Используйте измерения из мест, которые находятся близко друг к другу и далеко друг от друга. Какие измерения дают вам наиболее точную оценку окружности Земли?
Используйте измерения из мест, которые находятся близко друг к другу и далеко друг от друга. Какие измерения дают вам наиболее точную оценку окружности Земли?
Вакансии
Если вам нравится этот проект, вы можете изучить следующие родственные профессии:
- Руководство по проекту научной ярмарки
- Другие подобные идеи
- Идеи астрономического проекта
- Мои любимые
Лента новостей по этой теме
,
,
Процитировать эту страницу
Общая информация о цитировании представлена здесь. Обязательно проверьте форматирование, включая заглавные буквы, для используемого метода и при необходимости обновите цитату.
MLA Style
Сотрудники научных друзей.
«Вычисление окружности Земли». Друзья по науке ,
16 июля 2022 г.,
https://www.

 14159265358979323846f;
14159265358979323846f;
 Формулу обычно записывают следующим образом: C = π*D.
Формулу обычно записывают следующим образом: C = π*D. (2004). Оцените окружность Земли, используя расчеты Эратосфена, Технологический институт Стивенса, Центр инноваций в инженерном и научном образовании. Проверено 1 июля 2022 г.
(2004). Оцените окружность Земли, используя расчеты Эратосфена, Технологический институт Стивенса, Центр инноваций в инженерном и научном образовании. Проверено 1 июля 2022 г. Библиографию, SIT. (2004), Часть B)
Библиографию, SIT. (2004), Часть B) и С. Черчмен. (н.д.). Эратосфен. Астрономия 201: Наш дом во Вселенной, Корнельский университет. Проверено 2 ноября 2006 г.
и С. Черчмен. (н.д.). Эратосфен. Астрономия 201: Наш дом во Вселенной, Корнельский университет. Проверено 2 ноября 2006 г.
 Это будет немного нечетко; сделать все возможное, чтобы быть точным и последовательным. Отметьте время измерения рядом с отметкой.
Это будет немного нечетко; сделать все возможное, чтобы быть точным и последовательным. Отметьте время измерения рядом с отметкой.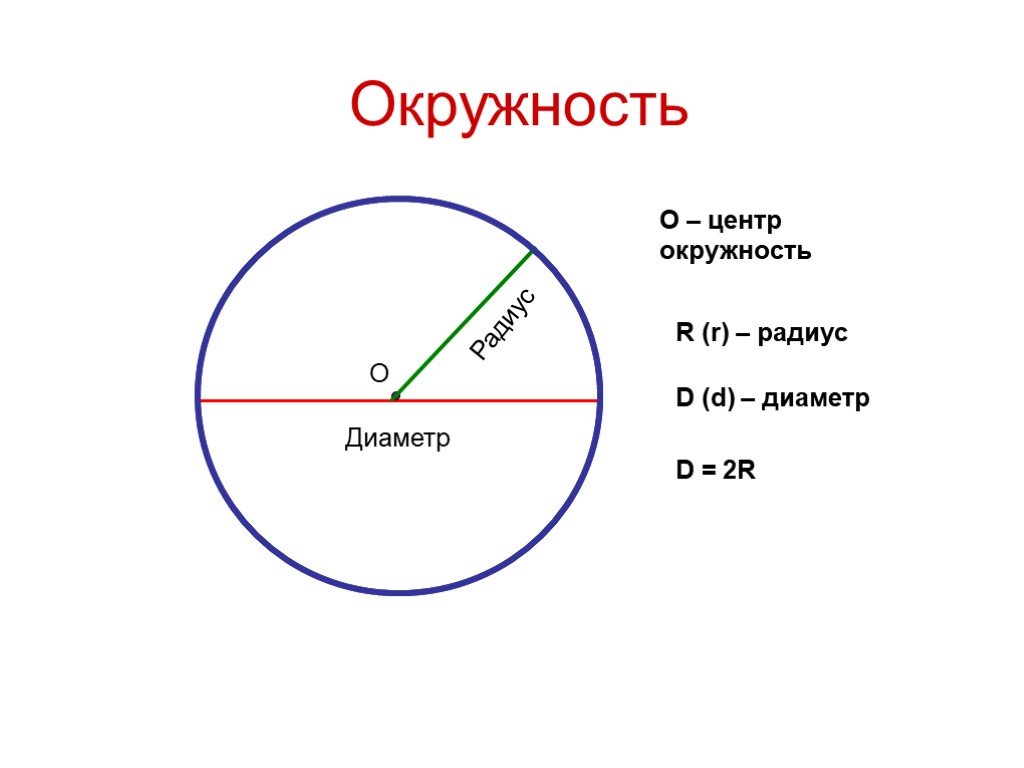
 Как и в случае с масштабом карты, вы хотите рассчитать расстояние каждого города от экватора (введите 0℃ для широты и ту же долготу, что и для интересующего города), а затем используйте эту информацию, чтобы определить расстояние с севера на юг между два города.
Как и в случае с масштабом карты, вы хотите рассчитать расстояние каждого города от экватора (введите 0℃ для широты и ту же долготу, что и для интересующего города), а затем используйте эту информацию, чтобы определить расстояние с севера на юг между два города.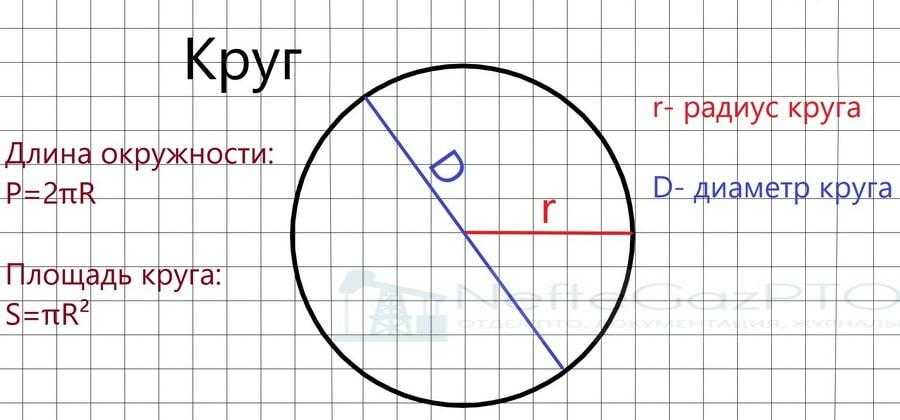 Используйте измерения из мест, которые находятся близко друг к другу и далеко друг от друга. Какие измерения дают вам наиболее точную оценку окружности Земли?
Используйте измерения из мест, которые находятся близко друг к другу и далеко друг от друга. Какие измерения дают вам наиболее точную оценку окружности Земли?