Расстояние от точки до прямой в пространстве онлайн: Онлайн калькулятор. Расстояние от точки до прямой в пространстве

Найти расстояние от точки до прямой в пространстве — онлайн калькулятор

Расстояние от точки до прямой в пространстве равно длине перпендикуляра, опущенного из точки на прямую. Чтобы быстро узнать ответ задачи, можно использовать автоматические подсчеты. Набор калькуляторов поможет вычислить результат любого задания по алгебре и геометрии.

Сервисом пользуются учащиеся школ и университетов. Также за готовым решением обращаются преподаватели, родители учеников и специалисты инженерного профиля.

1. Выберите, в какой форме представлено уравнение прямой.

Вариант 1

2. Введите данные в соответствующие окна. Отправьте задание на вычисление кнопкой «Рассчитать».

Вариант 1

3. Получите решение и ответ.

 

Вариант 2

2. Введите данные в соответствующие окна. Отправьте задание на вычисление кнопкой «Рассчитать».

 

Вариант 2

3. Получите решение и ответ.

Ответ:

Решение

Ответ:

• list» :key=»`error-${eIdx}`» v-html=»e»/>

Похожие калькуляторы:

• Длина отрезка. Расстояние между точками
• Середина отрезка
• Каноническое уравнение прямой проходящей через две точки
• Параметрическое Уравнение прямой проходящей через две точки
• Расстояние от точки до прямой на плоскости
• Уравнение плоскости (координаты трех точек)
• Уравнение плоскости (координаты вектора нормали и точки)
• Точка пересечения прямых (с угловыми коэффициентами)
• Расстояние от точки до плоскости
• Расстояние между плоскостями
• Угол между плоскостями
• Угол между прямой и плоскостью

Как найти расстояние от прямой до точки в пространстве.

Онлайн-калькулятор

Вычислить расстояние между точкой и прямой в пространстве можно по формуле:

Программа автоматически выполняет комплекс действий. Нет необходимости вычислять результат каждого действия отдельно. Это сокращает время на решение задания и исключает ошибки и потерю данных.

Почему калькуляторы на нашем сайте часто используют:

• Вы получаете быстрый расчет без ожидания регистрации и перехода по сторонним страницам. Во время проверки знаний особенно важно без промедлений получить решение.
• Расчеты на сайте не требуют платежей. Раздел с вычислениями позволяет ученикам повышать свой уровень знаний без посторонней помощи. Понятный интерфейс с подробными действиями позволяет лучше запомнить материал.
• На запросы не установлены ограничения. Тренироваться в подсчетах, используя любую программу раздела, можно необходимое количество раз в удобное для вас время.

Пошаговые вычисления помогут проверить собственные расчеты, выявить ошибки в алгоритме. Готовое решение можно использовать в качестве примера, запоминать и применять в аналогичных заданиях. Во время зачета или экзамена на сайте можно быстро решить задание и получить хорошую оценку. Если тема не поддается освоению, обратитесь к консультанту. Он найдет для вас преподавателя по выгодной цене.

Понравился калькулятор? Поделись с друзьями!

Расстояние от точки до прямой в пространстве

Похожие презентации:

Расстояние от точки до плоскости в пространстве

Расстояние между прямыми в пространстве

Расстояние между скрещивающимися прямыми

Расстояние от точки до плоскости в пространстве

Угол между прямой и плоскостью. Упражнения

Угол между прямыми в пространстве

Угол между прямыми в пространстве

Двугранный угол. Задачи

Двугранный угол. (1)

Задания С-2 по математике ЕГЭ-2014

1. РАССТОЯНИЕ ОТ ТОЧКИ ДО ПРЯМОЙ

Расстоянием от точки до прямой в пространстве
называется длина перпендикуляра, опущенного из
данной точки на данную прямую.

2. Нахождение расстояний 1

Для нахождения расстояния от точки A до прямой l перпендикуляр
AH, опущенный из данной точки на данную прямую, представляют
в качестве высоты треугольника, одной вершиной которого является
точка A, а сторона BC, противолежащая этой вершине, лежит на
прямой l. Зная стороны этого треугольника, можно найти и его
высоту.
При этом возможны следующие случаи:
1. Треугольник ABC – равнобедренный, AB = AC. Пусть AB = AC =
b, BC = a. Искомый перпендикуляр находится из прямоугольного
треугольника ABH:
2
AH b 2
a
.
4
H

3. Нахождение расстояний 2

2. Треугольник ABC – равнобедренный, AC = BC.
2
c
2
Пусть AB = c, AC = BC = a. Найдем высоту CG. CG a .
42 2
2
Площадь треугольника ABC равна 1 AB CG 1 c a 2 c c 4a c .
2
2
С другой стороны, площадь этого треугольника равна
4
1
1
BC AH a AH . Приравнивая первое и второе значения
2
2
площади, получим значение искомого перпендикуляра
c 4a 2 c 2
AH
.
2a
4

4. Нахождение расстояний 3

3. Треугольник ABC – прямоугольный, угол A – прямой.
Пусть AB = c, AC = b. Тогда гипотенуза BC равна b2 c 2 .
Удвоенная площадь треугольника ABC, с одной стороны,
bc
равна bc, а с другой h b 2 c 2 . Следовательно, h 2 2 .
b c

5. Нахождение расстояний 4

4. Треугольник ABC – произвольный.
Пусть AB = c, AC = b, BC = a, ACB . По теореме косинусов
имеет место равенство c2 a2 b2 2ab cos . Откуда
a 2 b2 c 2 Зная косинус угла, можно найти его синус
cos
.
2ab
sin 1 cos 2 , а зная синус , можно найти высоту AH b sin .

6. Куб 1

В единичном кубе A…D1 найдите расстояние от
точки A до прямой BC.

7. Куб 4

В единичном кубе A…D1 найдите расстояние от
точки A до прямой BC1.

8. Куб 5

В единичном кубе A…D1 найдите расстояние от
точки A до прямой DC1.

9. Куб 6

В единичном кубе A…D1 найдите расстояние от
точки A до прямой B1C1.
В единичном кубе A…D1 найдите расстояние от
точки A до прямой CC1.
В единичном кубе A…D1 найдите расстояние от
точки A до прямой BD.

12. Куб 12

В единичном кубе A…D1 найдите расстояние от точки A
до прямой B1D1.

13. Куб 13

В единичном кубе A…D1 найдите расстояние от точки A
до прямой CB1.

14. Куб 16

В единичном кубе A…D1 найдите расстояние от
точки A до прямой BD1.

15. Куб 18

В единичном кубе A…D1 точка E – середина ребра C1D1.
Найдите расстояние от точки A1 до прямой BE.

16. Пирамида 2

В правильной пирамиде SABCD, все ребра которой равны
1, найдите расстояние от вершины S до прямой AB.

17. Пирамида 3

В правильной пирамиде SABCD, все ребра которой равны
1, найдите расстояние от вершины A до прямой SB.

18. Пирамида 8

В правильной пирамиде SABCDEF, боковые ребра
которой равны 2, а ребра основания – 1, найдите
расстояние от точки A до прямой SB.

19. Призма 5

В правильной треугольной призме ABCA1B1C1, все ребра
которой равны 1, найдите расстояние от точки A до прямой BC.

20. Призма 10

В правильной треугольной призме ABCA1B1C1, все ребра которой
равны 1, найдите расстояние от точки A до прямой BD1, где D1 –
середина ребра A1C1.

English     Русский Правила

Трехмерный калькулятор расстояний

Базовый калькулятор

3D Калькулятор расстояний

(Х ₁ , Y ₁ , Z ₁ ) =

(X ₂ , Y ₂ , Z ₂ ) =

92} \)

\( d = \sqrt{100 + 4 + 1} \)

\( d = \sqrt105 \)

\( d = 10.246951 \)

Поделитесь этой ссылкой для ответа: help
Вставьте эту ссылку в электронное письмо, текст или социальные сети.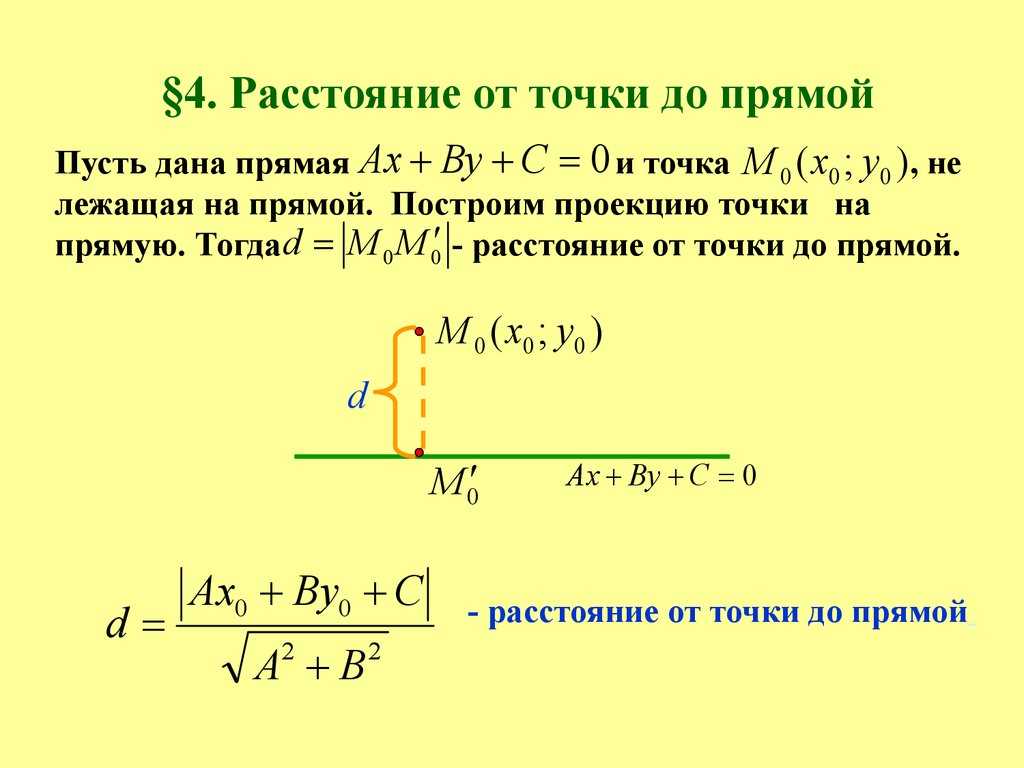

Получить виджет для этого калькулятора

© Calculator Soup

Поделитесь этим калькулятором и страницей

Калькулятор Использование

Введите 2 набора координат в трехмерной декартовой системе координат (X ₁ , Y ₁ , Z ₁ ) и (X ₂ , Y ₂ , Z ₂ ), чтобы получить расчет формулы расстояния для 2 точек и рассчитать расстояние между 2 точками.

Принимает положительные или отрицательные целые и десятичные дроби.

Формула расстояния:

Расстояние между двумя точками — это длина соединяющего их пути. Кратчайшее расстояние пути — прямая линия. В трехмерной плоскости расстояние между точками (X 92} \]

Возведение в квадрат слагаемых получаем,

\[d = \sqrt {144 + 25 + 225} \]

добавление 3 результатов,

\[d = \sqrt {394} \]

наконец,

\[ д = 19,849433 \]

 

Подписаться на калькуляторSoup:

евклидова геометрия — Расстояние между точкой и линией в пространстве

спросил 11 лет, 11 месяцев назад

Изменено 8 лет, 10 месяцев назад

Просмотрено 2к раз

$\begingroup$

У меня есть две точки $P_1(x_1, y_1, z_1)$ и $P_2(x_2, y_2, z_2)$ на прямой, $L$, и еще одна точка $P_0(x_0, y_0, z_0)$.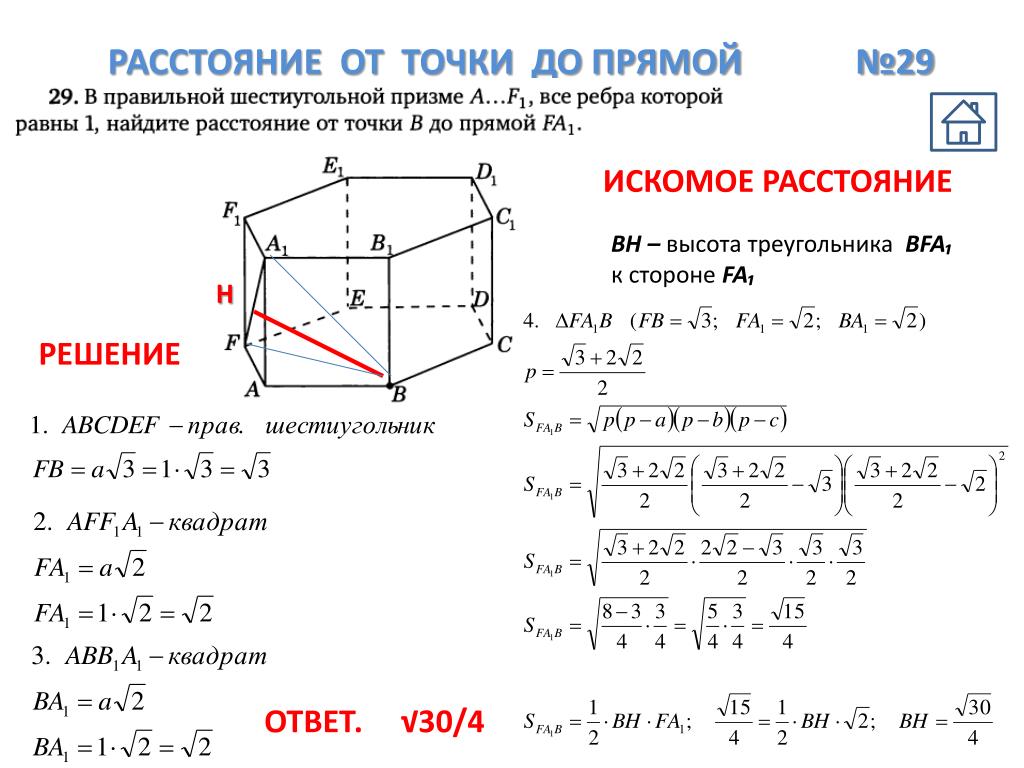

Я хочу найти расстояние между $P_0$ и $L$. Может ли кто-нибудь помочь?

• евклидова геометрия

$\endgroup$

11

$\begingroup$

Расстояние $h$ от точки $P_0=(x_0,y_0,z_0)$ до прямой, проходящей через точки $P_1=(x_1,y_1,z_1)$ и $P_2=(x_2,y_2,z_2)$, равно определяется выражением $h=2A/r$, где $A$ — площадь треугольника, определяемого тремя точками, а $r$ — расстояние от $P_1$ до $P_2$. Значения $r$ и $A$ можно вычислить следующим образом: 92},$

где

$a_1=x_0y_1+x_1y_2+x_2y_0 — (y_0x_1+y_1x_2+y_2x_0),\\ a_2=y_0z_1+y_1z_2+y_2z_0 — (z_0y_1+z_1y_2+z_2y_0),\\ a_3=x_0z_1+x_1z_2+x_2z_0 — (z_0x_1+z_1x_2+z_2x_0).$

$\endgroup$

$\begingroup$

Кратчайшее расстояние от точки до прямой всегда перпендикулярно данной прямой.