Преобразование графиков тригонометрических функций — презентация онлайн
Похожие презентации:
Преобразование графиков тригонометрических функций и их свойства
Преобразование графиков функций
Преобразование графиков тригонометрических функций
Преобразования графиков функций
Преобразование графиков функции
Преобразование графиков функции
Преобразование графиков тригонометрических функций
Творческая работа: «Преобразования графиков функции»
Преобразование графиков тригонометрических функций
Преобразование графиков функций
1. Преобразование графиков тригонометрических функций
Авторы проектаучителя математики
ГБС(К)ОУ школы –
интерната №113
г.о.Самара
Губарева Е.Г.
Пискаева С.В.
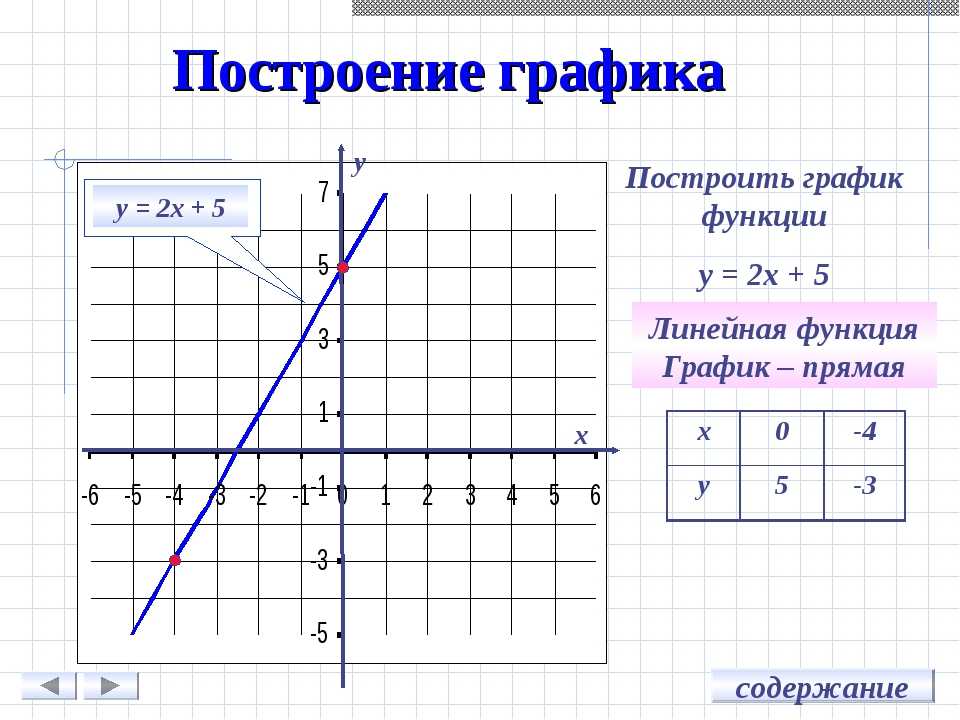
2. Параллельный перенос на вектор (0; b) вдоль оси ординат: График функции f(x)+b получается параллельным переносом графика f(x) в
положительном направлении оси ОУ на ǀbǀ единиц при b>0 и в отрицательномнаправлении этой оси на ǀbǀ единиц при b<0.

3. Параллельный перенос вдоль оси абсцисс на вектор (c; 0). График функции f(x+с) получается параллельным переносом в
отрицательном направлении оси ОХ на ǀсǀ при с>0 и в положительномнаправлении на ǀсǀ при с<0.
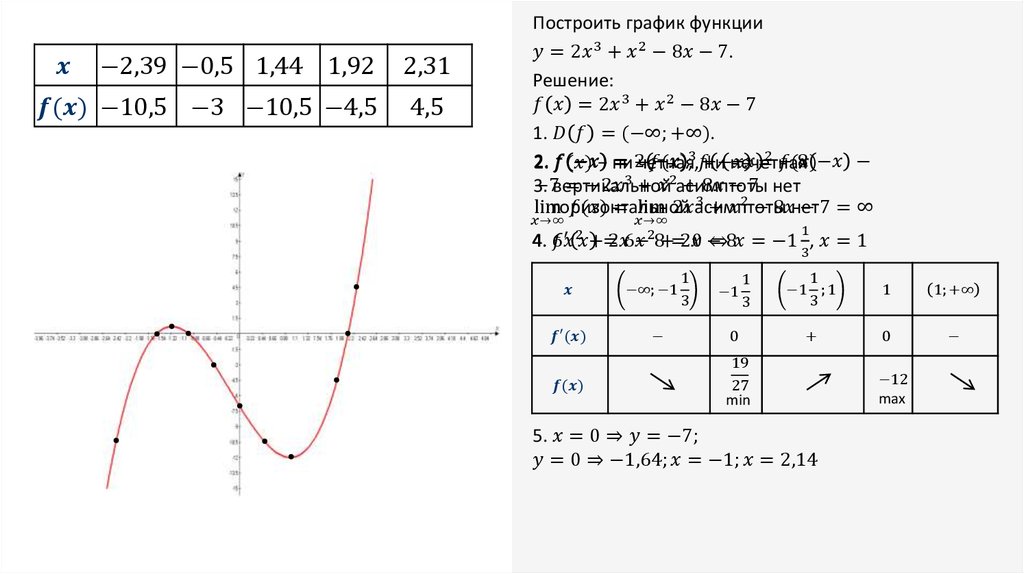
4. Растяжение вдоль оси ОX с коэффициентом k, которое задается формулами х₁=kх, у₁=y. График функции f(kx) получается сжатием
графика f(x) в k раз к оси ОУ при k>1 или растяжением в1/k раз от оси ОУ при 0<k<1.
5. Растяжение вдоль оси ОУ с коэффициентом a, которое задается формулами х₁=х, у₁=ay. График функции аf(x) получается растяжением
графика f(x) вдоль оси ОУ в а раз приа > 1 и сжатием вдоль оси ОУ в 1/a раз при 0 < a < 1.
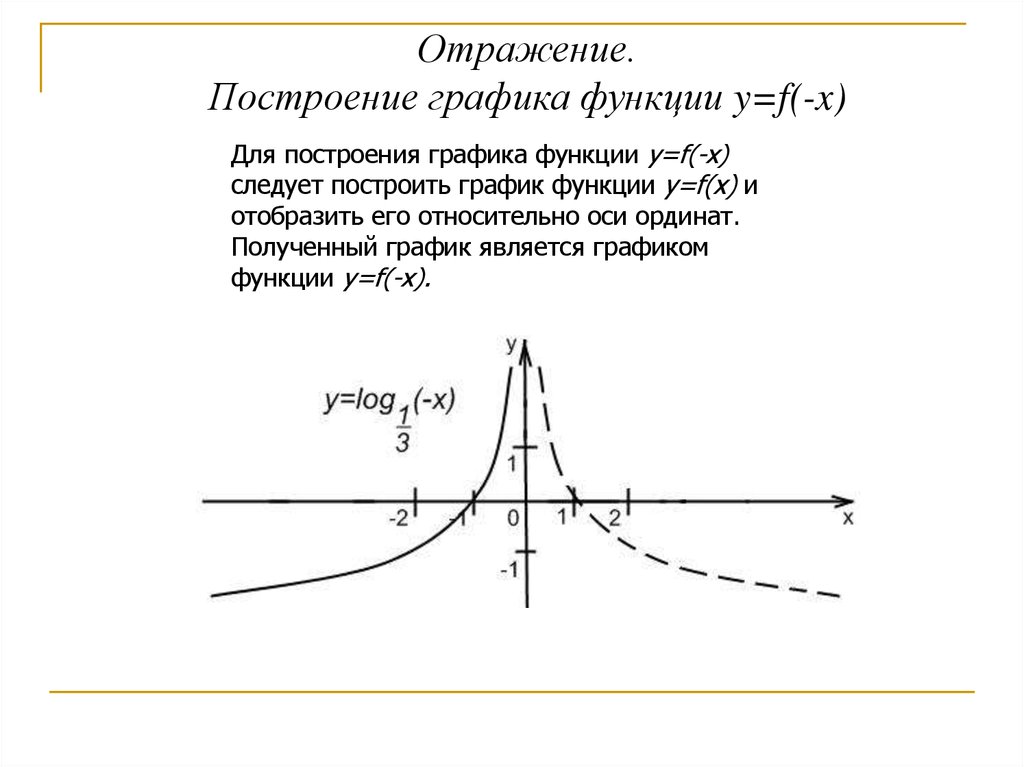
6. График функции y= f(-x) получается симметричным отображением графика f(x) относительно оси ОУ.
7. График функции y= -f(x) получается симметричным отображением графика f(x) относительно оси ОX.
8. График функции │f(x)│ получается из графика f(x) так: часть графика f(x), лежащая над осью ОХ, сохраняется, часть , лежащая под
осью ОХ, отображается симметричноотносительно оси ОХ.
9. График функции f(│x│) получается из графика функции f(x) так: при х ≥ 0 график f(x) сохраняется, а при х < 0 полученная часть
График функции f(│x│)получается из графика функции f(x) так: при х ≥ 0 график f(x) сохраняется, а при
х < 0 полученная часть графика отображается симметрично относительно оси ОУ.
10. Пошаговое построение графика функции у = 2sin(2x-π/3)
1. Построим график функции у = sin x2. Строим график функции y = sin 2x, сжимая
исходный график в 2 раза к оси ОУ
3. Строим график функции у = sin(2x – π/3), сдвигая
параллельным переносом в положительном
направлении на π/3 график
y = sin2x
4. Строим график функции у = 2sin(2x — π/3),
растяжением вдоль оси ОУ в 2 раза графика
у = sin(2x – π/3)
11. Проверь себя:
12. Итоговый график
1213. Список используемых источников
1. Учебник для 10-11 классов общеобразовательных учреждений«Алгебра и начала анализа» под редакцией А.
 Н.Колмогоров
Н.Колмогоров2. www.cleverstudents.ru/function_graph_transformations.html
3. www.distedu.ru/mirror/_fiz/archive.1september.ru/mat/2001/47/no47_01.htm
Построение графиков функций, содержащих знак модуля
t heory.html
Элементарные функции и их графики
5. uztes.ru/abstracts/?idabstract=51
Тригонометрические функции. Синус и косинус
13
English Русский Правила
Пошаговый график остаточного графика — MathCracker.com
Решатели Статистика
Инструкции: Используйте этот график остаточного графика, чтобы построить график остатка для значения, полученного с помощью анализа линейной регрессии, на основе предоставленных вами выборочных данных.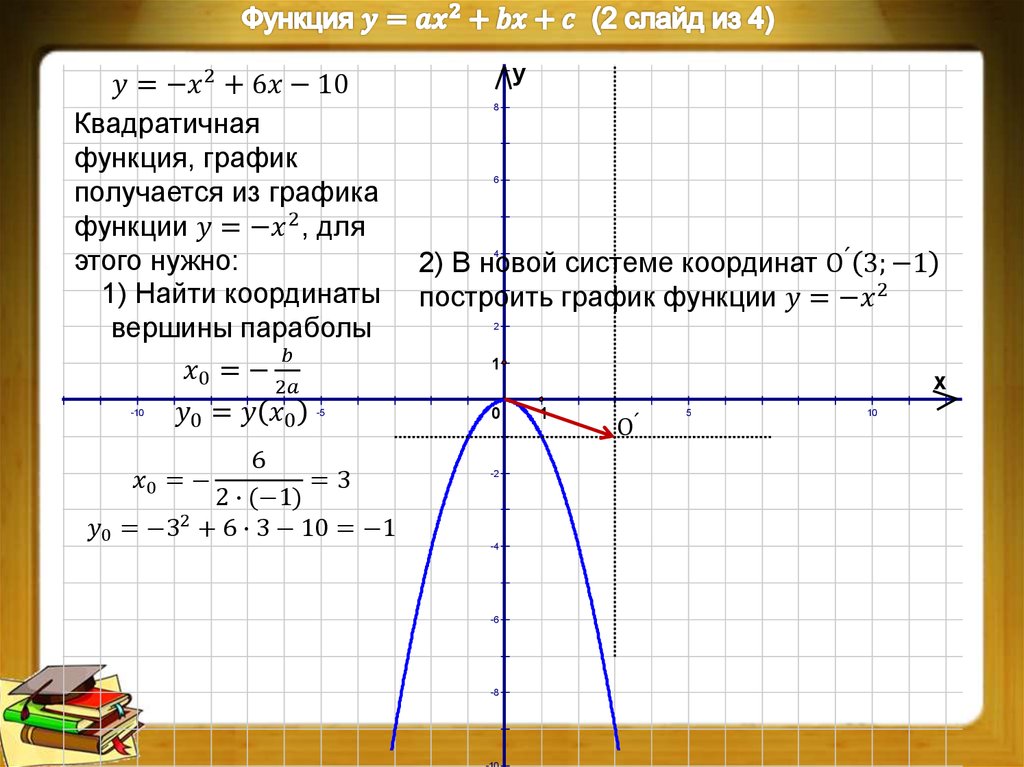
Независимая переменная \(X\) выборочные данные (разделенные запятой или пробелом) =
Зависимая переменная \(Y\) выборочные данные (разделенные запятой или пробелом) =
Имя независимой переменной (необязательно) =
Имя зависимой переменной ( опционально) =
Одним из основных требований, предъявляемых к результатам и прогнозам регрессионного анализа, является соблюдение допущений линейной регрессии. Предположения о независимости, нормальности и гомоскедастичности ошибок имеют решающее значение для получения надежных результатов регрессии.
Использование графиков, основанных на остатках, имеет решающее значение для быстрой оценки того, не выполняются ли допущения и требуется ли корректировка.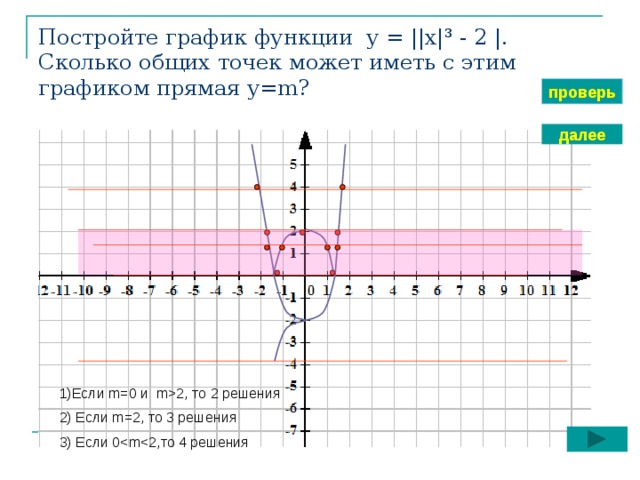
После того, как мы оценили коэффициенты регрессии, соответствующие отрезку y и наклону, \(\hat \beta_0\) и \(\hat \beta_1\), мы можем приступить к вычислению прогнозируемых значений.
Как вычислить остаточные значения регрессии?
Расчет прост. Первый шаг состоит из вычисления коэффициентов линейной регрессии, которые используются для вычисления прогнозируемых значений следующим образом:
\[ \ шляпа у = \ шляпа \ бета_0 + \ шляпа \ бета_1 х \]
Как только предсказанные значения \(\hat y\) вычислены, мы можем вычислить остатки следующим образом:
\[\text{Остаток} = y — \шляпа y\]
Что показывает остаточный график?
Остаточные графики используются для проверки предположений о линейной регрессии. Это визуальный способ быстро оценить, серьезно ли нарушены допущения или нет. Для более точной оценки выполнения допущений линейной регрессии для каждого допущения существует специальный статистический тест.
Это визуальный способ быстро оценить, серьезно ли нарушены допущения или нет. Для более точной оценки выполнения допущений линейной регрессии для каждого допущения существует специальный статистический тест.
Различают следующие типы графиков остатков: остатки по сравнению с числом наблюдений (обеспечиваемые этим калькулятором), которые используются для оценки гипотезы о независимости ошибки. Кроме того, у нас есть график нормальности остатков (который используется для оценки нормальности ошибок) и график остатков по сравнению с прогнозируемым значением, который используется для оценки предположения о гомоскедастичности ошибки.
Как построить график остатков модели линейной регрессии?
Существуют различные типы графиков с остатками. Этот калькулятор покажет вам расчет остатков и покажет вам график остатков в зависимости от числа наблюдений.
Этот создатель остаточного графика позволяет вам оценить, появляются ли остатки случайным образом во времени (чтобы они были независимыми), или есть ли какая-то закономерность во времени (что указывало бы на то, что остатки не будут независимыми, и предположение о регрессии будет нарушено).
Если вам нужно только вычислить результаты регрессии, вы можете использовать это калькулятор модели линейной регрессии , чтобы получить оценочные коэффициенты регрессии на основе предоставленных выборочных данных.
Базовый пакет статистики Создатель графиков Графический инструмент Предположения линейной регрессии Остаточный участок Остаточный графограф Остаточный производитель сюжета Калькулятор статистики Решатель статистики
Table View – GeoGebra
- Автор:
- GeoGebra Team
- Тема:
- Функции, График функций
Что такое Table View?
Создайте таблицу значений для функции, используя табличное представление графического калькулятора GeoGebra !
С Table View вы можете. ..
..
- создать таблицу значений в указанном диапазоне
- показать/скрыть сгенерированные точки в Графический вид
- изменить функцию
- изменить диапазон значений
Изучите таблицу значений функций, открыв
Исследуйте конструкцию…
Инструкции
| 1. | | Введите в строке ввода и нажмите Введите . Функция будет автоматически помечена как f(x) и отображается в графическом представлении . |
| 2. | | Откройте контекстное меню, нажав кнопку Еще справа от строки, содержащей f(x) . |
| 3. | | Выбрать Таблица значений . |
| 4. | | Открывается диалоговое окно, в котором вы можете определить Начальное значение для x , Конечное значение для x и Шаг . Нажмите OK для подтверждения настроек. Нажмите OK для подтверждения настроек. |
| 5. | | Табличное представление открывается автоматически, поэтому вы можете сразу увидеть значения. |
| 6. | | Вернитесь к Algebra View , введите в строку ввода и нажмите Enter . Функция будет автоматически помечена как g(x) и отображена в графическом представлении 9.0068 . |
| 7. | | Откройте контекстное меню, нажав кнопку Еще справа от строки, содержащей g(x) . |
| 8. | | Выбрать Таблица значений . |
| | Примечание: На этот раз диалоговое окно для определения начального и конечного значений не будет отображаться, поскольку вы уже установили эти значения на шаге 4. Вы можете изменить значения позже. | |
| 10. | | Таблица открывается автоматически, поэтому вы можете сразу увидеть значения.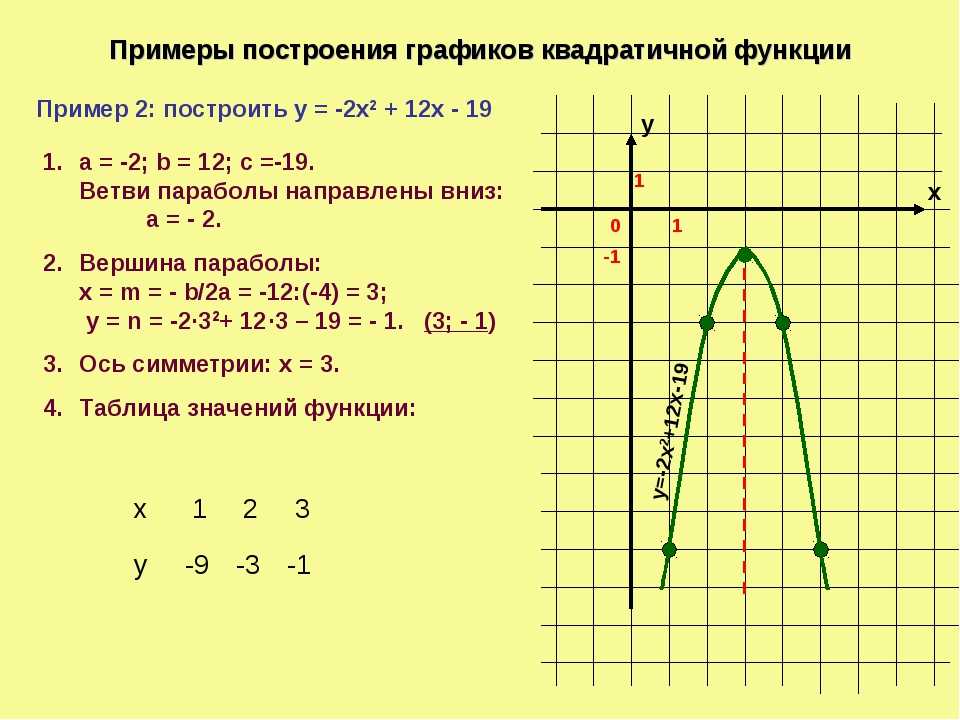 |
Попробуйте сами…
Параметры
Переключитесь на табличное представление , чтобы изменить следующие параметры. Изменить диапазон значений
| 1. | | Откройте контекстное меню, нажав кнопку Еще рядом с x. |
| 2. | | Выбрать Редактировать . |
| 3. | | Откроется диалоговое окно, в котором вы можете изменить Начальное значение для x , Конечное значение для x и Шаг . Нажмите OK для подтверждения настроек. |
Показать/скрыть точки в Графический вид
| 1. | | Откройте контекстное меню, нажав кнопку Еще рядом с функцией, для которой вы хотите скрыть точки, например.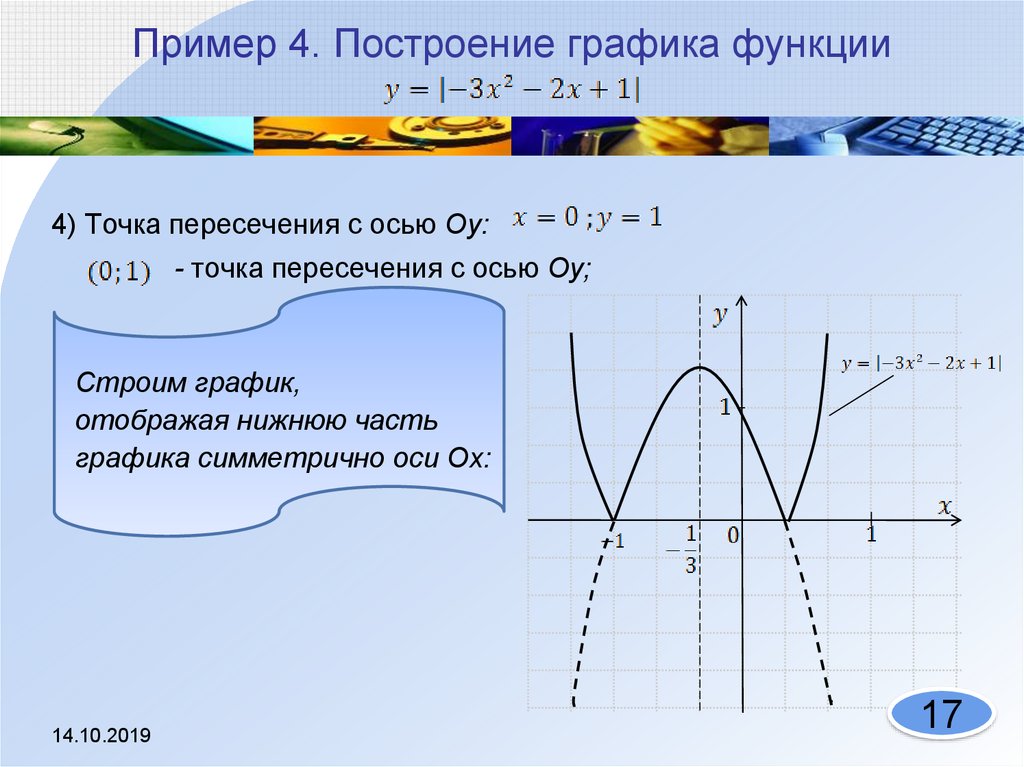 ф(х) . ф(х) . |
| 2. | | Выберите Скрыть точки . |
| 3. | | Точки теперь не отображаются в графическом виде . Чтобы показать их снова, откройте контекстное меню, нажав кнопку Нажмите кнопку «Дополнительно» и выберите Показать точки. |
Редактировать функцию
| 1. | | Откройте контекстное меню, нажав кнопку Еще рядом с функцией, которую вы хотите изменить, например. ф(х) . |
| 2. | | Выбрать Редактировать . |
| 3. | | Algebra View открывается автоматически. Теперь вы можете редактировать функцию. |
Удалить столбец
1. |
