Построение геометрических фигур в компьютерной среде «КОМПАС 3D»
В школьном курсе геометрии не только изучаются различные геометрические модели (теоремы), но и рассматривается процесс их построения с использованием линейки и циркуля. Для создания геометрических моделей на компьютере удобно использовать системы компьютерного черчения.
Рассмотрим систему компьютерного черчения КОМПАС 3D, которая специально предназначена для обучения компьютерному черчению в школах. КОМПАС можно использовать для выполнения геометрических построений с помощью циркуля и линейки, а также при создании чертежей деталей.
КОМПАС 3D – компьютерное средство моделирования, являющееся комплексной системой автоматизированного проектирования. Компас 3D используется в приоритете для разработки чертежей, проектирования кабельных систем и создания документов для инженерных проектов [1, c. 153]. Однако программа имеет и свои недостатки: могут возникать проблемы при загрузке 3d моделей из других программ, проектирование в 3d сложнее для новичка, чем 2d, требуется полноценное освоение моделирования, не очень хорошая возможность визуализации объектов, система поверхностного моделирования имеет недостатки в оформлении.
Примером выполнения геометрических построений в программе используем задачу из практической работы 2.3 «Выполнение геометрических построений в системе компьютерного черчения КОМПАС» (по учебнику информатики за 9 класс Н.Д. Угриновича) [3, с. 128].
1. Постановки задачи
Задача: построить угол, равный данному углу.
Геометрические объекты, заданные в условии задачи: произвольный угол и отрезок.
2. Математическая модель
Математическая модель процесса геометрического построения зафиксирована в форме алгоритма:
1. С помощью Компактной панели вызвать панель Геометрия.
Выбрать объект Отрезок и построить сначала произвольный угол А (начертить два отрезка, выходящих из одной точки), а затем построить произвольный луч ОМ (начертить отрезок).
Введем обозначения точек на чертеже с помощью панели Обозначения.
2. С помощью Компактной панели вызвать панель Обозначения.
Щелкнуть по кнопке Ввод текста и последовательно ввести обозначения угла и концов отрезка.
Построим окружность произвольного радиуса с центром в вершине заданного угла А, которая пересечет стороны угла в точках В и С.
3. На панели Геометрия выбрать объект Окружность и построить окружность с центром в точке А.
На панели Обозначения щелкнуть по кнопке Ввод текста и обозначить точки пересечения окружности со сторонами угла буквами В и С.
Построим окружность того же радиуса с центром в начале заданного луча ОМ, которая пересечет отрезок в точке D.
4. На панели Геометрия выбрать объект Окружность.
На Панели свойств щелкнуть правой кнопкой мыши по полю Радиус и в контекстном меню выбрать пункт Между 2 точками.
На чертеже навести курсор сначала на точку А, а затем на точку В.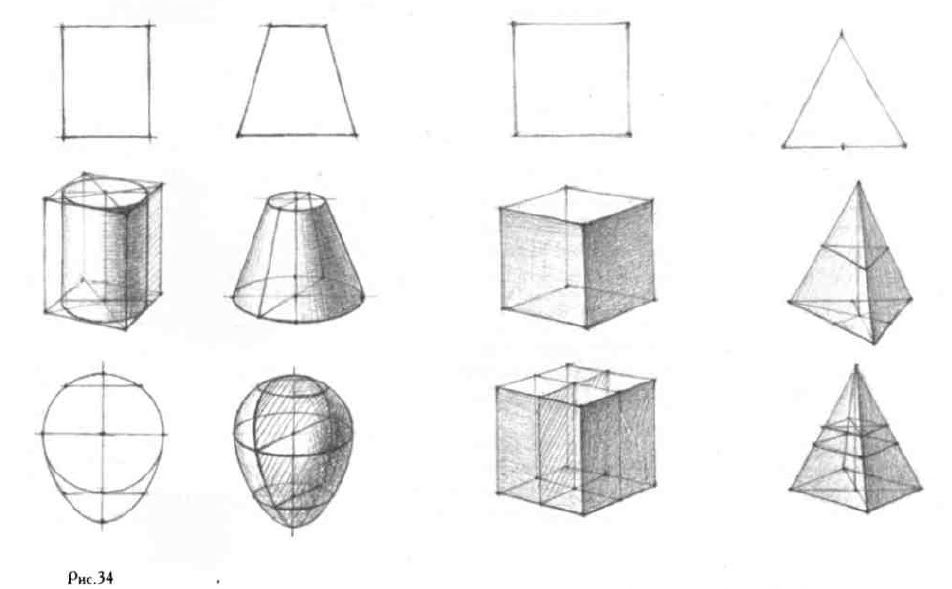
Центр появившейся окружности заданного радиуса переместить в точку О.
5. С помощью Компактной панели вызвать панель Обозначения. Щелкнуть по кнопке Ввод текста и обозначить точку пересечения окружности с отрезком ОМ буквой D.
Построим окружность с центром в точке D заданного радиуса ВС.
6. На панели Геометрия выбрать объект Окружность.
На Панели свойств щелкнуть правой кнопкой мыши по полю Радиус и в контекстном меню выбрать пункт Между 2 точками. На чертеже навести курсор сначала на точку С, а затем — на точку В.
Центр появившейся окружности заданного радиуса переместить в точку D.
7. С помощью Компактной панели вызвать панель Обозначения. Щелкнуть по кнопке Ввод текста и обозначить точку пересечения окружностей буквой Е.
8. Соединить отрезком точки О и Е, угол EOD, равный углу А, построен.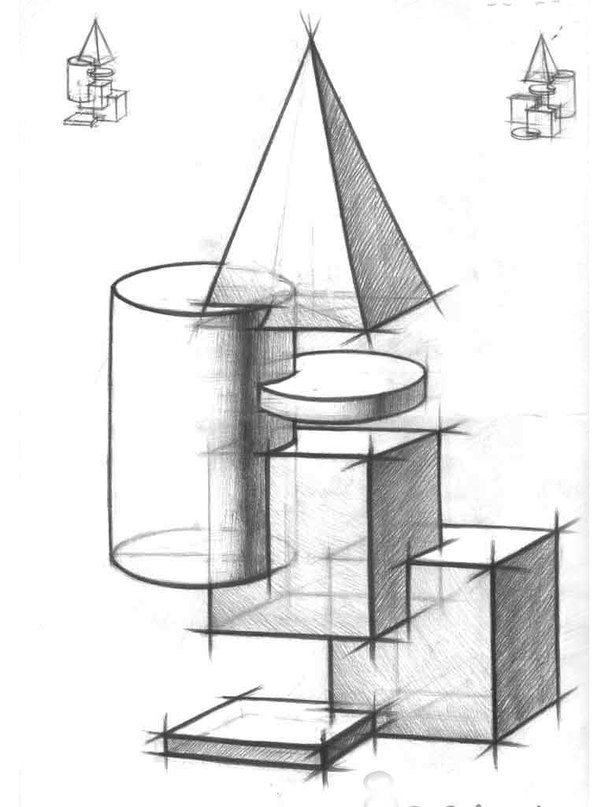
3. Компьютерная модель
Рис. 1. Компьютерная модель построенного угла
4. Эксплуатация модели. Анализ полученных результатов
Анализ полученных результатов заключается в сравнении градусной меры данного и получившегося углов. Проведение анализа возможно при помощи панели Измерения. Анализ градусных мер углов показал, что оба угла (данный и полученный) равны по 47˚ (рис. 2).
Рис. 2. Анализ полученных результатов
Таким образом, можно отметить, что в современных условиях учитель вправе реализовывать моделирование объектов в различных программных обеспечениях, средствах и пакетах, даже в ознакомительных целях [2, c. 16]. Это позволит современным школьникам не только научиться программировать в рамках раздела моделирование, но и самостоятельно ставить задачу, находить математические модели и области использования результатов решения задачи.
УРОК №1 Рисование простейших геометрических фигур
Построение рисунка линейки (рис 1)
Начнем с рисунка обычной линейки.
Линейка кладется на стол, лучше всего под углом 45° к рисующему. От художника ее должно отделять расстояние не меньшее, чем его вытянутая рука. Планшет с приколотым к нему листом бумаги следует одним краем опереть на спинку стула, а другим на колени и сесть так, чтобы, не поворачивая головы, можно было видеть и линейку и бумагу. После этого приступаем к рисунку, который ставит перед начинающим художником по существу первую изобразительную задачу. Ведь все, что он делал до сих пор в рисунке плоских фигур, сводилось главным образом к приобретению навыков в определении размеров линий и в умении точно передавать их характер, их направление и пропорции. Теперь же ему предстоит изобразить реальную форму. Можно попробовать начать рисовать, копируя, как в плоских фигурах, контур линейки. Но, рисуя так, начинающий художник быстро убедится, что его изображение будет мало походить на настоящую линейку: последняя не ляжет на стол и окажется неверной по своим пропорциям, размерам. По-видимому, необходим более точный подход к рисунку, и этот подход заключается в построении формы в пространстве.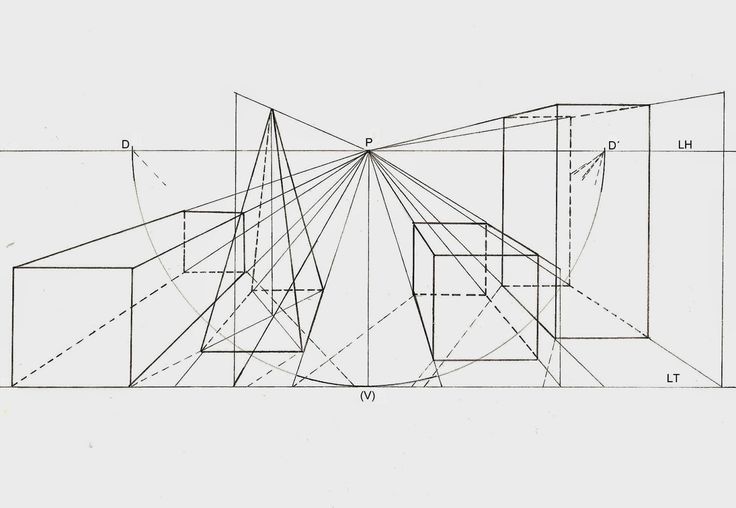
Глядя на линейку, мы видим, что одна ее часть находится к нам ближе, другая более удалена. И вот, если этот близко находящийся угол линейки каким-то образом обозначить на листе бумаги, то тогда можно, исходя из него, построить всю форму, рисуя ее от этой точки как бы в глубину. Так как линейка находится по отношению к рисующему под определенным углом, правильность ее положения в рисунке во многом зависит от точности определения этого угла. Чтобы легче определить угол, надо мысленно провести через его вершину прямую, параллельную нижнему основанию листа бумаги (или приложить к линейке полоску бумаги) и заметить на ней место соприкосновения с линейкой. Затем проводим на своем листе горизонтальную линию, соответствующую положению полоски бумаги на столе, ставим на ней точку касания линейки и приступаем к рисованию.
Намечая ребро линейки на бумаге, нужно все время сравнивать величину угла с натурой и. много раз, легко без нажима, водя карандашом по намечаемой части рисунка линейки, добиваться, чтобы ребро как бы легло на стол.
Когда это ощущение появится, художник должен еще раз сравнить свой рисунок с натурой и затем, нажимая на карандаш, провести линию, то есть нарисовать ребро линейки.
Нарисовав таким образом на листе бумаги одно ребро линейки, можно переходить к остальным. От намеченной точки строим ребро влево, а затем, отметив на нем ширину линейки, рисуем дальнее продольное ребро. Намечая последнее, художник не должен забывать основ наглядной перспективы — того, что ближайшие к нам части предметов кажутся больше, а дальние меньше.
Выполнив этот рисунок, художник не только сделает первое изображение натуры, но и познакомится с теми новыми качествами, которые приобретают лист бумаги и линии карандаша. Стремясь нарисовать линейку на плоскости стола, ему приходится с помощью своего воображения видеть лист бумаги неким пространством, и, соответственно, каждая проведенная линия становится не просто линией, а частью определенного предмета — линейки или стола.
Сущность геометрических построений — определение, основы геометрических построений, геометрические термины, построение треугольника, примеры.
Геометрия — понятие, имеющее дело с линиями, углами, формами объектов, размерами и размерами. Чтобы представить фигуры на бумаге, нам нужно точно нарисовать их с помощью таких инструментов, как линейки, транспортиры или циркуль. Самая простая конструкция – это линия. Мы начинаем с точки и медленно расширяем ее, чтобы нарисовать линию. Линия может иметь фиксированное измерение или бесконечную длину. Точно так же углы, круги и другие формы могут быть построены с правильной процедурой и заданными размерами.
| 1. | Определение геометрической конструкции |
| 2. | Основные геометрические построения |
| 3. | Термины и определения, используемые в геометрических построениях |
| 4. | Построение треугольника |
| 5. | Решенные примеры |
| 6. | Практические вопросы |
7. | Часто задаваемые вопросы по сущности геометрических построений |
Определение геометрической конструкции
Геометрическое построение означает точное рисование линий, отрезков, форм, окружностей и других фигур с помощью линейки, циркуля или транспортира. Большинство геометрических фигур включают в себя рисование отрезка, параллельных и перпендикулярных линий, перпендикулярных биссектрис, окружностей и даже касательных к окружностям.
Основные геометрические построения
В следующем разделе объясняются основные геометрические построения углов и окружностей.
Уголки
Есть три типа уголков. Следующие строки описывают, как эти типы углов можно нарисовать с помощью транспортира и линейки.
Острый угол: Угол, градусная мера которого меньше 90°, называется острым углом. Нарисуем острый угол 40° с помощью следующих шагов.
- Шаг 1: Нарисуйте прямую линию с помощью линейки и отметьте конечные точки как A и B.
- Шаг 2: Поместите транспортир в точку «А» так, чтобы точка совпала с центром транспортира.
- Шаг 3: Теперь, учитывая нижнюю шкалу транспортира, определите 40° и отметьте его буквой «С». Соедините точку ‘C’ с точкой ‘A’, чтобы образовался острый угол CAB = 40°
Конструкция острого угла показана на рисунке ниже.
Тупой угол: Угол, градусная мера которого больше 90°, называется тупым углом. Нарисуем острый угол 110° с помощью следующих шагов.
- Шаг 1: Нарисуйте прямую линию с помощью линейки и отметьте конечные точки как Q и R.
- Шаг 2: Поместите транспортир в точку Q так, чтобы точка совпала с центром транспортира.
- Шаг 3: Теперь, учитывая нижнюю шкалу транспортира, определите 110° и отметьте его буквой «P». Соедините точку ‘P’ с точкой ‘Q’, чтобы образовался тупой угол PQR = 110°
Конструкция тупого угла показана на рисунке ниже.
Прямой угол: Прямой угол равен 90°, и мы можем построить прямой угол с помощью следующих шагов.
- Шаг 1: Нарисуйте прямую линию с помощью линейки и отметьте конечные точки как A и B.
- Шаг 2: Поместите транспортир в точку «А» так, чтобы точка совпала с центром транспортира.
- Шаг 3: Теперь, учитывая нижнюю шкалу транспортира, определите 90° и обозначьте его буквой «С». Соедините точку «C» с точкой «A», чтобы образовался прямой угол CAB = 90°.
Конструкция прямого угла показана на рисунке ниже.
Круги
Некоторые важные термины, относящиеся к кругам, обсуждаются ниже.
- Окружность: Окружность определяется как граница круга.
- Радиус: Радиус измеряется как расстояние от центра круга до любой точки на окружности.
- Диаметр: Диаметр — это отрезок, проходящий через центр окружности, концы которого касаются окружности окружности.
- Хорда: Хорда — это отрезок, соединяющий любые две точки на окружности.
Выполните шаги, указанные ниже, чтобы нарисовать круг радиусом 5 единиц с помощью компаса.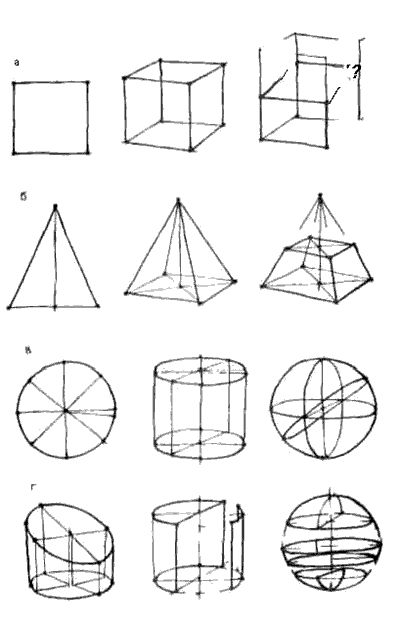
- Шаг 1: С помощью линейки установите на компасе необходимую ширину на 5 единиц.
- Шаг 2: Поместите заостренный конец компаса в точку, считающуюся центром круга, и полностью поверните его, чтобы нарисовать круг.
Окружность радиусом 5 единиц будет выглядеть так, как показано на следующем рисунке.
Термины и определения, используемые в геометрических построениях
- Биссектриса: В геометрических построениях биссектриса означает деление на две равные части. Мы можем разделить пополам линию, угол и даже фигуры.
- Параллельно : когда на плоскости нарисованы две линии, которые не пересекаются друг с другом, они называются параллельными линиями.
- Перпендикуляр: когда две нарисованные линии встречаются друг с другом под прямым углом или под углом 90°, они называются перпендикулярными линиями.
- Касательная: Касательная определяется как прямая линия, которая касается кривой в точке.
- Вписанный: когда многоугольник полностью нарисован внутри круга, мы можем сказать, что многоугольник вписан в круг. Можно также сказать, что вокруг многоугольника описана окружность.
- Описанный: Когда многоугольник окружает другую геометрическую фигуру (скажем, круг) так, что все вершины внутренней фигуры касаются сторон внешнего многоугольника, тогда говорят, что многоугольник описан вокруг окружности.
Следующие рисунки описывают каждый из рассмотренных выше геометрических терминов.
Построение треугольника
Теперь научимся строить треугольник, зная три его стороны. Построим треугольник ABC, где AB = 5 единиц, BC = 7 единиц и AC = 4 единицы. Нам понадобится линейка, циркуль и карандаш. Следующие шаги показывают способ построения треугольника.
- Шаг 1: Начертите с помощью линейки самый длинный заданный отрезок длиной 7 единиц и обозначьте его как BC.
- Шаг 2: Воспользуйтесь линейкой, измерьте 5 единиц с помощью циркуля и начертите дугу над линией с центром B.
- Шаг 3: Затем измерьте 4 единицы с помощью циркуля и нарисуйте дугу над линией с центром С так, чтобы она пересекала дугу, нарисованную на шаге 2, и отметьте точку пересечения как «А».
- Шаг 4: Соедините точки AB и AC.
На следующем рисунке показано построение треугольника с заданными размерами.
Темы, относящиеся к сущности геометрических построений
- Геометрическое построение
- Базовые треугольные конструкции
- Геометрические доказательства
- Круги
- Создание кругов
- Радиус
- Калькулятор радиуса окружности
Часто задаваемые вопросы о сущности геометрических построений
Что такое геометрическое построение?
Геометрическое построение означает рисование или построение геометрических фигур, состоящих из линий, углов, форм. Обычно мы используем циркуль, линейку, транспортир и карандаш для построения этих фигур.
Какие инструменты используются в геометрическом построении?
Линейка, циркуль, транспортир, угольники и делитель являются основными инструментами, используемыми для геометрического построения.
Каковы четыре основных геометрических построения?
Четыре основных построения в геометрии:
- Рисование линии по двум заданным точкам.
- Нахождение середины отрезка.
- Построение серединного перпендикуляра.
- Рисование биссектрисы угла.
Какие основные термины используются в геометрических построениях?
Основные термины, используемые в геометрических построениях, следующие:
- Точка: Точка описывает положение или местоположение. Для точки нет определенного размера.
- Линия: Линия — это фигура, имеющая только длину и не имеющую ширины. Он простирается бесконечно в обоих направлениях.
- Отрезок линии: Отрезок линии — это часть линии определенной длины с двумя конечными точками.
- Радиус: радиус измеряется как расстояние между центром круга и любой точкой на окружности.
- Биссект: Биссект означает точное деление на две равные части. Линия, угол или любая форма могут быть разделены пополам.
- Дуга: Изогнутая деталь обычно описывается как дуга. Дуга также является частью окружности.
Что значит разделить сегмент пополам?
Разделить отрезок пополам означает разделить его поровну на две части. Биссектриса определяется как отрезок, проходящий через середину данного отрезка.
Геометрические построения – Основы – Mathigon
Цель и обзор
В этом разделе учащиеся строят формальные геометрические построения с помощью геометрических инструментов (инструментов) Polypad, получая более глубокое представление о геометрических концепциях.
В древние времена геометрические построения фигур и длин ограничивались использованием только линейки и циркуля. Сегодня эту традицию можно использовать для создания серии уроков-головоломок.
Этот модуль посвящен основам геометрических построений:
- Копирование отрезка
- Разделение отрезка пополам
- Нахождение серединного перпендикуляра отрезка
- Построение центра окружности
- Создание перпендикулярных линий
- Построение прямой, параллельной заданной прямой через точку
- Копирование угла
- Разделение угла пополам
Введение
Поделитесь этим Полипадом со студентами. Попросите их скопировать сегмент линии, т.е. чтобы нарисовать отрезок, конгруэнтный AB‾\overline{AB} AB. Студенты могут заметить, что строка заблокирована на Polypad, поэтому они не могут ее выделить и просто скопировать. Предложите студентам поделиться своими методами. Возможно многие пользовались линейкой.
Затем попросите их сделать то же самое, не измеряя линейкой. Предложите им поделиться своими мыслями.
Объясните учащимся, что можно скопировать сегмент, не измеряя его. Вы можете использовать демонстрационное видео ниже или использовать этапы построения, чтобы скопировать сегмент.
Копирование AB‾\overline{AB} AB означает построение другого отрезка, скажем, CD‾\overline{CD}CD, конгруэнтного AB‾\overline{AB}AB.
Обсудите с учащимися значение слов «чертить», «рисовать» и «конструировать», используя задание «Скопировать сегмент».
В первом упражнении они чертят линию с помощью линейки, а во втором — строят отрезок с помощью циркуля. Геометрическое построение означает точное рисование линий, углов и форм без использования чисел или уравнений. Для этого нам нужно всего два инструмента! Линейка и компас. Напомните учащимся, что линейка похожа на линейку, но без маркировки. Компас позволяет нарисовать окружность заданного размера вокруг точки.
Основная деятельность
Греки сформулировали большую часть геометрии более 2000 лет назад. В частности, математик Евклид задокументировал геометрические понятия, аксиомы, логику и конструкции в своей книге «Элементы».
Поэтому эти конструкции также известны как евклидовы конструкции. Вы можете узнать больше об аксиомах Евклида на курсе Матигона по евклидовой геометрии.
Изучая геометрические построения, учащиеся увидят тесную связь с аксиоматической логикой, которую Евклид использовал для доказательства своих теорем. Он доказывал все с минимумом предположений, таких как аксиомы и постулаты, и строил самые сложные геометрические фигуры с минимумом инструментов, таких как циркуль и линейка.
С тех пор и до сих пор использование только линейки и циркуля для построения геометрических фигур стало почти загадкой для математиков. Пригласите студентов присоединиться к вам и пойти по стопам великих математиков! Поделитесь следующими проблемами и головоломками студентов. Варианты включают представление их по одному, предоставление общего доступа к ним всем учащимся или предоставление доступа к некоторым группам.
Разделение отрезка пополам и построение биссектрисы отрезка
Прежде всего, напомните учащимся, что есть два правила:
- Они могут пользоваться только циркулем и линейкой.
- Они не могут использовать линейку для измерения длины или транспортир для измерения углов.
Поделитесь этим Polypad со студентами. Вот решение:
- Поместите точку компаса в точку A и откройте компас больше, чем на половину длины сегмента, чтобы нарисовать дугу.
- Сохраняя постоянную ширину компаса, поместите точку компаса на B, чтобы нарисовать дугу. Убедитесь, что дуги пересекаются в двух точках. Обозначьте точки пересечения как C и D.
- Соедините точки C и D прямым краем. Отрезок CD пересекается с отрезком AB в одной точке. Обозначьте точку как E.
- E — середина (медиана) ABundefined\overlinesegment{AB}AB, а CDundefined\overlinesegment{CD}CD — биссектриса отрезка AB.
Центр окружности
Возможность найти середину отрезка без измерения и построения его биссектрисы помогает в более сложных построениях.
Одним из таких примеров является нахождение центра круга.
Покажите учащимся этот Полипад и попросите их построить его центр с помощью циркуля и линейки. Пусть они обсудят возможные свойства круга, которые могут помочь им построить (найти) его центр. Вот решение:
Один из самых простых способов — найти точку пересечения серединных перпендикуляров любых двух хорд окружности . Этот метод основан на том, что биссектриса хорды проходит через центр окружности.
Перпендикулярные линии
Поделитесь этим блокнотом, чтобы строить параллельные и перпендикулярные линии вместе с учениками. Вот решение:
Может быть два разных варианта построения перпендикуляра к заданной прямой:
- Построение перпендикулярной линии из точки, лежащей на прямой
- Построение перпендикулярной линии из точки, не лежащей на прямой
В обоих случаях: заданную точку и провести дугу так, чтобы она дважды пересекалась с заданным отрезком.
Параллельные линии
Существует несколько способов построения параллельных линий. Один из самых интуитивно понятных — использование свойств четырехугольников с параллельными прямыми. В ромбе конгруэнтные стороны можно построить, начертив радиус окружности.
- Сначала поместите компас в заданную точку.
- Нарисуйте длинную дугу (почти полный круг), дважды пересекающую исходный сегмент.
- Затем поместите компас в первую точку пересечения, сохраняя постоянную ширину компаса, и нарисуйте дугу, которая пересекается с отрезком.
- Теперь используйте эту точку пересечения, чтобы нарисовать еще одну дугу, пересекающуюся с предыдущей. На самом деле это четвертая вершина ромба.
- Наконец, соедините исходную точку с последней построенной точкой, чтобы провести параллельную линию.
- Этим методом можно построить параллельные прямые, а также ромб.
На самом деле это четвертая вершина ромба.Копирование угла
Поделитесь этим Полипадом со студентами и попросите их скопировать угол BAC. Вот решение:
Попросите учащихся измерить углы с помощью транспортира, чтобы доказать, что их измерения одинаковы. Вы также можете использовать дробную часть 15\frac{1}{5}51 для представления меры угла.
Разделение угла пополам (Построение биссектрисы угла)
Поделитесь этим Полипадом со студентами. Вот решение:
полипы для этого урока
Копирование сегмента — Polypad
Polypad.