Как решить систему уравнений если определитель равен 0: Решение систем линейных уравнений

Решение систем линейных уравнений

Каталин Дэвид

Системы линейных уравнений имеют следующий общий вид:

$ \begin{cases} a_{1,1}\cdot x_{1} + a_{1,2}\cdot x_{2} + a_{1,3}\cdot x_{3} + \cdots a_{1,n} \cdot x_{n} =b_{1} \\ a_{2,1}\cdot x_{1} + a_{2,2}\cdot x_{2}+ a_{2,3}\cdot x_{3} + \cdots + a_{2,n}\cdot x_{n} = b_{2} \\ a_{3,1}\cdot x_{1} + a_{3,2}\cdot x_{2}+a_{3,3}\cdot x_{3}+ \cdots + a_{3,n}\cdot x_{n}=b_{3} \\ \cdots\\ a_{m,1}\cdot x_{1}+ a_{m,2}\cdot x_{2}+a_{m,3}\cdot x_{3}+\cdots + a_{m,n}\cdot x_{n} =b_{n} \end{cases}$

$ A= \begin{pmatrix} a_{1,1} & a_{1,2} & a_{1,3} & . & . & a_{1,n} \\ a_{2,1} & a_{2,2} & a_{2,3} & . & . & a_{2,n} \\ a_{3,1} & a_{3,2} & a_{3,3} & . & . & a_{3,n} \\ \cdots \\ a_{m,1} & a_{m,2} & a_{m,3} & . & . & a_{m,n} \end{pmatrix}$ — матрица системы, а $b_{1}, b_{2},b_{3} \cdots b_{n}$ — свободные члены системы.

Если все свободные члены равны 0, то система однородна.

Матрица системы — квадратная (m=n)

Надо вычислить определитель матрицы системы.

$\Delta = \begin{vmatrix} a_{1,1} & a_{1,2} & a_{1,3} & . & . & a_{1,n} \\ a_{2,1} & a_{2,2} & a_{2,3} & . & . & a_{2,n} \\ a_{3,1} & a_{3,2} & a_{3,3} & . & . & a_{3,n} \\ \cdots \\ a_{n,1} & a_{n,2} & a_{n,3} & . & . & a_{n,n} \end{vmatrix}$

Определитель матрицы системы не равен 0

Система называется невырожденной системой с единственным решением. Чтобы найти решение системы, используем метод Крамера.

Вычислим $ \Delta_{x_{1}}$ — определитель матрицы, полученной заменой столбца с коэффициентами соответствующей переменной $x_{1}$ столбцом свободных членов.
$\Delta_{x_{1}}= \begin{vmatrix} b_{1} & a_{1,2} & a_{1,3} & . & . & a_{1,n} \\ b_{2} & a_{2,2} & a_{2,3} & . & . & a_{2,n} \\ b_{3} & a_{3,2} & a_{3,3} & . & .

& a_{3,n} \\ \cdots \\ b_{n} & a_{n,2} & a_{n,3} & . & . & a_{n,n} \end{vmatrix}$

Получаем $ x_{1} = \dfrac{\Delta_{x_{1}}}{\Delta}$

Вычислим $ \Delta_{x_{2}}$ — определитель матрицы, полученной заменой столбца с коэффициентами соответствующей переменной $x_{2}$ столбцом свободных членов.
$\Delta_{x_{2}}= \begin{vmatrix} a_{1,1} & b_{1} & a_{1,3} & . & . & a_{1,n} \\ a_{2,1} & b_{2} & a_{2,3} & . & . & a_{2,n} \\ a_{3,1} & b_{3} & a_{3,3} & . & . & a_{3,n} \\ \cdots \\ a_{n,1} & b_{n} & a_{n,3} & . & . & a_{n,n} \end{vmatrix}$

Получаем $ x_{2} = \dfrac{\Delta_{x_{2}}}{\Delta}$

Вычислим $ \Delta_{x_{3}}$ — определитель матрицы, полученной заменой столбца с коэффициентами соответствующей переменной $x_{3}$ столбцом свободных членов.
$\Delta_{x_{3}}= \begin{vmatrix} a_{1,1} & a_{1,2} & b_{1} & . & . & a_{1,n} \\ a_{2,1} & a_{2,2} & b_{2} & .

& . & a_{2,n} \\ a_{3,1} & a_{3,2} & b_{3} & . & . & a_{3,n} \\ \cdots \\ a_{n,1} & a_{n,2} & a_{n} & . & . & a_{n,n} \end{vmatrix}$

Получаем $ x_{3} = \dfrac{\Delta_{x_{3}}}{\Delta}$

Продолжаем делать это с остальными переменными, и в конце-концов записываем решение системы.
$x_{n}=\dfrac{\Delta_{x_{n}}}{\Delta}$

Пример 53
$\begin{cases} 2\cdot x + 3\cdot y -5\cdot z = \color{red}{-7}\\ -3 \cdot x + 2\cdot y + z = \color{red}{-9}\\ 4\cdot x — y + 2\cdot z = \color{red}{17} \end{cases}$

Матрица системы:
$ \begin{pmatrix} 2 & 3 & -5\\ -3 & 2 & 1\\ 4 & -1 & 2 \end{pmatrix}$

Вычисляем определитель матрицы и получаем $\Delta = 8 -15 + 12 +40 +2 + 18 = 65$

Вычисляем $ \Delta_{x}= \begin{vmatrix} \color{red}{-7} & 3 & -5\\ \color{red}{-9} & 2 & 1\\ \color{red}{17} & -1 & 2 \end{vmatrix}= -28 — 45 + 51 + 170 — 7 +54 = 195$

Вычисляем $ \Delta_{y}= \begin{vmatrix} 2 & \color{red}{-7} & -5\\ -3 & \color{red}{-9} & 1\\ 4 & \color{red}{17} & 2 \end{vmatrix}=-36 + 255 -28 -180 -34 -42 = -65$

Вычисляем $ \Delta_{z}= \begin{vmatrix} 2 & 3 &\color{red}{-7}\\ -3 & 2 & \color{red}{-9}\\ 4 & -1 & \color{red}{17} \end{vmatrix}= 68 -21 -108 + 56 -18 + 153 =130$

Решение системы:
$x = \dfrac{\Delta_{x}}{\Delta} =\dfrac{195}{65} = 3$
$y = \dfrac{\Delta_{y}}{\Delta} = -\dfrac{65}{65}= -1$
$z = \dfrac{\Delta_{z}}{\Delta} =\dfrac{130}{65}= 2$
$S=\{3;-1;2\}$

Пример 54
$\begin{cases} 4\cdot x + 5\cdot y -2\cdot z = \color{red}{3}\\ -2 \cdot x + 3\cdot y — z = \color{red}{-3}\\ -1\cdot x — 2\cdot y + 3\cdot z = \color{red}{-5} \end{cases}$

Матрица системы: $ \begin{pmatrix} 4 & 5 & -2\\ -2 & 3 & -1\\ -1 & -2 & 3 \end{pmatrix}$

Вычисляем определитель матрицы и получаем $\Delta = 36 -8 + 5 -6 -8 + 30 = 49$

Вычисляем $ \Delta_{x}= \begin{vmatrix} \color{red}{3} & 5 & -2\\ \color{red}{-3} & 3 &1\\ \color{red}{-5} & -2 & 3 \end{vmatrix}= 27 — 12 + 25 — 30 — 6 + 45 = 49$

Вычисляем $ \Delta_{y}= \begin{vmatrix} 4 & \color{red}{3} & -2\\ -2 & \color{red}{-3} & -1\\ -1 & \color{red}{-5} & 3 \end{vmatrix}=-36 -20+ 3 +6 -20 + 18 = -49$

Вычисляем $ \Delta_{z}= \begin{vmatrix} 4 & 5 & \color{red}{3}\\ -2 & 3 & \color{red}{-3}\\ -1& -2 & \color{red}{-5} \end{vmatrix}= -60 + 12 + 15 + 9 — 24 -50 = — 98$

Решение системы:
$x = \dfrac{\Delta_{x}}{\Delta} =\dfrac{49}{49} = 1$
$y = \dfrac{\Delta_{y}}{\Delta} = -\dfrac{-49}{49}= -1$
$z = \dfrac{\Delta_{z}}{\Delta} =\dfrac{-98}{4}= -2$

$S=\{1;-1;-2\}$

Если система однородна, то ее решение есть {0;0;0}, потому что в матрицах, определителями которых являются $\Delta_{x}$,$\Delta_{y}$ и $\Delta_{z}$, есть столбцы из одних нулей, следовательно, эти определители равны 0.

Пример 55
$\begin{cases} 2\cdot x + 3\cdot y -5\cdot z = \color{red}{0}\\ -3 \cdot x + 2\cdot y + z = \color{red}{0}\\ 4\cdot x — y + 2\cdot z = \color{red}{0} \end{cases}$

Матрица системы:
$ \begin{pmatrix} 2 & 3 & -5\\ -3 & 2 & 1\\ 4 & -1 & 2 \end{pmatrix}$

Вычисляем определитель матрицы и получаем $\Delta = 8 -15 + 12 +40 +2 + 18 = 65 $

$\Delta_{x}= \begin{vmatrix} \color{red}{0} & 3 & -5\\ \color{red}{0} & 2 & 1\\ \color{red}{0} & -1 & 2 \end{vmatrix}= 0 $

$\Delta_{y}= \begin{vmatrix} 2 & \color{red}{0} & -5\\ -3 & \color{red}{0} & 1\\ 4 & \color{red}{0} & 2 \end{vmatrix}= 0$

$\Delta_{z}= \begin{vmatrix} 2 & 3 &\color{red}{0}\\ -3 & 2 & \color{red}{0}\\ 4 & -1 & \color{red}{0} \end{vmatrix}= 0$

Решение системы:
$x = \dfrac{\Delta_{x}}{\Delta} =\dfrac{0}{65} = 0$
$y = \dfrac{\Delta_{y}}{\Delta} = -\dfrac{0}{65}= 0$
$z = \dfrac{\Delta_{z}}{\Delta} =\dfrac{0}{65}= 0$
$S = \{0;0;0\}$

Определитель матрицы системы равен 0.

Вычисляем ранг матрицы системы и ранг расширенной матрицы (исходной матрицы, к которой добавлен столбец свободных членов).

Возможны следующие варианты:

Пример 56
$\begin{cases} 2\cdot x + 3\cdot y +2\cdot z = \color{red}{5}\\ -3 \cdot x + 2\cdot y -3 \cdot z = \color{red}{-1}\\ 4\cdot x — y + 4\cdot z = \color{red}{3} \end{cases}$

Матрица системы:
$\begin{pmatrix} 2 & 3 & 2\\ -3 & 2 & -3\\ 4 & -1 & 4 \end{pmatrix}$

Вычисляем ранг матрицы:

$ 2\neq 0$

$\begin{vmatrix} 2 & 3\\ -3 & 2 \end{vmatrix}= 4 + 9 =13 \neq0$

$\begin{vmatrix} 2 & 3 & 2\\ -3 & 2 & -3\\ 4 & -1 & 4 \end{vmatrix}=0 $ (матрица имеет два равных столбца, следовательно, ее ранг равен 2)

Расширенная матрица:
$\begin{pmatrix} 2 & 3 & 2 & \color{red}{5}\\ -3 & 2 & -3 & \color{red}{-1}\\ 4 & -1 & 4 & \color{red}{3} \end{pmatrix}$

Вычисляем ранг расширенной матрицы:
$ 2\neq 0$

$\begin{vmatrix} 2 & 3\\ -3 & 2 \end{vmatrix}= 4 + 9 =13 \neq0$

$\begin{vmatrix} 2 & 3 & 2\\ -3 & 2 & -3\\ 4 & -1 & 4 \end{vmatrix}=0$
$\begin{vmatrix} 2 & 3 & \color{red}{5}\\ -3 & 2 & \color{red}{-1}\\ 4 & -1 & \color{red}{3} \end{vmatrix}=0 $ (матрица имеет два равных столбца, следовательно, ее ранг равен 2)

Поскольку ранги равны, система совместна и имеет бесконечное множество решений.

Минор соответствующего ранга становится базисным минором.
$ \Delta_{p} = \begin{vmatrix} 2 & 3\\ -3 & 2 \end{vmatrix}$

Переменные x и y, коэффициенты при которых входят в базисный минор, становятся базисными переменными, а z становится неосновной переменной. Пусть $z=\alpha$. Первые два уравнения, в которых находится базисный минор, становятся базисными уравнениями. Решаем систему, состоящую из базисных уравнений.
$\begin{cases} 2\cdot x + 3\cdot y +2\cdot \alpha = 5\\ -3 \cdot x + 2\cdot y -3 \cdot\alpha = -1\\ \end{cases}=$ $\begin{cases} 2\cdot x + 3\cdot y = 5 — 2\cdot \alpha\\ -3 \cdot x + 2\cdot y = -1 + 3\cdot\alpha\\ \end{cases}$

Умножаем первое уравнение на 3, а второе на 2.
$\begin{cases} 6\cdot x + 9\cdot y = 15 — 6\cdot \alpha\\ -6 \cdot x + 4\cdot y = -2 + 6 \cdot \alpha \\ \end{cases}$

Складываем два полученные уравнения и получаем:
$ 13\cdot y = 13 \Rightarrow y = \dfrac{13}{13} = 1$

Умножаем первое уравнение на -2, а второе на 3.
$ \begin{cases} -4\cdot x — 6\cdot y = -10 + 4\cdot \alpha\\ -9 \cdot x + 6\cdot y = -3 + 9 \cdot \alpha \\ \end{cases}$

Складываем два полученные уравнения и получаем:
$ -13\cdot x = 13 \Rightarrow y = \dfrac{13\cdot\alpha -13}{13} = \alpha -1$
Решение системы: $\{\alpha-1;1;\alpha \}$

Пример 57
$\begin{cases} 2\cdot x + y +5\cdot z = \color{red}{3}\\ 3 \cdot x + 2\cdot y +2 \cdot z = \color{red}{1}\\ 7\cdot x +y + 12\cdot z = \color{red}{2} \end{cases}$

Матрица системы:
$\begin{pmatrix} 2 & 1 & 5\\ 3 & 2 & 2\\ 7 & 4 & 12 \end{pmatrix}$

Вычисляем ранг матрицы:
$ 2\neq 0$
$\begin{vmatrix} 2 & 1\\ 3 & 2 \end{vmatrix}= 4 — 3 =1 \neq0$

$\begin{vmatrix} 2 & 1 & 5\\ 3 & 2 & 2\\ 7 & 4 & 12 \end{vmatrix}= 48 + 60 + 14 — 70 -16 -36 =0 $ (следовательно, ранг равен 2)

Расширенная матрица:
$\begin{pmatrix} 2 & 1 & 5 & \color{red}{3}\\ 3 & 2 & 2 & \color{red}{1}\\ 7 & 4 & 12 & \color{red}{2} \end{pmatrix}$

Вычисляем ранг расширенной матрицы:
$ 2\neq 0$
$\begin{vmatrix} 2 & 1\\ 3 & 2 \end{vmatrix}= 4 -3 =1 \neq0$

$\begin{vmatrix} 2 & 1 & 5\\ 3 & 2 & 2\\ 7 & 4 & 12 \end{vmatrix}=0$

$\begin{vmatrix} 2 & 1 & \color{red}{3}\\ 3 & 2 & \color{red}{1}\\ 7 & 4 & \color{red}{2} \end{vmatrix}= 8 + 36 + 7 — 42 -8 -6 = -5\neq 0 $

Ранг расширенной матрицы равен 3.

Поскольку ранги этих матриц различны, система не имеет решения. Это несовместная система. Однородная система всегда совместна и имеет бесконечное множество решений, поскольку ранг расширенной матрицы, содержащей столбец из одних нулей, всегда совпадает с рангом матрицы системы.

Пример 58
$\begin{cases} 2\cdot x + 3\cdot y +2\cdot z = \color{red}{0}\\ -3 \cdot x + 2\cdot y -3 \cdot z = \color{red}{0}\\ 4\cdot x — y + 4\cdot z = \color{red}{0} \end{cases}$

Матрица системы:
$\begin{pmatrix} 2 & 3 & 2\\ -3 & 2 & -3\\ 4 & -1 & 4 \end{pmatrix}$

Вычисляем ранг матрицы:
$ 2\neq 0$
$\begin{vmatrix} 2 & 3\\ -3 & 2 \end{vmatrix}= 4 + 9 = 13 \neq0$

$ \begin{vmatrix} 2 & 3 & 2\\ -3 & 2 & -3\\ 4 & -1 & 4 \end{vmatrix}=0 $ (матрица имеет два равных столбца, следовательно, ее ранг равен 2)

Расширенная матрица:
$\begin{pmatrix} 2 & 3 & 2 & \color{red}{0}\\ -3 & 2 & -3 & \color{red}{0}\\ 4 & -1 & 4 & \color{red}{0} \end{pmatrix}$

Вычисляем ранг расширенной матрицы:
$ 2\neq 0$
$\begin{vmatrix} 2 & 3\\ -3 & 2 \end{vmatrix}= 4 + 9 =13 \neq0$

$\begin{vmatrix} 2 & 3 & 2\\ -3 & 2 & -3\\ 4 & -1 & 4 \end{vmatrix}=0$

$ \begin{vmatrix} 2 & 3 & \color{red}{0}\\ -3 & 2 & \color{red}{0}\\ 4 & -1 & \color{red}{0} \end{vmatrix}=0 $ (матрица включает столбец из одних нулей, следовательно, ее ранг равен 2)

Поскольку ранги равны, система совместна и имеет бесконечное множество решений. Минор соответствующего ранга становится базисным минором.
$\Delta_{p} = \begin{vmatrix} 2 & 3\\ -3 & 2 \end{vmatrix}$

Переменные x и y, коэффициенты при которых входят в базисный минор, становятся базисными переменными, а z становится неосновной переменной. Пусть $z=\alpha$. Первые два уравнения, в которых находится базисный минор, становятся базисными уравнениями. Решаем систему, состоящую из базисных уравнений.
$\begin{cases} 2\cdot x + 3\cdot y +2\cdot \alpha = 0\\ -3 \cdot x + 2\cdot y -3 \cdot\alpha = 0\\ \end{cases}=$ $\begin{cases} 2\cdot x + 3\cdot y = — 2\cdot \alpha\\ -3 \cdot x + 2\cdot y = 3\cdot\alpha\\ \end{cases}$

Умножаем первое уравнение на 3, а второе на 2.
$\begin{cases} 6\cdot x + 9\cdot y = -6\cdot \alpha\\ -6 \cdot x + 4\cdot y = 6 \cdot \alpha \\ \end{cases}$

Складываем два полученные уравнения и получаем:
$13\cdot y = 0 \Rightarrow y = \dfrac{0}{13} = 0$
Делаем то же самое, чтобы найти x. Умножаем первое уравнение на -2, а второе на 3.
$ \begin{cases} -4\cdot x — 6\cdot y = 4\cdot \alpha\\ -9 \cdot x + 6\cdot y =9 \cdot \alpha \\ \end{cases}$

Складываем два полученные уравнения и получаем:
$ -13\cdot x = 13 \Rightarrow y = \dfrac{13\cdot\alpha}{-13} = -\alpha$
Решение системы: $ \{-\alpha;0;\alpha \}$

Матрица системы не квадратная $(m\neq n)$

Вычисляем ранг матрицы системы и ранг расширенной матрицы (исходной матрицы, к которой добавлен столбец свободных членов).

Возможны следующие варианты:

• Если ранг этих матриц различен, то система не имеет решения. Это несовместная система.
• Если ранги равны, то система совместна и имеет бесконечное множество решений.
  Решение системы находится следующим образом:
  
  • Минор соответствующего ранга становится базисным минором.
  • Переменные, коэффициенты при которых входят в базисный минор, становятся базисными (основными) переменными. Остальные переменные становятся свободными (неосновными), обозначаются другими буквами и переносятся в правую часть уравнений.
  • Уравнения, содержащие базисный минор, становятся базисными уравнениями.
  • Решаем систему, состоящую только из базисных уравнений, и находим решение системы, которое будет зависеть от неосновных переменных.
  • Записываем решение.

Пример 59
$\begin{cases} 2\cdot x + 3\cdot y +2\cdot z = \color{red}{5}\\ -3 \cdot x + 2\cdot y -3 \cdot z = \color{red}{-1}\\ \end{cases}$

Матрица системы:
$\begin{pmatrix} 2 & 3 & 2\\ -3 & 2 & -3\\ \end{pmatrix}$

Вычисляем ранг матрицы:
$ 2\neq 0$
$\begin{vmatrix} 2 & 3\\ -3 & 2 \end{vmatrix}= 4 + 9 =13 \neq0$ (ранг равен 2)

Расширенная матрица:
$\begin{pmatrix} 2 & 3 & 2 & \color{red}{5}\\ -3 & 2 & -3 & \color{red}{-1}\\ \end{pmatrix}$

Вычисляем ранг расширенной матрицы:
$ 2\neq 0$
$\begin{vmatrix} 2 & 3\\ -3 & 2 \end{vmatrix}= 4 + 9 =13 \neq0$ (ранг также равен 2)

Поскольку ранги равны, система совместна и имеет бесконечное множество решений. Минор соответствующего ранга становится базисным минором.

$ \Delta_{p} = \begin{vmatrix} 2 & 3\\ -3 & 2 \end{vmatrix}$

Переменные x и y, коэффициенты при которых входят в базисный минор, становятся базисными переменными, а z становится неосновной переменной. Пусть $z=\alpha$. Первые два уравнения, в которых находится базисный минор, становятся базисными уравнениями. Решаем систему, состоящую из базисных уравнений.

$\begin{cases} 2\cdot x + 3\cdot y +2\cdot \alpha = 5\\ -3 \cdot x + 2\cdot y -3 \cdot\alpha = -1\\ \end{cases}=$ $\begin{cases} 2\cdot x + 3\cdot y = 5 — 2\cdot \alpha\\ -3 \cdot x + 2\cdot y = -1 + 3\cdot\alpha\\ \end{cases}$

Умножаем первое уравнение на 3, а второе на 2.
$\begin{cases} 6\cdot x + 9\cdot y = 15 — 6\cdot \alpha\\ -6 \cdot x + 4\cdot y = -2 + 6 \cdot \alpha \\ \end{cases}$

Складываем два полученные уравнения и получаем:
$ 13\cdot y = 13 \Rightarrow y = \dfrac{13}{13} = 1$
Делаем то же самое, чтобы найти x. Умножаем первое уравнение на -2, а второе на 3.
$ \begin{cases} -4\cdot x — 6\cdot y = -10 + 4\cdot \alpha\\ -9 \cdot x + 6\cdot y = -3 + 9 \cdot \alpha \\ \end{cases}$

Складываем два полученные уравнения и получаем:
$-13\cdot x = 13 \Rightarrow y = \dfrac{13\cdot\alpha -13}{13} = \alpha -1$
Решение системы: $\{\alpha-1;1;\alpha \}$

Пример 60
$\begin{cases} 2\cdot x + 3\cdot y = \color{red}{5}\\ -3 \cdot x + 2\cdot y = \color{red}{-1}\\ 4\cdot x — y = \color{red}{3} \end{cases}$

Матрица системы:
$\begin{pmatrix} 2 & 3 \\ -3 & 2 \\ 4 & -1 \end{pmatrix}$

Вычисляем ранг матрицы:
$2\neq 0$
$\begin{vmatrix} 2 & 3\\ -3 & 2 \end{vmatrix}= 4 + 9 =13 \neq0$ (ранг равен 2)

Расширенная матрица:
$\begin{pmatrix} 2 & 3 & \color{red}{5}\\ -3 & 2 & \color{red}{-1}\\ 4 & -1 & \color{red}{3} \end{pmatrix}$

Вычисляем ранг расширенной матрицы:
$2\neq 0$
$\begin{vmatrix} 2 & 3\\ -3 & 2 \end{vmatrix}= 4 + 9 =13 \neq0$
$\begin{vmatrix} 2 & 3 & \color{red}{5}\\ -3 & 2 & \color{red}{-1}\\ 4 & -1 & \color{red}{3} \end{vmatrix}=0 $ (матрица имеет два равных столбца, следовательно, ее ранг равен 2)

Поскольку ранги равны, система совместна и имеет бесконечное множество решений. Минор соответствующего ранга становится базисным минором.
$\Delta_{p} = \begin{vmatrix} 2 & 3\\ -3 & 2 \end{vmatrix}$

Переменные x и y, коэффициенты при которых входят в базисный минор, становятся базисными переменными, а z становится неосновной переменной. Система не имеет неосновных переменных. Первые два уравнения, в которых находится базисный минор, становятся базисными уравнениями. Решаем систему, состоящую из базисных уравнений.
$\begin{cases} 2\cdot x + 3\cdot y = 5\\ -3 \cdot x + 2\cdot y = -1\\ \end{cases}$

Умножаем первое уравнение на 3, а второе на 2.
$\begin{cases} 6\cdot x + 9\cdot y = 15\\ -6 \cdot x + 4\cdot y = -2 \\ \end{cases}$

Складываем два полученные уравнения и получаем:
$13\cdot y = 13 \Rightarrow y = \dfrac{13}{13} = 1$
Делаем то же самое, чтобы найти x. Умножаем первое уравнение на -2, а второе на 3.
$ \begin{cases} -4\cdot x — 6\cdot y = -10\\ -9 \cdot x + 6\cdot y = -3\\ \end{cases}$

Складываем два полученные уравнения и получаем:
$ -13\cdot x = -13 \Rightarrow y = \dfrac{-13}{-13} = 1$
Убедимся, что результаты удовлетворяют неосновному уравнению.
$4\cdot1 -1\cdot1 = 3$
Решение системы: $\{1;1 \}$

Матрицы Умножение матриц Определители Ранг матрицы Обратные матрицы Матричные уравнения Калькуляторы для матриц

Системы линейных алгебраических уравнений — презентация онлайн

Похожие презентации:

Системы линейных уравнений

Матрицы. Определитель матрицы

Системы линейных алгебраических уравнений

Высшая математика. Лекция 2. Обратная матрица

Системы линейных уравнений

Решение систем линейных алгебраических уравнений по правилу Крамера, матричным методом, методом Гаусса

Элементы линейной алгебры

Матрицы и определители

Системы линейных алгебраических уравнений

Системы линейных уравнений

Системы линейных
алгебраических уравнений
(СЛАУ)
Система m линейных алгебраических уравнений c
n неизвестными имеет вид:
а11х1 + а12х2 + …..+ а1nхn = в1
а21х1 + а22х2 + ….+ а2nхn = в2
………………………………
аm1х1 + аm2х2 + …. + аmnхn = вm
аij – коэффициенты, хj — неизвестные, bi свободные члены уравнений.
Опр. Решить систему означает найти все совокупности
значений неизвестных (х1, х2,….хn), удовлетворяющих
системе или показать, что система не имеет решений.
1.Если система не имеет решений, то она называется
несовместимой.
2. Если она имеет единственное решение –
определенной.
3. Если она имеет бесконечно много решений –
неопределенной.
Опр: Если хотя бы одно из чисел bi, отлично от нуля,
система называется неоднородной. Если все свободные
члены равны нулю, то система называется однородной.
Опр: Матрица составленная из коэффициентов
системы называется основной матрицей, если к
основной матрице приписать справа столбец
свободных членов, то получится расширенная
матрица системы.

5. Метод Крамера

По формулам Крамера решаются только
неоднородные системы.
а11х1 а12 х2 а13 х3 в1
а21х1 а22 х2 а23 х3 в2
а х а х а х в
32 2
33 3
3
31 1
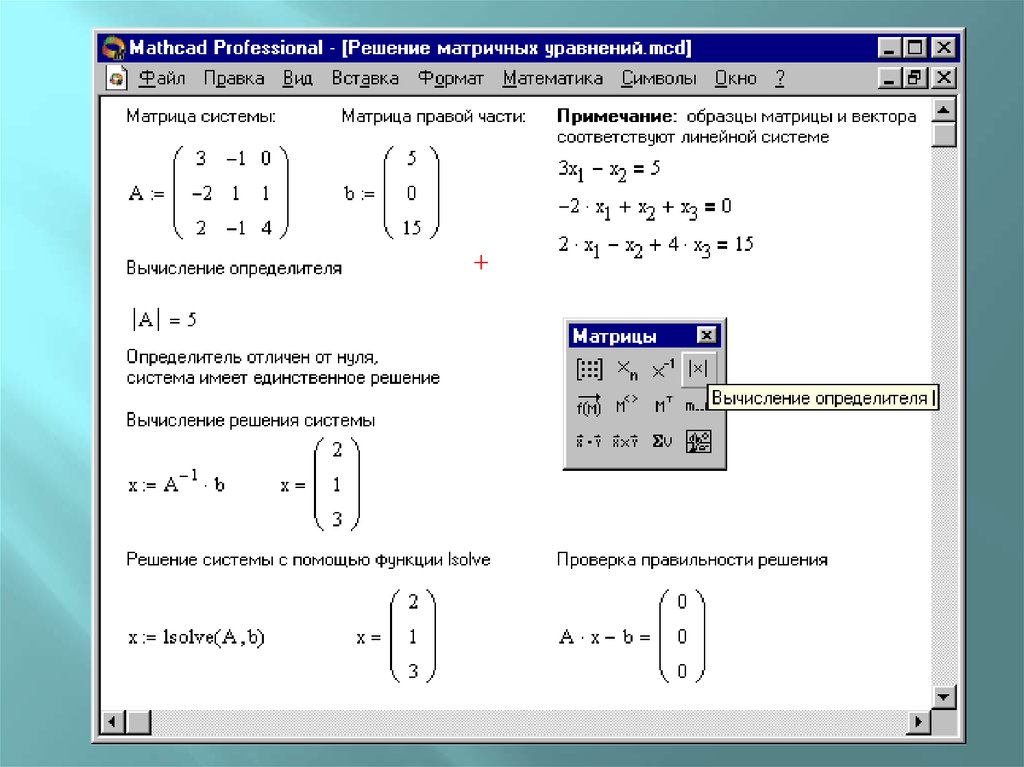
Опр: Определитель Δ основной матрицы
называется
главным
(основным)
определителем.
Δ=
а11 а12
а21 а22
а13
а23
а31 а32
а33
Опр: Дополнительным определителем
называется определитель полученный из
главного определителя путем замены j-го
столбца столбцом свободных членов.
.
Δ 1=
в1
в2
а12
а22
а13
а23
в3
а32
а33
Δ3=
Δ 2=
а11 а12 в1
а21 а22 в2
а31 а32
в3
а11 в1
а21 в2
а13
а23
а31 в3
а33
Теорема: Если определитель системы Δ не
равен 0, то система имеет единственное
решение, которое находится по формулам:
Х1 = Δ1/ Δ;
х2== Δ2/ Δ;
х3== Δ3/ Δ
Теорема: Если определитель системы Δ=0, и
хотя бы один из определителей ∆1, ∆2, ∆3
отличен от нуля, то система несовместна(т.е.
не имеет решений).
Теорема:Если определитель системы ∆=0, и
∆1=∆2=∆3=0, то система имеет бесконечное
множество решений. (неопределенная
система).

12. Матричный метод решения СЛАУ

Системе
3х
линейных
уравнений
соответствует матричное уравнение
АХ=В
А=
а11
а21
а31
а
а
а
12
22
32
23
33
а
а
а
13
х1
х
Х = 2
х
3
АХ=В
А-1АХ= А-1В
ЕХ = А-1В
Х = А-1В
в1
в2
В=
в3

14.

Метод не работает, если число уравнений не равно числу неизвестных, или когда матрица системы хотя и квадратна, но вырождена (тогда не сущес Метод не работает, если число уравнений не равно
числу неизвестных, или когда матрица системы хотя
и квадратна, но вырождена (тогда не существует
обратной матрицы, т.е определитель основной
матрицы равен нулю).

English     Русский Правила

линейная алгебра — Для $\det(A)=0$, как мы узнаем, что $A x = b$ не имеет решения или бесконечно много решений?

спросил 10 лет, 2 месяца назад

Изменено 3 месяца назад

Просмотрено 68 тысяч раз

$\begingroup$

Если определитель $\det(A)$ матрицы $A$ неоднородной системы уравнений равен $0$, то как узнать, не имеет ли она решений или имеет бесконечно много решений?

И пока мы этим занимаемся, пожалуйста, ответьте на следующие «подвопросы», вытекающие из этого. Я буду вам очень признателен, так как это будет иметь решающее значение для моего понимания всего этого:

а) Поскольку определитель равен нулю, это означает, что возникает ситуация «Деления на ноль» (используя правило Крамера), вариант понятен, так как деление на ноль не определено. Но меня смущает, как тогда, при любых обстоятельствах , система может иметь бесконечно много решений. Я имею в виду, не будем ли мы сталкиваться с делением на ноль во всех случаях, когда определитель равен нулю? Так пожалуйста дайте мне интуитивное и проницательное объяснение этому.

б) Не ошибусь ли я, если предположу, что в случае, когда определитель равен нулю, существует бесконечно много решений тогда и только тогда, когда это однородная система уравнений? Пожалуйста, объясните, почему или почему нет.

И, пожалуйста, не забудьте главный вопрос — «для определителя $=0$, как узнать, что решений нет или бесконечно много?»

• линейная алгебра
• матрицы
9{-1}\vec b=\vec x $$

Что касается (а) и вашего «основного вопроса»: если $\,\det A=0\,$, то можно еще проверить, нет ли решений или бесконечные решения (при условии, что мы работаем с бесконечным полем). Например, если система однородна (над бесконечным полем), она должна иметь бесконечные решения, тогда как если система неоднородна, она может не иметь решений или их может быть несколько:

$$\begin{cases}x+y=1 \\x+y=1\end{cases} \Longleftrightarrow \begin{pmatrix}1&1\\1&1\end{pmatrix}\binom{x}{y}=\binom{1}{1}\longrightarrow\,\ ,\text{бесконечное количество решений}$$

$$\begin{case}x+y=1\\x+y=0\end{cases} \Longleftrightarrow \begin{pmatrix}1&1\\1&1\end{pmatrix}\binom{x}{y} =\binom{1}{0}\longrightarrow\,\,\text{вообще нет решений}$$

и, конечно, в обоих вышеприведенных случаях имеем $\,\det A=0\,$

$\endgroup$

3

$\begingroup$

Для случая линейной системы неоднородных уравнений необходимо рассмотреть расширенную матрицу и сравнить ее ранг с рангом матрицы коэффициентов системы.

$\endgroup$

2

$\begingroup$

На самом деле возможны два случая: Если вектор b не находится в пространстве столбцов матрицы A, он не будет иметь решений. Если b находится в пространстве столбцов A и поскольку det(A)=0, то у него будет бесконечно много решений. Надеюсь, это может быть хорошей отправной точкой для вас.

$\endgroup$

$\begingroup$

Пусть система уравнений: $$ \левый\{ \начать{массив}{л} топор+by=е \\ сх+dy=f \конец{массив} \верно. $$ Если мы умножим определитель на $x$ и воспользуемся некоторыми свойствами определителей, то получим: $$x\begin{массив}{|cc|} а и б \\ CD \\ \end{массив}= \begin{массив}{|cc|} топор и б \\ сх & д \\ \конец{массив} \Rightarrow$$

$$\Rightarrow х\начало{массив}{|cc|} а и б \\ CD \\ \end{массив}= \begin{массив}{|cc|} е-б&б\ ф-ды&д\ \конец{массив} \Rightarrow$$ $$\стрелка вправо х\начало{массив}{|cc|} а и б \\ CD \\ \end{массив}= \begin{массив}{|cc|} е & б \\ ж и д \\ \конец{массив}+ \begin{массив}{|cc|} -by&b\ -ды&д\ \конец{массив} \Rightarrow$$ $$ \Rightarrow x\begin{массив}{|cc|} а и б \\ CD \\ \end{массив}= \begin{массив}{|cc|} е & б \\ ж и д \\ \конец{массив}+ 0 \Rightarrow$$ $$\Rightarrow x\begin{массив}{|cc|} а и б \\ CD \\ \end{массив}= \begin{массив}{|cc|} е & б \\ ж и д \\ \конец{массив} $$ Если у нас есть система, в которой $\begin{array}{|cc|} а и б \\ CD \\ \end{массив}=0$ и $\begin{массив}{|cc|} е & б \\ ж и д \\ \end{array}=0$, тогда $x$ может быть любым вещественным числом.

То же самое можно сделать и с $y$, но в этом случае мы получим: $$\Rightarrow y\begin{массив}{|cc|} а и б \\ CD \\ \end{массив}= \begin{массив}{|cc|} а & е \\ с и ж \\ \конец{массив} $$ Опять же, если $\begin{массив}{|cc|} а и б \\ CD \\ \end{массив}=0$ и $\begin{массив}{|cc|} а & е \\ с и ж \\ \end{массив}=0$, $y$ может принимать множество значений в зависимости от значений $x$ или наоборот.

$\endgroup$

$\begingroup$

У меня есть геометрическая интерпретация:

Матрица $2 \times 2$ $\bf{A}$ преобразует вектор $\bf{x}$ на плоскости в другой вектор $\bf{b}$.

Если $\text{det }\bf{A}=0$, то это преобразование фактически представляет собой уплощение (геометрическая интерпретация определителя состоит в том, что это площадь, полученная преобразованием единичного квадрата):

Любой вектор будет преобразован в вектор, который будет выровнен вдоль той же линии, проходящей через начало координат, независимо от вектора $\bf{x}$.

Итак, если у вас есть $\bf{}Ax=b$ и $\text{det }\bf{A}=0$:

• Если $\bf{b}$ выровнено по этой конкретной линии, вы действительно можете выбрать любой $\bf{x}$. То есть: бесконечное решение.
• Но если $\bf{b}$ не выровнен вдоль этой конкретной линии, невозможно найти вектор $\bf{x}$: сглаживание $\bf{}A$ всегда дает вектор, выровненный вдоль этой определенной строка, поэтому $\bf{b}$ никогда не может быть результатом преобразования $\bf{x}$ с помощью $\bf{}A$.

То же самое можно рассуждать и с однородным уравнением: это преобразование с помощью $\bf{A}$ вектора $\bf{x}$ в одну точку: начало координат $O\,(0,\quad 0)$ :

Следовательно, если $\text{det }\bf{A}=0$, это всегда верно, поскольку сглаживание создает векторы, выровненные вдоль определенной линии, всегда проходящие через начало координат.

$\endgroup$

Определитель — Линейная алгебра | Elevri

Линейная алгебра

Определитель

Определитель – это скалярное представление матрицы, определяемое специальным вычислением. Геометрическая интерпретация заключается в том, что это масштабный коэффициент для линейного преобразования, которое представляет матрица. Он также говорит о том, имеет ли система линейных уравнений, которую представляет матрица, единственное решение или нет.

Содержание

Почему это правило называется правилом Крамера?

В 1750 году Габриэль Крамер опубликовал статью, в которой изложил знаменитую технику, которая сегодня носит его имя: Правило Крамера . Швейцарский гений понял, что определителя можно использовать для решения систем линейных уравнений.

В возрасте всего 18 лет Крамер получил докторскую степень в Женевском университете. Учебное заведение было настолько впечатлено способностями молодого математика, что для него создали новую должность сопредседателя кафедры математики в университете.

Как оказалось, это был умный ход со стороны Университета, от которого выиграла вся Женева.

Крамер остался в университете до конца своей жизни, где он реформировал систему образования, чтобы математика преподавалась на французском языке, а не только на латыни, таким образом охватив более широкую аудиторию.

Каково определение определителя?

Определитель матрицы представляет собой скалярное значение, обозначаемое или . Чтобы существовать, матрица должна быть квадратной, и если она квадратная, то раскрывает информацию о решениях системы уравнений, которую составляет матрица.

Если определитель равен нулю, то у данной системы либо бесконечно много решений, либо их нет вообще. Все остальные значения означают, что существует единственное решение.

Для матриц, определители которых равны нулю, мы можем быть уверены, что существует либо бесконечное число решений, либо ни одного из них. Более того, ненулевой определитель всегда будет давать единственное решение.

Значение определителя также тесно связано с обратной матрицей. Тогда и только тогда, когда матрица имеет ненулевой определитель, она обратима, и мы можем использовать определитель, чтобы найти обратную матрицу.

Кроме того, определитель дает коэффициент масштабирования линейного преобразования, описываемого матрицей.

Как найти определитель квадратной матрицы?

Чтобы найти определитель квадратной матрицы (он должен быть квадратным), мы можем использовать такие методы, как формула Лейбница или разложение Лапласа, которые всегда будут работать. Однако есть короткие пути, которые мы можем использовать в определенных случаях.

Если — матрица, ее определитель можно быстро найти по следующей формуле:

В случае, если мы имеем дело с матрицей, используем следующую формулу:

Подробнее об определителе

Введение

Определитель является скаляром и отмечен:

Определитель может быть введен как поздно, так и рано в курсе линейной алгебры. Что касается того, что это такое, студентов традиционно сначала знакомят с тем, как вычисляется определитель, а затем с практической связью и ее геометрической интерпретацией.

Мы делаем наоборот.

Практическая связь

Определитель показывает, имеет ли линейная система уравнений решения. Помните три случая; единственное решение , бесконечно много решений или нет решений .

Если определитель равен нулю, система имеет «бесконечное множество решений» или «нет решений».

Если определитель отличен от нуля, система имеет единственное решение.

Геометрическая интерпретация

Определитель геометрически интерпретируется как масштабный коэффициент для линейного преобразования, с которым новичок, к сожалению, обычно не знакомится, когда необходимы вычисления определителя.

Короче говоря, каждое умножение матриц является линейным преобразованием, но с практической точки зрения можно сказать, что линейное преобразование — это матрица, которая умножается на вектор для получения желаемого результата.

Простым примером может быть линейное преобразование, которое поворачивает по часовой стрелке на угол и удваивает свою длину. Тогда масштабный коэффициент, то есть определитель, будет равен .

Определитель 2×2

Определение определителя -матрицы формирует основу для вычисления определителя -матрицы.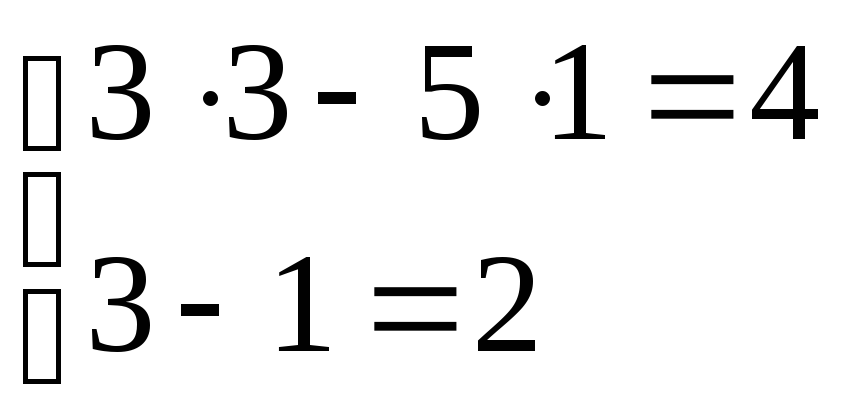

Пусть:

откуда определение определителя:

Определитель 3×3

Алгоритм вычисления определителя -матрицы выполняется с использованием суммы трех -определителей. Мы производим их, расширяя одну строку или столбец в определителе (называемый расширением кофактора ).

Пусть:

и тогда применимо, что определитель равен:

где мы сделали разложение первой строки, потому что скаляры каждой -матрицы — это просто элементы из первой строки.

Теперь рассмотрим, как делается расширение. Рассмотрим определитель:

Мы начнем с расширения вдоль первой строки и начнем с первого элемента:

Расширение затем происходит путем выбора строки и столбца текущего элемента для извлечения оставшихся элементов в виде -детерминанта, умноженного на :

Переходим к следующему элементу по первой строке и получаем:

Обратите внимание, что расширение вокруг идет со знаком минус! Мы скоро вернемся к этому.

Теперь мы продолжаем расширять следующий и последний элемент: .

Обратите внимание, что элемент идет со знаком плюс!

Теперь мы закончим вычисление, используя определение -определителя:

Которое завершает формулу для -определителя, а также алгоритм, облегчающий запоминание определения вместо того, чтобы заучивать формулу наизусть (что-то, что требуется для продвижения вперед). со статусом новичка).

Альтернативная формула

Приведенный выше метод можно легко аналогично распространить на более крупные матрицы, поэтому мы начали с него. Однако существует альтернативный алгоритм, применимый к -определителю, который визуально напоминает определение -определителя:

Если мы расширим этот образ мышления, мы получим метод, который работает, но работает только для вычисления -определителей. Метод называется правилом Сарру .

nxn определитель

Вычисление определителя, вне зависимости от размерности матрицы, производится аналогично -определителю — можно выразить в виде алгоритма для каждого -определителя. Но прежде чем мы это сделаем, мы объясним, почему элемент в вычислении -детерминанта имел знак минус.

Рассмотрим -матрицу . В этом случае каждый извлеченный элемент в своем определителе несет с собой знак плюс или минус в зависимости от его положения в соответствии со следующим «шахматным шаблоном»:

Это означает, что для -определителя скрытый знак для каждого элемента следующим образом:

Например, если бы мы выбрали расширение по второму столбцу, сумма произведений была бы:

Обратите внимание, что знаки плюс и минус, записанные в указанных выше определителях, не должны использоваться ни в каких вычислениях, но теперь они сделано только в образовательных целях.

Общая форма разложения вдоль линии (кофакторное разложение) для определителя -матрицы может быть записана как:

где — каждый элемент в выбранной строке , и — кофактор , который является -детерминантом другие элементы, которые не делят строку или столбец с соответствующим .

Алгоритм для определителя nxn

1. Выберите строку или столбец, которые необходимо разложить в произведение суммы матричных элементов и -определителей

2. Для каждого элемента в выбранной строке/столбце:
   \begin{enumerate}

3. Извлечь элемент со знаком плюс или минус, который он несет, и умножить на -детерминант элементов, которые не разделяют строку или столбец с выделенным элементом

4. Повторяйте до тех пор, пока не будут извлечены все элементы в выбранной строке/столбце

\item Повторяйте вышеуказанные шаги до тех пор, пока последняя сумма произведений не будет содержать только -детерминанты.
\конец{перечислить}
Алгоритм показывает, что вычисление определителя может быть чрезвычайно трудоемким, если размерность велика.

Однако обратите внимание на преимущество извлечения строки или столбца, число элементов которых равно нулю! Это означает, что сумма разработанного продукта значительно снижается. Например, как в:

Если в определителе, который вы вычисляете, не хватает 0-элементов или их недостаточно, чтобы значительно упростить вычисление, вы можете, как Гаусс-Жордан, сократить строку матрицы определителя, не изменяя определитель. Эти и другие функции обсуждаются в следующем разделе.

Сопряжение к матрице

Сопряжение к матрице основано на кофакторных разложениях . Это становится интересным в теореме для выражения , если обратное существует. Наше определение сопряженной матрицы:

Если -матрица и является кофактором , то отсюда следует, что матрица:

называется кофакторной матрицей матрицы A. Транспонирование этой матрицы называется примыкает к матрице и обозначается как .

Используя сопряженную матрицу , мы можем очень легко выразить, существует ли обратная, используя следующую теорему, которую мы оставляем недоказанной.

Если обратимая матрица, то:

Сейчас мы покажем все это на примерах. Пусть следующая обратимая матрица:

, кофакторы которой становятся:

и, таким образом, матрица кофакторов и сопряженная матрица становятся следующими:

Определяющие свойства

детерминантную матрицу перед расширением строки, чтобы максимизировать количество 0-элементов.

Для каждой -матрицы применяется следующее:

• Если матрица является результатом умножения скаляра на строку или столбец в матрице, то:

• Если матрица является результатом двух строк или столбцов, поменявшихся местами в , применяется следующее:

• Если матрица является результатом умножения строки или столбца матрицы на другую строку или столбец, то:

Доказательство первого и третьего пункта — хорошее упражнение для новичка, прямого доказательства -детерминанта и -детерминанта достаточно, чтобы убедиться. Чтобы создать устойчивое математическое доказательство, рекомендуется доказательство по индукции.

Второй пункт следует из определения определителя с «шахматной» схемой символов в предыдущем разделе.

С помощью предыдущего утверждения мы можем получить следующее утверждение:

Пусть — -матрица.

• Если две строки или столбца равны, то:

• Если строку или столбец можно уменьшить до 0, то:

• Если это скаляр, то:

  5

• 0 готовы к самой запоминающейся теореме для студентов, которая основана на последних теоремах и доказательствах, которые мы представили для того, как обратимая матрица может быть уменьшена по строкам до:

  Квадратная матрица обратима тогда и только тогда, когда .

  Предположим, что построчно можно свести к , тогда:

  Предположим противное, что нельзя построчно свести к , но к . Это означает, что необратимо, потому что по крайней мере две строки в линейно зависимы, и мы получаем по крайней мере одну нулевую строку в . Одна нулевая строка дает:

  Еще одна полезная теорема для арифметики:

  Если и — квадратные матрицы одинаковой размерности, то:

  Следующее утверждение применимо к обратному:

  Если матрица обратима, то применяется:

  Помните, что . Тогда у нас есть:

  Поскольку , у нас есть:

  Мы заканчиваем этот раздел, связывая теорему, которая вводится с обратными и линейными системами уравнений, а также наши идеи с определителем.

  Пусть -матрица. Тогда применяются следующие утверждения:

  • Сокращенная ступенчатая форма строки для is

  • может быть выражена как произведение элементарных матриц

  • IS Invertible

  • имеет только тривиальное решение

  • для каждого вектора в

  • имеет ровно одно решение для каждого вектора в

  • .

  • Векторы-строки линейно независимы. Правило Крамера — это утверждение, которое, прежде всего, облегчает выражение решения, так как у нас нет чисел в матрице.

    Правило Крамера Если является линейной системой уравнений с уравнениями и переменными, то система имеет единственное решение тогда и только тогда, когда , после чего решение может быть выражено как:

    где матрица где столбец в заменено на .

    No related posts.