11. Исследование функции, построение графика
Далее займемся исследованием функций, применяя полученные знания.
Если в некоторой окрестности точки Х0 выполняется неравенство F(X)<F(Х0) или F(X) > F(Х0), то точка Х0 называется Точкой экстремума функции F(X) (соответственно точкой максимума или минимума). Необходимое условие экстремума: если Х0 – экстремальная точка функции F(X), то первая производная (Х0) либо равна нулю или бесконечности, либо не существует. Достаточное условие экстремума: Х0 является экстремальной точкой функции F(X), если ее первая производная (X) меняет знак при переходе через точку Х0: с плюса на минус – при максимуме, с минуса на плюс – при минимуме.
Точка Х0 называется Точкой перегиба кривой y=F(Х), если при переходе через точку Х0 меняется направление выпуклости.
Прямая Yас=KХ+B называется Наклонной асимптотой кривой y=F(Х), если расстояние от точки (x; F(Х)) кривой до этой прямой стремится к нулю при Х®¥. При этом
При K=0 имеем Горизонтальную асимптоту:Y=B.
Если
То прямая Х=А называется Вертикальной асимптотой.
Общая схема исследования функции и построения ее графика.
I. Элементарное исследование:
1) найти область определения функции;
2) исследовать функцию на симметричность и периодичность;
3) вычислить предельные значения функции в ее граничных точках;
4) выяснить существование асимптот;
5) определить, если это не вызовет особых затруднений, точки пересечения графика функции с координатными осями;
6) сделать эскиз графика функции, используя полученные результаты.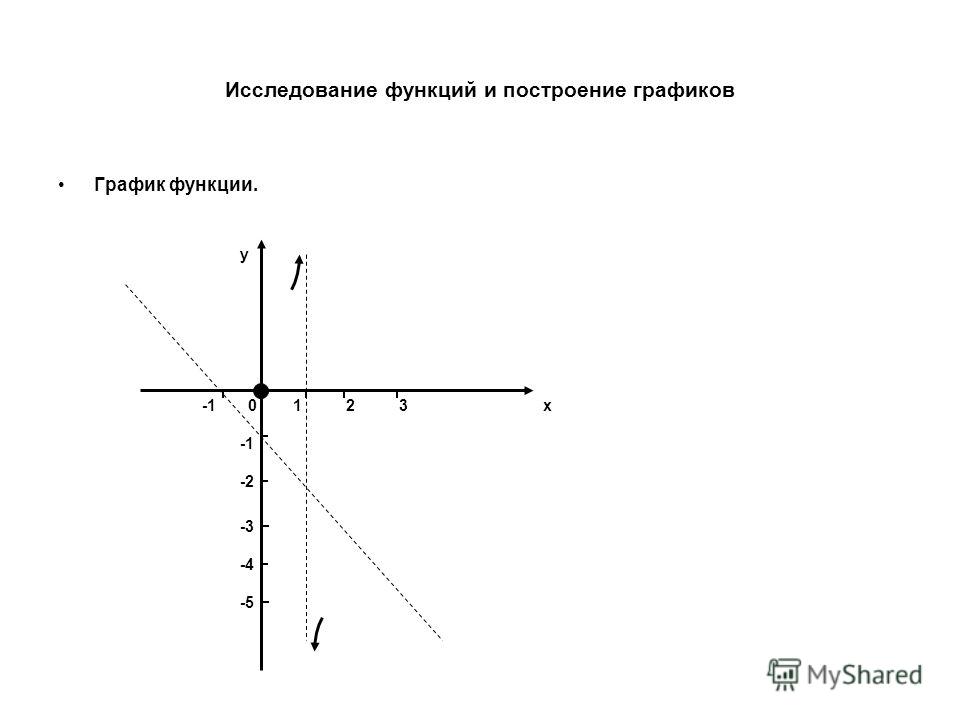
П. Исследование графика функции по первой производной:
1) найти решение уравнений Y’(Х)=0 и Y’(Х)=¥;
2) точки, «подозрительные» на экстремум, исследовать с помощью достаточного условия экстремума, определить вид экстремума;
3) вычислить значения функции в точках экстремума;
4) найти интервалы монотонности функции;
5) нанести на эскиз графика экстремальные точки;
6) уточнить вид графика функции согласно полученным результатам.
Ш. Исследование графика функции по второй производной
1) найти решения уравнений Y”(Х)=0 и Y”(Х)=¥;
2) точки, «подозрительные» на перегиб, исследовать с помощью достаточного условия;
3) вычислить значения функции в точках перегиба;
4) найти интервалы выпуклости и вогнутости графика функции;
5) нанести на эскиз графика точки перегиба;
6) окончательно построить график функции.
Если исследование проведено без ошибок, то результаты всех этапов должны согласовываться друг с другом.
Если же согласование отсутствует, необходимо проверить правильность результатов отдельных этапов и исправить найденные ошибки.
Рассмотрим на примерах
Пример 1. Исследовать на экстремум функцию .
Решение. Находим первую производную: . Из уравнений Y’=0 и Y’=¥ получаем точки, «подозрительные» на экстремум: . Исследуем их, определяя знак первой производной слева и справа от каждой точки. Для наглядности результаты представим в виде таблицы изменения знака Y’:
В первой строке указаны интервалы, на которые область определения функции разбивается точками и сами эти точки. Во второй строке указаны знаки производной Y’ в интервалах монотонности. В третьей строке приведено заключение о поведении функции.
Исследуемая функция, как следует из таблицы, имеет минимум в точке Х=-3: Y(-3)=27/4. Точки Х=-1 и Х=0 не являются точками экстремума, так как в первой точке функция не определена, а в окрестности второй точки первая производная сохраняет знак.
Пример 2. Найти асимптоты графика функции .
Решение. Точка Х=-1 является точкой разрыва функции. Так как , то прямая Х= -1 служит вертикальной асимптотой графика функции.
Ищем наклонные асимптоты ,
Таким образом, уравнение наклонной асимптоты имеет вид .
Пример 3. Построить график функции , используя общую схему исследования функции.
Решение. 1. Область определения: (-¥, -1), (-1, +¥). Функция не является симметричной и периодической. Находим предельные значения функции:
График функции имеет одну вертикальную асимптоту Х=-1 и одну наклонную асимптоту Y=-x+2 (см. пример 2). Он пересекает координатные оси в точке (0; 0).
П. Функция имеет один минимум при Х=-3 (см. пример 1).
Ш. Вторая производная обращается в бесконечность при Х=-1 и равна нулю в точке Х=0, которая является единственной точкой перегиба (см. таблицу):
Учитывая полученные результаты, строим график функции .
Вопросы для самопроверки:
1. Как найти область возрастания и убывания функции?
2. Каково необходимое условие экстремума Вам известны?
3. Как найти точку перегиба?
4. Укажите уравнение наклонной прямой?
5. Укажите уравнение наклонной асимптоты?
6. В каком случае существует вертикальная асимптота, а в каком горизонтальная?
| < Предыдущая | Следующая > |
|---|
Исследовать функцию и построить график. Полное исследование функции. Решение задач и контрольных работ по высшей математике онлайн
Краткая теория
Наиболее наглядное представление о ходе изменения функции дает ее график. Поэтому построение графика является заключительным этапом исследования функции, в котором используются все результаты ее исследования.
Схема исследования функции с последующим построением графика такова:
- Исследование области определения функции.
- Исследование функции на четность и нечетность.
- Нахождение точек пересечения графика с осями координат
- Исследование функции на точки разрыва. Нахождение вертикальных асимптот. Нахождение горизонтальных и наклонных асимптот.
- Исследование функции на экстремум и интервалы монотонности функции.
- Исследование функции на интервалы выпуклости и вогнутости графика функции. Нахождение точек перегиба графика функции.
- Построение графика функции.
Полученные данные следует использовать для построения графика функции. Если исследуемая функция является четной или нечетной, то ее достаточно исследовать при неотрицательных значениях аргумента из множества ее задания и принять во внимание, что график четной функции симметричен относительно оси ординат, а график нечетной функции симметричен относительно начала координат.
Если, например, функция имеет период
,
то следует построить график на отрезке
,
а затем продолжить его периодически на всю числовую ось.
Кроме того, если полученных данных окажется недостаточно, то следует, воспользовавшись уравнением , найти дополнительные точки графика, в которых его изменение менее ясно.
Разумеется, в процессе исследования функции не обязательно придерживаться приведенной схемы, иногда порядок исследования полезно выбрать, исходя из конкретных особенностей данной функции.
Примеры решения задач
Задача 1
Исследовать функцию и построить ее график:
Решение
1) Область определения функции:
2) Исследуем функцию на четность-нечетность:
Функция является четной
3) Находим точки пересечения с осями координат:
График функции пересекает ось в точках и . Ось график функции не пересекает.
4) Исследуем функцию на непрерывность, точки разрыва, вертикальные и наклонные асимптоты:
Если не находите примера, аналогичного вашему, если сами не успеваете выполнить работу, если впереди экзамен по предмету и нужна помощь — свяжитесь со мной:
ВКонтакте
WhatsApp
Telegram
Я буду работать с вами, над вашей проблемой, пока она не решится.
В точке существует разрыв 2-го рода.
Прямая –вертикальная асимптота.
Для нахождения наклонной асимптоты вычисляем пределы:
–горизонтальная асимптота
5) Исследуем функцию на экстремум. Найдем производную функции.
Первая производная на области определения в нуль не обращается
-функция возрастает
-функция убывает
6) Исследуем функцию на интервалы выпуклости и вогнутости.
Вторая производная функции не равна нулю на всей области определения
–график функции вогнутый
– график функции вогнутый
7) График функции имеет вид:
Задача 2
Исследовать функцию и построить ее график:
Решение
1) Область определения функции:
2) Исследуем функцию на четность-нечетность:
Функция является нечетной
3) График функции оси координат не пересекает
4) Исследуем функцию на непрерывность, точки разрыва, вертикальные и наклонные асимптоты:
В точке
существует разрыв 2-го рода.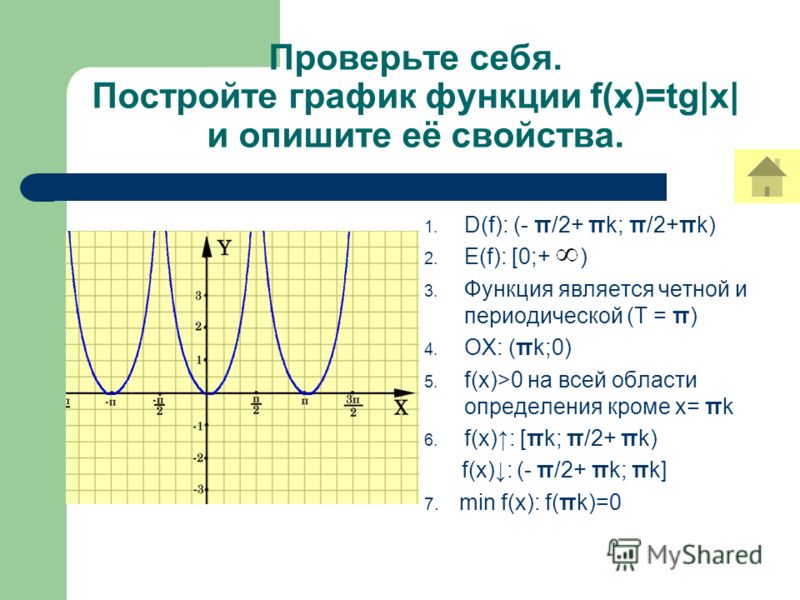
Прямая –вертикальная асимптота.
Для нахождения наклонной асимптоты вычисляем пределы:
–наклонная асимптота
5) Исследуем функцию на экстремум. Найдем производную функции.
Приравняем найденную производную к нулю и решим полученное уравнение:
-функция возрастает
-функция убывает
-функция убывает
-функция возрастает
6) Исследуем функцию на интервалы выпуклости и вогнутости.
Вторая производная функции не равна нулю на всей области определения
–график функции выпуклый
– график функции вогнутый
7) График функции имеет вид:
Задача 3
Исследовать функцию и
построить ее график.
Решение
1) Область определения функции:
2) Исследуем функцию на четность-нечетность:
Функция не обладает свойствами четности — нечетности
3) Находим точки пересечения с осями координат:
График пересекает ось в точке (-0618, 0) и (1.618, 0)
4) Исследуем функцию на непрерывность, точки разрыва, вертикальные и наклонные асимптоты:
Точка является точкой разрыва функции 2-го рода, а прямая -вертикальной асимптотой графика функции.
Точка является точкой разрыва функции 2-го рода, а прямая -вертикальной асимптотой графика функции.
Для нахождения наклонной асимптоты вычисляем пределы:
Прямая –горизонтальная асимптота
5) Исследуем функцию
на экстремум.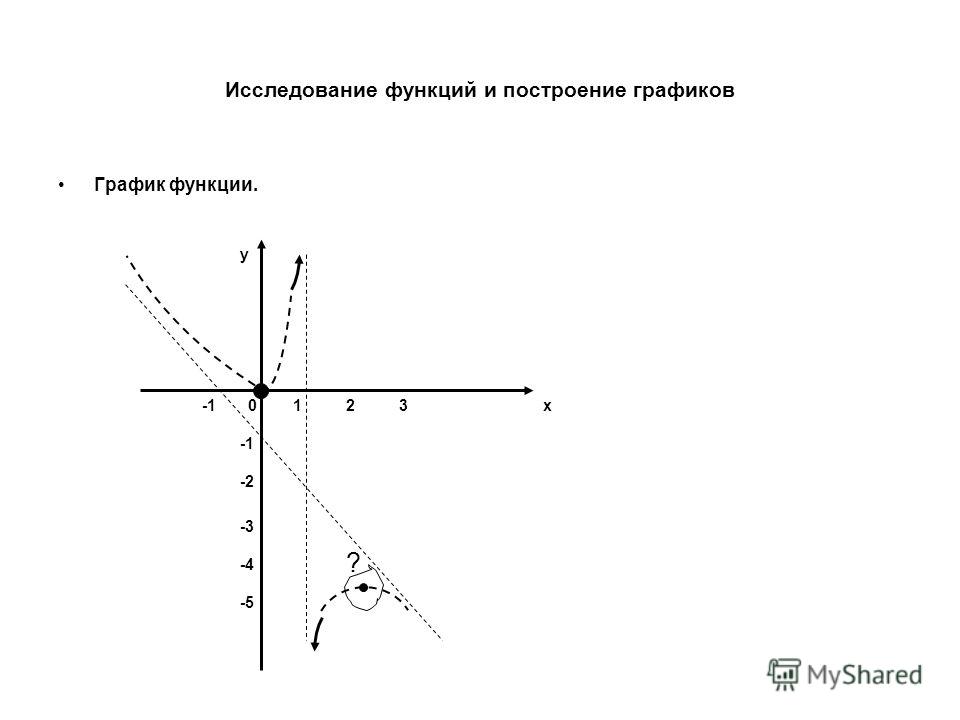
Найдем производную функции.
Приравняем найденную производную к нулю и решим полученное уравнение:
Полученное уравнение действительных корней не имеет
– функция убывает
– функция убывает
– функция убывает
6) Исследуем функцию на интервалы выпуклости и вогнутости.
– график функции выпуклый
– график функции вогнутый
– график функции выпуклый
– график функции вогнутый
7) График функции имеет вид:
3\вправо)$, я хочу учиться $$ г \ влево (х \ вправо) = \ гидроразрыва {е \ влево (2,5x \ вправо)} {е \ влево (х \ вправо)} $$
Например, для $x=0,8$ я хотел бы знать значение $f\left(0,8\right)$, $f\left(2\right)$ и в целом $g\left (0,8 \ справа) = \ гидроразрыва {е \ слева (2 \ справа)} {е \ слева (0,8 \ справа)} $.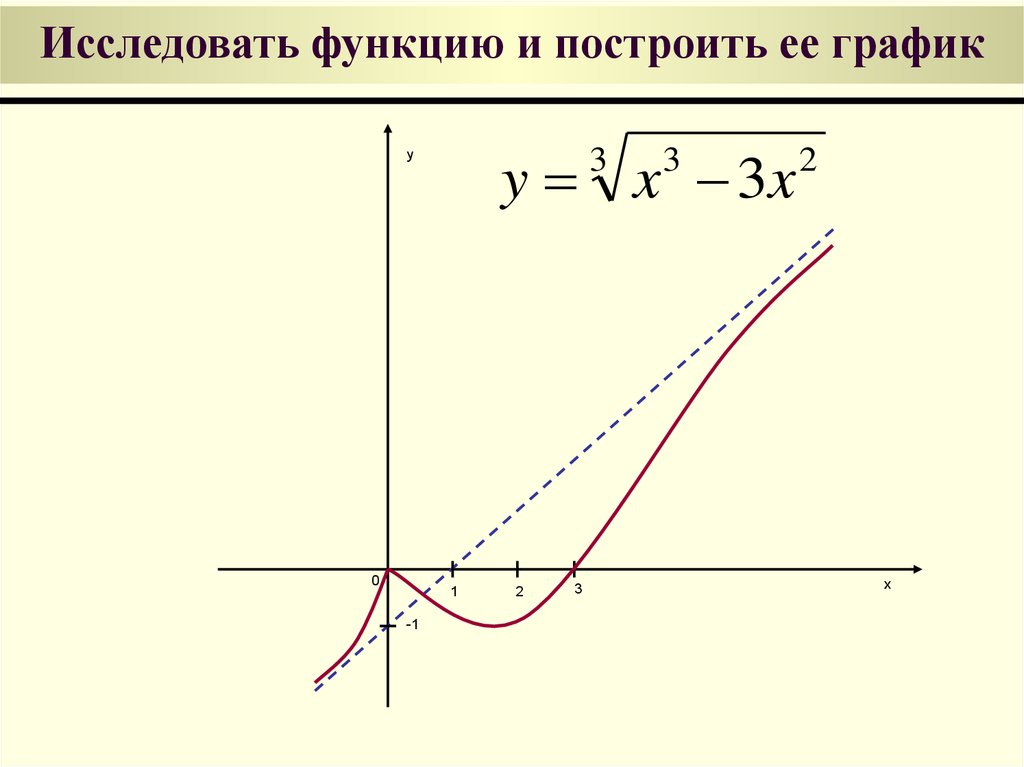
Однако каждое программное обеспечение, которое я пробовал, дает мне $f\left(0.8\right)=f\left(2\right)=0$, и тогда соотношение не существует. Я хотел бы знать, есть ли простой способ построить $g$ или хотя бы посмотреть, какой диапазон значений будет принимать эта функция? 93}\end{массив}$$
$\endgroup$
Зарегистрируйтесь или войдите в систему
Зарегистрируйтесь с помощью Google
Зарегистрироваться через Facebook
Зарегистрируйтесь, используя электронную почту и пароль
Опубликовать как гость
Электронная почта
Требуется, но не отображается
Опубликовать как гость
Электронная почта
Требуется, но не отображается
Нажимая «Опубликовать свой ответ», вы соглашаетесь с нашими условиями обслуживания, политикой конфиденциальности и политикой использования файлов cookie
.
R Функция plot() — Обучение на примере
Эффективная и точная визуализация данных является важной частью статистического анализа. Это может оживить ваши данные и эффективно передать ваше сообщение.
R имеет очень мощные графические возможности, которые помогут вам визуализировать ваши данные.
Функция plot()
В R базовой графической функцией для создания графика является функция plot() . Он имеет множество опций и аргументов для управления многими вещами, такими как тип графика, метки, заголовки и цвета.
Синтаксис
Синтаксис функции plot() :
plot(x,y,type,main,xlab,ylab,pch,col,las,bty,bg,cex,…)
Параметры
| x | The coordinates of points in the plot |
| y | The y coordinates of points in the plot |
| type | The type of plot to натяжной |
| основной | An overall title for the plot |
| xlab | The label for the x axis |
| ylab | The label for the y axis |
| pch | The shape of points |
| col | Цвет переднего плана символов и линий |
| las | Стиль меток осей |
| bty | Тип рамки вокруг области графика | 00 bg | The background color of symbols (only 21 through 25) |
| cex | The amount of scaling plotting text and symbols |
| … | Other graphical parameters |
Create a Simple Plot
To чтобы начать работу с графиком, вам нужен набор данных для работы.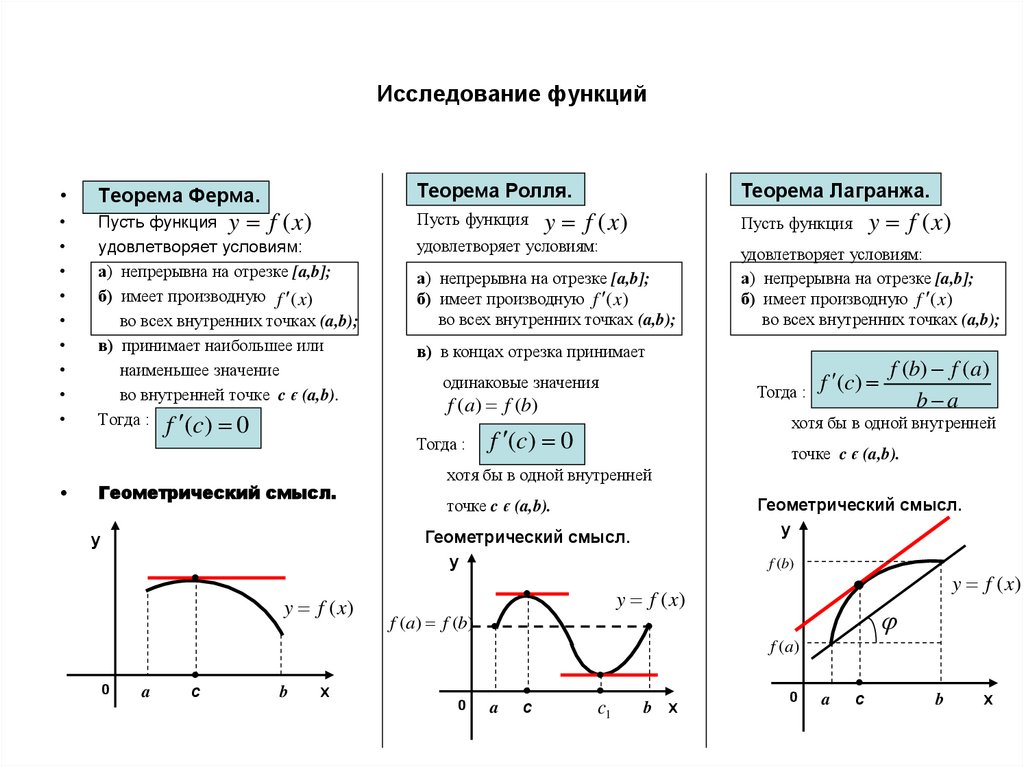
Давайте рассмотрим встроенный набор данных давления в качестве примера набора данных. Он содержит наблюдения за давлением паров ртути в диапазоне температур.
# Первые шесть наблюдений набора данных «Давление» напор (давление) температура давление 1 0 0,0002 2 20 0,0012 3 40 0,0060 4 60 0,0300 5 80 0,0900 6 100 0,2700
Чтобы создать график, просто укажите набор данных в функции plot() .
# Постройте набор данных «давление» участок (давление)
Изменение формы и размера точек
Вы можете использовать аргумент pch (графический символ), чтобы указать символы, используемые при построении точек.
Вот список символов, которые вы можете использовать.
# Изменить форму точек сюжет(давление, pch=17)
Для символов с 21 по 25 можно указать цвет границы с помощью аргумента col и цвет заливки с помощью аргумента bg.
# Изменить цвет границы на синий и цвет фона на голубой график (давление, pch = 21, col = "синий", bg = "голубой")
Чтобы изменить размер отображаемых символов, используйте аргумент cex (расширение символов).
# Масштабирование точек данных на 1,2 график (давление, cex = 1,2)
Изменение цвета
Вы можете изменить основной цвет символов, используя аргумент col.
# Изменить цвет символов на красный график (давление, цвет = "красный")
R имеет ряд предопределенных цветов, которые можно использовать в графике. Используйте функцию colors() , чтобы получить полный список доступных имен для цветов.
# Список предопределенных цветов в R цвета() [1] "белый" "aliceblue" "античный белый" [4] "античный белый1" "античный белый2" "античный белый3" ...
Или вы можете обратиться к следующей таблице цветов.
Цвета можно указывать по индексу, имени, шестнадцатеричному коду или значению RGB. Например, col=1 , col="white" и col="#FFFFFF" эквивалентны.
Различные типы графиков
Вы можете изменить тип отображаемого графика, используя аргумент типа.
Вот список всех типов, которые вы можете использовать.
| «p» | Точки | ||||
| «L» | Линии | ||||
| «B» | Оба точки и линии | ||||
| «C» | . | И точки, и линии «перегружены» | |||
| «H» | , такая как (или высокая плотность) Вертикальные линии | ||||
| «S» | Стальный график (горизонтальный первый) | 0 | « | ». | Ступенчатая диаграмма (сначала по вертикали) |
| «n» | Без построения графика |
Например, чтобы создать график с линиями между точками данных, используйте type="l" ; чтобы рисовать линии и точки, используйте type="b" .
Ниже показан ряд рисунков, показывающих различные типы.
Добавление заголовков и меток осей
Вы можете легко добавить собственные заголовки и метки осей, указав следующие аргументы.
| основной | Название основного сюжета |
| xlab | метка оси X |
| ylab | метка оси Y |
график (давление,
main = "Давление паров ртути",
xlab = "Температура (градусы C)",
ylab = «Давление (мм рт. ст.)»)
ст.)»)
Стиль метки осей
Указав аргумент las (стиль метки), можно изменить стиль метки осей. Это изменяет угол ориентации меток.
| 0 | По умолчанию, параллельно оси |
| 1 | Всегда горизонтальный |
| 2 | Perpendicular to The Axis |
| 3 | Все всегда Vertical | 9010
| «o» | (по умолчанию) Рисует полный прямоугольник вокруг графика. |
| «n» | Ничего не рисует вокруг участка. |
| «l», «7», «c», «u» или «]» | Рисует фигуру вокруг области графика. |
# Снимите коробку вокруг участка график (давление, bty = "n")
Добавить сетку
Функция plot() не рисует сетку автоматически.
Однако для некоторых сюжетов это полезно зрителю. Позвоните в grid() функция для рисования сетки после вызова plot() .
участок(давление) сетка()
Добавить легенду
Вы можете включить в свой график легенду – маленькую рамку, которая расшифровывает графику для зрителя. Вызовите функцию legend() после вызова plot() .
# Добавляем легенду в левый верхний угол
график (давление, col = "красный", pch = 19)
точки(давление$температура/2, давление$давление, col="синий", pch=17)
легенда ("верхний левый", c ("строка 1", "строка 2"), pch=c(19,17), col=c("красный","синий"))
Положение легенды можно указать с помощью следующих ключевых слов: «внизу справа», «внизу», «внизу слева», «слева», «сверху слева», «сверху», «сверху справа», «справа» и «по центру». .
Эффект от использования каждого из этих ключевых слов показан ниже.
Добавить точки на график
Вы можете добавить точки на график с помощью функции points() .
Например, давайте создадим подмножество давления, содержащее температуры выше 200 °C, и добавим эти точки на график.
график(давление, col = "красный") точки(давление[давление$температура > 200, ], col = "красный", pch = 19)
Добавление линий на график
Вы можете добавлять линии на график очень похоже на добавление точек, за исключением того, что для этого используется функция lines() .
участок(давление) линии(давление$температура/2, давление$давление)
Вы можете изменить тип линии, используя аргумент lty; и ширину линии с использованием аргумента lwd.
# Изменить тип и толщину линии участок (давление) линии(давление$температура/2, давление$давление, lwd=2, lty=3)
Вот список типов линий, которые вы можете использовать.
Есть еще одна функция, называемая abline() , которая позволяет рисовать горизонтальные, вертикальные или наклонные линии.
# Нарисуйте пунктирную горизонтальную линию на отметке 247 и вертикальную линию на отметке 300 участок (давление) abline (h = 247, v = 300, col = "красный", lty = 2)
Метки точек данных
Используйте функцию text() для добавления текстовых меток в любое место на графике.
Положение текста определяется аргументом pos. Значения 1, 2, 3 и 4 соответственно размещают текст ниже, слева, выше и справа от указанных координат.
# Добавляем текстовые метки над координатами график (давление, pch = 19, col = "красный") текст (давление, метки = давление $ давление, cex = 0,7, pos = 3, col = "синий")
Установить пределы осей
По умолчанию функция plot() определяет наилучший размер и масштаб каждой оси, чтобы они соответствовали области построения. Однако вы можете легко установить пределы каждой оси, используя аргументы xlim и ylim.
# Измените пределы осей так, чтобы оси x и y находились в диапазоне от 0 до 500 график (давление, ylim=c(0,500), xlim=c(0,500))
Отображение нескольких графиков на одной странице
С помощью графического параметра mfrow можно отображать несколько графиков на одной графической странице.
Чтобы использовать этот параметр, необходимо передать двухэлементный вектор, указав количество строк и столбцов.
Затем заполните каждую ячейку матрицы повторным вызовом plot.
Например, mfrow=c(1, 2) создает два параллельных графика.
пар(mfrow = c(1, 2)) сюжет (автомобили, main = "Скорость против расстояния", col = "красный") сюжет (mtcars $ миль на галлон, mtcars $ hp, main = «HP против MPG», col = «синий»)
Как только ваш график будет готов, вам нужно сбросить параметры par() . В противном случае все ваши последующие сюжеты будут появляться рядом.
# Сброс параметра mfrow номинал (mfrow = c (1,1))
Сохранить график в файл изображения
Чтобы сохранить график в файл изображения, вы должны последовательно выполнить три действия:
- Вызвать функцию для открытия нового графического файла, например
png(),jpg()илиpdf(). - Звоните
plot()для создания графического изображения. - Вызовите
dev.off(), чтобы закрыть графический файл.
