Построение графиков функций, содержащих знак модуля | План-конспект урока по алгебре (9 класс) по теме:
Тема: Построение графиков функций, содержащих знак модуля
Цели: Образовательная: обеспечить усвоение темы через осмысление ранее полученных знаний и исследовательскую деятельность учащихся, основываясь на этапах научного познания.
Развивающая: продолжать развитие проблемного мышления для решения познавательных задач; формировать представление о процессе научного познания; продолжить работу по овладению методами научного исследования.
Воспитательная: способствовать воспитанию у школьников культуры исследовательского труда, воспитанию навыков коммуникативного общения.
Формы организации учебной деятельности: фронтальная, групповая, индивидуальная.
Методы обучения: наглядно-иллюстративный, объяснительно-иллюстративный, частично-поисковый, исследовательский.
Оборудование:
- Раздаточный материал
- Мультимедийный комплекс для демонстрации презентации
Эпиграф к уроку:
«Мыслящий ум не чувствует себя счастливым, пока ему не удастся связать воедино разрозненные факты, им наблюдаемые».
Д.Хевеши
Ход урока:
- Организационный момент
Роль функций в жизни нашей неизменна,
Об этом знать должны вы непременно,
Описывать реальные процессы
Нельзя без функций в век науки и прогресса.
Наглядно представляя функций виды
Мы чертим графики, рисуем их эскизы,
И свойства функций так по ним легко читаются!
Что графики в ответ нам улыбаются…
Показ презентации «Графики улыбаются» (Приложение 1)
Вопросы учащимся:
Вы понимаете, что такие графики получаются с использованием не одной функции, а нескольких. Как называются такие функции? (кусочно-заданные функции)
- Проверка домашнего задания
Постройте и прочитайте график функции
Свойства функции:
- ;
- убывает возрастает ;
- функция ограниченная;
- функция непрерывная.

- Фронтальная работа с классом:
- Что называется областью определения функции?
- Какая функция называется возрастающей?
- Какая функция называется убывающей?
- Какая функция называется ограниченной? (функция называется ограниченной снизу, если существует такое число т, при котором для любого значения х из области определения выполняется неравенство ; функция называется ограниченной сверху, если существует такое число М, при котором для любого значения х из области определения выполняется неравенство )
- Что такое наибольшее и наименьшее значения функции? (число т называется наименьшим значением функции, если существует такая точка , что и выполняется неравенство ; число M называется наименьшим значением функции, если существует такая точка , что и выполняется неравенство )
- Что называется областью значения функции? (множество всех значений функции , называется областью значений функции)
- Какая функция называется непрерывной?
- Что такое выпуклость функции? (функцию называют выпуклой вниз (вверх), если соединив любые две точки ее графика, соответствующая часть графика лежит ниже (выше) проведенного отрезка)
А теперь обратим внимание на последние четыре графика функций.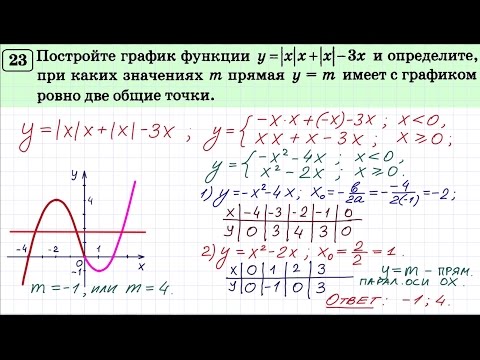
- Знакомы ли вам функции графики, которых изображены на слайде?
- Хотели бы вы научиться строить такие графики?
Построение графиков, содержащих модуль, осуществляется двумя способами:
- На основании определения модуля
Построение графика функции
Приводится пример построения графика функции
Построение графика функции
Приводится пример построения графика функции
- На основании правил геометрического преобразования графиков функций.
Какие геометрические преобразования, можно использовать при построение графиков функций? (параллельный перенос вдоль осей ОХ и ОУ, симметричное отображение относительно осей или точки)
Формулируется цель урока.
На сегодняшнем уроке мы с вами продолжим и усовершенствуем построение графиков функций, содержащих модуль.
Внимание на эпиграф.
Сегодня вам самим придется попробовать себя в роли исследователей, сделать новые открытия.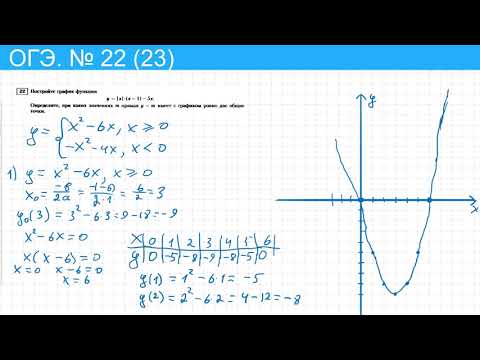
- Групповая исследовательская работа
Класс делится на 4 группы по 5-7 человек. В каждой группе назначается консультант. Группам раздается задание и правила выполнения исследовательской работы (Приложение 2).
На экране:
Правила работы в группах:
И стину познаем, а не соревнуемся!
Д аем высказаться товарищу!
Е динство цели и задачи!
А ктивность.
Л юбознательность.
Задания группам:
I и III группы
Постройте графики функций:
II и IV группы
Постройте графики функций:
После работы учащиеся выступают перед классом, делают выводы. Полученные выводы обобщаются вместе с учителем. Учащимся раздаются правила (алгоритмы) построения графиков функции, содержащих знак модуля (Приложение 3)
- Самостоятельная работа
Учащимся предлагается выполнить разноуровневую самостоятельную работу, на четыре варианта (Приложение 4)
- Домашнее задание
Постройте графики функций. Сделайте вывод, как построить график функции , с помощью геометрических преобразований графиков.
Сделайте вывод, как построить график функции , с помощью геометрических преобразований графиков.
- Подведение итогов
- Удалось ли нам углубить знания об основных свойствах функций?
- Усовершенствовали ли мы умения исследовать функции и строить графики?
- Рефлексия
Приложение 1
Презентация «ГРАФИКИ УЛЫБАЮТСЯ»
Приложение 2
ИССЛЕДОВАТЕЬСКАЯ РАБОТА
I группа
Постройте графики функций:
План исследования
Задание 1
- Постройте график функции .
Задание 2
- Используя определение модуля, запишите функцию , как кусочно-заданную.
- Постройте ее график.
- Проанализируйте, какое преобразование можно использовать при построении графика не прибегая к определению модуля?
- Сделайте вывод.
Задание 3
- Используя определение модуля, запишите функцию , как кусочно-заданную.

- Постройте ее график.
- Проанализируйте, какое преобразование можно использовать при построении графика не прибегая к определению модуля?
- Сделайте вывод.
ИССЛЕДОВАТЕЬСКАЯ РАБОТА
II группа
Постройте графики функций:
- ;
План исследования
Задание 1
- Постройте график функции .
Задание 2
- Используя определение модуля, запишите функцию , как кусочно-заданную.
- Постройте ее график.
- Проанализируйте, какое преобразование можно использовать при построении графика не прибегая к определению модуля?
- Сделайте вывод.
Задание 3
- Используя определение модуля запишите функцию , как кусочно-заданную.
- Постройте ее график.
- Проанализируйте, какое преобразование можно использовать при построении графика не прибегая к определению модуля?
- Сделайте вывод.
Приложение 3
Построение графика .
Чтобы построить график функции , если известен график функции , нужно оставить на месте ту его часть, где , и симметрично отобразить относительно оси Х другую его часть, где .
Алгоритм построения графика:
- Построить график функции ,
- Часть графика , лежащая над осью ОХ, сохраняется, а часть его, лежащая под осью ОХ, отображается симметрично относительно оси ОХ.
Построение графика .
Чтобы построить график функции , если известен график функции , нужно оставить на месте ту его часть, где , а при отразить построенную часть симметрично относительно оси ОУ.
Алгоритм построения графика:
- Построить график функции ,
- При график сохраняется, а при отражает построенную часть симметрично относительно оси ОУ.
Приложение 4
Самостоятельная работа «Построение графиков, содержащих знак модуля»
1 уровень
- Постройте график функции.

Вариант 1
Вариант 2
- Опишите его свойства.
2 уровень
- Постройте график функции.
Вариант 3
Вариант 4
- Опишите его свойства.
Приложение 4
Рефлексия урока
Ребята, мы с вами очень плодотворно поработали! Молодцы! Мне очень было приятно работать с вами! А вы не могли бы поделиться своими впечатлениями? Ответьте, пожалуйста, на вопросы рефлексии.
- Что вы узнали нового? ______________________________________________________________
- Смогли бы вы объяснить новый материал другу? _______________________
- Над чем вам надо еще поработать в данной теме? ______________________________________________________________
- Какой вопрос сегодняшнего урока был самым трудным? ______________________________________________________________
- Поставьте оценки по пятибалльной шкале за работу на уроке:
а) себе, оценив свою активность на уроке, самостоятельность, правильность выполнения заданий;
б) классу;
в) учителю.
Спасибо!
Построение графиков онлайн x y. Функции и графики
«Натуральный логарифм» — 0,1. Натуральные логарифмы. 4. «Логарифмический дартс». 0,04. 7. 121.
«Степенная функция 9 класс» — У. Кубическая парабола. У = х3. 9 класс учитель Ладошкина И.А. У = х2. Гипербола. 0. У = хn, у = х-n где n – заданное натуральное число. Х. Показатель – четное натуральное число (2n).
«Квадратичная функция» — 1 Определение квадратичной функции 2 Свойства функции 3 Графики функции 4 Квадратичные неравенства 5 Вывод. Свойства: Неравенства: Подготовил ученик 8А класса Герлиц Андрей. План: График: -Промежутки монотонности при а > 0 при а
«Квадратичная функция и её график» — Решение.у=4x А(0,5:1) 1=1 А-принадлежит. При а=1 формула у=аx принимает вид.
«8 класс квадратичная функция» — 1) Построить вершину параболы. Построение графика квадратичной функции. x. -7. Построить график функции. Алгебра 8 класс Учитель 496 школы Бовина Т. В. -1. План построения. 2) Построить ось симметрии x=-1. y.
2) Построить ось симметрии x=-1. y.
В золотой век информационных технологий мало кто будет покупать миллиметровку и тратить часы для рисования функции или произвольного набора данных, да и зачем заниматься столь муторной работой, когда можно построить график функции онлайн. Кроме того, подсчитать миллионы значений выражения для правильного отображения практически нереально и сложно, да и несмотря на все усилия получится ломаная линия, а не кривая. Потому компьютер в данном случае – незаменимый помощник.
Что такое график функций
Функция – это правило, по которому каждому элементу одного множества ставится в соответствие некоторый элемент другого множества, например, выражение y = 2x + 1 устанавливает связь между множествами всех значений x и всех значений y, следовательно, это функция. Соответственно, графиком функции будет называться множество точек, координаты которых удовлетворяют заданному выражению.
На рисунке мы видим график функции y = x . Это прямая и у каждой ее точки есть свои координаты на оси X и на оси Y . Исходя из определения, если мы подставим координату X некоторой точки в данное уравнение, то получим координату этой точки на оси Y .
Это прямая и у каждой ее точки есть свои координаты на оси X и на оси Y . Исходя из определения, если мы подставим координату X некоторой точки в данное уравнение, то получим координату этой точки на оси Y .
Сервисы для построения графиков функций онлайн
Рассмотрим несколько популярных и лучших по сервисов, позволяющих быстро начертить график функции.
Открывает список самый обычный сервис, позволяющий построить график функции по уравнению онлайн. Umath содержит только необходимые инструменты, такие как масштабирование, передвижение по координатной плоскости и просмотр координаты точки на которую указывает мышь.
Инструкция:
- Введите ваше уравнение в поле после знака «=».
- Нажмите кнопку «Построить график» .
Как видите все предельно просто и доступно, синтаксис написания сложных математических функций: с модулем, тригонометрических, показательных — приведен прямо под графиком. Также при необходимости можно задать уравнение параметрическим методом или строить графики в полярной системе координат.
В Yotx есть все функции предыдущего сервиса, но при этом он содержит такие интересные нововведения как создание интервала отображения функции, возможность строить график по табличным данным, а также выводить таблицу с целыми решениями.
Инструкция:
- Выберите необходимый способ задания графика.
- Введите уравнение.
- Задайте интервал.
- Нажмите кнопку «Построить» .
Для тех, кому лень разбираться, как записать те или иные функции, на этой позиции представлен сервис с возможностью выбирать из списка нужную одним кликом мыши.
Инструкция:
- Найдите в списке необходимую вам функцию.
- Щелкните на нее левой кнопкой мыши
- При необходимости введите коэффициенты в поле «Функция:» .
- Нажмите кнопку «Построить» .
В плане визуализации есть возможность менять цвет графика, а также скрывать его или вовсе удалять.
Desmos безусловно – самый навороченный сервис для построения уравнений онлайн. Передвигая курсор с зажатой левой клавишей мыши по графику можно подробно посмотреть все решения уравнения с точностью до 0,001. Встроенная клавиатура позволяет быстро писать степени и дроби. Самым важным плюсом является возможность записывать уравнение в любом состоянии, не приводя к виду: y = f(x).
Передвигая курсор с зажатой левой клавишей мыши по графику можно подробно посмотреть все решения уравнения с точностью до 0,001. Встроенная клавиатура позволяет быстро писать степени и дроби. Самым важным плюсом является возможность записывать уравнение в любом состоянии, не приводя к виду: y = f(x).
Инструкция:
- В левом столбце кликните правой кнопкой мыши по свободной строке.
- В нижнем левом углу нажмите на значок клавиатуры.
- На появившейся панели наберите нужное уравнение (для написания названий функций перейдите в раздел «A B C»).
- График строится в реальном времени.
Визуализация просто идеальная, адаптивная, видно, что над приложением работали дизайнеры. Из плюсов можно отметить огромное обилие возможностей, для освоения которых можно посмотреть примеры в меню в верхнем левом углу.
Сайтов для построения графиков функций великое множество, однако каждый волен выбирать для себя исходя из требуемого функционала и личных предпочтений.
К сожалению, не все студенты и школьники знают и любят алгебру, но готовить домашние задания, решать контрольные и сдавать экзамены приходится каждому. Особенно трудно многим даются задачи на построение графиков функций: если где-то что-то не понял, не доучил, упустил — ошибки неизбежны. Но кому же хочется получать плохие оценки?
Не желаете пополнить когорту хвостистов и двоечников? Для этого у вас есть 2 пути: засесть за учебники и восполнить пробелы знаний либо воспользоваться виртуальным помощником — сервисом автоматического построения графиков функций по заданным условиям. С решением или без. Сегодня мы познакомим вас с несколькими из них.
Лучшее, что есть в Desmos.com, это гибко настраиваемый интерфейс, интерактивность, возможность разносить результаты по таблицам и бесплатно хранить свои работы в базе ресурса без ограничений по времени.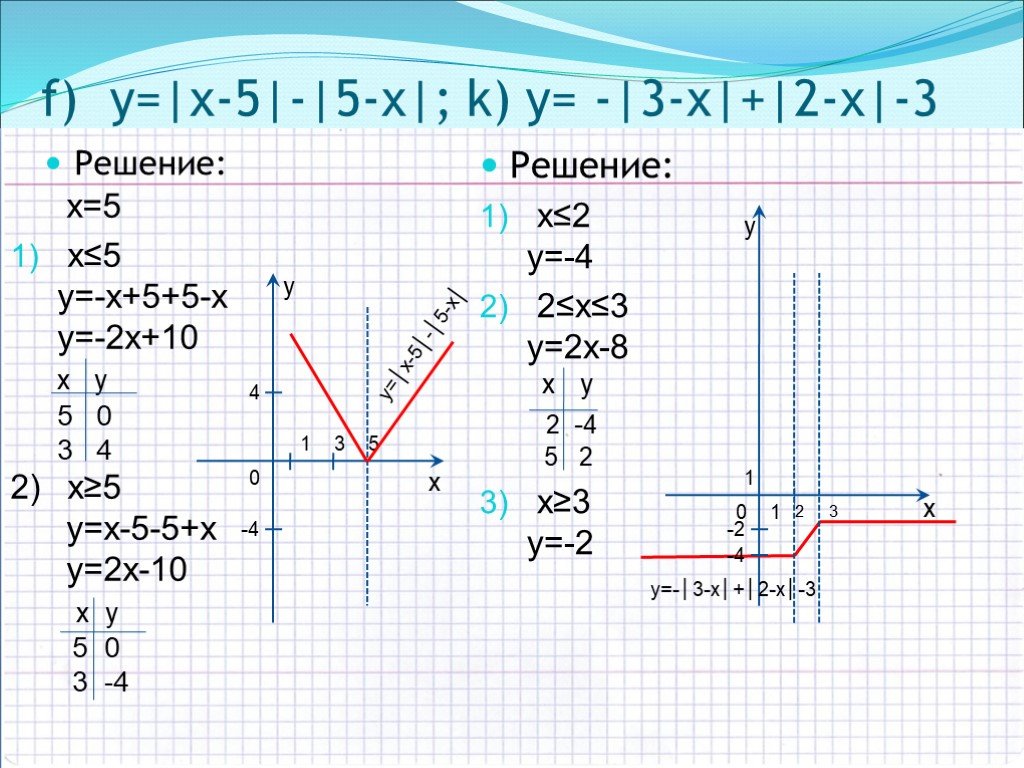
Grafikus.ru
Grafikus.ru — еще один достойный внимания русскоязычный калькулятор для построения графиков. Причем он строит их не только в двухмерном, но и в трехмерном пространстве.
Вот неполный перечень заданий, с которыми этот сервис успешно справляется:
- Черчение 2D-графиков простых функций: прямых, парабол, гипербол, тригонометрических, логарифмических и т. д.
- Черчение 2D-графиков параметрических функций: окружностей, спиралей, фигур Лиссажу и прочих.
- Черчение 2D-графиков в полярных координатах.
- Построение 3D-поверхностей простых функций.
- Построение 3D-поверхностей параметрических функций.
Координатная плоскость Grafikus.ru поддерживает изменение границ осей, подписей к ним, шага сетки, а также — ширины и высоты самой плоскости и размера шрифта.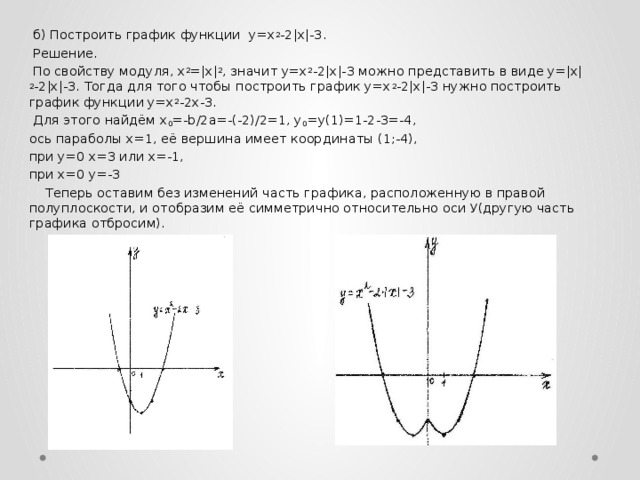
Самая сильная сторона Grafikus.ru — возможность построения 3D-графиков. В остальном он работает не хуже и не лучше, чем ресурсы-аналоги.
Построение графиков функций, содержащих модули, обычно вызывает немалые затруднения у школьников. Однако, все не так плохо. Достаточно запомнить несколько алгоритмов решения таких задач, и вы сможете без труда построить график даже самой на вид сложной функции. Давайте разберемся, что же это за алгоритмы.
1. Построение графика функции y = |f(x)|
Заметим, что множество значений функций y = |f(x)| : y ≥ 0. Таким образом, графики таких функций всегда расположены полностью в верхней полуплоскости.
Построение графика функции y = |f(x)| состоит из следующих простых четырех этапов.
1) Построить аккуратно и внимательно график функции y = f(x).
2) Оставить без изменения все точки графика, которые находятся выше оси 0x или на ней.
3) Часть графика, которая лежит ниже оси 0x, отобразить симметрично относительно оси 0x.
Пример 1. Изобразить график функции y = |x 2 – 4x + 3|
1) Строим график функции y = x 2 – 4x + 3. Очевидно, что график данной функции – парабола. Найдем координаты всех точек пересечения параболы с осями координат и координаты вершины параболы.
x 2 – 4x + 3 = 0.
x 1 = 3, x 2 = 1.
Следовательно, парабола пересекает ось 0x в точках (3, 0) и (1, 0).
y = 0 2 – 4 · 0 + 3 = 3.
Следовательно, парабола пересекает ось 0y в точке (0, 3).
Координаты вершины параболы:
x в = -(-4/2) = 2, y в = 2 2 – 4 · 2 + 3 = -1.
Следовательно, точка (2, -1) является вершиной данной параболы.
Рисуем параболу, используя полученные данные (рис. 1)
2) Часть графика, лежащую ниже оси 0x, отображаем симметрично относительно оси 0x.
3) Получаем график исходной функции (рис. 2 , изображен пунктиром).
2. Построение графика функции y = f(|x|)
Заметим, что функции вида y = f(|x|) являются четными:
y(-x) = f(|-x|) = f(|x|) = y(x).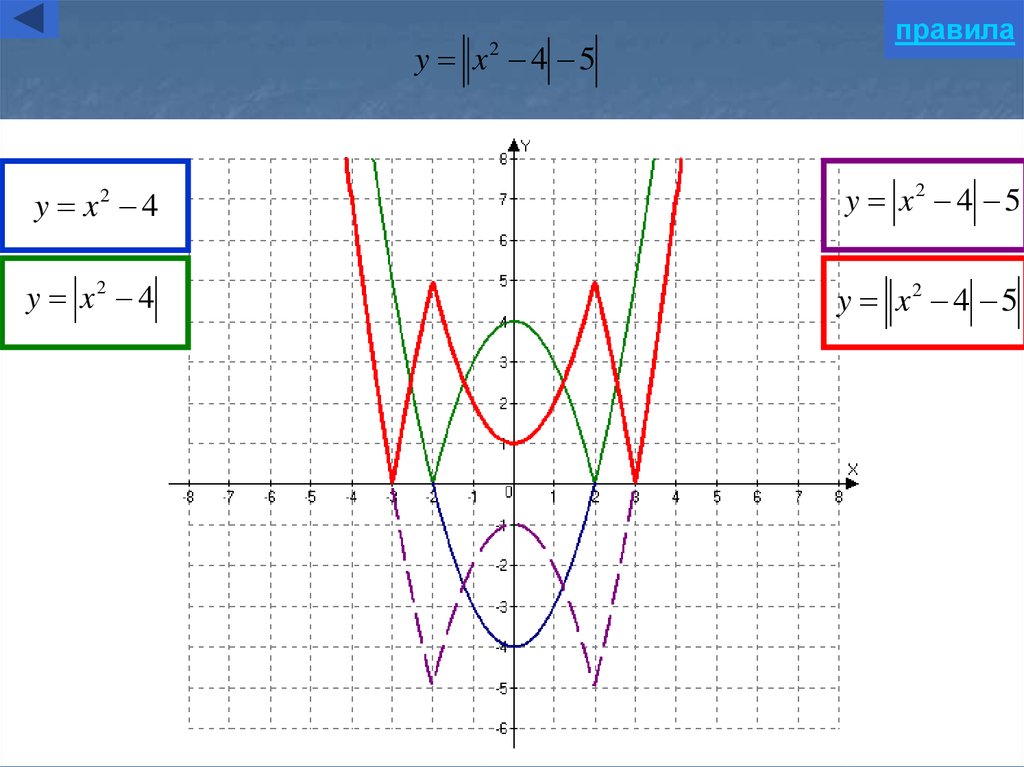 Значит, графики таких функций симметричны относительно оси 0y.
Значит, графики таких функций симметричны относительно оси 0y.
Построение графика функции y = f(|x|) состоит из следующей несложной цепочки действий.
1) Построить график функции y = f(x).
2) Оставить ту часть графика, для которой x ≥ 0, то есть часть графика, расположенную в правой полуплоскости.
3) Отобразить указанную в пункте (2) часть графика симметрично оси 0y.
4) В качестве окончательного графика выделить объединение кривых, полученных в пунктах (2) и (3).
Пример 2. Изобразить график функции y = x 2 – 4 · |x| + 3
Так как x 2 = |x| 2 , то исходную функцию можно переписать в следующем виде: y = |x| 2 – 4 · |x| + 3. А теперь можем применять предложенный выше алгоритм.
1) Строим аккуратно и внимательно график функции y = x 2 – 4 · x + 3 (см. также рис. 1 ).
2) Оставляем ту часть графика, для которой x ≥ 0, то есть часть графика, расположенную в правой полуплоскости.
3) Отображаем правую часть графика симметрично оси 0y.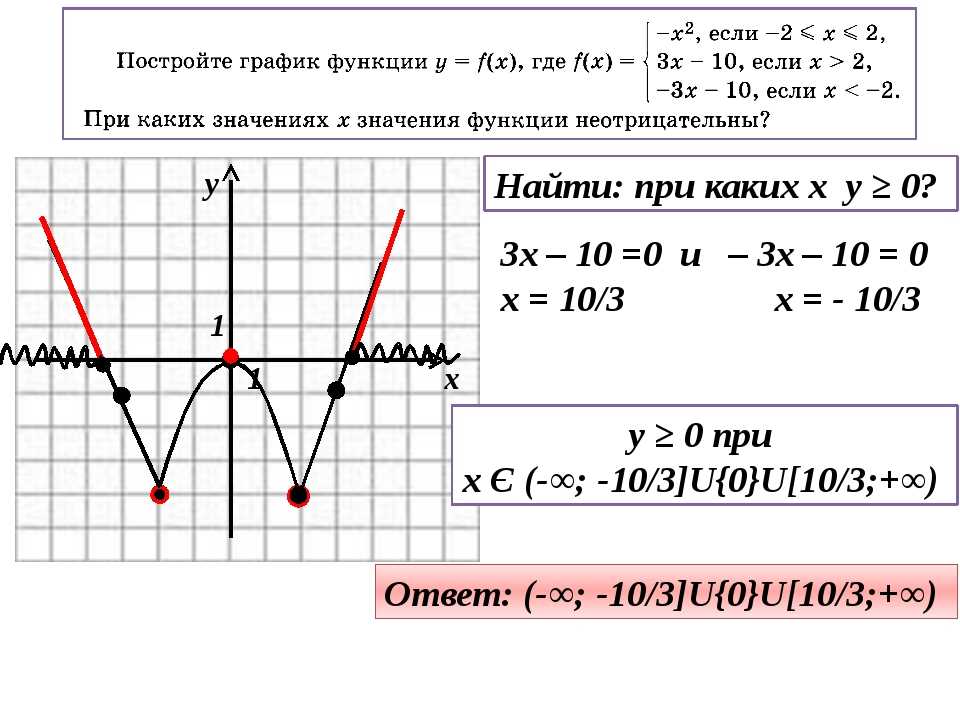
(рис. 3) .
Пример 3. Изобразить график функции y = log 2 |x|
Применяем схему, данную выше.
1) Строим график функции y = log 2 x (рис. 4) .
3. Построение графика функции y = |f(|x|)|
Заметим, что функции вида y = |f(|x|)| тоже являются четными. Действительно, y(-x) = y = |f(|-x|)| = y = |f(|x|)| = y(x), и поэтому, их графики симметричны относительно оси 0y. Множество значений таких функций: y ≥ 0. Значит, графики таких функций расположены полностью в верхней полуплоскости.
Чтобы построить график функции y = |f(|x|)|, необходимо:
1) Построить аккуратно график функции y = f(|x|).
2) Оставить без изменений ту часть графика, которая находится выше оси 0x или на ней.
3) Часть графика, расположенную ниже оси 0x, отобразить симметрично относительно оси 0x.
4) В качестве окончательного графика выделить объединение кривых, полученных в пунктах (2) и (3).
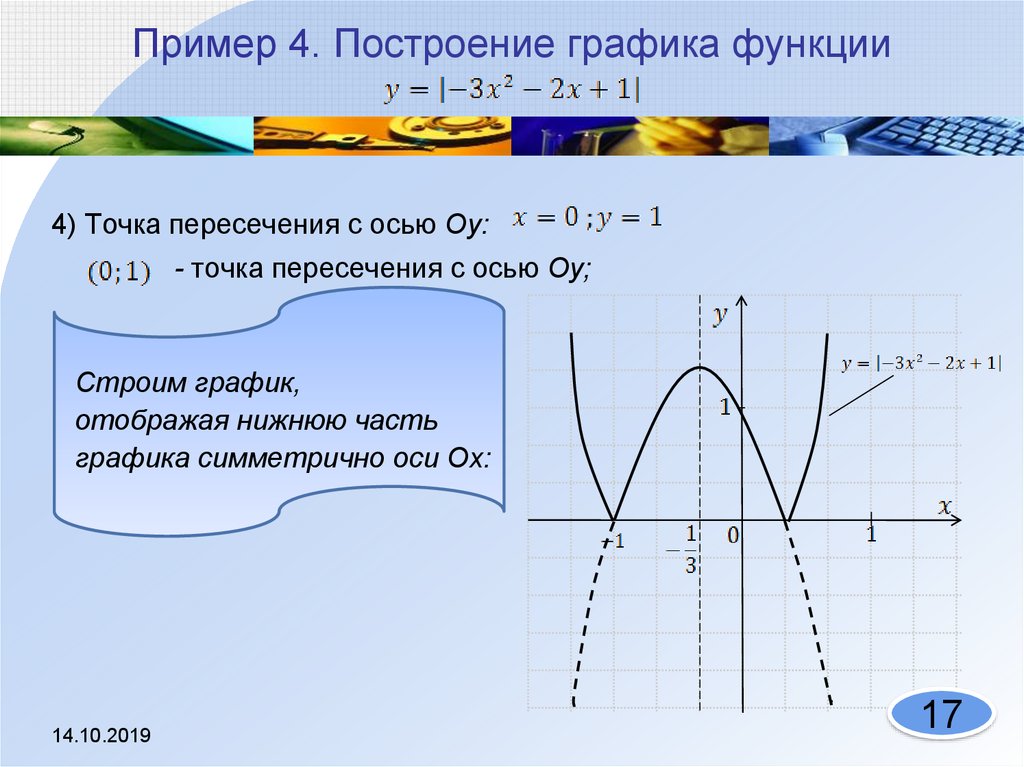
Пример 4. Изобразить график функции y = |-x 2 + 2|x| – 1|.
1) Заметим, что x 2 = |x| 2 . Значит, вместо исходной функции y = -x 2 + 2|x| – 1
можно использовать функцию y = -|x| 2 + 2|x| – 1, так как их графики совпадают.
Строим график y = -|x| 2 + 2|x| – 1. Для этого применяем алгоритм 2.
a) Строим график функции y = -x 2 + 2x – 1 (рис. 6) .
b) Оставляем ту часть графика, которая расположена в правой полуплоскости.
c) Отображаем полученную часть графика симметрично оси 0y.
d) Полученный график изображен на рисунке пунктиром (рис. 7) .
2) Выше оси 0х точек нет, точки на оси 0х оставляем без изменения.
3) Часть графика, расположенную ниже оси 0x, отображаем симметрично относительно 0x.
4) Полученный график изображен на рисунке пунктиром (рис. 8) .
Пример 5. Построить график функции y = |(2|x| – 4) / (|x| + 3)|
1) Сначала необходимо построить график функции y = (2|x| – 4) / (|x| + 3). Для этого возвращаемся к алгоритму 2.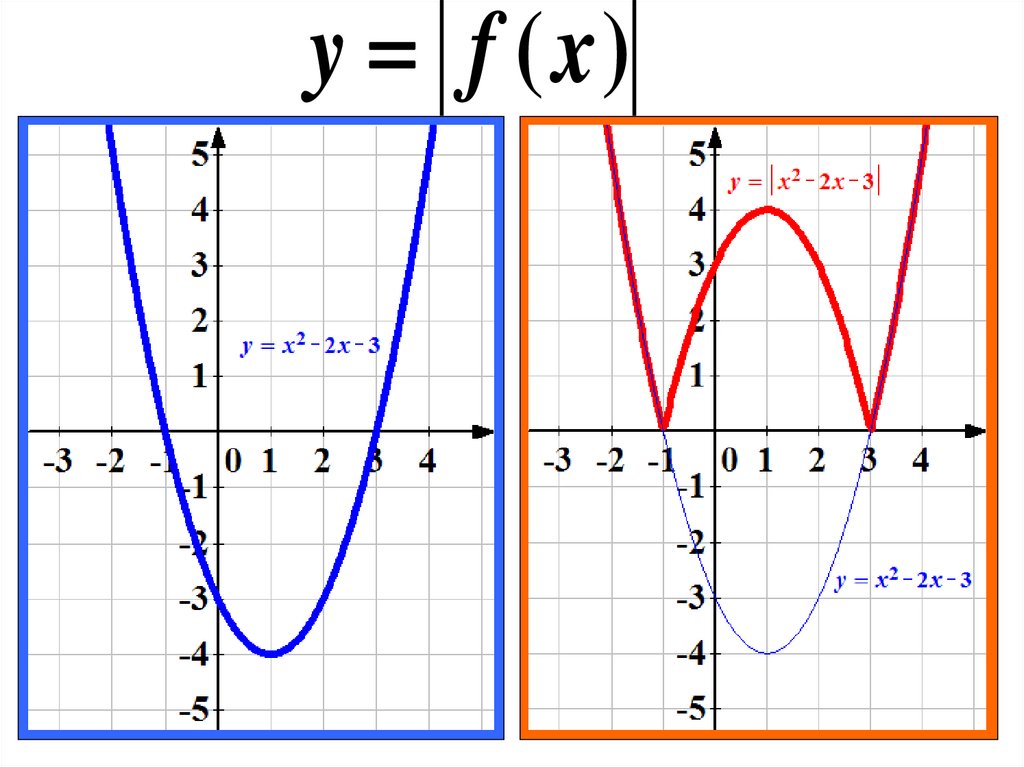 3$.
3$.
2. Найдем точку А, координата x, которой равна 1,5. Мы видим, что координата функции находится между значениями 3 и 4 (см. рис. 2). Значит надо заказать 4 куба.
Визуализация данных в Python: обзор, библиотеки и графики
При работе с данными может быть сложно по-настоящему понять ваши данные, когда они представлены только в табличной форме. Чтобы понять, что именно передают наши данные, а также лучше очистить их и подобрать для них подходящие модели, нам необходимо их визуализировать или представить в графическом виде. Это помогает выявить шаблоны, корреляции и тенденции, которые невозможно получить, когда данные находятся в таблице или файле CSV.
Процесс поиска тенденций и корреляций в наших данных путем их графического представления называется визуализацией данных. Чтобы выполнить визуализацию данных в Python, мы можем использовать различные модули визуализации данных Python, такие как Matplotlib, Seaborn, Plotly и т. д. В этой статье «Полное руководство по визуализации данных в Python» мы обсудим, как работать с некоторыми из этих модулей для визуализацию данных в Python и подробно осветить следующие темы.
- Что такое визуализация данных?
- Визуализация данных в Python
- Matplotlib и Сиборн
- Линейные графики
- Гистограммы
- Гистограммы
- Графики рассеяния
- Тепловые карты
Что такое визуализация данных?
Визуализация данных — это область анализа данных, которая занимается визуальным представлением данных. Он графически отображает данные и является эффективным способом передачи выводов на основе данных.
Используя визуализацию данных, мы можем получить визуальную сводку наших данных. С картинками, картами и графиками человеческому разуму легче обрабатывать и понимать любые данные. Визуализация данных играет значительную роль в представлении как малых, так и больших наборов данных, но она особенно полезна, когда у нас есть большие наборы данных, в которых невозможно увидеть все наши данные, не говоря уже об их обработке и понимании вручную.
Визуализация данных в Python
Python предлагает несколько библиотек построения графиков, а именно Matplotlib, Seaborn и многие другие подобные пакеты визуализации данных с различными функциями для создания информативных, настраиваемых и привлекательных графиков для представления данных наиболее простым и эффективным способом.
Рисунок 1: Визуализация данных
Matplotlib и Сиборн
Matplotlib и Seaborn — это библиотеки Python, которые используются для визуализации данных. В них встроены модули для построения различных графиков. В то время как Matplotlib используется для встраивания графиков в приложения, Seaborn в основном используется для статистических графиков.
Но когда мы должны использовать любой из двух? Давайте разберемся в этом с помощью сравнительного анализа. В таблице ниже представлено сравнение между двумя известными пакетами визуализации Python, Matplotlib и Seaborn.
Матплотлиб | Сиборн |
Используется для построения основных графиков, таких как линейные диаграммы, гистограммы и т. | Он в основном используется для визуализации статистики и может выполнять сложные визуализации с меньшим количеством команд. |
В основном работает с наборами данных и массивами. | Работает со всеми наборами данных. |
Seaborn значительно более организован и функционален, чем Matplotlib, и рассматривает весь набор данных как отдельную единицу. | Matplotlib продуктивно работает с массивами данных и фреймами. Он рассматривает тузы и цифры как объекты. |
Seaborn имеет больше встроенных тем и в основном используется для статистического анализа. | Matplotlib более настраиваемый и хорошо сочетается с Pandas и Numpy для исследовательского анализа данных. |
Таблица 1: Matplotlib против Seaborn
Линейные графики
Линейная диаграмма — это график, представляющий информацию в виде ряда точек данных, соединенных прямой линией. На линейных диаграммах каждая точка данных или маркер нанесены на график и соединены линией или кривой.
На линейных диаграммах каждая точка данных или маркер нанесены на график и соединены линией или кривой.
Рассмотрим урожайность яблок (тонн с гектара) в Канто. Давайте построим линейный график, используя эти данные, и посмотрим, как урожайность яблок меняется с течением времени. Начнем с импорта Matplotlib и Seaborn.
Рисунок 2: Импорт необходимых модулей
Использование Matplotlib
Мы используем случайные точки данных для представления урожайности яблок.
Рисунок 3: График урожайности яблок
Чтобы лучше понять график и его назначение, мы также можем добавить значения по оси X.
Рисунок 4: Значения осей
Давайте добавим метки к осям, чтобы мы могли показать, что представляет каждая ось.
Рисунок 5: Ось с метками
Чтобы отобразить несколько наборов данных на одном графике, просто используйте функцию plt.plot один раз для каждого набора данных. Давайте воспользуемся этим, чтобы сравнить урожайность яблок и апельсинов на одном графике.
Рисунок 6: Построение нескольких графиков
Мы можем добавить легенду, которая говорит нам, что означает каждая линия на нашем графике. Чтобы понять, что мы рисуем, мы можем добавить заголовок к нашему графику.
Рисунок 7: Построение нескольких графиков
Чтобы показать каждую точку данных на нашем графике, мы можем выделить их маркерами, используя аргумент marker. Matplotlib предоставляет множество различных форм маркеров, таких как круг, крест, квадрат, ромб и т. д.
Рисунок 8: Использование маркеров
Вы можете использовать функцию plt.figure для изменения размера фигуры.
Рисунок 9: Изменение размера графика
Использование Seaborn
Простой способ сделать ваши диаграммы красивыми — использовать некоторые стили по умолчанию из библиотеки Seaborn. Их можно применять глобально с помощью функции sns.set_style.
Рисунок 10: Использование Seaborn
Мы также можем использовать опцию darkgrid, чтобы изменить цвет фона на более темный оттенок.
Рисунок 11: Использование darkgrid в Seaborn
Гистограммы
Когда у вас есть категориальные данные, вы можете представить их в виде гистограммы. Гистограмма отображает данные с помощью столбцов, которые представляют значение по оси Y и категорию по оси X. Гистограммы используют столбцы разной высоты для отображения данных, относящихся к определенной категории.
Рисунок 12: Построение гистограмм
Мы также можем складывать стержни друг на друга. Давайте построим данные для яблок и апельсинов.
Рисунок 13: Построение гистограмм с накоплением
Далее давайте воспользуемся набором данных подсказок в Seaborn. Набор данных состоит из:
- Сведения о поле (поле)
- Время суток
- Общий счет
- Чаевые от посетителей ресторана за неделю
Рисунок 14: Набор данных Iris
Мы можем нарисовать гистограмму, чтобы визуализировать, как средняя сумма счета меняется в разные дни недели. Мы можем сделать это, вычислив средние значения за день, а затем используя plt.bar. Библиотека Seaborn также предоставляет функцию гистограммы, которая может автоматически вычислять средние значения.
Мы можем сделать это, вычислив средние значения за день, а затем используя plt.bar. Библиотека Seaborn также предоставляет функцию гистограммы, которая может автоматически вычислять средние значения.
Рисунок 15: График средних значений каждого бара
Если вы хотите сравнить гистограммы рядом друг с другом, вы можете использовать аргумент оттенка. Сравнение будет производиться по третьему признаку, указанному в этом аргументе.
Рисунок 16: Построение нескольких гистограмм
Вы можете сделать полосы горизонтальными, переключая оси.
Рисунок 17: Построение горизонтальных гистограмм
Гистограммы
Гистограмма – это столбчатое представление данных, которые варьируются в определенном диапазоне. Он отображает высоту данных, принадлежащих диапазону по оси y, и диапазону по оси x. Гистограммы используются для отображения данных в диапазоне значений. Они используют линейчатое представление для отображения данных, принадлежащих каждому диапазону. Давайте снова используем данные «Ирис», которые содержат информацию о цветах, для построения гистограмм.
Давайте снова используем данные «Ирис», которые содержат информацию о цветах, для построения гистограмм.
Рисунок 18: База данных Iris
Теперь построим гистограмму с помощью функции hist().
Рисунок 19: Построение гистограмм
Мы также можем контролировать количество или размер ячеек.
Рисунок 20: Изменение количества ячеек
Мы также можем изменить количество и размер бинов, используя numpy.
Рисунок 21: Изменение количества и размера ячеек
Мы также можем создавать контейнеры разного размера.
Рисунок 22: Корзины разного размера
Подобно линейным графикам, мы можем рисовать несколько гистограмм на одном графике. Мы можем уменьшить непрозрачность каждой гистограммы, чтобы столбцы одной гистограммы не скрывали столбцы других. Нарисуем отдельные гистограммы для каждого вида цветов.
Рисунок 23: Несколько гистограмм
Несколько гистограмм можно наложить друг на друга, установив для параметра Stacked значение True.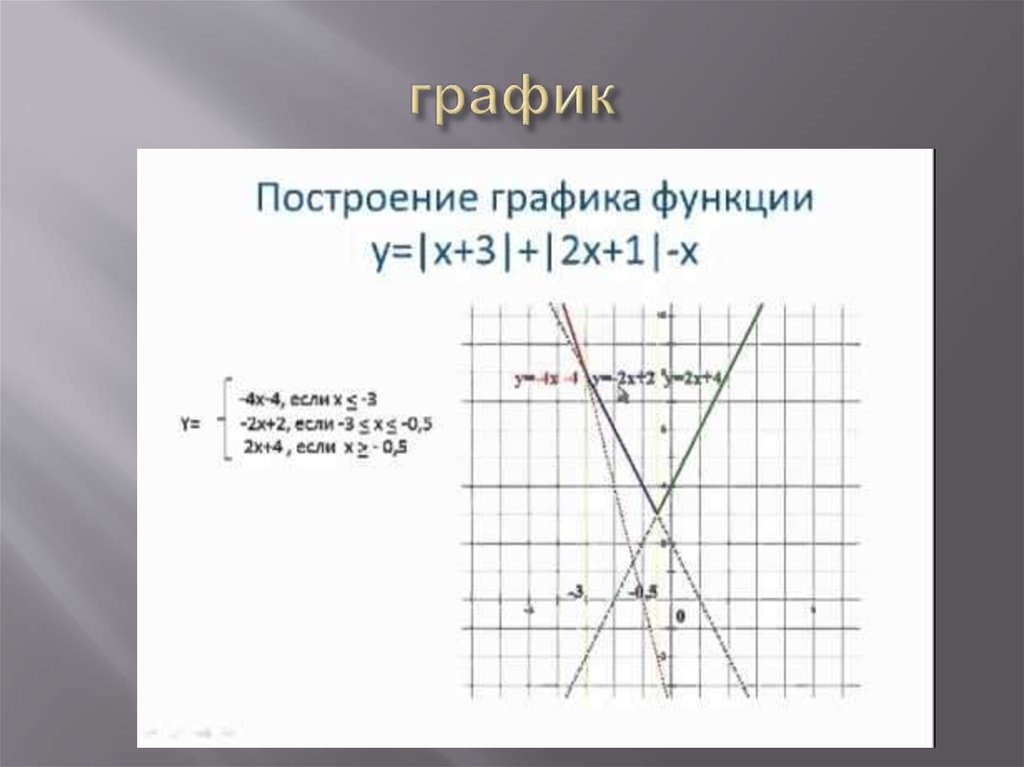
Рисунок 24: Гистограммы суммирования
Точечная диаграмма
Диаграммы рассеяния используются, когда нам нужно отобразить две или более переменных, присутствующих в разных координатах. Данные разбросаны по всему графику и не ограничены диапазоном. Две или более переменных отображаются на точечной диаграмме, причем каждая переменная представлена своим цветом. Давайте используем набор данных «Ирис» для построения точечной диаграммы.
Рисунок 25: Набор данных Iris
Во-первых, давайте посмотрим, сколько у нас разных видов цветов.
Рисунок 26: Уникальные виды цветов
Давайте попробуем изобразить данные с помощью линейного графика.
Рисунок 27: Построение линейной диаграммы
Это не очень информативно. Мы не можем выяснить взаимосвязь между различными точками данных.
Рисунок 28: Диаграмма рассеяния
Это намного лучше. Но мы по-прежнему не можем различать разные точки данных, принадлежащие к разным категориям. Мы можем раскрасить точки, используя виды цветов в качестве оттенка.
Мы можем раскрасить точки, используя виды цветов в качестве оттенка.
Рисунок 29: Диаграмма рассеяния с несколькими цветами
Поскольку Seaborn использует графические функции Matplotlib для внутреннего использования, мы можем использовать такие функции, как plt.figure и plt.title, для изменения рисунка.
Рисунок 30: Изменение размеров точечной диаграммы
Тепловые карты
Тепловые карты используются для наблюдения за изменениями в поведении или постепенными изменениями данных. Он использует разные цвета для представления разных значений. Основываясь на том, как эти цвета различаются по оттенкам, интенсивности и т. д., можно понять, как меняется явление. Давайте воспользуемся тепловыми картами, чтобы визуализировать ежемесячный пассажиропоток в аэропорту за 12 лет на основе набора данных о рейсах в Seaborn.
Рисунок 31. Набор данных о рейсах
Вышеприведенный набор данных, Flight_df, показывает нам ежемесячную посещаемость аэропорта за каждый год с 1949 по 1960 год.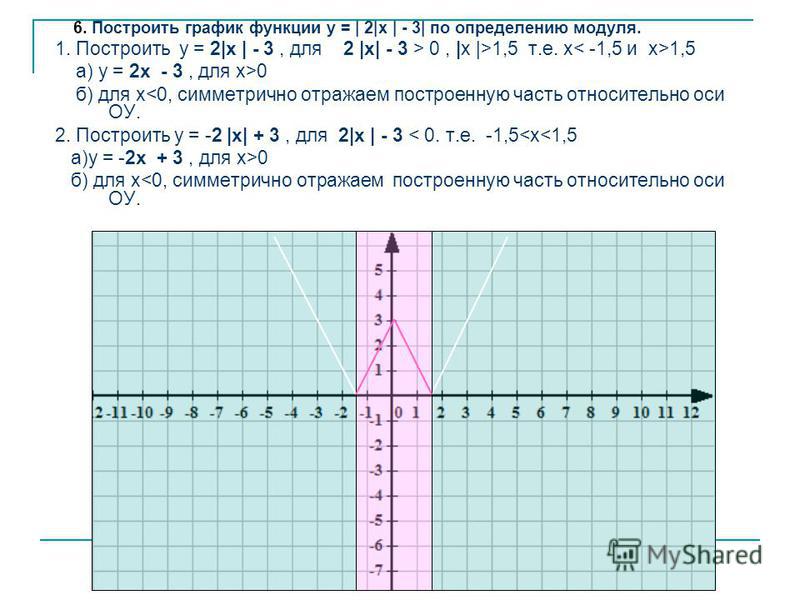 Значения представляют количество пассажиров (в тысячах), прошедших через аэропорт. Давайте используем тепловую карту для визуализации приведенных выше данных.
Значения представляют количество пассажиров (в тысячах), прошедших через аэропорт. Давайте используем тепловую карту для визуализации приведенных выше данных.
Рисунок 32: Построение тепловой карты
Чем ярче цвет, тем больше пешеходов в аэропорту. Глядя на график, мы можем сделать вывод, что:
- Годовая посещаемость в любой данный год самая высокая в июле и августе.
- Ежегодно увеличивается посещаемость. Каждый месяц в году будет иметь более высокую посещаемость по сравнению с предыдущими годами.
Давайте отобразим фактические значения на нашей тепловой карте и изменим оттенок на синий.
Рисунок 33: Построение тепловой карты со значениями
Мастер глубокого обучения, машинного обучения и других языков программирования с магистерской программой для инженеров искусственного интеллекта
Заключение
В этой статье «Полное руководство по визуализации данных в Python» мы представили обзор визуализации данных в Python и обсудили, как создавать линейные диаграммы, гистограммы, гистограммы, точечные диаграммы и тепловые карты с использованием различных пакетов визуализации данных, предлагаемых Python. как Matplotlib и Seaborn.
как Matplotlib и Seaborn.
Если вам нужны дополнительные разъяснения или вы хотите узнать больше о визуализации данных в Python и хотите понять, как выполнять визуализацию данных, поделитесь с нами своими запросами, упомянув их в разделе комментариев на этой странице. Мы попросим наших экспертов рассмотреть их в ближайшее время!
Python предлагает несколько других пакетов визуализации, которые можно использовать для создания различных типов визуализаций, а не только графиков и графиков. Поэтому также важно понимать проблемы и преимущества различных библиотек и то, как использовать их в полной мере. Ознакомьтесь с курсом искусственного интеллекта Simplilearn, чтобы освоить ключевые концепции, включая науку о данных с помощью Python, машинное обучение, глубокое обучение, НЛП и многое другое. Цель этого курса — подготовить вас к работе и обеспечить успех в карьере.
Графики в Excel — линейная регрессия
Содержание
- Создание начальной диаграммы рассеяния
- Создание линии линейной регрессии (линии тренда)
- Использование уравнения регрессии для расчета наклона и перехват
- Использование расчета коэффициента R-квадрата для оценки подходит
Введение
Линии регрессии можно использовать как способ визуального изображения отношений между независимыми (x) и зависимыми (y) переменными на графике.
Прямая линия изображает линейный тренд в данных (т. е. уравнение описывающая линию имеет первый порядок. Например, y = 3x + 4. Там в этом уравнении нет переменных, возведенных в квадрат или в куб). Изогнутая линия представляет тренд, описываемый уравнением более высокого порядка (например, y = 2x 2 + 5х — 8). Важно, чтобы вы могли защитить свое использование прямая или изогнутая линия регрессии. То есть теория, лежащая в основе вашего лаборатория должна указать, связаны ли отношения независимых и зависимых переменные должны быть линейными или нелинейными.
В дополнение к визуальному изображению тенденции в данных с регрессией линии, вы также можете рассчитать уравнение линии регрессии. Этот уравнение можно увидеть в диалоговом окне и/или показать на графике. Насколько хорошо это уравнение описывает данные («подгонка»), выражается как коэффициент корреляции, R 2 (Р-квадрат).
Доводчик R 2 до 1,00, тем лучше подходит. Это тоже можно рассчитать и отобразить на графике.
Приведенные ниже данные были впервые введены в базовой графический модуль и из химической лаборатории, исследующей поглощение света по решениям. Закон Бера утверждает, что существует линейная зависимость между концентрация окрашенного соединения в растворе и светопоглощение решения. Этот факт можно использовать для расчета концентрации неизвестных растворов, учитывая их показания поглощения. Это делается подгонка линии линейной регрессии к собранным данным.
Создание начальной диаграммы рассеяния
Прежде чем вы сможете создать линию регрессии, необходимо построить график из данные. Традиционно это будет точечная диаграмма. Этот модуль будет начните с точечной диаграммы, созданной в базовой графический модуль.
Рисунок 1 .
Вернуться к началу
Создание линии линейной регрессии (линии тренда)
Когда окно диаграммы выделено, вы можете добавить линию регрессии к график, выбрав Диаграмма > Добавить линию тренда…
Появится диалоговое окно (рис. 2). Выберите Linear Trend/Regression тип:
Рисунок 2 .
Выберите вкладку Параметры и выберите Показать уравнение на графике (Рисунок 3):
Рисунок 3 .
Щелкните OK , чтобы закрыть диалоговое окно. На диаграмме теперь отображается регрессия линия (рисунок 4)
Рисунок 4 .
Вернуться к началу
Использование уравнения регрессии для расчета концентраций
Линейное уравнение, показанное на графике, представляет зависимость между Концентрация (x) и абсорбция (y) соединения в растворе.
линию регрессии можно считать приемлемой оценкой истинного зависимость между концентрацией и абсорбцией. Нам дали показания абсорбции для двух растворов неизвестной концентрации.
Используя линейное уравнение (обозначенное буквой A на рис. 5), ячейка электронной таблицы может иметь уравнение, связанное с ним, чтобы сделать расчет для нас. У нас есть значение y (поглощение) и нужно решить для x (концентрация). Ниже приведены алгебраические уравнения для этого расчета:
у = 2071,9х + 0,111
г — 0,0111 = 2071,9 х
(г — 0,0111) / 2071,9 = х
Теперь мы должны преобразовать это окончательное уравнение в уравнение в электронной таблице. клетка. Уравнение, связанное с ячейкой электронной таблицы, будет выглядеть так то, что обозначено C на рисунке 8. «B12» в уравнении представляет собой y (значение поглощение неизвестного).
Тогда решение для x (концентрация) будет отображается в ячейке «C12».
- Выделите ячейку электронной таблицы для хранения ‘x’, результата итоговое уравнение (ячейка C12, обозначенная буквой B на рис. 5).
- Нажмите в области уравнений (обозначена C, рис. 5)
- Введите знак равенства и затем круглые скобки
- Щелкните в ячейке, представляющей ‘y’ в вашем уравнении (ячейка B12 на рисунке 5), чтобы поместить эту метку ячейки в уравнение
.- Завершите ввод уравнения
Примечание. Если ваше уравнение отличается от приведенного в этом примере, используйте уравнение
Продублируйте уравнение для другого неизвестного.
- Выделите исходную ячейку уравнения (C12 на рис. 5) и ячейка под ней (C13)
- Выберите Правка > Заливка > Вниз
Вернуться к началу
Обратите внимание: если вы выделите свое новое уравнение в C13, ссылка на ячейка B12 также увеличилась до ячейки B13.
Рисунок 5 .
Вернуться к началу
Использование расчета коэффициента R-квадрата для оценки подходит
Дважды щелкните на линии тренда, выберите вкладку Параметры в диалоговое окно Format Trendlines и установите флажок Display r-squared. значение на диаграмме . Теперь ваш график должен выглядеть так, как показано на рис. 6. Примечание. значение R-квадрата на графике. Чем ближе к 1.0, тем лучше соответствие линии регрессии. То есть чем ближе линия проходит через все точки.
Рисунок 6 .
Теперь давайте посмотрим на другой набор данных, сделанный для этой лаборатории (рис. 7). Уведомление что уравнение для линии регрессии отличается от того, которое было в Рисунок 6. Другое уравнение рассчитывало бы другую концентрацию для двух неизвестных.



 д.
д. Прямая линия изображает линейный тренд в данных (т. е. уравнение
описывающая линию имеет первый порядок. Например, y = 3x + 4. Там
в этом уравнении нет переменных, возведенных в квадрат или в куб). Изогнутая линия представляет
тренд, описываемый уравнением более высокого порядка (например, y = 2x 2 + 5х — 8). Важно, чтобы вы могли защитить свое использование
прямая или изогнутая линия регрессии. То есть теория, лежащая в основе вашего
лаборатория должна указать, связаны ли отношения независимых и зависимых
переменные должны быть линейными или нелинейными.
Прямая линия изображает линейный тренд в данных (т. е. уравнение
описывающая линию имеет первый порядок. Например, y = 3x + 4. Там
в этом уравнении нет переменных, возведенных в квадрат или в куб). Изогнутая линия представляет
тренд, описываемый уравнением более высокого порядка (например, y = 2x 2 + 5х — 8). Важно, чтобы вы могли защитить свое использование
прямая или изогнутая линия регрессии. То есть теория, лежащая в основе вашего
лаборатория должна указать, связаны ли отношения независимых и зависимых
переменные должны быть линейными или нелинейными. Доводчик R 2 до 1,00, тем лучше подходит. Это тоже можно рассчитать и отобразить
на графике.
Доводчик R 2 до 1,00, тем лучше подходит. Это тоже можно рассчитать и отобразить
на графике.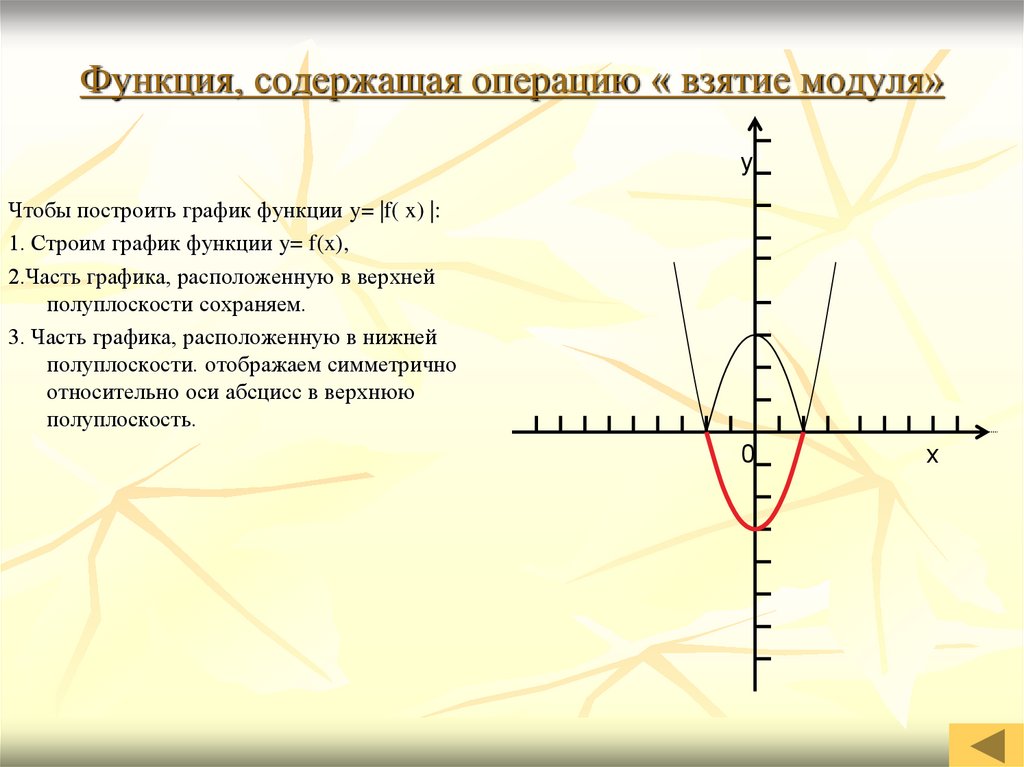
 линию регрессии можно считать приемлемой оценкой истинного
зависимость между концентрацией и абсорбцией. Нам дали
показания абсорбции для двух растворов неизвестной концентрации.
линию регрессии можно считать приемлемой оценкой истинного
зависимость между концентрацией и абсорбцией. Нам дали
показания абсорбции для двух растворов неизвестной концентрации.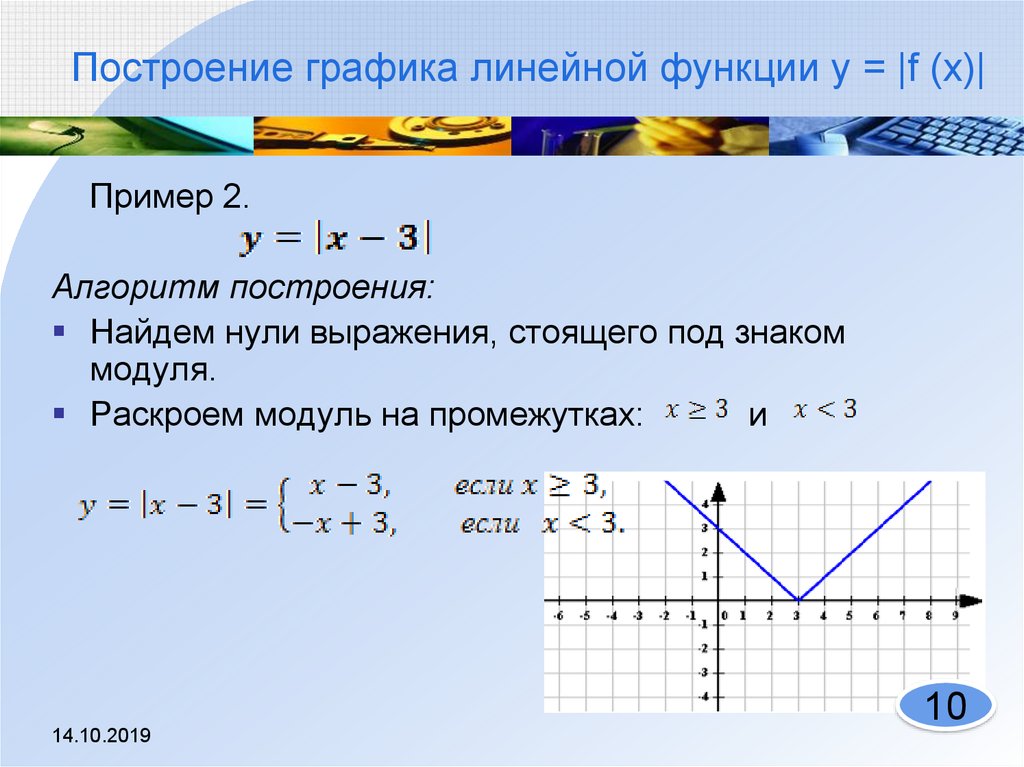 Тогда решение для x (концентрация) будет
отображается в ячейке «C12».
Тогда решение для x (концентрация) будет
отображается в ячейке «C12».
