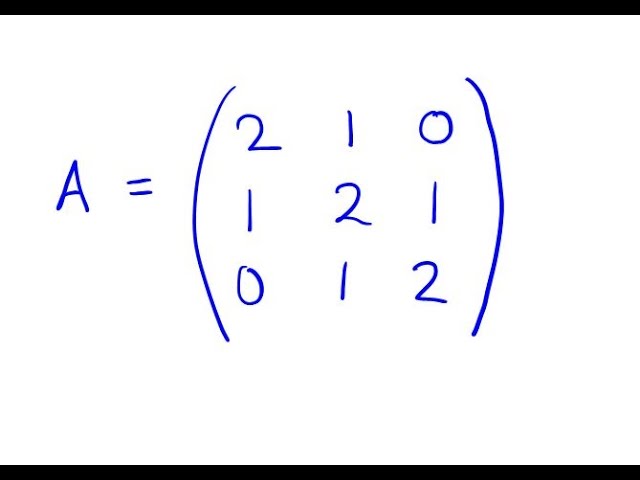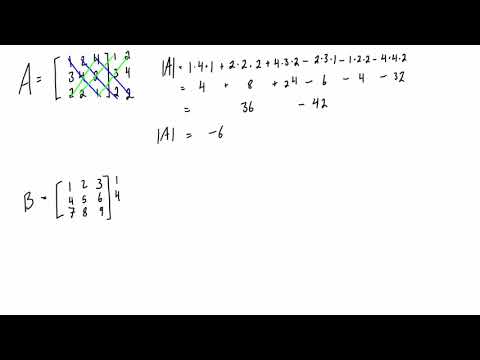trace | NumPy
numpy.trace(a, offset=0, axis1=0, axis2=1, dtype=None, out=None)
Функция trace() вычисляет cумму диагональных элементов (след) матрицы.
- Параметры:
- a — массив NumPy или подобный массиву объект.
- Двумерный или многомерный массив.
- offset — целое число (необязательный параметр).
- Определяет смещение диагонали по которой вычисляется сумма элементов, положительные числа смещают ее вверх, отрицательные — вниз.

- Определяют оси массива, относительно которых рассматриваются его подматрицы. По умолчанию
axis1 = 0иaxis2 = 1, что соответствует двум первым осям, а не двум последним как принято в пакете linalg. - dtype — тип данных NumPy (необязательный параметр).
- Определяет тип данных результата. По умолчанию
dtype=None, т.е. тип данных не преобразуется. - out — массив NumPy (необязательный параметр).
- Массив в который можно поместить результат функции. Данный массив должен соответствовать форме и типу данных результирующего массива функции (зачастую, тип данных может быть преобразован автоматически).
 Указание данного параметра, позволяет избежать лишней операции присваивания тем самым немного ускоряя работу вашего кода. Полезный параметр если вы очень часто обращаетесь к функции в цикле.
Указание данного параметра, позволяет избежать лишней операции присваивания тем самым немного ускоряя работу вашего кода. Полезный параметр если вы очень часто обращаетесь к функции в цикле.
- Возвращает:
- результат — массив NumPy или число
- Сумму диагональных элементов в виде числа если на вход подана одна матрица, в виде массива, если указан массив матриц.
Замечание
Данная функция может вычислять сумму диагональных элементов не только квадратных матриц, однако, такую операцию уже нельзя назвать следом матрицы.
Смотрите так же:diag, diagflat
Примеры
>>> import numpy as np >>> >>> a = np.eye(3) >>> a array([[1., 0., 0.], [0., 1., 0.], [0., 0., 1.]]) >>> >>> np.trace(a) 3.0 >>> >>> >>> b = np.arange(1, 10).reshape(3, 3) >>> b array([[1, 2, 3], [4, 5, 6], [7, 8, 9]]) >>> >>> np.trace(b, offset = 0) # по умолчанию offset = 0 15 >>> >>> np.trace(b, offset = 1) 8 >>> np.trace(b, offset = -1) 12 >>> >>> >>> # Массивы не обязаны быть квадратными: ... c = np.arange(1, 13).reshape(3, 4) >>> c array([[ 1, 2, 3, 4], [ 5, 6, 7, 8], [ 9, 10, 11, 12]]) >>> >>> np.trace(c) 18
По умолчанию axis1 = 0 и axis2 = 1, что немного нарушает правила модуля linalg, в котором принято, что подматрицы определяются на основании последних двух осей многомерного массива. Это приводит к немного странным результатам:
>>> d = np.arange(12).reshape(3, 2, 2) >>> d array([[[ 0, 1], [ 2, 3]], [[ 4, 5], [ 6, 7]], [[ 8, 9], [10, 11]]]) >>> >>> np.trace(d) array([6, 8])
Дело в том, что из-за установленных по умолчанию параметров axis1 = 0 и axis2 = 1 обрабатываются не те массивы, которые мы ожидаем:
>>> d[:, :, 0]
array([[ 0, 2],
[ 4, 6],
[ 8, 10]])
>>>
>>> np.trace(d[:, :, 0])
6
>>>
>>>
>>> d[:, :, 1]
array([[ 1, 3],
[ 5, 7],
[ 9, 11]])
>>>
>>> np.trace(d[:, :, 1])
8Если внутри вашего многомерного массива, по последним двум осям расположены матрицы, то достаточно указать именно две последние оси
>>> d
array([[[ 0, 1],
[ 2, 3]],
[[ 4, 5],
[ 6, 7]],
[[ 8, 9],
[10, 11]]])
>>>
>>> np. trace(d, axis1 = 1, axis2 = 2)
array([ 3, 11, 19])
>>>
>>> np.trace(d, axis1 = -2, axis2 = -1)
array([ 3, 11, 19])
trace(d, axis1 = 1, axis2 = 2)
array([ 3, 11, 19])
>>>
>>> np.trace(d, axis1 = -2, axis2 = -1)
array([ 3, 11, 19]) Параметр dtype позволяет указать тип данных результирующего массива:
>>> np.trace(d, axis1 = -2, axis2 = -1, dtype = np.float) array([ 3., 11., 19.])
Параметр out позволяет указать массив в который необходимо поместить результат вычислений:
>>> trace_d = np.ones(3) >>> trace_d array([1., 1., 1.]) >>> >>> np.trace(d, axis1 = -2, axis2 = -1, out = trace_d) array([ 3., 11., 19.]) >>> >>> trace_d array([ 3., 11., 19.])
Вычисление следа матрицы MatLab
RADIOMASTER
Лучшие смартфоны на Android в 2022 году
Серия iPhone от Apple редко чем удивляет. Когда вы получаете новый iPhone, общее впечатление, скорее всего, будет очень похожим на ваше предыдущее устройство. Однако всё совсем не так в лагере владельцев устройств на Android. Существуют телефоны Android всех форм и размеров, не говоря уже о разных ценовых категориях. Другими словами, Android-телефон может подойти многим. Однако поиск лучших телефонов на Android может быть сложной задачей.
Когда вы получаете новый iPhone, общее впечатление, скорее всего, будет очень похожим на ваше предыдущее устройство. Однако всё совсем не так в лагере владельцев устройств на Android. Существуют телефоны Android всех форм и размеров, не говоря уже о разных ценовых категориях. Другими словами, Android-телефон может подойти многим. Однако поиск лучших телефонов на Android может быть сложной задачей.
1021 0
Документация Схемотехника CAD / CAM Статьи
MathCAD 12 MatLab OrCAD P CAD AutoCAD MathCAD 8 — 11
- Главная /
- База знаний /
- CAD / CAM /
- MatLab
Урок 11. Матричные операции линейной алгебры
Вычисление
нормы и чисел обусловленности матрицы
Определитель
и ранг матрицы
Определение нормы вектора
Определение ортонормированного базиса матрицы
Определение угла между двумя подпространствами
Вычисление следа матрицы
Разложение Холецкого
Обращение матриц — функции inv, pinv
LU- и QR-разложения
Вычисление собственных значений и сингулярных чисел
Приведение матриц к форме Шура и Хессенберга
Что нового мы узнали?
След матрицы
А — это сумма ее диагональных элементов. Он вычисляется функцией trace:
Он вычисляется функцией trace:
trace(A)
— возвращает след матрицы. Пример:
» а=[2.3.4:5.6,7;8.9,1]
а =
2 3 4
5 6 7
» trace(a)
ans =
9
Теги MatLab САПР
Сюжеты MatLab
Знакомство с матричной лабораторией MATLAB MatLab
8079 0
Визуализация и графические средства MatLab
9572 0
Техническая документация по системе MatLab
6105 0
Комментарии (0)
Вы должны авторизоваться, чтобы оставлять комментарии.
Вход
О проекте Использование материалов Контакты
Новости Статьи База знаний
Радиомастер
© 2005–2022 radiomaster. ru
ru
При использовании материалов данного сайта прямая и явная ссылка на сайт radiomaster.ru обязательна. 0.2392 s
След матрицы
Марко Табога, доктор философии
След квадрата матрица представляет собой сумму своих диагональные входы.
Трассировка имеет несколько свойств, которые используются для доказательства важности приводит к матричной алгебре и ее приложениям.
СОДЕРЖАНИЕ
Определение
Примеры
Свойства
ТРЕЛО из суммы
- 0002 следы скалярной множественной
Трассия линейной комбинации
ТРЕЗИЙ ТРАНСПОРТАЦИИ Матрикса
ТРЕЗИ
Упражнение 1
Упражнение 2
Определение
Начнем с формального определения.
Определение Позволять быть матрица.
 Тогда его след, обозначаемый
или же
,
это сумма его диагоналей
записей:
Тогда его след, обозначаемый
или же
,
это сумма его диагоналей
записей:Примеры
Ниже приведены некоторые примеры.
Пример Определите матрица Тогда его след
Пример Определите матрица Тогда его след
Свойства
В следующих подразделах сообщается о некоторых полезных свойствах оператора трассировки.
След суммы
След суммы двух матриц равен сумме их следов.
Предложение Позволять и быть двумя матрицы. Затем,
Доказательство
Помните, что сумма двух матриц равна выполняется суммированием каждого элемента одной матрицы с соответствующим элементом другой матрицы (см. лекцию о Добавление матрицы). Как следствие,
След скалярного множителя
Следующее предложение говорит нам, что происходит со следом, когда матрица умножить на скаляр.

Предложение Позволять быть матрица и скаляр. Затем
Доказательство
Помните, что умножение матрицы скаляром выполняется путем умножения каждого элемента матрицы на заданное скаляр (см. лекцию о Умножение матрицы скаляром). Как следствие,
След линейной комбинации
Два вышеуказанных свойства (след сумм и скалярных кратных) подразумевают, что след линейного комбинация равна линейной комбинации трасс.
Предложение Позволять и быть двумя матрицы и и два скаляра. Затем,
След транспонирования матрицы
Транспонирование матрицы не меняет ее след.
Предложение Позволять быть матрица. Тогда
Доказательство
След матрицы есть сумма ее диагональные элементы, но транспозиция оставляет диагональные элементы без изменений.

След продукта
Следующее предложение касается следа произведения матриц.
Предложение Позволять быть матрица и ан матрица. Затем
Доказательство
Обратите внимание, что это матрица и является матрица. Тогда где по шагам и мы использовали определение матричного произведения, в частности, те факты, что равно скалярному произведению между -й ряд и -й столбец , и равно скалярному произведению между -й ряд и -й столбец .
След скаляра
Тривиальное, но часто полезное свойство состоит в том, что скаляр равен своему след , потому что скаляр можно рассматривать как матрица, имеющая единственный диагональный элемент, который в свою очередь равен следу.
Это свойство часто используется для записи скалярных произведений в виде следов.

Пример Позволять быть вектор строки и а вектор-столбец. Затем продукт является скаляром, и где на последнем шаге мы использовали предыдущее предложение о следе матрицы продукты. Таким образом, мы смогли записать скаляр как след от матрица .
Решенные упражнения
Ниже вы можете найти несколько упражнений с поясненными решениями.
Упражнение 1
Позволять быть матрица определена поНайти его след.
Решение
Суммируя диагональные элементы, мы получить
Упражнение 2
Позволять быть матрица и а вектор. Написать продуктыкак след произведения двух матрицы.
Раствор
С тех пор это скаляр, у нас есть это Более того, является и является . Следовательно, где обе и находятся .

Как цитировать
Пожалуйста, указывайте как:
Taboga, Marco (2021). «След матрицы», Лекции по матричной алгебре. https://www.statlect.com/matrix-алгебра/trace-of-a-matrix.
След матрицы
Марко Табога, доктор философии
След квадрата матрица представляет собой сумму своих диагональные входы.
Трассировка имеет несколько свойств, которые используются для доказательства важности приводит к матричной алгебре и ее приложениям.
СОДЕРЖАНИЕ
Определение
Примеры
Свойства
ТРЕЗИЙ3
ТРЕЗИЯ СКАЛАРЕ
ТРЕЗАНИ След транспонирования матрицы
След произведения
След скаляра
Решенные упражнения
Упражнение 1
Упражнение 2
Определение
Начнем с формального определения.

Определение Позволять быть матрица. Тогда его след, обозначаемый или же , это сумма его диагоналей записи:
Примеры
Ниже приведены некоторые примеры.
Пример Определите матрица Тогда его след
Пример Определите матрица Тогда его след
Свойства
В следующих подразделах сообщается о некоторых полезных свойствах оператора трассировки.
След суммы
След суммы двух матриц равен сумме их следов.
Предложение Позволять и быть двумя матрицы. Затем,
Доказательство
Помните, что сумма двух матриц равна выполняется суммированием каждого элемента одной матрицы с соответствующим элементом другой матрицы (см. лекцию о Добавление матрицы). Как следствие,
След скалярного множителя
Следующее предложение говорит нам, что происходит со следом, когда матрица умножить на скаляр.

Предложение Позволять быть матрица и скаляр. Тогда
Доказательство
Помните, что умножение матрицы скаляром выполняется путем умножения каждого элемента матрицы на заданное скаляр (см. лекцию о Умножение матрицы скаляром). Как следствие,
След линейной комбинации
Два вышеуказанных свойства (след сумм и скалярных кратных) подразумевают, что след линейного комбинация равна линейной комбинации трасс.
Предложение Позволять и быть двумя матрицы и и два скаляра. Затем,
След транспонирования матрицы
Транспонирование матрицы не меняет ее след.
Предложение Позволять быть матрица. Затем
Доказательство
След матрицы есть сумма ее диагональные элементы, но транспозиция оставляет диагональные элементы без изменений.

След продукта
Следующее предложение касается следа произведения матриц.
Предложение Позволять быть матрица и ан матрица. Затем
Доказательство
Обратите внимание, что это матрица и является матрица. Тогда где по шагам и мы использовали определение матричного произведения, в частности, те факты, что равно скалярному произведению между -й ряд и -й столбец , и равно скалярному произведению между -й ряд и -й столбец .
След скаляра
Тривиальное, но часто полезное свойство состоит в том, что скаляр равен своему след , потому что скаляр можно рассматривать как матрица, имеющая единственный диагональный элемент, который в свою очередь равен следу.
Это свойство часто используется для записи скалярных произведений в виде следов.

Пример Позволять быть вектор строки и а вектор-столбец. Затем продукт является скаляром, и где на последнем шаге мы использовали предыдущее предложение о следе матрицы продукты. Таким образом, мы смогли записать скаляр как след от матрица .
Решенные упражнения
Ниже вы можете найти несколько упражнений с поясненными решениями.
Упражнение 1
Позволять быть матрица определена поНайти его след.
Решение
Суммируя диагональные элементы, мы получить
Упражнение 2
Позволять быть матрица и а вектор. Написать продуктыкак след произведения двух матрицы.
Раствор
С тех пор это скаляр, у нас есть это Более того, является и является . Следовательно, где обе и находятся .



 Указание данного параметра, позволяет избежать лишней операции присваивания тем самым немного ускоряя работу вашего кода. Полезный параметр если вы очень часто обращаетесь к функции в цикле.
Указание данного параметра, позволяет избежать лишней операции присваивания тем самым немного ускоряя работу вашего кода. Полезный параметр если вы очень часто обращаетесь к функции в цикле. eye(3)
>>> a
array([[1., 0., 0.],
[0., 1., 0.],
[0., 0., 1.]])
>>>
>>> np.trace(a)
3.0
>>>
>>>
>>> b = np.arange(1, 10).reshape(3, 3)
>>> b
array([[1, 2, 3],
[4, 5, 6],
[7, 8, 9]])
>>>
>>> np.trace(b, offset = 0) # по умолчанию offset = 0
15
>>>
>>> np.trace(b, offset = 1)
8
>>> np.trace(b, offset = -1)
12
>>>
>>>
>>> # Массивы не обязаны быть квадратными:
... c = np.arange(1, 13).reshape(3, 4)
>>> c
array([[ 1, 2, 3, 4],
[ 5, 6, 7, 8],
[ 9, 10, 11, 12]])
>>>
>>> np.trace(c)
18
eye(3)
>>> a
array([[1., 0., 0.],
[0., 1., 0.],
[0., 0., 1.]])
>>>
>>> np.trace(a)
3.0
>>>
>>>
>>> b = np.arange(1, 10).reshape(3, 3)
>>> b
array([[1, 2, 3],
[4, 5, 6],
[7, 8, 9]])
>>>
>>> np.trace(b, offset = 0) # по умолчанию offset = 0
15
>>>
>>> np.trace(b, offset = 1)
8
>>> np.trace(b, offset = -1)
12
>>>
>>>
>>> # Массивы не обязаны быть квадратными:
... c = np.arange(1, 13).reshape(3, 4)
>>> c
array([[ 1, 2, 3, 4],
[ 5, 6, 7, 8],
[ 9, 10, 11, 12]])
>>>
>>> np.trace(c)
18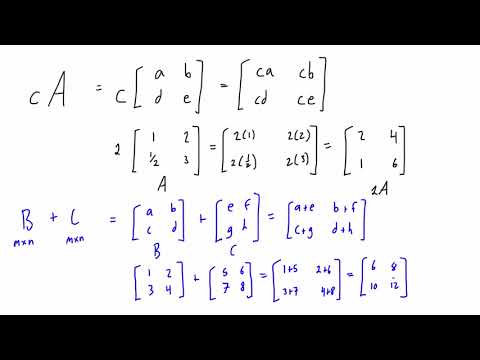 arange(12).reshape(3, 2, 2)
>>> d
array([[[ 0, 1],
[ 2, 3]],
[[ 4, 5],
[ 6, 7]],
[[ 8, 9],
[10, 11]]])
>>>
>>> np.trace(d)
array([6, 8])
arange(12).reshape(3, 2, 2)
>>> d
array([[[ 0, 1],
[ 2, 3]],
[[ 4, 5],
[ 6, 7]],
[[ 8, 9],
[10, 11]]])
>>>
>>> np.trace(d)
array([6, 8]) trace(d, axis1 = 1, axis2 = 2)
array([ 3, 11, 19])
>>>
>>> np.trace(d, axis1 = -2, axis2 = -1)
array([ 3, 11, 19])
trace(d, axis1 = 1, axis2 = 2)
array([ 3, 11, 19])
>>>
>>> np.trace(d, axis1 = -2, axis2 = -1)
array([ 3, 11, 19]) Тогда его след, обозначаемый
или же
,
это сумма его диагоналей
записей:
Тогда его след, обозначаемый
или же
,
это сумма его диагоналей
записей: