Гиперболический синус в маткаде: Часть 1. Набор встроенных функций MathCAD

Самоучитель MathCAD

Самоучитель MathCAD

И другие программы этой серии

 

Самоучитель MathCAD

Все углы в
тригонометрических функциях измеряются в радианах.
• acosh(X) – возвращает гиперболический арккосинус для каждого элемен
та X. Пример:
>>Y = acosh (0.7)
Y=
0 + 0.7954i
Рис. 3.3. Графики синусоиды, прямоугольных,
пилообразных и треугольных колебаний
• acoth(X) – возвращает гиперболический арккотангенс для каждого эле
мента X. Пример:
>>Y = acoth (0.1)
Y = 0.1003 + 1.5708i
• acsch(X) – возвращает гиперболический арккосеканс для каждого эле
мента X. Пример:
>> Y = acsch(1)
Y=
0.8814
• asech(X) – возвращает гиперболический арксеканс для каждого элемента
X. Пример:
>> Y = asech(4)
Y=
0 + 1.3181i
• asinh(X) – возвращает гиперболический арксинус для каждого элемента
X. Пример:
>> Y = asinh (2.456)
Y=
1. 6308

• atanh(X) – возвращает гиперболический арктангенс для каждого элемен
та X. Пример:
>> X=[0.84 0.16 1.39];
>> atanh (X)
ans = 1.2212
0.1614
0.9065 + 1.5708i
Рис. 3.4. Графики периодических сигналов без разрывов
• cosh(X) – возвращает гиперболический косинус для каждого элемента X.

178
Пример:
Программные средства математических вычислений
Встроенные элементарные функции
179
>> X=[1 2 3];
>> cosh(X)
ans = 1.5431 3.7622
10.0677
• coth(X) – возвращает гиперболический котангенс для каждого элемента
X. Пример:
>> Y = coth(3.987)
Y=
1.0007
• csch(x) – возвращает гиперболический косеканс для каждого элемента X.
Пример:
>> X=[2 4.678 5;0.987 1 3];
>> Y = csch(X)
Y=
0.2757
0.0186
0.0135
0.8656
0.8509
0.0998
• sech(X) – возвращает гиперболический секанс для каждого элемента X.

Пример:
>> X=[pi/2 pi/4 pi/6 pi];
>> sech(X)
ans = 0. 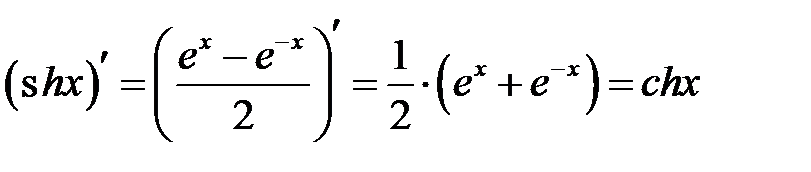3985 0.7549 0.8770
Рис. 3.5. Графики гиперболических функций
0.0863
• sinh(X) – возвращает гиперболический синус для каждого элемента X.
Пример:
>> X=[pi/8 pi/7 pi/5 pi/10];
>> sinh(X)
ans = 0.4029 0.4640 0.6705
0.3194
• tanh(X) – возвращает гиперболический тангенс для каждого элемента X.
Пример:
>> X=[pi/2 pi/4 pi/6 pi/10];
>> tanh(X)
ans = 0.9172 0.6558 0.4805
0.3042
Следующий m файл сценарий (программа) строит графики (рис.

<< Назад   1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121 122 123 124 125 126 127 128 129 130 131 132 133 134 135 136 137 138 139 140 141 142 143 Вперед >>

 

Глава 2.

Элементарные функции MathCad.

Тригонометрические

sin(z) — синус,

cos(z) — косинус,

tan(z) — тангенс,

cot(z) — котангенс,

sec(z) — секанс

csc(z) — косеканс.

Обратные тригонометрические

asin(z) — арксинус,

acos(z) — арккосинус,

atan(z) — арктангенс

Гиперболические

sinh(z) — гиперболический синус,

cosh(z) — гиперболический косинус,

tanh(z) — гиперболический тангенс,

coth(z) — гиперболический котангенс,

sech(z) — гиперболический секанс

csch(z) — гиперболический косеканс.

Обратные гиперболические

asinh(z) — арксинус гиперболический,

acosh(z) — арккосинус гиперболический,

atanh(z) — арктангенс гиперболический

Показательные и логарифмические

exp(z) — экспонента,

ln(z) — натуральный логарифм,

log(z) — десятичный логарифм.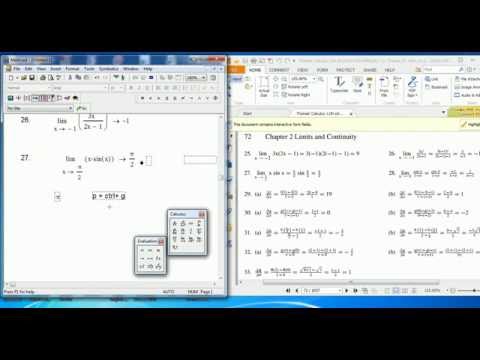

Комплексного аргумента

Re(z) — вещественная часть,

Im(z) — мнимая часть,

|z| — модуль,

arg(z) — фаза (для формата экспоненты),

— сопряженный комплекс

Встроенные функции можно ввести в документ с помощью команды

Insert / Function…или кнопкой f(x) Из одноименного окна диалога выбрать нужную категорию, а в ней соответствующую функцию.

Программа Visio предназначена для создания различного вида чертежей: от схем сетей до календарей, от планов офиса до блок-схем. Microsoft Visio — это универсальная графическая программа, предоставляющая средства для визуализации большинства технических и деловых задач при помощи одного простого в использовании продукта. Программы Microsoft Office Visio 2003 и Microsoft Office Visio 2007 дают возможность всем пользователям в таких отраслях, как коммерция, проектирование и информационные технологии, создавать и распространять схемы процессов, систем и графики числовых данных.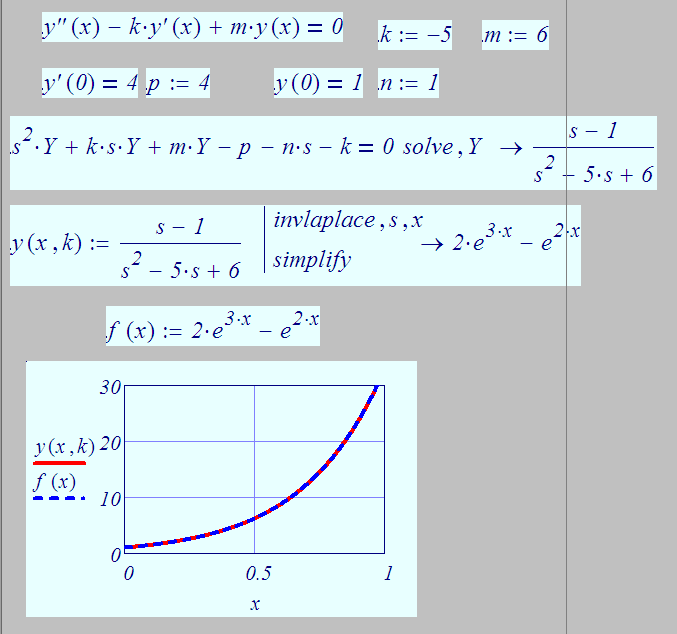

В Microsoft Office Visio 2007 представлены тысячи фигур и более шестидесяти шаблонов схем, одни из которых простые, а другие — довольно сложные. Каждый шаблон предназначен для конкретных целей — от создания планов водопроводных сетей до компьютерных сетей. Шаблоны разбиты по темам – например, план офиса, машиностроение, блок-схемы, расписание, бизнес, техника и прочее.

Кроме всего прочего Вы можете создавать свои Шаблоны со своими наборами фигур.

Файловые форматы

VSD — диаграмма

VSS — Фигура

VST — шаблон

VDX — диаграмма в формате XML

VSX

VTX

VSL — надстройка

Немного истории

Первоначально Visio разрабатывался и выпускался компанией Visio Corporation. Microsoft приобрела компанию в 2000 году, когда продукт назывался Visio 2000.

Был выполнен ребрендинг и продукт был включен в состав Microsoft Office.

Visio 1.0 (Standard, Lite, Home)

Visio 2.0

Visio 3.0

Visio 4.0 (Standard, Technical)

Visio 4.1 (Standard, Technical)

Visio 4.5 (Standard, Professional, Technical)

Visio 5.0 (Standard, Professional, Technical)

Visio 2000 (6.0; Standard, Professional, Technical, Enterprise)

Visio 2002 (10.0; Standard, Professional)

Visio Enterprise Network Tools, Visio Network Center

Visio for Enterprise Architects 2003 (VEA 2003) (based on Visio 2002 and included with Visual Studio .NET 2003 Enterprise Architect)

Office Visio 2003 (11.0; Standard, Professional)

Office Visio for Enterprise Architects 2005 (VEA 2005) (based on Visio 2003 and included with Visual Studio 2005 Team Suite and Team Architect editions)

Office Visio 2007 (12.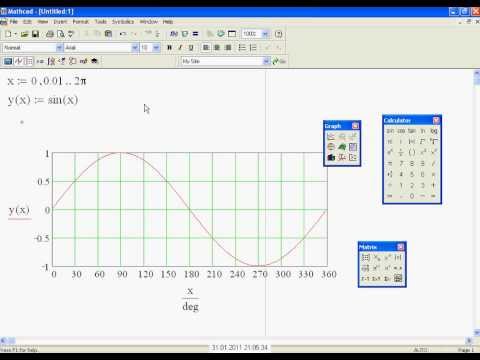 0; Standard, Professional).

Office Visio 2010 (14.0; планируемая версия, в настоящее время в статусе Release Candidate (RC))

Замечание: Не существует версий 7, 8, и 9, после покупки Visio компанией Microsoft, входила в состав Office, соответственно версия Visio соответствует версии Office.

Microsoft Office Visio относится к семейству продуктов Microsoft Office, но не входит ни в один стандартный комплект, поэтому приобретается отдельно. Программа выпускается в двух редакциях: Standard и Professional.

Ниже Вы найдете две таблицы со сравнением версий Visio Standard и Professional. Первая таблица посвящена сравнению функционала в области проектирования, во второй таблице приведено сравнение общезначимых функций программы.

sin-in-steps-matlab — Googlesuche

AlleBilderVideosBücherMapsNewsShopping

suchoptionen

Tipp: Begrenze diesuche auf deutschsprachige Ergebnisse. Du kannst deinesuchsprache in den Einstellungen ändern.

Y = sind( X ) возвращает синус элементов в X , выраженных в градусах.

Синус аргумента в градусах — MATLAB sind — MathWorks

www.mathworks.com › … › Элементарная математика › Тригонометрия

Hervorgehobene Snippets

Ähnliche Fragen

Как перевести MATLAB в градусы?

Как написать sin в MATLAB?

MATLAB в радианах или градусах?

Грех в MATLAB в радианах?

Синус аргумента в градусах — MATLAB sind — MathWorks Deutschland

de.mathworks.com › … › Тригонометрия

Y = sind( X ) возвращает синус элементов в X , которые выражены в . ..

Примеры · Входные аргументы

Обратный синус в градусах — MATLAB asind — MathWorks

www.mathworks.com › … › Тригонометрия

Y = asind( X ) возвращает арксинус (sin-1) элементов X в градусах.

Описание · Примеры · Входные аргументы

Синус аргумента в радианах — MATLAB sin — MathWorks

www. mathworks.com › … › Тригонометрия

Функция sin работает с массивами поэлементно. Функция принимает как вещественные, так и комплексные входные данные. Для реальных значений X функция sin(X) возвращает реальные значения …

sind (Функции MATLAB)

matlab.izmiran.ru › help › techdoc › ref › sind

sind. Синус аргумента в градусах. Синтаксис. Y = синд(Х). Описание. Y = sind(X) — синус элементов X , выраженный в градусах.

MATLAB sin() vs sind() — градусы (n*pi) отражает точность значения pi с плавающей запятой. Итак, если вы …

Как MATLAB sind дает синус аргументов в градусах — YouTube

www.youtube.com › смотреть

14.03.2019 · MATLAB TUTORIAL — Как MATLAB sind дает синус аргументов в градусах.
Dauer: 0:29
Прислан: 14.03.2019

Тригонометрические функции в MATLAB — GeeksforGeeks

www.geeksforgeeks.org синус ввода в радианах. Ввод может быть числом, массивом или матрицей.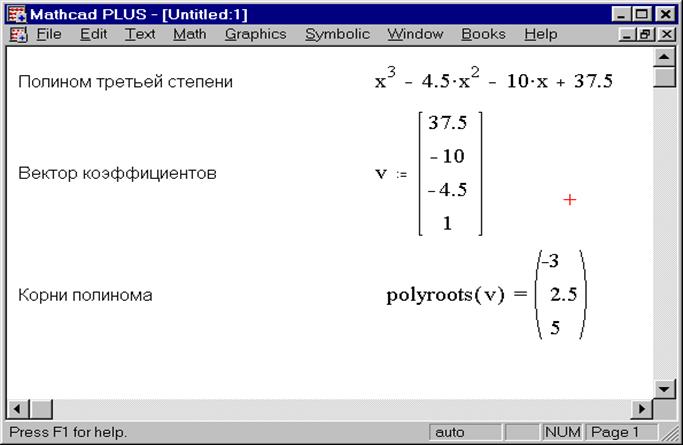 · : sin(значение) ; sind: Эта функция …

Грех в градусах Matlab

woeh.alexandrupostamia.it › sin-in-grades-matlab

Как ввести тригонометрические функции в градусах и. Триггерные функции MATLAB (градусы синуса, косинуса и родственные функции с результатами в радианах или градусах.

sin (функции MATLAB)

www.ece.northwestern.edu › techdoc › ref › sin

sin. . Синтаксис. Y = sin(X). Описание. Функция sin работает с массивами поэлементно. Домены и диапазоны функции включают комплексные значения. 92

MATLAB sin(pi не равно нулю)

MATLAB asin

MATLAB plot

[PDF] Превосходная производительность использования гиперболических синусоидальных функций активации в ZNN, проиллюстрированная нахождением квадратного корня из изменяющейся во времени матрицы

• DO29/80. CSIS120121043Z
• Идентификатор корпуса: 7612571

 @article{Zhang2012SuperiorPO,
  title={Превосходная производительность использования функций активации гиперболического синуса в ZNN, проиллюстрированная нахождением квадратного корня изменяющейся во времени матрицы},
  автор = {Юнун Чжан, Лун Цзинь и Чжэндэ Кэ},
  журнал={Вычисл.  науч. Инф. сист.},
  год = {2012},
  громкость = {9},
  страницы={1603-1625}
} 

• Юнонг Чжан, Лун Цзинь, Чжэндэ Кэ
• Опубликовано в 2012 г.
• Информатика
• Вычисл. науч. Инф. Сист.

Особый класс рекуррентных нейронных сетей (RNN), называемый нейронными сетями Чжан. сеть (ZNN), изображенная в неявной динамике, недавно была предложена для онлайн-решения нестационарных квадратных корней матрицы. Такая модель ZNN может быть построено с использованием монотонно возрастающих нечетных функций активации для получить теоретические квадратные корни изменяющейся во времени матрицы в безошибочном способ. Различные варианты массивов функций активации могут привести к различным производительность модели ZNN… 

Нелинейная и устойчивая к помехам модель ZNN и ее применение к статической и изменяющейся во времени матрице Нахождение квадратного корня

Предлагаемая модель NNT-ZNN с двумя свойствами нелинейности и помехоустойчивости для переменной во времени и статической матрицы поиск квадратного корня полностью учитывает ошибку, вызванную возможным шумом в аппаратной реализации ZNN.

Анализ производительности рекуррентных моделей нейронных сетей, используемых для онлайновой нелинейной оптимизации во времени

Теоретические результаты показывают, что остаточные ошибки модели ZNN с непрерывным временем обладают свойством глобальной экспоненциальной сходимости и что максимальная установившаяся остаточная ошибка любого метода, предназначенного по своей сути для решения задачи статической оптимизации и используемого для онлайн-решения OTVNO, равна O(τ), где τ обозначает интервал выборки.

Адаптивные расчеты коэффициентов для нелинейной функции активации и ее применение к обнулению нейронной сети для решения изменяющегося во времени уравнения Сильвестра

• Чжэнь Цзянь, Линь Сяо, Кенли Ли, Цююэ Цзо, Юншэн Чжан

• Информатика

  Дж. Франкл. Инст.

• 2020

Zeroing neural networks: A survey

• Long Jin, Shuai Li, Bolin Liao, Zhijun Zhang

• Computer Science

  Neurocomputing

• 2017

An Integration-Enhanced Noise-Resistant RNN Модель с превосходными характеристиками, проиллюстрированная с помощью решения уравнения Сильвестра, изменяющегося во времени

Путем определения новой матричнозначной функции ошибки рекуррентная нейронная сеть с улучшенным интегрированием (IENRRNN) обобщается для решения изменяющегося во времени уравнения Сильвестра в этой статье.

Рекуррентная нейронная сеть с ускорением сходимости с переменными параметрами для онлайн-решения псевдообратной динамической матрицы и ее применение для роботов -устойчивый, по сравнению с традиционной нейронной сетью Чжана, предназначенной для динамических задач.

Обнуление нейронных сетей: обзор (cid:2)

• Л. Джин, Болин Ляо, Чжицзюнь Чжан

• Информатика

• 2017

Всесторонние обзоры, включая непрерывные исследования ZNNtimes и модели ZNN с дискретным временем для решения различных задач, а также их применение в планировании движения и управлении избыточными манипуляторами, отслеживании управления хаотическими системами или даже управлении популяциями в математических биологических науках.

Новая 5-шаговая нейросеть с дискретным временем для нахождения квадратного корня из матрицы, зависящей от времени остаточные ошибки состояния пропорциональны четвертой степени периода дискретизации.

Обнуление нейронной сети с нечетким параметром для вычисления псевдообратной произвольной матрицы

• В. Кацикис, П. Станимирович, Спиридон Д. Муртас, Линь Сяо, Д. Карабашевич, Д. Стануйкич

• Информатика

  Транзакции IEEE в нечетких системах

• 2022

FLS, который включает в себя надлежащим образом определенные функции принадлежности и правила нечеткой логики.

Активируемая нелинейностью шумоустойчивая нейронная сеть с обнулением для инверсии изменяющейся матрицы в реальном времени

Активируемая нелинейностью устойчивая к шуму нейронная сеть обнуления построена и используется для инверсии матриц, зависящей от времени, в шумной среде, активируется специально построенными нелинейными функциями активации и обладает лучшими характеристиками сходимости.

ПОКАЗАНЫ 1-10 ИЗ 33 ССЫЛОК

СОРТИРОВАТЬ ПОРелевантность Наиболее влиятельные статьиНедавность

Моделирование и сравнение решения нейронной сети Чжана и градиентной нейронной сети для квадратных корней изменяющейся во времени матрицы

В этой статье разрабатываются, обобщаются, моделируются и сравниваются модели ZNN и GNN для онлайн-решения квадратных корней изменяющейся во времени матрицы, а результаты с помощью функций активации степенной сигмы дополнительно подтверждают превосходную сходимость ZNN при решении изменяющихся во времени задач по сравнению с модель ГНН.

Разработка и анализ общей модели рекуррентной нейронной сети для инверсии изменяющейся во времени матрицы

Результаты моделирования подтверждают теоретический анализ и демонстрируют эффективность нейронной модели для инверсии изменяющейся во времени матрицы, особенно при использовании степенной сигмовидной функции активации .

Моделирование в MATLAB Simulink и моделирование нейронных сетей Чжана для онлайн-решения уравнения Сильвестра, изменяющегося во времени

• Weimu Ma, Yunong Zhang, Jiahai Wang

• Информатика

  2008 IEEE International Joint Conference on Neural Networks (IEEE World Congress on Neural Networks (IEEE World Congress on Neural Networks) Вычислительный интеллект)

• 2008

В этой статье исследуется моделирование MATLAB Simulink и имитационная верификация моделей ZNN для решения уравнения Сильвестра с переменным временем, а результаты обосновывают эффективность ZNN при решении нестационарных задач в режиме онлайн.

Нейронная сеть Чжана для линейного изменяющегося во времени уравнение и ее роботизированное применение

• Ю.-Нонг Чжан, Хайфенг Пенг

• Компьютерная наука, математика

  2007 Международная конференция по машинному обучению и кибернетике 9000 3

9
• 3333333333333333333333333333333333333333333333333333333333333333333333333333333333333333333333333333н. Результаты моделирования подтверждают теоретический анализ и демонстрируют эффективность нейронной сети Чжана при решении линейных уравнений, изменяющихся во времени, особенно при использовании степенной сигмовидной функции активации.

  Моделирование в MATLAB и сравнение нейронной сети Чжана и градиентной нейронной сети для онлайн-решения линейного матричного уравнения, изменяющегося во времени AXB-C=0

  • Ке Чен, Шуай Юэ, Юнонг Чжан

  • Информатика

    6

    ICIC

  • 2008

  Исследование MATLAB-моделирования нейронных сетей Чжана (ZNN) для решения в реальном времени линейного переменного матричного уравнения AXB- C = 0,1 и результаты обосновывают теоретический анализ и эффективность ZNN при решении линейного матричного уравнения, изменяющегося во времени.

  Рекуррентные нейронные сети для вычисления псевдообратных матриц с дефицитом ранга

  • J. Wang

  • Информатика, математика

    SIAM J. Sci. вычисл.

  • 1997

  Представлены три рекуррентные нейронные сети для вычисления псевдообратных матриц без ранга с динамическим уравнением, аналогичным предложенному ранее для обращения матриц и способным к обращению Мура—Пенроуза при условии нулевых начальных состояний.

  Устойчивые итерации для матричного квадратного корня

  Показано, что кажущиеся безобидными алгоритмические модификации итерации Паде могут привести к нестабильности, и анализ возмущений дан для некоторого объяснения.

  Новый взгляд на аналоговый компьютер и градиентную нейронную систему для инверсии матриц

  • Юнонг Чжан

  • Информатика

    Материалы Международного симпозиума IEEE 2005 г., Средиземноморская конференция по управлению и автоматизации, интеллектуальное управление, 9005.

    No related posts.