Умножение иррациональных чисел: Иррациональные числа — урок. Алгебра, 8 класс.

II. Действия на иррациональными числами

Приближенное значения иррациональных чисел по недостатку и по избытку являются конечными десятичными дробями. Поэтому можно определить операцию сложения на множестве I₊.

Определение. Суммой положительных иррациональных чисел a и b, таких, что и , называется число a +b, которое удовлетворяет условию

Найти сумму этих чисел с точностью до 0,01 и 0,001.

III. Умножение положительных иррациональных чисел

Пусть даны числа a и b, которые принадлежат множеству положительных иррациональных чисел. Произведением чисел a и b называется число a^.b. , где a_n и b_n – приближенные значения a и b с точностью до по недостатку, а

a_n’ и b_n’ – приближенные значения a и b с точностью до по избытку.

Пример. Найдем произведение с точностью до 0,01.

IV. Аксиоматика множества положительных действительных чисел

Определение. Положительные рациональные числа – числа, которые могут быть записаны в виде бесконечных десятичных дробей. Но десятичная дробь – одна из форм записи действительных чисел. Существует бесконечные двоичные, бесконечные троичные и т.д. дроби. Чтобы понятие действительного числа не зависело от формы записи, формулируют аксиомы, которым они удовлетворяют. Можно предложить несколько аксиоматик действительного числа. Одним из примеров может служить система аксиом, опирающаяся на свойства сложения. В ней неопределяемые понятия – это единица, операция сложения. Названные понятия должны удовлетворять следующей системе аксиом:

1. Множество натуральных чисел является подмножеством множества положительных действительных чисел. ( )

2. Операция сложения ставит в соответствие любой паре действительных чисел a и b число , называемое суммой чисел.

3. Сложение в R₊ коммутативно:

4. Сложение в R₊ ассоциативно:

5.

6.

7.

Аксиомы 1–7 позволяют ввести на множестве положительных действительных чисел отношение порядка:

8. Аксиома непрерывности. Если числовое множество X лежит слева от числового множества

Y, т.е. и , то существует число , разделяющее множества X и Y, так, что .

Другую систему аксиом см. в книге Сендер, А.Н. «Методология формирования понятия о числе», с. 145.

V. Действительные отрицательные числа. Число 0. Модуль действительного числа

С помощью положительных действительных чисел можно выразить результат измерения любой скалярной величины: длины, площади, объема, массы и т.д. Но на практике часто бывает нужно выразить числом не результат измерения величины, а ее изменение, т.е. показать, на сколько изменилась эта величина. Изменение величины может идти в двух направлениях: она может как увеличиваться, так и уменьшаться, а может и остаться неизменной. Поэтому, чтобы выразить изменение величины, кроме положительных действительных чисел, нужны иные числа, нужно расширить множество R

+. Мы расширим его, присоединив к нему число 0 (ноль) и отрицательные числа. Число 0 характеризует такое состояние при измерении, когда величина не изменяется, остается прежней.

Итак, возьмем множество R₊ положительных действительных чисел и поставим в соответствие каждому числу х из R₊ новое число, которое будем обозначать –х (читается «минус х»). Например, числу 5 ставится в соответствие число –5, числу 8,14 — число –8,14 и т.д. Числа вида –х, где , назовем отрицательными числами, а их множество обозначим R_–.

Определение. Множеством действительных чисел называется объединение множества положительных действительных чисел с множеством отрицательных действительных чисел и 0. , причем множества R_–

, R и {0} попарно не пересекаются (ни одно число не может быть одновременно и положительным, и отрицательным; или и положительным, и нулем).

Между множеством действительных чисел и множеством точек координатной прямой существует взаимно-однозначное соответствие, т.е. каждому действительному числу соответствует вполне определенная и единственная точка на координатной прямой. И наоборот: каждой точке соответствует определенное единственное действительное число.

При этом непрерывность числовой прямой является подтверждением непрерывности множества действительных чисел. Это значит, что на прямой не существует точки, которая не соответствовала бы какому-либо действительному числу.

Определение. Все точки на координатной прямой, расположенные правее точки 0, соответствуют положительным действительным числам, а все точки левее точки 0 – отрицательным.

Числа х и (–х), где , изображаются точками координатной прямой, симметрично расположенными относительно начала отсчета 0. Эти числа называют противоположными друг другу, причем считают, что –(–х) = х. Например, –(–6) = 6. Число 0 считают противоположным самому себе: – 0 = 0.

Множество действительных чисел является бесконечным, т.е. не существует наименьшей и наибольший элемент. Оно имеет мощность континуума.

Множество R упорядочено, несчетно.

Определение. Модулем действительного числа называется расстояние от точки 0 до точки, изображающей это число. Геометрический смысл модуля:

Поскольку расстояние есть величина неотрицательная, то модуль любого числа тоже выражается неотрицательным числом.

Числа рациональные и иррациональные

Числа рациональные и иррациональные

Айвен Нивен. Числа рациональные и иррациональные Эта книга посвящена одному из основных понятий математики — понятию действительного числа. Ученики старших классов (именно на них она в первую очередь и рассчитана) узнают из нее некоторые свойства чисел, о которых они раньше и не подозревали, и познакомятся с доказательствами теорем, принимаемых в школьном курсе алгебры на веру. Изложение очень простое и живое. Оно сопровождается рядом вопросов и задач, облегчающих активное усвоение материала. Автор книги — известный американский специалист по теории чисел. Оглавление От редактора Введение ГЛАВА I. Натуральные и целые числа § 1. Простые числа § 2. Единственность разложения на простые множители § 3. Целые числа § 4. Четные и нечетные целые числа § 5. Свойства замкнутости § 6. Замечания о природе доказательства ГЛАВА II. Рациональные числа § 1. Определение рациональных чисел § 2. Конечные и бесконечные десятичные дроби § 3. Различные сгюсобы формулировки и доказательства предложений § 4. Периодические десятичные дроби § 5. Всякую конечную десятичную дробь можно представить в виде периодической десятичной дроби § 6. Краткие выводы ГЛАВА III. Действительные числа § 1. Геометрическая точка зрения § 2. Десятичные представления § 3. Иррациональность числа V2 § 4. Иррациональность числа V3 § 5. Иррациональность чисел V6 и V2+V3 § 6. Слова, которыми мы пользуемся § 7. Приложение к геометрии § 8. Краткие выводы ГЛАВА IV. Иррациональные числа § 1. Свойства замкнутости § 2. Алгебраические уравнения § 3. Рациональные корни алгебраических уравнений § 4. Дальнейшие примеры § 5. Краткие выводы ГЛАВА V. Значения тригонометрических и логарифмической функций § 1. Иррациональные значения тригонометрических функций § 2. Одно общее правило § 3. Иррациональные значения десятичных логарифмов § 4. Трансцендентные числа § 5. Три знаменитые задачи на построение § 6. Дальнейший анализ числа V2 § 7. Краткие выводы ГЛАВА VI. Приближение иррациональных чисел рациональными § 1. Неравенства § 2. Приближение целыми числами § 3. Приближение рациональными числами § 4. Лучшие приближения § 5. Приближения с точностью до 1/n2 § 6. Ограничения точности приближений § 7. Краткие выводы ГЛАВА VII. Существование трансцендентных чисел § 1. Предварительные сведения из алгебры § 2. Один способ приближения числа а § 3. План доказательства § 4. Свойства многочленов § 5. Трансцендентность числа а § 6. Краткие выводы ПРИЛОЖЕНИЕ А. Доказательство бесконечности числа простых чисел ПРИЛОЖЕНИЕ Б. Доказательство основной теоремы арифметики ПРИЛОЖЕНИЕ В. Доказательство Кантора существования трансцендентных чисел ПРИЛОЖЕНИЕ Г. Доказательство иррациональности значений тригонометрических фуннций И. М. Яглом Ответы и указания к упражнениям ПРИЛОЖЕНИЕ В Литература

умножение иррациональных чисел — 2 типа

Содержание

Этот пост также доступен в: हिन्दी (хинди)

Умножение — одно из четырех основных математических действий. Как вы можете выполнять умножение с натуральными числами, целыми числами, целыми числами и рациональными числами, так же вы можете выполнять эту операцию с иррациональными числами.

Давайте разберемся, как можно выполнять умножение иррациональных чисел.

Умножение иррациональных чисел

Вы можете выполнять умножение между рациональными и иррациональными числами, а также между двумя иррациональными числами. Когда вы имеете дело с действительными числами и умножаете их, следует помнить о следующих указателях:

• Когда операция умножения выполняется над рациональным и иррациональным числом, результатом является иррациональное число.
• Когда операция умножения выполняется над иррациональным и иррациональным числом, результатом может быть иррациональное или рациональное число.

Вы можете умножать иррациональное число на любое действительное число, т. е. иррациональное число можно умножать на натуральное, целое, целое или рациональное число.

Примечание:

• Все натуральные числа, целые числа и целые числа являются рациональными числами
• Рациональные и иррациональные числа вместе образуют набор действительных чисел

Умножение рационального числа на иррациональное число

Когда рациональное число умножается на иррациональное, их произведение можно записать одним из двух способов.

• $a\sqrt[n]{b}$ $\left(a \text{ — рациональное число и } \sqrt[n]{b} \text { — иррациональная часть}   \right)$
• $\sqrt[n]{c}$ $\left(\sqrt[n]{c} \text{ является иррациональным числом} \right)$

Примеры

Давайте рассмотрим несколько примеров, чтобы понять умножение иррациональных чисел на рациональные числа.

Пример 1: Найдите произведение $3$ и $\sqrt {5}$.

$3 \times \sqrt{5} = 3\sqrt{5}$

9{3} \times 7} = \sqrt[3] {8 \times 7} = \sqrt[3] {56}$.

Примечание: \sqrt[3] {56} также является иррациональным числом.

Умножение иррационального числа на иррациональное число

Произведение иррационального числа на другое иррациональное число может быть как иррациональным, так и рациональным числом.

Умножение двух или более иррациональных чисел может быть любого из двух типов

• Умножение иррациональных чисел с одинаковыми корнями $\left( \sqrt[n]{a} \times \sqrt[n]{b} \right)$
• Умножение иррациональных чисел с разными корнями $\left( \sqrt[m]{a} \times \sqrt[n]{b} \right)$

СКАЧАТЬ БЕСПЛАТНО КАРТОЧКИ ПО МАТЕМАТИКЕ:

Красиво оформленные карточки для печати, которые помогут вам запомнить все важные математические понятия и формулы.

Умножение иррациональных чисел с одинаковым корнем

При умножении двух или более иррациональных чисел с одинаковыми корнями найдите произведение чисел внутри корней.

Математически это можно выразить как $\sqrt [n]{a} \times \sqrt [n]{b} = \sqrt [n]{a \times b}$.

Примеры

Чтобы понять произведение двух или более иррациональных чисел, рассмотрим несколько примеров.

Пример 1: Найдите произведение $\sqrt {2}$ и $\sqrt {3}$.

Обратите внимание, что два иррациональных числа имеют одинаковые корни, поэтому их можно умножать напрямую.

$\sqrt {2} \times \sqrt {3} = \sqrt {2 \times 3} = \sqrt {6}$.

Примечание: Результат — иррациональное число.

Пример 2: Найдите произведение $\sqrt [5]{7}$ и $\sqrt [5]{2}$.

Здесь также два иррациональных числа имеют одинаковые корни.

$\sqrt [5]{7} \times \sqrt [5]{2} = \sqrt [5]{7 \times 2} = \sqrt [5]{14}$.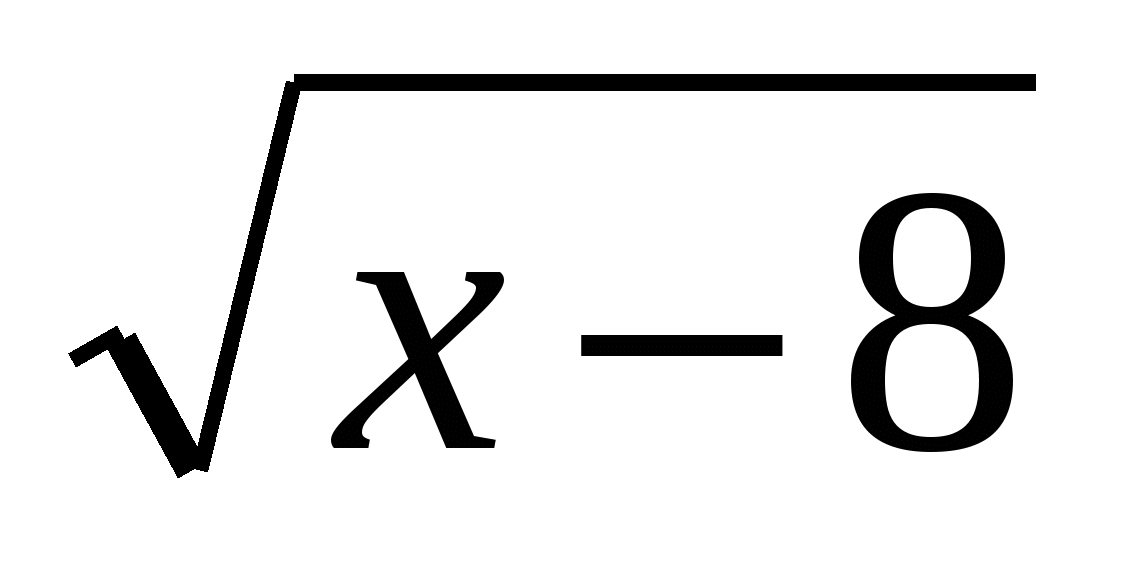 {3}} = \sqrt[3]{27}$ 9{2}} = 4$.

Примечание: Результатом является рациональное число.

Известные математики для вдохновения вашего ребенка

Умножение иррациональных чисел с разными корнями

Когда вы умножаете два или более иррациональных числа с разными корнями, то первым делом нужно преобразовать все иррациональные числа с одинаковыми корнями, а затем использовать процедуру умножения иррациональных чисел с одинаковыми корнями.

Чтобы преобразовать иррациональные числа с разными корнями, возьмите L.C.M. корней (единственного числа) корней. Л.К.М. будет основанием корня результата. 9{4}} = 2$.

Примечание: Результатом является рациональное число.

Заключение

Вы можете умножать иррациональное число на рациональное число или на иррациональное число. Когда вы умножаете иррациональное число на рациональное, результатом всегда будет иррациональное число, тогда как произведение двух или более иррациональных чисел может быть иррациональным или рациональным числом.

Практические задачи

Выполните следующие операции

• $4 \times \sqrt{3}$
• $2 \times \sqrt[4]{3}$
• $4 \times \sqrt[3]{5}$
• $\sqrt{5} \times \sqrt{3}$
• $\sqrt[5]{2} \times \sqrt[5]{3}$
• $\sqrt{7} \times \sqrt[3]{2}$
• $\sqrt[3]{3} \times \sqrt{9}$
• $\sqrt[4]{2} \times \sqrt[5]{3}$

Рекомендуемое чтение

• Ассоциативное свойство – значение и примеры
• Распределительная собственность – значение и примеры
• Коммутативное свойство – определение и примеры
• Свойство закрытия (определение и примеры)
• Аддитивная идентичность десятичных чисел (определение и примеры)
• Мультипликативное тождество десятичных чисел (определение и примеры)
• Натуральные числа — определение и свойства
• Целые числа — определение и свойства
• Что такое целое число — определение и свойства

Часто задаваемые вопросы

Как умножать иррациональные числа?

Чтобы умножить два или более иррациональных чисел, прежде всего проверьте, совпадают ли основания иррациональных чисел. Если одинаковые, умножьте числа в корне напрямую. Если основания разные, сначала преобразуйте иррациональные числа с общими основаниями, а затем умножьте.

Что получится, если умножить иррациональное число на иррациональное?

При умножении двух или более иррациональных чисел результатом может быть как иррациональное, так и рациональное число.

Что такое умножение рациональных и иррациональных чисел?

Произведение рационального числа на иррациональное число всегда является иррациональным числом.

Вам также может понравиться

Как решать линейные уравнения с матрицами (с методом и примерами)

Содержание Как решать линейные уравнения с матрицамиУсловие непротиворечивости

Читать далее

Правило Крамера – определение, формулы и примеры

Содержание Что такое правило Крамера?Формула правила КрамераПравило Крамера 2 x

Читать далее

Карточки по математике для бесплатной печати – скачать PDF

Этот пост также доступен на: हिन्दी (хинди) Карточки по математике — это

Читать далее

Произведение рациональных и иррациональных чисел иррационально (Доказательство + Вопросы) – Новичок в математике

Доказательство

Докажем это от противного.

Пусть yx — рациональное число, а p — иррациональное число.

Предположим, что произведение этих чисел есть рациональное число ba​. Мы надеемся получить противоречие из-за этого предположения. Предположение приводит к следующему уравнению:

yx​×p=ba​

Умножение обеих сторон на xy​:

p=ba​×xy​=bxay​

Уравнение выражает p как произведение двух рациональных чисел. Так что это должно быть рационально. Этот результат противоречит тому факту, что р — иррациональное число.

Итак, наше предположение (произведение рационального числа yx на иррациональное число p является рациональным числом) неверно. Следовательно, результатом этого произведения является иррациональное число.

✩ Известные иррациональные числа

1. Квадратный корень из простых чисел (Prime​): √2, √3, √5, √7, √11, √13, √17, √19…
2. Специальные числа: Pi ( π ), число Эйлера ( e ), золотое сечение в следующих примерах является иррациональным числом. Почему?

   Одно из чисел при умножении — это квадратный корень из простого числа, что является иррациональным.

   Пример 1

   2×3​=23​

   • 2 рационально
   • √3 иррационально
   • Product is irrational

   Example 2

   53​×5​=535​​

   • 53​ is rational
   • √5 is irrational
   • Product is irrational

   Example 3

   (2129​+ 35​)×11​

   =(2129+35​)×11​

   =2164​11​

   2164​ рационально, 11​ иррационально

   Их произведение иррационально.

   Пример 4

   Следующие произведения иррациональны, потому что π — иррациональное число.

   • 21×π=2π​
   • 23×π=23π​
   • 2 × π = 2π

   ✩ Иррациональный результат операций

   . Каким бы ни был порядок операций, результатом всегда будет иррациональное число.
   1. Рациональное + Иррациональное: [ 3 + √2 ], [ 4 + √7 ], …
   2. Рациональное − Иррациональное: [ 5 – √2 ], [ √3 – 6 ], …
   3. Рациональное × Иррациональное: [ 4 × π = 4π], [6 × √3 = 6√3], …
   4. Рациональное ÷ Иррациональное: [ 2 ÷ √2 ], [ π ÷ 2 ], …

   Произведение двух иррациональных чисел

   Мы знаем, что произведение двух рациональных чисел рационально. Единственный оставшийся случай — это произведение двух иррациональных чисел. При этом результирующее число может быть рациональным или иррациональным, в зависимости от множимого и множителя.

   Давайте рассмотрим несколько примеров.

   Пример 5

   √2 × √6

   =12​

   = 2√3

   Это произведение является иррациональным числом из-за наличия квадратного корня из √3, которое является иррациональным числом.

   Пример 6

   √3 × √3

   = √9

   = 3

   3 — рациональное число. Произведение двух иррациональных чисел может быть рациональным.

   Пример 7

   (2 + √3) × (2 − √3)

   Полученное число в каждой скобке выше является суммой рационального и иррационального чисел. Значит, это иррациональное число. Посмотрим, что будет с продуктом.

   (2 + √3) × (2 − √3)

   = 4 − 2√3 + 2√3 − (√3) ²

   = 4 − 3 = 1

   Произведение является рациональным числом!

   Вопросы

   1 Вопрос

   231​ рациональный или иррациональный?

   Ответ

   Является ли 31 простым числом?

   2 Вопрос

   80​×5​ является рациональным или иррациональным?

   Ответить

   Можете ли вы умножить числа?

   3 Вопрос

   Найдите произведение (4 − √7)(4 + √7). Это рационально?

   Ответ

   Можете ли вы применить формулу (a − b)(a + b) = a ² − б ² ?

   4 Question

   Докажите, что площадь круга с радиусом π3 – рациональное число.

   Ответ

   Можете ли вы найти площадь по формуле Площадь = πr ² ?

   5 Вопрос

   Дано 2−5​2+5​=x+y5​, где x, y — рациональные числа. Найдите х, у.

   Ответ

   Можете ли вы рационализировать знаменатель?

   Ответы

   1 Ответ

   31 — простое число.

   Квадратный корень из простых чисел иррационален, поэтому его произведение на 2 также иррационально.

   2 Ответ

   При умножении получаем:

   80×5=16×5×5

   4√5 × √5 = 4 × 5 = 20

   Это рациональное число.

   3 Ответ

   Применяя формулу разности квадратов, получаем:

   (4 − √7)(4 + √7) = 4 ² − (√7) ²

   −
   = 16 = 9

   Результатом является рациональное число.

   No related posts.