Построение графиков комплексных чисел: Играемся с комплексными числами / Хабр

Играемся с комплексными числами / Хабр

Привет!

Очередной очерк. На этот раз поиграемся с комплексными числами, с формулами и их визуализацией.

Идея

Комплексное число — это некоторое расширение вещественного числа, по сути вектор, для которого определено целое множество аксиом. Любое комплексное (а значит и вещественное) число можно записать в виде , где a — вещественная часть, b — мнимая, i — корень уравнения . Для него определено много операций, которые определены для вещественного числа, к примеру, . Интересно, что если проделывать различные операции с ними, возводить в степень, умножать и т. д. а затем брать (вещественную часть) для оси Ox, а (мнимую часть) для оси Oy, можно получать забавные картинки.

Кстати все следующие формулы я сам придумал.

Функция визуализации

Рутина. Функция, которая по данной итеративной функции рисует все на поле:

import random
import numpy as np
def vis(A, f, step=1. 0, c=None):
    x = []
    y = []
    for B in np.arange(0, A, step):
        v = f(A, B)
        x.append(v.real)
        y.append(v.imag)
    plt.figure(figsize=[8, 8])
    mxabs = max([i[0] ** 2 + i[1] ** 2 for i in zip(x, y)]) ** 0.5
    x = np.array(x) / mxabs
    y = np.array(y) / mxabs
    if c is None:
        plt.scatter(x, y)
    else:
        plt.scatter(x, y, color=[c(x[i], y[i]) for i in range(len(x))])
    plt.show()

Все наши функции зависят от двух параметров A и B. Причем по B мы итерируемся внутри vis(), а A — глобальный параметр функции.

Функция «Завитушки»

Ее объявление в python:

def func_1(A, B):
    return math.sin(B) * B * math.e ** (1j * (B * math.cos(A)))

И запустим

A = 121.5
vis(A, func_1, step=0.1)

И результат для A=121.5:

И для A=221.5:

Заметьте, эти числа вовсе не следуют из расчета какого-нибудь определенного интеграла на гладком многообразии и других умных бессмысленных в этом контексте слов.

Это действительно рандомные числа, и существует еще ровно бесконечность разных A, в результате которых получается красота.

Надо покрасить

Объявим функцию цвета (такую функцию, которая по координатам возвращает tuple из трех чисел):

def sigm(x):  # Эта функция позволяет нормализировать все что угодно от 0 до 1
    return (1 / (1 + 1.2 ** (-x*50)) - 0.5) * 2
color_1 = lambda x, y: (0.2, sigm(x ** 2 + y ** 2) / 1.4, 1 - sigm(x ** 2 + y ** 2))
color_2 = lambda x, y: (sigm(x ** 2 + y ** 2), 0.5, 0.5)

Выберем рандомный параметр A, пусть будет 149:

vis(149, func_1, step=0.1, c=color_1)

Функция «Гуси»

Гуси описываются так:

Объявление на python:

def func_2(A, B):
    return math.cos(B) * math.sin(B) * B * math.e ** (1j * (B * math.cos(A)))

Ее результат для A=106:

Функция «Фокачча»

def func_3(A, B):
    return math. cos((A + 1) * B) * math.e ** (1j * (B * math.cos(A)))

vis(246, func_3, step=0.1, c=color_2)

vis(246, func_3, step=0.1, c=color_2)

Функция «Без названия»

color_3 = lambda x, y: (0.5, 0.5, sigm(x ** 2 + y ** 2))
vis(162, func_4, step=0.1, c=color_3)

vis(179, func_4, step=0.1, c=color_3)

Формула красоты

def func_5(A, B):
    return math.cos((A + 1) * B) ** 1.5 * math.e ** (1j * (B * math.cos(A)))

color_4 = lambda x, y: (sigm(x ** 2 + y ** 2) / 2, 0.5, 1 - sigm(x ** 2 + y ** 2))
vis(345, func_5, step=0.1, c=color_4)

vis(350, func_5, step=0.1, c=color_4)

Пока все.

Весь код

import numpy as np
import random
import matplotlib.pyplot as plt
import math
def vis(A, f, step=1.0, c=None):
    x = []
    y = []
    for B in np.arange(0, A, step):
        v = f(A, B)
        x.append(v.real)
        y.append(v. imag)
    plt.figure(figsize=[7, 7])
    mxabs = max([i[0] ** 2 + i[1] ** 2 for i in zip(x, y)]) ** 0.5
    x = np.array(x) / mxabs
    y = np.array(y) / mxabs
    if c is None:
        plt.scatter(x, y)
    else:
        plt.scatter(x, y, color=[c(x[i], y[i]) for i in range(len(x))])
    plt.show()
def func_1(A, B):
    return math.sin(B) * B * math.e ** (1j * (B * math.cos(A)))
def func_2(A, B):
    return math.cos(B) * math.sin(B) * B * math.e ** (1j * (B * math.cos(A)))
def func_3(A, B):
    return math.cos((A + 1) * B) * math.e ** (1j * (B * math.cos(A)))
def func_4(A, B):
    return math.sin(A + B) * B * math.e ** (1j * B * math.sin(A))
def func_5(A, B):
    return math.cos((A + 1) * B) ** 1.5 * math.e ** (1j * (B * math.cos(A)))
def sigm(x):
    return (1 / (1 + 1.2 ** (-x*50)) - 0.5) * 2
color_1 = lambda x, y: (0.2, sigm(x ** 2 + y ** 2) / 1.4, 1 - sigm(x ** 2 + y ** 2))
color_2 = lambda x, y: (sigm(x ** 2 + y ** 2), 0.5, 0.5)
color_3 = lambda x, y: (0.5, 0.5, sigm(x ** 2 + y ** 2))
color_4 = lambda x, y: (sigm(x ** 2 + y ** 2) / 2, 0.  5, 1 - sigm(x ** 2 + y ** 2))
colors = [color_1, color_2, color_3, color_4]
funcs = [func_1, func_2, func_3, func_4, func_5]
while True:
    col = random.choice(colors)
    func = random.choice(funcs)
    vis(random.random() * 200 + 100, func, step=0.1, c=col)
    if input() == "exit":
        break

Еще скриншоты

3.26. Комплексные числа

3.26.1. Комплексные числа в алгебраической форме

а) Определения.

• Комплексным числом называется выражение вида , в котором a и b – вещественные числа (действительные), а i — так называемая мнимая единица – число, квадрат которого считается равным минус единице: .

— вещественная часть, — мнимая часть комплексного

числа

Также пишут .

= .

б). Действия над комплексными числами в алгебраической форме

1. Степени числа .

2. Сложение, вычитание, умножение и возведение в целую положительную степень комплексных чисел можно выполнять по правилам этих действий над обычными алгебраическими выражениями, но с заменой степеней числа .

3. Деление комплексных чисел:

3.26.2. Тригонометрическая форма комплексного числа

1. Комплексное число определяется парой вещественных чисел и . Это позволяет изображать комплексные числа как точки плоскости в декартовой (прямоугольной) системе координат или радиусом-вектором этой точки .

2. Модулем комплексного числа называется длина вектора , угол называется аргументом комплексного числа.

3. Из прямоугольного треугольника OAM имеем:

,

тогда ) —

тригонометрическая форма

комплексного числа.

4. Действия над комплексными числами в тригонометрической форме

тогда .

• Деление: .

• Извлечение корня:

=

где

,

Формулы возведения в степень и извлечения корня называются формулами Муавра.

3.26.3. Показательная форма комплексного числа

.

ДЛЯ ЗАМЕТОК.

3.27. Элементарные приёмы построения

ГРАФИКОВ ФУНКЦИЙ

3.

27.1. Преобразования графиков

Исходя из графика функции , можно построить графики

функций:

1. — первоначальный график отображается симметрично оси Ох (“зеркальное отображение” ).

2. — первоначальный график сдвигается вдоль оси Ох на величину а вправо, если и влево, если .

3. — исходный график перемещается вдоль оси Оу на величину : вверх, если , и вниз, если .

4. — исходный график растягивается вдоль оси Оу в А раз (если А>1) и сжимается в раз, если .

5. — тот же график, но растянутый вдоль оси Ох от начала координат в раз.

Таким образом, используя график функции , можно построить график функции

6.

.

Примеры.

1). , 2).

Примеры. (1): ; (2): — сдвиг на 1 ед. вправо (3) : — сдвиг на 2 ед. влево

3). 4).

Примеры. (1)  :  ; (2) : — сдвиг на 2 ед. вверх ; (3) : — сдвиг на 1 ед. вниз.

Примеры. (1) :  ; (2) :  — растяжение в 3 раза вдоль оси Оу;  (3): — сжатие в 2 раза.

5).

Примеры. (1): ; (2): — сжатие в два раза к началу координат вдоль оси Ох; (3): — растяжение в два раза от начала координат вдоль оси Ох.

6).

Пример. +1 Приведём к виду: . Строим цепочку графиков в следующей последовательности: ; — сжатие в 2 раза ; -сдвиг на 2 ед. вправо вдоль оси Ох; -растяжение в 3 раза вдоль оси Оу;  -зеркальное отображение относительно оси Ох 6. — график построен.

Исследовательская работа «Различные способы решения кубических уравнений. Роль комплексных чисел при решении уравнений» • Наука и образование ONLINE

Главная Работы на конкурс Предметное образование Физико-математические дисциплины Исследовательская работа «Различные способы решения кубических уравнений. Роль комплексных чисел при решении уравнений»

Автор: Волкова Ларина Владимировна

Место работы/учебы (аффилиация): МОУ СОШ № 2, ст.Григорополсская, Ставропольский край, 10 класс

Научный руководитель: Колбасова Лариса Александровна

Математическое образование, получаемое в общеобразовательной школе, является важнейшим компонентом общего образования и общей культуры современного человека. Практически все, что окружает современного человека – это все так или иначе связано с математикой. А последние достижения в физике, технике и информационных технологиях не оставляют никакого сомнения, что и в будущем положение вещей останется прежним. Поэтому решение многих практических задач сводится к решению различных видов уравнений, которые необходимо научиться решать.

Цель исследования: изучить различные способы решения кубических уравнений и понятие комплексного числа.

Объект исследования: кубические уравнения.

Задачи исследования:

1. Изучить различные способы решения кубических уравнений.
2. Изучить теорию комплексных чисел.
3. Применение изученного материала на практике:

• разложение многочлена на множители;
• решение кубических и  квадратных уравнений;
• исследование функций и построение графиков.

Данная работа является попыткой обобщить и систематизировать изученный материал по решению кубических уравнений. Хотя уравнения высоких степеней в общем случае неразрешимы в радикалах, да и формулы Кардано  для уравнений третьей и четвертой степеней в школе не проходят.  но уже планируется включение в КИМ ЕГЭ математики профильного уровня задания с комплексными числами, а с ними мы сталкиваемся когда  при решении уравнений невозможно  ограничиваться только действительным решением, считаю, что иначе  решение уравнения просто не законченно. Ведь если в уравнении нет действительных корней, то это еще не значит, что оно не имеет решений. Квадратные корни из отрицательных чисел- мнимые или комплексные числа,  неизбежно возникают при решении кубического уравнения по способу Кардано, даже если такое уравнение имеет три действительных корня.

Загрузка…

Физико-математические дисциплины

Исследовательская работа «Создание домашнего термоса»

Доступна к просмотру полнотекстовая версия работы

Я люблю смотреть познавательную программу «Галилео». В ней рассказывают о различных явлениях, окружающих человека, научных фактах, технике. В одной из передач говорили про такой предмет, как термос. И здесь я узнал, что его можно применять не только…

Посмотреть работу

Физико-математические дисциплины

Исследовательская работа по математике «Финансовая математика. Вклады»

Доступна к просмотру полнотекстовая версия работы

В современном мире люди проводят миллионы банковских операций. С развитием технологий можно управлять своими средствами через гаджеты, стали возможны переводы средств другому человеку/организации и т.д., Online инвестиции, вклады, расчеты пенсии. Воз…

Посмотреть работу

Физико-математические дисциплины

Исследовательская работа «Компьютерные вирусы и борьба с ними»

В настоящее время компьютер прочно вошел в повседневную жизнь. Его возможности используются в школе, на работе, при проведении досуга, в быту и других сферах жизни человека. Несмотря на принятые во многих странах законы о борьбе с компьютерными прест…

Посмотреть работу

Технические дисциплины, Физико-математические дисциплины

Исследовательская работа «Три телефона, созданные в домашних условиях»

Летние каникулы я провела у бабушки и дедушки. Мое внимание привлек их домашний телефон. Он был с необычной трубкой и диском. Такого я еще никогда не видела. У нас дома тоже есть домашний телефон. Он немного похож на мобильный, с ним можно легко пере…

Посмотреть работу

Физико-математические дисциплины

Исследовательская работа «Влияют ли числа на судьбу человека»

Доступна к просмотру полнотекстовая версия работы

Мир нас восхищает многообразием, как мы с вами постоянно говорим, различных загадок. Мало кто знает, что пароль к загадкам вселенной — это числа. Разумеется, ученые в глубочайшей древности увидели связь личности и числа. Конечно же, все мы знаем, что…

Посмотреть работу

Мероприятие завершено

3.1: Комплексные числа — Математика LibreTexts

1. Последнее обновление

2. Сохранить как PDF

Идентификатор страницы

17359

• OpenStax
• OpenStax

Навыки для развития

• Выразите квадратные корни отрицательных чисел как кратные \(i\).
• Нанесение комплексных чисел на комплексную плоскость.
• Сложение и вычитание комплексных чисел.
• Умножать и делить комплексные числа.

Изучение математики постоянно саморазвивается. Отрицательные целые числа, например, заполняют пустоту, оставленную набором положительных целых чисел. Множество рациональных чисел, в свою очередь, заполняет пустоту, оставленную множеством целых чисел. Множество действительных чисел заполняет пустоту, оставленную множеством рациональных чисел. Неудивительно, что множество действительных чисел также имеет пустоты. Например, у нас до сих пор нет решения таких уравнений, как 92+4=0\не число\]

Нашим лучшим предположением может быть \(x=+2\) или \(x=–2\). Но если мы проверим +2 в этом уравнении, это не сработает. Если мы проверим -2, это не сработает. Если мы хотим получить решение этого уравнения, нам придется пойти дальше, чем мы до сих пор. В конце концов, до сих пор мы описывали квадратный корень из отрицательного числа как неопределенный. К счастью, есть другая система чисел, которая обеспечивает решение подобных проблем. В этом разделе мы рассмотрим эту систему счисления и то, как в ней работать.

Выражение квадратных корней из отрицательных чисел в виде кратных

\(i\)

Мы знаем, как найти квадратный корень из любого положительного действительного числа. Аналогичным образом мы можем найти квадратный корень из отрицательного числа. Отличие в том, что рут не настоящий. Если значение подкоренного числа отрицательное, корень называется мнимым числом. Мнимое число \(i\) определяется как квадратный корень из \(-1\).

\[\sqrt{-1}=i\nonumber\]

Итак, используя свойства радикалов, 92=−1\nonumber\]

Мы можем записать квадратный корень любого отрицательного числа как кратное \(i\). Возьмем квадратный корень из –25.

\[\begin{align} \sqrt{-25}&=\sqrt{25 {\cdot} (-1)}\nonumber\\ &=\sqrt{25}\sqrt{-1} \nonumber\ \ &= 5i\nonumber \end{align}\nonumber\]

Мы используем 5 i , а не −5 i , потому что главный корень из 25 является положительным корнем.

Комплексное число представляет собой сумму действительного числа и мнимого числа. Комплексное число выражается в стандартной форме при записи \(a+bi\) (с \(a, b\) действительными числами), где \(a\) — действительная часть, а \(bi\) — мнимая часть. Например, \(5+2i\) — комплексное число. То же самое и с \(3+4\sqrt{3}i\).

Примечание: поскольку очень легко ошибиться, думая, что \(i\) в конце числа находится под знаком корня, это число принято записывать как \(3+4i\sqrt{ 3}\). Кроме того, как обычно, если член равен 0 или коэффициент равен 1, мы часто его опускаем; поэтому \(0+1i\) (правильная стандартная форма) часто записывается просто как \(i\).

Рисунок \(\PageIndex{1}\)

Мнимые числа отличаются от действительных, поскольку возведение в квадрат мнимого числа дает отрицательное действительное число. Вспомните, когда возводится в квадрат положительное действительное число, результатом является положительное действительное число, а когда возводится в квадрат отрицательное действительное число, снова получается положительное действительное число. Комплексные числа представляют собой комбинацию действительных и мнимых чисел.

Определение: мнимые и комплексные числа

Комплексное число — это число вида \(a+bi\), где

• \(a\) — действительная часть комплексного числа.
• \(bi\) — мнимая часть комплексного числа.

Если \(b=0\), то \(a+bi\) — действительное число. Если \(a=0\) и \(b\) не равно 0, комплексное число называется мнимым числом . Мнимое число – это четный корень из отрицательного числа.

Дано мнимое число, представить его в стандартной форме

1. Запишите \(\sqrt{-a}\) как \(\sqrt{a}\sqrt{-1}\).
2. Выразите \(\sqrt{−1}\) как \(i\) .
3. Напишите \(\sqrt{a}{\cdot}i\) в простейшей форме.

Пример \(\PageIndex{1}\): Выражение мнимого числа в стандартной форме

Выражение \(\sqrt{−9}\) в стандартной форме.

Решение

\[\sqrt{−9}=\sqrt{9}\sqrt{−1}=3i\nonnumber\]

В стандартной форме это \(0+3i\).

\(\PageIndex{1}\)

Экспресс \(\sqrt{−24}\) в стандартной форме.

Ответить

\(\sqrt{−24}=0+2i\sqrt{6}\)

Нанесение комплексного числа на комплексную плоскость

Мы не можем наносить на числовую прямую комплексные числа, как настоящие числа. Однако мы все еще можем представить их графически. Чтобы представить комплексное число, нам нужно обратиться к двум компонентам числа. Мы используем комплексную плоскость, которая представляет собой систему координат, в которой горизонтальная ось представляет действительную составляющую, а вертикальная ось представляет мнимую составляющую. Комплексные числа — это точки на плоскости, выраженные в виде упорядоченных пар \((a,b)\), где \(a\) представляет собой координату по горизонтальной оси, а \(b\) представляет собой координату по вертикальной оси.

Рассмотрим число \(−2+3i\). Действительная часть комплексного числа равна \(−2\), а мнимая часть равна \(3i\). Мы строим упорядоченную пару \((−2,3)\) для представления комплексного числа \(−2+3i\), как показано на рисунке \(\PageIndex{2}\)

Рисунок \( \PageIndex{2}\): График комплексного числа, \(-2 + 3i\). Обратите внимание, что действительная часть \((-2)\) откладывается по оси \(x\), а мнимая часть \((3i)\) — по оси \(y\).

Сложная плоскость

На комплексной плоскости горизонтальная ось является реальной осью, а вертикальная ось — мнимой осью, как показано на рисунке \(\PageIndex{3}\).

Рисунок \(\PageIndex{3}\): Комплексная плоскость, показывающая, что горизонтальная ось (в реальной плоскости ось \(x\)) известна как действительная ось, а вертикальная ось (в реальной плоскости ось \(y\)) известна как воображаемая ось.

Для заданного комплексного числа представить его компоненты на комплексной плоскости.

1. Определите действительную и мнимую части комплексного числа.
2. Перемещайтесь по горизонтальной оси, чтобы показать действительную часть числа.
3. Перемещение параллельно вертикальной оси для отображения мнимой части числа.
4. Нанесите точку.

Пример \(\PageIndex{2}\): построение комплексного числа на комплексной плоскости

Нанесение комплексного числа \(3−4i\) на комплексную плоскость.

Решение

Действительная часть комплексного числа равна 3, а мнимая часть равна \(−4i\). Наносим упорядоченную пару \((3,−4)\), как показано на рисунке \(\PageIndex{4}\).

Рисунок \(\PageIndex{4}\): График комплексного числа, \(3 — 4i\). Обратите внимание, что действительная часть \((3)\) отложена по оси x, а мнимая часть \((-4i)\) отложена по оси y.

\(\PageIndex{2}\)

Постройте комплексное число \(−4−i\) на комплексной плоскости.

Ответить

Рисунок \(\PageIndex{5}\)

Сложение и вычитание комплексных чисел

Как и с действительными числами, мы можем выполнять арифметические операции над комплексными числами. Чтобы сложить или вычесть комплексные числа, мы объединяем действительные части и объединяем мнимые части.

Комплексные числа: сложение и вычитание

Сложение комплексных чисел:

\[(a+bi)+(c+di)=(a+c)+(b+d)i\nonumber\]

Вычитание комплексных чисел:

\[(a+bi)−(c+ di)=(a−c)+(b−d)i\nonumber\]

Даны два комплексных числа, найдите их сумму или разность.

1. Определите действительную и мнимую части каждого числа.
2. Добавить или вычесть действительные части.
3. Сложите или вычтите мнимые части.

Пример \(\PageIndex{3}\): добавление комплексных чисел

Добавьте \(3−4i\) и \(2+5i\).

Решение

Складываем действительные части и складываем мнимые части.

\[\begin{align} (a+bi)+(c+di)&=(a+c)+(b+d)i \nonumber\\ (3−4i)+(2+5i)& =(3+2)+(−4+5)i \не число\\ &=5+i \не число\конец{выравнивание}\не число\]

\(\PageIndex{3}\)

Вычесть \( 2+5i\) из \(3–4i\).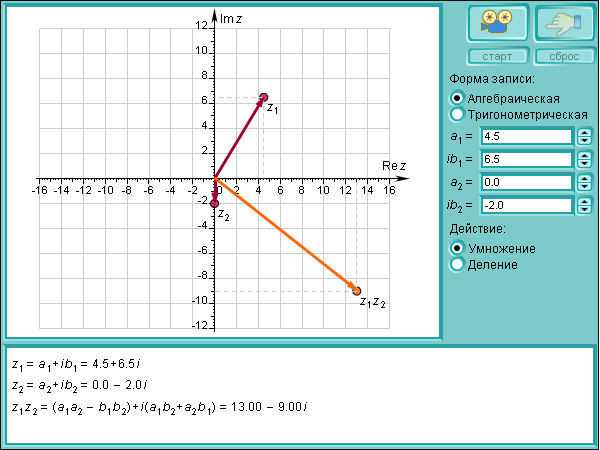 2\) как \(-1\).

Умножение комплексного числа на вещественное число

Начнем с умножения комплексного числа на действительное число. Мы распределяем действительное число так же, как и биномиальное. Так, например,

Рисунок \(\PageIndex{6}\)

Учитывая комплексное число и действительное число, умножьте его, чтобы найти произведение.

1. Используйте свойство дистрибутива.
2. Упростить.

Пример \(\PageIndex{4}\): умножение комплексного числа на вещественное число

Найдите произведение \(4(2+5i).\)

Решение

Распределите 4.

\ [\begin{align} 4(2+5i)&=(4⋅2)+(4⋅5i) \nonumber\\ &=8+20i \nonumber\end{align}\nonumber\]

\(\ PageIndex{4}\)

Найдите произведение \(−4(2+6i)\).

Ответить

\(−8−24i\)

Умножение комплексных чисел 92\номер\\ &=(8+15)+(-20+6)i \неномер\\ &=23-14i \неномер\конец{выравнивание}\неномер\]

\(\PageIndex{5}\ )

Умножить \((3−4i)(2+3i)\).

Ответить

\(18+я\)

Деление комплексных чисел

Деление двух комплексных чисел сложнее, чем сложение, вычитание и умножение, поскольку стандартная форма комплексного числа не допускает мнимого числа в знаменателе. «Деление» комплексных чисел превращается в задачу переписать дробь так, чтобы результат был в стандартной форме. Нам нужен член, на который мы можем умножить числитель и знаменатель, который исключит мнимую часть знаменателя. Этот термин называется комплексное сопряжение знаменателя, которое находится при изменении знака мнимой части комплексного числа. Другими словами, комплексное сопряжение \(a+bi\) равно \(a−bi\).

Определение: комплексное сопряжение

Комплексное сопряжение комплексного числа \(a+bi\) равно \(a−bi\). Его находят изменением знака мнимой части комплексного числа. Действительная часть числа остается неизменной.

• Когда комплексное число умножается на его комплексно-сопряженное, результатом является действительное число: \((a+bi)(a-bi)=a^2+b^2\).
• Когда комплексное число добавляется к его комплексно-сопряженному, результатом является действительное число: \((a+bi) +(a-bi)=2a\).

Обратите внимание, что комплексно-сопряженные числа имеют обратную связь: комплексно-сопряженное число \(a+bi\) равно \(a−bi\), а комплексно-сопряженное число \(a−bi\) равно \(a+bi\ ). Примечание: как мы увидим в разделе 3.2, когда квадратное уравнение с действительными коэффициентами имеет комплексные решения, решения всегда комплексно сопряжены друг другу.

Предположим, мы хотим разделить \(c+di\) на \(a+bi\), где ни a, ни \(b\) не равны нулю. Сначала запишем деление в виде дроби, затем найдем комплексно-сопряженную часть знаменателя и умножим. 92}\nonumber\]

 

Пример \(\PageIndex{6}\): Поиск комплексно-сопряженных чисел

Найдите комплексно-сопряженное число каждого числа.

1. \(2+i\sqrt{5}\)
2. \(−\frac{1}{2}i\)

Раствор

а. Число уже находится в форме \(a+bi\). Комплексное сопряжение равно \(a−bi\) или \(2−i\sqrt{5}\).
б. Перепишите это число в виде \(a+bi\), чтобы получить \(0−\frac{1}{2}i\). Комплексное сопряжение равно \(a−bi\) или \(0-(-\frac{1}{2}i)\), что упрощается до \(0+\frac{1}{2}i\) . Обычно это записывается просто как \(\frac{1}{2}i\).

Даны два комплексных числа, разделите одно на другое.

1. Запишите задачу деления в виде дроби.
2. Определите комплексное сопряжение знаменателя.
3. Умножить числитель и знаменатель дроби на комплексное сопряжение знаменателя.
4. Упростить.

Пример \(\PageIndex{7}\): деление комплексных чисел

Разделите \((2+5i)\) на \((4−i)\).

Решение

Начнем с записи задачи в виде дроби.

\[\dfrac{(2+5i)}{(4−i)}\nonumber\]

Умножаем числитель и знаменатель на комплексное сопряжение знаменателя.

\[\dfrac{(2+5i)}{(4−i)}{\cdot}\dfrac{(4+i)}{(4+i)}\nonumber\]

Чтобы умножить два сложных чисел, мы расширяем произведение, как если бы мы использовали биномы (процесс, обычно называемый FOIL). 2=-1$}\\ &=\dfrac{3+22i}{17} \\ &=\dfrac{3}{17}+\dfrac{22} {17}i & & \text{Разделить действительную и мнимую части.} \end{align*}\]

Обратите внимание, что это выражает частное в стандартной форме.

Дополнительный кредит : Мы умножаем исходную дробь на \(\frac{4+i}{4+i}\). (a) Каково значение \(\frac{4+i}{4+i}\)? (b) Объясните важность этого значения в процессе деления комплексных чисел. Запишите это и передайте своему инструктору для получения дополнительных баллов.

Пример \(\PageIndex{8}\): подстановка комплексного числа в полиномиальную функцию 92−3x\). Вычислите \(f(8−i)\).

Ответить

\(102−29i\)

Пример \(\PageIndex{9}\): замена мнимого числа в рациональной функции

Пусть \(f(x)=\frac{2+x}{x+3}\). Вычислите \(f(10i)\).

Решение

Подставьте \(x=10i\) и упростите. 2}{92$.}\\[5pt] &\dfrac{106+10i}{109} & & \text{Упростить.}\\[5pt] &\dfrac{106}{109}+\dfrac{10}{109 } & & \text{Разделите действительную и мнимую части.} \end{align*}\]

\(\PageIndex{7}\)

Пусть \(f(x)=\frac{x+1} {х−4}\). Вычислите \(f(−i)\).

Ответить

\(−\frac{3}{17}+\frac{5i}{17}\)

Упрощающие степени \(i\)

Степени \(i\) цикличны. Давайте посмотрим, что произойдет, если мы поднимем 9.{19}\)

Ключевые понятия

• Квадратный корень из любого отрицательного числа может быть записан как кратное \(i\).
• Чтобы построить комплексное число, мы используем две числовые линии, которые пересекаются, образуя комплексную плоскость. Горизонтальная ось — это реальная ось, а вертикальная ось — воображаемая ось.
• Комплексные числа можно складывать и вычитать, комбинируя действительные части и комбинируя мнимые части.
• Комплексные числа можно умножать и делить.
• Чтобы умножить комплексные числа, распределите так же, как и многочлены.
• Чтобы разделить комплексные числа, умножьте и числитель, и знаменатель на комплексное сопряжение знаменателя, чтобы исключить комплексное число из знаменателя.
• Степени \(i\) цикличны, повторяя каждую четвертую.

Глоссарий

комплексное сопряжение
комплексное число, в котором знак мнимой части изменен, а действительная часть числа оставлена ​​без изменений; при добавлении или умножении на исходное комплексное число результатом является действительное число

комплексное число
сумма действительного и мнимого чисел, записанная в стандартной форме
\(a+bi\) (\(a,b \in \mathbb{R}\)),
где \(a\) — действительная часть, а \(bi\) — мнимая часть

комплексная плоскость
система координат, в которой горизонтальная ось используется для представления действительной части комплексного числа, а вертикальная ось используется для представления мнимой части комплексного числа

мнимого числа
число в форме \(bi\), где \(i=\sqrt{−1}\)

Авторы

---

Эта страница под названием 3.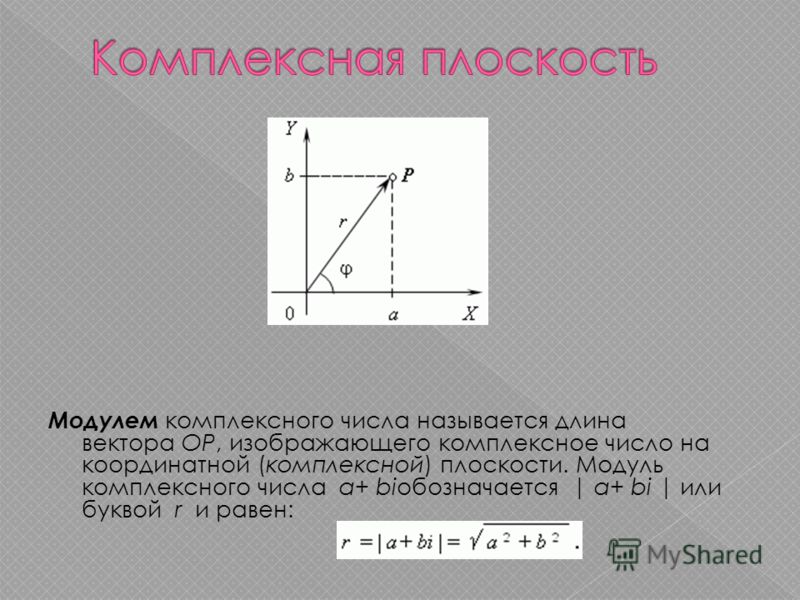 1: Комплексные числа распространяется под лицензией CC BY-NC-SA 4.0 и была создана, изменена и/или курирована OpenStax.

1. Наверх
• Была ли эта статья полезной?

1. Тип изделия

   Раздел или Страница

   Автор

   ОпенСтакс

   Лицензия

   CC BY-NC-SA

   Версия лицензии

   4,0

   Показать страницу TOC

   да

   Включено

   да

2. Теги

   1. расчет: да
   2. комплексно-сопряженный
   3. комплексный номер
   4. сложный самолет
   5. Воображаемое число
   6. воображаемая единица

python — Как строить комплексные числа (диаграмма Арганда) с использованием matplotlib

Вопрос задан 9 лет, 3 месяца назад

Изменено 2 года, 11 месяцев назад

Просмотрено 71k раз

21

Новинка! Сохраняйте вопросы или ответы и организуйте свой любимый контент.
Узнать больше.

Я хочу создать диаграмму Арганда из набора комплексных чисел, используя matplotlib.

_{Изображение LeonardoG, CC-SA-3.0}

• python
• numpy
• matplotlib
• plot
• комплексные числа

Я не совсем уверен, что вы здесь ищете… у вас есть набор комплексных чисел, и вы хотите отобразить их на плоскости, используя их действительную часть как x координата и мнимая часть как y?

Если это так, вы можете получить реальную часть любого мнимого числа Python с number.real и мнимую часть с number.imag . Если вы используете numpy, он также предоставляет набор вспомогательных функций numpy.real и numpy.imag и т. д., которые работают с массивами numpy.

Например, если у вас есть массив комплексных чисел, хранящийся примерно так:

 В [13]: a = n.arange(5) + 1j*n.arange(6,11)
В [14]: а
Out[14]: array([ 0. +6.j, 1. +7.j, 2. +8.j, 3. +9. j, 4.+10.j])
 

…вы можете просто сделать

 В [15]: fig,ax = subplots()
В [16]: ax.scatter(a.real,a.imag)
 

Отображает точки на диаграмме Аргана для каждой точки.

редактирование: для части построения графика вы, конечно, должны импортировать matplotlib.pyplot через из matplotlib.pyplot import * или (как я сделал) использовать оболочку ipython в режиме pylab.

1

Чтобы продолжить ответ @inclement; следующая функция создает график Аргана, который центрируется вокруг 0,0 и масштабируется до максимального абсолютного значения в наборе комплексных чисел.

Я использовал функцию построения графика и указал сплошные линии от (0,0). Их можно удалить, заменив ro- на ro .

 по аргану(а):
    импортировать matplotlib.pyplot как plt
    импортировать numpy как np
    для x в диапазоне (len (a)):
        plt.plot([0,a[x].real],[0,a[x].imag],'ro-',label='python')
    limit=np. max(np.ceil(np.absolute(a))) # установить ограничения для оси
    plt.xlim((-лимит,лимит))
    plt.ylim((-лимит,лимит))
    plt.ylabel('Воображаемый')
    plt.xlabel('Настоящий')
    plt.show()
 

Например:

 >>> a = n.arange(5) + 1j*n.arange(6,11)
>>> из аргана импортировать арган
>>> арган(а)
 

производит:

РЕДАКТИРОВАТЬ:

Я только что понял, что есть также функция графика полярных :

 для x в a:
    plt.polar([0,угол(х)],[0,абс(х)],маркер='o')
 

2

Если вы предпочитаете график, подобный приведенному ниже

один тип графика

или этот односекундный график

вы можете сделать это просто с помощью этих двух строк (в качестве примера для графиков выше):

 z=[20+10j,15,-10-10j,5+15j] # массив комплексных значений
complex_plane2(z,1) # вызываемая функция
 

с помощью простого кода jupyter отсюда https://github. com/osnove/other/blob/master/complex_plane.py

Я написал это для своих целей. Еще лучше, если это поможет другим.

 импортировать matplotlib.pyplot как plt
из импорта numpy *
'''
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~`
Это рисует ось для диаграммы Аргана
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~`
'''
р = 1
Y = [r*exp(1j*theta) для тета в linspace(0,2*pi, 200)]
Y = массив (Y)
plt.plot (реальный (Y), образ (Y), 'r')
plt.ylabel('Воображаемый')
plt.xlabel('Настоящий')
plt.axhline(y=0,color='черный')
plt.axvline(x=0, цвет='черный')
деф арганд (complex_number):
    '''
    Эта функция принимает комплексное число.
    '''
    у = комплексное_число
    x1,y1 = [0,вещественное(y)], [0, imag(y)]
    x2,y2 = [действительное (y), действительное (y)], [0, imag (y)]
    plt.plot(x1,y1, 'r') # Рисуем гипотенузу
    plt.plot(x2,y2, 'r') # Рисуем проекцию на действительную ось
    plt.plot (реальный (у), образ (у), 'бо')
[argand(r*exp(1j*theta)) для тета в linspace(0,2*pi,100)]
plt.show()
 

https://github. com/QuantumNovice/Matplotlib-Argand-Diagram/blob/master/argand.py

Зарегистрируйтесь или войдите в систему

Зарегистрируйтесь с помощью Google

Зарегистрироваться через Facebook

Зарегистрируйтесь, используя электронную почту и пароль

Опубликовать как гость

Электронная почта

Обязательно, но не отображается

Опубликовать как гость

Электронная почта

Требуется, но не отображается

комплексная плоскость, сложение и вычитание

Комплексные числа: комплексная плоскость, сложение и вычитание Поскольку Гаусс доказал основную теорему алгебры, мы знаем, что все комплексные числа имеют вид x  +  yi, , где x и y — действительные числа, действительные числа — все те числа, которые являются положительными, отрицательными или нулевыми. Следовательно, мы можем использовать плоскость xy для отображения комплексных чисел. Мы даже назовем ее комплексной плоскостью , когда используем таким образом плоскость xy . Это дает нам второй путь к комплексным числам, первый путь — алгебраический, как в выражении x  +  yi.

Обозначение.

Стандартный символ для набора всех комплексных чисел — C , и мы также будем обозначать комплексную плоскость как C .

Мы попробуем использовать x и y для вещественных переменных и z и z для комплексных переменных. Например, уравнение z  =  x  +  yi следует понимать как говорящее, что комплексное число z — это сумма действительного числа x и действительного числа y , умноженного на i. In general, the x part of a complex number z  =  x  +  yi is called the real part of z , while y is called the imaginary part of z . (Иногда и называют мнимой частью.)

Когда мы используем xy -плоскость для комплексной плоскости C , мы будем называть ось x реальной осью , и ось y мы будем называть мнимой осью.

Вещественные числа следует рассматривать как частные случаи комплексных чисел; это просто цифры x  +  yi , когда y равно 0, то есть это числа на действительной оси. Например, действительное число 2 равно 2 + 0 , т.е. Числа на мнимой оси иногда называют чисто мнимые числа.

Арифметические операции над

C Операции сложения и вычитания понятны. Чтобы сложить или вычесть два комплексных числа, просто сложите или вычтите соответствующие действительные и мнимые части. Например, сумма 5 + 3 i и 4 + 2 i равна 9 + 5 i. Во-вторых, сумма 3 +  i и 1 + 2 i равна 2 + 3 i.

Дополнение может быть представлено графически на комплексной плоскости C . Возьмем последний пример. Комплексное число z  = 3 +  i расположено на 3 единицы правее мнимой оси и на 1 единицу выше действительной оси, а w  = 1 + 2 i расположено на 1 единицу левее и 2 единиц вверх. Таким образом, сумма z + w  = 2 + 3 i равна 2 единицам вправо и 3 единицам вверх.

Правило параллелограмма.

Обратите внимание, что в последнем примере четыре комплексных числа 0, z  = 3 +  i, w  = 1 + 2 i, и z  +  w i 3 = 908 8 равны углы параллелограмма. В целом это правда. Чтобы найти, где в плоскости C находится сумма z  +  w двух комплексных чисел z и w , начертите z и w, линии от 0 до каждого из них, и завершите параллелограмм. Четвертая вершина будет z  +  w.

Дополнение в виде перевода.

Используя правило параллелограмма, можно интерпретировать сложение w как преобразование плоскости C . Добавление w к 0 дает w, конечно, , поэтому в этом преобразовании 0 перемещается в w . Любая другая точка z перемещается в z  +  w, , поэтому z перемещается в том же направлении на то же расстояние. Другими словами, каждая точка в C перемещается в том же направлении и на то же расстояние, когда к нему добавляется w . Можно сказать, что сложение w дает перевод плоскости C в направлении и на расстояние от 0 до w. Термин «вектор» обычно используется в описании: «плоскость переводится по вектору 0 w.

Отрицание и вычитание.

Есть и хорошая геометрическая интерпретация отрицания. Конечно, отрицание x  +  yi равно x    yi, , поэтому отрицание комплексного числа будет располагаться как раз напротив 0 и на таком же расстоянии от него. Например, z  = 2 +  i расположено на 2 единицы вправо и на одну единицу вверх, поэтому его отрицание z  = 2   i расположено на 2 единицы влево и на одну единицу вниз.

No related posts.