Свойства средней линии треугольника — онлайн справочник для студентов
ОПРЕДЕЛЕНИЕ
Средняя линия треугольника — это сегмент, соединяющий середины двух сторон.
Свойства треугольника треугольника
Средняя линия треугольника параллельна одной стороне и равна половине ее. Например, на картинке
\(\ K N \| A C \), \(\ K N=\frac{1}{2} A C \)
В любом треугольнике есть три средние линии, на пересечении которых образуются 4 равных треугольника, аналогичные исходным с коэффициентом 1/2.
Средняя линия обрезает треугольник, который похож на этот, и его площадь равна одной четверти исходного треугольника.
Примеры решения проблем
ПРИМЕР 1
В треугольнике \(\ A B C \) со сторонами \(\ A B=5 \mathrm{см} \), \(\ B=7 \mathrm{см} \) и \(\ A C=8 \mathrm{см} \), были вычерчены средние линии \(\ \mathrm{KN} \), \(\ \mathrm{NL} \) и \(\ \mathrm{KL} \). Найдите периметр треугольника \(\ \mathrm{KNL} \).

Поскольку средняя линия равна половине стороны, в которой она параллельна, мы можем найти длины всех средних линий:
\(\ K N=\frac{1}{2} A C=4 \mathrm{см} \), \(\ N L=\frac{1}{2} A B=2,5 \mathrm{см} \), \(\ K L=\frac{1}{2}=3,5 \mathrm{cm} \)
Теперь вы можете найти периметр треугольника \(\ \mathrm{KNL} \) как сумму длин всех его сторон:
\(\ P_{K N L}=K N+N L+K L=4+2,5+3,5=10 \mathrm{см} \)
\(\ P_{K N L}=10 \)
ПРИМЕР 2
В треугольнике \(\ A B C \) со стороной \(\ A C=7 \mathrm{см} \) и высотой \(\ \mathrm{BK}=4 \mathrm{см} \) центральная линия \(\ \mathrm{MN} \) была проведена параллельно стороне \(\ \mathrm{AC} \). Найдите область треугольника \(\ \mathrm{MBN} \).
Средняя линия \(\ \mathrm{MN} \) разрезает треугольник \(\ \mathrm{MBN} \), площадь которого равна одной четверти исходного треугольника \(\ \mathrm{ABC} \). Найдите область треугольника \(\ \mathrm{ABC} \):
\(\ S_{A B C}=\frac{1}{2} A C \cdot B K=\frac{1}{2} 7 \cdot 4=14 \mathrm{cm}^{2} \)
Тогда площадь треугольника \(\ \mathrm{MBN} \) равна:
\(\ S_{M B N}=\frac{1}{4} S_{A B C}=\frac{1}{4} \cdot 14=3,5 \mathrm{cm}^{2} \)
\(\ S_{M B N}=3,5 \)
Физика
166
Реклама и PR
31
Педагогика
80
Психология
72
Социология
7
Астрономия
9
Биология
30
Культурология
86
Экология
8
Право и юриспруденция
36
Политология
13
Экономика
49
Финансы
9
История
16
Философия
8
Информатика
20
Право
35
Информационные технологии
6
Экономическая теория
7
Менеджент
719
Математика
338
Химия
20
Микро- и макроэкономика
1
Медицина
5
Государственное и муниципальное управление
2
География
542
Информационная безопасность
2
Аудит
11
Безопасность жизнедеятельности
3
Архитектура и строительство
1
Банковское дело
1
Рынок ценных бумаг
6
Менеджмент организации
2
Маркетинг
238
Кредит
3
Инвестиции
2
Журналистика
1
Конфликтология
15
Этика
9
Формулы дифференцирования Свойства высоты треугольника Свойства медианы треугольника Свойства биссектрисы треугольника Свойства прямоугольного треугольника
Узнать цену работы
Узнай цену
своей работы
Имя
Выбрать тип работыЧасть дипломаДипломнаяКурсоваяКонтрольнаяРешение задачРефератНаучно — исследовательскаяОтчет по практикеОтветы на билетыТест/экзамен onlineМонографияЭссеДокладКомпьютерный набор текстаКомпьютерный чертежРецензияПереводРепетиторБизнес-планКонспектыПроверка качестваЭкзамен на сайтеАспирантский рефератМагистерскаяНаучная статьяНаучный трудТехническая редакция текстаЧертеж от рукиДиаграммы, таблицыПрезентация к защитеТезисный планРечь к дипломуДоработка заказа клиентаОтзыв на дипломПубликация в ВАКПубликация в ScopusДиплом MBAПовышение оригинальностиКопирайтингДругоеПодпишись на рассылку, чтобы не пропустить информацию об акциях
Средняя линия треугольника — свойства, признаки и формулы
Одним из важных понятий, с помощью которого легко решается целый класс задач по геометрии, является средняя линия треугольника.
Разберём данное понятие, рассмотрим свойства, и научимся правильно решать задачи на эту тему.
Содержание
- Определение и признаки средней линии треугольника
- Теорема о средней линии треугольника
- Доказательства
- Следствия из теоремы с доказательствами
- Следствие №1
- Следствие №2
- Свойства средней линии треугольника
- Средняя линия прямоугольного треугольника
- Пример решения задачи
Определение и признаки средней линии треугольника
Отрезок, соединяющий середины двух сторон треугольника, называется его средней линией.
Отрезок, у которого один из концов совпадает с серединой одной из сторон, другой находится на второй стороне, проведённый параллельно третьей стороне, является средней линией треугольника.
Доказательство следует из теоремы Фалеса.
Теорема о средней линии треугольника
Средняя линия треугольника параллельна основанию (третьей стороне) и равна её половине.
Существует три вида доказательств этого положения. Каждое из них базируется на одной из ключевых позиций планиметрии.
Пусть дан треугольник ABC, M – середина стороны AB, N – середина BC.
По определению, MN – средняя линия ΔABC.
Необходимо доказать, что MN II AC, MN = ½AC.
Доказательства
Первый способ
Пусть прямая MK II AC. Тогда по теореме Фалеса MK пересекает сторону BC в её середине. В этом случае отрезок MN лежит на прямой MK.
Следовательно, MN II AC.
Пусть NP II AB.
Тогда NP – средняя линия по теореме Фалеса, то есть AP = PC.
Так как AMNP – параллелограмм по определению, то AP = MN. Из этого и предыдущего утверждения следует, что длина MN равна ½AC.
Доказано.
Второй способ
Рассматриваются треугольники MBN и ABC. В них угол B является общим,
По второму признаку подобия треугольников ΔMBN ∼ ΔABC. Следовательно, углы BMN и BAC равны.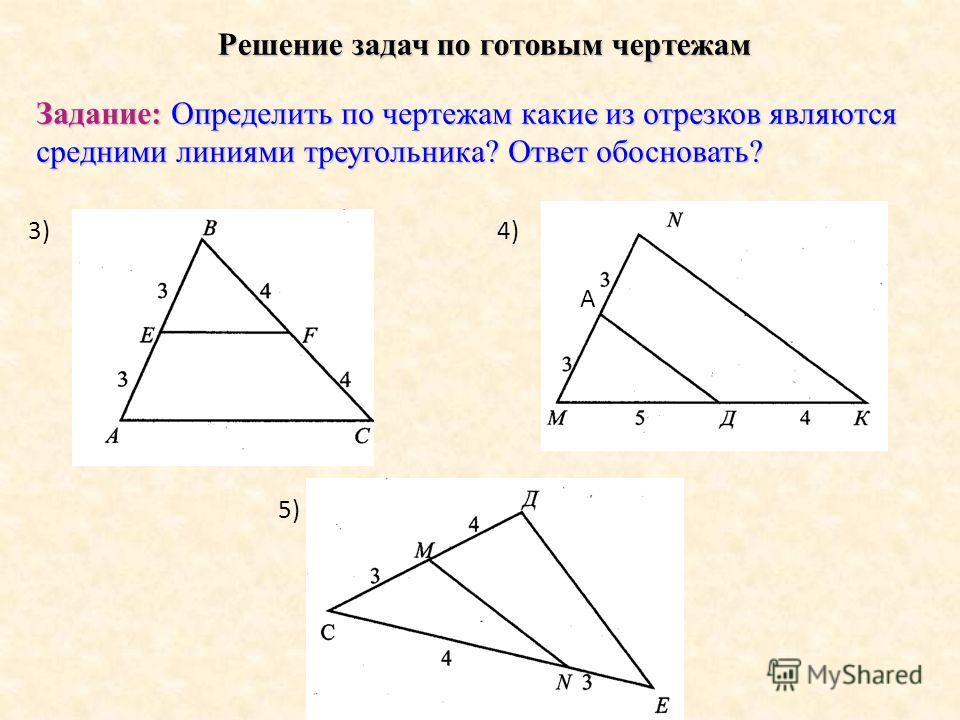
Поскольку эти углы являются соответственными, то прямые MN и AC параллельны.
Формула MN = ½AC следует из условий
поскольку пропорциональность двух пар сторон влечёт соответствующее отношение для третьей пары сторон.
Доказано.
Третий способ
Рассматривается сумма векторов
Поскольку в результате образуется замкнутая ломаная, то
Отсюда следует, что
Так как
то
Из последнего равенства следуют условия теоремы.
Доказано.
Следствия из теоремы с доказательствами
Следствие №1
Средняя линия отсекает треугольник, подобный данному, с коэффициентом подобия ½ и площадью, составляющий ¼ площади заданного треугольника.
Доказательство.
По определению стороны AB и BC делятся пополам, поэтому
Согласно теореме,
Из третьего признака подобия вытекает рассматриваемое свойство.
Поскольку площади подобных фигур относятся как квадрат коэффициента подобия, то получается вторая часть свойства, то есть площадь маленького треугольника относится к площади большого как
Доказано.
Следствие №2
Три средних линии треугольника разбивают его на четыре равных треугольника, подобные заданному, с коэффициентом подобия ½.
Доказательство.
Поскольку MN – средняя линия, то MN II AC, поэтому ∠BMN = ∠BAP, ∠BNM = ∠BCA как соответственные при MN II AC и секущей AB или BC соответственно.
Поскольку MP – средняя линия, то MP II BC, поэтому ∠MPA = ∠BCA как соответственные при MP II BC и секущей AC.
Таким образом: ∠BNM = ∠BCA = ∠MPA.
Так как MN – средняя линия, то сторона MN = ½AC, поэтому MN = AP.
Следовательно, ΔAMP = ΔMBN по второму признаку равенства треугольников.
Равенство остальных пар треугольников доказывается аналогично.
По основному свойству ΔMBN ∼ ΔABC с коэффициентом подобия ½.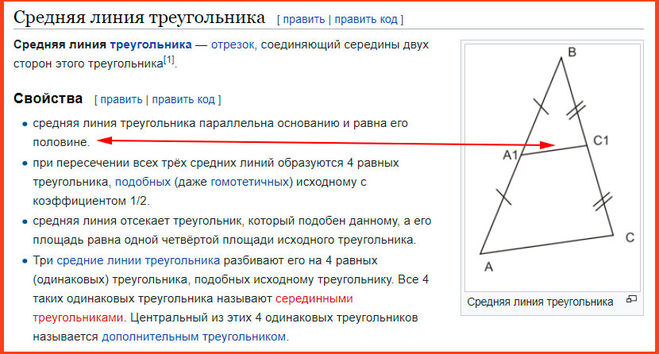 Так как все полученные маленькие треугольники равны между собой, то каждый из них, следовательно, подобен большому с тем же коэффициентом.
Так как все полученные маленькие треугольники равны между собой, то каждый из них, следовательно, подобен большому с тем же коэффициентом.
Доказано.
Свойства средней линии треугольника
Теорема и следствия из неё составляют основные свойства средней линии треугольника.
Согласно второму утверждению, вид большого треугольника такой же, как и у маленьких. То есть для равностороннего и равнобедренного треугольников средние линии отсекают равносторонние и равнобедренные треугольники.
Высоты тупоугольного треугольника, проведённые к тупому углу из вершин острых, располагаются вне треугольника. Поэтому часто рассматривают не саму среднюю линию, а её продолжение. Учитывая подобие получаемых фигур, можно утверждать, что точкой пересечения с продолжением средней линии высота делится на две равные части.
Биссектриса угла треугольника точкой пересечения со средней линией также делится пополам.
Средняя линия прямоугольного треугольника
Для прямоугольного треугольника две средние линии перпендикулярны катетам, а третья равна медиане, проведённой к гипотенузе.
Остроугольный разносторонний треугольник не имеет средних линий, обладающих подобными характеристиками.
Пример решения задачи
Доказать, что середины сторон произвольного выпуклого четырёхугольника являются вершинами параллелограмма.
Решение.
Проводя диагональ четырёхугольника, получают разбиение на два треугольника, в каждом из которых построена средняя линия, параллельная по основной теореме диагонали, как основанию.
Так как две прямые, параллельные третьей, параллельны между собой, то противолежащие стороны образованного средними линиями четырёхугольника параллельны.
Аналогично доказывается параллельность двух других сторон нового четырёхугольника. По определению четырёхугольник, полученный соединением середин сторон заданного четырёхугольника, является параллелограммом.
По определению четырёхугольник, полученный соединением середин сторон заданного четырёхугольника, является параллелограммом.
Доказано.
Предыдущая
ГеометрияПараллелепипед — определение, свойства и измерение фигуры
Следующая
ГеометрияВсе формулы прямоугольного треугольника — примеры расчетов
Средние линии геометрических фигур (стр. 1 из 2)
Гомельская научно-практическая конференция школьников по математике, ее приложениям и информационным технологиям «Поиск»
Учебно-исследовательская работа
Средние линии геометрических фигур
Ученика:
Морозовой Елизаветы
Гомель 2010
Оглавление
Введение
1.Свойства средних линий
2. Треугольник, четырехугольник, параллелограмм
Треугольник, четырехугольник, параллелограмм
3. Четырехугольник, тетраэдр. Центры масс
4. Тетраэдр, октаэдр, параллелепипед, куб
Заключение
Список использованной литературы
Приложение
Введение
Геометрия является неотъемлемой составляющей общей культуры, а геометрические методы служат инструментом познания мира, способствуют формированию научных представлений об окружающем пространстве, раскрытию гармонии и совершенства Вселенной. Геометрия начинается с треугольника. Вот уже два тысячелетия треугольник является как бы символом геометрии, но он не символ. Треугольник – атом геометрии. Треугольник неисчерпаем – постоянно открываются его новые свойства. Чтобы рассказать обо всех известных его свойствах, необходим том сравнимый по объему с томом Большой энциклопедии. Мы хотим рассказать о средних линиях геометрических фигур и их свойствах.
В нашей работе прослеживается цепочка теорем, которая охватывает весь курс геометрии. Она начинается с теоремы о средних линиях треугольника и приводит к интересным свойствам тетраэдра и других многогранников.
Средняя линия фигур — отрезок, соединяющий середины двух сторон данной фигуры.
1. Свойства средних линий
1. Свойства треугольника:
· при проведении всех трёх средних линий образуются 4 равных треугольника, подобных исходному с коэффициентом 1/2.
· средняя линия параллельна основанию треугольника и равна его половине;
· средняя линия отсекает треугольник, который подобен данному, а его площадь равна одной четверти его площади.
2. Свойства четырёхугольника:
· если в выпуклом четырехугольнике средняя линия образует равные углы с диагоналями четырехугольника, то диагонали равны.
· длина средней линии четырехугольника меньше полусуммы двух других сторон или равна ей, если эти стороны параллельны, и только в этом случае.
· середины сторон произвольного четырёхугольника — вершины параллелограмма. Его площадь равна половине площади четырехугольника, а его центр лежит на точке пересечения средних линий. Этот параллелограмм называется параллелограммом Вариньона;
· Точка пересечения средних линий четырехугольника является их общей серединой и делит пополам отрезок, соединяющий середины диагоналей.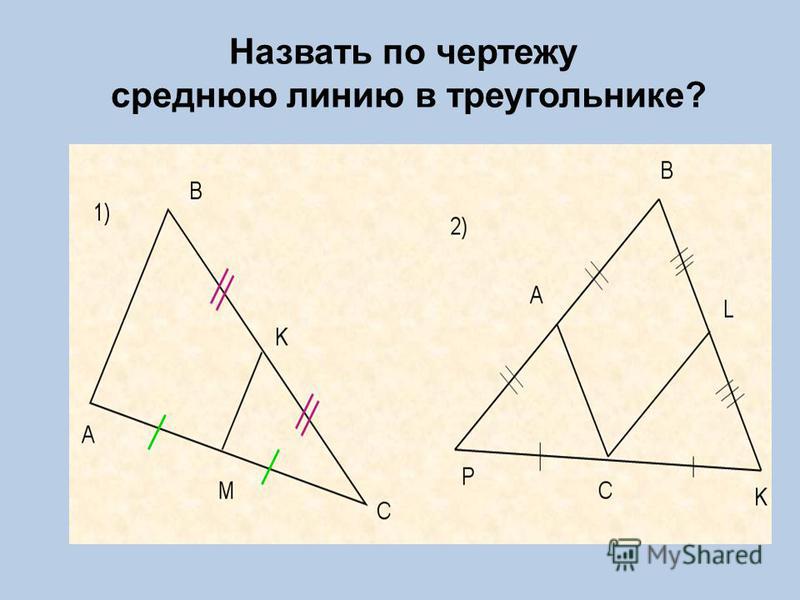 Кроме того, она является центроидом вершин четырехугольника.
Кроме того, она является центроидом вершин четырехугольника.
3. Свойства трапеции:
· средняя линия параллельна основаниям трапеции и равна их полусумме;
· середины сторон равнобедренной трапеции являются вершинами ромба.
2. Треугольник, четырехугольник, параллелограмм
К любому треугольнику KLM можно пристроить три равных ему треугольника АКМ, BLK, CLM, каждый из которых образует вместе с треугольником KLM параллелограмм (рис. 1). При этом AK = ML=KB, и к вершине К примыкают три угла, равные трем разным углам треугольника, в сумме составляющие 180°, поэтому К — середина отрезка АВ; аналогично, L — середина отрезка ВС, а М — середина отрезка СА.
Теорема 1. Если соединить в любом треугольнике середины сторон, мы получим четыре равных треугольника, причем средний составляет с каждым из трех других параллелограмм.
В этой формулировке участвуют сразу все три средние линии треугольника.
Теорема 2. Отрезок, соединяющий середины двух сторон треугольника, параллелен третьей стороне треугольника и равен ее половине (см. рис. 1).
рис. 1).
Именно эта теорема и обратная к ней — о том, что прямая, параллельная основанию и проходящая через середину одной боковой стороны треугольника, делит пополам и другую боковую сторону,— чаще всего нужны при решении задач.
Из теоремы о средних линиях треугольника вытекает свойство средней линии трапеции (рис. 2), а также теоремы об отрезках, соединяющих середины сторон произвольного четырехугольника.
Теорема 3. Середины сторон четырехугольника являются вершинами параллелограмма. Стороны этого параллелограмма параллельны диагоналям четырехугольника, а их длины равны половинам длин диагоналей.
В самом деле, если К и L — середины сторон АВ и ВС (рис. 3), то KL — средняя линия треугольника ABC, поэтому отрезок KL параллелен диагонали АС и равен ее половине; если М и N — середины сторон CD и AD, то отрезок MN также параллелен АС и равен АС/2. Таким образом, отрезки KL и MN параллельны и равны между собой, значит, четырехугольник KLMN — параллелограмм.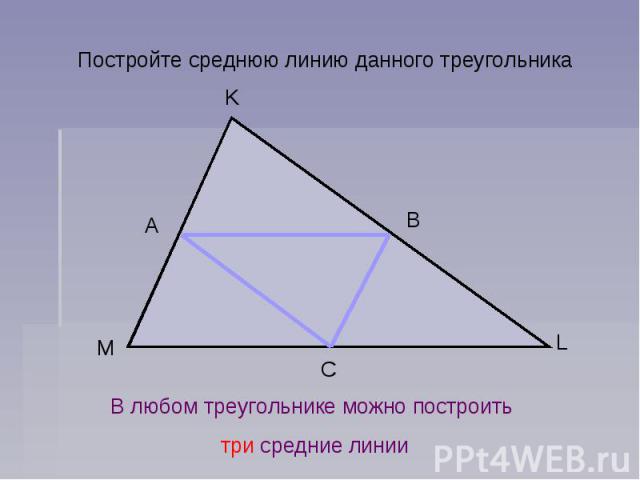
В качестве следствия из теоремы 3 получаем интересный факт (т. 4).
Теорема 4. В любом четырехугольнике отрезки, соединяющие середины противоположных сторон, делятся точкой пересечения пополам.
В этих отрезках можно увидеть диагонали параллелограмма (см. рис. 3), а в параллелограмме диагонали делятся точкой пересечения пополам (эта точка — центр симметрии параллелограмма).
Мы видим, что теоремы 3 и 4 и наши рассуждения остаются верными и для невыпуклого четырехугольника, и для самопересекающейся четырехугольной замкнутой ломаной (рис. 4; в последнем случае может оказаться, что параллелограмм KLMN «вырожденный» — точки К, L, М, N лежат на одной прямой).
Покажем, как из теорем 3 и 4 можно вывести основную теорему о медианах треугольника.
Теорема 5. Медианы треугольника пересекаются в одной точке и делятся ею в отношении 2:1 (считая от вершины, из которой проведена медиана).
Проведем две медианы AL и СК треугольника ABC. Пусть О — точка их пересечения. Середины сторон невыпуклого четырехугольника АВСО — точки К, L,MиN (рис. 5) — вершины параллелограмма, причем точкой пересечения его диагоналей КМ и LN для нашей конфигурации будет точка пересечения медиан О. Итак, AN = NO = OL и CM=MO = OK, т. е. точка О делит каждую из медиан AL и СК в отношении 2:1.
Середины сторон невыпуклого четырехугольника АВСО — точки К, L,MиN (рис. 5) — вершины параллелограмма, причем точкой пересечения его диагоналей КМ и LN для нашей конфигурации будет точка пересечения медиан О. Итак, AN = NO = OL и CM=MO = OK, т. е. точка О делит каждую из медиан AL и СК в отношении 2:1.
Вместо медианы СК мы могли бы рассмотреть медиану, проведенную из вершины В, и убедиться точно так же, что и она делит медиану AL в отношении 2:1, т. е. проходит через ту же точку О.
3.Четырехугольник и тетраэдр. Центры масс
Теоремы 3 и 4 верны и для любой пространственной замкнутой ломаной из четырех звеньев АВ, ВС, CD, DA, четыре вершины А, В, С, D которой не лежат в одной плоскости.
Такой пространственный четырехугольник можно получить, вырезав из бумаги четырехугольник ABCD и согнув его по диагонали под некоторым углом (рис. 6, а). При этом ясно, что средние линии KL и MN треугольников ABC и ADC остаются по-прежнему их средними линиями и будут параллельны отрезку АС и равны АС/2. (Здесь мы используем тот факт, что для пространства остается верным основное свойство параллельных прямых: если две прямые KL и MN параллельны третьей прямой АС, то KL и MN лежат в одной плоскости и параллельны между собой.)
(Здесь мы используем тот факт, что для пространства остается верным основное свойство параллельных прямых: если две прямые KL и MN параллельны третьей прямой АС, то KL и MN лежат в одной плоскости и параллельны между собой.)
Таким образом, точки К, L, М, N — вершины параллелограмма; тем самым отрезки КМ и LN пересекаются и делятся точкой пересечения пополам. Вместо четырехугольника здесь можно говорить о тетраэдре — треугольной пирамиде ABCD: середины К, L, М, N его ребер АВ, AC, CD и DA всегда лежат в одной плоскости. Разрезав тетраэдр по этой плоскости (рис. 6, б), мы получим параллелограмм KLMN, две стороны которого параллельны ребру АС и равны
АС/2, а две другие — параллельны ребру BD и равны BD/2.
Такой же параллелограмм — «среднее сечение» тетраэдра — можно построить и для других пар противоположных ребер. Каждые два из этих трех параллелограммов имеют общую диагональ. При этом середины диагоналей совпадают. Итак, мы получаем интересное следствие:
Теорема 6. Три отрезка, соединяющие середины противоположных ребер тетраэдра, пересекаются в одной точке и делятся ею пополам (рис. 7).
Три отрезка, соединяющие середины противоположных ребер тетраэдра, пересекаются в одной точке и делятся ею пополам (рис. 7).
Этот и другие обсуждавшиеся выше факты естественно объясняются на языке механики — с помощью понятия центра масс. В теореме 5 говорится об одной из замечательных точек треугольника — точке пересечения медиан; в теореме 6 — о замечательной точке для четверки вершин тетраэдра. Эти точки — центры масс соответственно треугольника и тетраэдра. Вернемся сначала к теореме 5 о медианах.
Поместим в вершинах треугольника три одинаковых груза (рис. 8).
Массу каждого примем за единицу. Найдем центр масс этой системы грузов.
Рассмотрим сначала два груза, находящихся в вершинах А и В: их центр масс расположен в середине отрезка АВ, так что эти грузы можно заменить одним грузом массой 2, помещенным в середину К отрезка АВ (рис. 8, а). Теперь нужно найти центр масс системы из двух грузов: одного массой 1 в точке С и второго — массой 2 в точке К. По правилу рычага, центр масс такой системы находится в точке О, делящей отрезок СК в отношении 2:1 (ближе к грузу в точке К с большей массой — рис. 8, б).
8, б).
Мы могли сначала объединить грузы в точках В и С, а затем — полученный груз массой 2 в середине L отрезка ВС — с грузом в точке А. Или сначала объединить грузы А и С, а. затем присоединить В. В любом случае мы должны получить тот же результат. Центр масс находится, таким образом, в точке О, делящей каждую из медиан в отношении 2:1, считая от вершины. Подобными соображениями можно было объяснить и теорему 4 — тот факт, что отрезки, соединяющие середины противоположных сторон четырехугольника, делят друг друга пополам (служат диагоналями параллелограмма): достаточно поместить в вершинах четырехугольника одинаковые грузы и объединить их попарно двумя способами (рис. 9).
Треугольник срединного сегмента
Треугольник срединного сегмента
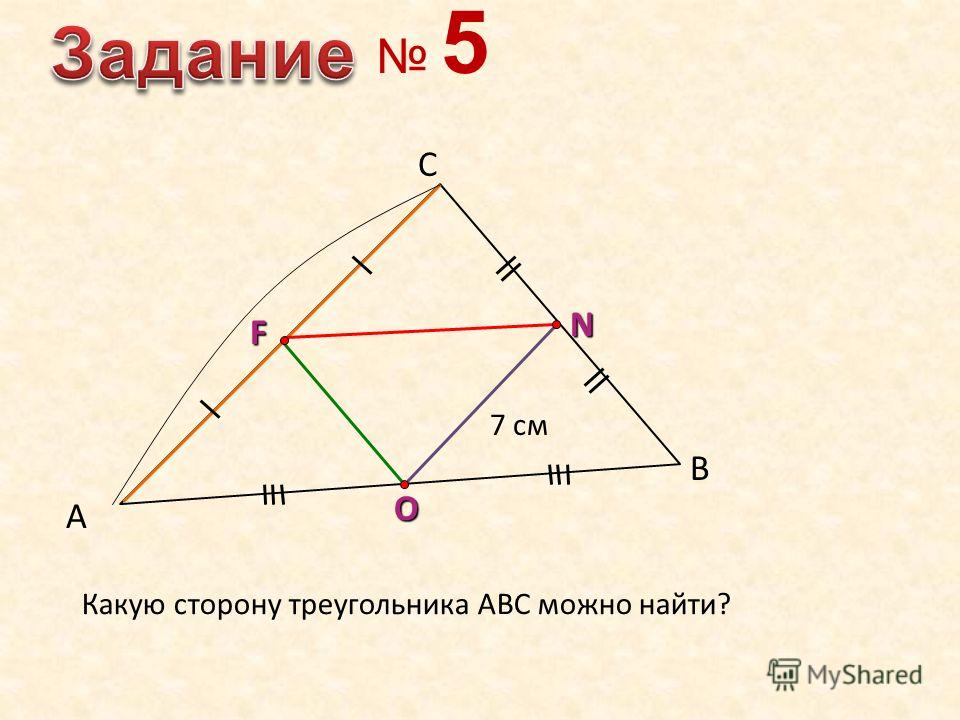
Назначение 4
Треугольник срединного сегмента
на
Кейтлин Спунер
Возьмем остроугольный треугольник ABC.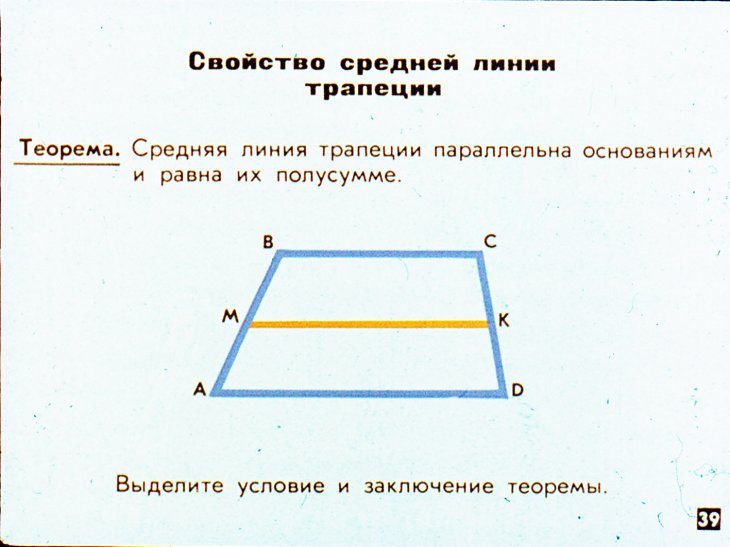 Постройте H и отрезки HA, HB и HC. Постройте середины HA, HB и HC. Соедините середины, чтобы сформировать треугольник. Докажите, что этот треугольник подобен треугольнику ABC и равен медиальному треугольнику. Постройте G, H, C и I для этого треугольника. Сравнивать.
Постройте H и отрезки HA, HB и HC. Постройте середины HA, HB и HC. Соедините середины, чтобы сформировать треугольник. Докажите, что этот треугольник подобен треугольнику ABC и равен медиальному треугольнику. Постройте G, H, C и I для этого треугольника. Сравнивать.
Чтобы построить ортоцентр H треугольника ABC, мы строим три высоты треугольника. H — точка пересечения этих трех высот. Чтобы построить треугольник срединного сегмента, мы строим сегменты между A и H, B и H, C и H. Возьмите середины каждого из этих сегментов и соедините их, чтобы построить треугольник срединного сегмента DEF, который показан красным.
Сначала докажем, что треугольник DEF со средним отрезком подобен треугольнику ABC. Проведите прямую через A и H. Затем проведите прямую, параллельную прямой AH, через точку B. Проведите прямую через точки D и E и постройте точку N на пересечении прямой, проходящей через B, и прямой DE. Эта прямая является секущей параллельных прямых AH и BN. Растяните отрезок AB так, чтобы он образовал прямую через две точки, чтобы он также стал секущей через две параллельные прямые. При наложенных друг на друга внутренних углах угол EDH равен углу ENB. При соответствующих углах угол ENB равен углу ABO. Тогда по свойству транзитивности, поскольку угол EDH равен углу ENB, а угол ENB равен углу ABO, угол EDH равен углу ABO. Далее, угол ABO равен углу BAD, так как они являются альтернативными внутренними углами. Наконец, угол EDH равен углу BAD по свойству транзитивности.
Растяните отрезок AB так, чтобы он образовал прямую через две точки, чтобы он также стал секущей через две параллельные прямые. При наложенных друг на друга внутренних углах угол EDH равен углу ENB. При соответствующих углах угол ENB равен углу ABO. Тогда по свойству транзитивности, поскольку угол EDH равен углу ENB, а угол ENB равен углу ABO, угол EDH равен углу ABO. Далее, угол ABO равен углу BAD, так как они являются альтернативными внутренними углами. Наконец, угол EDH равен углу BAD по свойству транзитивности.
Мы показали, что угол EDH равен углу BAD. Теперь мы должны показать, что угол FDH равен углу DAC. Мы пройдем тот же процесс удлинения линий, что и в предыдущем разделе. Проведите прямую, параллельную прямой AH, через точку C. Проведите прямую через точки D и F и постройте точку P на пересечении прямой, проходящей через C, и прямой DF. Эта прямая является секущей параллельных прямых AH и CQ. Растяните отрезок AC, чтобы провести линию через две точки.
Теперь мы знаем, что угол EDH равен углу BAD, а угол FDH равен углу DAC. Каждый из них является лишь частью внутреннего угла в каждом треугольнике, и мы хотим показать, что весь внутренний угол в исходном треугольнике равен целому углу в треугольнике среднего сегмента. В нашем исходном треугольнике угол BAC равен углу BAD плюс угол DAC. Точно так же в нашем треугольнике со средним сегментом угол EDF равен углу EDH плюс угол FDH. Используя выводы, к которым мы пришли в двух предыдущих разделах, мы можем заключить:
BAC = BAD + DAC = EDH + FDH = EDF
Следовательно, угол BAC равен углу EDF. Используя аналогичный метод, мы также можем доказать, что угол ABC равен углу DEF, а угол BCA равен углу EFD. Тогда по подобию угла-угла наш первоначальный треугольник ABC подобен нашему треугольнику среднего сегмента DEF.
Используя аналогичный метод, мы также можем доказать, что угол ABC равен углу DEF, а угол BCA равен углу EFD. Тогда по подобию угла-угла наш первоначальный треугольник ABC подобен нашему треугольнику среднего сегмента DEF.
Теперь мы хотим доказать, что треугольник срединного сегмента конгруэнтен срединному треугольнику. Срединный треугольник, показанный ниже зеленым, строится путем соединения средних точек каждого из сегментов исходного треугольника.
Сначала мы рассмотрим треугольник FEH и покажем, что он подобен треугольнику CBH, используя сходство стороны-угла-стороны. По построению отрезок EH вдвое короче отрезка BH, а отрезок HF вдвое длиннее отрезка HC. Угол EHF равен углу BHC по свойству тождества. Тогда по подобию стороны-угла-стороны треугольник EHF подобен треугольнику BHF. Поскольку эти два треугольника подобны, мы знаем, что все их соответствующие стороны имеют одинаковое отношение. Следовательно, отрезок EF вдвое короче отрезка BC.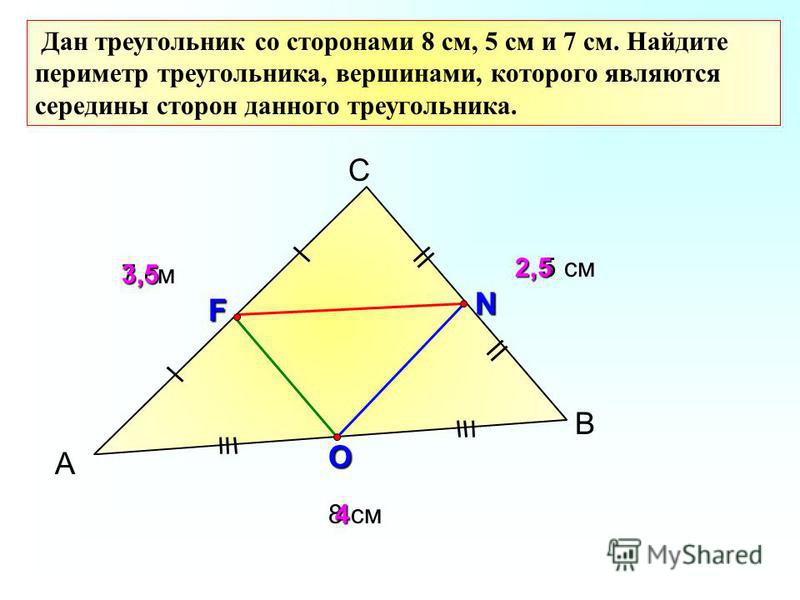
Далее мы обсудим длины сторон медиального треугольника. Помните, что для построения срединного треугольника мы соединяем середины каждой из сторон исходного треугольника. Возьмите сторону JK срединного треугольника. По теореме отрезок JK параллелен отрезку AC, а длина JK составляет половину длины AC. Также по этой теореме отрезок JL составляет половину длины отрезка BC, а отрезок KL — половину длины отрезка AB.
Подводя итог:
Следовательно, по конгруэнтности сторон треугольник DEF со средними сегментами конгруэнтен медиальному треугольнику KLJ.
Наконец, мы посмотрим на центры треугольника срединного сегмента. Эти центры включают центр тяжести, ортоцентр, центр описанной окружности и центр вписанной окружности. Как вы думаете, как каждый из этих центров будет относиться к центрам исходного треугольника?
Как вы думаете, как каждый из этих центров будет относиться к центрам исходного треугольника?
Как, по вашему мнению, центр тяжести исходного треугольника будет относиться к центру тяжести треугольника срединного сегмента? В приведенной ниже конструкции центроид помечен буквой G для каждого треугольника. Центроид — это точка, построенная на пересечении трех медиан треугольника. На диаграмме для каждого треугольника показан один набор соответствующих медиан. Эти медианы параллельны, поэтому мы можем предположить, что для каждой медианы в исходном треугольнике существует соответствующая медиана, параллельная срединному сегменту треугольника. Для этого треугольника каждый из центроидов находится внутри треугольника срединного сегмента, но это не всегда так. Центроиды находятся в одной и той же точке, когда у нас есть равносторонний треугольник. Медианы — это одна и та же линия, когда у нас есть равнобедренный треугольник, поэтому центроиды находятся на одной линии.
Каковы ваши прогнозы для ортоцентра? Кажется, что два треугольника имеют один и тот же ортоцентр в точке H. Давайте подумаем, как строится ортоцентр. Помните, что ортоцентр — это пересечение трех высот треугольника. Когда мы берем высоту исходного треугольника, она также образует высоту треугольника срединного сегмента. На линии построена вершина, образующая треугольник срединного сегмента, а линия перпендикулярна противоположной стороне треугольника срединного сегмента. Поскольку эти два треугольника имеют одинаковые высоты, они также имеют один и тот же ортоцентр.
Давайте подумаем, как строится ортоцентр. Помните, что ортоцентр — это пересечение трех высот треугольника. Когда мы берем высоту исходного треугольника, она также образует высоту треугольника срединного сегмента. На линии построена вершина, образующая треугольник срединного сегмента, а линия перпендикулярна противоположной стороне треугольника срединного сегмента. Поскольку эти два треугольника имеют одинаковые высоты, они также имеют один и тот же ортоцентр.
Центр описанной окружности является точкой пересечения биссектрисы каждой стороны треугольника и равноудален от каждой из вершин треугольника. Подобно медианам каждого треугольника, мы можем видеть, что набор соответствующих серединных перпендикуляров для двух треугольников параллельны. Здесь центр описанной окружности для каждого треугольника находится внутри соответствующего треугольника, и они оба находятся внутри треугольника срединного сегмента. Если треугольник изменить, мы заметим, что центр описанной окружности для треугольника срединного сегмента находится в том же положении в треугольнике срединного сегмента, что и центр описанной окружности в исходном треугольнике по отношению к исходному треугольнику. Например, если исходный центр описанной окружности находится за пределами исходного треугольника, центр описанной окружности треугольника срединного сегмента находится вне треугольника срединного сегмента.
Например, если исходный центр описанной окружности находится за пределами исходного треугольника, центр описанной окружности треугольника срединного сегмента находится вне треугольника срединного сегмента.
Наконец, как, по вашему прогнозу, будут связаны центры двух треугольников? Центр вписанной окружности образован пересечением трех биссектрис каждого треугольника и равноудален от трех сторон треугольника. И снова мы можем видеть, что набор соответствующих биссектрис угла для каждого треугольника кажется параллельным, как мы наблюдали с медианами и серединными перпендикулярами сторон треугольника. В этом треугольнике оба центра инцентрации всегда находятся внутри треугольника срединного сегмента. Хотя это не всегда так, верно то, что центр инцентрации всегда будет внутри своего родительского треугольника.
Вернуться на домашнюю страницу Кейтлин Спунер
Свойства треугольников: определение, формулы, примеры
- Автор Прия_Сингх
- Последнее изменение 19-07-2022
Ранее мы изучали Треугольники и типы треугольников. Чтобы лучше понять концепцию, дайте нам знать Свойства треугольника . Как известно, треугольник — это замкнутый многоугольник с тремя сторонами, тремя углами и вершинами. Существуют типы треугольников в зависимости от длины их сторон и углов. Свойства треугольников основаны на сторонах и углах треугольника.
Чтобы лучше понять концепцию, дайте нам знать Свойства треугольника . Как известно, треугольник — это замкнутый многоугольник с тремя сторонами, тремя углами и вершинами. Существуют типы треугольников в зависимости от длины их сторон и углов. Свойства треугольников основаны на сторонах и углах треугольника.
В этой статье вы узнаете больше о свойствах треугольников, формулах и типах с некоторыми решенными примерами.
Треугольник — это многоугольник с тремя сторонами. Его также можно определить фигурой, ограниченной или заключенной в трехлинейные отрезки.
Ясно, что треугольник будет иметь три стороны и три вершины.
Ниже мы обсудим некоторые свойства.
Типы треугольников
Треугольники бывают 6 типов в зависимости от их сторон и углов
На основе бок Острый угловой треугольник
Наклонный угловой треугольник
ПРАВИЛЬНЫЙ КРЕЙНГЛИЯ
На основе углов
Equilateral Triangle
Sliangle
Isosceles Triangle
66601101166666.
 \circ }\) или двум прямым углам. . Это называется свойством суммы углов треугольника. 9\circ }\) Сумма внешних углов
\circ }\) или двум прямым углам. . Это называется свойством суммы углов треугольника. 9\circ }\) Сумма внешних углов В треугольнике \(PQR,\) если одна из сторон равна \(QR\) (скажем) продолжается до\(S,\), то \ (\угол PRS\) называется внешним углом треугольника в точке \(R,\)
Существует очень важное свойство, связанное с внешним углом треугольника. Можно доказать, что внешний угол треугольника равен сумме двух крайних внутренних углов треугольника.
В приведенном выше треугольнике \(PQR,\угол PRS = \угол PQR + \угол QPR.\) 9\circ }.\)
Высоты треугольника встречаются в одной точке. Эта точка называется ортоцентром треугольника.
Изучение концепций экзамена на Embibe
Медианы в треугольникеВ любом треугольнике три медианы пересекаются в одной точке.
Центроид: Точка пересечения медиан в треугольнике называется центром треугольника.
В приведенном выше треугольнике \(ABC,\) медианы \(AD,BE\) и \(CF,\) пересекаются в точке \(G.\) Итак, точка \(G\) называется центроидом треугольника.
В треугольнике центр тяжести делит каждую медиану в отношении \(2:1.\). Это показано на рисунке.
Итак, в треугольнике \(ABC,\) имеем \(AG:GD = BG:GE = CG:GF = 2:1\)
Центр: Точка пересечение внутренних биссектрис трех ангелов в треугольнике называется центром треугольника.
Теперь из точки \(I\) (центр), если провести перпендикуляр к любой стороне треугольника, а затем при такой длине перпендикуляра от центра до точки, где он пересекает сторону, круг нарисован, этот круг касается двух других сторон. Эта окружность называется вписанной окружностью треугольника.
Центр треугольника всегда лежит внутри треугольника, независимо от формы треугольника, то есть, является ли треугольник остроугольным, тупоугольным или прямоугольным, центр всегда лежит внутри треугольника.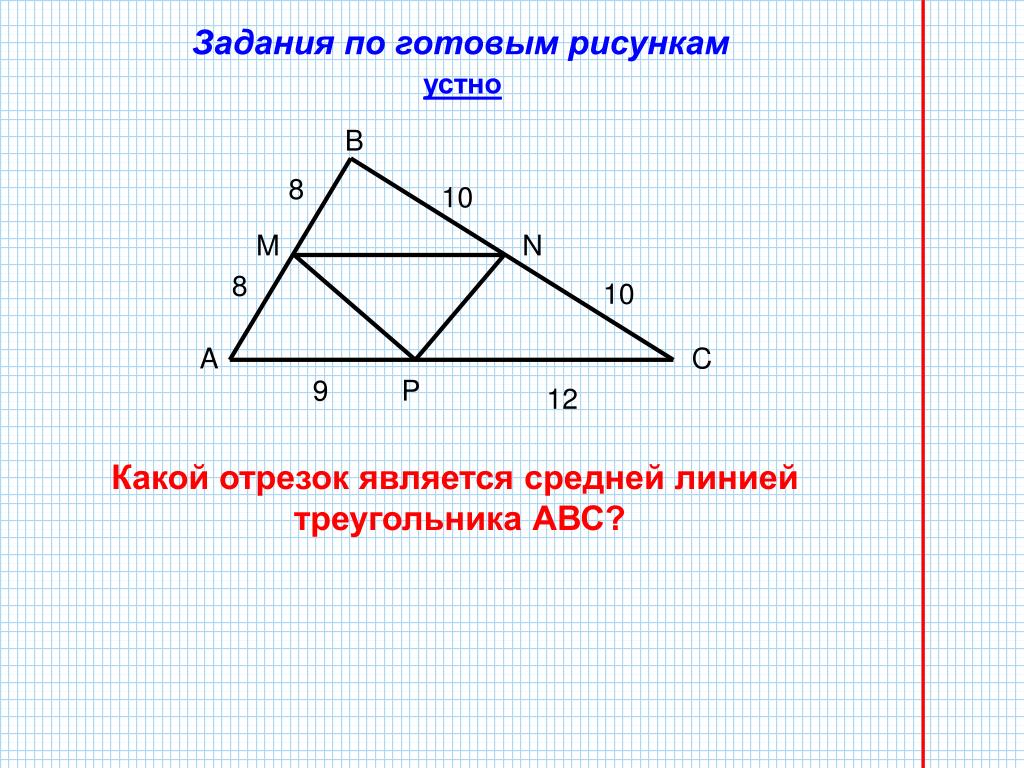
Центр окружности: Три биссектрисы треугольника всегда пересекаются в одной точке, и эта точка называется центром описанной окружности треугольника.
В треугольнике \(ABC,\) серединные перпендикуляры \(PD,NE\) и \(MF\) пересекаются в точке \(O.\). Эта точка \(O\) является центром описанной окружности треугольника.
Окружность: Это окружность, нарисованная с центром описанной окружности в качестве центра и расстоянием между центром описанной окружности и любой из ее вершин треугольника в качестве радиуса.
В приведенном выше треугольнике нарисована описанная окружность, принимая \(O\) за центр и \(OA\) за радиус. Нарисованная окружность проходит через две другие вершины \(B\) и \(C.\)
Примечание:- Для остроугольного треугольника центр описанной окружности всегда лежит внутри треугольника, как показано на рисунке выше.
- В тупоугольном треугольнике центр описанной окружности всегда лежит вне треугольника, как показано на рисунке ниже.

3. Для прямоугольного треугольника центр описанной окружности всегда лежит на гипотенузе треугольника, как показано на рисунке ниже.
Неравенство треугольникаСтороны треугольника обладают важным свойством, которое приведено ниже:
Свойство: Сумма любых двух сторон треугольника больше третьей стороны. То есть в треугольнике \(ABC,\) мы имеем 90 125 \(b + c > a, c + a > b\) и \(a + b > c\) 90 125. Это важное свойство треугольника известно как Неравенство треугольника.
Подобие в треугольнике:Если два треугольника подобны, то их
- Соответствующие углы равны и
- Соответствующие стороны пропорциональны
Если \(\Delta ABC\) подобен \(\Delta DEF,\), то \(\угол A = \угол D,\угол B = \угол E = \угол F\) и \(\frac{{AB}}{{DE}} = \frac{{BC}}{{EF}} = \frac{{AC}}{{DF }}.\)
Практические экзаменационные вопросы
Конгруэнтные свойства треугольника: Определение Два треугольника называются конгруэнтными, если они имеют одинаковую форму и размер, т. е. .
е. .
На рисунках выше треугольник \(ABC\) и треугольник \(DEF\) выглядят одинаково. Они имеют одинаковую форму и размер. Следовательно, эти два треугольника будем называть конгруэнтными треугольниками. Символ, используемый для обозначения конгруэнтности, — это \( \cong ,\), и он читается как «конгруэнтно». Следовательно, в этом случае соответствие между треугольниками \(ABC\) и \(DEF\) представлено как \(\Delta ABC \cong \Delta DEF.\)
СвойстваВ двух конгруэнтных треугольниках соответствующие стороны имеют одинаковую длину и соответствующие углы имеют одинаковую меру.
В \(\Delta ABC\) и \(\Delta DEF,\) ясно, \(AB = DE,AC = DF,BC = EF\) и \(\угол A = \угол D,\угол B = E,\угол C = \угол F.\)
Формулы Формула периметра треугольникаПериметр получается сложением длин трех сторон треугольника.
Периметр разностороннего треугольника
\(ABC\) — это разносторонний треугольник со сторонами \(AB = c,BC = a\) и \(AC = b. \)
\)
Итак, периметр \(\Delta ABC = \) длина стороны \( = AB + BC + CA = c + a + b = a + b + c.\)
\(ABC\) является равнобедренным треугольником со сторонами \(AB = BC = a\) и \(BC = b.\)
Итак, периметр \(\Delta ABC = \) длина стороны \( = AB + BC + = a + b + a = 2a + b.\)
\(ABC\) является равносторонний треугольник со сторонами \(AB = BC = АС = а.\)
Итак, периметр \(\Delta ABC = \) длина сторон \( = AB + BC + CA = a + a + a = 3a = 3 \times {\rm{side}}\)
Определение площади: Площадь треугольника – это область или пространство, ограниченное тремя сторонами треугольника
Площадь треугольника, если известны основание и высота:Площадь треугольника \( = \frac{1}{2} \times {\rm{основание}} \times {\rm{высота}}\)
Площадь треугольника, если даны длины трех сторон: Формула Герона Согласно этой формуле, площадь треугольника определяется как площадь \( = \sqrt {s\left({s – a} \ right)\left({s – b} \right)\left({s – c}\right),} \)
где \(a,b\) и \(c\) — длины сторон треугольника, а s — полупериметр треугольника, определяемый формулой \(s = \frac{{a + b + c}}{2}. 2}.\)
2}.\)
В этом случае формула площади треугольника задается следующим образом:
\(Площадь = \frac{1}{2}ab\,\sin \,C \)
\(Площадь = \frac{1}{2}bc\,\sin \,A\)
\(Площадь = \frac{1}{2}ca\,\sin \,B\)
Отсюда , площадь равна, \({\rm{площадь}} = \frac{1}{2} \times {\rm{product}}\,{\rm{of}}\,{\rm{любой}} \, {\ rm {два}} \, {\ rm {стороны}} \ times \ sin \, {\ rm {e}} \, {\ rm {of}} \, {\ rm {the}} \ , {\ rm {угол}} \, {\ rm {включая}} \, {\ rm {те}} \, {\ rm {два}} \, {\ rm {стороны}} {\ rm {.} }\)
Площадь этого треугольника можно рассчитать по формуле \(area = \frac{1}{2}\left[{{x_1} \left( {{y_2} – {y_3}} \right) + {x_2}\left({{y_3} – {y_1}} \right) + {x_3}\left({{y_1} – {y_2}} \right)} \right]\)
Решаемые примеры Q.1. На приведенной диаграмме \(\Delta ABC,AB = 3\,{\text{см}},BC = 4\,{\text{см}}\) и \(AC = 5\,{\text {см}}.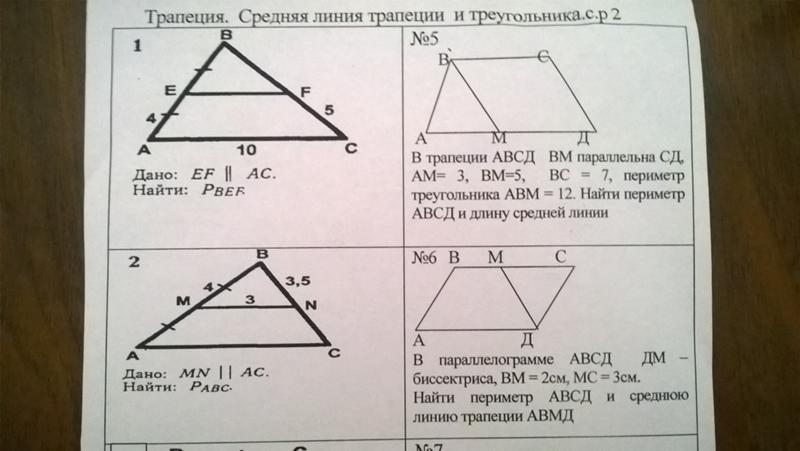 \) Назовите наименьший и наибольший углы треугольника.
\) Назовите наименьший и наибольший углы треугольника.
Ответ: Как известно, наибольший угол всегда лежит против наибольшей стороны.
Следовательно, \(\угол B\) — наибольший угол.
Здесь наименьший угол противоположен наименьшей стороне.
\(\следовательно \угол C\) — наименьший угол.
Q.2. На рисунке ниже показан треугольник \(ABC\) с \(AB = AC,E\) и \(F\) две точки на \(BC\) такие, что \(BF = CE.\) Показать, что \(AE = AF.\)
Ответ: In \(\Delta ABE\) и \(\Delta ACF,AB = AC.\)
Поскольку углы, лежащие напротив равных сторон, равны, \(\угол B = \угол C.\)
Кроме того, \(BF = CE\)
Итак, \(BF – EF = CE – EF\)
, то есть \(BE = FC\)
Таким образом, используя правило сравнения \(SAS\), мы заключаем, что \(\Delta ABE \cong \Delta ACF.\ )
Следовательно, \(AE = AF.\)
9\circ }\)
Q. 4. Объясните, могут ли эти числа быть длинами сторон треугольника: \(2,3,4.\)
4. Объясните, могут ли эти числа быть длинами сторон треугольника: \(2,3,4.\)
+ 4 > 3\) и \(3 + 4 > 2\)
Здесь сумма любых двух данных чисел больше третьего числа.
Следовательно, \(2\,{\text{см}},3\,{\text{см}}\) и \(4\,{\text{см}}\) могут быть длинами сторон треугольника.
5. Объясните, могут ли эти числа быть длинами сторон треугольника: \(4,5,3.\)
Ответ: Имеем
\(4 + 5 > 3,4 > 5\) и \(5 + 3 > 4\)
То есть, сумма любых двух из заданных чисел больше третьего числа.
Итак, \(4\,{\text{см}},5\,{\text{см}}\) и \(3\,{\text{см}}\) могут быть длинами сторон треугольника.
Попытка пробных тестов
Резюме В этой статье мы узнали об определении треугольника, различных свойствах треугольника, связанных со сторонами, углами, высотами, медианами, центроидом, биссектрисами угла, вписанной окружностью, описанная окружность, сходство, конгруэнтность и т. д. Мы также рассмотрели формулы, основанные на треугольнике, и обсудили несколько примеров для большей ясности по треугольникам.
д. Мы также рассмотрели формулы, основанные на треугольнике, и обсудили несколько примеров для большей ясности по треугольникам.
Q.1. Что такое \(3\) атрибутов треугольника?
Ответ: Треугольник имеет три стороны, три угла и три вершины.
Q.2. Как найти \(R\) свойств треугольников?
Ответ: Окружность, проходящая через вершины треугольника, называется описанной окружностью треугольника. Радиус описанной окружности известен как радиус описанной окружности треугольника, который обозначается \(‘R’,\) и формула для этого \(2R = \ frac {a}{{\sin \,A}} = \frac{b}{{\sin \,B}} = \frac{c}{{\sin \,C}}.\)
Q.3. Какова формула периметра разностороннего треугольника?
Ответ: ABC — разносторонний треугольник со сторонами \(AB = c,BC = a\) и \(AC = b. \)
\)
Итак, периметр \(\Delta ABC = \) длина сторон \( = AB + BC + CA = c + a + b = a + b + c.\)
Q.4. Какими свойствами обладает тупоугольный треугольник?
Ответ: Свойства тупоугольного треугольника Вы знаете, что сумма двух углов, отличных от тупого, меньше \({9\circ }.\)
2. Сумма длин двух сторон треугольника больше длины третьей стороны.
3. Разница между двумя сторонами треугольника меньше длины третьей стороны.
4. Сторона, лежащая против большего угла, является наибольшей стороной из всех трех сторон треугольника.
5. Внешний угол треугольника всегда равен сумме двух внутренних противоположных углов при противоположных сторонах. Это свойство треугольника известно как свойство внешнего угла.
6. Два треугольника подобны, если соответствующие углы обоих треугольников равны, а длины их сторон пропорциональны.
Brilliant Math & Science Wiki
Содержание
- Поиск центра
- Доказательство существования
- Основные свойства
- Расширенные свойства
- Другие полигоны
- Смотрите также
У всех треугольников есть вписанный центр, и он всегда лежит внутри треугольника.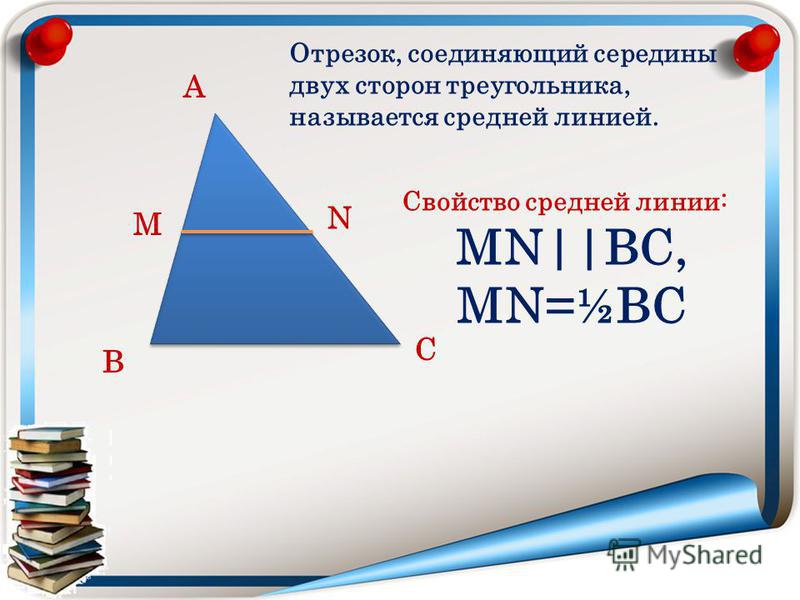 Один из способов найти вписанный центр использует свойство, согласно которому входящий центр является пересечением трех биссектрис, используя координатную геометрию для определения местоположения входящего центра. К сожалению, это часто утомительно с вычислительной точки зрения.
Один из способов найти вписанный центр использует свойство, согласно которому входящий центр является пересечением трех биссектрис, используя координатную геометрию для определения местоположения входящего центра. К сожалению, это часто утомительно с вычислительной точки зрения.
Как правило, самый простой способ найти центр вписанной окружности — сначала определить внутренний радиус или радиус вписанной окружности, обычно обозначаемый буквой rrr (буква RRR зарезервирована для радиуса описанной окружности). Это можно сделать несколькими способами, подробно описанными в разделе «Основные свойства» ниже. После того, как известен внутренний радиус, каждую сторону треугольника можно перевести на длину внутреннего радиуса, и пересечение полученных трех линий будет центром вписанной стороны. Это, опять же, можно сделать с помощью координатной геометрии.
В качестве альтернативы можно использовать следующую формулу. Для треугольника со сторонами a,b,ca,b,ca,b,c с вершинами в точках (x1,y1),(x2,y2),(x3,y3)(x_1, y_1), (x_2 , y_2), (x_3, y_3)(x1,y1), (x2,y2), (x3,y3), центр вписанной дуги лежит на
(ax1+bx2+cx3a+b+c, ay1+by2+cy3a+b+c).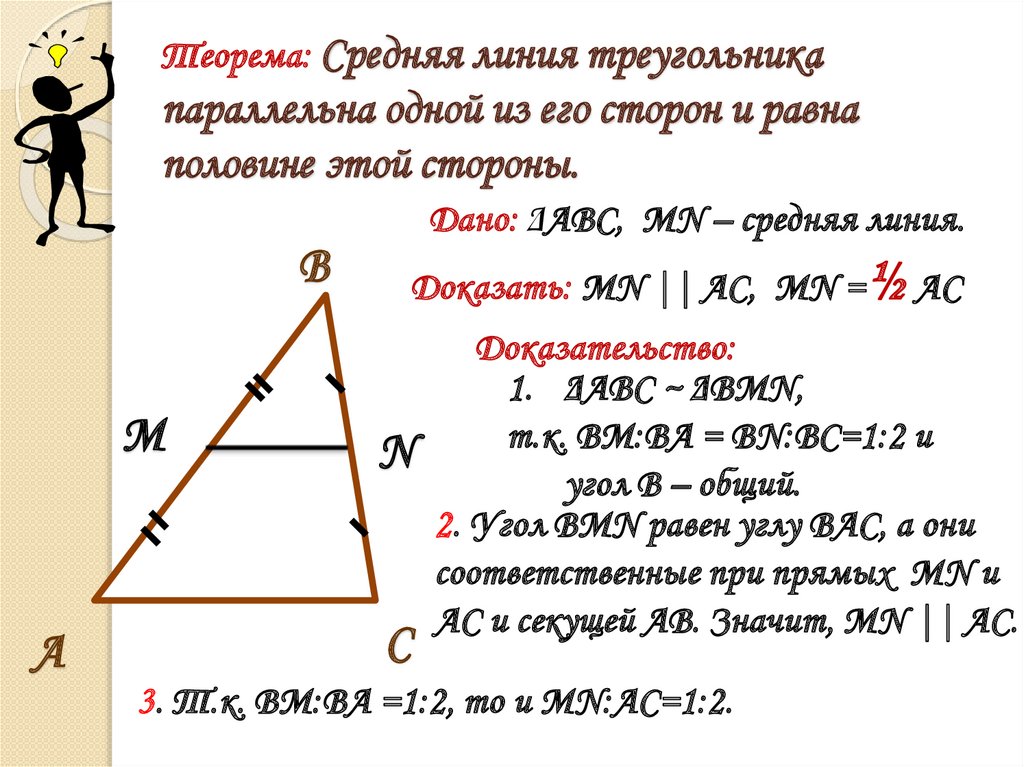 \left(\dfrac{ax_1+bx_2+cx_3}{a+b+c}, \dfrac{ay_1+by_2+cy_3}{a+b+c}\right) .(a+b+cax1+bx2+cx3, a+b+cay1+by2+cy3).
\left(\dfrac{ax_1+bx_2+cx_3}{a+b+c}, \dfrac{ay_1+by_2+cy_3}{a+b+c}\right) .(a+b+cax1+bx2+cx3, a+b+cay1+by2+cy3).
Треугольник имеет вершины в точках A=(0,0),B=(14,0)A=(0,0), B=(14,0)A=(0,0),B=(14,0) ) и С=(5,12)С=(5,12)С=(5,12). Каковы координаты центра? 92}=14.a=(14−5)2+(12−0)2=15,b=(5−0)2+(12−0)2=13,c=(14−0) 2+(0−0)2=14. Теперь можно использовать приведенную выше формулу: I=(15⋅0+13⋅14+14⋅513+14+15,15⋅0+13⋅0+14⋅1213+14+15)=(6,4). □I = \left(\dfrac{15 \cdot 0+13 \cdot 14+14 \cdot 5}{13+14+15}, \dfrac{15 \cdot 0+13 \cdot 0+14 \cdot 12} {13+14+15}\right)=\left(6, 4\right).\ _\squareI=(13+14+1515⋅0+13⋅14+14⋅5,13+14+1515⋅ 0+13⋅0+14⋅12)=(6,4). □
Простейшее доказательство является следствием тригонометрической версии теоремы Чевы, которая утверждает, что AD, BE, CFAD, BE, CFAD, BE, CF совпадают тогда и только тогда, когда
sin∠BADsin∠ABE⋅sin∠CBEsin∠BCF⋅sin∠ACFsin∠CAD=1.\frac{\sin\angle BAD}{\sin\angle ABE} \cdot \frac{\ sin \angle CBE}{\sin \angle BCF} \cdot \frac{\sin\angle ACF}{\sin \angle CAD} = 1. sin∠ABEsin∠BAD⋅sin∠BCFsin∠CBE⋅sin∠CADsin ∠ACF=1.
sin∠ABEsin∠BAD⋅sin∠BCFsin∠CBE⋅sin∠CADsin ∠ACF=1.
В этом случае D,E,FD,E,FD,E,F — основания биссектрисы угла, поэтому ∠BAD=∠CAD\угол BAD=\угол CAD∠BAD=∠CAD, ∠ABE=∠ CBE\угол ABE=\угол CBE∠ABE=∠CBE и ∠ACF=∠BCF\угол ACF=\угол BCF∠ACF=∠BCF. В результате
sin∠BADsin∠CAD⋅sin∠ABEsin∠CBE⋅sin∠ACFsin∠BCF=1⋅1⋅1=1\frac{\sin\angle BAD}{\sin\ угол CAD} \cdot \frac{\sin\angle ABE}{\sin\angle CBE} \cdot \frac{\sin\angle ACF}{\sin\angle BCF} = 1 \cdot 1 \cdot 1 = 1sin∠ CADsin∠BAD⋅sin∠CBEsin∠ABE⋅sin∠BCFsin∠ACF=1⋅1⋅1=1
и перестановка левой части дает
sin∠BADsin∠ABE⋅sin∠CBEsin∠BCF⋅sin∠ACFsin∠CAD=1.\frac{\sin\angle BAD}{\sin\ угол ABE} \cdot \frac{\sin \angle CBE}{\sin \angle BCF} \cdot \frac{\sin\angle ACF}{\sin \angle CAD} = 1.sin∠ABEsin∠BAD⋅sin ∠BCFsin∠CBE⋅sin∠CADsin∠ACF=1.
Следовательно, три биссектрисы пересекаются в одной точке, III.
Кроме того, поскольку III лежит на биссектрисе угла ∠BAC\угла BAC∠BAC, расстояние от III до ABABAB равно расстоянию от III до ACACAC.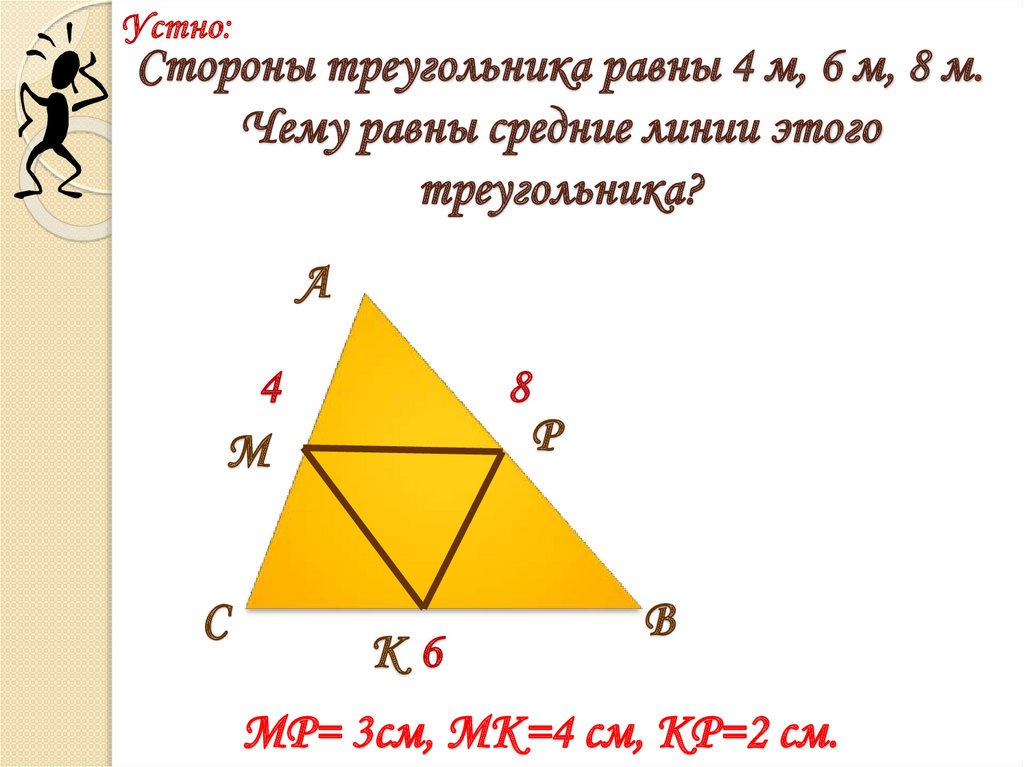 Точно так же это также равно расстоянию от III до BCBCBC. Следовательно, III является центром вписанной окружности, что доказывает существование центра вписанной окружности.
Точно так же это также равно расстоянию от III до BCBCBC. Следовательно, III является центром вписанной окружности, что доказывает существование центра вписанной окружности.
Альтернативное доказательство включает версию теоремы Чевы о длине и теорему о биссектрисе угла.
Выше было отмечено, что центр вписанной окружности является пересечением трех биссектрис.
Для треугольника с полупериметром (половиной периметра) sss и внутренним радиусом rrr,
Площадь треугольника равна srsrsr.
Это особенно полезно для нахождения длины внутреннего радиуса по длинам сторон, поскольку площадь можно вычислить другим способом (например, по формуле Герона), а полупериметр легко вычислить.
3 6 4 5
В треугольнике ABCABCABC AB=13,BC=14AB=13, BC=14AB=13,BC=14 и CA=15CA=15CA=15.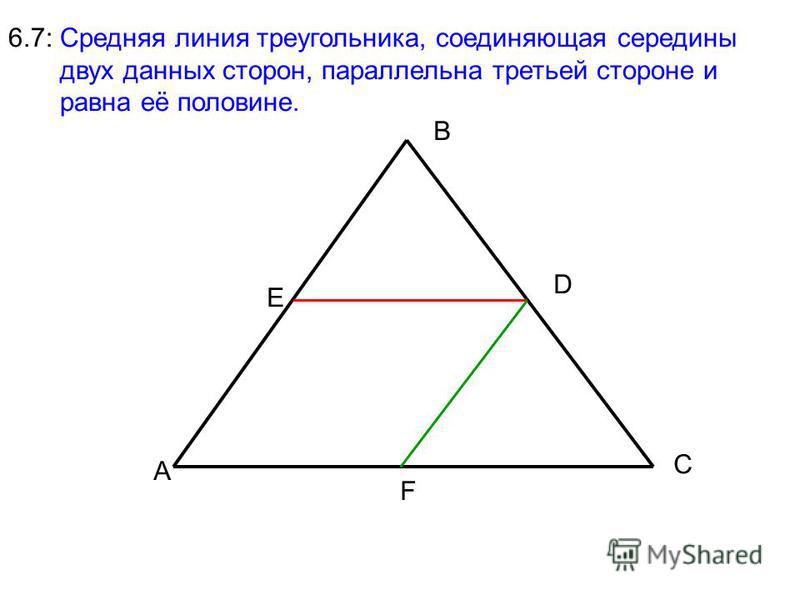 Какова длина внутреннего радиуса △ABC\треугольника ABC△ABC?
Какова длина внутреннего радиуса △ABC\треугольника ABC△ABC?
Как следствие,
В прямоугольном треугольнике с целыми длинами сторон внутренний радиус всегда является целым числом.
Если DDD — это точка, где вписанная окружность касается BCBCBC, и, аналогично, E,FE,FE,F — это точки, где вписанная окружность касается ACACAC и ABABAB соответственно, тогда AE=AF=s-a,BD=BF=s-b,CD =CE=s-cAE=AF=s-a, BD=BF=s-b, CD=CE=s-cAE=AF=s-a,BD=BF=s-b,CD=CE=s-c. Как следствие,
AE+BF+CD=sAE+BF+CD=sAE+BF+CD=s, а также r=AE⋅BF⋅CDAE+BF+CD.r = \sqrt{\dfrac{AE \cdot BF \cdot CD {AE+BF+CD}}.r=AE+BF+CDAE⋅BF⋅CD.
Кроме того, AD, BE, AD, BE, AD, BE и CFCFCF пересекаются в одной точке, называемой Жергон-пойнт .
Если высоты треугольника имеют длину h2,h3,h4h_1, h_2, h_3h2,h3,h4, то
1h2+1h3+1h4=1r.\dfrac{1}{h_1}+\dfrac{1}{h_2}+\dfrac{1}{h_3}=\dfrac{1}{r}.
h21+ h31+h41=r1.
Пусть стороны треугольника равны a,b,ca,b,ca,b,c. Тогда, поскольку 12ah2=Δ\frac{1}{2} a h_1= \Delta 21ah2=Δ, и аналогично для других сторон, ∑1h2=∑a2Δ=2s2Δ=1Δ/s=1r.\sum \frac {1}{h_1} = \sum \frac{a}{2 \Delta} = \frac{2s}{2 \Delta} = \frac{1}{ \Delta/s}= \frac{1}{r }.∑h21=∑2Δa=2Δ2s=Δ/s1=r1. 92.rR=2(a+b+c)abc, и IA⋅IB⋅IC=4Rr2.Вписанные в круги также хорошо относятся друг к другу. Если r1,r2,r3r_1, r_2, r_3r1,r2,r3 — это радиусы трех окружностей, касающихся вписанной окружности и двух сторон треугольника, то
r=r1r2+r2r3+r3r1.r=\sqrt{r_1r_2}+\sqrt{r_2r_3}+\sqrt{r_3r_1}.r=r1r2+r2r3+r3r1.
С другой стороны, если описанная окружность ABCABCABC нарисована, а MMM является серединой малой дуги BCBCBC, то
MMM также является центром описанной окружности △BIC\треугольника BIC△BIC.
Эквивалентно MB=MI=MCMB=MI=MCMB=MI=MC.

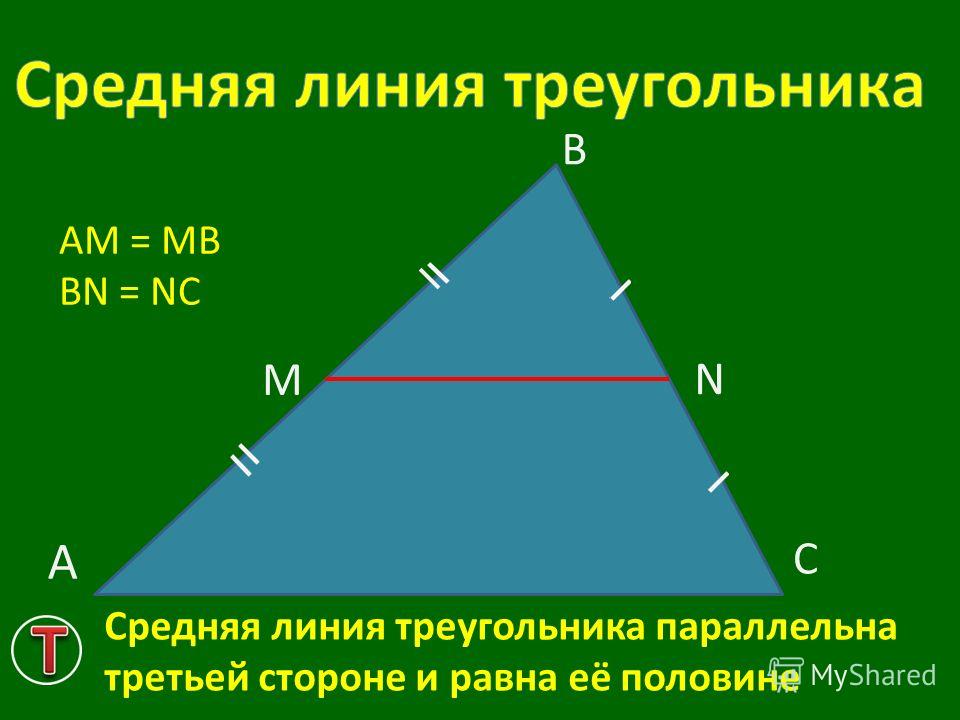
 h21+ h31+h41=r1.
h21+ h31+h41=r1.