Ответы
DEN23567893 09.08.2020 14:58
(x-1)(x+1)≤0
x=1 x=-1
x∈[-1;1]
ПОКАЗАТЬ ОТВЕТЫ
Маруся200117 26.10.2020 16:35
ПОКАЗАТЬ ОТВЕТЫ
fredkalash 26.10.2020 16:35
ответ:
ПОКАЗАТЬ ОТВЕТЫ
 2 — 10x + 21 > 0
2 — 10x + 21 > 0(x — 7) ( x — 3) > 0
+ — +
(3) (7) > x
x ∈ ( — ω; 3) ∨ ( 7; + ω)
ПОКАЗАТЬ ОТВЕТЫ
динька2 26.10.2020 16:35
X²-10x+21>0
x²-10x+21=0
x1=7
x2=3
по теореме Виетта
(x-7)(x-3)>0
+ _ +
37
x∈(-∞;3)∨(7;+∞)
ПОКАЗАТЬ ОТВЕТЫ
domka123456789 26.10.2020 16:35 Ну вот так (-1;11) прости за некачественный снимок
ПОКАЗАТЬ ОТВЕТЫ
999999апро
26. -6…
-6…
Yuliy5321 14.08.2019 10:00
Решити систему уравнений методом подстоновкм [3x+y=2 x+2y=-6…
двоищник3 28.05.2019 12:10
Поиск результатов по фразе преобразовав линейное уравнение 5х+4у-4=0 к виду линейной функции у=кх+m, найдите ее угловой коэффициент….
MaliaCr 27.10.2020 19:28
Расположите числа в порядке возрастания ( подсказка: — внесите множитель под знак корня) √(19 ) , 2√5 , 3√2…
соня1581
29. 2-1≥0… -reshimne.ru
2-1≥0… -reshimne.ru
Новые вопросы
Ответы
Похожие вопросы
I2x-1I=4х+7
3x +4меньше или равно x2меньше или равно 9…
X²+2x -6=√x²+2x-4 корень над всей второй частью примера…
В равнобедреной трапеции одно основание равно 18, а другое -12.Диоганали этой трапеции взаимно перпендикулярно.Найдите площадь трапеции
…
Потяг мав проїхати 300 км. Проїхав ⅓ шляху він зупинився на 1 год, а потім рухався зі швидкістю на 10 км/ год менше.Знайти швидкість до зупинки , якщо він прибув до місця через 8 год після виїзду. ..
..
215,216,217… Найдите все значение a, при каждом из которых уравнение имеет ровно один корень.
Решить с объяснениями)
…
Математика
Литература
Алгебра
Русский язык
Геометрия
Английский языкХимия
Физика
Биология
Другие предметы
История
Обществознание
География
Українська мова
Українська література
Қазақ тiлi
Беларуская мова
Информатика
Экономика
Музыка
Право
Французский язык
Немецкий язык
МХК
ОБЖ
Психология
ГДЗ Математика 4 класс Петерсон на Решалка
ГДЗ Математика 4 класс Петерсон
авторы: Петерсон.
издательство: «Фгос» 2013 год
Задачи
- ЧАСТЬ 1
- 1 урок. Решение неравенства
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 2 урок. Множество решений
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 3 урок.
 Знаки ≥ (больше или равно) и ≤ (меньше или равно)
Знаки ≥ (больше или равно) и ≤ (меньше или равно)- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 4 урок. Двойное неравенство
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 5 урок.
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 6 урок.
 Оценка суммы
Оценка суммы- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 7 урок. Оценка разности
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 8 урок. Оценка произведения
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 9 урок.
 Оценка частного
Оценка частного- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 10 урок. Прикидка результатов арифметических действий
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 11 урок. Деление с однозначным частным
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 12 урок.

- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 13 урок. Деление на двузначное и трехзначное число
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 14 урок.
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 15 урок.
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 16 урок.

- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 17 урок. Оценка площади
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 18 урок. Приближенное вычисление площадей
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 19 урок. Измерения дробей
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 20 урок.
 Из истории дробей
Из истории дробей- 1
- 2
- 3
- 4
- 5
- 21 урок. Доли
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 22 урок. Сравнение долей
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 23 урок. Нахождение доли числа
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 24 урок.
 Проценты
Проценты- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 25 урок. Нахождение числа по доле
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 26 урок.
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 27 урок. Дроби
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 28 урок.
 Сравнение дробей
Сравнение дробей- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 29 урок. Нахождение части числа
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 30 урок. Нахождение числа по его части
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 31 урок.
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 32 урок.
 Площадь прямоугольного треугольника
Площадь прямоугольного треугольника- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 1 урок. Решение неравенства
- ЧАСТЬ 2
- 1 урок. Деление и дроби
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 2 урок. Нахождение части, которую одно число составляет от другого
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 3 урок.
 Сложение дробей
Сложение дробей- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 4 урок. Вычитание дробей
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 5 урок. Правильные и неправильные дроби
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 6 урок.
 Правильные и неправильные части величин
Правильные и неправильные части величин- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 7 урок. Задачи на части
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 8 урок. Смешанные числа
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 9 урок.
 Выделение целой части из неправильной дроби
Выделение целой части из неправильной дроби- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 10 урок. Запись смешанного числа в виде неправильной дроби
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 11 урок. Сложение и вычитание смешанных чисел
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 12 урок.

- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 13 урок.
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14 урок.
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 15 урок.
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16 урок.

- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 17 урок. Шкалы
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 18 урок. Числовой луч
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 19 урок. Координаты на луче
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 20 урок.
 Расстояние между точками координатного луча
Расстояние между точками координатного луча- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 21 урок. Движение по координатному лучу
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 22 урок.
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 23 урок.
 Одновременное движение по координатному лучу
Одновременное движение по координатному лучу- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 24 урок. Скорость сближения и скорость удаления
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 25 урок.
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 26 урок.
 Встречное движение
Встречное движение- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 27 урок. Движение в противоположных направлениях
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 28 урок. Движение вдогонку
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 29 урок.
 Движение с отставанием
Движение с отставанием- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 30 урок. Формула одновременного движения
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 31 урок.
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 32 урок.

- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 33 урок.
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 34 урок.
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 35 урок. Действия над составными именнованными числами
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 36 урок.
 Новые единицы площади
Новые единицы площади- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 1 урок. Деление и дроби
- ЧАСТЬ 3
- 1 урок. Сравнение углов
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 2 урок. Развернутый угол. Смежные углы
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 3 урок.
 Измерение углов
Измерение углов- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 4 урок. Угловой градус
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 5 урок. Транспортир
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 6 урок.

- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 7 урок.
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 8 урок.
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 9 урок.
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 10 урок.
 Круговые диаграммы
Круговые диаграммы- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 11 урок. Столбчатые и линейные диаграммы
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 12 урок. Игра «Морской бой». Пара элементов
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 13 урок. Передача изображений
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 14 урок.
 Координаты на плоскости
Координаты на плоскости- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15 урок. Построение точек по их координатам
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 16 урок. Точки на осях координат
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 17 урок.

- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 18 урок. График движения
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 19 урок.
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 20 урок.
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 21 урок.

- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- Задачи на повторение
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
- 31
- 32
- 33
- 34
- 35
- 36
- 37
- 38
- 39
- 40
- 41
- 42
- 43
- 44
- 45
- 46
- 47
- 48
- 49
- 50
- 51
- 52
- 53
- 54
- 55
- 56
- 57
- 58
- 59
- 60
- 61
- 62
- 63
- 64
- 65
- 66
- 67
- 68
- 69
- 70
- 71
- 72
- 73
- 74
- 75
- 76
- 77
- 78
- 79
- 80
- 81
- 82
- 83
- 84
- 85
- 86
- 87
- 1 урок. Сравнение углов
Начальная школа уже с первых лет связана с постоянно увеличивающейся нагрузкой. Причем уже в младших классах приходится решать много нелегких заданий по разным дисциплинам, в том числе и по математике. Это один из самых сложных предметов в программе и неудивительно, что его изучение не всем дается легко. Четвероклассникам из-за ожидающихся вскоре контрольных работ и экзаменов нередко приходится нанимать репетиторов, задействовать решебники. Индивидуальные занятия требуют финансовых трат, а вот онлайн-сборник с ГДЗ по математике (4 класс) — нет.
Причем уже в младших классах приходится решать много нелегких заданий по разным дисциплинам, в том числе и по математике. Это один из самых сложных предметов в программе и неудивительно, что его изучение не всем дается легко. Четвероклассникам из-за ожидающихся вскоре контрольных работ и экзаменов нередко приходится нанимать репетиторов, задействовать решебники. Индивидуальные занятия требуют финансовых трат, а вот онлайн-сборник с ГДЗ по математике (4 класс) — нет.
Готовые домашние задания по пособию Петерсона
Учебник удобно структурирован на 3 части, где есть теория и практические упражнения для закрепления материала. В первую очередь решебник пригодится четверокласснику. Он сможет улучшить средние баллы, научиться быстрее решать однотипные задания, эффективнее готовиться к занятиям, рациональнее расходовать свое время. Также учителям-математикам, преподающим предмет для 4 класса по пособию Петерсона, готовые ответы будут полезными в целях экономии времени на проверку домашки и подготовки материала ученикам. Все материалы в нем составлены в соответствии с Федеральным государственным образовательным стандартом. По структуре он повторяет учебник: ресурс разделен на три части, в каждой из которых имеются разобранные задания. Также тут есть ответы на проверочные и контрольные работы после всех параграфов.
Все материалы в нем составлены в соответствии с Федеральным государственным образовательным стандартом. По структуре он повторяет учебник: ресурс разделен на три части, в каждой из которых имеются разобранные задания. Также тут есть ответы на проверочные и контрольные работы после всех параграфов.
Онлайн-решебник доступен везде, где есть Интернет
С хорошей базой материалов ребенку интереснее получать новые знания, у него будет больше мотивации хорошо учиться, а проработать на будущее самодисциплину, аналитическое и логическое мышление поможет решебник для 4 класса.
3-8
Решите каждое неравенство и нарисуйте решение: -2(1-3x)>16-Turito
Вопрос
Подсказка:
Линейные неравенства — это выражения, в которых любые два значения сравниваются с помощью символов неравенства
<,>,≤ &≥ .
Нас просят решить неравенство и построить его график.
Правильный ответ: x>3
Шаг 1 из 2:
Переставьте и решите неравенство;
Шаг 2 из 2:
Нарисуйте график решения неравенства;
‘Хотите узнать больше?
Зарегистрируйтесь в Turito, чтобы просмотреть полное решение
У вас уже есть учетная запись? Войдите, чтобы продолжить
Когда у нас есть неравенство с символами < или >, мы используем пунктирные линии для их графического отображения. Это потому, что мы не включаем конечную точку неравенства.
Забронировать бесплатную демоверсию
Mobile*
+
91
Электронная почта*
класс*
Я согласен с уведомлениями WhatsApp и маркетинговыми обновлениями
6
. Что является решением системы уравнений?
Что является решением системы уравнений?
Y= 2x-3
Y=-5x+6
Подсказка:-
Решим данные одновременные уравнения и найдем решение.
Пошаговое решение:-
Из приведенной информации получаем-
y = 2x — 3
∴ 3 = 2x — y
т.е. 2x — y = 3 ………………… …………………………… (Уравнение i)
y = -5x + 6
∴ 5x + y = 6 ……………………………………………. …. (Уравнение ii)
Складывая уравнения i и ii, мы получаем-
2x — y = 3
+ 5x + y = 6
7x = 9
∴ x = 9/7 …….. (Деление обеих сторон на 7) ……………………………….. (Уравнение iii)
Подстановка Уравнение iii в уравнении i, мы получаем-
2x — y = 3
∴ 2 (9/7) — y = 3
∴ 18/7 — y = 3
∴ 18/7 — 3 = y
∴ -3/7 = y
Окончательный ответ: —
∴ Решением данной системы уравнений является (9/7, -3/7), т.е. x = 9/7 и y = -3/7
Примечание:-
В качестве альтернативы, мы можем нанести данные уравнения на график и найти точка пересечения как решение.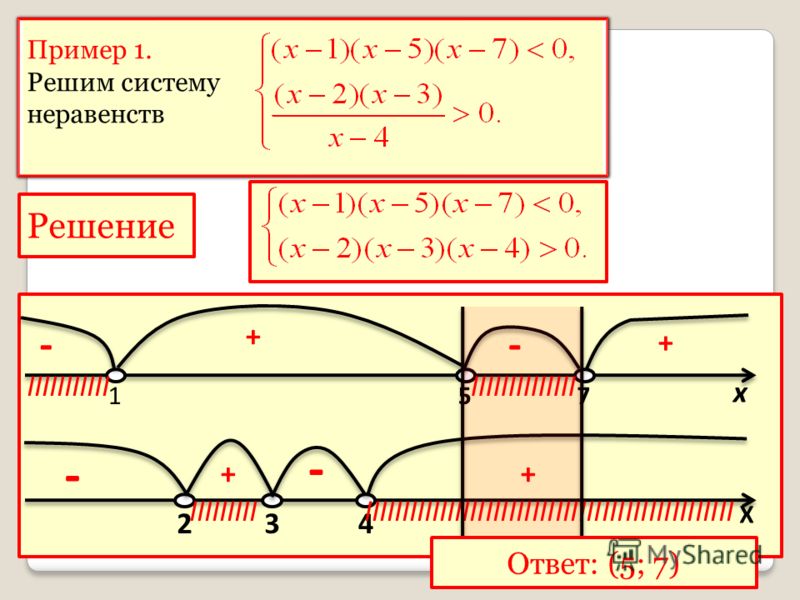 См. соседнюю диаграмму).
См. соседнюю диаграмму).
Какое решение системы уравнений?
Y= 2x-3
Y=-5x+6
Общая математика
Подсказка:-
Решим данные одновременные уравнения и найдем решение.
Пошаговое решение:-
Из данной информации получаем-
y = 2x — 3
∴ 3 = 2x — y
т.е. 2x — y = 3 ………….. …………………………… (Уравнение i)
y = -5x + 6
∴ 5x + y = 6 ………………………………. …………. (Уравнение ii)
Складывая уравнения i и ii, мы получаем-
2x — y = 3
+ 5x + y = 6
7x = 9
∴ x = 9/ 7 …….. (Деление обеих сторон на 7) …………………… … (Уравнение III)
Подставляя уравнение iii в уравнение i, получаем-
2x — y = 3
∴ 2 (9/7) — y = 3
∴ 18/7 — y = 3
∴ 18/7 — 3 = y
∴ — 3/7 = y
Окончательный ответ: —
∴ Решением данной системы уравнений является (9/7, -3/7), т. е. x = 9/7 и y = -3/7
Примечание: —
В качестве альтернативы, мы можем изобразить данные уравнения на графике и найти точку пересечения как решение. См. соседнюю диаграмму).
См. соседнюю диаграмму).
Общее
Математика-
Решите каждое неравенство и нарисуйте решение:
2(1-3x)<20
Подсказка:
Линейные неравенства — это выражения, в которых любые два значения сравниваются с помощью символов неравенства <,>,≤&≥ .
Нас просят решить неравенство и построить его график.
Шаг 1 из 2:
Переставьте и решите неравенство:
Шаг 2 из 2:
Постройте график решения неравенства;
Примечание:
Когда у нас есть неравенство с символами < или > , мы используем пунктирные линии для их графического отображения. Это потому, что мы не включаем конечную точку неравенства.
Решите каждое неравенство и нарисуйте решение:
2(1-3x)<20
Maths-General
Подсказка:
Линейные неравенства — это выражения, в которых любые два значения сравниваются с помощью символов неравенства <,>,≤&≥ .
Нас просят решить неравенство и построить его график.
Шаг 1 из 2:
Переставьте и решите неравенство:
Шаг 2 из 2:
Постройте график решения неравенства;
Примечание:
Когда у нас есть неравенство с символами < или > , мы используем пунктирные линии для их графического отображения. Это потому, что мы не включаем конечную точку неравенства.
Общий
Математика-
У Мониши и Холли есть еще 14 дней, чтобы закончить чтение того же романа для класса. Мониша планирует читать по 9 страниц каждый день. Пока Холли планирует читать по 20 страниц каждый день. Предположим, что Холли и Мониша придерживаются своего плана чтения. Когда Холли догонит Монишу? Кто первым закончит читать роман?
Подсказка:-
1. Страницы, ожидающие чтения = количество страниц, которые нужно прочитать каждый день * количество. дней для чтения
2. Всего кол. страниц в книге = Количество уже заполненных страниц + Количество страниц, ожидающих прочтения
Пошаговое решение:-
Пусть нет. дней и Мониша, и Холли будут читать отложенные страницы через x.
дней и Мониша, и Холли будут читать отложенные страницы через x.
Общее количество страниц в книге = 220 ……………………………………………………………………….. … (Уравнение i)
Количество страниц, уже заполненных Монишей = 96 …………………….. (Уравнение ii)
Нет страниц, уже заполненных Холли = 6 ………………………….. (уравнение iii)
Для Мониши —
Страниц, ожидающих чтения = Количество страниц, которые нужно прочитать каждый день * количество. дней для чтения
∴ Страниц, ожидающих чтения = 9 * x ………………………………… …. (Из предоставленной информации)
∴ Страниц, ожидающих чтения = 9x ………………………….. …………… (Уравнение iv)
Всего № страниц в книге = Количество уже заполненных страниц + Количество страниц, ожидающих прочтения
∴ Всего кол. страниц в книге = 96 + 9x ………. (из уравнений ii и iv) ……………. (уравнение v)
220 = 96 + 9x ……………………………….. (из уравнения i)
∴ 220 — 96 = 9 х
∴ 124 = 9 х
∴ 124/9 = х . ………………………… …………… (делим обе части на 9)
………………………… …………… (делим обе части на 9)
∴ 13,8 = x
∴ Мониша закончит читать книгу на 14-й день (поскольку дни не могут быть десятичными).
Аналогично, для Holly-
Количество страниц, ожидающих чтения = количество страниц, которые необходимо прочитать каждый день * количество. количество дней для чтения
∴ Страниц, ожидающих чтения = 20 * x ……………………………. ……… (Из предоставленной информации)
∴ Страниц, ожидающих чтения = 20x ……………………… ……………….. (Уравнение vi)
Общее количество страниц в книге = Количество уже заполненных страниц + Количество страниц, ожидающих прочтения
∴ Всего кол. страниц в книге = 6 + 20x ………. (из уравнений iii и vi) …………. (уравнение vii)
220 = 6 + 20x . ……………………………. (Из уравнения i)
∴ 220 — 6 = 20x
∴ 214 = 20x
∴ 214/20 = x ………………………………………….. …. (делим обе части на 20)
∴ 10,7 = x
∴ Холли закончит читать книгу на 11-й день (поскольку дни не могут быть десятичными). 909:11 Теперь нам нужно выяснить, когда Холли догонит Монишу.
909:11 Теперь нам нужно выяснить, когда Холли догонит Монишу.
т.е. №. дней после чего, нет. количество страниц, прочитанных ими обоими, будет одинаковым.
∴ Приравниваем уравнения их скорости чтения и находим решение.
∴ Приравнивая уравнения v и vii, получаем-
96 + 9x = 6 + 20x
∴ 96 — 6 = 20x — 9x
∴ 90 = 11x
∴ 90 / 11 = x ………. …………………………………………. (делим обе части на 11)
∴ 8.2 ≈ x
∴ На 9-й день Холли догонит Монишу.
Окончательный ответ:-
∴ Холли догонит Монишу примерно на 9-й день (8,2 дня) и Холли закончит читать роман (примерно через 11 дней) первой.
У Мониши и Холли есть еще 14 дней, чтобы закончить чтение того же романа для класса. Мониша планирует читать по 9 страниц каждый день. Пока Холли планирует читать по 20 страниц каждый день. Предположим, что Холли и Мониша придерживаются своего плана чтения. Когда Холли догонит Монишу? Кто первым закончит читать роман?
Maths-General
Подсказка:-
1. Страницы, ожидающие чтения = количество страниц, которые нужно читать каждый день * количество. дней для чтения
Страницы, ожидающие чтения = количество страниц, которые нужно читать каждый день * количество. дней для чтения
2. Всего кол. страниц в книге = Количество уже заполненных страниц + Страниц, ожидающих чтения
Пошаговое решение:-
Пусть нет. дней и Мониша, и Холли будут читать отложенные страницы через x.
Общее количество страниц в книге = 220 ……………………………………………………………………….. … (Уравнение i)
Количество страниц, уже заполненных Монишей = 96 …………………….. (Уравнение ii)
Количество страниц, уже заполненных Холли = 6 …….. …………………….. (Уравнение iii)
Для Monisha-
Страниц, ожидающих чтения = Количество страниц, которые нужно читать каждый день * нет. количество дней для чтения
∴ Страниц, ожидающих чтения = 9 * x …………………………… ……… (Из предоставленной информации)
∴ Страниц, ожидающих чтения = 9x ……………………… ……………….. (Уравнение iv)
Всего № страниц в книге = Количество уже заполненных страниц + Количество страниц, ожидающих прочтения
∴ Общее количество страниц в книге = 96 + 9x . ……… (из уравнений ii и iv) ……………. (уравнение v)
……… (из уравнений ii и iv) ……………. (уравнение v)
220 = 96 + 9x ………………………………. (из уравнения i)
∴ 220 — 96 = 9x
∴ 124 = 9x
∴ 124/9 = x ………………………………… ……. (делим обе части на 9)
∴ 13,8 = x
∴ Мониша закончит читать книгу на 14-й день (поскольку дни не могут быть десятичными).
Аналогично, для Holly-
Количество страниц, ожидающих чтения = количество страниц, которые необходимо прочитать каждый день * количество. дней для чтения
∴ Страниц, ожидающих чтения = 20 * x ………………………………… …. (Из предоставленной информации)
∴ Страниц, ожидающих чтения = 20x ………………………….. …………… (Уравнение vi)
Всего № страниц в книге = Количество уже заполненных страниц + Количество страниц, ожидающих прочтения
∴ Всего кол. страниц в книге = 6 + 20x ………. (из уравнений iii и vi) …………. (уравнение vii)
220 = 6 + 20x . …………………………… (Из уравнений i)
…………………………… (Из уравнений i)
∴ 220 — 6 = 20 х
∴ 214 = 20 х
∴ 214/20 = х …………………………. …………… (делим обе части на 20)
∴ 10,7 = x
∴ Холли закончит читать книгу на 11-й день (поскольку дни не могут быть десятичными).
Теперь нам нужно узнать, когда Холли догонит Монишу.
т.е. №. дней после чего, нет. количество страниц, прочитанных ими обоими, будет одинаковым.
∴ Приравниваем уравнения их скорости чтения и находим решение.
∴ Приравнивая уравнения v и vii, получаем-
96 + 9х = 6 + 20х
∴ 96 — 6 = 20х — 9х
∴ 90 = 11х
∴ 90 / 11 = х ………………… …………………………… (Деление обеих сторон на 11)
∴ 8,2 ≈ x
∴ В 9-й день , Холли догонит Монишу.
Окончательный ответ:-
∴ Холли догонит Монишу примерно на 9-й день (8,2 дня), а Холли закончит читать роман (примерно через 11 дней) первой.
Общее
Математика-
Используйте график для решения каждой системы уравнений
3X+2Y=9
3-X= 2y/3
Подсказка:-
Мы подставляем различные значения x в данные уравнения, чтобы найти соответствующие значения y, и наносим полученные таким образом координаты для обоих уравнений на график, чтобы найти решение.
Приведенные выше уравнения могут быть записаны как-
i. 3x + 2y = 9
2y = -3x + 9
y = -3/2 x + 9/2
y = -1,5x + 4,5 ……………… ……………………. (Уравнение i)
ii. 3 — х = 2/3 у
9 — 3х = 2у
4,5 — 1,5х = у
т. е. y = -1,5x + 4,5 …………………………………. , (Уравнение ii)
Пошаговое решение:-
i. Y = -1,5x + 4,5
Подставляя x = 1 в вышеприведенное уравнение, получаем: )
Подставляя x = 0 в приведенное выше уравнение, мы получаем-
y = -1,5(0) + 4,5
y = 0 + 4,5
y = 4,5
Следовательно, точка B (0,4,5)
Подставляя x = -1 в приведенном выше уравнении мы получаем-
y = -1,5 (-1) + 4,5
y = 1,5 + 4,5
y = 6
Следовательно, точка C (-1,6)
ii. Y = -1,5x + 4,5
Подставив x = 1 в вышеприведенное уравнение, получим: )
Подставляя x = 0 в приведенное выше уравнение, мы получаем-
y = -1,5(0) + 4,5
y = 0 + 4,5
y = 4,5
Следовательно, точка E (0,4,5)
Подставляя x = -1 в приведенном выше уравнении мы получаем-
y = -1,5 (-1) + 4,5
y = 1,5 + 4,5
y = 6
Следовательно, точка F (-1,6) 909:11 Наносим указанные выше координаты на график, чтобы найти решение двух уравнений.
Окончательный ответ: —
∴ Из соседнего графика видно, что графики заданных линий одинаковы.
Следовательно, данная система уравнений имеет бесконечно много решений.
Используйте график для решения каждой системы уравнений
3X+2Y=9
3-X= 2y/3
Maths-General
Подсказка:-
Мы подставляем различные значения x в данные уравнения, чтобы найти соответствующие значения y и нанесите полученные таким образом координаты для обоих уравнений на график, чтобы найти решение.
Приведенные выше уравнения можно записать в виде-
i. 3x + 2y = 9
2y = -3x + 9
y = -3/2 x + 9/2
y = -1,5x + 4,5 ……………… ……………………. (Уравнение i)
ii. 3 — x = 2/3 y
9 — 3x = 2y
4,5 — 1,5x = y
т.е. y = -1,5x + 4,5 ………………….. …………………. (Уравнение ii)
Пошаговое решение:-
i. Y = -1,5x + 4,5
Подставляя x = 1 в вышеприведенное уравнение, получаем:0911 Следовательно, точка A (1,3)
Подставляя x = 0 в вышеприведенное уравнение, получаем: ,4. 5)
5)
Подставляя x = -1 в вышеприведенное уравнение, получаем-
y = -1,5(-1) + 4,5
y = 1,5 + 4,5
y = 6
Следовательно, точка C (-1,6)
II. Y = -1,5x + 4,5
Подставив x = 1 в вышеприведенное уравнение, получим: )
Подставив x = 0 в приведенное выше уравнение, мы получим-
y = -1,5(0) + 4,5
y = 0 + 4,5
y = 4,5
Следовательно, точка E (0,4,5)
Подставляя x = -1 в приведенное выше уравнение, мы получаем-
y = -1,5( -1) + 4,5
y = 1,5 + 4,5
y = 6
Следовательно, точка F (-1,6)
. Наносим вышеуказанные координаты на график, чтобы найти решение двух уравнений.
Окончательный ответ: —
∴ Из соседнего графика видно, что графики заданных линий одинаковы.
Следовательно, данная система уравнений имеет бесконечно много решений.
Общий
Математика-
Используйте график для решения каждой системы уравнений соответствующие значения y и нанесите полученные таким образом координаты для обоих уравнений на график, чтобы найти решение.

Данные уравнения можно записать в виде-
i. у = 0,5х + 7 ………………………………………… ( Уравнение i)
ii. 4х — 8у = 12
х — 2у = 3
-2y = -x + 1,5
y = 1/2x + 1,5
y = 0,5x + 1,5 ……………………… …… (Уравнение ii)
Пошаговое решение:-
i. Y= 0,5X+7
. Подставив x = 1 в вышеприведенное уравнение, мы получим: x = 0 в приведенном выше уравнении, мы получаем-
y = 0,5 (0) + 7
y = 0 + 7
y = 7
Следовательно, точка B (0,7)
Подставляя x = -1 в приведенное выше уравнение , получаем-
у = 0,5(-1) + 7
y = -0,5 + 7
y = 6,5
Следовательно, точка C (-1,6,5)
ii. Y = 0,5x — 1,5
Подставляя x = 1 в вышеприведенное уравнение, получаем:
Подставляя x = 0 в вышеприведенное уравнение, мы получаем-
y = 0,5(0) — 1,5
y = 0 — 1,5
y = -1,5
Следовательно, точка E (0,-1,5)
Подставляя x = -1 в приведенном выше уравнении мы получаем-
y = 0,5(-1) — 1,5
y = -0,5 — 1,5
y = -2
Следовательно, точка F (-1,-2) 909:11 Наносим указанные выше координаты на график, чтобы найти решение двух уравнений.

Окончательный ответ:-
∴ Из соседнего графика видно, что график данных прямых параллельен. Мы знаем, что параллельные прямые никогда не пересекаются. Следовательно, данная система уравнений не имеет решения.
Используйте график для решения каждой системы уравнений
Y= 0,5X+7
4X-8Y=12
Maths-General
Подсказка:-
Мы подставляем различные значения x в данные уравнения, чтобы найти соответствующие значения y и нанесите полученные таким образом координаты для обоих уравнений на график, чтобы найти решение.
Данные уравнения можно записать в виде-
i. у = 0,5х + 7 ………………………………………… ( Уравнение i)
ii. 4x — 8y = 12
x — 2y = 3
-2y = -x + 1,5
y = 1/2x + 1,5
y = 0,5x + 1,5 ……………. …………….. (Уравнение ii)
Пошаговое решение:-
i. Y= 0,5X+7
Подставив x = 1 в вышеприведенное уравнение, мы получим: x = 0 в приведенном выше уравнении, мы получаем-
y = 0,5(0) + 7
y = 0 + 7
y = 7
Следовательно, точка B (0,7)
Подставляя x = -1 в вышеприведенное уравнение, получаем —
y = 0,5(-1 ) + 7
y = -0,5 + 7
y = 6,5
Следовательно, точка C (-1,6,5)
ii. Y = 0,5x — 1,5
Y = 0,5x — 1,5
Подставляя x = 1 в вышеприведенное уравнение, получаем:
Подставляя x = 0 в вышеприведенное уравнение, получаем-
y = 0,5(0) — 1,5
y = 0 — 1,5
y = -1,5
Следовательно, точка E (0,-1,5)
Подставляя x = -1 в вышеприведенное уравнение, получаем-
y = 0,5(-1) — 1,5
y = -0,5 — 1,5
y = -2
Следовательно, точка F (-1,-2)
We нанесите указанные выше координаты на график, чтобы найти решение двух уравнений.
Окончательный ответ:-
∴ Из соседнего графика видно, что график данных прямых параллельен. Мы знаем, что параллельные прямые никогда не пересекаются. Следовательно, данная система уравнений не имеет решения.
Общий
Математика-
Каково решение каждой системы уравнений ?Используйте график, чтобы пояснить свои ответы.
Y-2X=6
-4x+2Y=8
Подсказка:-
Мы подставляем различные значения x в данные уравнения, чтобы найти соответствующие значения y, и наносим полученные таким образом координаты для обоих уравнений на график найти решение.
Данные уравнения можно записать в виде-
i. y — 2x = 6
y = 2x + 6 ____________ (уравнение i)
ii. -4x + 2y = 8
2y = 8 + 4x
y = 4 + 2x __________________ (Уравнение ii)
Пошаговое решение:-
i. Y = 2x + 6
Подставляя x = 1 в вышеприведенное уравнение, мы получаем-
y = 2(1) + 6
y = 2 + 6
y = 8
Следовательно, точка A (1,8)
Подставляя x = 0 в приведенное выше уравнение, мы получаем-
y = 2(0) + 6
y = 0 + 6
y = 6
Следовательно, точка B (0,6)
Подставляя x = -1 в вышеприведенное уравнение, получаем-
y = 2(-1) + 6
y = -2 + 6
y = 4
Следовательно, точка C (-1,4)
ii. Y = 2x + 4
Подставив x = 1 в вышеприведенное уравнение, мы получим: = 0 в приведенном выше уравнении, мы получаем-
y = 2(0) + 4
y = 0 + 4
y = 4
Следовательно, точка E (0,4)
Подставляя x = -1 в вышеприведенное уравнение, получаем-
y = 2(-1 ) + 4
y = -2 + 4
y = 2
Следовательно, точка F (-1,2)
Мы наносим указанные выше координаты на график, чтобы найти решение двух уравнений.
Окончательный ответ:-
∴ Из соседнего графика видно, что график данных прямых параллельен. Мы знаем, что параллельные прямые никогда не пересекаются. Следовательно, данная система уравнений не имеет решения.
Каково решение каждой системы уравнений ?Используйте график, чтобы пояснить свои ответы.
Y-2X=6
-4x+2Y=8
Maths-General
Подсказка:-
Мы подставляем различные значения x в данные уравнения, чтобы найти соответствующие значения y и наносим координаты, полученные таким образом для обоих уравнения на графике, чтобы найти решение.
Данные уравнения можно записать в виде-
i. y — 2x = 6
y = 2x + 6 ____________ (уравнение i)
ii. -4х + 2у = 8
2y = 8 + 4x
y = 4 + 2x _____________ (уравнение ii)
Пошаговое решение:-
i. Y = 2x + 6
Подставив x = 1 в вышеприведенное уравнение, мы получим: = 0 в приведенном выше уравнении, мы получаем-
y = 2(0) + 6
y = 0 + 6
y = 6
Следовательно, точка B (0,6)
Подставляя x = -1 в приведенное выше уравнение, получаем-
y = 2(-1) + 6
y = -2 + 6
y = 4
Следовательно, точка C (-1,4)
ii. Y = 2x + 4
Y = 2x + 4
Подставив x = 1 в вышеприведенное уравнение, мы получим: = 0 в приведенном выше уравнении, мы получаем-
y = 2(0) + 4
y = 0 + 4
y = 4
Следовательно, точка E (0,4)
Подставляя x = -1 в приведенное выше уравнение, мы получаем-
y = 2 (-1) + 4
y = -2 + 4
y = 2
Следовательно, точка F (-1,2)
Мы наносим вышеуказанные координаты на график, чтобы найти решение 2 уравнения.
Окончательный ответ:-
∴ Из соседнего графика видно, что график заданных линий параллелен. Мы знаем, что параллельные прямые никогда не пересекаются. Следовательно, данная система уравнений не имеет решения.
Общий
Математика-
Каково решение каждой системы уравнений ?Используйте график, чтобы пояснить свои ответы.
15x+5y= 25
Y= 5-3x
Подсказка:-
Подставим различные значения x в данные уравнения, чтобы найти соответствующие значения y, и нанесем полученные таким образом координаты для обоих уравнений на график, чтобы найти решение.
Пошаговое решение:-
i. 15x+5y= 25
Подставляя x = 1 в вышеприведенное уравнение, получаем: (Деление обеих частей на 5)
y = 2
Следовательно, точка A (1,2)
Подставляя x = 0 в приведенное выше уравнение, мы получаем-
15(0) + 5y = 25
0 + 5y = 25
5y = 25
y = 25/5 __________ (делим обе части на 5)
y = 5
Следовательно, точка B (0,5)
Подставляя x = -1 в вышеприведенное уравнение, получаем-
15(-1) + 5y = 25
-15 + 5y = 25
5y = 25 + 15
5y = 40
y = 40/5 ___________ (делим обе части на 5)
y = 8
Следовательно, точка C (-1,8)
Наносим вышеуказанные координаты на график, чтобы найти решение двух уравнений.
Окончательный ответ: —
∴ Из соседнего графика видно, что графики заданных линий одинаковы.
Следовательно, данная система уравнений имеет бесконечно много решений.
Каково решение каждой системы уравнений ?Используйте график, чтобы пояснить свои ответы.

15x+5y= 25
Y= 5-3x
Maths-General
Подсказка:-
Мы подставляем различные значения x в данные уравнения, чтобы найти соответствующие значения y, и наносим координаты, полученные таким образом, для обоих уравнения на графике, чтобы найти решение.
Пошаговое решение:-
i. 15x+5y= 25
Подставляя x = 1 в вышеприведенное уравнение, получаем: (Деление обеих сторон на 5)
y = 2
Следовательно, точка A (1,2)
Подставив x = 0 в вышеприведенное уравнение, получим: /5 __________ (делим обе части на 5)
y = 5
Следовательно, точка B (0,5)
Подставляя x = -1 в вышеприведенное уравнение, получаем-
15(-1) + 5y = 25
— 15 + 5y = 25
5y = 25 + 15
5y = 40
y = 40/5 ___________ (делим обе части на 5)
y = 8
Следовательно, точка C (-1,8)
Наносим указанные выше координаты на графике, чтобы найти решение 2 уравнений.
Окончательный ответ:-
∴ Из соседнего графика видно, что графики заданных линий одинаковы.
Следовательно, данная система уравнений имеет бесконечно много решений.
Общий
Математика-
Используйте график для решения этой системы уравнений:
Y=2X+10
Y= -0,5X+1
Подсказка:-
Мы подставляем разные значения x в данные уравнения чтобы найти соответствующие значения y и нанести полученные таким образом координаты для обоих уравнений на график, чтобы найти решение.
Пошаговое решение:-
i. Y= 2X+10
Подставив x = -5 в вышеприведенное уравнение, мы получим: )
Подставляя x = 0 в вышеприведенное уравнение, мы получаем-
y = 2(0) + 10
y = 0 + 10
y = 10
Следовательно, точка B (0,10)
Подставляя x = 3 в приведенное выше уравнение, мы получаем-
y = 2(3) + 10
y = 6 + 10
y = 16
Следовательно, точка C (3,16)
ii. Y= -0,5X+1
Подставив x = -5 в приведенное выше уравнение, мы получим-
y = -0,5(-5) + 1
y = 2,5 + 1
y = 3,5
Следовательно, точка D (-5,3,5)
Подставляя x = 0 в приведенное выше уравнение, мы получаем —
y = -0,5 (0) + 1
y = 0 + 1
y = 1
Следовательно, точка E (0,1)
Подставляя x = 3 в приведенное выше уравнение, мы получаем —
y = -0,5(3) + 1
y = -1,5 + 1
y = -0,5
Следовательно, точка F (3,-0,5)
Нанесем вышеуказанные координаты на график, чтобы найти решение двух уравнений.
Окончательный ответ: —
∴ Из соседнего графика видно, что график заданных прямых пересекается в точке (-3.6,2.8). Следовательно, решение вышеуказанного вопроса равно (-3,6,2,8), т. е. x = -3,6 и y = 2,8.
Используйте график для решения этой системы уравнений:
Y=2X+10
Y= -0,5X+1
Maths-General
Подсказка:-
Мы подставляем различные значения x в данные уравнения, чтобы найти соответствующие значения y и нанесите полученные таким образом координаты для обоих уравнений на график, чтобы найти решение.
Пошаговое решение:-
i. Y= 2X+10
Подставив x = -5 в вышеприведенное уравнение, мы получим:
y = 2(-5) + 10
y = -10 + 10
y = 0,
Отсюда точка A (-5,0)
. Подставляя x = 0 в вышеприведенное уравнение, получаем-
y = 2(0) + 10
y = 0 + 10
y = 10
Следовательно, точка B (0 ,10)
Подставляя x = 3 в приведенное выше уравнение, мы получаем-
y = 2(3) + 10
y = 6 + 10
y = 16
Следовательно, точка C (3,16)
ii. Y= -0,5X+1
Y= -0,5X+1
. Подставив x = -5 в вышеприведенное уравнение, получим: ,3.5)
Подставляя x = 0 в приведенное выше уравнение, мы получаем-
y = -0,5(0) + 1
y = 0 + 1
y = 1
Следовательно, точка E (0,1)
Подставляя x = 3 в приведенное выше уравнение, мы получаем —
y = -0,5(3 ) + 1
y = -1,5 + 1
y = -0,5
Следовательно, точка F (3,-0,5)
Нанесем вышеуказанные координаты на график, чтобы найти решение двух уравнений.
Окончательный ответ: —
∴ Из соседнего графика видно, что график заданных прямых пересекается в точке (-3.6,2.8). Следовательно, решение вышеуказанного вопроса равно (-3,6,2,8), т. е. x = -3,6 и y = 2,8.
Общий
Математика-
Используйте график для решения этой системы уравнений:
Y= 0,5X-2
Y= 3X-7
Подсказка:-
Мы подставляем различные значения x в данные уравнения найдите соответствующие значения y и нанесите полученные таким образом координаты для обоих уравнений на график, чтобы найти решение.
Пошаговое решение:-
i. Y= 0,5X-2
Подставив x = 1 в вышеприведенное уравнение, получим:
y = 0,5(1) — 2
y = 0,5 — 2
y = -1,5
Следовательно, точка A (1,-1,5)
Подставляя x = 2 в вышеприведенное уравнение, получаем-
y = 0,5(2) — 2
y = 1 — 2
y = -1
Следовательно, точка B (2,-1)
. Подставляя x = 3 в вышеприведенное уравнение, получаем: ,-0,5)
ii. Y= 3X-7
Подставив x = 1 в приведенное выше уравнение, мы получим-
y = 3(1) — 7
y = 3 — 7
y = -4
Следовательно, точка D (1,-4)
Подставляя x = 2 в приведенное выше уравнение, мы получаем-
y = 3(2) — 7
y = 6 — 7
y = -1
Следовательно, точка E (2,-1)
Подставляя x = 3 в вышеприведенное уравнение, получаем —
y = 3(3 ) — 7
y = 9 — 7
y = 2
Следовательно, точка F (3,2)
. Наносим вышеуказанные координаты на график, чтобы найти решение двух уравнений.
Окончательный ответ:-
∴ Из соседнего графика видно, что график заданных прямых пересекается в точке (2,-1). Следовательно, решение приведенного выше вопроса равно (2,-1), т.е.
Следовательно, решение приведенного выше вопроса равно (2,-1), т.е.
Окончательный ответ: —
∴ Из соседнего графика видно, что график заданных линий пересекается в точке (2,-1). Следовательно, решение вышеуказанного вопроса равно (2,-1), т. е. x = 2 и y = -1.
Используйте график для решения этой системы уравнений:
Y= 0,5X-2
Y= 3X-7
Maths-General
Подсказка:-
Мы подставляем различные значения x в данные уравнения, чтобы найти соответствующие значения y и нанесите полученные таким образом координаты для обоих уравнений на график, чтобы найти решение.
Пошаговое решение:-
i. Y= 0,5X-2
Подставляя x = 1 в вышеприведенное уравнение, получаем:
y = 0,5(1) — 2
y = 0,5 — 2
y = -1,5
Отсюда точка А (1,-1,5)
Подставляя x = 2 в вышеприведенное уравнение, получаем-
y = 0,5(2) — 2
y = 1 — 2
y = -1
Отсюда точка B ( 2,-1)
Подставляя x = 3 в вышеприведенное уравнение, получаем-
y = 0,5(3) — 2
y = 1,5 — 2
y = -0,5
Следовательно, точка C (3,-0,5)
II. Y= 3X-7
Y= 3X-7
Подставив x = 1 в приведенное выше уравнение, мы получим-
y = 3(1) — 7
y = 3 — 7
y = -4
Следовательно, точка D (1,-4)
Подставляя x = 2 в приведенное выше уравнение, мы получаем-
y = 3(2) — 7
y = 6 — 7
y = -1
Следовательно, точка E (2,-1)
Подставляя x = 3 в вышеприведенное уравнение, получаем —
y = 3(3 ) — 7
y = 9 — 7
y = 2
Следовательно, точка F (3,2)
. Наносим вышеуказанные координаты на график, чтобы найти решение двух уравнений.
Окончательный ответ:-
∴ Из соседнего графика видно, что график заданных прямых пересекается в точке (2,-1). Следовательно, решение приведенного выше вопроса равно (2,-1), т.е.
Окончательный ответ: —
∴ Из соседнего графика видно, что график заданных линий пересекается в точке (2,-1). Следовательно, решение вышеуказанного вопроса равно (2,-1), т. е. x = 2 и y = -1.
Общий
Математика-
Решите систему уравнений графически:
Y= -2x-4
Y= 0,5x+6 соответствующие значения y и нанесите полученные таким образом координаты для обоих уравнений на график, чтобы найти решение.

Пошаговое решение:-
i. Y= -2x-4
Подставляя x = -5 в приведенное выше уравнение, мы получаем-
y = -2(-5) — 4
y = 10 — 4
y = 6
Следовательно, точка A (-5,6)
Подставляя x = 2 в вышеприведенное уравнение, получаем-
y = -2(2) — 4
y = -4 — 4
y = -8
Следовательно, точка B (2,-8)
Подставляя x = 3 в вышеприведенное уравнение, получаем-
y = -2(3) — 4
y = -6 — 4
y = -10
-10)
ii. Y= 0,5x+6
Подставляя x = -5 в вышеприведенное уравнение, получаем: 3.5)
Подставляя x = 2 в приведенное выше уравнение, мы получаем-
y = 0,5(2) + 6
y = 1 + 6
y = 7
Следовательно, точка E (2,7)
Подставляя x = 3 в вышеприведенное уравнение, получаем:
y = 0,5(3) + 6
y = 1,5 + 6
y = 7,5
Следовательно, точка F (3,7.5)
. Наносим вышеуказанные координаты на график, чтобы найти решение двух уравнений.
Окончательный ответ:-
∴ Из соседнего графика видно, что график заданных линий пересекается в точке (-4,4).
 Следовательно, решение вышеуказанного вопроса равно (-4,4), т. е. x = -4 & y = 4.
Следовательно, решение вышеуказанного вопроса равно (-4,4), т. е. x = -4 & y = 4.Решите систему уравнений графически:
Y= -2x-4
Y= 0,5x+6
Maths-General
Подсказка:-
Мы подставляем различные значения x в данные уравнения, чтобы найти соответствующие значения от y и нанесите полученные таким образом координаты обоих уравнений на график, чтобы найти решение.
Пошаговое решение:-
i. Y= -2x-4
Подставляя x = -5 в вышеприведенное уравнение, получаем-
y = -2(-5) — 4
y = 10 — 4
y = 6
Следовательно, точка A (-5, 6)
Подставив x = 2 в приведенное выше уравнение, мы получим-
y = -2(2) — 4
y = -4 — 4
y = -8
Следовательно, точка B (2,-8)
Подставив x = 3 в приведенном выше уравнении мы получаем-
y = -2(3) — 4
y = -6 — 4
y = -10
Следовательно, точка C (3,-10)
ii. Y= 0,5x+6
Подставляя x = -5 в вышеприведенное уравнение, получаем: 3.5)
Подставляя x = 2 в вышеприведенное уравнение, получаем:
y = 0,5(2) + 6
y = 1 + 6
y = 7
Следовательно, точка E (2,7)
Подставляя x = 3 в вышеприведенное уравнение, получаем:
y = 0,5(3) + 6
y = 1,5 + 6
y = 7,5
Следовательно, точка F (3,7,5)
Нанесем указанные выше координаты на график, чтобы найти решение двух уравнений.
Окончательный ответ:-
∴ Из соседнего графика видно, что график заданных линий пересекается в точке (-4,4). Следовательно, решение вышеуказанного вопроса равно (-4,4), т. е. x = -4 и y = 4.
Общее
Maths-
Решите каждое неравенство и нарисуйте решение
-2(3x-1)>20
Подсказка:
Линейные неравенства — это выражения, в которых любые два значения сравниваются с помощью символов неравенства <,>,≤&≥ .
Нас просят решить неравенство и построить его график.
Шаг 1 из 2:
Переставьте и решите неравенство;
Шаг 2 из 2:
Постройте график решения неравенства;
Примечание:
Когда у нас есть неравенство с символами < или > , мы используем пунктирные линии для их графического отображения. Это потому, что мы не включаем конечную точку неравенства.
Решите каждое неравенство и нарисуйте решение
-2(3x-1)>20
Maths-General
Подсказка:
Линейные неравенства — это выражения, в которых любые два значения сравниваются с помощью символов неравенства <,>,≤&≥ .
Нас просят решить неравенство и построить его график.
Шаг 1 из 2:
Переставьте и решите неравенство;
Шаг 2 из 2:
Постройте график решения неравенства;
Примечание:
Когда у нас есть неравенство с символами < или > , мы используем пунктирные линии для их графического отображения. Это потому, что мы не включаем конечную точку неравенства.
Общий
Математика-
Скорость роста подсолнуха с 14 по 35 день почти постоянна. На этом интервале какое из следующих уравнений лучше всего описывает высоту h в сантиметрах подсолнуха через t дней после того, как он начал расти?
В 1919 году Х. С. Рид и Р. Х. Холланд опубликовали статью о выращивании подсолнечника. В документ были включены таблица и график выше, которые показывают высоту h в сантиметрах подсолнуха через t дней после того, как подсолнух начал расти.
Решение:
Подсказка:
- Для записи уравнения прямой нам нужны две точки
- Затем используем формулы
Объяснение:
- Мы привели данные и график роста подсолнуха за разные периоды времени.

- Нам нужно найти уравнение, связывающее h, t на интервале .
Шаг 1 из 2:
Мы знаем, что высота на
Поскольку скорость постоянна, график представляет собой прямую линию.
Чей наклон будет
Используя форму точки-наклона, мы можем записать уравнение как
Итак, вариант (B) правильный.
Скорость роста подсолнечника с 14 по 35 день почти постоянна. На этом интервале какое из следующих уравнений лучше всего описывает высоту h в сантиметрах подсолнуха через t дней после того, как он начал расти?
В 1919 году Х. С. Рид и Р. Х. Холланд опубликовали статью о выращивании подсолнечника. В документ были включены таблица и график выше, которые показывают высоту h в сантиметрах подсолнуха через t дней после того, как подсолнух начал расти.
Maths-General
Решение:
Подсказка:
- Для записи уравнения прямой нам нужны две точки
- Затем используем формулы
Объяснение:
- Мы привели данные и график роста подсолнуха за разные периоды времени.

- Нам нужно найти уравнение, связывающее h, t на интервале .
Шаг 1 из 2:
Мы знаем, что высота на
Т.к. скорость постоянная, то график представляет собой прямую линию.
Чей наклон будет
Используя форму точки-наклона, мы можем записать уравнение как
Итак, Вариант (B) правильный.
Общее
Математика-
Решите каждое неравенство и нарисуйте решение:
4x+1+2x≥5
Подсказка:
Линейные неравенства — это выражения, в которых любые два значения сравниваются с помощью символов неравенства <,>,≤& ≥ .
Нас просят решить неравенство и построить его график.
Шаг 1 из 2:
Переставьте и решите неравенство;
Шаг 2 из 2:
Постройте график решения неравенства;
Примечание:
Всякий раз, когда мы используем символ ≤ или ≥ , мы также используем конечную точку. Итак, мы используем полную линию для построения графика решения.
Решите каждое неравенство и нарисуйте решение:
4x+1+2x≥5
Maths-General
Подсказка:
Линейные неравенства — это выражения, в которых любые два значения сравниваются с помощью символов неравенства <,>,≤&≥ .
Нас просят решить неравенство и построить его график.
Шаг 1 из 2:
Переставьте и решите неравенство;
Шаг 2 из 2:
Постройте график решения неравенства;
Примечание:
Всякий раз, когда мы используем символ ≤ или ≥ , мы также используем конечную точку. Итак, мы используем полную линию для построения графика решения.
Общий
Математика-
Если a является решением приведенного выше уравнения и a > 0, каково значение a ?
Подсказка:
Мы используем метод факторинга для решения данного квадратного уравнения.
Объяснения:
Шаг 1 из 3 :
Данное квадратное уравнение
Теперь мы можем записать приведенное выше уравнение в такой форме
Шаг 2 из 3 :
Мы знаем, что если произведение двух чисел равно нулю, то либо числа должны быть равны нулю.
Следовательно, или
Шаг 3 из 3:
Так как a является решением данного уравнения и a > 0, т. е. a положительно, то a должно быть равно 3 .
∴ a = 3
Окончательный ответ:
Значение a равно 3.
Если а является решением приведенного выше уравнения и а > 0, каково значение а ?
Maths-General
Подсказка:
Для решения данного квадратного уравнения мы используем метод факторинга.
Объяснения:
Шаг 1 из 3 :
Данное квадратное уравнение
Теперь мы можем записать приведенное выше уравнение в такой форме
Шаг 2 из 3 :
Мы знаем, что если произведение двух чисел равно нулю, то либо числа должны быть равны нулю.
Следовательно, или
Шаг 3 из 3:
Так как а является решением данного уравнения и а > 0, т. е. а положительно, то а должно быть 3 .
∴ a = 3
Окончательный ответ:
Значение a равно 3.
Общее
Математика-
миллиарды фунтов стерлингов.
 На графике ниже показаны данные и линия наилучшего соответствия. Уравнение линии наилучшего соответствия: , где x – количество лет, прошедших с 19 лет.85, а y — количество ежегодно производимого пластика в миллиардах фунтов стерлингов.
На графике ниже показаны данные и линия наилучшего соответствия. Уравнение линии наилучшего соответствия: , где x – количество лет, прошедших с 19 лет.85, а y — количество ежегодно производимого пластика в миллиардах фунтов стерлингов. Что из следующего ближе всего к процентному увеличению миллиардов фунтов пластика, произведенного в Соединенных Штатах с 2000 по 2003 год?
Подсказка:
Мы наблюдаем за точками данных, особенно выделенными, и пытаемся решить проблему интуитивно.
Формула процентного увеличения выглядит следующим образом:
Пояснения:
Шаг 1 из 2:
Нам нужно найти процентное увеличение производства пластика в США с 2000 по 2003 год9.0911 Обратите внимание на выделенные точки на рисунке.
Левая — это точка данных за 2000 год, поскольку она находится на 15-й -й x -осевой линии и (1985+15)=2000. Эта точка точно равна 100 от линии оси y .
А правый — 2003 года, и он где-то посередине 100 и 120 линий и оси. Для простоты мы рассматриваем значение как 110.
Для простоты мы рассматриваем значение как 110.
Шаг 2 из 2:
Теперь, согласно формуле процентного увеличения, мы имеем новое значение = 110 и исходное значение = 100.
Итак, % прироста определяется как %-прирост
Окончательный ответ:
Ближайший к процентному приросту из приведенных вариантов — А) 10% пластика, ежегодно производимого в США, в миллиардах фунтов стерлингов. На графике ниже показаны данные и линия наилучшего соответствия. Уравнение линии наилучшего соответствия , где x – количество лет, прошедших с 1985 года, а y – количество ежегодно производимого пластика в миллиардах фунтов.
Что из следующего ближе всего к процентному увеличению миллиардов фунтов пластика, произведенного в Соединенных Штатах с 2000 по 2003 год?
Maths-General
Подсказка:
Мы наблюдаем за точками данных, особенно выделенными, и пытаемся решить задачу интуитивно.
Формула процентного увеличения выглядит следующим образом:
Пояснения:
Шаг 1 из 2:
Нам нужно найти процентное увеличение производства пластика в США с 2000 по 2003 год9. 0911 Обратите внимание на выделенные точки на рисунке.
0911 Обратите внимание на выделенные точки на рисунке.
Левая — это точка данных за 2000 год, поскольку она находится на 15-й -й x -осевой линии и (1985+15)=2000. Эта точка точно равна 100 от линии оси y .
А правый — 2003 года, и он где-то посередине 100 и 120 линий и оси. Для простоты мы рассматриваем значение как 110.
Шаг 2 из 2:
Теперь, согласно формуле процентного увеличения, мы имеем новое значение = 110 и исходное значение = 100.
Таким образом, % прироста определяется как %-прирост
Окончательный ответ:
Ближайший к процентному приросту из заданных вариантов – А) 10%
Цели обучения
К концу этого раздела вы сможете:
- Решать квадратные неравенства графически
- Алгебраическое решение квадратных неравенств
Прежде чем начать, пройдите этот тест на готовность.
- Решить:
Если вы пропустили эту проблему, просмотрите (рисунок).

- Решить: .
Если вы пропустили эту проблему, просмотрите (рисунок).
- Решить
Если вы пропустили эту проблему, просмотрите (рисунок).
Ранее мы научились решать линейные неравенства и рациональные неравенства. Некоторые из методов, которые мы использовали для их решения, были одинаковыми, а некоторые отличались.
Теперь мы научимся решать неравенства, имеющие квадратное выражение. Мы будем использовать некоторые приемы решения линейных и рациональных неравенств, а также квадратных уравнений.
Квадратные неравенства будем решать двумя способами — и графически, и алгебраически.
Решить квадратное неравенство графически
Квадратное уравнение имеет стандартную форму, если записать его как x 2 + bx + c = 0. Если мы заменим знак равенства знаком неравенства, мы получим квадратное неравенство в стандартной форме.
Квадратное неравенство
Квадратное неравенство — это неравенство, содержащее квадратное выражение.
Стандартная форма квадратного неравенства записывается:
График квадратичной функции Когда мы спрашиваем, когда ax 2 + bx + c < 0, мы спрашиваем, когда f( x ) < 0. Мы хотим знать, когда парабола находится ниже оси x .
Когда мы спрашиваем, когда x 2 + bx + c > 0, мы спрашиваем, когда f ( x ) > 0. Мы хотим знать, когда парабола выше и -ось.
Как решить квадратное неравенство графически
Решить графически. Запишите решение в интервальной записи.
ⓐ Решите графически и ⓑ запишите решение в интервальной записи.
ⓐ
ⓑ
ⓐ Решите графически и ⓑ запишите решение в интервальной записи.
ⓐ
ⓑ
Перечислим шаги, необходимые для графического решения квадратного неравенства.
Решите квадратное неравенство графически.
- Запишите квадратное неравенство в стандартной форме.
- График функции
- Определите решение по графику.
В последнем примере парабола открылась вверх, а в следующем — вниз. В обоих случаях мы ищем ту часть параболы, которая ниже 9.2157 x , но обратите внимание, как положение параболы влияет на решение.
Решить графически. Запишите решение в интервальной записи.
 The x-intercepts are (negative 6, 0) and (negative 2, 0). The graph shown is the curve formed when plotting all the points just found. Then, determine the solution from the graph, (negative infinity, negative 6] in union with [negative 2, infinity). We include the x-intercepts as the inequality is “less than or equal to.”» data-label=»»>
The x-intercepts are (negative 6, 0) and (negative 2, 0). The graph shown is the curve formed when plotting all the points just found. Then, determine the solution from the graph, (negative infinity, negative 6] in union with [negative 2, infinity). We include the x-intercepts as the inequality is “less than or equal to.”» data-label=»»>Вершина
 Позволять .
Позволять .Использовать свойство нулевого продукта.
Мы включаем x -отрезков как неравенство
— «меньше или равно».
ⓐ Решите графически и ⓑ запишите решение в интервальной записи.
ⓐ
ⓑ
ⓐ Решите графически и ⓑ запишите решение в интервальной записи.
ⓐ
ⓑ
Алгебраическое решение квадратных неравенств
Алгебраический метод, который мы будем использовать, очень похож на метод, который мы использовали для решения рациональных неравенств. Найдем критические точки неравенства, которые будут решениями соответствующего квадратного уравнения. Помните, что полиномиальное выражение может менять знак только тогда, когда оно равно нулю.
Найдем критические точки неравенства, которые будут решениями соответствующего квадратного уравнения. Помните, что полиномиальное выражение может менять знак только тогда, когда оно равно нулю.
Мы будем использовать критические точки, чтобы разделить числовую прямую на интервалы, а затем определить, будет ли квадратное выражение положительным или отрицательным в интервале. Затем находим решение неравенства.
Алгебраическое решение квадратных неравенств
Алгебраическое решение. Запишите решение в интервальной записи.
Решить алгебраически. Запишите решение в интервальной записи.
Решить алгебраически. Запишите решение в интервальной записи.
В этом примере, поскольку выражение хорошо влияет на множители, мы также можем найти знак в каждом интервале так же, как мы делали это при решении рациональных неравенств. Находим знак каждого из сомножителей, а затем знак произведения. Наша числовая строка будет выглядеть так:
Результат будет таким же, как и при использовании другого метода.
Здесь мы суммируем шаги.
Алгебраически решить квадратное неравенство.
- Запишите квадратное неравенство в стандартной форме. г.
- Определите критические точки — решения соответствующего квадратного уравнения.
- Используйте критические точки, чтобы разделить числовую прямую на интервалы.
- Над числовой прямой покажите знак каждого квадратного выражения, используя контрольные точки из каждого интервала, подставленного в исходное неравенство.
- Определите интервалы, на которых неравенство верно. Запишите решение в интервальной записи.
Решить алгебраически. Запишите решение в интервальной записи.
 A number line is shown with 1 and 6 tenths and 4 and 4 tenths. Test the numbers from each interval in the original inequality. On the number line, negative x squared plus 6 times x minus 7 is shown with the signs negative, positive, and negative. Determine the intervals where the inequality is correct. Write the solution in interval notation. negative x squared plus 6 times x minus 7 is greater than or equals to 0 in the middle interval, so the final answer is [3 minus square root of 2, 3 plus square root of 2″ data-label=»»>
A number line is shown with 1 and 6 tenths and 4 and 4 tenths. Test the numbers from each interval in the original inequality. On the number line, negative x squared plus 6 times x minus 7 is shown with the signs negative, positive, and negative. Determine the intervals where the inequality is correct. Write the solution in interval notation. negative x squared plus 6 times x minus 7 is greater than or equals to 0 in the middle interval, so the final answer is [3 minus square root of 2, 3 plus square root of 2″ data-label=»»>Не забудьте поменять знак неравенства.
соответствующее квадратное уравнение.
номер строки на интервалы.
Тестовые номера из каждого интервала
в исходном неравенстве.
неравенство верно. Напишите решение
Напишите решение
в интервальной записи.
Решить алгебраически. Запишите решение в интервальной записи.
Решить алгебраически. Запишите решение в интервальной записи.
Решениями квадратных неравенств в каждом из предыдущих примеров были либо интервал, либо объединение двух интервалов. Это произошло из-за того, что в каждом случае было найдено два решения соответствующего квадратного уравнения x 2 + bx + c = 0. Затем эти два решения дали нам либо две точки пересечения x- для графика, либо две критические точки для разделения числовой прямой на интервалы.
Это коррелирует с нашим предыдущим обсуждением количества и типа решений квадратного уравнения с использованием дискриминанта.
Для квадратного уравнения вида ах 2 + bx + с = 0,
Последняя строка таблицы показывает нам, когда параболы никогда не пересекают ось x . Используя квадратную формулу для решения квадратного уравнения, подкоренное число является отрицательным. Получаем два комплексных решения.
В следующем примере решения квадратного неравенства будут получены в результате комплексного решения квадратного уравнения.
Решить, записав любое решение в интервальной записи:
ⓐⓑ
ⓐ
соответствующее квадратное уравнение.
Также парабола открывается вверх. Это
говорит нам, что парабола находится полностью над осью x .
Требуется найти решение задачи Поскольку для всех значений графика выше оси x , все значения x делают неравенство верным. В интервальных обозначениях мы пишем
В интервальных обозначениях мы пишем
ⓑ
Поскольку соответствующее квадратное уравнение такое же, как в части (а), то и парабола будет такой же. Парабола открывается вверх и находится полностью над осью x — ни одна ее часть не находится ниже оси x .
Нам нужно найти решение задачи Поскольку для всех значений x график никогда не находится ниже оси x , никакие значения x не делают неравенство верным. Неравенство не имеет решения.
Решите и запишите любое решение в интервальной записи: 9
Решите и запишите любое решение в виде интервалов:
Основные понятия
- Графическое решение квадратного неравенства
- Запишите квадратное неравенство в стандартной форме.
- Постройте график функции, используя свойства или преобразования.

- Определите решение по графику.
- Как решить квадратное неравенство алгебраически
- Запишите квадратное неравенство в стандартной форме.
- Определите критические точки — решения соответствующего квадратного уравнения.
- Используйте критические точки, чтобы разделить числовую прямую на интервалы.
- Над числовой прямой покажите знак каждого квадратного выражения, используя контрольные точки из каждого интервала, подставленного в исходное неравенство.
- Определите интервалы, на которых неравенство верно. Запишите решение в интервальной записи. г.
Раздел Упражнения
Практика делает совершенным
Решите квадратные неравенства графически
В следующих упражнениях ⓐ решите графически и ⓑ запишите решение в интервальной записи.
В следующих упражнениях решите каждое неравенство алгебраически и запишите любое решение в интервальной записи.
no solution
Письменные упражнения
Объясните критические точки и то, как они используются для алгебраического решения квадратных неравенств.
Ответы будут разными.
Решите как графически, так и алгебраически. Какой метод вы предпочитаете и почему?
Опишите шаги, необходимые для графического решения квадратного неравенства.
Ответы будут разными.
Опишите шаги, необходимые для алгебраического решения квадратного неравенства.
Самопроверка
ⓐ После выполнения упражнений используйте этот контрольный список, чтобы оценить свое мастерство в выполнении целей этого раздела.
ⓑ По шкале от 1 до 10, как бы вы оценили свое знание этого раздела в свете ваших ответов на контрольный список? Как вы можете улучшить это?
Упражнения на обзор глав
Решение квадратных уравнений с использованием свойства квадратного корня
Решение квадратных уравнений вида ax 2 = k Использование свойства квадратного корня
7 9 Корневое свойство.
11.
Решение квадратных уравнений вида с использованием свойства квадратного корня
В следующих упражнениях решите уравнение с использованием свойства квадратного корня.
Solve Quadratic Equations by Completing the Square
Solve Quadratic Equations Using Completing the Square
In the following exercises , завершите квадрат так, чтобы получился идеальный квадратный трехчлен. Затем запишите результат в виде бинома в квадрате.
Затем запишите результат в виде бинома в квадрате.
В следующих упражнениях решите, заполнив квадрат.
Solve Quadratic Equations of the form ax 2 + bx + c = 0, заполнив квадрат
В следующих упражнениях решите, заполнив квадрат.
Solve Quadratic Equations Using the Quadratic Formula
In the following exercises, solve by using the Quadratic Formula.
Use the Discriminant to Predict Количество решений квадратного уравнения
В следующих упражнениях определите количество решений для каждого квадратного уравнения.
ⓐ 1 ⓑ 2 ⓒ 2 ⓓ 2
Определите наиболее подходящий метод решения квадратного уравнения решать каждое квадратное уравнение. Не решить.
ⓐ множитель ⓑ Квадратная формула ⓒ квадратный корень
Решение уравнений в квадратной форме
Решение уравнений в квадратной форме
В следующих упражнениях решите.
Solve Applications of Quadratic Equations
Solve Applications Modeled by Quadratic Equations
In the following упражнения, решите, используя метод факторинга, принцип квадратного корня или квадратную формулу. Округлите свои ответы до десятых, если необходимо.
Найдите два последовательных нечетных числа, произведение которых равно 323.
Найдите два последовательных четных числа, произведение которых равно 624.
Два последовательных четных числа, произведение которых равно 624, это 24 и 26, а также -24 и -26.
Треугольный баннер имеет площадь 351 квадратный сантиметр. Длина основания на два сантиметра больше, чем в четыре раза больше высоты. Найдите высоту и длину основания.
Юлий построил треугольную витрину для своей коллекции монет. Высота витрины на шесть дюймов меньше, чем удвоенная ширина основания. Площадь задней части корпуса составляет 70 квадратных дюймов. Найдите высоту и ширину корпуса.
Высота 14 дюймов, ширина 10 дюймов.
Плитка-мозаика в форме прямоугольного треугольника используется в качестве угла прямоугольной дорожки. Гипотенуза мозаики равна 5 футам. Одна сторона мозаики в два раза длиннее другой. Каковы длины сторон? Округлите до десятых.
Прямоугольный кусок фанеры имеет диагональ, которая на два фута больше ширины. Длина фанеры в два раза больше ширины. Какова длина диагонали фанеры? Округлите до десятых.
Какова длина диагонали фанеры? Округлите до десятых.
Длина диагонали 3,6 фута.
Проход от улицы к дому Пэм имеет площадь 250 квадратных футов. Его длина в два раза меньше ширины в четыре раза. Найдите длину и ширину тротуара. Округлите до десятых.
Для выпускного вечера Софии несколько столов одинаковой ширины будут расставлены встык, чтобы получился сервировочный стол общей площадью 75 квадратных футов. Общая длина столов будет в два раза больше ширины. Найдите длину и ширину сервировочного стола, чтобы София могла купить скатерть нужного размера. Ответ округлить до десятых.
Ширина сервировочного стола 4,7 фута, а длина 16,1 фута.
Мяч брошен вертикально в воздух со скоростью 160 футов/сек. Используйте формулу ч = -16 t 2 + v 0 t , чтобы определить, когда мяч будет на высоте 384 фута от земли. Округлите до десятых.
Округлите до десятых.
Пара на маленьком самолете совершила быстрый полет в винную страну для романтического ужина, а затем вернулась домой. Самолет летел в общей сложности 5 часов и в одну сторону расстояние составило 360 миль. Если самолет летел со скоростью 150 миль в час, какова была скорость ветра, действовавшего на самолет?
Скорость ветра была 30 миль в час.
Эзра плыл вверх по реке и обратно в общей сложности за 6 часов. Путь был 4 мили в одну сторону, и течение было трудным. Если Рой плыл на байдарке со скоростью 5 миль в час, какова была скорость течения?
Два мастера могут сделать ремонт дома за 2 часа, если они будут работать вместе. Одному из мужчин требуется на 3 часа больше, чем другому, чтобы закончить работу самостоятельно. Сколько времени требуется каждому мастеру на ремонт дома индивидуально?
Одному человеку требуется 3 часа, а другому 6 часов, чтобы закончить ремонт в одиночку.
График квадратичных функций с использованием свойств
Распознавание графика квадратичной функции
В следующих упражнениях постройте график по точкам.
График
График
В следующих упражнениях определите, раскрываются ли следующие параболы вверх или вниз.
ⓐ
ⓑ
ⓐ
ⓑ
ⓐ вверх ⓑ вниз
Найдите ось симметрии и вершину параболы
В следующих упражнениях найдите ⓐ уравнение оси симметрии и ⓑ вершину.
Найдите точки пересечения параболы
В следующих упражнениях найдите точки пересечения x и y .
Построение графика квадратичных функций с использованием свойств
В следующих упражнениях построение графика с использованием его свойств.
.Максимальное значение равно 2, когда x = 2,
В следующих упражнениях решите. Округление ответов до десятых.
Округление ответов до десятых.
Мяч брошен вверх с земли с начальной скоростью 112 футов/сек. Используйте квадратное уравнение ч = -16 t 2 + 112 t , чтобы найти, сколько времени потребуется мячу, чтобы достичь максимальной высоты, а затем найдите максимальную высоту.
Детский сад огораживает прямоугольную площадку вдоль стены своего здания, чтобы дети могли играть на открытом воздухе. Им нужно максимально увеличить площадь, используя 180-футовое ограждение с трех сторон двора. Квадратное уравнение A = −2 x 2 + 180 x дает площадь A двора для длины x здания, которое будет ограничивать двор. Найдите длину здания, которое должно граничить с двором, чтобы площадь была максимальной, а затем найдите максимальную площадь.
Примыкающая к зданию длина составляет 90 футов, что дает максимальную площадь 4050 квадратных футов.
График квадратичных функций с использованием преобразований
График квадратичных функций вида
В следующих упражнениях постройте график каждой функции, используя сдвиг по вертикали.
В следующих упражнениях постройте график каждой функции, используя сдвиг по горизонтали.
В следующих упражнениях постройте график каждой функции, используя преобразования.
График квадратичных функций вида
В следующих упражнениях постройте график каждой функции.
График квадратичных функций с использованием преобразований
В следующих упражнениях перепишите каждую функцию в форме, заполнив квадрат.
В следующих упражнениях ⓐ перепишите каждую функцию в форме и ⓑ нарисуйте ее, используя преобразования.
В следующих упражнениях ⓐ перепишите каждую функцию в форме и ⓑ нарисуйте ее, используя свойства.
Найдите квадратичную функцию по ее графику
В следующих упражнениях запишите квадратичную функцию в форме.
Решение квадратных неравенств
Решение квадратных неравенств графически
В следующих упражнениях решите графически и запишите решение в интервальной записи.
В следующих упражнениях решите каждое неравенство алгебраически и запишите любое решение в интервальной записи.
нет решения
Практический тест
Использование свойства «Квадратный корень» для решения квадратного уравнения
Использование «Заполнение квадрата» для решения квадратного уравнения
Использование квадратной формулы для решения квадратного уравнения
Решите следующие квадратные уравнения. Используйте любой метод.
Используйте любой метод.
Используйте дискриминант для определения количества и типа решений каждого квадратного уравнения.
2 комплекса
Решите каждое уравнение.
Для каждой параболы найти ⓐ направление, в котором она раскрывается, ⓑ уравнение оси симметрии, ⓒ вершину, ⓓ x- и y -максимальные точки пересечения, e) или минимальное значение.
ⓐ вниз ⓑ
ⓒ ⓓ
ⓔ минимальное значение, когда
Постройте график каждой квадратичной функции, используя точку пересечения, вершину и уравнение оси симметрии.
В следующих упражнениях постройте график каждой функции, используя преобразования.
В следующих упражнениях решите каждое неравенство алгебраически и запишите любое решение в интервальной записи.
Смоделируйте ситуацию квадратным уравнением и решите любым методом.

 Знаки ≥ (больше или равно) и ≤ (меньше или равно)
Знаки ≥ (больше или равно) и ≤ (меньше или равно)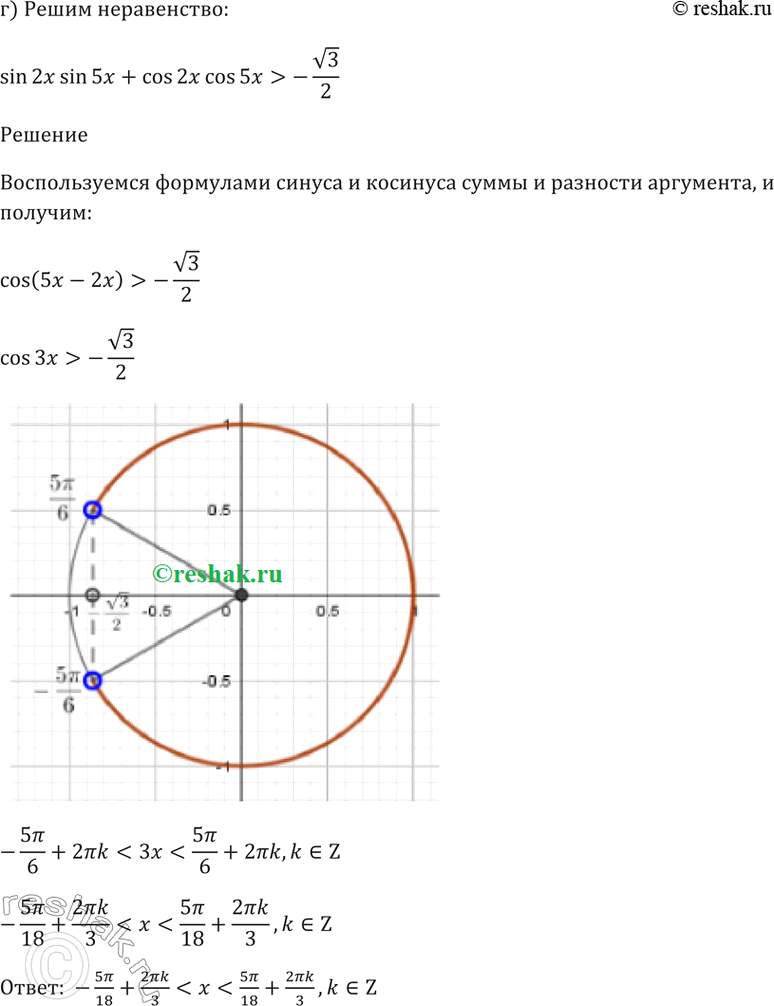 Оценка суммы
Оценка суммы Оценка частного
Оценка частного

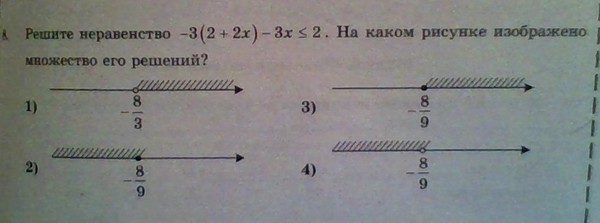 Из истории дробей
Из истории дробей Проценты
Проценты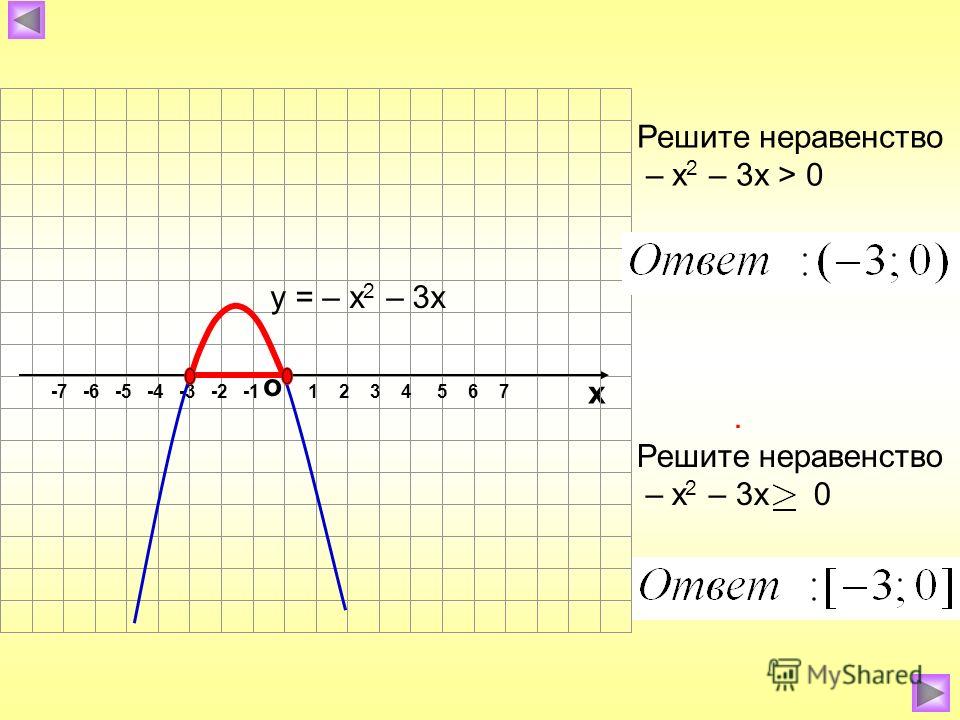 Сравнение дробей
Сравнение дробей Площадь прямоугольного треугольника
Площадь прямоугольного треугольника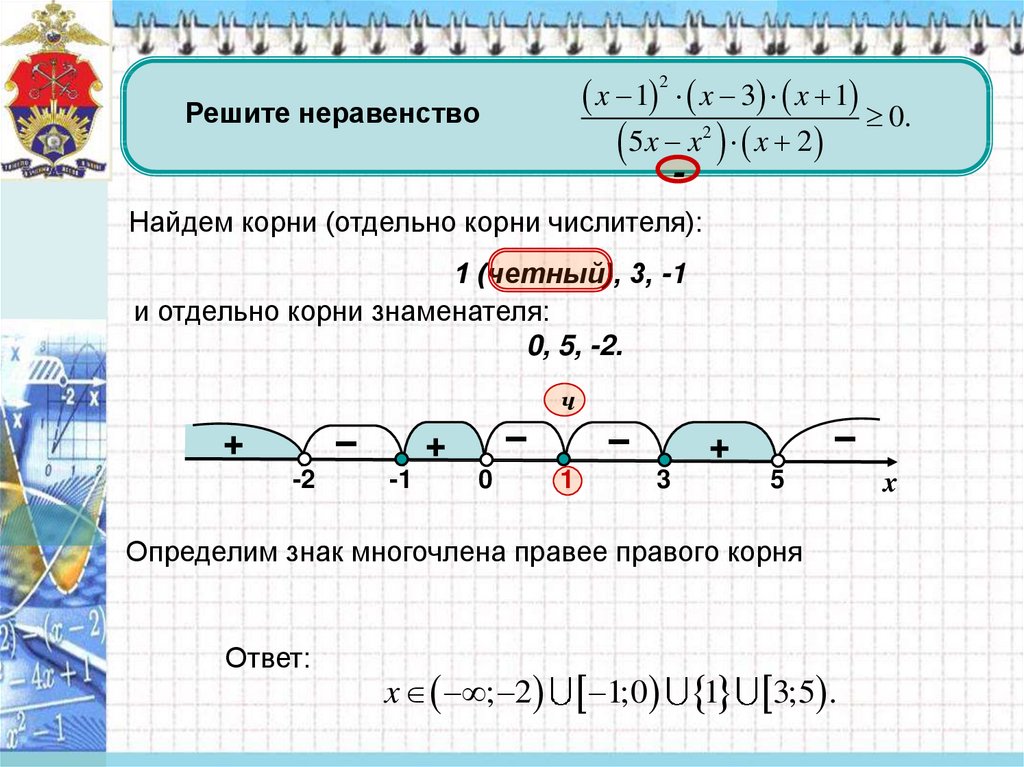 Сложение дробей
Сложение дробей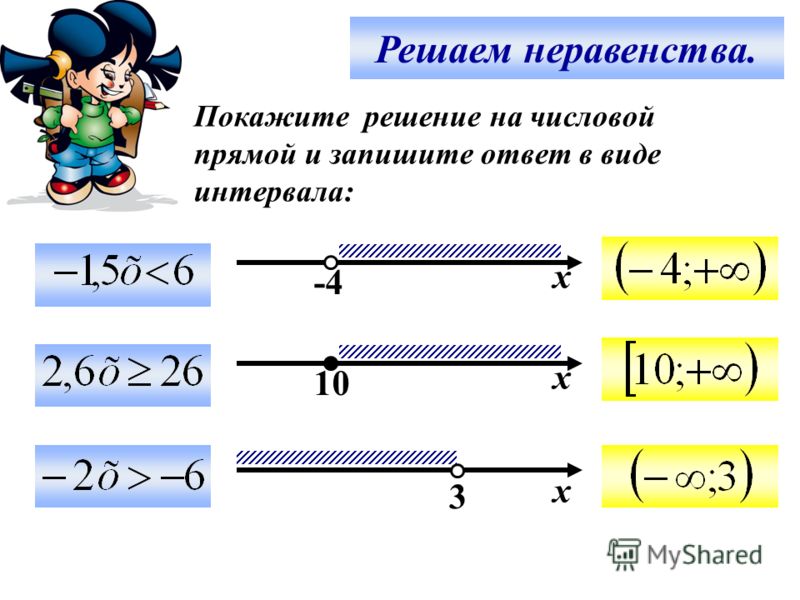 Правильные и неправильные части величин
Правильные и неправильные части величин Выделение целой части из неправильной дроби
Выделение целой части из неправильной дроби

 Расстояние между точками координатного луча
Расстояние между точками координатного луча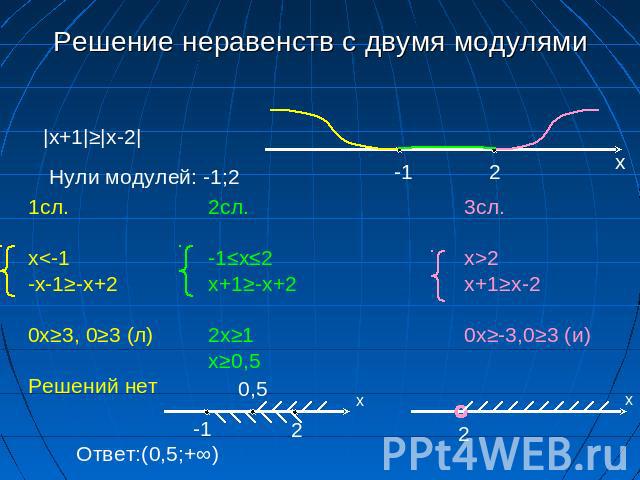 Одновременное движение по координатному лучу
Одновременное движение по координатному лучу Встречное движение
Встречное движение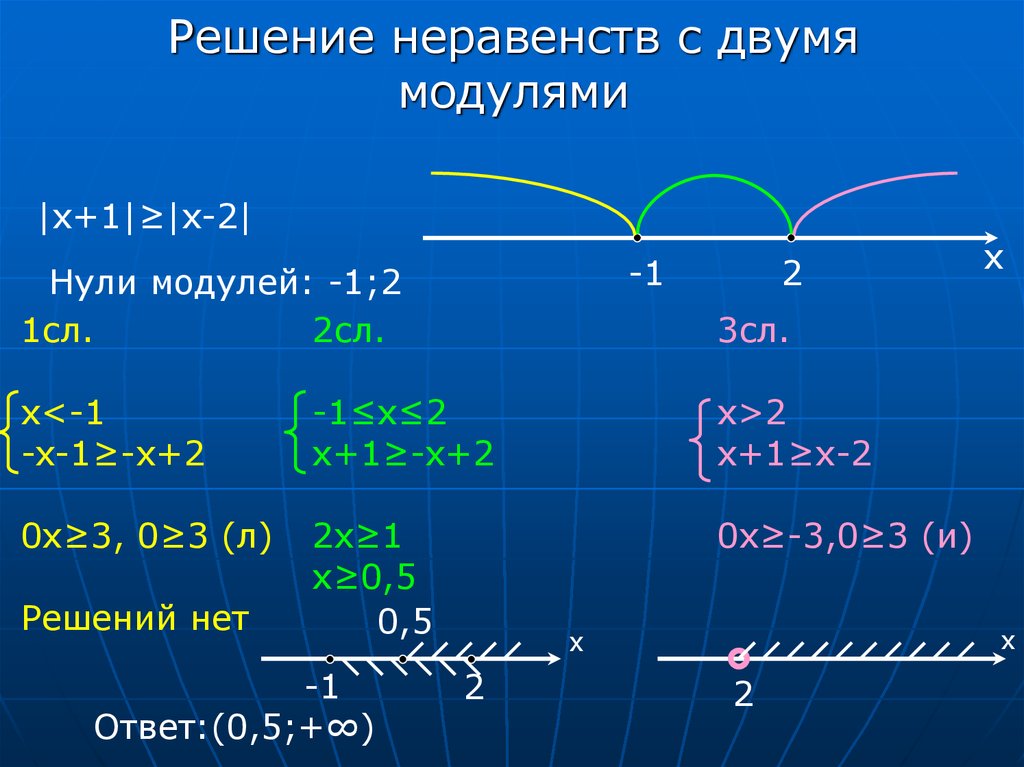 Движение с отставанием
Движение с отставанием
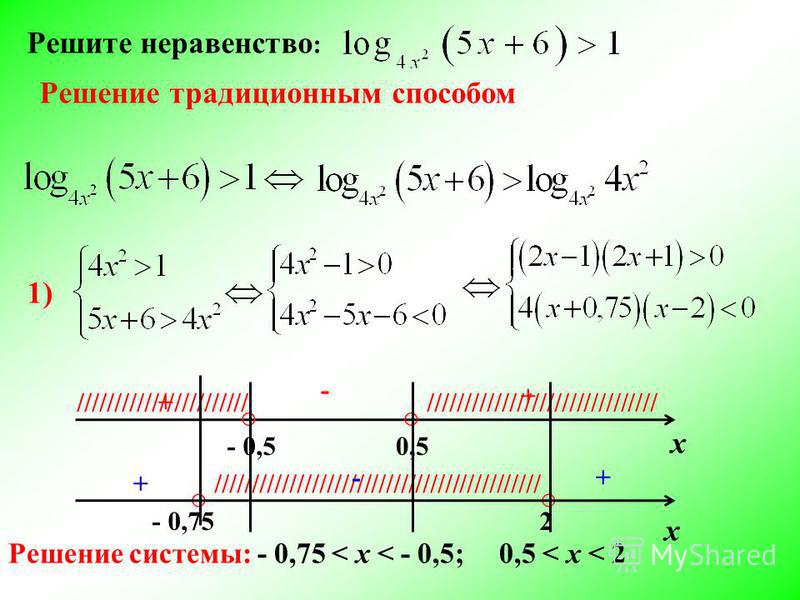 Новые единицы площади
Новые единицы площади Измерение углов
Измерение углов
 Круговые диаграммы
Круговые диаграммы Координаты на плоскости
Координаты на плоскости