Раздел недели: Плоские фигуры. Свойства, стороны, углы, признаки, периметры, равенства, подобия, хорды, секторы, площади и т.д. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Поиск на сайте DPVA Поставщики оборудования Полезные ссылки О проекте Обратная связь Ответы на вопросы. Оглавление Таблицы DPVA.ru — Инженерный Справочник | Адрес этой страницы (вложенность) в справочнике dpva.ru: главная страница / / Техническая информация/ / Математический справочник / / Таблицы численных значений. (Таблица квадратов, кубов, синусов ….) + Таблицы Брадиса / / Таблица квадратов натуральных (целых) чисел от 1 до 999. Поделиться:
 Введите свой запрос: Введите свой запрос: | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Если Вы не обнаружили себя в списке поставщиков, заметили ошибку, или у Вас есть дополнительные численные данные для коллег по теме, сообщите , пожалуйста. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Коды баннеров проекта DPVA.ru Консультации и техническая | Проект является некоммерческим. Информация, представленная на сайте, не является официальной и предоставлена только в целях ознакомления. Владельцы сайта www.dpva.ru не несут никакой ответственности за риски, связанные с использованием информации, полученной с этого интернет-ресурса. Free xml sitemap generator | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Способы извлечения квадратного корня из многозначных чисел
Похожие презентации:
Элементы комбинаторики ( 9-11 классы)
Применение производной в науке и в жизни
Проект по математике «Математика вокруг нас. Узоры и орнаменты на посуде»
Узоры и орнаменты на посуде»
Знакомство детей с математическими знаками и монетами
Тренажёр по математике «Собираем урожай». Счет в пределах 10
Методы обработки экспериментальных данных
Лекция 6. Корреляционный и регрессионный анализ
Решение задач обязательной части ОГЭ по геометрии
Дифференциальные уравнения
Подготовка к ЕГЭ по математике. Базовый уровень Сложные задачи
Исследовательская работа
на тему:
«Способы извлечения
квадратного корня
из многозначных чисел»
Выполнил:
ученик 8 класса
СОШ №22 г. Саратова
Талдыкин Дмитрий
Руководитель: Акимова Вера Михайловна
Саратов — 2020
«Нужно ли Вам уметь извлекать квадратные
корни многозначных чисел без
калькулятора?»
«да»
8%
«затрудняюсь
ответить»
92%
Какие способы извлечения квадратных
корней из многозначных чисел Вы
знаете?
25
25
15
20
15
1
10
5
0
С помощью
таблицы на
форзаце
учебника
алгебры 8
класс
Разложение
на простые
множители
Способ
отбрасывания
полного
квадрата
Вывод:
Результаты показали, что ученики хорошо
умеют пользоваться таблицей квадратов
двузначных чисел, но не умеют извлекать корни
из многозначных чисел больших 1002.
Цель работы:
изучить способы вычисления арифметических
корней и выбрать самый рациональный для
практического применения.
Задачи проекта:
1. Проанализировать путём соцопроса умение
учащихся извлекать квадратные корни без
калькулятора;
2.Изучить математическую литературу по данной теме,
используя Интернет-ресурсы;
3. Изучить способы и алгоритмы вычисления
арифметического корня и рассмотреть примеры
быстрого извлечения квадратного корня;
3. Классифицировать найденные способы извлечения
корней по степени сложности, погрешности и
практическому применению;
4. Познакомить одноклассников с самым
рациональным способом извлечения корней.
Актуальность
В школьном курсе математики часто
встречаются задания с извлечением
квадратного корня, в заданиях ОГЭ, в
практических вычислениях и быту.
Умения извлекать квадратные корни нужны
при изучении некоторых тем химии и
физики .
Способ разложения на простые множители
Для извлечения квадратного корня можно разложить число
на простые множители и извлечь квадратный корень из
произведения.
1936 | 2
968 | 2
482| 2
242| 2
121| 11
11| 11
1| 1
1521 | 3
507 | 3
169 | 13
13 | 13
1|1
√1521 = √132 ∙ 32= 13∙3 = 39
√1936 = √24∙11² = 2∙2∙11 = 44
Не всегда легко можно
разложить, занимает
много времени.
Способ использования таблицы квадратов
двузначных чисел
5
Закрыть две
последние
цифры, найти
число, которое
меньше
подкоренного
8
7225
Используется только
для корней до100,
имеет точность
только до десятых.
Поможет на экзамене
ученику.
?
73 = 8,5
Формула Древнего Вавилона.
Древние вавилоняне пользовались следующим
способом нахождения приближенного значения
квадратного корня их числа х. Число х они
представляли в виде суммы а2+b
Формула:
Пример:
—
3
28 =
52+ 3
~
~ 5 + 2 * 5 = 5,3
Сложность состоит в том,
что нужно знать полные
квадраты больших чисел,
уметь их быстро находить, а
также много и правильно
считать.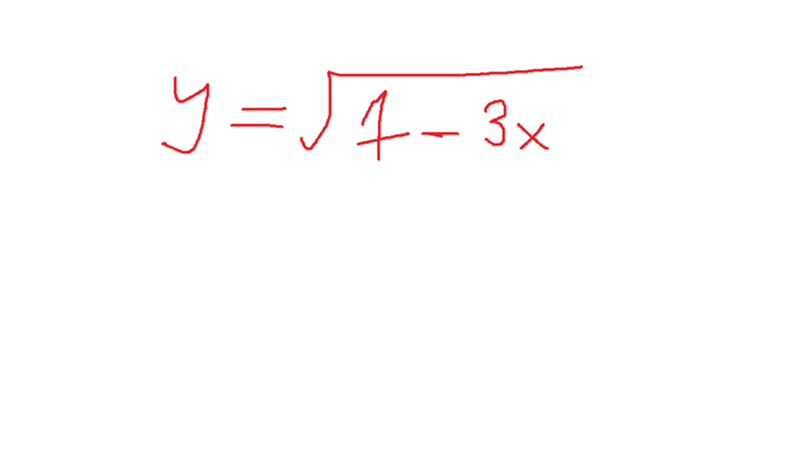
Через решение уравнения
√129 = ?
√121< √129 < √144
11 < √129 < 12
√129= 11 + х
(√129) ² = (11 + х)²
Такой способ
интересный, но
трудоёмкий. Больше
применим к
небольшим корням,
где легко можно
определить границы
корня.
129 = (11 + х)² = 121 + 22х + х²
129 = 121 + 22х
х = 0,3636
Значит √ 129 ≈ 11 + 0,3636 ≈ 11,3636
Способ отбрасывание полного квадрата
Извлечение корней до числа 752 =5625
Выделяем из
числа квадрат,
который
оканчивается
той же цифрой,
что и данное
число
2704 =
2700+4 = 27+25= 52
4624 =
4300+324= 43+25=68
Извлечение корней после 752 =5625
8836 =
8800+36=88+6= 94
Этот способ плох, так как
применим только для
извлечения квадратного
корня из точного
квадрата, и имеет 2
алгоритма
Графический метод
11 = ?
Состоит в решении уравнения
графически.
у = 11 – прямая, параллельная оси абсцисс,
у = Х ² — классическая парабола.
Точка их пересечения на [0 ; +∞]
имеет абсциссу ≈ 3,3, поэтому
11 ≈ 3,3
11
Ограниченность
пространством листа
и из-за неточности в
построении
получение больших
погрешностей.
3,3
Заключение
В ходе исследования, я убедился, что актуальность темы я выбрал
правильную, ведь не только дети, но и взрослые не умеют вычислять
квадратные корни без калькулятора, а это является важной составляющей в
жизни людей. В результате проведённой работы, было найдено огромное
количество способов вычисления квадратного корня, а также выявлено, что
современной науке известно много таких способов, начиная со способа
математиков Древнего Вавилона и заканчивая способом «Степенных рядов
сложных степеней» из разделов высшей математики, но, к сожалению, не
все они являются удобными и легкими в вычислениях. Методом проб и
ошибок, я пришел к выводу, что самым рациональным и точным является
способ «Решение уравнения». В ходе исследования были проработаны все
способы, а их практическое применение доказало все недостатки и
преимущества каждого из методов. Была дана характеристика каждого
Была дана характеристика каждого
способа по таким критериям, как точность вычислений, трудоёмкость,
«требует знания формул», «для каких корней применим», «требует логики
или дополнительных знаний», а также насколько способ удобен,
математически красив и практичен. В результате исследовательской работы
я пришел к выводу, что извлечение квадратного корня без калькулятора
является не только полезным занятием, но еще и очень увлекательным.
English Русский Правила
Квадратный корень из 1521 — Как найти квадратный корень из 1521?
LearnPracticeDownload
Совершенное квадратное число — это число, полученное после возведения целого числа в квадрат. Его также можно определить как число, квадратный корень которого всегда дает целое число. 1521 — это такое число, которое получается после возведения в квадрат 39. Таким образом, квадратный корень из 1521 дает целое число (39). Это делает 1521 совершенным квадратным числом. Следовательно, квадратный корень из 1521 — рациональное число. В этом мини-уроке мы научимся находить квадратный корень из 1521 вместе с решенными примерами. Теперь найдем квадратный корень из 1521.
В этом мини-уроке мы научимся находить квадратный корень из 1521 вместе с решенными примерами. Теперь найдем квадратный корень из 1521.
- Квадратный корень из 1521: √1521 = 39
- Квадрат 1521: 1521 ² = 2 313 441
| 1. | Что такое квадратный корень из 1521? |
| 2. | Является ли квадратный корень из 1521 рациональным или иррациональным? |
| 3. | Как найти квадратный корень из 1521? |
| 4. | Важные примечания |
| 5. | Сложные вопросы |
| 6. | Часто задаваемые вопросы о квадратном корне из 1521 |
Что такое квадратный корень из 1521?
Квадратный корень числа — это значение, которое при возведении в квадрат дает исходное число. Например, квадратный корень из 1521 (обозначается √1521) равен 39.
Например, квадратный корень из 1521 (обозначается √1521) равен 39.
- Квадратный корень — это число (целое число), которое при умножении само на себя дает исходное число.
- 1521 = а × а = 39²
- Тогда а = √1521 = √(39 × 39)
- 39 × 39 = 1521 или -39 × -39 = 1521
- Квадратный корень из 1521 равен +39 или -39.
- Это показывает, что 1521 — правильный квадрат.
Является ли квадратный корень из 1521 рациональным или иррациональным?
Рациональное число определяется как число, которое может быть выражено в виде частного или деления двух целых чисел, т. е. p/q, где q не равно 0. Число, не являющееся рациональным, называется иррациональное число. Неконечные десятичные числа, которые имеют повторяющиеся числа после запятой, являются рациональными числами. Давайте поговорим о числе 1521. Квадратный корень из 1521 можно выразить как 39./1 и -39/1. Оба числа могут быть представлены в виде рационального числа. Следовательно, квадратный корень из 1521 — рациональное число.
Следовательно, квадратный корень из 1521 — рациональное число.
Как найти квадратный корень из 1521?
Вычислим квадратный корень из 1521, используя метод простой факторизации.
Квадратный корень из 1521 методом простой факторизации
- Простая факторизация 1521: 3 × 3 × 13 × 13
- Простые множители числа 1521 в парах: (3 × 3) × (13 × 13)
- Квадратный корень из 1521: (3) ² × (13) ² = ±39
- Следовательно, √1521 = ±39
Важные примечания:
- 1521 — это число, представляющее собой полный квадрат. Это указывает на то, что в качестве квадратного корня используется натуральное число.
- Квадратный корень из 1521 равен 39.
- Квадратный корень из 1521 может быть выражен как дробь в форме p/q. Это говорит нам о том, что квадратный корень из 1 521 — рациональное число.
- Квадратный корень из 1521 равен 39 или -39.

- 39 и -39 могут быть выражены как 39/1 и -39/1.
- Оба числа 39 и -39 могут быть представлены в виде рационального числа.
Изучение квадратных корней с помощью иллюстраций и интерактивных примеров
- Квадратный корень из 1600
- Квадратный корень из 1225
- Квадратный корень из 1296
- Квадратный корень из 1156
- Квадратный корень из 1369
- Квадратный корень из 1681
- Квадратный корень из 21
- Квадратный корень из 15
- Квадратный корень из 52
Загадочные вопросы
- Какой отрицательный корень из 15210?
- Найти квадратный корень из 152 с точностью до 5 знаков после запятой?
- Чему равен квадратный корень из:
а) √√√1521
б) √1521
Пример 1: Найдите квадратный корень из 1521, используя метод деления в большую сторону.

Решение:
Квадратный корень из 1521 можно найти с помощью метода деления в большую сторону. Вот шаги:
- Шаг 1 : Мы соединяем цифры заданного числа, начиная с цифр справа. Поместите горизонтальную черту над числами, чтобы обозначить сопряжение.
- Шаг 2 : Теперь мы находим число, которое при умножении на себя дает произведение, меньшее или равное 15. Как мы знаем, 3 × 3 = 9 < 15. Следовательно, полученная разность равна 6, а частное равно 3.
- Шаг 3 : Теперь мы должны уменьшить 21 и умножить частное на 2. Это даст нам 6. Следовательно, 6 – начальная цифра нового делителя.
- Шаг 4 : 9 теперь ставится на место нового делителя. 69, умноженное на 9, дает 621. Полученный остаток равен 0, .
- Шаг 5 : Следовательно, квадратный корень из 1521 равен 39.
Пример 2: Рози умножает число само на себя.
 Если произведение равно 1521, помогите Рози найти это число. Найдите квадратный корень из полученного числа.
Если произведение равно 1521, помогите Рози найти это число. Найдите квадратный корень из полученного числа.Решение:
Чтобы найти число, предположим, что число = q
При умножении q на q = q × q = 1521
q² = 1521
q = √1521
д = 39
(39 × 39 = 1521)
Число 39.
Квадратный корень из 39 с использованием метода деления в длинную сторону:Квадратный корень из 39 равен 6,244.
Пример 3: Рози хочет купить новую настенную картину. В магазине она находит квадратную картину со стороной 39.единицы. Рассчитайте площадь настенной росписи.
Решение:
Сторона квадратной картины = 39 единиц
Площадь = сторона × сторона = 39 × 39 = 1521
Площадь настенной росписи составляет 1521 кв. ед.
перейти к слайдуперейти к слайдуперейти к слайду
Есть вопросы по основным математическим понятиям?
Станьте чемпионом по решению проблем, используя логику, а не правила. Узнайте, почему стоит математика, с сертифицированными экспертами ourCuemath.
Узнайте, почему стоит математика, с сертифицированными экспертами ourCuemath.
Записаться на бесплатный пробный урок
перейти к слайдуперейти к слайду
Часто задаваемые вопросы о квадратном корне из 1521
Чему равен квадратный корень из 1521 с использованием простой факторизации?
Разложение числа 1521 на простые множители: 3 × 3 × 13 × 13
Простые множители числа 1521 в парах: (3 × 3) × (13 × 13) 90 166
Квадратный корень из 1521: (3)² × (13)² = ±39
Следовательно, √1521 = ±39
Является ли число 1521 идеальным квадратом?
1521 — идеальный квадрат. 1521 – натуральное число. Существует еще одно натуральное число – 39., которое можно возвести в квадрат, чтобы получить 1 521 в результате. Таким образом, 1 521 – идеальный квадрат.
Каково значение квадратного корня из 1521?
Значение квадратного корня из 1521 √1521 = 39.
Является ли квадратный корень из 1521 рациональным числом?
Да, квадратный корень из 1521 является рациональным числом, поскольку квадратный корень из 1521 может быть представлен в виде p/q.
Можем ли мы найти квадратный корень из 1521, используя метод повторного вычитания?
Да, мы можем найти квадратный корень из 1521 методом повторного вычитания, так как его можно использовать только для полных квадратов, а 1521 это идеальный квадрат. 93-8
Квадратный корень из 1521
Sqrt(1521). Найдите квадратный корень из 1521 или любого другого действительного числа, положительного или отрицательного. Вот ответы на такие вопросы, как: Квадратный корень из 1521 или что такое квадратный корень из 1521?
Найдите квадратный корень из 1521 или любого другого действительного числа, положительного или отрицательного. Вот ответы на такие вопросы, как: Квадратный корень из 1521 или что такое квадратный корень из 1521?
Что такое квадратный корень? Определение квадратного корня
Квадратный корень из числа ‘x’ – это число y такое, что y 2 = x, другими словами, число y, квадрат которого равен y. Например, 39 — это квадратный корень из 1521, потому что 39 2 = 39•39 = 1521, -39 — это квадратный корень из 1521, потому что (-39) 2 = (-39)•(-39) = 1521. означает квадратный корень из х. Подробнее о квадратном корне читайте здесь: Квадратный корень — Википедия и здесь: Квадратный корень — Wolfram
Квадратный символ?
Вот символ квадратного корня. Он обозначается √, известным как радикальный знак или основание.
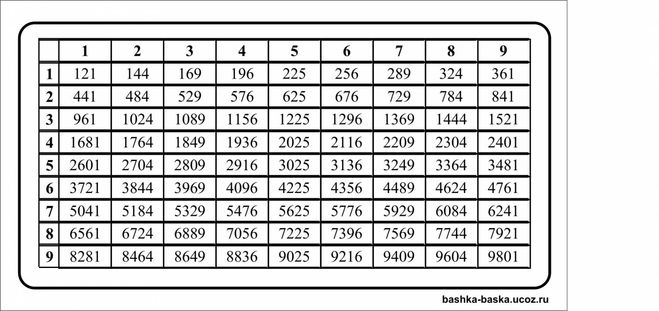
Таблица квадратного корня 1-100
Квадратные корни от 1 до 100 округляются до тысячных.
| номер | квадрат | квадрат корень |
|---|---|---|
| 1 | 1 | 1. 000 000 |
| 2 | 4 | 1.414 |
| 3 | 9 | 1.732 |
| 4 | 16 | 2.000 |
| 5 | 25 | 2.236 |
| 6 | 36 | 2.449 |
| 7 | 49 | 2.646 |
| 8 | 64 | 2.828 |
| 9 | 81 | 3.000 |
| 10 | 100 | 3.162 |
| 11 | 121 | 3.317 |
| 12 | 144 | 3.464 |
| 13 | 169 | 3.606 |
| 14 | 196 | 3.742 |
| 15 | 225 | 3.873 |
| 16 | 256 | 4.000 |
| 17 | 289 | 4.123 |
| 18 | 324 | 4. 243 243 |
| 19 | 361 | 4.359 |
| 20 | 400 | 4.472 |
| 21 | 441 | 4.583 |
| 22 | 484 | 4.690 |
| 23 | 529 | 4.796 |
| 24 | 576 | 4.899 |
| 25 | 625 | 5.000 |
| number | square | square корень |
|---|---|---|
| 26 | 676 | 5.099 |
| 27 | 729 | 5,196 |
| 28 | 784 40024 | |
| 28 | 784 40024 | |
| 28 | 784 | 28 |
| 28 | ||
| 28 | ||
| 28 | ||
| 29 | 841 | 5.385 |
| 30 | 900 | 5.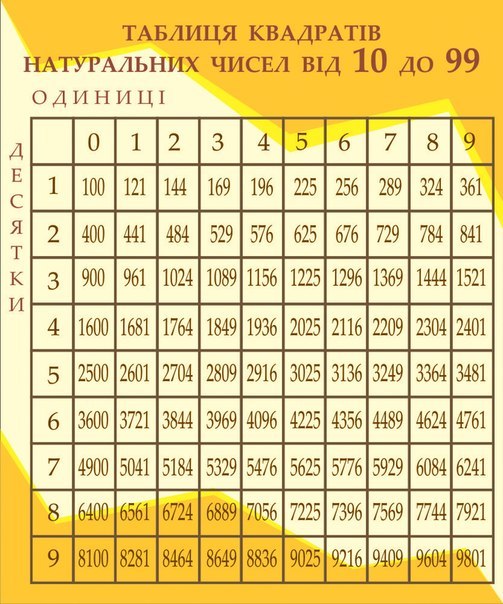 477 477 |
| 31 | 961 | 5.568 |
| 32 | 1,024 | 5.657 |
| 33 | 1,089 | 5.745 |
| 34 | 1,156 | 5.831 |
| 35 | 1,225 | 5.916 |
| 36 | 1,296 | 6.000 |
| 37 | 1,369 | 6.083 |
| 38 | 1,444 | 6.164 |
| 39 | 1,521 | 6.245 |
| 40 | 1,600 | 6.325 |
| 41 | 1,681 | 6.403 |
| 42 | 1,764 | 6.481 |
| 43 | 1,849 | 6.557 |
| 44 | 1,936 | 6.633 |
| 45 | 2,025 | 6.708 |
| 46 | 2,116 | 6. 782 782 |
| 47 | 2,209 | 6.856 |
| 48 | 2,304 | 6.928 |
| 49 | 2,401 | 7.000 |
| 50 | 2,500 | 7.071 |
| номер | квадрат | квадрат корень |
|---|---|---|
| 51 | 2,601 | 7.141 |
| 52 | 2,704 | 7.211 |
| 53 | 2,809 | 7.280 |
| 54 | 2,916 | 7.348 |
| 55 | 3,025 | 7.416 |
| 56 | 3 136 | 7.483 |
| 57 | 3,249 | 7.550 |
| 58 | 3,364 | 7.616 |
| 59 | 3,481 | 7.681 |
| 60 | 3,600 | 7.746 |
| 61 | 3,721 | 7. 810 810 |
| 62 | 3,844 | 7.874 |
| 63 | 3,969 | 7.937 |
| 64 | 4,096 | 8.000 |
| 65 | 4,225 | 8.062 |
| 66 | 4,356 | 8.124 |
| 67 | 4,489 | 8.185 |
| 68 | 4,624 | 8.246 |
| 69 | 4,761 | 8.307 |
| 70 | 4,900 | 8.367 |
| 71 | 5,041 | 8.426 |
| 72 | 5,184 | 8.485 |
| 73 | 5,329 | 8.544 |
| 74 | 5,476 | 8.602 |
| 75 | 5,625 | 8.660 |
| номер | квадрат | квадрат корень |
|---|---|---|
| 76 | 5 776 | 8,718 |
| 77 | 5,929 | 8. 775 775 |
| 78 | 6,084 | 8.832 |
| 79 | 6,241 | 8.888 |
| 80 | 6,400 | 8.944 |
| 81 | 6,561 | 9.000 |
| 82 | 6,724 | 9.055 |
| 83 | 6,889 | 9.110 |
| 84 | 7,056 | 9.165 |
| 85 | 7,225 | 9.220 |
| 86 | 7,396 | 9.274 |
| 87 | 7,569 | 9.327 |
| 88 | 7,744 | 9.381 |
| 89 | 7,921 | 9.434 |
| 90 | 8,100 | 9.487 |
| 91 | 8,281 | 9.539 |
| 92 | 8,464 | 9.592 |
| 93 | 8,649 | 9.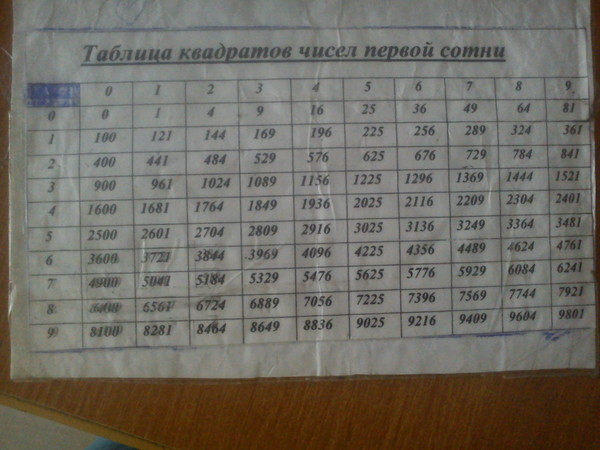 |


 То есть, для того, чтобы узнать квадрат
То есть, для того, чтобы узнать квадрат То есть, для того, чтобы узнать квадрат
То есть, для того, чтобы узнать квадрат То есть, для того, чтобы узнать квадрат
То есть, для того, чтобы узнать квадрат То есть, для того, чтобы узнать квадрат
То есть, для того, чтобы узнать квадрат То есть, для того, чтобы узнать квадрат
То есть, для того, чтобы узнать квадрат

 Если произведение равно 1521, помогите Рози найти это число. Найдите квадратный корень из полученного числа.
Если произведение равно 1521, помогите Рози найти это число. Найдите квадратный корень из полученного числа.