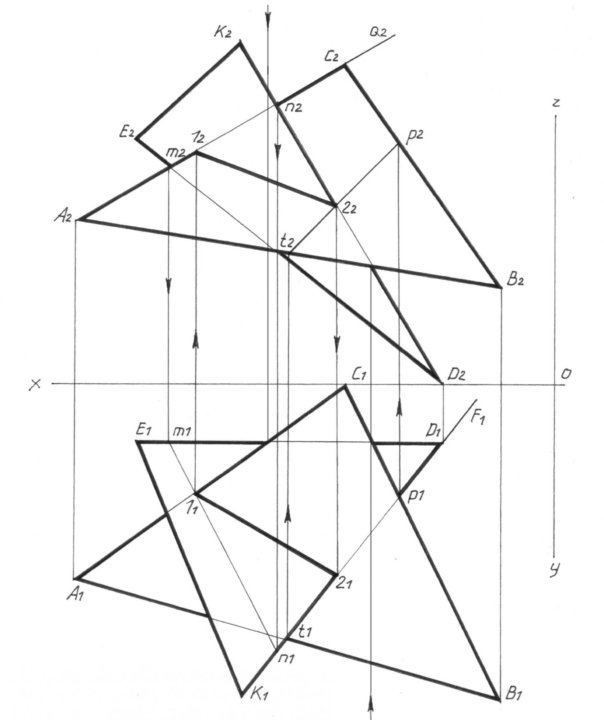
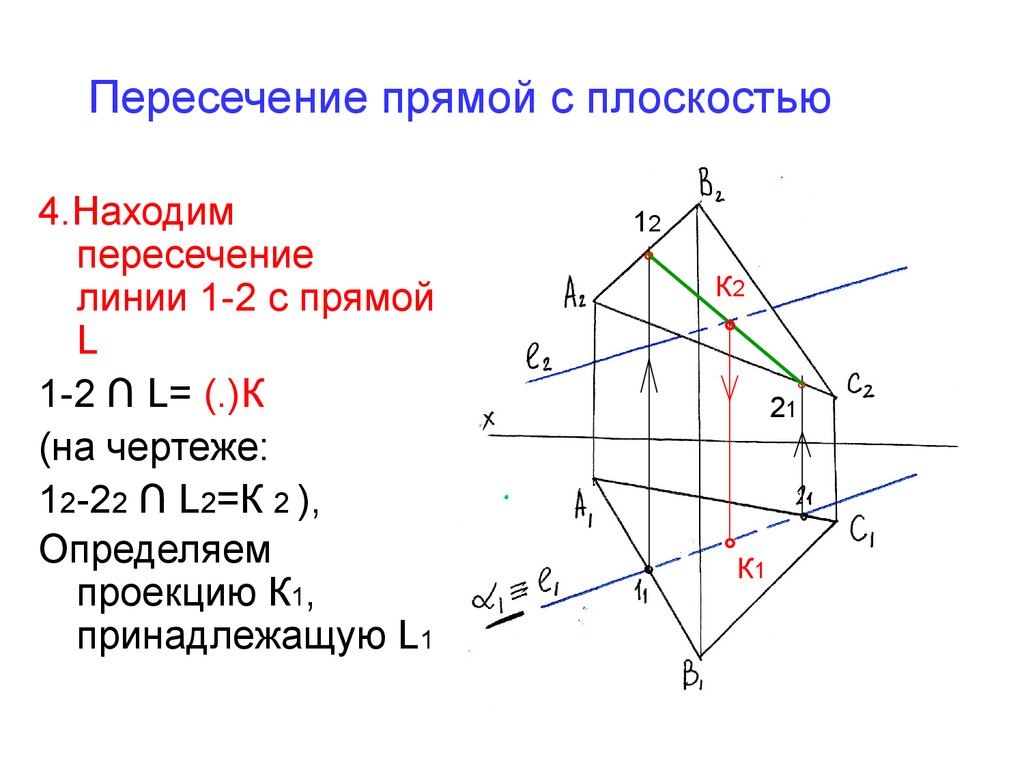
Как построить плоскость?
Несмотря на обилие программ и онлайн сервисов, ручное построение чертежей сохранит актуальность и через много лет, хотя бы потому, что позволит учащимся качественно усвоить материал. Что нужно знать и уметь в самых суровых условиях?
Прежде всего, вы должны на полном автомате узнавать уравнения плоскостей, которые параллельны координатным плоскостям . Фрагменты плоскостей стандартно обозначают прямоугольниками, которые в последних двух случаях выглядят,
как параллелограммы. Размеры выбираем разумные, при этом желательно, чтобы точка, в которой координатная ось «протыкает» плоскость являлась
центром симметрии:
! Все помнят неформальный смысл этих уравнений?
Повторим заодно и неравенства:
– неравенство (левый чертёж) задаёт дальнее от нас полупространство,
исключая саму плоскость ;
– неравенство
– двойное неравенство (правый чертёж) задаёт «слой», расположенный
между плоскостями , включая обе плоскости.
Задача 124
Изобразить тело, ограниченное плоскостями , составить систему неравенств, определяющих данное тело.
Это задание для самостоятельного решения. Из-под грифеля вашего карандаша должен выйти старый знакомый прямоугольный параллелепипед. Не забывайте, что невидимые рёбра и грани следует прочертить пунктиром. Готовый чертёж в конце книги.
НЕ ПРЕНЕБРЕГАЙТЕ учебными задачами!
Особенно, если они кажутся простыми
А то может статься, раз пропустили, два пропустили, а затем потратили битый час, вымучивая трёхмерный чертёж в каком-нибудь реальном примере. Причём, несложный.
Следующую группу плоскостей условно назовём «прямыми пропорциональностями» – это плоскости, проходящие через координатные оси:
1) уравнение вида (здесь и далее ) задаёт плоскость, проходящую через ось ;
2) уравнение вида задаёт плоскость, проходящую через ось ;
3) уравнение вида задаёт плоскость, проходящую через ось .
Задача 125
Построить плоскость
Как лучше осуществить построение? Предлагаю следующий алгоритм:
Сначала перепишем уравнение в виде , из которого хорошо видно, что «игрек» может принимать любые значения. Зафиксируем значение , то есть, будем рассматривать координатную плоскость . Уравнения задают пространственную прямую, лежащую в этой плоскости. Данная прямая проходит через начало координат, поэтому для её построения достаточно найти одну точку. Пусть . Откладываем точку и проводим прямую:
Теперь возвращаемся к уравнению плоскости . Поскольку «игрек» принимает любые значения, то построенная в плоскости прямая
непрерывно «тиражируется» влево и вправо. Именно так и образуется наша плоскость , проходящая через ось . Чтобы завершить
чертёж, слева и справа от прямой откладываем две параллельные линии и
поперечными горизонтальными отрезками «замыкаем» символический параллелограмм.
И ещё раз повторим смысл пространственного линейного неравенства на примере . Как определить полупространство, которое оно задаёт? Берём какую-нибудь точку, не
принадлежащую плоскости , например, точку из ближнего к нам полупространства и подставляем её координаты в неравенство:
Задача 126
Построить плоскости
а) , б) .
Это задания для самостоятельного решения, в случае затруднений используйте аналогичные рассуждения. Краткие указания и чертежи в конце книги.
На практике особенно распространены плоскости, параллельные оси . Частный случай, когда плоскость проходит через ось, только что был в пункте «бэ», и сейчас мы разберём более общую задачу:
Задача 127
Построить плоскость
Решение: в уравнение в явном виде не участвует переменная «зет», а значит, плоскость
параллельна оси аппликат.
Перепишем уравнение плоскости в виде , из которого понятно, что «зет» может принимать любые значения. Зафиксируем и в «родной» плоскости начертим обычную «плоскую» прямую . Для её построения удобно взять опорные точки .
Поскольку «зет» принимает все значения, то построенная прямая непрерывно «размножается» вверх и вниз, образуя тем самым искомую плоскость . Аккуратно оформляем параллелограмм разумной величины.
5.1.5. Уравнение плоскости в отрезках
5.1.3. Линейные неравенства в пространстве
| Оглавление |
Автор: Aлeксaндр Eмeлин
Построение плоскости
Зная
уравнение плоскости, легко построить
саму плоскость. Для этого достаточно
найти три какие-либо ее точки, не лежащие
на одной прямой. Для того чтобы найти
какую-либо точку на плоскости достаточно
задать произвольно значения двух
координат, а третью найти из уравнения
плоскости.
Проще всего определять точки пересечения плоскости с осями координат.
Пусть точки M1, M2, M3 не лежат на одной прямой. Как известно, три такие точки однозначно определяют некоторую плоскость р (рис. 199).
Выведем уравнение плоскости р. Пусть М — произвольная точка пространства. Очевидно, что точка М принадлежит плоскости р тогда и только тогда, когда векторы M1M>, M1M2>, M1M3>компланарны. Необходимым и достаточным условием компланарности трех векторов является равенство нулю их смешанного произведения (§ 23*, теорема 2). Поэтому уравнение плоскости, проходящей через три точки, не лежащие на одной прямой, может быть записано следующим образом:
(M1M>, M1M2>, M1M3>)
= 0.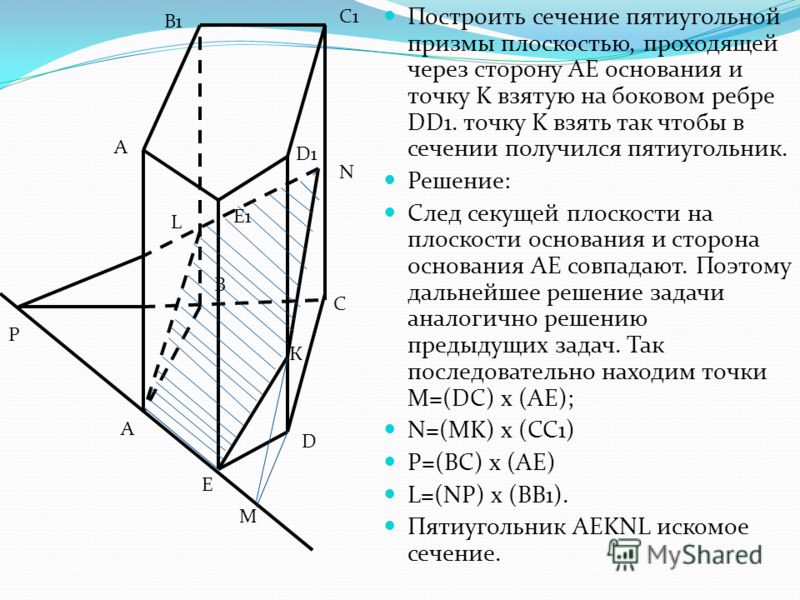 (1)
(1)
Если точки M1, M2 и M3 заданы координатами в некоторой прямоугольной декартовой системе координат, то уравнение (1) можно записать в координатах. Пусть M1(x1; y1; z1), M2(х2; у2; z2), M3(х3; у3; z3) — данные точки. Обозначим координаты произвольной точки М плоскости р через х, у и z. Найдем координаты векторов, входящих в уравнение (1):
M1M>
= (х — х1; у — у1; z — z1),M1M2> = (x2 — x1 ; y2 — y1; z2 — z1),
M1M3> =
(x3 —
x1;
у3 —
y1;
z3 —
z1).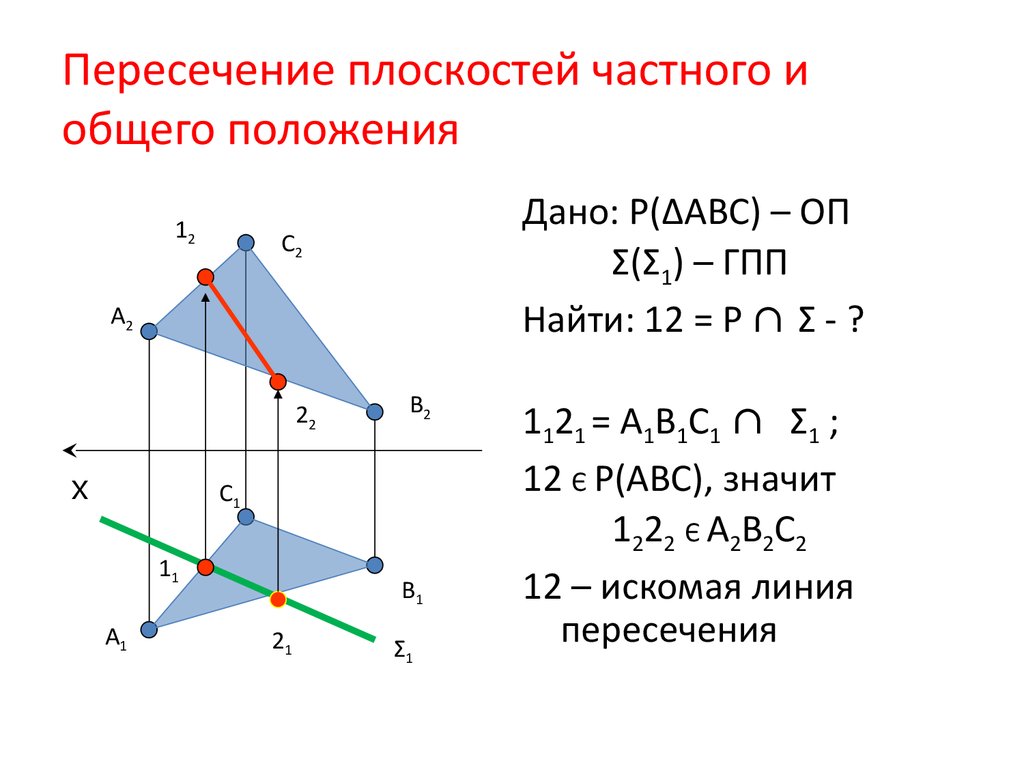
Смешанное произведение трех векторов равно определителю третьего порядка, в строках которого стоят координаты векторов . Следовательно, уравнение (1) в координатах имеет вид
Уравнение плоскости в отрезках
где a, b, c
Расстояние от точки до плоскости — равно длине перпендикуляра, опущенного из точки на плоскость.
Формула для вычисления расстояния от точки до плоскости
Если задано уравнение плоскости Ax + By + Cz + D = 0, то расстояние от точки M(Mx, My, Mz) до плоскости можно найти, используя следующую формулу:
d = | |A·Mx + B·My + C·Mz + D| |
√A2 + B2 + C2 |
Двугранный
угол между плоскостями равен
углу образованному нормальными векторами
этих плоскостей.
Двугранный угол между плоскостями равен углу образованному прямыми l1 и l2, лежащими в соответствующих плоскостях и перпендикулярными линии пересечения плоскостей.
Формула для вычисления угла между плоскостями
Если заданы уравнения плоскостей A1x + B1y + C1z + D1 = 0 и A2x + B2y + C2z + D2 = 0, то угол между плоскостями можно найти, используя следующую формулу
cos α = | |A1·A2 + B1·B2 + C1·C2| |
√A12 + B12 + C1 |
Условия перпендикулярности
2х плоскостей. Ясно,
что две плоскости перпендикулярны
тогда и только тогда, когда их нормальные
векторы перпендикулярны, а
следовательно, или.
Ясно,
что две плоскости перпендикулярны
тогда и только тогда, когда их нормальные
векторы перпендикулярны, а
следовательно, или.
Таким образом, .
Условия параллельности 2х плоскостей. Две плоскости α1 и α2 параллельны тогда и только тогда, когда их нормальные векторы ипараллельны, а значит
Геометрические построения на плоскости — РЦ Гильдия наук
Геометрические построения
- Post category:Обо всем на свете / Олимпиада по математике
При начале изучения геометрии достаточно много внимания уделяется формированию навыков учащихся производить грамотные построения различных фигур. Геометрические построения – важный этап изучения предмета. В данной статье мы приведем примеры навыков, которыми должны владеть учащиеся 7-8 класса средних школ.
Геометрические построения на плоскости
При выполнении всех задач, требующих изображения геометрических фигур, используются следующие инструменты:
- Транспортир.

- Циркуль.
- Линейка.
- Набор треугольников.
Для построения геометрических фигур инструменты используются так:
- Линейка позволяет произвести построение отрезка определенной длины. Ею также можно провести прямую на плоскости.
- Транспортир применяется для построения углов.
- Циркуль позволяет провести дугу, окружность и отложить отрезок заданной длины.
- Геометрические построения параллельных и перпендикулярных прямых выполняются с помощью треугольников.
Какие бывают построения
В общем случае при изучении геометрии учащимся требуется при решении задач использовать наглядные рисунки. Также построения могут быть также отражением решения задачи или иллюстрировать ее условие.
На вводных занятиях к курсу геометрии на уроках рассматриваются основные геометрические построения, к которым относятся:
• Прямая.
• Треугольник.
• Прямоугольник.
• Угол.
• Луч.
Для построения прямой достаточно провести на плоскости линию, пользуясь только линейкой.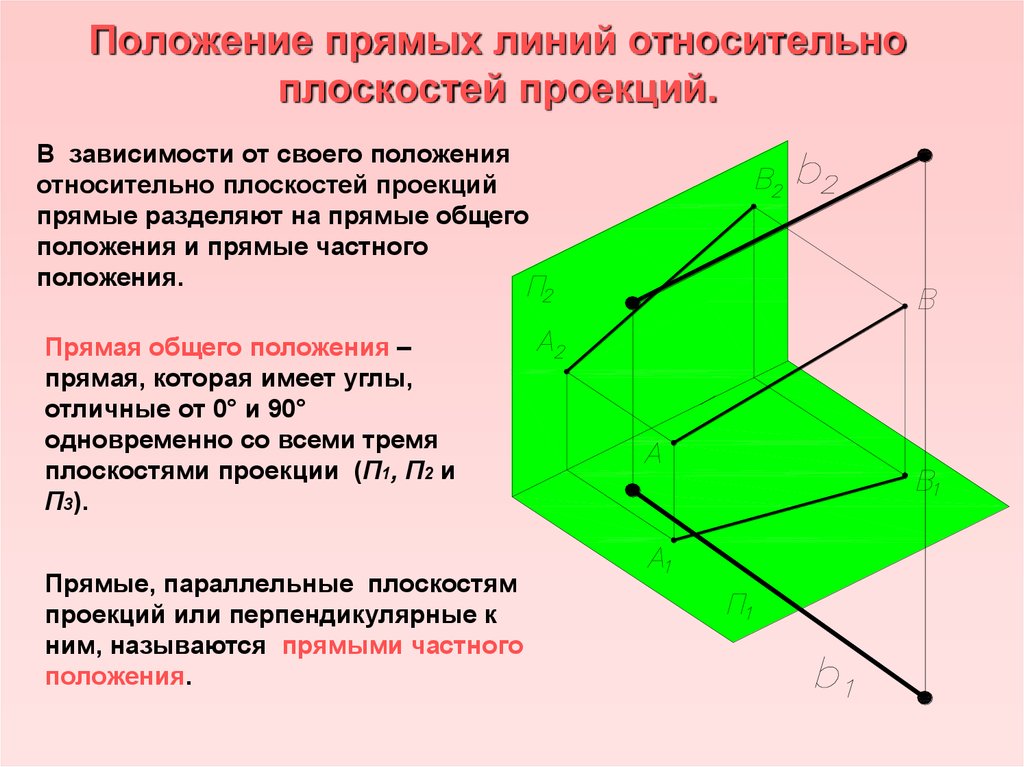
Если прямую необходимо провести через две произвольные точки, то для этого также достаточно обозначить точки на плоскости, и затем провести через них прямую при помощи линейки.
Как построить заданный угол
Общий алгоритм выполнения такой работы выглядит следующим образом:
- На плоскости проводится произвольная прямая.
- На ней отмечается точка, которая будет центром построения, — допустим, О.
- К этой точке прикладывается транспортир, на котором отмечается угол нужного размера. Он фиксируется точкой, к примеру, В.
- Далее точка А и точка В соединяются между собой отрезком.
- Угол, получившийся между прямой и построенным отрезком, является искомым углом.
Геометрические построения: как построить треугольник
Чаще всего в решении задач используются треугольники. В этом отношении их можно назвать наиболее интересными геометрическими фигурами. Самые простые построения, которые с ними связаны, включают изображение с заданными сторонами.
Если у треугольника заданы размеры сторон, то их откладывают на плоскости следующим образом:
- Проводят произвольную прямую.
- На ней отмечают точку А, которая будет центром построения.
- Далее циркулем на линейке снимаем нужное расстояние, равное одной из сторон, которые необходимо построить и откладываем его на прямой от точки А. Полученную таким образом точку назовем В.
- Циркулем снимаем с линейки расстояние второй стороны и откладываем его, путем рисования дуги на свободном пространстве по одной из сторон прямой, на которой отложены точки А и В, от точки А.
- Затем снимаем циркулем на линейке расстояние, равное третьей стороне, которую нужно отложить и откладываем его путем рисования дуги, до пересечения с первой дугой. В точке пересечения двух дуг отмечаем точку С.
Построение биссектрисы угла
Чтобы выполнить построение биссектрисы угла, нужно
Отложить из центра вершины угла (точки А) окружность произвольного радиуса.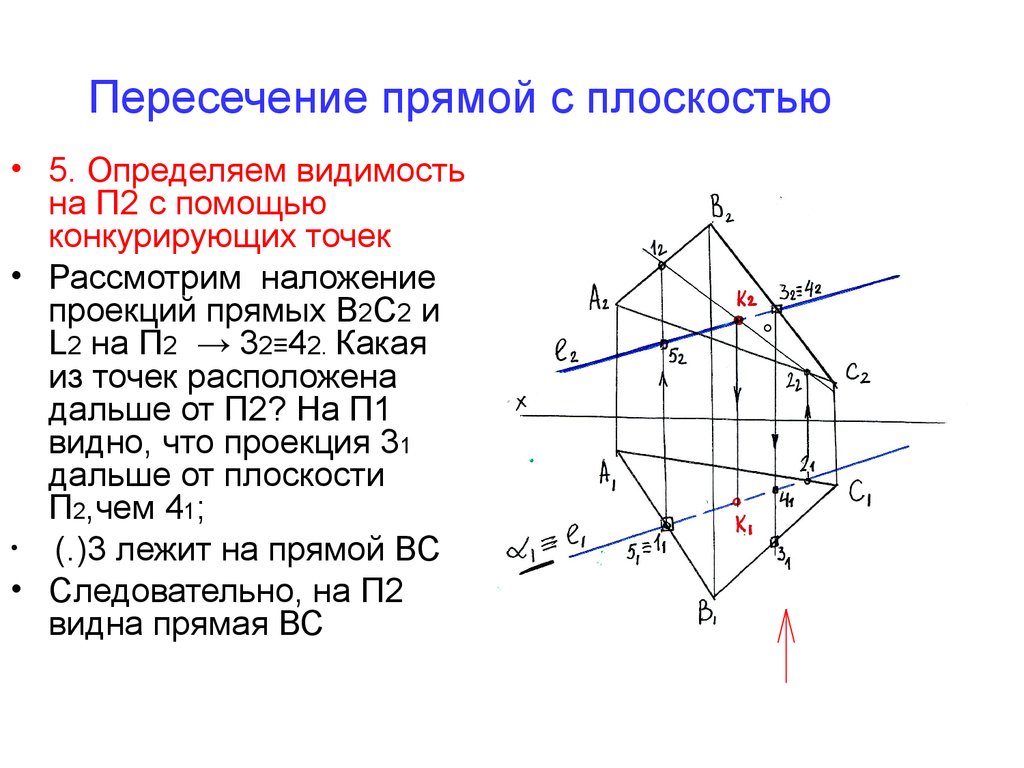 Точки пересечения окружности со сторонами угла обозначим как В и С.
Точки пересечения окружности со сторонами угла обозначим как В и С.
Затем при помощи циркуля из полученных точек откладываем такого же размера дуги. В точке пересечения дуг отметим точку D.
Соединим точку А с точкой D.
Полученный отрезок – биссектриса угла АВС.
Геометрические построения: перпендикуляр к отрезку
Чтобы отложить серединный перпендикуляр к отрезку АВ, необходимо использовать циркуль. Произвольным раствором циркуля по обе стороны отрезка проводятся дуги, которые откладываются из каждой точки – А и В.
Пересечение дуг с каждой стороны отрезка образует точки С и D. Если соединить эти точки, то получим перпендикуляр к отрезку А и В.
Таким же образом можно построить середину отрезка А и В.
Проведение перпендикулярной прямой
Существует два случая:
- Точка О, через которую надо провести перпендикуляр, находится на прямой.

- Точка О, через которую надо провести перпендикуляр находится вне прямой.
В первом случае необходимо из точки о отложить произвольным радиусом две окружности, которые пересекут прямую в точках А и В. Далее из каждой из полученных точек нужно провести окружность радиусом, равным расстоянию между А и В. Из точки С пересечения данных окружностей опускаем на прямую перпендикуляр в точку О, находящуюся на прямой между А и В.
Треугольник АСВ – равнобедренный, поэтому СО – его высота.
О правилах быстрого счета читайте здесь.
Самолетостроение: Как делают самолеты?
Самолет — это летательный аппарат с двигателем, который движется вперед в воздухе за счет тяги двигателя. Мы все это знаем, но как мы доходим до этой стадии? Как делают самолеты?
Самолеты производятся серийно? Завод выпускает сотни самолетов одновременно с мелкой бытовой техникой? Или он производит по одному самолету, как антиквариат ручной работы? Или правда смесь обоих утверждений?
Требуется несколько этапов проектирования и производства, чтобы сконструировать нечто такое огромное, способное летать в небе. Давайте вместе посмотрим на эти этапы и узнаем, как делаются самолеты.
Давайте вместе посмотрим на эти этапы и узнаем, как делаются самолеты.
Как изготавливаются самолеты: Этап проектирования
Цели и технические характеристики самолета устанавливаются в процессе проектирования и планирования.
Первый шаг — использование рисунков и уравнений. На этом этапе компании используют компьютеры для рисования и планирования дизайна.
Затем наступает этап моделирования, компьютеры снова используются для первоначального моделирования самолета. После этого изготавливаются небольшие модели всей конструкции или только отдельных частей самолета, которые испытываются в аэродинамических трубах, чтобы испытать его аэродинамику.
Этап проектирования и планирования может занять до четырех лет.
Как изготавливаются самолеты: Стадия строительства
Самолет состоит из ряда основных компонентов, таких как фюзеляж, крылья, оперение, шасси и один или несколько двигателей.
Каждый из этих компонентов состоит из тысяч мелких деталей. Меньшие части строятся по отдельности, а затем собираются вместе.
Меньшие части строятся по отдельности, а затем собираются вместе.
Когда два или более компонентов самолета необходимо соединить сваркой, процесс должен соответствовать самым строгим и конкретным правилам и стандартам безопасности. Национальная программа аккредитации подрядчиков в области аэрокосмической и оборонной промышленности (Nadcap) устанавливает глобальные требования к качеству, управлению качеством и обеспечению качества для всего авиастроения.
Очень немногие компании в мире производят самолеты в больших масштабах. Но авиастроение — это процесс, в который, помимо основного предприятия-производителя, обычно вовлечено множество других компаний и заводов.
Другие компании часто производят компоненты, которые идут в самолет. Или просто производить детали, из которых изготавливаются основные компоненты. Например, компания может нести ответственность за производство иллюминаторов для самолетов. И поскольку этот процесс не ограничивается компаниями, находящимися в том же городе, что и завод-изготовитель, или даже в одной стране, иногда детали для самолетов могут поступать со всего мира.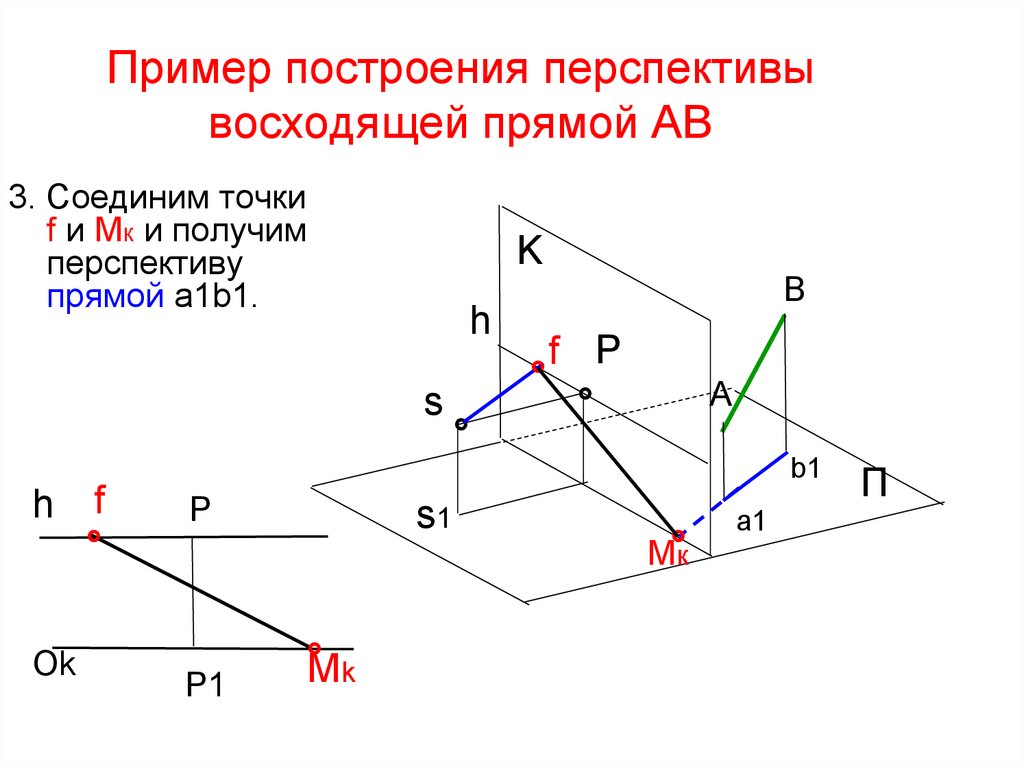
Как производятся самолеты: Стадия сборки
Готовые и проверенные детали отправляются на головной завод авиастроительной компании, где находится производственная линия. Части теперь готовы к соединению вместе, чтобы сформировать самолет.
Иногда существуют производственные линии, предназначенные для сборки определенных частей самолета, особенно крыльев и фюзеляжа в случае очень больших самолетов.
После того, как весь самолет собран, его тщательно осматривают на наличие каких-либо недостатков или дефектов.
После того, как инспекторы дают свое согласие, самолет подвергается серии летных испытаний, чтобы убедиться, что все его системы работают должным образом и что самолет работает плавно и без заминок.
Но это не финальный этап, после прохождения всех этих испытаний самолет готов к «финальной доработке», которая может включать в себя внутреннюю настройку или покраску, или любые косметические работы.
После этого этапа самолет окончательно готов к передаче заказчику.
1- Самолеты авиации общего назначения.
2- Коммерческие транспортные самолеты.
3- Боевые самолеты.
Деятельность авиации общего назначения подразделяется на личную авиацию, рекреационную авиацию и спасательные службы, и большинство самолетов авиации общего назначения имеют небольшие размеры и имеют один или два двигателя, а некоторые из них оснащены реактивными двигателями, но большинство из них приводится в движение воздушными винтами. Коммерческие транспортные самолеты большие и подходят для перевозки пассажиров, товаров или только товаров Авиакомпании эксплуатируют эти самолеты, самый маленький из которых может вместить от 20 до 100 пассажиров, самый большой из которых может вместить более ста человек. Что касается боевых самолетов, то к ним относятся бомбардировщики, истребители и военные корабли, принадлежащие правительствам стран.
Материалы для изготовления самолетов
Процесс изготовления самолетов включает в себя множество материалов для его изготовления, включая древесину, некоторые композитные материалы, синтетические волокна и несколько типов металлов. Первые самолеты изготавливались из дерева и обтягивались тканью, а затем развилась авиапромышленность и стала производиться из смеси металлов и алюминия, который также отличается своей прочностью и легкостью, и авиастроительные материалы не ограничиваются только теми , металлический титан также входит в состав некоторых частей самолетов, таких как двигатель, и есть некоторые композитные материалы с очень легким весом в обмен на его прочность, так как доля композитных материалов в некоторых самолетах может достигать половины, что делает этот лучшие варианты в процессе постройки самолета
Первые самолеты изготавливались из дерева и обтягивались тканью, а затем развилась авиапромышленность и стала производиться из смеси металлов и алюминия, который также отличается своей прочностью и легкостью, и авиастроительные материалы не ограничиваются только теми , металлический титан также входит в состав некоторых частей самолетов, таких как двигатель, и есть некоторые композитные материалы с очень легким весом в обмен на его прочность, так как доля композитных материалов в некоторых самолетах может достигать половины, что делает этот лучшие варианты в процессе постройки самолета
Самые известные страны-производители самолетов
Соединенные Штаты Америки: Производитель самого известного в мире самолета Boeing.
Франция, Германия, Испания и Великобритания: Все эти страны участвуют в производстве самолета-конкурента Boeing, которым является «Эйрбас».
Россия: Производство военных самолетов составляет важную часть российской экономики.
Канада. Италия. Япония. Бразилия
самолет | Определение, типы, механика и факты
Air New Zealand Limited
См. все средства массовой информации
- Ключевые сотрудники:
- Игорь Сикорский Говард Хьюз Чарльз Линдберг Олив Энн Бич Жаклин Кокран
- Похожие темы:
- С-47 гидросамолет Конкорд ДС-3 Боинг 367-80
Просмотреть весь связанный контент →
Резюме
Прочтите краткий обзор этой темы
самолет , также называемый самолет или самолет , любой из класса самолетов с неподвижным крылом, который тяжелее воздуха, приводится в движение винтовым винтом или высокоскоростной реактивной струей и поддерживается динамической реакцией воздух против своих крыльев. За отчет о развитии самолета и появлении гражданской авиации см. историю полетов.
Основными компонентами самолета являются система крыла, поддерживающая его в полете, хвостовое оперение для стабилизации крыльев, подвижные поверхности для управления ориентацией самолета в полете и силовая установка, обеспечивающая тягу, необходимую для толкания летательного аппарата через воздух. Должна быть предусмотрена поддержка самолета, когда он находится в состоянии покоя на земле, а также во время взлета и посадки. Большинство самолетов имеют закрытый корпус (фюзеляж) для размещения экипажа, пассажиров и груза; кабина — это место, из которого пилот управляет органами управления и приборами для управления самолетом.
Должна быть предусмотрена поддержка самолета, когда он находится в состоянии покоя на земле, а также во время взлета и посадки. Большинство самолетов имеют закрытый корпус (фюзеляж) для размещения экипажа, пассажиров и груза; кабина — это место, из которого пилот управляет органами управления и приборами для управления самолетом.
Принципы полета и эксплуатации самолета
На самолет в горизонтальном полете без ускорения действуют четыре силы. (При повороте, нырянии или полете с набором высоты в игру вступают дополнительные силы.) Этими силами являются подъемная сила, сила, действующая вверх; сопротивление, тормозящая сила сопротивления подъемной силе и трению самолета, движущегося по воздуху; вес, нисходящий эффект гравитации на самолет; и тяга, сила прямого действия, обеспечиваемая двигательной установкой (или, в случае самолета без двигателя, за счет использования силы тяжести для преобразования высоты в скорость). Сопротивление и вес — элементы, присущие любому объекту, в том числе и летательному аппарату.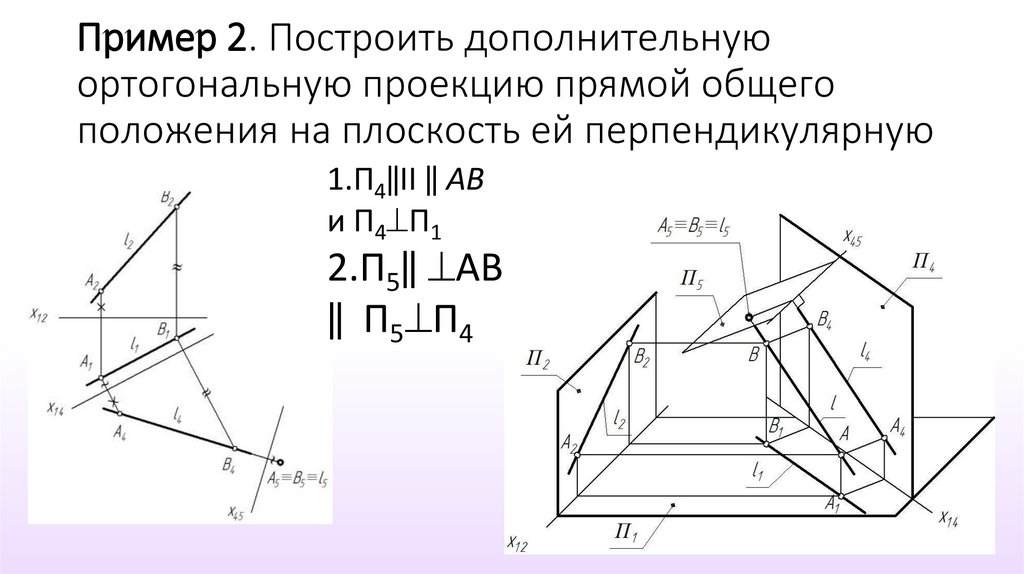 Подъемная сила и тяга — это искусственно созданные элементы, разработанные для того, чтобы самолет мог летать.
Подъемная сила и тяга — это искусственно созданные элементы, разработанные для того, чтобы самолет мог летать.
Чтобы понять подъемную силу, в первую очередь необходимо понять аэродинамический профиль, который представляет собой конструкцию, предназначенную для получения реакции на его поверхность от воздуха, в котором он движется. Ранние аэродинамические поверхности обычно имели немного больше, чем слегка изогнутую верхнюю поверхность и плоскую нижнюю поверхность. На протяжении многих лет аэродинамические поверхности адаптировались для удовлетворения меняющихся потребностей. К 1920-м годам аэродинамические поверхности обычно имели закругленную верхнюю поверхность, при этом наибольшая высота достигалась в первой трети хорды (ширины). Со временем как верхняя, так и нижняя поверхности искривлялись в большей или меньшей степени, а наиболее толстая часть аэродинамического профиля постепенно смещалась назад. По мере роста скорости полета возникла потребность в очень плавном прохождении воздуха над поверхностью, что было достигнуто в аэродинамическом профиле с ламинарным потоком, где изгиб был дальше назад, чем того требовала современная практика.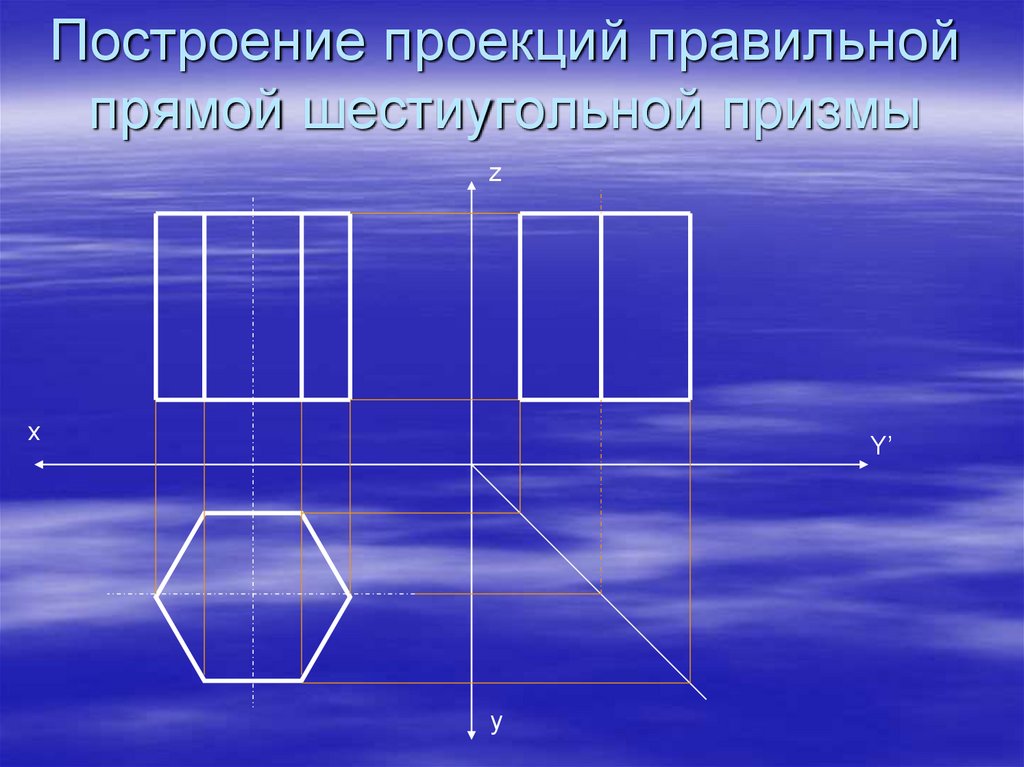 Сверхзвуковые самолеты потребовали еще более радикальных изменений в форме аэродинамического профиля, некоторые из которых потеряли округлость, ранее связанную с крылом, и приобрели форму двойного клина.
Сверхзвуковые самолеты потребовали еще более радикальных изменений в форме аэродинамического профиля, некоторые из которых потеряли округлость, ранее связанную с крылом, и приобрели форму двойного клина.
Викторина «Британника»
Самолет: правда или вымысел?
Является ли авиационная отрасль крупнейшим в мире потребителем нефти? Можно ли дозаправлять Air Force One в воздухе? Проверьте, подходите ли вы для первоклассной работы, ответив на вопросы этой увлекательной викторины.
Двигаясь вперед в воздухе, аэродинамический профиль крыла получает полезную для полета реакцию от воздуха, проходящего над его поверхностью. (В полете аэродинамическая поверхность крыла обычно создает наибольшую подъемную силу, но гребные винты, хвостовое оперение и фюзеляж также функционируют как аэродинамические поверхности и создают подъемную силу различной величины.) В 18 веке швейцарский математик Даниэль Бернулли обнаружил, что если скорость воздуха над определенной точкой профиля увеличивается, давление воздуха уменьшается.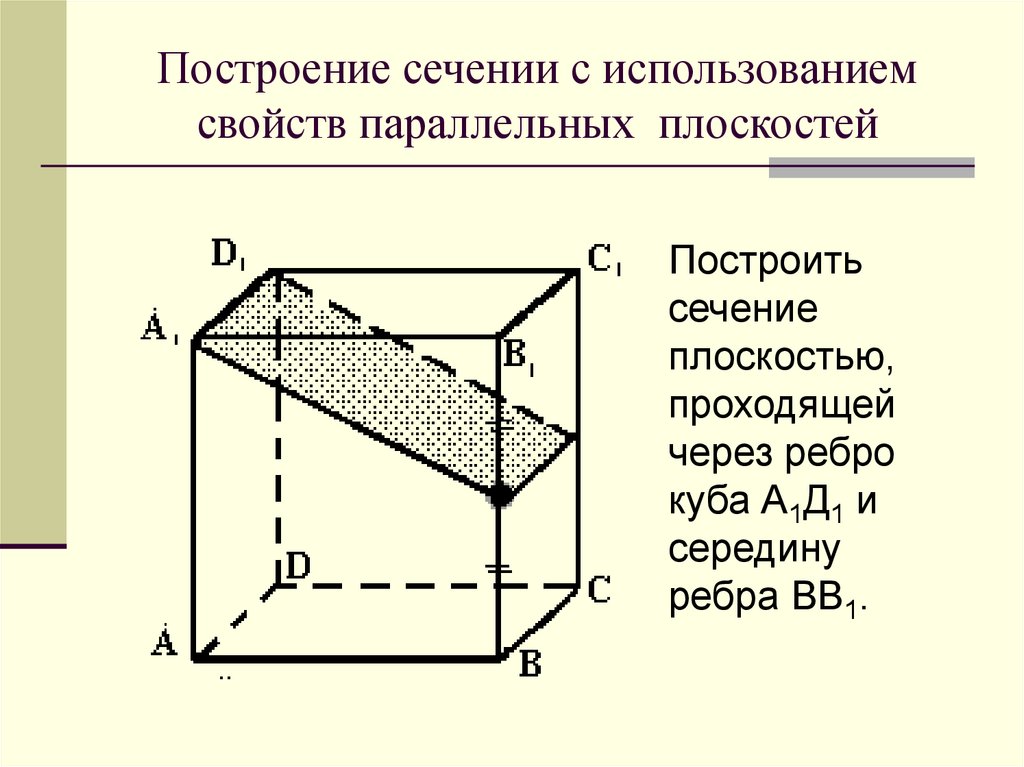 Воздух, протекающий над изогнутой верхней поверхностью аэродинамического профиля крыла, движется быстрее, чем воздух, протекающий по нижней поверхности, уменьшая давление сверху. Более высокое давление снизу толкает (поднимает) крыло вверх в область более низкого давления. Одновременно воздух, обтекающий нижнюю часть крыла, отклоняется вниз, обеспечивая ньютоновскую равную и противоположную реакцию и внося свой вклад в общую подъемную силу.
Воздух, протекающий над изогнутой верхней поверхностью аэродинамического профиля крыла, движется быстрее, чем воздух, протекающий по нижней поверхности, уменьшая давление сверху. Более высокое давление снизу толкает (поднимает) крыло вверх в область более низкого давления. Одновременно воздух, обтекающий нижнюю часть крыла, отклоняется вниз, обеспечивая ньютоновскую равную и противоположную реакцию и внося свой вклад в общую подъемную силу.
На подъемную силу аэродинамического профиля также влияет его «угол атаки», то есть его угол по отношению к ветру. И подъемную силу, и угол атаки можно сразу, хотя и грубо, продемонстрировать, выставив руку из окна движущегося автомобиля. Когда рука повернута плашмя к ветру, ощущается большое сопротивление и создается небольшой «подъем», поскольку за рукой находится турбулентная область. Отношение подъемной силы к сопротивлению низкое. Когда рука держится параллельно ветру, сопротивление гораздо меньше и создается умеренная подъемная сила, турбулентность сглаживается, а отношение подъемной силы к сопротивлению лучше. Однако если руку немного повернуть так, чтобы ее передний край был поднят на больший угол атаки, подъемная сила увеличится. Это положительное увеличение отношения подъемной силы к сопротивлению создаст тенденцию руки «летать» вверх и вверх. Чем больше скорость, тем больше будет подъемная сила и сопротивление. Таким образом, полная подъемная сила связана с формой аэродинамического профиля, углом атаки и скоростью, с которой крыло проходит через воздух.
Однако если руку немного повернуть так, чтобы ее передний край был поднят на больший угол атаки, подъемная сила увеличится. Это положительное увеличение отношения подъемной силы к сопротивлению создаст тенденцию руки «летать» вверх и вверх. Чем больше скорость, тем больше будет подъемная сила и сопротивление. Таким образом, полная подъемная сила связана с формой аэродинамического профиля, углом атаки и скоростью, с которой крыло проходит через воздух.
Оформите подписку Britannica Premium и получите доступ к эксклюзивному контенту. Подписаться сейчас
Вес – это сила, действующая противоположно подъемной силе. Таким образом, конструкторы пытаются сделать самолет максимально легким. Поскольку все конструкции самолетов имеют тенденцию к увеличению веса в процессе разработки, в штатах современных аэрокосмических инженеров есть специалисты в области контроля веса с самого начала проектирования. Кроме того, пилоты должны контролировать общий вес, который разрешено перевозить воздушному судну (пассажиры, топливо и груз), как по количеству, так и по местоположению.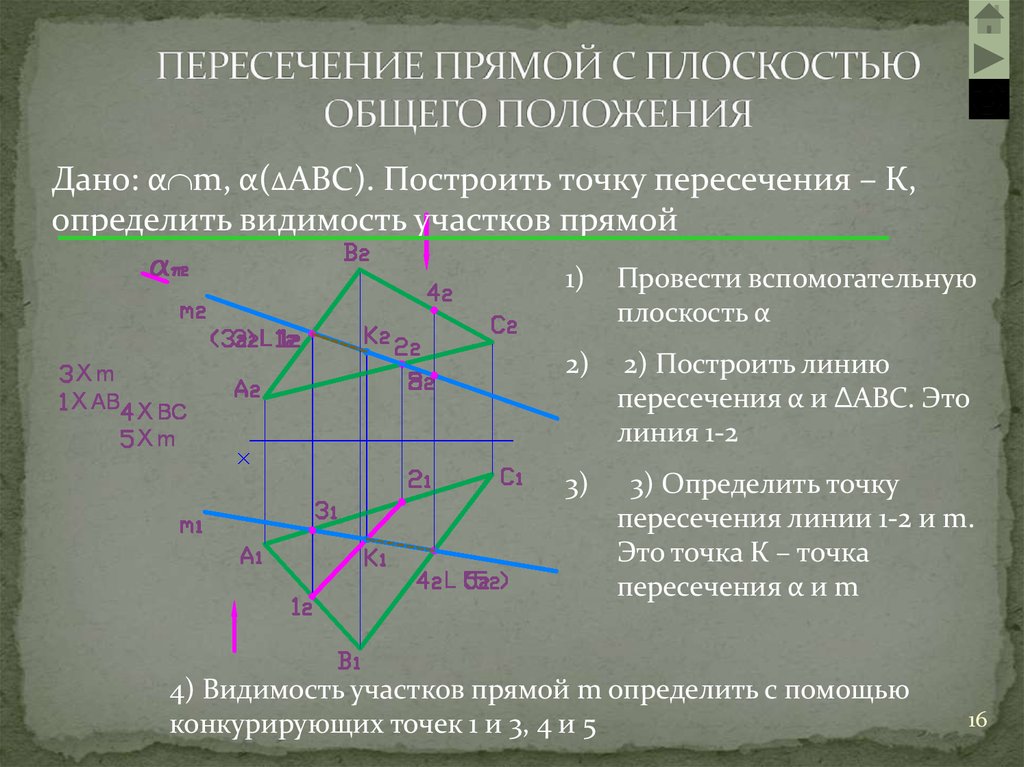 Распределение веса (то есть управление центром тяжести самолета) так же важно с точки зрения аэродинамики, как и величина переносимого веса.
Распределение веса (то есть управление центром тяжести самолета) так же важно с точки зрения аэродинамики, как и величина переносимого веса.
Тяга, сила, действующая вперед, противостоит сопротивлению, как подъемная сила противостоит весу. Тяга получается за счет ускорения массы окружающего воздуха до скорости, превышающей скорость самолета; равной и противоположной реакцией является движение самолета вперед. В поршневых или турбовинтовых самолетах тяга создается за счет движущей силы, вызванной вращением воздушного винта, а остаточная тяга обеспечивается выхлопом. В реактивном двигателе тяга создается движущей силой вращающихся лопастей турбины, сжимающей воздух, который затем расширяется за счет сгорания введенного топлива и выбрасывается из двигателя. В самолете с ракетным двигателем тяга создается за счет равной и противоположной реакции на горение ракетного топлива. В планере высота, достигнутая с помощью механических, орографических или тепловых методов, преобразуется в скорость посредством гравитации.
Действуя в постоянном противодействии тяге, есть сопротивление, состоящее из двух элементов. Паразитическое сопротивление вызвано сопротивлением формы (из-за формы), трением кожи, помехами и всеми другими элементами, которые не способствуют подъемной силе; Индуктивное сопротивление создается в результате создания подъемной силы.
Паразитное сопротивление увеличивается по мере увеличения скорости полета. Для большинства полетов желательно, чтобы все сопротивление было сведено к минимуму, и по этой причине значительное внимание уделяется оптимизации формы самолета за счет устранения как можно большего количества конструкций, вызывающих сопротивление (например, ограждение кабины фонарем, уборка шасси, заклепка заподлицо, покраска и полировка поверхностей). Некоторые менее очевидные элементы сопротивления включают относительное расположение и площадь поверхностей фюзеляжа и крыла, двигателя и оперения; пересечение крыльев и оперения; непреднамеренная утечка воздуха через конструкцию; использование избыточного воздуха для охлаждения; и использование отдельных форм, которые вызывают локальное разделение воздушного потока.
Индуктивное сопротивление вызывается той частью воздуха, которая отклоняется вниз и не является вертикальной по отношению к траектории полета, а немного наклонена назад от нее. По мере увеличения угла атаки увеличивается и сопротивление; в критической точке угол атаки может стать настолько большим, что поток воздуха разбивается о верхнюю поверхность крыла, и подъемная сила теряется при увеличении сопротивления. Это критическое состояние называется сваливанием.
Подъемная сила, сопротивление и сваливание по-разному зависят от формы крыла в плане. Например, эллиптическое крыло, подобное тому, что использовалось на истребителе Supermarine Spitfire времен Второй мировой войны, хотя и идеально с точки зрения аэродинамики для дозвукового самолета, имеет более нежелательную схему сваливания, чем простое прямоугольное крыло.
Аэродинамика сверхзвукового полета сложна. Воздух сжимаем, и по мере увеличения скорости и высоты скорость воздуха, обтекающего самолет, начинает превышать скорость движения самолета по воздуху. Скорость, с которой эта сжимаемость действует на самолет, выражается как отношение скорости самолета к скорости звука, называемое числом Маха в честь австрийского физика Эрнста Маха. Критическое число Маха для самолета было определено как то, при котором в какой-то точке самолета скорость воздушного потока достигает скорости звука.
Скорость, с которой эта сжимаемость действует на самолет, выражается как отношение скорости самолета к скорости звука, называемое числом Маха в честь австрийского физика Эрнста Маха. Критическое число Маха для самолета было определено как то, при котором в какой-то точке самолета скорость воздушного потока достигает скорости звука.
При числах Маха, превышающих критическое число Маха (то есть скоростях, при которых воздушный поток превышает скорость звука в локальных точках планера), происходят значительные изменения сил, давлений и моментов, действующих на крыло и фюзеляжа в результате образования ударных волн. Одним из наиболее важных эффектов является очень большое увеличение сопротивления, а также снижение подъемной силы. Первоначально конструкторы стремились достичь более высоких критических чисел Маха, проектируя самолеты с очень тонкими сечениями аэродинамического профиля крыла и горизонтальных поверхностей и обеспечивая как можно более высокое отношение тонкости (длины к диаметру) фюзеляжа. Соотношение толщины крыла (толщина крыла, деленная на его ширину) составляла от 14 до 18 процентов на типичных самолетах 19-го века.40–45 период; в более поздних самолетах это соотношение было снижено до менее 5 процентов. Эти методы задержали локальный воздушный поток, достигший скорости 1,0 Маха, что позволило немного увеличить критические числа Маха для самолета. Независимые исследования, проведенные в Германии и США, показали, что достижение критического числа Маха можно еще больше отсрочить, если откинуть крылья назад. Размах крыла был чрезвычайно важен для разработки немецкого Messerschmitt Me 262 времен Второй мировой войны, первого боевого реактивного истребителя, а также для послевоенных истребителей, таких как North American F-86 Sabre и советский МиГ-15. Эти истребители работали на высоких дозвуковых скоростях, но конкурентное давление разработки требовало самолетов, которые могли бы работать на околозвуковых и сверхзвуковых скоростях. Мощность реактивных двигателей с форсажной камерой делала эти скорости технически возможными, но конструкторам все еще мешало огромное увеличение лобового сопротивления в околозвуковой области.
Соотношение толщины крыла (толщина крыла, деленная на его ширину) составляла от 14 до 18 процентов на типичных самолетах 19-го века.40–45 период; в более поздних самолетах это соотношение было снижено до менее 5 процентов. Эти методы задержали локальный воздушный поток, достигший скорости 1,0 Маха, что позволило немного увеличить критические числа Маха для самолета. Независимые исследования, проведенные в Германии и США, показали, что достижение критического числа Маха можно еще больше отсрочить, если откинуть крылья назад. Размах крыла был чрезвычайно важен для разработки немецкого Messerschmitt Me 262 времен Второй мировой войны, первого боевого реактивного истребителя, а также для послевоенных истребителей, таких как North American F-86 Sabre и советский МиГ-15. Эти истребители работали на высоких дозвуковых скоростях, но конкурентное давление разработки требовало самолетов, которые могли бы работать на околозвуковых и сверхзвуковых скоростях. Мощность реактивных двигателей с форсажной камерой делала эти скорости технически возможными, но конструкторам все еще мешало огромное увеличение лобового сопротивления в околозвуковой области. Решение заключалось в увеличении объема фюзеляжа перед и позади крыла и уменьшении его возле крыла и хвоста, чтобы создать площадь поперечного сечения, которая более всего приближалась к идеальной площади для ограничения околозвукового сопротивления. Раннее применение этого правила привело к появлению «осиной талии», такой как у Convair F-102. В более поздних реактивных самолетах применение этого правила не так очевидно в плане самолета.
Решение заключалось в увеличении объема фюзеляжа перед и позади крыла и уменьшении его возле крыла и хвоста, чтобы создать площадь поперечного сечения, которая более всего приближалась к идеальной площади для ограничения околозвукового сопротивления. Раннее применение этого правила привело к появлению «осиной талии», такой как у Convair F-102. В более поздних реактивных самолетах применение этого правила не так очевидно в плане самолета.
Как строятся самолеты: полное руководство
Мы все смотрели в небо и восхищались удивительными машинами, которыми являются самолеты. В этом руководстве вы узнаете, как именно строятся самолеты.
В следующий раз, когда вы поедете в аэропорт, умоляю вас внимательно посмотреть на самолеты вокруг. Огромный их размер. Какие они невероятные. Дело в том, что эти гигантские металлические машины могут поднять нас в небо и облететь вокруг света. Если вы уже сделали это, готов поспорить, что в какой-то момент вы задавались вопросом, как строятся самолеты, верно?
Самолеты строятся в четыре этапа. Прежде всего, инженеры должны планировать и проектировать самолет. Затем выполняется компьютерное моделирование с использованием программного обеспечения САПР для проверки конструкций. Затем строятся различные части самолета. Наконец, части собираются вместе.
Прежде всего, инженеры должны планировать и проектировать самолет. Затем выполняется компьютерное моделирование с использованием программного обеспечения САПР для проверки конструкций. Затем строятся различные части самолета. Наконец, части собираются вместе.
Хотя мы можем немного предвзято относиться ко всему, что связано с авиацией, я думаю, мы все можем согласиться с тем, что самолеты удивительны. Я знаю, что лично я был поражен ими с детства, и это побудило меня заняться авиацией как страстью. В этой статье я надеюсь поделиться с вами своей страстью к самолетам и авиации, предоставив вам полное руководство о том, как строятся самолеты.
Здесь, в SkyTough, мы стремимся предоставить нашим читателям только лучший авиационный контент, который они могут найти в Интернете. Таким образом, когда вы закончите читать эту статью, вы будете точно знать, как строятся самолеты, и вам не придется искать ответ в Интернете. Для этого мы тщательно изучаем каждую тему и объединяем полученные результаты с нашими собственными знаниями и опытом, а также с опытом других специалистов в этой великой отрасли.
Как строятся самолеты?
Я хотел бы иметь неограниченное время и пространство, чтобы по-настоящему погрузиться в детали того, как строятся самолеты, потому что этот процесс, несомненно, вызывает восхищение. Сложные детали каждой фазы, все различные части и кусочки, которые идут вместе. И, конечно же, как все эти детали сочетаются друг с другом. То, как устроены самолеты, и тот факт, что они летают на тысячи футов в воздухе, до сих пор поражает меня.
Но, к сожалению, вы бы читали эту статью несколько дней, если бы я действительно углубился в мельчайшие детали. Поэтому вместо этого я собираюсь дать вам общий обзор того, что связано с созданием самолетов, которое состоит из четырех основных этапов. К ним относятся планирование и проектирование, компьютерное моделирование, изготовление деталей и сборка.
Давайте перейдем к самому интересному.
Планирование и проектирование самолетов
Первым шагом в процессе создания самолета, конечно же, является планирование и проектирование самолета. Если речь идет о самолете, который уже был спроектирован и построен в течение многих лет, то в этом может не быть необходимости. Но для того, чтобы строить новые самолеты и чтобы инновации в авиации продолжались, необходимо регулярно проектировать новые самолеты. Вот что задействовано.
Если речь идет о самолете, который уже был спроектирован и построен в течение многих лет, то в этом может не быть необходимости. Но для того, чтобы строить новые самолеты и чтобы инновации в авиации продолжались, необходимо регулярно проектировать новые самолеты. Вот что задействовано.
Этот шаг может занять от нескольких недель до нескольких месяцев, и его выполняют авиаконструкторы, являющиеся экспертами в своей области. На этом этапе они определят форму и размер самолета, а также то, как он будет питаться и как он будет управляться. Этот первоначальный проект помогает гарантировать, что после постройки самолета он сможет успешно выполнять свою миссию — будь то перевозка людей или товаров из одного места в другое или предоставление таких услуг, как тушение пожаров по воздуху.
После того, как авиаконструкторы завершили разработку конструкции самолета, они передают чертежи инженерам. Инженеры — это следующая группа профессионалов, которые участвуют в процессе строительства самолета. Они берут проекты, созданные авиаконструкторами, и придумывают, как воплотить их в жизнь.
Они берут проекты, созданные авиаконструкторами, и придумывают, как воплотить их в жизнь.
Это включает в себя определение таких вещей, как, какой вес может выдержать каждая часть самолета, какие материалы должны использоваться для каждой части самолета и как все должно быть соединено вместе. Сколько времени займет этот процесс, будет зависеть от того, какой тип самолета строится, но инженеры нередко тратят годы на проработку всех этих деталей, прежде чем какие-либо детали будут заказаны или изготовлены.
Сколько времени уходит на проектирование самолета?
Процесс проектирования самолета занимает примерно шесть лет. Первый этап проекта — это набросок того, как вы хотите, чтобы он выглядел, где все части будут сочетаться друг с другом, и что он сможет делать, когда вы закончите строительство. После того, как ваша идея была изложена на бумаге, начинается поиск материалов, которые были бы одновременно легкими и прочными.
Шесть лет могут показаться довольно долгим сроком для конструкции самолета, но это просто потому, что это так! Но если подумать, на самом деле не так много новых и улучшенных конструкций самолетов выпускается каждый год или что-то в этом роде. По большей части многие из тех же самолетов, которые используются сегодня, использовались десятилетиями. Таким образом, первоначальные затраты времени на разработку надежного самолета в конечном итоге окупятся.
По большей части многие из тех же самолетов, которые используются сегодня, использовались десятилетиями. Таким образом, первоначальные затраты времени на разработку надежного самолета в конечном итоге окупятся.
Компьютерное моделирование конструкций самолетов
Чтобы ускорить (и подчеркнуть) процесс проектирования, некоторые авиаконструкторы используют компьютерное моделирование. Здесь они создают трехмерную модель самолета с помощью программного обеспечения, а затем проверяют, как он будет работать в различных условиях. В конце концов, гораздо проще ввести некоторую информацию и цифры в симуляцию, чем протестировать даже масштабную модель реального объекта.
Например, они могут смоделировать, что происходит, когда самолет сталкивается с турбулентностью, или как он будет себя вести, если совершит жесткую посадку. Эти симуляции можно использовать для проверки того, насколько быстро может летать самолет и как высоко он может подняться. Вещи, которые нельзя проверить в реальном мире. Затем результаты компьютерного моделирования можно использовать для корректировки конструкции самолета перед изготовлением каких-либо деталей.
Затем результаты компьютерного моделирования можно использовать для корректировки конструкции самолета перед изготовлением каких-либо деталей.
Компьютерное моделирование также можно использовать для проверки того, насколько хорошо будет работать самолет после его использования. Например, они могут смоделировать, сколько энергии будут производить двигатели и достаточно ли места для багажа под всеми сиденьями. Они даже могли определить, будет ли у пассажиров место для хранения ручной клади над головой во время взлета и посадки.
Без компьютерного моделирования проектирование самолета заняло бы не только значительно больше времени, но и вовлеченные инженеры не получили бы полного представления о том, как самолет будет вести себя в различных условиях. Моделирование значительно ускорило процесс создания самолета, а также сделало конечный продукт гораздо более удобным в использовании и дало участникам более точную картину того, как он на самом деле будет реагировать.
Сколько времени нужно, чтобы испытать самолет с помощью моделирования?
После завершения проектирования нового самолета его необходимо протестировать с помощью моделирования, прежде чем он может быть одобрен для использования авиакомпаниями.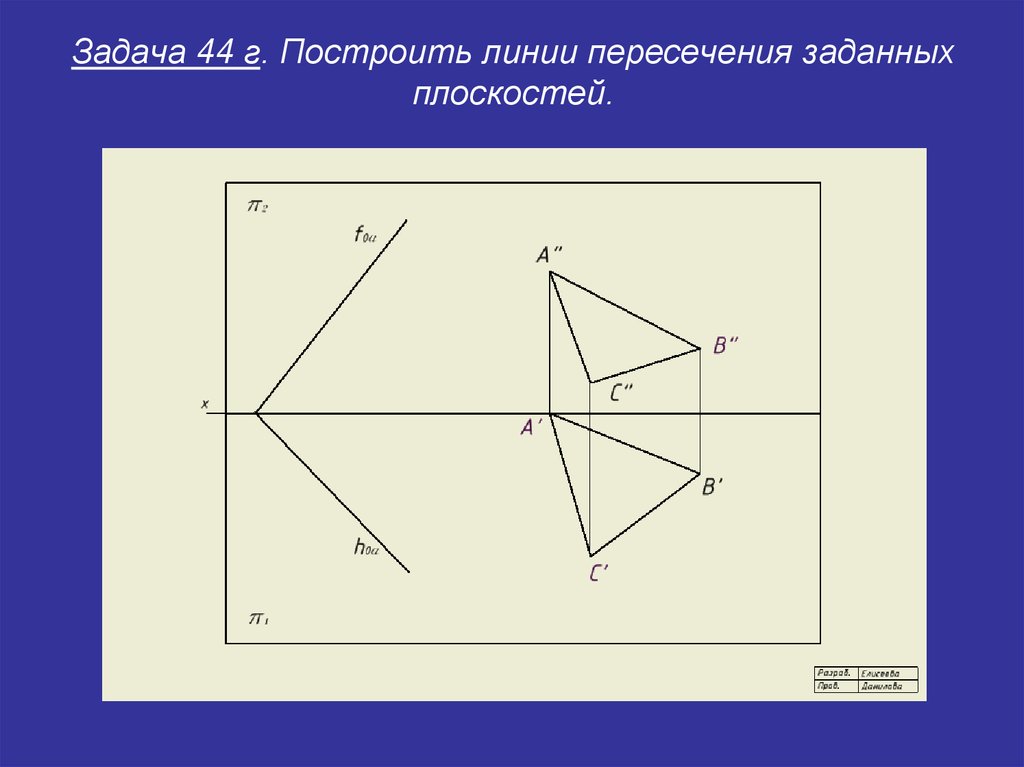 Сколько времени занимает этот процесс?
Сколько времени занимает этот процесс?
Обычно испытание самолета с помощью моделирования занимает около двух лет. Однако этот срок может варьироваться в зависимости от сложности самолета. Например, тестирование нового дизайна может занять больше времени, чем тестирование обновления существующей модели. И, как упоминалось выше, большинство самолетов, используемых сегодня, на самом деле представляют собой не совершенно новые модели, а просто существующие модели с обновленными функциями и дизайном.
По большей части время, необходимое для запуска моделирования, учитывается в общем времени проектирования, поскольку дизайнеры и инженеры должны работать бок о бок, чтобы создать идеальный самолет и при необходимости настроить конструктивные особенности на основе моделирования. полученные результаты. Таким образом, проектирование и моделирование на самом деле не являются двумя отдельными шагами сами по себе, а скорее выполняются одновременно, чтобы ускорить процесс, опираясь друг на друга.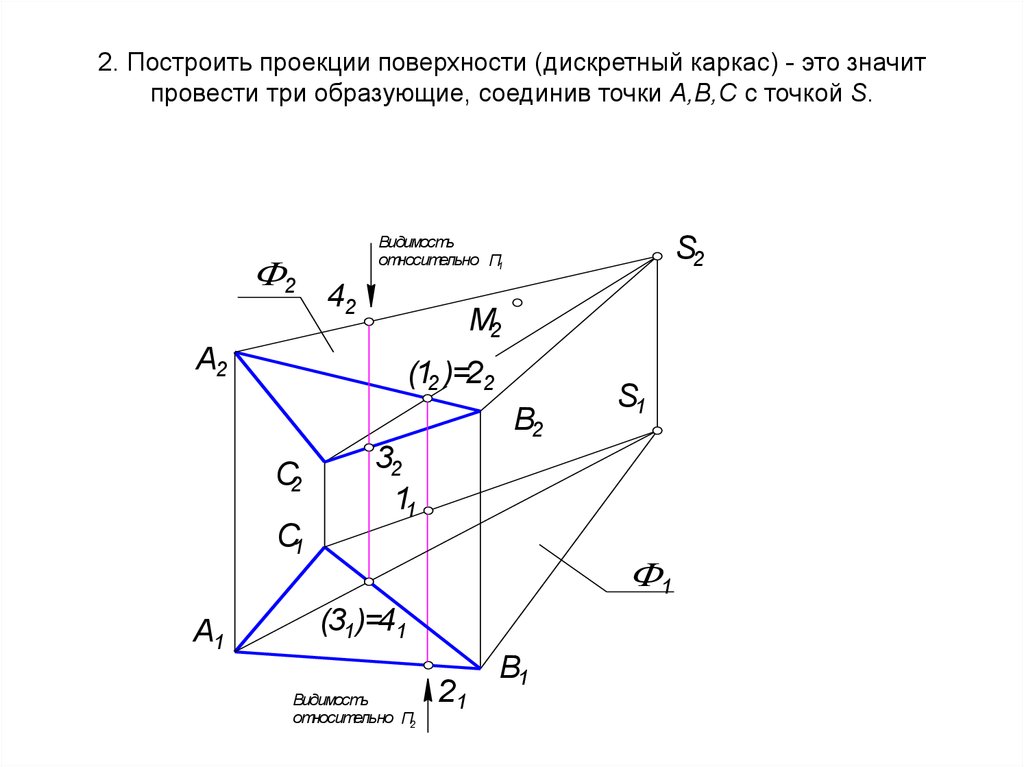
Изготовление частей самолета
После того, как обширные процессы планирования, проектирования и моделирования завершены, мы, наконец, приступаем к фактической конструкции самолета. Прежде чем можно будет построить сам самолет, необходимо построить все отдельные части и детали. Тогда это, вероятно, заставит вас задуматься обо всех различных частях и деталях, которые на самом деле задействованы в самолете.
По правде говоря, существуют тысячи и тысячи различных частей самолета, которые должны работать вместе, чтобы действительно летать. Учитывая сложность полета, это чудо, как вообще летают самолеты, но все это было бы невозможно без тщательного процесса строительства. Вот что задействовано.
Какие части самолета?
Части самолета — это все отдельные части, которые собираются вместе, чтобы сформировать целое. Сами по себе они не имеют никакой реальной пользы или функции, кроме того, что являются маленькими частями того, что составляет большую картину. Но объединенные друг с другом и правильно подобранные, эти отдельные компоненты работают вместе, чтобы создать конечный продукт, который представляет собой настоящий самолет, способный летать по воздуху.
Но объединенные друг с другом и правильно подобранные, эти отдельные компоненты работают вместе, чтобы создать конечный продукт, который представляет собой настоящий самолет, способный летать по воздуху.
В самолет входят самые разные детали, но наиболее примечательными являются крылья, фюзеляж, хвостовое оперение и двигатели. Каждый из них имеет определенную цель и является неотъемлемой частью того, чтобы самолет работал должным образом.
Что делают крылья?
Крылья, вероятно, являются одной из самых известных частей самолета. Это большие изогнутые части, которые торчат сбоку самолета и отвечают за создание подъемной силы. Этот лифт помогает удерживать самолет в воздухе и летать по небу. Чем больше площадь поверхности крыла, тем большую подъемную силу оно может создать, поэтому на коммерческих самолетах они имеют тенденцию быть такими большими.
Что такое фюзеляж?
Фюзеляж является основной частью самолета и удерживает все остальные части на своих местах. Как правило, он имеет цилиндрическую форму и состоит из множества различных панелей, собранных вместе, как пазл. Это одна из самых важных частей самолета, потому что она отвечает за скрепление всего остального.
Как правило, он имеет цилиндрическую форму и состоит из множества различных панелей, собранных вместе, как пазл. Это одна из самых важных частей самолета, потому что она отвечает за скрепление всего остального.
Что такое хвост?
Хвост — это задняя часть самолета, которая в основном используется для управления самолетом. Он состоит из множества различных частей, включая руль направления, который помогает контролировать движение самолета, и лифты, отвечающие за движение самолета вверх или вниз. Без хвоста пилот практически не мог бы управлять самолетом.
Что такое двигатели?
Как вы, наверное, знаете, именно двигатели обеспечивают мощность, которая в первую очередь позволяет самолетам летать. Не вдаваясь слишком далеко в детали авиационных двигателей, достаточно сказать, что они большие и чрезвычайно мощные. На большинстве коммерческих самолетов они все еще могут продолжать полет, даже если один двигатель выйдет из строя, что свидетельствует о том, насколько мощными на самом деле являются эти двигатели.
Сколько времени уходит на изготовление всех частей самолета?
В зависимости от сложности деталей и способа их изготовления изготовление деталей самолета может быть одним из самых длительных этапов производственного процесса. Тем не менее, пока существуют подходящие производственные процессы, которые могут обрабатывать необходимые детали, это не должно занимать столько же времени, сколько упомянутый выше потенциальный 6-летний процесс проектирования.
В среднем на постройку и/или приобретение всех различных частей самолета уходит от одного до двух лет. Это включает в себя все, от создания деталей с нуля до сборки десятков тысяч более мелких деталей, таких как гайки, болты, заклепки и т. д., для формирования некоторых основных систем самолета.
Но не волнуйтесь, как только все детали собраны, самолет почти готов к полету, даже если он состоит из множества разных частей!
Сборка частей самолета
Когда самолеты только производятся, их собирают из частей, а затем собирают, как пазл. Большинство деталей поставляются предварительно изготовленными, чтобы сократить расходы и сэкономить время, но, поскольку каждая деталь имеет свой уникальный размер, который необходимо соединить вместе, ее нельзя просто собрать волей-неволей. Сборка самолета требует большой точности и планирования, чтобы все подошло правильно и работало так, как должно.
Большинство деталей поставляются предварительно изготовленными, чтобы сократить расходы и сэкономить время, но, поскольку каждая деталь имеет свой уникальный размер, который необходимо соединить вместе, ее нельзя просто собрать волей-неволей. Сборка самолета требует большой точности и планирования, чтобы все подошло правильно и работало так, как должно.
Сначала детали доставляются с завода в аэропорт. Как быстро это происходит, зависит от того, насколько велик и тяжел самолет, а также от того, какой тип транспорта используется, но обычно требуется около дня или двух, чтобы все было перемещено на место. После того, как все детали доставлены, они распределяются по типам в так называемом авиационном ангаре.
Следующим шагом является начало процесса сборки, и этим занимается команда рабочих, специально обученных сборке самолетов. Весь процесс может занять от двух недель до месяца, в зависимости от размера и сложности самолета. Самая большая секция, которая собирается первой, — это корпус самолета, и он состоит из нескольких более мелких частей, которые нужно собрать вместе, как пазл.
Когда тело готово, прикрепляются крылья и, наконец, хвост. После того, как все эти основные секции собраны, рабочие устанавливают все двигатели, шасси и другие мелкие детали. Последним шагом в процессе сборки является проверка всего. Затем самолет проходит тщательное тестирование, чтобы увидеть, насколько хорошо он работает и нужно ли делать какой-либо ремонт, прежде чем он будет готов к своему первому полету.
Сколько времени занимает сборка самолета?
Хотя идея сборки гигантского, дорогого и тяжелого металлического пазла может показаться сложной задачей, на самом деле это самый быстрый этап всего процесса сборки самолета. Пока все тщательно спланировано и спроектировано до того, как будет построено с точными допусками, сборка должна быть намного более коротким этапом, чем любая другая часть процесса.
Зависит от размера и сложности самолета, но может занять от двух недель до месяца. Более крупные и сложные самолеты, как правило, занимают больше времени, потому что нужно собрать больше деталей. Это также занимает гораздо больше времени, если они работают с более новой технологией, а процесс сборки требует даже большей точности, чем в противном случае с хорошо известным процессом проектирования и сборки.
Это также занимает гораздо больше времени, если они работают с более новой технологией, а процесс сборки требует даже большей точности, чем в противном случае с хорошо известным процессом проектирования и сборки.
Сколько самолетов строится в год?
В США ежегодно строится более 11 000 самолетов. Но это не означает, что каждый используемый самолет внезапно заменяется каждый год. В конце концов, производство этих самолетов от начала до конца стоит миллионы и миллионы долларов, поэтому авиакомпании делают все возможное, чтобы максимально продлить жизнь самолетам.
На сегодняшний день в мире насчитывается около 19 000 самолетов, средний возраст которых превышает 20 лет. Боинг 747, ответственный за почти половину этих самолетов, находится в процессе вывода из эксплуатации. Он существует с 1970, но до сих пор остается одним из самых продаваемых больших пассажирских самолетов на рынке.
Хотя 11 000 самолетов, строящихся в год, безусловно, много, вы должны помнить, что каждый отдельный самолет не должен проходить этот процесс с самого начала. Как уже отмечалось, Boeing 747, например, существует с 1970 года и используется до сих пор. Таким образом, каждый построенный и/или используемый Боинг 747 не должен начинаться с нуля с новой конструкцией.
Как уже отмечалось, Boeing 747, например, существует с 1970 года и используется до сих пор. Таким образом, каждый построенный и/или используемый Боинг 747 не должен начинаться с нуля с новой конструкцией.
На самом деле, процесс проектирования используется очень редко, но его стоит включить, так как создание нового самолета с нуля, безусловно, требует этого. Но для огромного, подавляющего большинства построенных самолетов дизайн не нужен. Просто настройки и улучшения здесь и там. Поэтому только в этой стране можно производить более 10 000 самолетов в год.
Какая компания ежегодно производит больше всего самолетов?
Большинство этих самолетов производятся компанией Boeing. Они производят самолеты уже почти 100 лет и в настоящее время имеют портфель заказов более чем на 5000. Airbus находится на втором месте, производя около 1600 самолетов в год. Остальные производители каждый год строят значительно меньше самолетов.
Таким образом, даже если вы можете столкнуться с некоторыми из этих других брендов во время полета, я готов поспорить, что чаще всего вы летите на самолете, построенном Boeing или на самолете, построенном Airbus.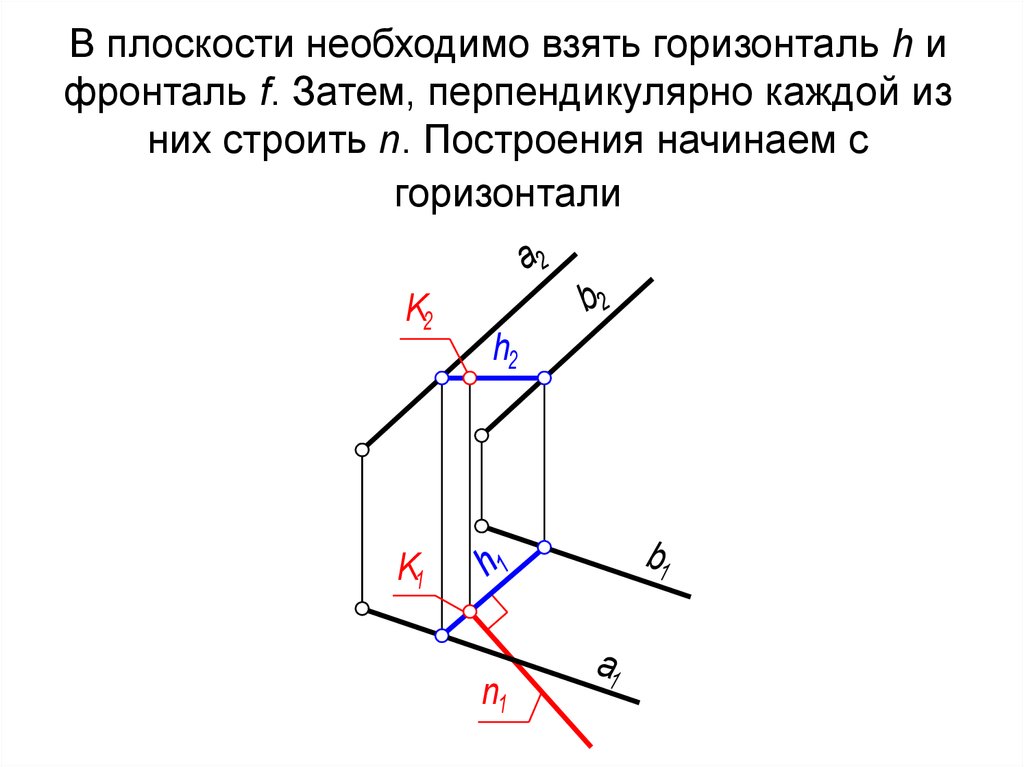 Это не ограничивается только Соединенными Штатами. Самолеты Boeing и Airbus используются во всем мире почти всеми существующими крупными авиакомпаниями.
Это не ограничивается только Соединенными Штатами. Самолеты Boeing и Airbus используются во всем мире почти всеми существующими крупными авиакомпаниями.
Тем не менее, если вы решите стать коммерческим пилотом, велики шансы, что вы научитесь управлять самолетами этих двух производителей. И хотя коммерческие пилоты не могут управлять всеми существующими моделями самолетов, знание того, как управлять наиболее распространенными самолетами Airbus и Boeing, будет иметь большое значение для успешной карьеры пилота, полной привилегий и преимуществ от начала до конца. финиш.
Сколько стоит построить или купить коммерческий авиалайнер?
Коммерческий самолет обычно измеряется вместимостью пассажиров. Чем больше самолет, тем больше стоит производство и покупка самолета. Средняя стоимость небольшого коммерческого самолета вместимостью от 50 до 79 человек.пассажиров оценивается в 50 миллионов долларов. Чем больше самолет, тем дороже он становится: более крупные модели от Boeing и Airbus стоят более 442 миллионов долларов.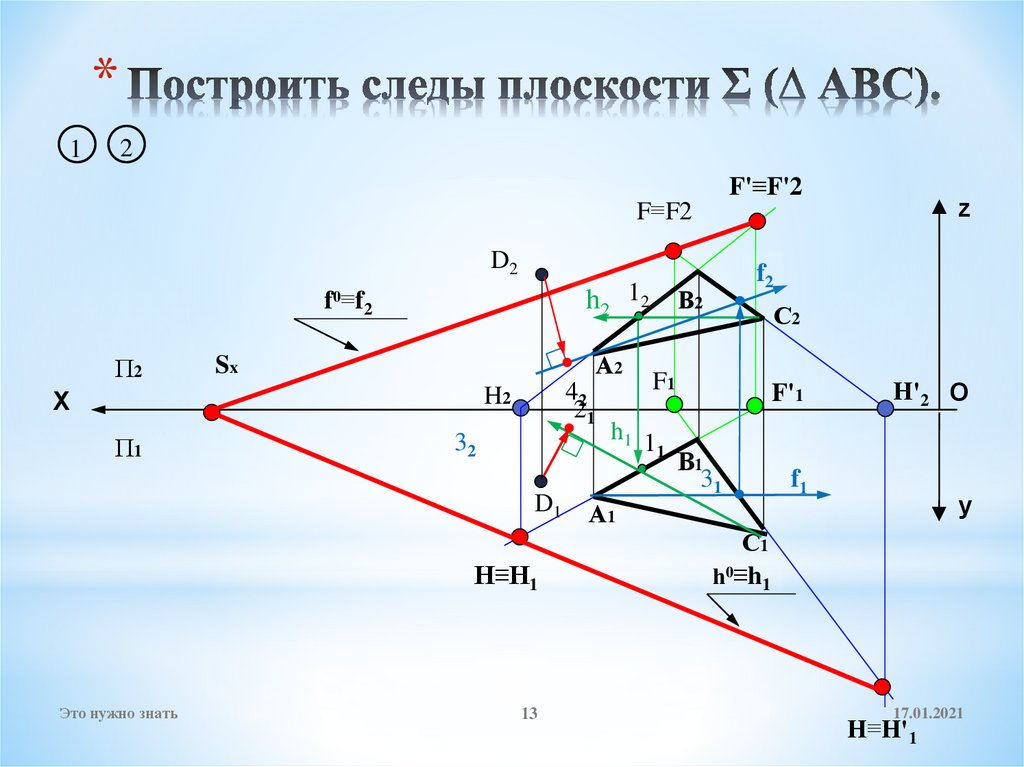
Airbus и Boeing — два основных производителя коммерческих самолетов в мире. У них обоих есть множество моделей, которые варьируются от малых, средних, больших и очень больших самолетов. Что касается ценников, Airbus предлагает более дешевые самолеты, чем Boeing. Однако, когда дело доходит до заказов (количество заказанных самолетов), в этом году Boeing получил больше заказов, чем Airbus.
Так что же влияет на окончательную цену? Затраты на производство составляют около 60% от общих расходов, в то время как расходы на приобретение и лицензирование составляют оставшиеся 40%. В конце концов, Boeing и Airbus не собираются тратить деньги на производство и терять деньги на своем бизнесе. Вместо этого эти компании переложат производственные затраты на клиентов, то есть на различные авиакомпании по всему миру.
Но если вы хотите узнать точную стоимость конкретной модели коммерческого самолета и пассажировместимости, свяжитесь напрямую с производителями Airbus или Boeing. Они могут дать более точную цитату на основе ваших спецификаций. Цены также различаются в зависимости от региона, в котором вы находитесь. Например, Airbus A320 будет дешевле в Европе, чем в Северной Америке.
Они могут дать более точную цитату на основе ваших спецификаций. Цены также различаются в зависимости от региона, в котором вы находитесь. Например, Airbus A320 будет дешевле в Европе, чем в Северной Америке.
В заключение отметим, что стоимость коммерческого самолета зависит от его размера, модели и производителя. Но по общей оценке вы можете заплатить около 50 миллионов долларов за небольшой самолет, вмещающий от 50 до 79 пассажиров.
Могу ли я построить свой собственный самолет?
Многие люди задавались вопросом, могут ли они построить свой собственный самолет. Ответ: вы можете! Но это не так просто, как можно подумать. В самолет входит много разных деталей, и каждый этап процесса сборки имеет решающее значение для безопасного полета самолета. Давайте подробнее рассмотрим, как строятся самолеты меньшего размера.
Первый шаг в постройке самолета — приобретение деталей. Есть много разных поставщиков запчастей, и каждый из них имеет свою специализацию. Например, одна компания может специализироваться на поставке фюзеляжей, а другая — на поставке двигателей. Важно найти подходящего поставщика для каждой части самолета.
Важно найти подходящего поставщика для каждой части самолета.
После того, как все детали будут получены, следующим шагом будет их сборка. Это можно сделать на заводе или дома, в зависимости от вашего уровня знаний. Самая важная часть процесса сборки — убедиться, что каждая деталь правильно прикреплена и подходит друг к другу. Если одна деталь окажется не на месте, это может привести к падению всего самолета.
Наконец, самолет необходимо проверить, чтобы убедиться, что он безопасен для полета. Этот процесс может занять несколько недель или даже месяцев и включает в себя ряд испытаний как на земле, так и в воздухе. Если все в порядке, самолет готов к взлету!
Итак, сколько времени нужно, чтобы построить самолет? Ответ зависит от типа самолета и уровня знаний строителя. Однако в среднем на постройку небольшого самолета с нуля уходит около года. Это можно ускорить еще быстрее, если вы купите самолет в комплекте и пойдете по этому пути, независимо от того, собираете ли вы его на заводе или делаете это сами.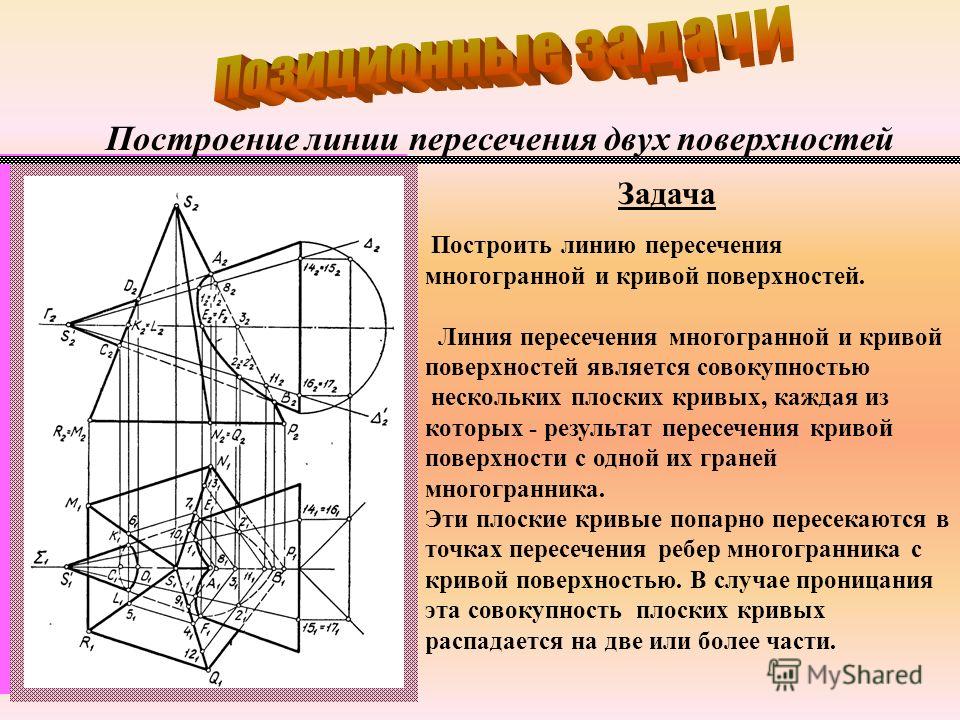
Самое замечательное в комплектных самолетах то, что в них есть почти все, что вам нужно. По крайней мере, в большинстве случаев в наборы будет входить все необходимое для сборки базовой части самолета, даже если вам, возможно, придется поставить двигатель или приборную панель отдельно. Но когда все части спроектированы таким образом, чтобы идеально сочетаться друг с другом, как большая головоломка, процесс намного проще, чем начинать с нуля.
Некоторые из лучших кит-самолетов — это различные типы кустовых самолетов, которые позволят вам летать в некоторые области , куда вы не можете попасть ни на каком другом типе самолета. По крайней мере, однажды вы станете опытным пилотом, который сможет посадить самолет на разных типах местности. Но это другая статья для другого дня!
Сколько стоит построить собственный самолет?
Создание собственного самолета может оказаться сложной задачей. Чтобы построить самолет, вам нужны не только знания и навыки, но и соответствующие инструменты и материалы. А если этого недостаточно, постройка собственного самолета может обойтись довольно дорого. В некоторых случаях может быть выгодно найти и купить готовый к полету недорогой самолет самостоятельно.
А если этого недостаточно, постройка собственного самолета может обойтись довольно дорого. В некоторых случаях может быть выгодно найти и купить готовый к полету недорогой самолет самостоятельно.
Так сколько же стоит построить собственный самолет?
Стоимость постройки собственного самолета будет варьироваться в зависимости от типа самолета, который вы решите построить, а также от уровня сложности его постройки. Но в среднем рассчитывайте потратить от 20 000 до 50 000 долларов только на запчасти и материалы. Конечно, это не включает стоимость рабочей силы, которая может добавить к общей цене еще несколько тысяч долларов.
Так оно того стоит?
Это зависит от вашего уровня знаний в области авиации и суммы, которую вы готовы потратить. Если вы начинающий пилот с небольшим опытом в авиастроении, лучше всего доверить постройку самолета профессионалам. Но если вы опытный летчик с ноу-хау и инструментами, необходимыми для создания собственного самолета, то дерзайте! Просто будьте готовы к сложному и дорогому проекту.