«Пропорции». 6-й класс
Цели.
1) Повторить знания и умения учащихся по теме “Пропорция”, ввести алгоритм решения задач на пропорциональные величины.
2) Содействовать развитию математического мышления учащихся, умению комментировать, расширение кругозора при решении задач.
3) Формирование стремления к достижению конечного результата на основе совместной деятельности.
Оборудование: интерактивная доска, раздаточный материал.
Структура урока
- Сообщение темы и цели урока (1 мин.)
- Проверка домашнего задания (3 мин.)
- Систематизация знаний и умений по пройденному материалу (5 мин.)
- Обьяснение нового материала (15 мин.)
- Решение задач (6 мин.)
- Инструктирование по выполнению самостоятельной работы (1 мин.)
- Выполнение заданий в группах. Проверка и
обсуждение полученных результатов (12 мин.

- Подведение итогов урока. Рефлексия. (2 мин.)
Ход урока
1. Сообщение темы и цели урока.
Ребята, сегодня на уроке мы повторим свойства пропорции, прямую и обратную пропорциональные зависимости, научимся решать задачи на пропорции.
2. Проверка домашнего задания.
На дом были даны уравнения. Проверьте ваше решение по интерактивной доске.
Слайд №1
1) 12,1:1,1=х:2 х=22 5) 4,8:х=2,4:0,2 х=0,4
2) 3,6:0,9=64:х х=16 6) х:8=3,2:0,4 х=64
3) 6:х=3:11 х=22 7) 7,5:2,5=1,5:х х=0,5
4) 9,6:1,2=х:8 х=64 8) ? : х = 1/64 : 1/2 х=16
Корни уравнений замените буквами, используя соответствие “число-буква”. И вы узнаете какое название дали математике древние индусы.
| 22 | 0,4 | 64 | 0,5 | 16 |
| л | в | а | т | и |
Древние индусы дали название математике
“лилавати”, что означает “прекрасная” или
“красавица со сверкающими глазами”.
3. Разминка (устная работа).
1) Найдите “сбежавшие” числа:
а) 36:4 = 18:_ ;
б) _ : _ = 6:12
2) Используя основное свойство пропорции составьте пропорции из чисел: 4; 6; 20; 30
3) Что такое пропорция? Каким основным свойством обладают члены пропорции?
4) Определите вид зависимости между величинами:
а) Обьемом прямоугольного параллелепипеда и его длиной. (Прямо пропорциональная зависимость)
б) Площадью квадрата и его стороной. (Нет пропорциональной зависимости)
в) Временем движения автомобиля и путем, который он проедет с определенной скоростью. (Обратно пропорциональная зависимость)
г) Возрастом человека и его ростом. (Нет пропорциональной зависимости)
д) Как аукнется, так и откликнется. (Прямо пропорциональная зависимость)
е) Чем больше народа, тем меньше кислорода. (Обратно пропорциональная зависимость)
4. Обьяснение нового материала. Применим
знания о зависимостях при решении задач.
Применим
знания о зависимостях при решении задач.
Задача 1.
Ученик прочитал 161 страницу, что составляет 23% числа всех страниц в книге. Сколько страниц в книге?
Вопросы.
1. О каких двух величинах говорится в задаче?
2. Какая зависимость между величинами? Составим краткое условие задачи.
В краткой записи стрелки направлены в одну сторону. Это значит, что если первая величина возрастает (первая стрелка вверх), то и вторая величина возрастает (вторая стрелка вверх).
Составим пропорцию: х:161= 100:23 х=700
Ответ: 700 страниц.
Задача №2.
Рабочие бригады, состоящей из 10 человек, могут выложить бассейн плиткой за 7 дней. Сколько человек в другой бригаде, если они могут выполнить эту работу за 5 дней?
Вопросы:
1. О каких двух величинах говорится в задаче?
2. Какая зависимость между величинами? Составим
краткое условие задачи.
Стрелки в краткой записи направлены в противоположные стороны. Это значит, если первая величина возрастает (первая стрелка вверх), то вторая величина убывает (вторая стрелка вниз). Составим отношения. Так как стрелки направлены в разные стороны, одно из отношений переворачиваем и приравниваем. Получим пропорцию.
10 : х = 5 : 7
х =14
Ответ: 14 человек.
Учащиеся вместе с учителем составляют алгоритм решения задач с помощью пропорций.
1) Неизвестное число обозначаем буквой х.
2) Условие задачи записываем с помощью таблицы.
3) Устанавливаем вид зависимости между величинами.
4) Составляем и решаем пропорцию.
5. Решение задач с помощью пропорций.
1) Для приготовления пирога массой 0,8 кг нужно 0,32 кг начинки. Сколько начинки нужно для приготовления пирога массой 2,5 кг? Ответ: 1 кг начинки.
2) В семенах льна содержится 47% масла. Сколько
льняного масла можно получить из 85 кг семян льна?
Ответ: 39,95 кг льняного масла.
Сколько
льняного масла можно получить из 85 кг семян льна?
Ответ: 39,95 кг льняного масла.
3) Ученик каждый день читает по 42 страницы книги и дочитывает ее целиком за 5 дней. Сколько времени ему понадобится на эту книгу, если он будет читать по 35 страниц в день? Ответ: 6 дней.
6. Инструктирование по выполнению самостоятельной работы.
Учитель передает задания каждой группе из 4-5 учащихся раздаточный материал с заданиями для групп. Содержание одного из вариантов задания.
Решите задачи с помощью пропорций:
1. Если печенье из большой коробки разложить в пакеты по 0,4 кг каждый, получится 60 пакетов. Сколько пакетов по 0,15 кг можно заполнить этим печеньем?
2. Из 20 кг яблок получается 16 кг яблочного пюре. Сколько яблочного пюре получится из 45 кг яблок?
3. В 2,5 кг баранины содержится 0,4 кг белков. Сколько белков содержится в 3,2 кг баранины?
7. Выполнение заданий в группах. Проверка и
обсуждение полученных результатов.
Выполнение заданий в группах. Проверка и
обсуждение полученных результатов.
Проверьте по интерактивной доске решение работы.
Учащиеся осуществляют самопроверку и самооценку заданий. Получают разъяснения по возникающим при этом вопросам.
Ответы к рассмотренному варианту.
Слайд №2
1.
Решение:
0,4:0,15 = х:60
х=160
Ответ: 160 пакетов.
2.
Решение:
20:45=16:х
х=36
Ответ: 36 кг яблочного пюре.
3.
Решение:
5,4:3,6=1,5:хх=1
Ответ: 1 кг белка.
8. Подведение итогов урока. Учащимся
предлагается оценить свою работу на уроке по
направлениям: — “я” — как я себя чувствовал в
процессе урока, доволен ли я своей работой; -
“мы” — насколько комфортно и эффективно мне было
работать в малой группе; — “дело” — достиг ли я
цели обучения, в чем испытывал затруднения, как
преодолеть проблемы.
Учитель благодарит учащихся за их работу на уроке, сообщает оценки за урок и домашнее задание.
Работа с пропорциями в Premiere Pro
Руководство пользователя Отмена
Поиск
- Руководство пользователя Adobe Premiere Pro
- Выпуски бета-версии
- Обзор программы бета-тестирования
- Домашняя страница бета-версии Premiere Pro
- Начало работы
- Начало работы с Adobe Premiere Pro
- Новые возможности Premiere Pro
- Заметки о выпуске | Premiere Pro
- Сочетания клавиш в Premiere Pro
- Специальные возможности в Premiere Pro
- Руководство по рабочим процессам с длинным форматами и эпизодами
- Начало работы с Adobe Premiere Pro
- Требования к оборудованию и операционной системе
- Рекомендации по аппаратному обеспечению
- Системные требования
- Требования к ГП и драйверу ГП
- Рендеринг с ускорением графического процессора и аппаратное кодирование/декодирование
- Рекомендации по аппаратному обеспечению
- Создание проектов
- Создать проект
- Открытие проектов
- Перемещение и удаление проектов
- Работа с несколькими открытыми проектами
- Работа с ссылками проекта
- Обратная совместимость проектов Premiere Pro
- Как открыть и редактировать проекты Premiere Rush в Premiere Pro
- Передовой опыт: создание собственных шаблонов проектов
- Рабочие среды и рабочие процессы
- Рабочие среды
- Вопросы и ответы | Импорт и экспорт в Premiere Pro
- Работа с панелями
- Управление касанием и жестами в Windows
- Использование Premiere Pro в конфигурации с двумя мониторами
- Рабочие среды
- Захват и импорт
- Захват
- Захват и оцифровка видеоматериала
- Захват видео в форматах HD, DV или HDV
- Пакетный захват и повторный захват
- Настройка системы для захвата медиаданных в форматах HD, DV или HDV
- Захват и оцифровка видеоматериала
- Импорт
- Передача файлов
- Импорт неподвижных изображений
- Импорт цифрового аудио
- Импорт из Avid или Final Cut
- Импорт AAF-файлов проекта из Avid Media Composer
- Импорт XML-файлов проекта из Final Cut Pro 7 и Final Cut Pro X
- Импорт AAF-файлов проекта из Avid Media Composer
- Поддерживаемые форматы файлов
- Оцифровка аналогового видео
- Работа с тайм-кодом
- Захват
- Эпизоды
- Создание и изменение последовательностей
- Добавление клипов в последовательности
- Изменение порядка клипов в последовательностях
- Поиск, выбор и группировка клипов в последовательностях
- Редактирование эпизодов, загруженных в исходный монитор
- Упрощение последовательностей
- Рендеринг и предпросмотр последовательностей
- Работа с маркерами
- Исправление источника и определение целевых дорожек
- Определение редактирования сцен
- Видео
- Создание и воспроизведение клипов
- Обрезка клипов
- Синхронизация аудио и видео с помощью функции «Объединение клипов»
- Рендеринг и замена медиа
- Отмена, история и события
- Заморозка и удерживание кадров
- Работа с соотношением сторон
- Создание и воспроизведение клипов
- Аудио
- Обзор аудио в Premiere Pro
- Микшер аудиодорожек
- Настройка уровней громкости
- Редактирование, восстановление и улучшение звука с помощью панели Essential Sound
- Автоматическое понижение громкости аудио
- Ремикс аудио
- Управление громкостью и панорамированием клипа с помощью микширования аудиоклипа
- Балансировка и панорамирование аудио
- Усовершенствованное аудио — фонограммы, понижающее микширование и маршрутизация
- Аудиоэффекты и переходы
- Работа с аудиопереходами
- Применение аудиоэффектов
- Измерение уровня звука с помощью эффекта «Акустический локатор»
- Запись аудиомиксов
- Редактирование аудио на таймлайне
- Сопоставление аудиоканалов в Premiere Pro
- Использование аудиодорожки Adobe Stock в Premiere Pro
- Обзор аудио в Premiere Pro
- Дополнительные функции редактирования
- Редактирование многокамерной передачи
- Настройка и использование головного дисплея для видео с эффектом погружения в Premiere Pro
- Редактирование VR-материалов
- Редактирование многокамерной передачи
- Передовой опыт
- Передовой опыт: ускорение микширования аудио
- Передовой опыт: эффективное редактирование
- Рабочие процессы редактирования для полнометражных фильмов
- Эпизоды
- Видеоэффекты и переходы
- Обзор видеоэффектов и переходов
- Эффекты
- Типы эффектов в Premiere Pro
- Применение и удаление эффектов
- Шаблоны настроек эффектов
- Автоматическое переформатирование видео для различных каналов социальных сетей
- Эффекты цветокоррекции
- Изменить продолжительность и скорость клипов
- Корректирующие слои
- Стабилизация видеоряда
- Переходы
- Применение переходов в Premiere Pro
- Изменение и настройка переходов
- Морфо-вырезка
- Заголовки, графика и подписи
- Обзор панели «Основные графические элементы»
- Заголовки
- Создание заголовка
- Графика
- Создание фигуры
- Выравнивание и распределение объектов
- Применение градиентов
- Добавление возможностей гибкого дизайна к графическим элементам
- Установка и использование шаблонов анимационного дизайна
- Замена изображений или видео в шаблонах анимационного дизайна
- Используйте шаблоны анимационного дизайна на основе данных
- Подписи
- Перевод речи в текст
- Работа с подписями
- Проверка орфографии, поиск и замена
- Экспорт текста
- Перевод речи в текст в Premiere Pro | Вопросы и ответы
- Рекомендации: ускорение обработки графики
- Удаление прежней версии конструктора заголовков в Premiere Pro | Вопросы и ответы
- Обновление устаревших заголовков до графики источника
- Анимация и ключевые кадры
- Добавление, навигация и установка ключевых кадров
- Эффекты анимации
- Используйте эффект движения для редактирования и анимации клипов
- Оптимизация автоматизации ключевого кадра
- Перемещение и копирование ключевых кадров
- Просмотр и настройка эффектов и ключевых кадров
- Добавление, навигация и установка ключевых кадров
- Создание композиции
- Создание композиции, альфа-каналы и управление непрозрачностью клипа
- Маскирование и отслеживание
- Режимы наложения
- Создание композиции, альфа-каналы и управление непрозрачностью клипа
- Цветовая коррекция и градация
- Обзор: рабочие процессы цветокоррекции в Premiere Pro
- Автоматитческая цветовая коррекция
- Творческие эксперименты с цветами при помощи стилей Lumetri
- Регулировка цветов с помощью RGB и кривых цветового тона / насыщенности
- Коррекция и совмещение цветов разных кадров
- Использование вторичных элементов управления HSL на панели «Цвет Lumetri»
- Создание виньеток
- Представления Look и таблицы LUT
- Области Lumetri
- Управление цветом дисплея
- HDR для трансляций
- Включить поддержку DirectX HDR
- Экспорт медиа
- Экспорт видео
- Экспорт Управления наборами
- Рабочий процесс и обзор экспорта
- Быстрый экспорт
- Экспорт для мобильных устройств и публикации в Интернете
- Экспорт неподвижного изображения
- Экспорт проектов для других приложений
- Экспортирование OMF-файлов для Pro Tools
- Экспорт в формат Panasonic P2
- Настройки экспорта
- Ссылка на настройки экспорта
- Основные настройки видео
- Параметры кодирования
- Рекомендации: ускорение экспорта
- Совместная работа: Frame.
 io, продукты и проекты группы
io, продукты и проекты группы- Совместная работа в Premiere Pro
- Frame.io
- Установка и активация Frame.io
- Использование Frame.io с Premiere Pro и After Effects
- Вопросы и ответы
- Продукты
- Использование продуктов
- Работа с клипами в проектах продукта
- Передовой опыт: работа с продуктами
- Проекты группы
- Начало работы с командными проектами
- Создать проект группы
- Добавление мультимедиа и управление ими в командных проектах
- Совместная работа с помощью проектов группы
- Общий доступ к изменениям и управление ими вместе с соавторами проекта группы
- Архивация, восстановление и удаление командных проектов
- Начало работы с командными проектами
- Работа с другими приложениями Adobe
- After Effects и Photoshop
- Dynamic Link
- Audition
- Prelude
- Организация ресурсов и управление ими
- Работа с панелью «Проект»
- Организуйте ресурсы на панели «Проект»
- Воспроизведение ресурсов
- Поиск ресурсов
- Библиотеки Creative Cloud
- Синхронизация настроек в Premiere Pro
- Объединение, преобразование и архивирование проектов
- Управление метаданными
- Рекомендации
- Передовой опыт: уроки телевещания
- Передовой опыт: работа с нативными форматами
- Передовой опыт: уроки телевещания
- Работа с панелью «Проект»
- Повышение производительности и устранение неполадок
- Настройка параметров
- Сброс настроек
- Работа с прокси
- Обзор прокси
- Процесс использования поглощения и прокси
- Обзор прокси
- Проверьте, совместима ли ваша система с Premiere Pro
- Premiere Pro для процессоров Apple
- Удаление мерцания
- Чересстрочная развертка и порядок полей
- Интеллектуальный рендеринг
- Поддержка панели управления
- Передовой опыт: работа с нативными форматами
- База знаний
- Выявленные неполадки
- Исправленные ошибки
- Устранение проблем с сбоем Premiere Pro
- Зеленое и розовое видео в Premiere Pro или Premiere Rush
- Как управлять медиа-кэшем в Premiere Pro
- Исправление ошибок при рендеринге или экспорте
- Устранение проблем c воспроизведением и производительностью в Premiere Pro
- Настройка параметров
- Мониторинг ресурсов и автономные медиафайлы
- Мониторинг ресурсов
- Использование исходного монитора и программного монитора
- Использование контрольного монитора
- Офлайн медиа
- Работа с офлайн клипами
- Создание клипов для автономного редактирования
- Повторное связывание автономных медиаданных
- Работа с офлайн клипами
- Мониторинг ресурсов
Пропорция определяет отношение ширины к высоте. Кадры видео и фотоснимков обладают пропорцией кадра (формат кадра), а пикселы, составляющие кадр, — попиксельной пропорцией (иногда называемой PAR). В различных стандартах видеозаписи используются разные пропорции. Например, видео для телевидения записывается с пропорцией кадра (форматом кадра) 4:3 или 16:9. Дополнительную информацию см. в разделе Пропорция кадра.
Кадры видео и фотоснимков обладают пропорцией кадра (формат кадра), а пикселы, составляющие кадр, — попиксельной пропорцией (иногда называемой PAR). В различных стандартах видеозаписи используются разные пропорции. Например, видео для телевидения записывается с пропорцией кадра (форматом кадра) 4:3 или 16:9. Дополнительную информацию см. в разделе Пропорция кадра.
Пропорции кадра и попиксельные пропорции задаются при создании проекта в Premiere Pro. После создания пропорций для проекта их изменение невозможно. Однако пропорцию эпизода можно изменить. В проекте можно использовать ресурсы, созданные с другими пропорциями.
Premiere Pro автоматически пытается компенсировать пропорции пиксела для исходных файлов. Если ресурс по-прежнему выглядит искаженным, можно вручную задать его пропорции пиксела. Перед согласованием пропорций кадра сначала необходимо согласовать попиксельные пропорции, так как ошибочные пропорции кадра могут привести к неправильной интерпретации попиксельных пропорций.
Типы пропорций
Часто используемые пропорции:
Широкий экран (16:9)
Это стандартная пропорция, широко используемая в веб-видео, документальных и художественных фильмах. Она позволяет получить большие объемы данных с подробностями.
Широкий экран (16:9)Вертикальная (9:16)
Видео, записанного на телефоне.
Вертикальная (9:16)Полный экран (4:3)
Эта пропорция использовалась в телевидении, до появления широких экранов. Она позволяет одномоментно сфокусироваться на определенном элементе.
Полный экран (4:3)Квадрат (1:1)
Это точная квадратная пропорция, которая широко используется в Instagram.
Квадрат (1:1)Анаморфная (2.40:1)
Это широкоэкранная пропорция часто используется в фильмах. Она похожа на 16:9, но при этом верхняя и нижняя части обрезаны. Этот эффект дает ощущение кинематографичности.
Чтобы задать пропорцию эпизода:
Создайте новый эпизод. Выберите Файл > Создать > Эпизод.
Дополнительные сведения см. в разделе Создание и изменение эпизодов.
Перейдите на вкладку «Настройки» диалогового окна «Создать эпизод».
Перейдите на вкладку «Настройки».
В разделе «Видео» введите размер кадра по высоте и по горизонтали (ширина). Premiere Pro автоматически создает пропорцию.
Заполните соответствующие поля, назовите эпизод и нажмите кнопку ОК.
Пропорция эпизода задана.
Пропорции кадра задают отношение ширины к высоте в размерах изображения. Кадры видео и фотоснимков обладают пропорцией кадра.
Например, DV NTSC использует пропорции кадра 4:3 (ширина 4,0 к высоте 3,0). Типичный широкоэкранный кадр обладает пропорциями 16:9. Многие камеры, поддерживающие широкоэкранный режим, могут вести запись с пропорциями кадра 16:9. Многие пленки были отсняты даже с еще более широкими пропорциями кадра.
Пропорции кадра 4:3 (слева) и более широкие пропорции кадра 16:9 (справа)В Premiere Pro можно реализовать леттербоксинг или метод панорамирования и сканирования, используя свойства эффекта «Движение», такие как «Положение» и «Масштаб».
Леттербоксинг
При импорте клипов, снятых с одними пропорциями кадра, в проект, использующий другие пропорции кадра, нужно выбрать способ согласования разных значений. В этом случае над и под кадром фильма отображаются черные полосы, что называется почтовым ящиком (леттербоксинг).
Например, для показа фильма 16:9 на стандартном телевизоре 4:3 используются два типичных метода. Можно поместить кадр фильма 16:9 в кадр телевизора 4:3 по всей ширине.
Панорамирование и сканирование
Панорамирование и сканирование — это альтернативный способ использования проекта с другой пропорцией. Сохраняется только часть кадра, а все остальное теряется.
Например, еще один способ показа фильма с пропорцией 16:9 на стандартном телевизоре 4:3 — заполнить кадр 4:3 по вертикали кадром 16:9 так, чтобы их высоты совпадали. Затем, кадр 16:9 панорамируется по горизонтали в более узком кадре 4:3 так, чтобы важные действия всегда оказывались в кадре 4:3.
Леттербоксинг и панорамирование и сканированиеПопиксельная пропорция определяет отношение ширины к высоте для одного пиксела кадра. Пикселы, составляющие кадр, обладают попиксельной пропорцией (иногда называемой PAR). Попиксельные пропорции могут меняться, так как разные видеосистемы делают собственные предположения о числе пикселов, необходимых для заполнения кадра.
Например, во многих компьютерных видеостандартах кадр с пропорцией 4:3 определен как 640 пикселов в ширину на 480 пикселов в высоту, что приводит к квадратному пикселу. Пикселы компьютерного видео имеют попиксельную пропорцию 1:1 (квадратную). В таких видеостандартах, как DV NTSC, кадр с пропорцией 4:3 определяется как кадр размером 720×480 пикселей, что приводит к более узким, прямоугольным пикселам. Пикселы DV NTSC имеют пропорцию пиксела 0,91 (неквадратная). Пикселы DV, всегда прямоугольные, ориентированы вертикально в системах, создающих видео NTSC, и горизонтально в системах, создающих видео PAL. Premiere Pro отображает пропорции пиксела клипа рядом с его миниатюрой на панели «Проект».
Пикселы компьютерного видео имеют попиксельную пропорцию 1:1 (квадратную). В таких видеостандартах, как DV NTSC, кадр с пропорцией 4:3 определяется как кадр размером 720×480 пикселей, что приводит к более узким, прямоугольным пикселам. Пикселы DV NTSC имеют пропорцию пиксела 0,91 (неквадратная). Пикселы DV, всегда прямоугольные, ориентированы вертикально в системах, создающих видео NTSC, и горизонтально в системах, создающих видео PAL. Premiere Pro отображает пропорции пиксела клипа рядом с его миниатюрой на панели «Проект».
A. Изображение 4:3 с квадратными пикселами, выведенное на монитор 4:3 (компьютерном) с квадратными пикселами B. Изображение 4:3 с квадратными пикселами, правильно интерпретированное для отображения на мониторе 4:3 (ТВ) с неквадратными пикселами C. Изображение 4:3 с квадратными пикселами, неправильно интерпретированное для отображения на мониторе 4:3 (ТВ) с неквадратными пикселами
Чистая диафрагма — часть изображения, свободная от артефактов и искажений, появляющихся на краях изображения. Производственная диафрагма представляет собой все изображение.
Производственная диафрагма представляет собой все изображение.
Искаженные изображения
Если без изменений отобразить прямоугольные пикселы на мониторе с квадратными пикселами, изображения будут выглядеть искаженными, например, круги превратятся в овалы. Но при отображении на контрольном видеомониторе пропорции изображений выглядят правильно, поскольку на контрольных видеомониторах используются прямоугольные пикселы. Premiere Pro может без искажений отображать и выводить клипы с разными пропорциями пиксела. Premiere Pro пытается автоматически согласовать их с попиксельной пропорцией проекта.
Иногда, если Premiere Pro неправильно интерпретирует попиксельную пропорцию, клип может выглядеть искаженно. Можно исправить искажение отдельного клипа вручную, указав попиксельную пропорцию исходного клипа в диалоговом окне «Интерпретировать материал».
Искаженное изображениеПри импорте ресурса Premiere Pro пытается сохранить пропорции кадров, попиксельные пропорции и размеры кадров, чтобы ресурс не отображался обрезанным или искаженным.
Для ресурсов с метаданными такие вычисления выполняются автоматически и точно. Например:
- При съемке или импорте видеоряда NTSC с размером кадра ATSC 704×480, размером кадра D1 720×486 или размером кадра DV 720×480 попиксельные пропорции задаются как отношение D1/DV NTSC (0,91).
- При съемке или импорте видеоряда высокой четкости с размером кадра 1440×1080 задается попиксельная пропорция HD 1080 Анаморфная (1,33).
- При съемке или импорте материала PAL с разрешением D1 или DV 720×576 попиксельные пропорции задаются как отношение D1/DV PAL (1,094).
Для других размеров кадра Premiere Pro предполагает, что ресурс был разработан с квадратными пикселами, и изменяет попиксельные пропорции и размер кадра так, чтобы сохранить для пропорции изображения. Если импортированный ресурс искажен, можно задать попиксельные пропорции вручную.
Ресурсы в эпизоде
Если перетащить ресурс в эпизод, ресурс по умолчанию размещается в центре кадра программы. В зависимости от размера кадра получившееся изображение может быть слишком мало или слишком сильно обрезано для потребностей проекта. Premiere Pro может изменить его масштаб автоматически при перетаскивании ресурса на эпизод или его можно изменить вручную.
В зависимости от размера кадра получившееся изображение может быть слишком мало или слишком сильно обрезано для потребностей проекта. Premiere Pro может изменить его масштаб автоматически при перетаскивании ресурса на эпизод или его можно изменить вручную.
Это всегда важно для правильной интерпретации файлов. Размеры кадра и пропорции пиксела для ресурса можно узнать рядом с миниатюрой предпросмотра и в столбце «Данные видео» на панели «Проект». Эти данные также можно найти в диалоговом окне «Свойства» ресурса, в диалоговом окне «Интерпретировать материал» и на панели «Информация».
Искажение пропорций в эпизоде
Шаблон настроек эпизода, выбранный при его создании, определяет для эпизода пропорции кадра и попиксельные пропорции. После создания эпизода пропорции изменить нельзя, но можно изменить попиксельные пропорции, предполагаемые в Premiere Pro для отдельных ресурсов.
Например, если ресурс с квадратными пикселами, созданный в графической программе, искажен в Premiere Pro, попиксельные пропорции можно исправить, чтобы изображение выглядело правильно. Убедившись, что все файлы правильно интерпретированы, можно объединить материал с различными пропорциями в одном проекте. Затем можно создать выходной материал без искажений получившихся изображений.
Убедившись, что все файлы правильно интерпретированы, можно объединить материал с различными пропорциями в одном проекте. Затем можно создать выходной материал без искажений получившихся изображений.
Исправление неправильных интерпретаций отдельных пропорций
Чтобы исправить интерпретацию отдельных пропорций, выполните указанные ниже действия.
Щелкните правой кнопкой мыши неподвижное изображение на панели «Проект».
Выберите Клип > Изменить > Интерпретировать материал.
Если выбрать клип на панели «Таймлайн» или в программном мониторе, эта возможность не доступна.
Выберите один из следующих вариантов в разделе Попиксельная пропорция:
Использовать попиксельные пропорции из файла
Использует исходное соотношение сторон, сохраненное с неподвижным изображением.
Соответствует
Позволяет выбрать в списке стандартных пропорций.
Изменить клип
При использовании Photoshop для создания изображений с целью применения в видеопроектах лучше всего использовать шаблон настроек Photoshop с именем, соответствующим видеоформату, который предполагается использовать. Использование этого шаблона настроек гарантирует создание изображений с правильными пропорциями.
Нажмите кнопку ОК.
Попиксельная пропорция | Рекомендации к применению | |
Квадратные пикселы | Материал имеет размер кадра 640 x 480 или 648 x 486, записан в формате 1920 x 1080 HD (не HDV или DVCPRO HD), записан в формате 1280 x 720 HD либо HDV или же экспортирован из программы, которая не поддерживает неквадратные пикселы. | |
D1/DV NTSC | Материал имеет размер кадра 720 x 486 или 720 x 480, и требуется получить кадр с пропорциями 4:3. Этот параметр также подходит для материалов, которые были экспортированы из программы, работающей с неквадратными пикселами (например, программы для трехмерной анимации). | |
D1/DV NTSC, широкоэкранный | Материал имеет размер кадра 720 x 486 или 720 x 480, и требуется получить кадр с пропорциями 16:9. | |
D1/DV PAL | Материал имеет размер кадра 720 x 576, и требуется получить кадр с пропорциями 4:3. | |
D1/DV PAL, широкоэкранный | Материал имеет размер кадра 720 x 576, и требуется получить кадр с пропорциями 16:9. | |
Анаморфный 2:1 | Материал был снят с помощью анаморфного объектива или перенесен с помощью анаморфирования с пленки, пропорции кадра которой составляют 2:1. | |
HDV 1080/DVCPRO HD 720, анаморфный HD 1080 | Материал имеет размер кадра 1440 x 1080 или 960 x 720, и требуется получить кадр с пропорциями 16:9. | |
DVCPRO HD 1080 | Материал имеет размер кадра 1280 x 1080, и требуется получить кадр с пропорциями 16:9. |
Справки по другим продуктам
- Автоматическое центрирование клипов и эпизодов для различных каналов социальных сетей
- Импорт неподвижных изображений
- Создание заголовков и анимированной графики
Вход в учетную запись
Войти
Управление учетной записью
Как решать пропорции крест накрест с процентами.
 Как решать рациональные уравнения по математике. Соблюдение вашей конфиденциальности на уровне компании
Как решать рациональные уравнения по математике. Соблюдение вашей конфиденциальности на уровне компанииФормула пропорций
Пропо́рция — это равенство двух отношений, когда a:b=c:d
отношение 1 : 10 равно отношению 7 : 70, что также можно записать в виде дроби: 1 10 = 7 70 читается как: «один относится к десяти так же, как семь относится к семидесяти»
Основные свойства пропорции
Произведение крайних членов равно произведению средних членов (крест-накрест): если a:b=c:d , то a⋅d=b⋅c
1 10 ✕ 7 70 1 ⋅ 70 = 10 ⋅ 7
Обращение пропорции: если a:b=c:d , то b:a=d:c
1 10 7 70 10 1 = 70 7
Перестановка средних членов: если a:b=c:d , то a:c=b:d
1 10 7 70 1 7 = 10 70
Перестановка крайних членов: если a:b=c:d , то d:b=c:a
1 10 7 70 70 10 = 7 1
Решение пропорции с одним неизвестным | Уравнение
1 : 10 = x : 70 или 1 10 = x 70
Чтобы найти икс, нужно перемножить два известных числа крест-накрест и поделить на противоположное значение
x = 1 ⋅ 70 10 = 7
Как посчитать пропорцию
Задача: нужно пить 1 таблетку активированного угля на 10 килограмм веса. Сколько таблеток нужно выпить, если человек весит 70 кг?
Сколько таблеток нужно выпить, если человек весит 70 кг?
Составим пропорцию: 1 таблетка — 10 кг x таблеток — 70 кг Чтобы найти икс, нужно перемножить два известных числа крест-накрест и поделить на противоположное значение: 1 таблетка x таблеток ✕ 10 кг 70 кг x = 1 ⋅ 70 : 10 = 7 Ответ: 7 таблеток
Задача: за пять часов Вася пишет две статьи. Сколько статей он напишет за 20 часов?
Составим пропорцию: 2 статьи — 5 часов x статей — 20 часов x = 2 ⋅ 20 : 5 = 8 Ответ: 8 статей
Будущим выпускникам школ могу сказать, что умение составлять пропорции мне пригодилось и , и для того, чтобы пропорционально уменьшать картинки, и в HTML-вёрстке интернет-страницы, и в бытовых ситуациях.
Это наиболее простая и довольно точная однородная разностная схема счета газодинамики. Ее шаблзн приведен на рис. 98; значения радиусов приписываются узлам сетки, значения скорости — границам пространственных интервалов на полуцелых слоях, а значения плотности, давления и внутренней энергии — серединам интервалов на целых слоях.
Построение схемы напоминает акустический «крест». Для простоты записи выберем равномерные по массе и времени шаги и t и аппроксимируем систему следующими разностными уравнениями:
Эти уравнения записаны в том порядке, который удобен для вычислений.
Обсудим разностное выражение для вязкого давления (65). Чтобы выполнить предельный переход от разностной схемы к уравнениям газодинамики, надо сначала устремить к нулю при фиксированном коэффициенте вязкости, а затем построить серию таких предельных решений для неограниченно уменьшающихся значений . Но это очень трудоемко. Поэтому на практике объединяют эти предельные переходы в один общий, полагая хотя законность такой процедуры не доказана (плотность введена в формулу для того, чтобы коэффициенты были безразмерны).
Таким образом, вязкое давление (65) принимает вид
где — скорость звука. Выражение (67) написано для плоского случая; но обычно им пользуются при любой симметрии задачи.
Аппроксимация. Из вида шаблона на рис. 98 и симметричного написания схемы (66) нетрудно заметить, что на течениях без сжатий, когда псевдовязкость (67) обращается в нуль, схема «крест» имеет локальную аппроксимацию
Из вида шаблона на рис. 98 и симметричного написания схемы (66) нетрудно заметить, что на течениях без сжатий, когда псевдовязкость (67) обращается в нуль, схема «крест» имеет локальную аппроксимацию
На течениях со сжатиями (в том числе — с ударными волнами) псевдовязкость отлична от нуля. Правда, квадратичный член в (67а) имеет величину но линейный член имеет величину и, тем самым, ухудшает порядок аппроксимации. Кроме того, вязкие члены записываются не вполне симметрично по времени. В итоге аппроксимация ухудшается до
Нахождение разностного решения. Схема (66) — явная; вычисления по ней проводятся следующим образом. Пусть все величины на исходном слое известны. Тогда из разностного уравнения импульса (66а) находим во всех интервалах; затем из второго уравнения (66б) определяем а из уравнения (66в) — .
Последним решается уравнение энергии (66г). Формально оно является неявным алгебраическим уравнением для определения в данном интервале. Но при каждом значении индекса уравнения (66г) решаются независимо, не образуя связанной системы уравнений, так что разностная схема, по существу, остается явной.
Замечание 1. Уравнение энергии в (66) можно сделать яным, используя в нем только значение с исходного слоя:
Это несколько упрощает расчет, не влияет на устойчивость, но заметно ухудшает точность, так как погрешность аппроксимации становится даже на гладких течениях. Такой вариант используется редко.
Устойчивость схемы можно исследовать методом разделения переменных, линеаризируя схему и замораживая коэффициенты. Громоздкие выкладки приводят к условию устойчивости типа Куранта.
Например, на гладких течениях с нулевой вязкостью схема устойчива при
Для идеального газа и условие (69) принимает вид где есть адиабатическая скорость звука. На течениях с ненулевой вязкостью ограничение на шаг несколько более сильное; при квадратичной вязкости условие устойчивости принимает вид
где — скачок скорости на ударной волне. Хотя это исследование не является строгим, тем не менее данное условие устойчивости хорошо подтверждается на практике.
Таким образом, «крест» — условно устойчивая схема. Отметим любопытное обстоятельство. Для расчета гладких течений вязкость не нужна. А если рассчитать без вязкости ударную волну (выбирая небольшое удовлетворяющее условию (70)), то получим «разболтку», изображенную на рис. 99. Этот расчет устойчив, поскольку амплитуда колебаний не возрастает со временем. Но сходимости к физически правильному решению при нет, так как на разрыве потеряна аппроксимация.
Отметим любопытное обстоятельство. Для расчета гладких течений вязкость не нужна. А если рассчитать без вязкости ударную волну (выбирая небольшое удовлетворяющее условию (70)), то получим «разболтку», изображенную на рис. 99. Этот расчет устойчив, поскольку амплитуда колебаний не возрастает со временем. Но сходимости к физически правильному решению при нет, так как на разрыве потеряна аппроксимация.
Сходимость газодинамической схемы «крест» не доказана. Однако эта схема успешно используется в расчетах примерно с 1950 г. и проверена на многих трудных задачах с известными точными решениями. При стремлении шагов к нулю наблюдалась сходимость к правильному решению, если шаги удовлетворяли условию устойчивости.
Замечание 2. Схема (66) неконсервативна; однако ее дисбаланс стремится к нулю при
Замечание 3. Газодинамические задачи с очень тонкими слоями особенно трудны для расчета. В самом деле, если , то для вычисления с удовлетворительной точностью по формуле (66в) надо знать радиусы с очень высокой точностью, сравнимой с ошибками округления на ЭВМ. В подобных задачах иногда приходится вести расчет с двойным числом знаков или специально видоизменять разностную схему.
В подобных задачах иногда приходится вести расчет с двойным числом знаков или специально видоизменять разностную схему.
Сегодня мы продолжаем серию видеоуроков, посвященных задачам на проценты из ЕГЭ по математике. В частности, разберем две вполне реальных задачи из ЕГЭ и еще раз убедимся, насколько важно внимательно читать условие задачи и правильно его интерпретировать.
Итак, первая задача:
Задача. Только 95% и 37 500 выпускников города правильно решили задачу B1. Сколько человек правильно решили задачу B1?
На первый взгляд кажется, что это какая-то задача для кэпов. Наподобие:
Задача. На дереве сидело 7 птичек. 3 из них улетело. Сколько птичек улетело?
Тем не менее, давай все-таки сосчитаем. Решать будем методом пропорций. Итак, у нас есть 37 500 учеников — это 100%. А также есть некое число x учеников, которое составляет 95% тех самых счастливчиков, которые правильно решили задачу B1. Записываем это:
37 500 — 100%
X
— 95%
Нужно составить пропорцию и найти x
. Получаем:
Получаем:
Перед нами классическая пропорция, но прежде чем воспользоваться основным свойством и перемножить ее крест-накрест, предлагаю разделить обе части уравнения на 100. Другими словами, зачеркнем в числителе каждой дроби по два нуля. Перепишем полученное уравнение:
По основному свойству пропорции, произведение крайних членов равно произведению средних членов. Другими словами:
x = 375 · 95
Это довольно большие числа, поэтому придется умножать их столбиком. Напоминаю, что пользоваться калькулятором на ЕГЭ по математике категорически запрещено. Получим:
x = 35 625
Итого ответ: 35 625. Именно столько человек из исходных 37 500 решили задачу B1 правильно. Как видите, эти числа довольно близки, что вполне логично, потому что 95% тоже очень близки к 100%. В общем, первая задача решена. Переходим к второй.
Задача на проценты №2
Задача. Только 80% из 45 000 выпускников города правильно решили задачу B9. Сколько человек решили задачу B9 неправильно?
Решаем по той же самой схеме. Изначально было 45 000 выпускников — это 100%. Затем из этого количества надо выбрать x
выпускников, которые должны составить 80% от исходного количества. Составляем пропорцию и решаем:
Изначально было 45 000 выпускников — это 100%. Затем из этого количества надо выбрать x
выпускников, которые должны составить 80% от исходного количества. Составляем пропорцию и решаем:
45 000 — 100%
x
— 80%
Давайте сократим по одному нулю в числителе и знаменателе 2-й дроби. Еще раз перепишем полученную конструкцию:
Основное свойство пропорции: произведение крайних членов равно произведению средних. Получаем:
45 000 · 8 = x · 10
Это простейшее линейное уравнение. Выразим из него переменную x :
x = 45 000 · 8: 10
Сокращаем по одному нулю у 45 000 и у 10, в знаменателе остается единица, поэтому все, что нам нужно — это найти значение выражения:
x = 4500 · 8
Можно, конечно, поступить так же, как в прошлый раз, и перемножить эти числа столбиком. Но давайте не будем сами себе усложнять жизнь, и вместо умножения столбиком разложим восьмерку на множители:
x = 4500 · 2 · 2 · 2 = 9000 · 2 · 2 = 36 000
А теперь — самое главное, о чем я говорил в самом начале урока. Нужно внимательно читать условие задачи!
Нужно внимательно читать условие задачи!
Что от нас требуется узнать? Сколько человек решили задачу B9 неправильно . А мы только что нашли тех людей, которые решили правильно. Таких оказалось 80% от исходного числа, т.е. 36 000. Это значит, что для получения окончательного ответа надо вычесть из исходной численности учеников наши 80%. Получим:
45 000 − 36 000 = 9000
Полученное число 9000 — это и есть ответ к задаче. Итого в этом городе из 45 000 выпускников 9000 человек решили задачу B9 неправильно. Все, задача решена.
Я надеюсь, что этот ролик поможет тем, кто самостоятельно готовится к ЕГЭ по математике. А у меня на этом все. С вами был Павел Бердов. До новых встреч!:)
Многие важные вопросы изучения курса химии по
ряду причин исключены из школьной программы.
Среди них закон эквивалентов, разные способы
выражения концентрации растворов, правило
креста и многие другие. Однако на факультативных
занятиях, при подготовке ребят к олимпиадам без
них не обойтись. Да и в жизни ребятам они
пригодятся, особенно тем, кто свяжет будущую
профессию с химией (заводские лаборатории,
аптеки, научно-исследовательская работа, да и
просто химия в быту).
Да и в жизни ребятам они
пригодятся, особенно тем, кто свяжет будущую
профессию с химией (заводские лаборатории,
аптеки, научно-исследовательская работа, да и
просто химия в быту).
Особенно трудно в этом отношении молодым
учителям – у них нет той массы дополнительной
литературы, которую накопили старые учителя за
десятки лет работы в школе, а что издает
современная книгопечатная отрасль
промышленности – известно всем. Поэтому
предлагаемая методика решения задач на растворы
с применением правила креста, думается, хоть
сколько-то поможет молодым коллегам в этом деле.
Очень часто в лабораторной практике и при
решении олимпиадных задач приходится
встречаться со случаями приготовления растворов
с определенной массовой долей растворенного
вещества, смешением двух растворов разной
концентрации или разбавлением крепкого раствора
водой. В некоторых случаях можно провести
достаточно сложный арифметический расчет.
Однако это малопродуктивно. Чаще для этого лучше
применить правило смешения (диагональную модель
«конверта Пирсона», или, что то же самое, правило
креста).
Допустим, нужно приготовить раствор
определенной концентрации, имея в распоряжении
два раствора с более высокой и менее высокой
концентрацией, чем нужно нам. Тогда, если
обозначить массу первого раствора через m 1 ,
а второго – через m 2 , то при смешивании
общая масса смеси будет слагаться из суммы этих
масс. Пусть массовая доля растворенного вещества
в первом растворе – 1 , во втором – 2 , а в их смеси – 3 . Тогда общая масса
растворенного вещества в смеси будет слагаться
из масс растворенного вещества в исходных
растворах:
m 1 1 + m 2 2 = 3 (m 1 + m 2) .
Отсюда
m 1 ( 1 – 3) = m 2 ( 3 – 2),
m 1 /m 2 = ( 3 – 2)/( 1 – 3).
Видно, что отношение массы первого раствора к массе второго раствора есть отношение разности массовых долей растворенного вещества в смеси и во втором растворе к разности соответствующих величин в первом растворе и в смеси.
При решении задач на растворы с разными
концентрациями чаще всего применяют
диагональную схему правила смешении. При
расчетах записывают одну над другой массовые
доли растворенного вещества в исходных
растворах, справа между ними – его массовую долю
в растворе, который нужно приготовить, и вычитают
по диагонали из большего меньшее значение.
Разности их вычитаний показывают массовые доли
для первого и второго растворов, необходимые для
приготовления нужного раствора.
При
расчетах записывают одну над другой массовые
доли растворенного вещества в исходных
растворах, справа между ними – его массовую долю
в растворе, который нужно приготовить, и вычитают
по диагонали из большего меньшее значение.
Разности их вычитаний показывают массовые доли
для первого и второго растворов, необходимые для
приготовления нужного раствора.
Для пояснения этого правила сначала решим простейшую задачу.
ЗАДАЧА 1
Определите концентрацию раствора, полученного при слиянии 150 г 30%-го и 250 г 10%-го растворов какой-либо соли.
Дано:
m 1 = 150 г,
m 2 = 250 г,
1 = 30%,
2 = 10%.
Найти:
Решение
1-й способ (метод пропорций).
Общая масса раствора:
m 3 = m 1 + m 2 = 150 + 250 = 400 г.
Массу вещества в первом растворе находим методом пропорций, исходя из определения: процентная концентрация раствора показывает, сколько граммов растворенного вещества находится в 100 г раствора:
100 г 30%-го р-ра – 30 г в-ва,
150 г 30%-го р-ра – х г в-ва,
х = 150 30/100 = 45 г.
Для второго раствора составляем аналогичную пропорцию:
100 г 10%-го р-ра – 10 г в-ва,
250 г 10%-го р-ра – y г в-ва,
y = 250 10/100 = 25 г.
Следовательно, 400 г нового раствора содержит 45 + 25 = 70 г растворенного вещества.
Теперь можно определить концентрацию нового раствора:
400 г р-ра – 70 г в-ва,
100 г р-ра – z г в-ва,
z = 100 70/400 = 17,5 г, или 17,5%.
2-й способ (алгебраический).
m 1 1 + m 2 2 = 3 (m 1 + m 2).
3 = (m 1 1 + m 2 2)/(m 1 + m 2).
В результате находим:
3 = (150 30 + 250 10)/(150 + 250) = 17,5%.
3-й способ (правило креста).
( 3 – 10)/(30 – 3) = 150/250.
(30 – 3) 150 = ( 3 – 10) 250,
4500 – 150 3 = 250 3 – 2500,
4500 – 2500 = 250 3 – 150 3 ,
7000 = 400 3 , 3 = 7000/400 = 17,5%.
Ответ. При слиянии взятых
растворов получится новый раствор с
концентрацией 3
= 17,5%.
Теперь решим задачи посложнее.
ЗАДАЧА 2
Определите, сколько нужно взять 10%-го раствора соли и 30%-го раствора этой же соли для приготовления 500 г 20%-го раствора.
Дано:
1 = 10%,
2 = 30%,
3 = 20%,
m 3 = 500 г.
Найти:
m 1 , m 2 .
Решение
Используем правило креста.
Для приготовления 500 г 20%-го раствора соли нужно
взять по 10 частей растворов исходных
концентраций.
Проверим правильность нашего решения, учитывая,
что 1 часть равна 500/(10 + 10) = 25 г.
250 г 10%-го р-ра – х г соли,
х = 250 10/100 = 25 г.
250 г 30%-го р-ра – y г соли,
100 г 30%-го р-ра – 30 г соли,
y = 250 30/100 = 75 г.
m (р-ра) = 250 + 250 = 500 г.
m (соли) = 25 + 75 = 100 г.
Отсюда находим 3:
500 г р-ра – 100 г соли,
100 г р-ра – 3 г соли,
3 =
100 100/500 = 20 г, или 20%.
Ответ . Для приготовления 500 г 20%-го
раствора нужно взять исходные растворы по 250 г
(m 1 = 250 г, m 2 = 250 г).
ЗАДАЧА 3
Определите, сколько нужно взять растворов соли 60%-й и 10%-й концентраций для приготовления 300 г раствора 25%-й концентрации.
Дано:
1 = 60%,
2 = 10%,
3 = 25%,
3 = 300 г.
Найти:
m 1 , m 2 .
Решение
Масса одной части: 300/50 = 6 г.
m 1 = 6 15 = 90 г, m 2 = 6 35 = 210 г.
100 г 60%-го р-ра – 60 г соли,
90 г 60%-го р-ра – х г соли,
х = 54 г.
100 г 10%-го р-ра – 10 г соли,
210 г 30%-го р-ра – y г соли,
y = 21 г.
m (соли) = 54 + 21 = 75 г.
Находим концентрацию нового раствора:
300 г р-ра – 75 г соли,
100 г р-ра – z г соли,
z = 100 75/300 = 25 г, или 25%.
Ответ . m 1 = 90 г, m 2
= 210 г.
m 1 = 90 г, m 2
= 210 г.
Теперь перейдем к еще более сложным задачам.
ЗАДАЧА 4
Определите массу раствора Nа 2 СО 3 10%-й концентрации и массу сухого кристаллогидрата Na 2 CO 3 10H 2 O, которые нужно взять для приготовления 540 г раствора 15%-й концентрации .
Дано:
1 = 10%,
3 = 15%,
m 3 = 540 г.
Найти:
m 1 , m 2 .
Решение
1-й способ (через систему уравнений с двумя неизвестными).
Определяем массу соли Na 2 CO 3 в 540 г 15%-го раствора:
100 г 15%-го р-ра – 15 г соли,
540 г 15%-го р-ра – z г соли,
z = 540 15/100 = 81 г.
Cоставляем систему уравнений:
Находим молярную массу:
Избавляемся от лишних неизвестных:
m 2 = 286y /106;
100 г 10%-го р-ра – 10 г соли,
m 1 г 10%-го р-ра – х г соли,
m 1 = 100х /10 = 10х .
Подставляем m 2 и m 1 в систему уравнений:
С учетом того, что х = 81 – y , избавляемся от второго неизвестного:
10(81 – y ) + 286y /106 = 540.
y = 270/7,3 = 37 г.
Тогда m 2 = 286y /106 = 2,7 37 100 г – это масса необходимого
количества кристаллогидрата Na 2 СО 3 10H 2 O.
Далее находим: х = 81 – y = 81 – 37 = 44 г – это
масса соли из 10%-го раствора.
Находим массу 10%-го раствора:
100 г 10%-го р-ра – 10 г соли,
m 1 г 10%-го р-ра – 44 г соли,
m 1 = 100 44/10 = 440 г.
Видно, что так можно решить данную задачу – способ надежный, но, к сожалению, достаточно длинный, громоздкий и сложный. Им успешно могут воспользоваться учащиеся с достаточно развитым логическим мышлением. Для других он будет сложноват.
2-й способ (правило креста).
Допустим, что Na 2 СО 3 10H 2 O – это
«сухой раствор» (ведь он же содержит воду). Тогда
найдем его «концентрацию»:
Тогда
найдем его «концентрацию»:
286 г – 106 г соли,
100 г – х г соли,
х = 100 106/286 = 37 г, или 37%.
Применяем правило креста.
Находим массу одной части и массы веществ:
m 1 = 20 22 = 440 г, m 2 = 20 5 = 100 г.
Ответ. Для приготовления 540 г
раствора Na 2 CO 3 15%-й концентрации
необходимо взять 440 г 10%-го раствора и 100 г
кристаллогидрата.
Таким образом, применение правила креста удобнее
и проще при решении подобных задач. Этот способ
более экономичен по времени и менее трудоемок.
Правило креста можно применять и в тех случаях,
когда нужно получить раствор меньшей
концентрации путем разбавления водой более
концентрированного раствора или получить более
концентрированный раствор путем добавления к
исходному раствору сухой смеси. Рассмотрим это
на примерах.
ЗАДАЧА 5
Сколько воды нужно добавить к 250 г раствора соли для понижения его концентрации с 45% до 10%?
Дано:
1 = 45%,
3 = 10%,
m 1 = 250 г.
Найти:
Решение
Принимаем, что концентрация для добавляемой воды – 2 = 0%. Используем правило креста.
Определяем массу одной части через первый
раствор: 250/10 = 25 г.
Тогда масса необходимой воды равна:
m 2 = 25 35 = 875 г.
Проверим правильность решения.
Масса нового раствора:
m 3 = 250 + 875 = 1125 г.
250 г 45%-го р-ра – х г соли,
100 г 45%-го р-ра – 45 г соли,
х = 250 45/100 = 112,5 г.
Находим 3:
1125 г р-ра – 112,5 г соли,
100 г р-ра – y г соли,
y = 100 112,5/1125 = 10 г, или 10%.
Ответ . m 2 = 875 г.
ЗАДАЧА 6
Сколько сухой соли нужно добавить к 250 г раствора 10%-й концентрации для ее увеличения до 45%?
Дано:
1 = 10%,
m 1 = 250 г,
3 = 45%.
Найти:
m (с. с.).
Решение
Принимаем, что сухая соль – это раствор с 2 = 100%. Используем правило креста.
Используем правило креста.
Определяем массу одной части через первый
раствор: 250/55 = 4,5 г.
Определяем массу сухой соли:
m (с. с.) = 4,5 35 = 158 г.
Проверяем правильность решения.
Масса нового раствора:
m 3 = 250 + 158 = 408 г.
Масса соли в исходном растворе:
100 г 10%-го р-ра – 10 г соли,
250 г 10%-го р-ра – х г соли,
х = 250 10/100 = 25 г.
Общая масса соли в новом растворе:
25 + 158 = 183 г.
Концентрация нового раствора:
408 г р-ра – 183 г соли,
100 г р-ра – y г соли,
y = 100 183/408 = 45 г, или 45%.
Ответ . m (с. с.) = 158 г.
Думается, что опытный учитель всегда найдет
несколько способов решения любой задачи. Но как
учила меня моя первая учительница по химии
Клавдия Макаровна в школе № 17 г. Иркутска, так и я
стараюсь учить своих учеников: всегда глубоко
продумывать и понимать химическую сущность
задачи и находить наиболее рациональный способ
ее решения, а не просто подгонять под ответ в
конце учебника.
Применение уравнений широко распространено в нашей жизни. Они используются во многих расчетах, строительстве сооружений и даже спорте. Уравнения человек использовал еще в древности и с тех пор их применение только возрастает. Если вы видите выражение с дробями с переменной в числителе/знаменателе, то перед вами выражение, именуемое в математике рациональным уравнением. В целом можно назвать рациональными уравнениями все уравнения, имеющие в своем составе 1 рациональное выражение. Что касается решений рациональных уравнений, то они решаются следующим образом: производятся операции в левой и правой стороне до момента, когда переменная не обособляется на одной стороне. Существует два способа решения таких уравнений:
Умножение крест-накрест;
НОЗ (наименьший общий знаменатель).
Первые метод используется в том случае, если после того как было переписанное уравнение, на каждой его стороне образовалась одна дробь. Например:
\[\frac {x+3}{4}- \frac{x}{2}= 0\]
Чтобы использовать метод умножения крест-накрест необходимо преобразовать уравнения к виду:
\[\frac {x+3}{4}= \frac {x}{-2}\]
Второй метод можно использовать тогда, когда перед вами уравнение с 3/более дробями. Например:
Например:
\[\frac {x}{3}+ \frac {1}{2}=\frac{3x+1}{6} \]
Для данного уравнения наименьшим общим кратным числом будет 6, что позволит легко решить данное уравнение.
Где можно бесплатно решить рациональное уравнение онлайн?
Решить рациональное уравнение онлайн с решением вы можете на нашем сайте https://сайт. Бесплатный онлайн решатель позволит решить уравнение онлайн любой сложности за считанные секунды. Все, что вам необходимо сделать — это просто ввести свои данные в решателе. Так же вы можете посмотреть видео инструкцию и узнать, как решить уравнение на нашем сайте. А если у вас остались вопросы, то вы можете задать их в нашей групе Вконтакте http://vk.com/pocketteacher. Вступайте в нашу группу, мы всегда рады помочь вам.
Читайте также…
- Можно ли менять свой характер, и как?
- Личность – что это такое, структура, характеристики
- Как используется принцип парето в продажах Когда используется правило 80 20
- Саморазвитие и самосовершенствование, с чего начать
Решение пропорций
Этот урок посвящен решению пропорций с использованием перекрестного произведения для поиска неизвестных членов.
Мы также покажем некоторые принципы, специальные приемы или сокращения, которые можно использовать для быстрого решения пропорции.
Термины, которые необходимо знать:
x, y или любая другая буква используется для обозначения неизвестного числа.
Неизвестный термин: Отсутствующее или неизвестное число в пропорции.
В уроке о пропорциях мы видели, что мы можем использовать перекрестное произведение, чтобы определить, являются ли дроби или отношения пропорциями.
Перекрестные произведения также можно использовать для нахождения неизвестного члена в пропорции. Вот как!
Если а / б знак равно | с / д тогда a × d = b × c |
Если а / б знак равно | с / д тогда a × d = b × c |
Проиллюстрируем это парой примеров.
Пример №1:
Найдите х, если 5 / х | знак равно 10 / 16 |
Поскольку эти две дроби или отношения находятся в пропорциях, мы знаем, что перекрестный продукт должен быть равен.
Используя векторное произведение, мы получаем:
5 × 16 = x × 10
80 = 10x
Если вы знаете свою таблицу умножения, вы можете быстро получить ответ.
Если 10 × х = 80, то х должно быть равно 8, потому что 10 × 8 равно 80.
х = 8
Пропорция становится 5 / 8 | знак равно 10 / 16 |
Обратите внимание, что 5 × 16 = 8 × 10 = 80
Вы также можете разбить задачу на несколько шагов, если хотите, как показано ниже:
Первое векторное произведение: 5 × 16 = 80
Второе векторное произведение: 10 × x
Приравняв векторные произведения, мы получим:
10 × х = 80
Есть более быстрый способ получить ответ при решении пропорций. Посмотрите еще раз на пропорцию:
Посмотрите еще раз на пропорцию:
знак равно 10 / 16 |
Обратите внимание: чтобы получить 10, нужно 5 умножить на 2. Точно так же, чтобы получить 16, нужно что-то или число умножить на 2. Какое число, умноженное на 2, даст вам 16? Без сомнения, это 8!
Пример №2:
Решите для n, если 8 / 10 | знак равно нет / 25 |
Используя векторное произведение, мы получаем:
8 × 25 = 10 × n
200 = 10n
Вместо того, чтобы спрашивать себя «10 умножить на то, что равно 200?», мы на этот раз решим уравнение, чтобы показать вы другой способ получить n.
Разделите обе стороны на 10
200 / 10 | знак равно 10н / 10 |
200 разделить на 10 равно 20, а 10 разделить на 10 равно 1
20 = 1n
20 = n
Полезные эквивалентные пропорции, которые можно использовать при решении пропорций.

Принцип №1:
Если а / б | знак равно с / д тогда, | а + б / б | знак равно в + г / д |
Доказательство:
Добавьте 1 к обеим частям уравнения и выполните математические действия, как показано:
х — 8 / 8
знак равно
6 / 4
Приведенное выше уравнение становится
х — 8 + 8 / 8 | знак равно 6 + 4 / 4 |
или
знак равно 10 / 4 |
Приведенное выше, конечно, намного проще решить
Принцип №2:
Если х / г | знак равно х / 4 тогда у = 4 |
Например, если 50 / г | знак равно 50 / 100 тогда у = 100 |
Если 18 / г | знак равно х / у тогда х = 18 |
Принцип №3:
Если а / б | знак равно с / д тогда, | а + в / б + д | знак равно а / б |
а + в / б + д | знак равно а / б |
Почему принцип №3 полезен при решении пропорций?
Скажи, что у тебя есть х + 2 / 8 + 4 | знак равно х / 8 |
Это эквивалентно х / 8 | знак равно 2 / 4 |
Опять же последний формат имеет дружественный вид и решается быстрее.
Просто помните эти 3 принципа при решении пропорций, и это облегчит вам упражнение с пропорциями. Спасибо за чтение!
Спасибо за чтение!
Проиллюстрируем это парой примеров.
Пример №1:
Найдите х, если 5 / х | знак равно 10 / 16 |
Поскольку эти две дроби или отношения находятся в пропорциях, мы знаем, что перекрестное произведение должно быть равно.
Используя перекрестное произведение, мы получаем:
5 × 16 = x × 10
80 = 10x
Если вы знаете свою таблицу умножения, вы можете быстро получить ответ.
Если 10 × x = 80, то x должно быть равно 8, потому что 10 × 8 равно 80.
x = 8
Пропорция становится 5 / 8 | знак равно 10 / 16 |
Обратите внимание, что 5 × 16 = 8 × 10 = 80
Вы также можете разбить проблему на несколько шагов, если хотите, как показано ниже:
Первое векторное произведение: 5 × 16 = 80
Второе векторное произведение: 10 × x
Приравняв векторные произведения, мы получим:
10 × x = 80
Есть более быстрый способ получить ответ, когда решение пропорций. Посмотрите еще раз на пропорцию:
Посмотрите еще раз на пропорцию:
знак равно 10 / 16 |
Обратите внимание: чтобы получить 10, нужно 5 умножить на 2. Точно так же, чтобы получить 16, нужно что-то или число умножить на 2. Какое число, умноженное на 2, даст вам 16? Без сомнения, это 8!
Пример #2:
Решите для n, если 8 / 10 | знак равно нет / 25 |
Используя векторное произведение, мы получаем:
8 × 25 = 10 × n
200 = 10n
Вместо того, чтобы спрашивать себя «10 умножить на то, что равно 200?», мы на этот раз решим уравнение, чтобы показать есть другой способ получить n
Разделите обе части на 10
200 / 10 | знак равно 10н / 10 |
200, разделенные на 10 — 20 и 10, разделенные на 10 — 1
20 = 1n
20 = N
Полезные эквивалентные пропорции. Вы можете использовать при решении пропорций:
Вы можете использовать при решении пропорций:
Принцип № 1:
Если а / б | знак равно с / д тогда, | а + б / б | знак равно в + г / д |
Доказательство:
Добавьте 1 к обеим частям уравнения и выполните математические действия, как показано:
х — 8 / 8
знак равно
6 / 4
Приведенное выше уравнение становится
х — 8 + 8 / 8 | знак равно 6 + 4 / 4 |
Или
знак равно 10 / 4 |
Приведенное выше, конечно, намного проще решить
Принцип №2:
Если х / г | знак равно х / 4 тогда у = 4 |
Например,
Если 50 / г | знак равно 50 / 100 тогда у = 100 |
Если 18 / г | знак равно х / у тогда х = 18 |
Принцип №3:
Если а / б | знак равно с / д тогда, | а + в / б + д | знак равно а / б | ||||||||||||||
а + в / б + д | знак равно а / б |
Почему принцип №3 полезен при решении пропорций?
Скажи, что у тебя есть х + 2 / 8 + 4 | знак равно х / 8 |
Это эквивалентно х / 8 | знак равно 2 / 4 |
Опять же последний формат имеет дружественный вид и решается быстрее.
Просто помните эти 3 принципа при решении пропорций, и это облегчит вам упражнение на пропорции. Спасибо, что прочитали
Спасибо, что прочитали
Решение викторины пропорций. Сможете ли вы пройти этот тест на 100%?
Математические задачи третьего класса
13, 22 октября 09:58
Разнообразные математические задачи третьего класса, которые учащиеся должны уметь решать в 3-м классе.
Подробнее
Как решить пропорцию — Полный курс арифметики
(Евклид, VII. 17.)
Мы уже видели, что отношение сохранится, если мы разделим оба слагаемых на одно и то же число.
Пример 5. Заполните пропорцию:
.6 : 7 = ? : 28
Раствор . 7 умножили на 4, чтобы получить 28. Следовательно, 6 также нужно умножить на 4:
6 : 7 = 24 : 28.
Чтобы решить эту пропорцию —
6 : 7 = ? : 28
— мы могли бы сказать:
«7 входит в число 28 четыре раза. Четыре раза по 6 получается 24.»
Четыре раза по 6 получается 24.»
Все примеры и задачи в этом уроке должны быть простыми расчетами в уме.
Пример 6. Решите эту пропорцию:
2 : 3 = 12 : ?
Решение . «2 шесть раз входит в число 12. Шесть раз 3 равно 18».
2 : 3 = 12 : 18.
На самом деле, рассмотрим эти столбцы кратные 2 и 3:
2 3
4 6
6
8 12
10 15
12 18
14 21
И так далее.
Теперь 2 составляет две трети от 3. (Урок 17.) И каждое кратное 2 составляет две трети от то же кратное 3:
4 составляет две трети от 6.
6 составляет две трети от 9.
8 составляет две трети от 12.
И так далее. На самом деле это единственные натуральные числа, в которых первое составляет две трети второго.
Обратите внимание, что у каждой пары есть общий делитель. И при делении на этот делитель в каждом случае частное будет 2 и 3. Это теорема об общем делителе. 2 и 3 – самые низкие условия. Это наименьшие числа, имеющие отношение «две трети».
Это теорема об общем делителе. 2 и 3 – самые низкие условия. Это наименьшие числа, имеющие отношение «две трети».
Пример 7. Назовите три пары чисел, первая из которых составляет три пятых от второй.
Решение . Элементарной парой являются 3 и 5. Чтобы сгенерировать другие, возьмите одно и то же число, кратное обоим: 6 и 10, 9 и 15, 12 и 20 и так далее.
Пример 8. 27 составляет три четверти какого числа?
Раствор . Пропорционально:
3 : 4 = 27 : ?
«27 — это девять раз по 3. Девять раз по 4 равно 36.»
3 : 4 = 27 : 36.
27 составляет три четверти от 36.
Только кратное 3 может быть тремя четвертями другого числа, которое должно быть тем же самым кратным 4.
Как 3 равно 4, так и любое количество троек соответствует равному количеству 4.
Пример 9. Решите эту пропорцию:
9: 45 = 2 : ?
Раствор . Здесь надо смотреть прямо:
Здесь надо смотреть прямо:
9 – пятая часть от 45. А 2 – пятая часть от 10.
9 : 45 = 2 : 10.
Пример 10. Общий делитель. Заполните эту пропорцию:
12 : 200 = ? : 100.
Раствор . С другой стороны, мы видим, что 200 равно , разделенному на 2 . Следовательно, 12 также нужно разделить на 2.
12 : 200 = 6 : 100.
Вместо деления 12 и 200 на 2 можно взять половину. Половина от 200 равна 100. Половина от 12 равна 6.
Правило трех
Мы видим, что если мы знаем три члена пропорции, то всегда можем найти четвертый. Это называется правилом трех. Мы можем резюмировать это следующим образом.
1-й : 2-й = 3-й : 4-й.
| • | Если 4-й член неизвестен, а 3-й член кратен или часть 1-го (пример 6), , то 4-й должен быть таким же кратным или частью 2-го. |
| (Аналогично, если 3-й член неизвестен, а 4-й кратен 2-му; Пример 5) | |
| • | Если 4-й член неизвестен, а 2-й член кратен или части 1-го (пример 9), , то 4-й должен быть таким же кратным или частью 3-го.  |
Самое главное, мы будем применять это правило, чтобы найти, сколько процентов одно число составляет от другого.
Что касается теоремы об общем делителе , то это то, что мы называем симметричной версией теоремы об одном и том же кратном. Для этой пропорции
6 соответствует 100, как 12 соответствует 200,
, в котором 3-й и 4-й члены появляются как двойники 1-го и 2-го, логически эквивалентна этой пропорции,
12 соответствует 200, а 6 соответствует 100,
, в котором 3-й и 4-й члены появляются как половинки 1-го и 2-го.
Пример 11. В классе соотношение девочек и мальчиков 3 к 4.
Есть 24 мальчика. Сколько девочек?
Решение . Пропорционально,
Девочки : Мальчики = 3 : 4 = ? : 24.
Обратите внимание, что 24 соответствует мальчикам.
Теперь 4 входит в число 24 шесть раз. Таким образом, число девушек равно шести, умноженным на 3: 18 .
Таким образом, число девушек равно шести, умноженным на 3: 18 .
Это еще один подход к Примеру 7 из предыдущего урока. А следующий пример — еще один способ приблизиться к Примеру 8 этого Урока.
Пример 12. Целое равно сумме частей. В классе количество девочек составляет 75% от количества мальчиков. Есть 35 студентов. Сколько девочек и сколько мальчиков?
Раствор . Сказать, что девочки составляют 75% — три четверти — мальчиков,
означает, что соотношение девочек и мальчиков составляет 3 к 4. Но это означает, что 3 из каждых 7 учащихся — девочки (3 + 4 = 7), а 4 из каждых 7 — мальчики.
Следовательно, составим пропорцию:
девочек: общее количество учеников =
3 : 7 = ? : 35.
Поскольку 35 равно 5 × 7, пропущенный член равен 5 × 3 = 15.
Есть 15 девушек. И так 20 мальчиков.
В этот момент, пожалуйста, «переверните» страницу и выполните несколько задач .
или
Перейдите к следующему разделу.
1-й урок по пропорциям.
1-й урок о частях натуральных чисел
Введение | Главная | Содержание
Copyright © 2021 Лоуренс Спектор
Вопросы или комментарии?
Электронная почта: [email protected]
Пропорции – объяснение и примеры
Трудно представить, какой была бы наша жизнь без таких математических понятий, как пропорции. В нашей повседневной жизни мы часто сталкиваемся с пропорциями и пропорциями, когда ходим за покупками, готовим пищу, в служебные поездки и т. д.
Соотношения и пропорции необходимы для эффективной работы. В этой статье мы научимся рассчитывать пропорции и применять полученные знания для решения типовых задач, но перед этим давайте начнем с определения пропорций.
Соотношение — это способ сравнения двух или более величин. Знаком, используемым для обозначения отношения, является двоеточие ‘: ’ Предположим, что a и b — две разные величины или числа, тогда отношение a к b может быть записано как a/b или a:b. Точно так же отношение b к a также может быть представлено как b: a или b/a. Первая величина в соотношении называется антецедентом, а второе значение называется консеквентом.
Точно так же отношение b к a также может быть представлено как b: a или b/a. Первая величина в соотношении называется антецедентом, а второе значение называется консеквентом.
Примеры отношений: : ¾ или 3: 4, 1/5 или 1: 5, 199/389 или 199:389 и т. д. Из этого примера видно, что отношение – это просто дробь, в которой числитель, а следствие — знаменатель.
Знаменитый рисунок Витрувианского человека Леонардо да Винчи был основан на идеальных пропорциях человеческого тела. Каждая часть тела занимает различное соотношение, например, лицо занимает около 1/10 от общей высоты, а голова занимает около 1/8 от общей высоты. Писатели средневековья использовали слово пропорция (пропорция) впервые. В 1948 году Ле Корбюзье ввел систему пропорций
Что такое пропорция?
Пропорция — это выражение, которое говорит нам, что два отношения эквивалентны. Два отношения называются пропорциональными, если они эквивалентны. Пропорции обозначаются знаком «:» или «=». Например, если a, b, c и d являются целыми числами, то пропорция записывается как a: b = c: d или a/b = c/d или b: a = d: c. Например, соотношения 3:5 и 15:25 пропорциональны и записываются как 3:5=15:25
Например, если a, b, c и d являются целыми числами, то пропорция записывается как a: b = c: d или a/b = c/d или b: a = d: c. Например, соотношения 3:5 и 15:25 пропорциональны и записываются как 3:5=15:25
Четыре числа a, b, c и d известны как члены пропорции. Первый член a и последний член d называются крайними членами, а второй и третий члены в пропорциональном выражении называются средними членами.
Как решить пропорции?
Легко вычислить, если пропорции пропорциональны. Проверить, пропорциональны ли отношения a:b и c:d.
- Умножение первого слагаемого на последнее: a x d
- Умножение второго слагаемого на третье: b x c
- Если произведение крайних членов равно произведению средних членов, то отношения пропорциональны: a x d = b x c
Непрерывная пропорция
Два отношения a:b и b:c называются непрерывными пропорциями, если а: б = б: в. В этом случае термин c называется третьей пропорцией a и b, тогда как b называется средней пропорцией между терминами a и c.
Когда члены a, b и c находятся в непрерывной пропорции, получается следующая формула:
a/b = b/c
Перемножение членов крестом дает; a x c =b x b, Следовательно,
b² = ac
Объяснение
- Умножьте первый и четвертый члены соотношений.
8 × 15 = 120
- Теперь умножьте второй и третий члены.
10 × 12 = 120
- Так как произведение крайних равно произведению средних,
- Так как произведение средних (120) = произведение крайних (120),
- Следовательно, 8: 10 и 12:15 пропорциональны. Пример 2
Объяснение
- Это случай непрерывной пропорции, поэтому применим формулу a x c =b x b,
- В этом случае a: b:c =6:12:24, поэтому a=6, b=12 и c=24
- Умножьте первый и третий члены:
6 × 24 = 144
- Квадрат средних членов:
(12) ² = 12 × 12 = 144
- Следовательно, отношение 6:12:24 пропорционально.

Пример 3
Если 12:18::20: с. Найдите значение x, чтобы отношения были пропорциональны?
Объяснение
Дано: 12: 18::20: p
Приравнять произведение крайностей к произведению средних;
⇒ 12 × p = 20 × 18
⇒ p = (20 × 18)/12Найдите p;
⇒ P = 30
Следовательно, значение P = 30Пример 4
Найти третье пропорциональное до 3 и 6.
. пропорциональный быть c.
- Тогда, B² = AC
6 x 6 = 3 x C
C = 36/3
= 12
Таким образом, третий пропорциональный до 3 и 6 — 12
9103 Пример 5
Пример.
Вычислить среднее пропорциональное между 3 и 27
Объяснение
- Пусть среднее пропорциональное между 3 и 27 будет m.

- Применяя формулу b² = ac; ‘
Следовательно, m x m = 27 x 3 = 81
m 2 =81
⇒ m = √81
⇒ m = 9
Следовательно, среднее пропорциональное между 3 и 27 равно 9
Пример 6
5 и b:c = 6 :7, Определить соотношение a:b:c.Объяснение
- Так как b является общим термином между двумя отношениями;
- Умножьте каждое слагаемое в первом соотношении на значение b во втором соотношении;
а: б = 4: 5 = 24:30,
- Также умножьте каждое слагаемое во втором соотношении на значение b в первом соотношении;
b: c = 6: 7 = 30: 35
Следовательно, отношение a: b: c = 24:30:35
Золотое сечение
Самое большое применение пропорции золотое сечение , которые очень помогли в анализе пропорций различных объектов и искусственных систем, таких как финансовые рынки. Говорят, что две величины находятся в золотом сечении, если их отношение равно отношению их суммы к большей из двух величин, т.


 io, продукты и проекты группы
io, продукты и проекты группы
 Этот параметр также подходит для материалов, которые были перенесены с пленки или предназначены для проектов с индивидуальной настройкой.
Этот параметр также подходит для материалов, которые были перенесены с пленки или предназначены для проектов с индивидуальной настройкой.


 Фактор a с правой стороны.
Фактор a с правой стороны.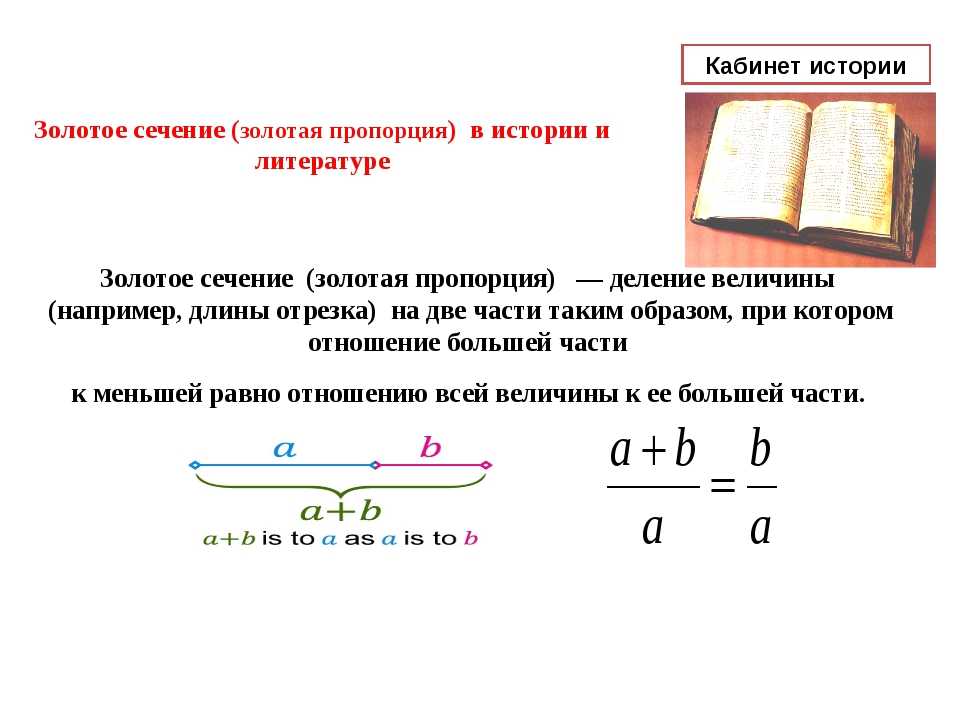 Фактор a из правой части
Фактор a из правой части
