Формула силы тока в физике
Содержание:
- Определение и формула силы тока
- Некоторые виды силы тока
- Плотность тока
- Сила тока в соединениях проводников
- Закон Ома
- Единицы измерения силы тока
- Примеры решения задач
Определение и формула силы тока
Определение
Электрическим током называют упорядоченное движение носителей зарядов. В металлах таковыми являются электроны, отрицательно заряженные частицы с зарядом, равным элементарному заряду. Направлением тока считают направление движения положительно заряженных частиц.
Силой тока (током) через некоторую поверхность S называют скалярную физическую величину, которую обозначают I, равную:
$$I=\frac{d q}{d t}$ (1)$
где q – заряд, проходящий сквозь поверхность S, t – время прохождения заряда. Выражение (1) определяет величину силы тока в
момент времени t (мгновенное значение величины силы тока). {2} d t}(3)$$
{2} d t}(3)$$
$$I=I_{m} \sin \omega t$$
то Im – амплитуда силы тока ($\omega$ – частота силы переменного тока).
Плотность тока
Распределение электрического тока по сечению проводника характеризуют при помощи вектора плотности тока ($\bar{j}$). При этом:
$$j_{n}=j \cos \alpha=\frac{d I}{d S}(5)$$
где $\alpha$ – угол между векторами $\bar{j}$ и $\bar{n}$ ( $\bar{n}$ – нормаль к элементу поверхности dS), jn – проекция вектора плотности тока на направление нормали ($\bar{n}$).
Сила тока в проводнике определяется при помощи формулы:
$$I=\int_{S} j d S(6)$$
где интегрирование в выражении (6) проводится по всему поперечному сечению проводника S ($\alpha \equiv 0$)
Для постоянного тока имеем:
$I = jS (7)$
Если рассматривать два проводника с сечениями S 1 и S2 и постоянными токами, то выполняется соотношение:
$$\frac{j_{1}}{j_{2}}=\frac{S_{2}}{S_{1}}(8)$$
Сила тока в соединениях проводников
При последовательном соединении проводников сила тока в каждом из них одинакова:
$$I=I_{1}=I_{2}=\cdots=I_{i}(9)$$
При параллельном соединении проводников сила тока (I) вычисляется как сумма токов в каждом проводнике (Ii):
$$I=\sum_{i=1}^{n} I_{i}(10)$$
Закон Ома
Сила тока входит в один из основных законов постоянного тока – закон Ома (для участка цепи):
$$I=\frac{\varphi_{1}-\varphi_{2}+\varepsilon}{R}(11)$$
где $\varphi_{1}$ —
$\varphi_{2}$ – разность потенциалов на концах, рассматриваемого участка,
$\varepsilon$ — ЭДС источника, который входит в участок цепи, R – сопротивление участка цепи.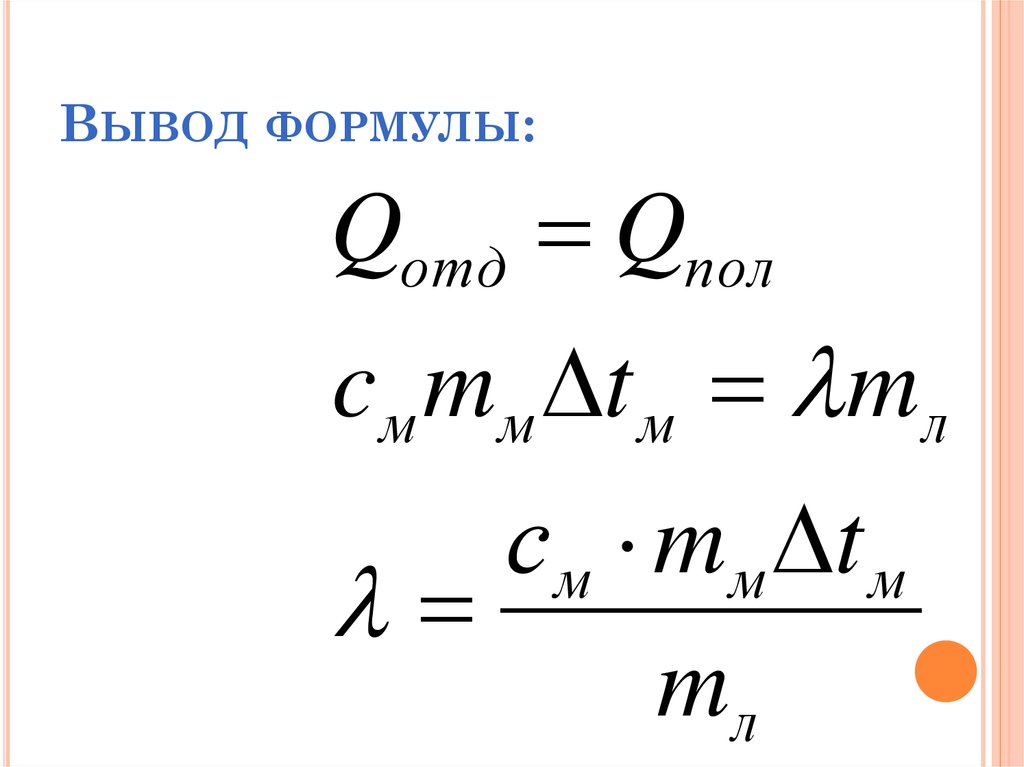 {6}=(30-6)=24$ (Кл)
{6}=(30-6)=24$ (Кл)
Ответ. q=24 Кл
236
проверенных автора готовы помочь в написании работы любой сложности
Мы помогли уже 4 396 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!
Пример
Задание. Плоский конденсатор составлен из двух квадратных пластин со стороной A, находящихся на расстоянии dдруг от друга. Этот конденсатор подключен к источнику постоянного напряжения U. Конденсатор погружают в сосуд с керосином (пластины конденсатора вертикальны) со скоростью v=const. Какова сила тока, которая будет течь по подводящим проводам в описанном выше процессе. Считать, что диэлектрическая проницаемость керосина равна $\varepsilon$.
Решение. Основой для решения задачи станет формул для вычисления силы тока вида:
$$I=\frac{d q}{d t}(2.1)$$
При погружении в керосин на глубину xописанной выше системы мы получаем два конденсатора, соединенных параллельно (над керосином и в керосине)
рис.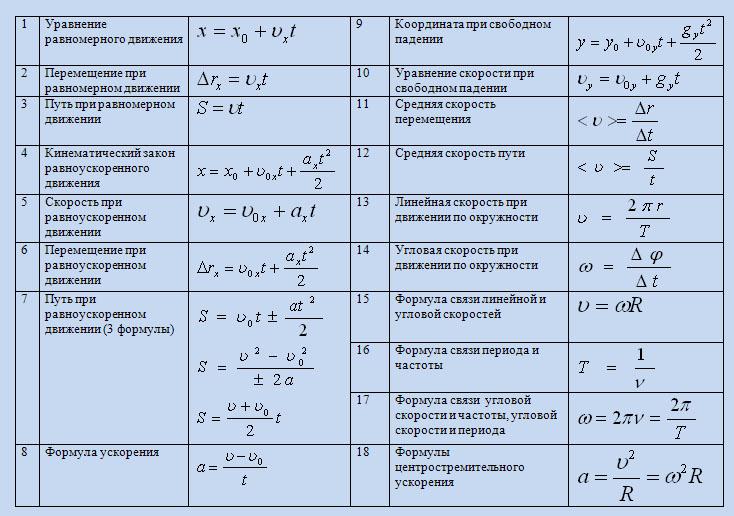 {2}-A v t\right) \rightarrow C_{2}=\frac{\varepsilon \varepsilon_{0}(A v t)}{d}(2.4)$$
{2}-A v t\right) \rightarrow C_{2}=\frac{\varepsilon \varepsilon_{0}(A v t)}{d}(2.4)$$
где $\varepsilon_{0}$ – электрическая постоянная, переменной величиной при погружении системы в керосин является площадь обкладок S:
$$S_{2}=A \cdot v \cdot t ; S_{1}=A \cdot(A-v t)$$
Из выражений (2.4), (2.5) и условий задачи имеем:
$$d C=d C_{1}+d C_{2}=\frac{\varepsilon \varepsilon_{0} A v d t}{d}-\frac{\varepsilon_{0}}{d} A v d t(2.6)$$
Тогда подставив dC в формулу для силы тока (2.1) получаем:
$$I=U\left(\frac{\varepsilon \varepsilon_{0} A v}{d}-\frac{\varepsilon_{0}}{d} A v\right)=\frac{\varepsilon_{0} U A v}{d}(\varepsilon-1)$$
Ответ. $I=\frac{\varepsilon_{0} U A v}{d}(\varepsilon-1)$
Читать дальше: Формула силы.
Все формулы q. Формулы по физике для егэ. Параллельное соединение проводников
Для того чтобы успешно подготовиться к ЦТ по физике и математике, среди прочего, необходимо выполнить три важнейших условия:
- Изучить все темы и выполнить все тесты и задания приведенные в учебных материалах на этом сайте.

- Выучить все формулы и законы в физике, и формулы и методы в математике . На самом деле, выполнить это тоже очень просто, необходимых формул по физике всего около 200 штук, а по математике даже чуть меньше. В каждом из этих предметов есть около десятка стандартных методов решения задач базового уровня сложности, которые тоже вполне можно выучить, и таким образом, совершенно на автомате и без затруднений решить в нужный момент большую часть ЦТ. После этого Вам останется подумать только над самыми сложными задачами.
- Посетить все три этапа репетиционного тестирования по физике и математике.
 Каждый РТ можно посещать по два раза, чтобы прорешать оба варианта. Опять же на ЦТ, кроме умения быстро и качественно решать задачи, и знания формул и методов необходимо также уметь правильно спланировать время, распределить силы, а главное правильно заполнить бланк ответов, не перепутав ни номера ответов и задач, ни собственную фамилию. Также в ходе РТ важно привыкнуть к стилю постановки вопросов в задачах, который на ЦТ может показаться неподготовленному человеку очень непривычным.
Каждый РТ можно посещать по два раза, чтобы прорешать оба варианта. Опять же на ЦТ, кроме умения быстро и качественно решать задачи, и знания формул и методов необходимо также уметь правильно спланировать время, распределить силы, а главное правильно заполнить бланк ответов, не перепутав ни номера ответов и задач, ни собственную фамилию. Также в ходе РТ важно привыкнуть к стилю постановки вопросов в задачах, который на ЦТ может показаться неподготовленному человеку очень непривычным.
Успешное, старательное и ответственное выполнение этих трех пунктов, а также ответственная проработка итоговых тренировочных тестов , позволит Вам показать на ЦТ отличный результат, максимальный из того, на что Вы способны.
Нашли ошибку?
Если Вы, как Вам кажется, нашли ошибку в учебных материалах, то напишите, пожалуйста, о ней на электронную почту (). В письме укажите предмет (физика или математика), название либо номер темы или теста, номер задачи, или место в тексте (страницу) где по Вашему мнению есть ошибка.
Абсолютно необходимы для того, чтобы человек, решивший изучать эту науку, вооружившись ими, мог чувствовать себя в мире физики как рыба в воде. Без знания формул немыслимо решение задач по физике. Но все формулы запомнить практически невозможно и важно знать, особенно для юного ума, где найти ту или иную формулу и когда ее применить.
Расположение физических формул в специализированных учебниках распределяется обычно по соответствующим разделам среди текстовой информации, поэтому их поиск там может отнять довольно-таки много времени, а тем более, если они вдруг понадобятся Вам срочно!
Представленные ниже шпаргалки по физике содержат все основные формулы из курса физики , которые будут полезны учащимся школ и вузов.
Все формулы школьного курса по физике с сайта http://4ege. ru
ru
I. Кинематика скачать
1. Основные понятия
2. Законы сложения скоростей и ускорений
3. Нормальное и тангенциальное ускорения
4. Типы движений
4.1. Равномерное движение
4.1.1. Равномерное прямолинейное движение
4.1.2. Равномерное движение по окружности
4.2. Движение с постоянным ускорением
4.2.1. Равноускоренное движение
4.2.2. Равнозамедленное движение
4.3. Гармоническое движение
1. Второй закон Ньютона
2. Теорема о движении центра масс
3. Третий закон Ньютона
4. Силы
5. Гравитационная сила
6. Силы, действующие через контакт
III. Законы сохранения. Работа и мощность скачать
1. Импульс материальной точки
2. Импульс системы материальных точек
3. Теорема об изменении импульса материальной точки
4. Теорема об изменении импульса системы материальных точек
5. Закон сохранения импульса
6. Работа силы
7. Мощность
8. Механическая энергия
9. Теорема о механической энергии
10.
 Закон сохранения механической энергии
Закон сохранения механической энергии11. Диссипативные силы
12. Методы вычисления работы
13. Средняя по времени сила
IV. Статика и гидростатика скачать
1. Условия равновесия
2. Вращающий момент
3. Неустойчивое равновесие, устойчивое равновесие, безразличное равновесие
4. Центр масс, центр тяжести
5. Сила гидростатического давления
6. Давлением жидкости
7. Давление в какой-либо точке жидкости
8, 9. Давление в однородной покоящейся жидкости
10. Архимедова сила
V. Тепловые явления скачать
1. Уравнение Менделеева-Клапейрона
2. Закон Дальтона
3. Основное уравнение МКТ
4. Газовые законы
5. Первый закон термодинамики
6. Адиабатический процесс
7. КПД циклического процесса (теплового двигателя)
8. Насыщенный пар
VI. Электростатика скачать
1. Закон Кулона
2. Принцип суперпозиции
3. Электрическое поле
3.1. Напряженность и потенциал электрического поля, созданного одним точечным зарядом Q
3.
 2. Напряженность и потенциал электрического поля, созданного системой точечных зарядов Q1, Q2, …
2. Напряженность и потенциал электрического поля, созданного системой точечных зарядов Q1, Q2, …3.4. Напряженность и потенциал однородного электрического поля, (созданного равномерно заряженной плоскотью или плоским конденсатором)
4. Потенциальная энергия системы электрических зарядов
5. Электроемкость
6. Свойства проводника в электрическом поле
VII. Постоянный ток скачать
1. Упорядоченная скорость
2. Сила тока
3. Плотность тока
4. Закон Ома для участка цепи, не содержащего ЭДС
5. Закон Ома для участка цепи, содержащего ЭДС
6. Закон Ома для полной (замкнутой) цепи
7. Последовательное соединение проводников
8. Параллельное соединение проводников
9. Работа и мощность электрического тока
10. КПД электрической цепи
11. Условие выделения максимальной мощности на нагрузке
12. Закон Фарадея для электролиза
VIII. Магнитные явления скачать
1.
 Магнитное поле
Магнитное поле2. Движение зарядов в магнитном поле
3. Рамка с током в магнитном поле
4. Магнитные поля, создаваемые различными токами
5. Взаимодействие токов
6. Явление электромагнитной индукции
7. Явление самоиндукции
IX. Колебания и волны скачать
1. Колебания, определения
2. Гармонические колебания
3. Простейшие колебательные системы
4. Волна
X. Оптика скачать
1. Закон отражения
2. Закон преломления
3. Линза
4. Изображение
5. Возможные случаи расположения предмета
6. Интерференция
7. Дифракция
Большая шпаргалка по физике . Все формулы изложены в компактном виде с небольшими комментариями. Шпаргалка также содержит полезные константы и прочую информацию. Файл содержит следующие разделы физики:
Механика (кинематика, динамика и статика)
Молекулярная физика. Свойства газов и жидкостей
Термодинамика
Электрические и электромагнитные явления
Электродинамика. Постоянный ток
Постоянный ток
Электромагнетизм
Колебания и волны. Оптика. Акустика
Квантовая физика и теория относительности
Маленькая шпора по физике . Все самое необходимое для экзамена. Нарезка основных формул по физике на одной странице. Не очень эстетично, зато практично. 🙂
Кинематика
Путь при равномерном движении:
Перемещение S (расстояние по прямой между начальной и конечной точкой движения) обычно находится из геометрических соображений. Координата при равномерном прямолинейном движении изменяется по закону (аналогичные уравнения получаются для остальных координатных осей):
Средняя скорость пути:
Средняя скорость перемещения:
Выразив из формулы выше конечную скорость, получаем более распространённый вид предыдущей формулы, которая теперь выражает зависимость скорости от времени при равноускоренном движении:
Средняя скорость при равноускоренном движении:
Перемещение при равноускоренном прямолинейном движении может быть рассчитано по нескольким формулам:
Координата при равноускоренном движении изменяется по закону:
Проекция скорости при равноускоренном движении изменяется по такому закону:
Скорость, с которой упадет тело падающее с высоты h без начальной скорости:
Время падения тела с высоты h без начальной скорости:
Максимальная высота на которую поднимется тело, брошенное вертикально вверх с начальной скоростью v 0 , время подъема этого тела на максимальную высоту, и полное время полета (до возвращения в исходную точку):
Время падения тела при горизонтальном броске с высоты H может быть найдено по формуле:
Дальность полета тела при горизонтальном броске с высоты H :
Полная скорость в произвольный момент времени при горизонтальном броске, и угол наклона скорости к горизонту:
Максимальная высота подъема при броске под углом к горизонту (относительно начального уровня):
Время подъема до максимальной высоты при броске под углом к горизонту:
Дальность полета и полное время полета тела брошенного под углом к горизонту (при условии, что полет заканчивается на той же высоте с которой начался, т. е. тело бросали, например, с земли на землю):
е. тело бросали, например, с земли на землю):
Определение периода вращения при равномерном движении по окружности:
Определение частоты вращения при равномерном движении по окружности:
Связь периода и частоты:
Линейная скорость при равномерном движении по окружности может быть найдена по формулам:
Угловая скорость вращения при равномерном движении по окружности:
Связь линейной и скорости и угловой скорости выражается формулой:
Связь угла поворота и пути при равномерном движении по окружности радиусом R (фактически, это просто формула для длины дуги из геометрии):
Центростремительное ускорение находится по одной из формул:
Динамика
Второй закон Ньютона:
Здесь: F — равнодействующая сила, которая равна сумме всех сил действующих на тело:
Второй закон Ньютона в проекциях на оси (именно такая форма записи чаще всего и применяется на практике):
Третий закон Ньютона (сила действия равна силе противодействия):
Сила упругости:
Общий коэффициент жесткости параллельно соединённых пружин:
Общий коэффициент жесткости последовательно соединённых пружин:
Сила трения скольжения (или максимальное значение силы трения покоя):
Закон всемирного тяготения:
Если рассмотреть тело на поверхности планеты и ввести следующее обозначение:
Где: g — ускорение свободного падения на поверхности данной планеты, то получим следующую формулу для силы тяжести:
Ускорение свободного падения на некоторой высоте от поверхности планеты выражается формулой:
Скорость спутника на круговой орбите:
Первая космическая скорость:
Закон Кеплера для периодов обращения двух тел вращающихся вокруг одного притягивающего центра:
Статика
Момент силы определяется с помощью следующей формулы:
Условие при котором тело не будет вращаться:
Координата центра тяжести системы тел (аналогичные уравнения для остальных осей):
Гидростатика
Определение давления задаётся следующей формулой:
Давление, которое создает столб жидкости находится по формуле:
Но часто нужно учитывать еще и атмосферное давление, тогда формула для общего давления на некоторой глубине h в жидкости приобретает вид:
Идеальный гидравлический пресс:
Любой гидравлический пресс:
КПД для неидеального гидравлического пресса:
Сила Архимеда (выталкивающая сила, V — объем погруженной части тела):
Импульс
Импульс тела находится по следующей формуле:
Изменение импульса тела или системы тел (обратите внимание, что разность конечного и начального импульсов векторная):
Общий импульс системы тел (важно то, что сумма векторная):
Второй закон Ньютона в импульсной форме может быть записан в виде следующей формулы:
Закон сохранения импульса. Как следует из предыдущей формулы, в случае если на систему тел не действует внешних сил, либо действие внешних сил скомпенсировано (равнодействующая сила равна нолю), то изменение импульса равно нолю, что означает, что общий импульс системы сохраняется:
Как следует из предыдущей формулы, в случае если на систему тел не действует внешних сил, либо действие внешних сил скомпенсировано (равнодействующая сила равна нолю), то изменение импульса равно нолю, что означает, что общий импульс системы сохраняется:
Если внешние силы не действуют только вдоль одной из осей, то сохраняется проекция импульса на данную ось, например:
Работа, мощность, энергия
Механическая работа рассчитывается по следующей формуле:
Самая общая формула для мощности (если мощность переменная, то по следующей формуле рассчитывается средняя мощность):
Мгновенная механическая мощность:
Коэффициент полезного действия (КПД) может быть рассчитан и через мощности и через работы:
Потенциальная энергия тела поднятого на высоту:
Потенциальная энергия растянутой (или сжатой) пружины:
Полная механическая энергия:
Связь полной механической энергии тела или системы тел и работы внешних сил:
Закон сохранения механической энергии (далее – ЗСЭ). Как следует из предыдущей формулы, если внешние силы не совершают работы над телом (или системой тел), то его (их) общая полная механическая энергия остается постоянной, при этом энергия может перетекать из одного вида в другой (из кинетической в потенциальную или наоборот):
Как следует из предыдущей формулы, если внешние силы не совершают работы над телом (или системой тел), то его (их) общая полная механическая энергия остается постоянной, при этом энергия может перетекать из одного вида в другой (из кинетической в потенциальную или наоборот):
Молекулярная физика
Химическое количество вещества находится по одной из формул:
Масса одной молекулы вещества может быть найдена по следующей формуле:
Связь массы, плотности и объёма:
Основное уравнение молекулярно-кинетической теории (МКТ) идеального газа:
Определение концентрации задаётся следующей формулой:
Для средней квадратичной скорости молекул имеется две формулы:
Средняя кинетическая энергия поступательного движения одной молекулы:
Постоянная Больцмана, постоянная Авогадро и универсальная газовая постоянная связаны следующим образом:
Следствия из основного уравнения МКТ:
Уравнение состояния идеального газа (уравнение Клапейрона-Менделеева):
Газовые законы. Закон Бойля-Мариотта:
Закон Бойля-Мариотта:
Закон Гей-Люссака:
Закон Шарля:
Универсальный газовый закон (Клапейрона):
Давление смеси газов (закон Дальтона):
Тепловое расширение тел. Тепловое расширение газов описывается законом Гей-Люссака. Тепловое расширение жидкостей подчиняется следующему закону:
Для расширения твердых тел применяются три формулы, описывающие изменение линейных размеров, площади и объема тела:
Термодинамика
Количество теплоты (энергии) необходимое для нагревания некоторого тела (или количество теплоты выделяющееся при остывании тела) рассчитывается по формуле:
Теплоемкость (С — большое) тела может быть рассчитана через удельную теплоёмкость (c — маленькое) вещества и массу тела по следующей формуле:
Тогда формула для количества теплоты необходимой для нагревания тела, либо выделившейся при остывании тела может быть переписана следующим образом:
Фазовые превращения. При парообразовании поглощается, а при конденсации выделяется количество теплоты равное:
При плавлении поглощается, а при кристаллизации выделяется количество теплоты равное:
При сгорании топлива выделяется количество теплоты равное:
Уравнение теплового баланса (ЗСЭ). Для замкнутой системы тел выполняется следующее (сумма отданных теплот равна сумме полученных):
Для замкнутой системы тел выполняется следующее (сумма отданных теплот равна сумме полученных):
Если все теплоты записывать с учетом знака, где «+» соответствует получению энергии телом, а «–» выделению, то данное уравнение можно записать в виде:
Работа идеального газа:
Если же давление газа меняется, то работу газа считают, как площадь фигуры под графиком в p –V координатах. Внутренняя энергия идеального одноатомного газа:
Изменение внутренней энергии рассчитывается по формуле:
Первый закон (первое начало) термодинамики (ЗСЭ):
Для различных изопроцессов можно выписать формулы по которым могут быть рассчитаны полученная теплота Q , изменение внутренней энергии ΔU и работа газа A . Изохорный процесс (V = const):
Изобарный процесс (p = const):
Изотермический процесс (T = const):
Адиабатный процесс (Q = 0):
КПД тепловой машины может быть рассчитан по формуле:
Где: Q 1 – количество теплоты полученное рабочим телом за один цикл от нагревателя, Q 2 – количество теплоты переданное рабочим телом за один цикл холодильнику.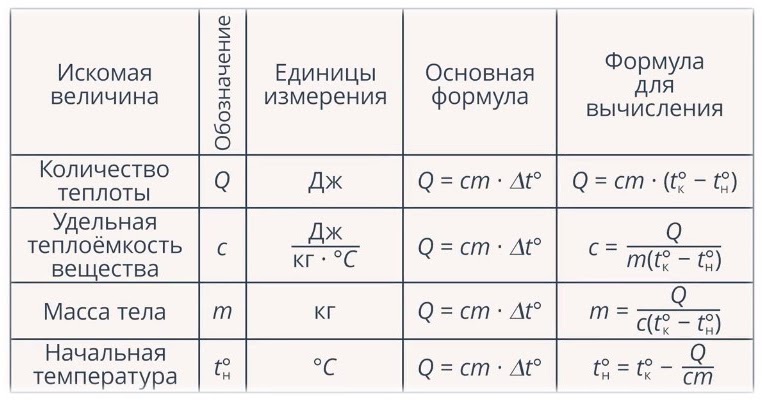 Работа совершенная тепловой машиной за один цикл:
Работа совершенная тепловой машиной за один цикл:
Наибольший КПД при заданных температурах нагревателя T 1 и холодильника T 2 , достигается если тепловая машина работает по циклу Карно. Этот КПД цикла Карно равен:
Абсолютная влажность рассчитывается как плотность водяных паров (из уравнения Клапейрона-Менделеева выражается отношение массы к объему и получается следующая формула):
Относительная влажность воздуха может быть рассчитана по следующим формулам:
Потенциальная энергия поверхности жидкости площадью S :
Сила поверхностного натяжения, действующая на участок границы жидкости длиной L :
Высота столба жидкости в капилляре:
При полном смачивании θ = 0°, cos θ = 1. В этом случае высота столба жидкости в капилляре станет равной:
При полном несмачивании θ = 180°, cos θ = –1 и, следовательно, h
Электростатика
Электрический заряд может быть найден по формуле:
Линейная плотность заряда:
Поверхностная плотность заряда:
Объёмная плотность заряда:
Закон Кулона (сила электростатического взаимодействия двух электрических зарядов):
Где: k — некоторый постоянный электростатический коэффициент, который определяется следующим образом:
Напряжённость электрического поля находится по формуле (хотя чаще эту формулу используют для нахождения силы действующей на заряд в данном электрическом поле):
Принцип суперпозиции для электрических полей (результирующее электрическое поле равно векторной сумме электрических полей составляющих его):
Напряженность электрического поля, которую создает заряд Q на расстоянии r от своего центра:
Напряженность электрического поля, которую создает заряженная плоскость:
Потенциальная энергия взаимодействия двух электрических зарядов выражается формулой:
Электрическое напряжение это просто разность потенциалов, т. е. определение электрического напряжения может быть задано формулой:
е. определение электрического напряжения может быть задано формулой:
В однородном электрическом поле существует связь между напряженностью поля и напряжением:
Работа электрического поля может быть вычислена как разность начальной и конечной потенциальной энергии системы зарядов:
Работа электрического поля в общем случае может быть вычислена также и по одной из формул:
В однородном поле при перемещении заряда вдоль его силовых линий работа поля может быть также рассчитана по следующей формуле:
Определение потенциала задаётся выражением:
Потенциал, который создает точечный заряд или заряженная сфера:
Принцип суперпозиции для электрического потенциала (результирующий потенциал равен скалярной сумме потенциалов полей составляющих итоговое поле):
Для диэлектрической проницаемости вещества верно следующее:
Определение электрической ёмкости задаётся формулой:
Ёмкость плоского конденсатора:
Заряд конденсатора:
Напряжённость электрического поля внутри плоского конденсатора:
Сила притяжения пластин плоского конденсатора:
Энергия конденсатора (вообще говоря, это энергия электрического поля внутри конденсатора):
Объёмная плотность энергии электрического поля:
Электрический ток
Сила тока может быть найдена с помощью формулы:
Плотность тока:
Сопротивление проводника:
Зависимость сопротивления проводника от температуры задаётся следующей формулой:
Закон Ома (выражает зависимость силы тока от электрического напряжения и сопротивления):
Закономерности последовательного соединения:
Закономерности параллельного соединения:
Электродвижущая сила источника тока (ЭДС) определяется с помощью следующей формулы:
Закон Ома для полной цепи:
Падение напряжения во внешней цепи при этом равно (его еще называют напряжением на клеммах источника):
Сила тока короткого замыкания:
Работа электрического тока (закон Джоуля-Ленца). Работа А электрического тока протекающего по проводнику обладающему сопротивлением преобразуется в теплоту Q выделяющуюся на проводнике:
Работа А электрического тока протекающего по проводнику обладающему сопротивлением преобразуется в теплоту Q выделяющуюся на проводнике:
Мощность электрического тока:
Энергобаланс замкнутой цепи
Полезная мощность или мощность, выделяемая во внешней цепи:
Максимально возможная полезная мощность источника достигается, если R = r и равна:
Если при подключении к одному и тому же источнику тока разных сопротивлений R 1 и R 2 на них выделяются равные мощности то внутреннее сопротивление этого источника тока может быть найдено по формуле:
Мощность потерь или мощность внутри источника тока:
Полная мощность, развиваемая источником тока:
КПД источника тока:
Электролиз
Масса m вещества, выделившегося на электроде, прямо пропорциональна заряду Q , прошедшему через электролит:
Величину k называют электрохимическим эквивалентом. Он может быть рассчитан по формуле:
Где: n – валентность вещества, N A – постоянная Авогадро, M – молярная масса вещества, е – элементарный заряд.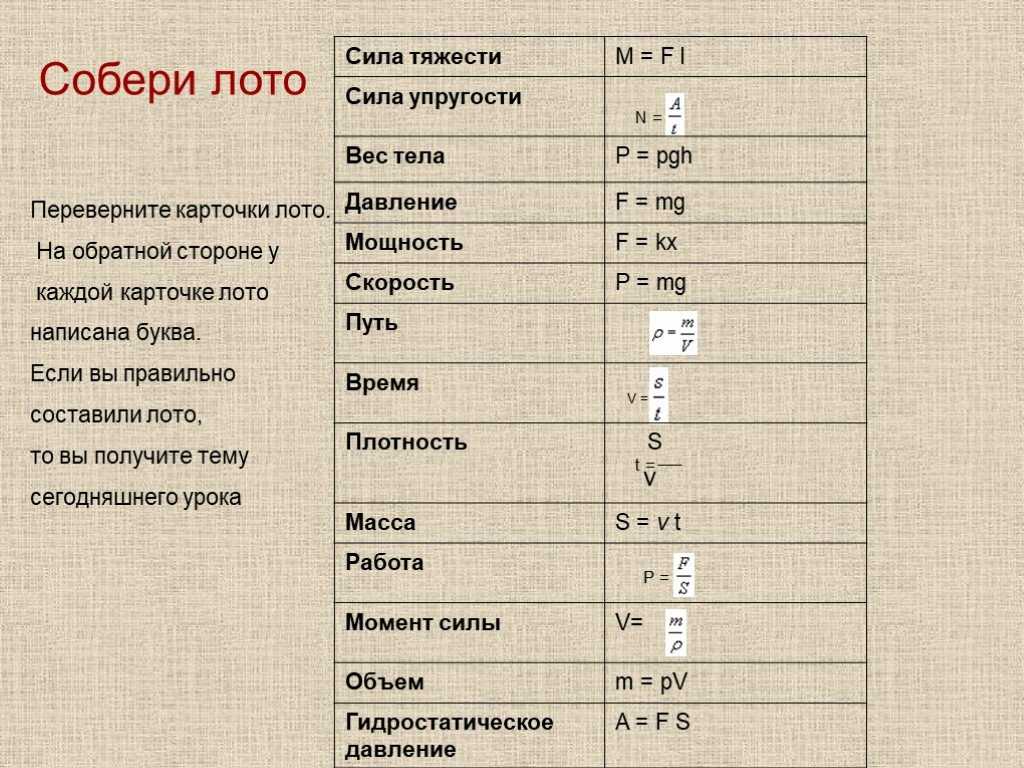 Иногда также вводят следующее обозначение для постоянной Фарадея:
Иногда также вводят следующее обозначение для постоянной Фарадея:
Магнетизм
Сила Ампера , действующая на проводник с током помещённый в однородное магнитное поле, рассчитывается по формуле:
Момент сил действующих на рамку с током:
Сила Лоренца , действующая на заряженную частицу движущуюся в однородном магнитном поле, рассчитывается по формуле:
Радиус траектории полета заряженной частицы в магнитном поле:
Модуль индукции B магнитного поля прямолинейного проводника с током I на расстоянии R от него выражается соотношением:
Индукция поля в центре витка с током радиусом R :
Внутри соленоида длиной l и с количеством витков N создается однородное магнитное поле с индукцией:
Магнитная проницаемость вещества выражается следующим образом:
Магнитным потоком Φ через площадь S контура называют величину заданную формулой:
ЭДС индукции рассчитывается по формуле:
При движении проводника длиной l в магнитном поле B со скоростью v также возникает ЭДС индукции (проводник движется в направлении перпендикулярном самому себе):
Максимальное значение ЭДС индукции в контуре состоящем из N витков, площадью S , вращающемся с угловой скоростью ω в магнитном поле с индукцией В :
Индуктивность катушки:
Где: n — концентрация витков на единицу длины катушки:
Связь индуктивности катушки, силы тока протекающего через неё и собственного магнитного потока пронизывающего её, задаётся формулой:
ЭДС самоиндукции возникающая в катушке:
Энергия катушки (вообще говоря, это энергия магнитного поля внутри катушки):
Объемная плотность энергии магнитного поля:
Колебания
Уравнение описывающее физические системы способные совершать гармонические колебания с циклической частотой ω 0:
Решение предыдущего уравнения является уравнением движения для гармонических колебаний и имеет вид:
Период колебаний вычисляется по формуле:
Частота колебаний:
Циклическая частота колебаний:
Зависимость скорости от времени при гармонических механических колебаниях выражается следующей формулой:
Максимальное значение скорости при гармонических механических колебаниях:
Зависимость ускорения от времени при гармонических механических колебаниях:
Максимальное значение ускорения при механических гармонических колебаниях:
Циклическая частота колебаний математического маятника рассчитывается по формуле:
Период колебаний математического маятника:
Циклическая частота колебаний пружинного маятника:
Период колебаний пружинного маятника:
Максимальное значение кинетической энергии при механических гармонических колебаниях задаётся формулой:
Максимальное значение потенциальной энергии при механических гармонических колебаниях пружинного маятника:
Взаимосвязь энергетических характеристик механического колебательного процесса:
Энергетические характеристики и их взаимосвязь при колебаниях в электрическом контуре:
Период гармонических колебаний в электрическом колебательном контуре определяется по формуле:
Циклическая частота колебаний в электрическом колебательном контуре:
Зависимость заряда на конденсаторе от времени при колебаниях в электрическом контуре описывается законом:
Зависимость электрического тока протекающего через катушку индуктивности от времени при колебаниях в электрическом контуре:
Зависимость напряжения на конденсаторе от времени при колебаниях в электрическом контуре:
Максимальное значение силы тока при гармонических колебаниях в электрическом контуре может быть рассчитано по формуле:
Максимальное значение напряжения на конденсаторе при гармонических колебаниях в электрическом контуре:
Переменный ток характеризуется действующими значениями силы тока и напряжения, которые связаны с амплитудными значениями соответствующих величин следующим образом. Действующее значение силы тока:
Действующее значение силы тока:
Действующее значение напряжения:
Мощность в цепи переменного тока:
Трансформатор
Если напряжение на входе в трансформатор равно U 1 , а на выходе U 2 , при этом число витков в первичной обмотке равно n 1 , а во вторичной n 2 , то выполняется следующее соотношение:
Коэффициент трансформации вычисляется по формуле:
Если трансформатор идеальный, то выполняется следующее соотношение (мощности на входе и выходе равны):
В неидеальном трансформаторе вводится понятие КПД:
Волны
Длина волны может быть рассчитана по формуле:
Разность фаз колебаний двух точек волны, расстояние между которыми l :
Скорость электромагнитной волны (в т.ч. света) в некоторой среде:
Скорость электромагнитной волны (в т.ч. света) в вакууме постоянна и равна с = 3∙10 8 м/с, она также может быть вычислена по формуле:
Скорости электромагнитной волны (в т.ч. света) в среде и в вакууме также связаны между собой формулой:
При этом показатель преломления некоторого вещества можно рассчитать используя формулу:
Оптика
Оптическая длина пути определяется формулой:
Оптическая разность хода двух лучей:
Условие интерференционного максимума:
Условие интерференционного минимума:
Закон преломления света на границе двух прозрачных сред:
Постоянную величину n 21 называют относительным показателем преломления второй среды относительно первой. Если n 1 > n 2 , то возможно явление полного внутреннего отражения, при этом:
Если n 1 > n 2 , то возможно явление полного внутреннего отражения, при этом:
Линейным увеличением линзы Γ называют отношение линейных размеров изображения и предмета:
Атомная и ядерная физика
Энергия кванта электромагнитной волны (в т.ч. света) или, другими словами, энергия фотона вычисляется по формуле:
Импульс фотона:
Формула Эйнштейна для внешнего фотоэффекта (ЗСЭ):
Максимальная кинетическая энергия вылетающих электронов при фотоэффекте может быть выражена через величину задерживающего напряжение U з и элементарный заряд е :
Существует граничная частота или длинна волны света (называемая красной границей фотоэффекта) такая, что свет с меньшей частотой или большей длиной волны не может вызвать фотоэффект. Эти значения связаны с величиной работы выхода следующим соотношением:
Второй постулат Бора или правило частот (ЗСЭ):
В атоме водорода выполняются следующие соотношения, связывающие радиус траектории вращающегося вокруг ядра электрона, его скорость и энергию на первой орбите с аналогичными характеристиками на остальных орбитах:
На любой орбите в атоме водорода кинетическая (К ) и потенциальная (П ) энергии электрона связаны с полной энергией (Е ) следующими формулами:
Общее число нуклонов в ядре равно сумме числа протонов и нейтронов:
Дефект массы:
Энергия связи ядра выраженная в единицах СИ:
Энергия связи ядра выраженная в МэВ (где масса берется в атомных единицах):
Закон радиоактивного распада:
Ядерные реакции
Для произвольной ядерной реакции описывающейся формулой вида:
Выполняются следующие условия:
Энергетический выход такой ядерной реакции при этом равен:
Основы специальной теории относительности (СТО)
Релятивистское сокращение длины:
Релятивистское удлинение времени события:
Релятивистский закон сложения скоростей. Если два тела движутся навстречу друг другу, то их скорость сближения:
Если два тела движутся навстречу друг другу, то их скорость сближения:
Релятивистский закон сложения скоростей. Если же тела движутся в одном направлении, то их относительная скорость:
Энергия покоя тела:
Любое изменение энергии тела означает изменение массы тела и наоборот:
Полная энергия тела:
Полная энергия тела Е пропорциональна релятивистской массе и зависит от скорости движущегося тела, в этом смысле важны следующие соотношения:
Релятивистское увеличение массы:
Кинетическая энергия тела, движущегося с релятивистской скоростью:
Между полной энергией тела, энергией покоя и импульсом существует зависимость:
Равномерное движение по окружности
В качестве дополнения, в таблице ниже приводим всевозможные взаимосвязи между характеристиками тела равномерно вращающегося по окружности (T – период, N – количество оборотов, v – частота, R – радиус окружности, ω – угловая скорость, φ – угол поворота (в радианах), υ – линейная скорость тела, a n – центростремительное ускорение, L – длина дуги окружности, t – время):
Расширенная PDF версия документа «Все главные формулы по школьной физике»:
- Назад
- Вперёд
Как успешно подготовиться к ЦТ по физике и математике?
Для того чтобы успешно подготовиться к ЦТ по физике и математике, среди прочего, необходимо выполнить три важнейших условия:
- Изучить все темы и выполнить все тесты и задания приведенные в учебных материалах на этом сайте.
 Для этого нужно всего ничего, а именно: посвящать подготовке к ЦТ по физике и математике, изучению теории и решению задач по три-четыре часа каждый день. Дело в том, что ЦТ это экзамен, где мало просто знать физику или математику, нужно еще уметь быстро и без сбоев решать большое количество задач по разным темам и различной сложности. Последнему научиться можно только решив тысячи задач.
Для этого нужно всего ничего, а именно: посвящать подготовке к ЦТ по физике и математике, изучению теории и решению задач по три-четыре часа каждый день. Дело в том, что ЦТ это экзамен, где мало просто знать физику или математику, нужно еще уметь быстро и без сбоев решать большое количество задач по разным темам и различной сложности. Последнему научиться можно только решив тысячи задач. - Выучить все формулы и законы в физике, и формулы и методы в математике . На самом деле, выполнить это тоже очень просто, необходимых формул по физике всего около 200 штук, а по математике даже чуть меньше. В каждом из этих предметов есть около десятка стандартных методов решения задач базового уровня сложности, которые тоже вполне можно выучить, и таким образом, совершенно на автомате и без затруднений решить в нужный момент большую часть ЦТ. После этого Вам останется подумать только над самыми сложными задачами.
- Посетить все три этапа репетиционного тестирования по физике и математике.
 Каждый РТ можно посещать по два раза, чтобы прорешать оба варианта. Опять же на ЦТ, кроме умения быстро и качественно решать задачи, и знания формул и методов необходимо также уметь правильно спланировать время, распределить силы, а главное правильно заполнить бланк ответов, не перепутав ни номера ответов и задач, ни собственную фамилию. Также в ходе РТ важно привыкнуть к стилю постановки вопросов в задачах, который на ЦТ может показаться неподготовленному человеку очень непривычным.
Каждый РТ можно посещать по два раза, чтобы прорешать оба варианта. Опять же на ЦТ, кроме умения быстро и качественно решать задачи, и знания формул и методов необходимо также уметь правильно спланировать время, распределить силы, а главное правильно заполнить бланк ответов, не перепутав ни номера ответов и задач, ни собственную фамилию. Также в ходе РТ важно привыкнуть к стилю постановки вопросов в задачах, который на ЦТ может показаться неподготовленному человеку очень непривычным.
Успешное, старательное и ответственное выполнение этих трех пунктов, а также ответственная проработка итоговых тренировочных тестов , позволит Вам показать на ЦТ отличный результат, максимальный из того, на что Вы способны.
Нашли ошибку?
Если Вы, как Вам кажется, нашли ошибку в учебных материалах, то напишите, пожалуйста, о ней на электронную почту (). В письме укажите предмет (физика или математика), название либо номер темы или теста, номер задачи, или место в тексте (страницу) где по Вашему мнению есть ошибка. Также опишите в чем заключается предположительная ошибка. Ваше письмо не останется незамеченным, ошибка либо будет исправлена, либо Вам разъяснят почему это не ошибка.
Также опишите в чем заключается предположительная ошибка. Ваше письмо не останется незамеченным, ошибка либо будет исправлена, либо Вам разъяснят почему это не ошибка.
Шпаргалка с формулами по физике для ЕГЭ
Шпаргалка с формулами по физике для ЕГЭ
И не только (может понадобиться 7, 8, 9, 10 и 11 классам). Для начала картинка, которую можно распечатать в компактном виде.
И не только (может понадобиться 7, 8, 9, 10 и 11 классам). Для начала картинка, которую можно распечатать в компактном виде.
Шпаргалка с формулами по физике для ЕГЭ и не только (может понадобиться 7, 8, 9, 10 и 11 классам).
и не только (может понадобиться 7, 8, 9, 10 и 11 классам).
А потом вордовский файл , который содержит все формулы чтобы их распечатать, которые находятся внизу статьи.
Механика
- Давление Р=F/S
- Плотность ρ=m/V
- Давление на глубине жидкости P=ρ∙g∙h
- Сила тяжести Fт=mg
- 5. Архимедова сила Fa=ρ ж ∙g∙Vт
- Уравнение движения при равноускоренном движении
X=X 0 +υ 0 ∙t+(a∙t 2)/2 S=(υ 2 —υ 0 2) /2а S=(υ +υ 0) ∙t /2
- Уравнение скорости при равноускоренном движении υ =υ 0 +a∙t
- Ускорение a=(υ —υ 0)/t
- Скорость при движении по окружности υ =2πR/Т
- Центростремительное ускорение a=υ 2 /R
- Связь периода с частотой ν=1/T=ω/2π
- II закон Ньютона F=ma
- Закон Гука Fy=-kx
- Закон Всемирного тяготения F=G∙M∙m/R 2
- Вес тела, движущегося с ускорением а Р=m(g+a)
- Вес тела, движущегося с ускорением а↓ Р=m(g-a)
- Сила трения Fтр=µN
- Импульс тела p=mυ
- Импульс силы Ft=∆p
- Момент силы M=F∙ℓ
- Потенциальная энергия тела, поднятого над землей Eп=mgh
- Потенциальная энергия упруго деформированного тела Eп=kx 2 /2
- Кинетическая энергия тела Ek=mυ 2 /2
- Работа A=F∙S∙cosα
- Мощность N=A/t=F∙υ
- Коэффициент полезного действия η=Aп/Аз
- Период колебаний математического маятника T=2π√ℓ/g
- Период колебаний пружинного маятника T=2 π √m/k
- Уравнение гармонических колебаний Х=Хmax∙cos ωt
- Связь длины волны, ее скорости и периода λ= υ Т
Молекулярная физика и термодинамика
- Количество вещества ν=N/ Na
- Молярная масса М=m/ν
- Cр.
 кин. энергия молекул одноатомного газа Ek=3/2∙kT
кин. энергия молекул одноатомного газа Ek=3/2∙kT - Основное уравнение МКТ P=nkT=1/3nm 0 υ 2
- Закон Гей — Люссака (изобарный процесс) V/T =const
- Закон Шарля (изохорный процесс) P/T =const
- Относительная влажность φ=P/P 0 ∙100%
- Внутр. энергия идеал. одноатомного газа U=3/2∙M/µ∙RT
- Работа газа A=P∙ΔV
- Закон Бойля — Мариотта (изотермический процесс) PV=const
- Количество теплоты при нагревании Q=Cm(T 2 -T 1)
- Количество теплоты при плавлении Q=λm
- Количество теплоты при парообразовании Q=Lm
- Количество теплоты при сгорании топлива Q=qm
- Уравнение состояния идеального газа PV=m/M∙RT
- Первый закон термодинамики ΔU=A+Q
- КПД тепловых двигателей η= (Q 1 — Q 2)/ Q 1
- КПД идеал. двигателей (цикл Карно) η= (Т 1 — Т 2)/ Т 1
Электростатика и электродинамика — формулы по физике
- Закон Кулона F=k∙q 1 ∙q 2 /R 2
- Напряженность электрического поля E=F/q
- Напряженность эл.
 поля точечного заряда E=k∙q/R 2
поля точечного заряда E=k∙q/R 2 - Поверхностная плотность зарядов σ = q/S
- Напряженность эл. поля бесконечной плоскости E=2πkσ
- Диэлектрическая проницаемость ε=E 0 /E
- Потенциальная энергия взаимод. зарядов W= k∙q 1 q 2 /R
- Потенциал φ=W/q
- Потенциал точечного заряда φ=k∙q/R
- Напряжение U=A/q
- Для однородного электрического поля U=E∙d
- Электроемкость C=q/U
- Электроемкость плоского конденсатора C=S∙ε ∙ε 0 /d
- Энергия заряженного конденсатора W=qU/2=q²/2С=CU²/2
- Сила тока I=q/t
- Сопротивление проводника R=ρ∙ℓ/S
- Закон Ома для участка цепи I=U/R
- Законы послед. соединения I 1 =I 2 =I, U 1 +U 2 =U, R 1 +R 2 =R
- Законы паралл. соед. U 1 =U 2 =U, I 1 +I 2 =I, 1/R 1 +1/R 2 =1/R
- Мощность электрического тока P=I∙U
- Закон Джоуля-Ленца Q=I 2 Rt
- Закон Ома для полной цепи I=ε/(R+r)
- Ток короткого замыкания (R=0) I=ε/r
- Вектор магнитной индукции B=Fmax/ℓ∙I
- Сила Ампера Fa=IBℓsin α
- Сила Лоренца Fл=Bqυsin α
- Магнитный поток Ф=BSсos α Ф=LI
- Закон электромагнитной индукции Ei=ΔФ/Δt
- ЭДС индукции в движ проводнике Ei=Вℓυ sinα
- ЭДС самоиндукции Esi=-L∙ΔI/Δt
- Энергия магнитного поля катушки Wм=LI 2 /2
- Период колебаний кол.
 контура T=2π ∙√LC
контура T=2π ∙√LC - Индуктивное сопротивление X L =ωL=2πLν
- Емкостное сопротивление Xc=1/ωC
- Действующее значение силы тока Iд=Imax/√2,
- Действующее значение напряжения Uд=Umax/√2
- Полное сопротивление Z=√(Xc-X L) 2 +R 2
Оптика
- Закон преломления света n 21 =n 2 /n 1 = υ 1 / υ 2
- Показатель преломления n 21 =sin α/sin γ
- Формула тонкой линзы 1/F=1/d + 1/f
- Оптическая сила линзы D=1/F
- max интерференции: Δd=kλ,
- min интерференции: Δd=(2k+1)λ/2
- Диф.решетка d∙sin φ=k λ
Квантовая физика
- Ф-ла Эйнштейна для фотоэффекта hν=Aвых+Ek, Ek=U з е
- Красная граница фотоэффекта ν к = Aвых/h
- Импульс фотона P=mc=h/ λ=Е/с
Физика атомного ядра
- Закон радиоактивного распада N=N 0 ∙2 — t / T
- Энергия связи атомных ядер
E CB =(Zm p +Nm n -Mя)∙c 2
СТО
- t=t 1 /√1-υ 2 /c 2
- ℓ=ℓ 0 ∙√1-υ 2 /c 2
- υ 2 =(υ 1 +υ)/1+ υ 1 ∙υ/c 2
- Е = mс 2
Сессия приближается, и пора нам переходить от теории к практике. На выходных мы сели и подумали о том, что многим студентам было бы неплохо иметь под рукой подборку основных физических формул. Сухие формулы с объяснением: кратко, лаконично, ничего лишнего. Очень полезная штука при решении задач, знаете ли. Да и на экзамене, когда из головы может «выскочить» именно то, что накануне было жесточайше вызубрено, такая подборка сослужит отличную службу.
На выходных мы сели и подумали о том, что многим студентам было бы неплохо иметь под рукой подборку основных физических формул. Сухие формулы с объяснением: кратко, лаконично, ничего лишнего. Очень полезная штука при решении задач, знаете ли. Да и на экзамене, когда из головы может «выскочить» именно то, что накануне было жесточайше вызубрено, такая подборка сослужит отличную службу.
Больше всего задач обычно задают по трем самым популярным разделам физики. Это механика , термодинамика и молекулярная физика , электричество . Их и возьмем!
Основные формулы по физике динамика, кинематика, статика
Начнем с самого простого. Старое-доброе любимое прямолинейное и равномерное движение.
Формулы кинематики:
Конечно, не будем забывать про движение по кругу, и затем перейдем к динамике и законам Ньютона.
После динамики самое время рассмотреть условия равновесия тел и жидкостей, т.е. статику и гидростатику
Теперь приведем основные формулы по теме «Работа и энергия». Куда же нам без них!
Куда же нам без них!
Основные формулы молекулярной физики и термодинамики
Закончим раздел механики формулами по колебаниям и волнам и перейдем к молекулярной физике и термодинамике.
Коэффициент полезного действия, закон Гей-Люссака, уравнение Клапейрона-Менделеева — все эти милые сердцу формулы собраны ниже.
Кстати! Для всех наших читателей сейчас действует скидка 10% на любой вид работы .
Основные формулы по физике: электричество
Пора переходить к электричеству, хоть его и любят меньше термодинамики. Начинаем с электростатики.
И, под барабанную дробь, заканчиваем формулами для закона Ома, электромагнитной индукции и электромагнитных колебаний.
На этом все. Конечно, можно было бы привести еще целую гору формул, но это ни к чему. Когда формул становится слишком много, можно легко запутаться, а там и вовсе расплавить мозг. Надеемся, наша шпаргалка основных формул по физике поможет решать любимые задачи быстрее и эффективнее.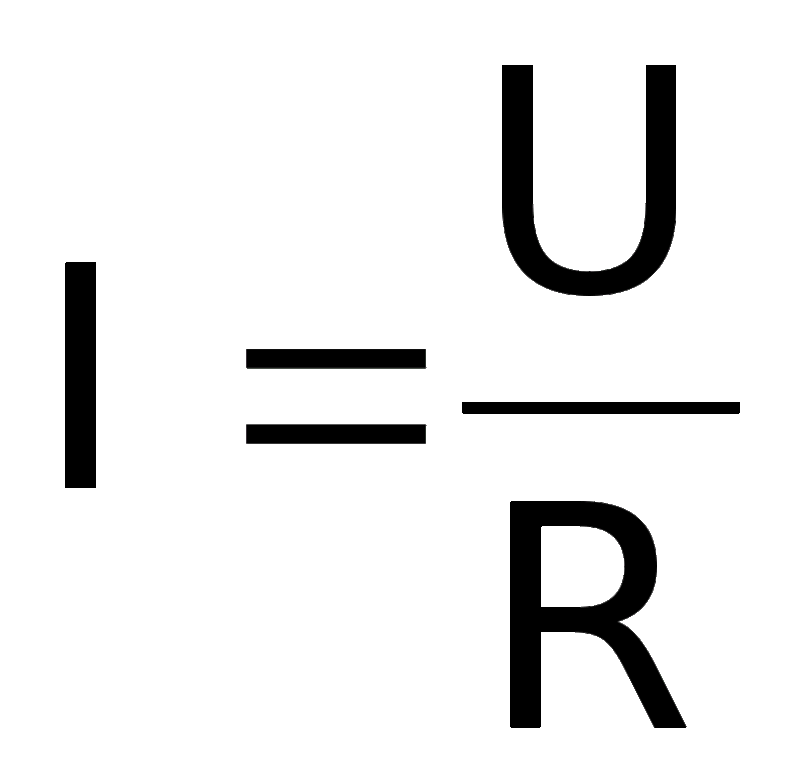 А если хотите уточнить что-то или не нашли нужной формулы: спросите у экспертов студенческого сервиса . Наши авторы держат в голове сотни формул и щелкают задачи, как орешки. Обращайтесь, и вскоре любая задача будет вам «по зубам».
А если хотите уточнить что-то или не нашли нужной формулы: спросите у экспертов студенческого сервиса . Наши авторы держат в голове сотни формул и щелкают задачи, как орешки. Обращайтесь, и вскоре любая задача будет вам «по зубам».
| введение физические величины библиотека ресурсы |
|
7.3: Электрический потенциал и разность потенциалов
- Последнее обновление
- Сохранить как PDF
- Идентификатор страницы
- 4387
- OpenStax
- OpenStax
Цели обучения
К концу этого раздела вы сможете:
- Определять электрический потенциал, напряжение и разность потенциалов
- Дайте определение электрон-вольту
- Расчет электрического потенциала и разности потенциалов по потенциальной энергии и электрическому полю
- Опишите системы, в которых электрон-вольт является полезной единицей
- Применить сохранение энергии к электрическим системам
Напомним, что ранее мы определили электрическое поле как величину, не зависящую от пробного заряда в данной системе, что, тем не менее, позволило бы нам вычислить силу, действующую на произвольный пробный заряд. (Предположение по умолчанию в отсутствие другой информации состоит в том, что пробный заряд положительный.) Мы кратко определили поле для гравитации, но гравитация всегда притягивает, тогда как электрическая сила может быть как притягивающей, так и отталкивающей. Поэтому, хотя потенциальной энергии вполне достаточно в гравитационной системе, удобно определить величину, позволяющую вычислить работу над зарядом, не зависящим от величины заряда. Прямой расчет работы может быть затруднен, поскольку \(W = \vec{F} \cdot \vec{d}\), а направление и величина \(\vec{F}\) могут быть сложными для нескольких зарядов, для объекты необычной формы и по произвольным траекториям. Но мы знаем, что, поскольку \(\vec{F}\), работа и, следовательно, \(\Delta U\) пропорциональна испытательному заряду \(q\). Чтобы иметь физическую величину, независимую от пробного заряда, мы определяем электрический потенциал \(В\) (или просто потенциал, поскольку понимается электрический) быть потенциальной энергией на единицу заряда:
(Предположение по умолчанию в отсутствие другой информации состоит в том, что пробный заряд положительный.) Мы кратко определили поле для гравитации, но гравитация всегда притягивает, тогда как электрическая сила может быть как притягивающей, так и отталкивающей. Поэтому, хотя потенциальной энергии вполне достаточно в гравитационной системе, удобно определить величину, позволяющую вычислить работу над зарядом, не зависящим от величины заряда. Прямой расчет работы может быть затруднен, поскольку \(W = \vec{F} \cdot \vec{d}\), а направление и величина \(\vec{F}\) могут быть сложными для нескольких зарядов, для объекты необычной формы и по произвольным траекториям. Но мы знаем, что, поскольку \(\vec{F}\), работа и, следовательно, \(\Delta U\) пропорциональна испытательному заряду \(q\). Чтобы иметь физическую величину, независимую от пробного заряда, мы определяем электрический потенциал \(В\) (или просто потенциал, поскольку понимается электрический) быть потенциальной энергией на единицу заряда:
Электрический потенциал
Электрическая потенциальная энергия на единицу заряда равна
\[V = \dfrac{U}{q}. \label{eq-1}\]
\label{eq-1}\]
Поскольку U пропорционально q , зависимость от q отменяется. Таким образом, V не зависит от q . Изменение потенциальной энергии \(\Delta U\) имеет решающее значение, поэтому нас интересует разность потенциалов или разность потенциалов \(\Delta V\) между двумя точками, где
Разность электрических потенциалов
Разность электрических потенциалов между точками A и B , \(V_B — V_A\) определяется как изменение потенциальной энергии заряда q , перемещенного от A к B , разделить на стоимость. Единицами разности потенциалов являются джоули на кулон, получившие название вольт (В) в честь Алессандро Вольта.
\[1 \, V = 1 \, J/C \label{eq0}\]
Знакомый термин напряжение — это общее название разности электрических потенциалов. Имейте в виду, что всякий раз, когда указывается напряжение, подразумевается разность потенциалов между двумя точками. Например, у каждой батареи есть две клеммы, а ее напряжение — это разность потенциалов между ними. Более того, точка, которую вы выбираете как ноль вольт, является произвольной. Это аналогично тому факту, что гравитационная потенциальная энергия имеет произвольный нуль, например, уровень моря или, возможно, пол лекционного зала. Стоит подчеркнуть различие между разностью потенциалов и электрической потенциальной энергией.
Имейте в виду, что всякий раз, когда указывается напряжение, подразумевается разность потенциалов между двумя точками. Например, у каждой батареи есть две клеммы, а ее напряжение — это разность потенциалов между ними. Более того, точка, которую вы выбираете как ноль вольт, является произвольной. Это аналогично тому факту, что гравитационная потенциальная энергия имеет произвольный нуль, например, уровень моря или, возможно, пол лекционного зала. Стоит подчеркнуть различие между разностью потенциалов и электрической потенциальной энергией.
Разность потенциалов и электрическая потенциальная энергия
Отношение между разностью потенциалов (или напряжением) и электрической потенциальной энергией определяется выражением
\[\Delta V = \dfrac{\Delta U}{q} \label{eq1}\]
или
\[ \Delta U = q \Delta V. \label{eq2}\]
Напряжение не равно энергии. Напряжение – это энергия на единицу заряда. Таким образом, аккумулятор мотоцикла и автомобильный аккумулятор могут иметь одинаковое напряжение (точнее, одинаковую разность потенциалов между клеммами аккумулятора), но один из них хранит гораздо больше энергии, чем другой, потому что \(\Delta U = q\Delta V\) . Автомобильный аккумулятор может передавать больше заряда, чем аккумулятор мотоцикла, хотя оба являются аккумуляторами на 12 В.
Автомобильный аккумулятор может передавать больше заряда, чем аккумулятор мотоцикла, хотя оба являются аккумуляторами на 12 В.
Пример \(\PageIndex{1}\): расчет энергии
У вас есть мотоциклетная батарея на 12,0 В, которая может заряжать 5000 Кл, и автомобильная батарея на 12,0 В, которая может заряжать 60 000 Кл. Сколько энергии дает каждый? (Предположим, что числовое значение каждого заряда соответствует трем значащим цифрам.)
Стратегия
Если мы говорим, что у нас есть батарея на 12,0 В, это означает, что ее клеммы имеют разность потенциалов 12,0 В. Когда такая батарея перемещает заряд, она проводит заряд через разность потенциалов 12,0 В, и заряду сообщается изменение потенциальной энергии, равное \(\Delta U = q\Delta V\). Чтобы найти выходную энергию, мы умножаем перемещенный заряд на разность потенциалов. 95 \, J. \nonumber\]
Значение
Напряжение и энергия связаны, но это не одно и то же. Напряжения батарей идентичны, но энергия, выдаваемая каждой из них, совершенно разная. Автомобильный аккумулятор имеет гораздо больший двигатель для запуска, чем мотоцикл. Обратите также внимание на то, что по мере разрядки аккумулятора часть его энергии расходуется внутри, и напряжение на его клеммах падает, например, когда фары тускнеют из-за разряженного автомобильного аккумулятора. Энергия, поставляемая батареей, по-прежнему рассчитывается, как в этом примере, но не вся энергия доступна для внешнего использования.
Автомобильный аккумулятор имеет гораздо больший двигатель для запуска, чем мотоцикл. Обратите также внимание на то, что по мере разрядки аккумулятора часть его энергии расходуется внутри, и напряжение на его клеммах падает, например, когда фары тускнеют из-за разряженного автомобильного аккумулятора. Энергия, поставляемая батареей, по-прежнему рассчитывается, как в этом примере, но не вся энергия доступна для внешнего использования.
Упражнение \(\PageIndex{1}\)
Сколько энергии имеет батарея AAA 1,5 В, которая может двигаться на 100 C?
- Ответить
\(\Дельта U = q\Дельта V = (100 \, С)(1,5 \, В) = 150 \, Дж \)
Обратите внимание, что энергии, рассчитанные в предыдущем примере, являются абсолютными значениями. Изменение потенциальной энергии для батареи отрицательно, так как она теряет энергию. Эти батареи, как и многие электрические системы, на самом деле перемещают отрицательный заряд, в частности электроны. Батареи отталкивают электроны от своих отрицательных клемм ( A ) через любую задействованную схему и притяните их к их положительным клеммам ( B ), как показано на рисунке \(\PageIndex{1}\). Изменение потенциала равно \(\Delta V = V_B — V_A = +12 \, V\), а заряд q отрицателен, так что \(\Delta U = q \Delta V\) отрицательна, что означает потенциальная энергия батареи уменьшилась, когда q переместилось с A на B .
Батареи отталкивают электроны от своих отрицательных клемм ( A ) через любую задействованную схему и притяните их к их положительным клеммам ( B ), как показано на рисунке \(\PageIndex{1}\). Изменение потенциала равно \(\Delta V = V_B — V_A = +12 \, V\), а заряд q отрицателен, так что \(\Delta U = q \Delta V\) отрицательна, что означает потенциальная энергия батареи уменьшилась, когда q переместилось с A на B .
 Внутри батареи движутся как положительные, так и отрицательные заряды.
Внутри батареи движутся как положительные, так и отрицательные заряды.Пример \(\PageIndex{2}\): Сколько электронов проходит через фару каждую секунду?
Когда автомобильный аккумулятор на 12,0 В питает одну фару мощностью 30,0 Вт, сколько электронов проходит через него каждую секунду?
Стратегия
Чтобы найти количество электронов, мы должны сначала найти заряд, который перемещается за 1,00 с. Перемещенный заряд связан с напряжением и энергией через уравнения \(\Delta U = q \Delta V\). Лампа мощностью 30,0 Вт потребляет 30,0 Дж в секунду. Поскольку батарея теряет энергию, мы имеем \(\Delta U = — 30 \, Дж\) и, поскольку электроны движутся от отрицательной клеммы к положительной, мы видим, что \(\Delta V = +12,0 \, V \).
Решение
Чтобы найти перемещенный заряд q , решаем уравнение \(\Delta U = q\Delta V\):
\[q = \dfrac{\Delta U}{\Delta V }.\]
Вводя значения для \(\Delta U\) и \(\Delta V\), получаем
\[q = \dfrac{-30. {-19{19} \, электроны.\]
{-19{19} \, электроны.\]
Значение
Это очень большое число. Неудивительно, что мы обычно не наблюдаем отдельных электронов, когда их так много в обычных системах. Фактически, электричество использовалось в течение многих десятилетий, прежде чем было установлено, что движущиеся заряды во многих случаях были отрицательными. Положительный заряд, движущийся в направлении, противоположном направлению отрицательного заряда, часто производит идентичные эффекты; это затрудняет определение того, что движется или движутся ли оба. 9{19} \, электроны\)
Электрон-Вольт
Энергия одного электрона в макроскопических ситуациях, как в предыдущем примере, очень мала — крошечная доля джоуля. Но в субмикроскопическом масштабе такая энергия, приходящаяся на одну частицу (электрон, протон или ион), может иметь большое значение. Например, даже крошечной доли джоуля может быть достаточно для того, чтобы эти частицы разрушили органические молекулы и нанесли вред живым тканям. Частица может нанести ущерб при прямом столкновении или создать вредное рентгеновское излучение, которое также может нанести ущерб. Полезно иметь единицу энергии, связанную с субмикроскопическими эффектами.
Частица может нанести ущерб при прямом столкновении или создать вредное рентгеновское излучение, которое также может нанести ущерб. Полезно иметь единицу энергии, связанную с субмикроскопическими эффектами.
На рисунке \(\PageIndex{2}\) показана ситуация, связанная с определением такой единицы энергии. Электрон ускоряется между двумя заряженными металлическими пластинами, как в телевизионной трубке старой модели или в осциллографе. Электрон приобретает кинетическую энергию, которая затем преобразуется в другую форму — например, в свет в телевизионной трубке. (Обратите внимание, что с точки зрения энергии «вниз» для электрона «вверх» для положительного заряда.) Поскольку энергия связана с напряжением соотношением \(\Delta U = q\Delta V\), мы можем думать о джоуле как кулон-вольт.
Рисунок \(\PageIndex{2}\): Типичная электронная пушка ускоряет электроны, используя разность потенциалов между двумя разделенными металлическими пластинами. По закону сохранения энергии кинетическая энергия должна равняться изменению потенциальной энергии, поэтому \(KE = qV\). Энергия электрона в электрон-вольтах численно равна напряжению между пластинами. Например, разность потенциалов в 5000 В производит электроны с энергией 5000 эВ. Концептуальная конструкция, а именно две параллельные пластины с отверстием в одной, показана на (а), а реальная электронная пушка показана на (б). 9{-19} \, J.\]
Энергия электрона в электрон-вольтах численно равна напряжению между пластинами. Например, разность потенциалов в 5000 В производит электроны с энергией 5000 эВ. Концептуальная конструкция, а именно две параллельные пластины с отверстием в одной, показана на (а), а реальная электронная пушка показана на (б). 9{-19} \, J.\]Электрон, ускоренный разностью потенциалов в 1 В, получает энергию 1 эВ. Отсюда следует, что электрон, ускоренный через 50 В, приобретает 50 эВ. Разность потенциалов 100 000 В (100 кВ) дает электрону энергию 100 000 эВ (100 кэВ) и так далее. Точно так же ион с двойным положительным зарядом, ускоренный до 100 В, получает 200 эВ энергии. Эти простые соотношения между ускоряющим напряжением и зарядами частиц делают электрон-вольт простой и удобной единицей энергии в таких обстоятельствах.
Электрон-вольт обычно используется в субмикроскопических процессах — химические валентные энергии, молекулярные и ядерные энергии связи входят в число величин, часто выражаемых в электрон-вольтах. Например, для разрушения некоторых органических молекул требуется около 5 эВ энергии. Если протон ускорить из состояния покоя через разность потенциалов 30 кВ, он приобретает энергию 30 кэВ (30 000 эВ) и может разорвать до 6000 таких молекул \((30 000 \, эВ \, : \, 5 \, эВ \, на \, молекула = 6000 \, молекул)\). Энергия ядерного распада составляет порядка 1 МэВ (1 000 000 эВ) на событие и, таким образом, может привести к значительным биологическим повреждениям.
Например, для разрушения некоторых органических молекул требуется около 5 эВ энергии. Если протон ускорить из состояния покоя через разность потенциалов 30 кВ, он приобретает энергию 30 кэВ (30 000 эВ) и может разорвать до 6000 таких молекул \((30 000 \, эВ \, : \, 5 \, эВ \, на \, молекула = 6000 \, молекул)\). Энергия ядерного распада составляет порядка 1 МэВ (1 000 000 эВ) на событие и, таким образом, может привести к значительным биологическим повреждениям.
Сохранение энергии
Полная энергия системы сохраняется, если нет чистого прибавления (или вычитания) за счет работы или теплопередачи. Для консервативных сил, таких как электростатическая сила, закон сохранения энергии утверждает, что механическая энергия является константой.
Механическая энергия представляет собой сумму кинетической энергии и потенциальной энергии системы; то есть \(K + U = константа\). Потеря U для заряженной частицы становится увеличением ее K . Сохранение энергии выражается в форме уравнения как
Сохранение энергии выражается в форме уравнения как
\[K + U = константа\] или \[K_i + U_i = K_f + U_f\]
, где i и f обозначают начальные и конечные условия. Как мы уже много раз убеждались, рассмотрение энергии может дать нам понимание и облегчить решение проблем.
Пример \(\PageIndex{3}\): преобразование электрической потенциальной энергии в кинетическую
Рассчитайте конечную скорость свободного электрона, ускоренного из состояния покоя при разности потенциалов 100 В. (Предположим, что это численное значение с точностью до три значащие цифры.) 96 \, м/с.\]
Значимость
Обратите внимание, что и заряд, и начальное напряжение отрицательны, как на рисунке \(\PageIndex{2}\). Из обсуждения электрического заряда и электрического поля мы знаем, что электростатические силы, действующие на малые частицы, обычно очень велики по сравнению с силой гравитации. Большая конечная скорость подтверждает, что гравитационной силой здесь действительно можно пренебречь. Большая скорость также указывает на то, насколько легко ускорять электроны при малых напряжениях из-за их очень малой массы. Напряжения, намного превышающие 100 В в этой задаче, обычно используются в электронных пушках. Эти более высокие напряжения создают настолько большие скорости электронов, что необходимо учитывать эффекты специальной теории относительности, которые будут обсуждаться в другом месте. Вот почему мы рассматриваем низкое напряжение (точно) в этом примере.
Большая скорость также указывает на то, насколько легко ускорять электроны при малых напряжениях из-за их очень малой массы. Напряжения, намного превышающие 100 В в этой задаче, обычно используются в электронных пушках. Эти более высокие напряжения создают настолько большие скорости электронов, что необходимо учитывать эффекты специальной теории относительности, которые будут обсуждаться в другом месте. Вот почему мы рассматриваем низкое напряжение (точно) в этом примере.
Упражнение \(\PageIndex{3}\)
Как изменится этот пример с позитроном? Позитрон идентичен электрону, за исключением того, что заряд положительный.
- Ответить
Он будет двигаться в противоположном направлении, что не повлияет на представленные расчеты.
Напряжение и электрическое поле
До сих пор мы исследовали взаимосвязь между напряжением и энергией. Теперь мы хотим исследовать взаимосвязь между напряжением и электрическим полем. 2 } \шляпа{г}\). Когда мы вычисляем интеграл 92} dr = \dfrac{kq}{r} — \dfrac{kq}{\infty} = \dfrac{kq}{r}.\]
2 } \шляпа{г}\). Когда мы вычисляем интеграл 92} dr = \dfrac{kq}{r} — \dfrac{kq}{\infty} = \dfrac{kq}{r}.\]
Этот результат,
\[V_r = \dfrac{kq} {r}\]
— стандартная форма потенциала точечного заряда. Это будет рассмотрено далее в следующем разделе.
Чтобы исследовать другой интересный частный случай, предположим, что однородное электрическое поле \(\vec{E}\) создается путем помещения разности потенциалов (или напряжения) \(\Delta V\) на две параллельные металлические пластины, обозначенные A и B (рис. \(\PageIndex{3}\)). Изучение этой ситуации подскажет нам, какое напряжение необходимо для создания определенной напряженности электрического поля. Это также раскроет более фундаментальную связь между электрическим потенциалом и электрическим полем.
Рисунок \(\PageIndex{3}\): Соотношение между V и E для параллельных проводящих пластин равно \(E = V/d\). (Обратите внимание, что \(\Delta V = V_{AB}\) по величине. Для заряда, который перемещается с пластины A с более высоким потенциалом на пластину B с более низким потенциалом, необходимо включить знак минус следующим образом. : \(- \Delta V = V_A — V_B = V_{AB}\).)
Для заряда, который перемещается с пластины A с более высоким потенциалом на пластину B с более низким потенциалом, необходимо включить знак минус следующим образом. : \(- \Delta V = V_A — V_B = V_{AB}\).) С точки зрения физики, либо \(\Delta V\), либо \(\vec{E}\) можно использовать для описать любое взаимодействие между зарядами. Однако \(\Delta V\) является скалярной величиной и не имеет направления, тогда как \(\vec{E}\) является векторной величиной, имеющей как величину, так и направление. (Обратите внимание, что величина электрического поля, скалярная величина, представлена E .) Соотношение между \(\Delta V\) и \(\vec{E}\) выявляется путем расчета работы, совершаемой электрической силой при перемещении заряда из точки A в точку B . Но, как отмечалось ранее, произвольное распределение заряда требует исчисления. Поэтому мы рассматриваем однородное электрическое поле как интересный частный случай.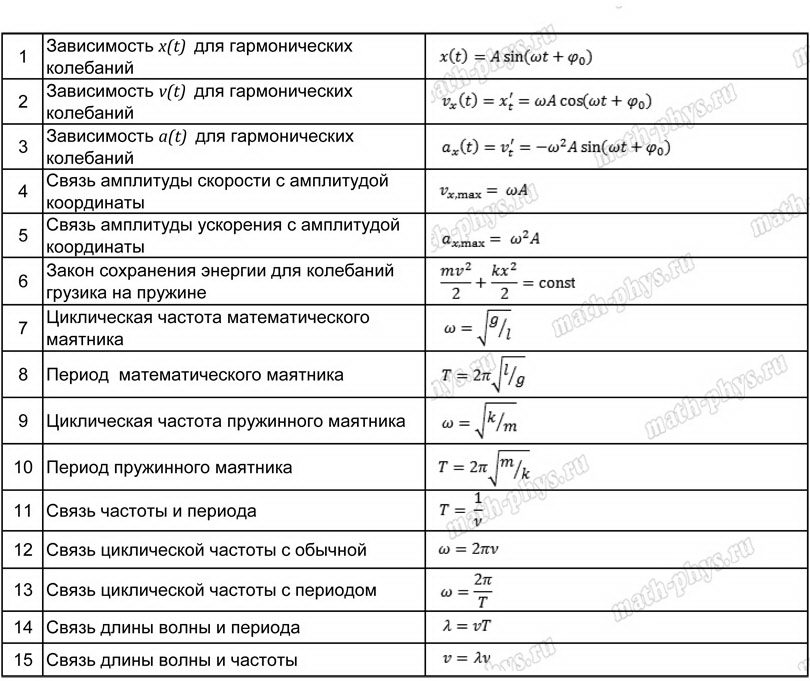
Работа, совершаемая электрическим полем на рисунке \(\PageIndex{3}\) для перемещения положительного заряда q от A положительной пластины с более высоким потенциалом к B , отрицательная пластина, более низкий потенциал, равна
\[W = — \Delta U = — q\Delta V.\]
Разность потенциалов между точками A и B равна
\[ — \Delta V = — (V_B — V_A) = V_A — V_B = V_{AB}.\]
Ввод этого выражения в выражение для работы дает
\[W = qV_{AB}.\]
Работа равна \(W = \vec{F} \cdot \vec{d} = Fd \, cos \, \theta\): здесь \(cos \, \theta = 1\), так как путь параллелен полю. Таким образом, \(W = Fd\). Поскольку \(F = qE\), мы видим, что \(W = qEd\).
Подстановка этого выражения для работы в предыдущее уравнение дает
\[qEd = qV_{AB}.\]
Заряд аннулируется, поэтому мы получаем для напряжения между точками A и B .
Только в однородном E-поле: \[V_{AB} = Ed\] \[E = \dfrac{V_{AB}}{d}\], где d — расстояние от A до B или расстояние между пластинами на рисунке \(\PageIndex{3}\). Обратите внимание, что это уравнение подразумевает, что единицами измерения электрического поля являются вольты на метр. Мы уже знаем, что единицами измерения электрического поля являются ньютоны на кулон; таким образом, справедливо следующее соотношение между единицами: 9B \vec{E} \cdot d\vec{l}.\]
В качестве демонстрации из этого мы можем вычислить разность потенциалов между двумя точками ( A и B ), равноудаленными от точечного заряда q в начале координат, как показано на рисунке \(\PageIndex{4}\).
Рисунок \(\PageIndex{4}\): Дуга для расчета разности потенциалов между двумя точками, равноудаленными от точечного заряда в начале координат. Для этого проинтегрируем дугу окружности постоянного радиуса r между 96 В/м\). Выше этого значения поле создает в воздухе достаточную ионизацию, чтобы сделать воздух проводником. Это позволяет разряду или искре, которая уменьшает поле. Чему тогда равно максимальное напряжение между двумя параллельными проводящими пластинами, разделенными 2,5 см сухого воздуха?
Выше этого значения поле создает в воздухе достаточную ионизацию, чтобы сделать воздух проводником. Это позволяет разряду или искре, которая уменьшает поле. Чему тогда равно максимальное напряжение между двумя параллельными проводящими пластинами, разделенными 2,5 см сухого воздуха?
Стратегия
Заданы максимальное электрическое поле E между пластинами и расстояние d между ними. Мы можем использовать уравнение \(V_{AB} = Ed\) для расчета максимального напряжения. 94 \, V\] или \[V_{AB} = 75 \, кВ.\]
(Ответ приведен только до двух цифр, так как максимальная напряженность поля является приблизительной.)
Значение
Один Одним из следствий этого результата является то, что требуется около 75 кВ, чтобы искра перескочила через зазор в 2,5 см (1 дюйм), или 150 кВ для 5-сантиметровой искры. Это ограничивает напряжения, которые могут существовать между проводниками, например, на линии электропередачи. Меньшее напряжение может вызвать искру, если на поверхности есть шипы, поскольку острые точки имеют большую напряженность поля, чем гладкие поверхности. Влажный воздух разрушается при более низкой напряженности поля, а это означает, что меньшее напряжение вызовет скачок искры во влажном воздухе. Наибольшее напряжение может создаваться статическим электричеством в сухие дни (Рисунок \(\PageIndex{5}\)).
Меньшее напряжение может вызвать искру, если на поверхности есть шипы, поскольку острые точки имеют большую напряженность поля, чем гладкие поверхности. Влажный воздух разрушается при более низкой напряженности поля, а это означает, что меньшее напряжение вызовет скачок искры во влажном воздухе. Наибольшее напряжение может создаваться статическим электричеством в сухие дни (Рисунок \(\PageIndex{5}\)).
 (кредит b: модификация работы Джека Коллинза)
(кредит b: модификация работы Джека Коллинза)Пример \(\PageIndex{1B}\): поле и сила внутри электронной пушки
Электронная пушка (рис. \(\PageIndex{2}\)) имеет параллельные пластины, разделенные расстоянием 4,00 см, и дает электронам энергию 25,0 кэВ. . а) Чему равна напряженность электрического поля между пластинами? б) С какой силой это поле будет действовать на кусок пластика с зарядом \(0,500 мкКл\), который попадет между пластинами?
Стратегия
Поскольку напряжение и расстояние между пластинами заданы, напряженность электрического поля можно рассчитать непосредственно из выражения \(E = \frac{V_{AB}}{d}\). Зная напряженность электрического поля, мы можем найти силу, действующую на заряд, используя \(\vec{F} = q\vec{E}\). Поскольку электрическое поле имеет только одно направление, мы можем записать это уравнение в терминах величин \(F = qE\). 95 В/м) = 0,313 \, Н.\]
Значение Обратите внимание, что единицами измерения являются ньютоны, поскольку \(1 \, В/м = 1 \, Н/Кл\). Поскольку электрическое поле между пластинами однородно, сила, действующая на заряд, одинакова независимо от того, где находится заряд между пластинами.
Поскольку электрическое поле между пластинами однородно, сила, действующая на заряд, одинакова независимо от того, где находится заряд между пластинами.
Пример \(\PageIndex{4C}\): расчет потенциала точечного заряда ) расстояние \(a = 4,0 \, см\) от 92} \hat{r} \cdot r\hat{\varphi}d\varphi\), но \(\hat{r} \cdot \hat{\varphi} = 0\) и, следовательно, \(\Delta V = 0\). Складывая две части вместе, мы получаем 300 В.
Значение
Мы продемонстрировали использование интегральной формы разности потенциалов для получения числового результата. Обратите внимание, что в этой конкретной системе мы могли бы также использовать формулу для потенциала, обусловленного точечным зарядом в двух точках, и просто взять разницу.
Упражнение \(\PageIndex{4}\)
Как из примеров зависит энергия удара молнии в зависимости от высоты облаков над землей? Рассмотрим систему облако-земля как две параллельные пластины.
- Ответить
При фиксированной максимальной напряженности электрического поля потенциал, при котором происходит удар, увеличивается с увеличением высоты над землей.
 Следовательно, каждый электрон будет нести больше энергии. Определение того, есть ли влияние на общее число электронов, лежит в будущем.
Следовательно, каждый электрон будет нести больше энергии. Определение того, есть ли влияние на общее число электронов, лежит в будущем.
Прежде чем приступить к рассмотрению задач, связанных с электростатикой, мы предлагаем стратегию решения проблем по этой теме.
Стратегия решения проблем: электростатика
- Изучите ситуацию, чтобы определить, связано ли это со статическим электричеством; это может касаться отдельных стационарных зарядов, сил между ними и создаваемых ими электрических полей.
- Определите интересующую систему. Это включает в себя указание количества, мест и типов связанных сборов.
- Определите, что именно нужно определить в задаче (идентифицируйте неизвестные). Письменный список полезен. Определите, следует ли рассматривать кулоновскую силу напрямую — если да, то может быть полезно нарисовать диаграмму свободного тела, используя силовые линии электрического поля.
- Составьте список того, что дано или может быть выведено из заявленной проблемы (укажите известное).
 Например, важно отличать кулоновскую силу F от электрического поля E .
Например, важно отличать кулоновскую силу F от электрического поля E . - Решите соответствующее уравнение для определяемой величины (неизвестной) или начертите линии поля в соответствии с запросом.
- Проверьте ответ, чтобы убедиться, что он разумен: Имеет ли он смысл? Верны ли единицы измерения и разумны ли задействованные числа?
Эта страница под названием 7.3: Electric Potential and Potential Difference распространяется под лицензией CC BY 4.0 и была создана, изменена и/или курирована OpenStax с помощью исходного контента, который был отредактирован в соответствии со стилем и стандартами платформы LibreTexts; подробная история редактирования доступна по запросу.
- Наверх
- Была ли эта статья полезной?
- Тип изделия
- Раздел или Страница
- Автор
- ОпенСтакс
- Лицензия
- СС BY
- Версия лицензии
- 4,0
- Программа OER или Publisher
- ОпенСтакс
- Показать оглавление
- нет
- Теги
- электрический потенциал
- разность электрических потенциалов
- электрон-вольт
- источник@https://openstax.
 org/details/books/university-physics-volume-2
org/details/books/university-physics-volume-2 - напряжение
Общая физика II
Закон Кулона говорит нам о силе между двумя точками обвинения. Наш вариант сообщает нам Электрическое поле из-за одноточечный заряд . Что нам делать, если у нас есть непрерывных распределение заряда? Мы можем суммировать электрическое поле вызвано каждой крошечной, бесконечно малой частью заряда распределение. Это означает интеграл по распределению заряда:
Для одноточечного заряда Q мы имели
, где r — расстояние от заряда Q. Помните, что E — это всего лишь величина электрического поля; мы должны позаботиться о
свой вектор природа отдельно! Это важно! Теперь у нас есть
распределение заряда, и мы должны заменить Q на dQ и E на dE
— и позаботьтесь о направлении E .
r, расстояние от крошечного, элементарного, бесконечно малого заряда dQ к рассматриваемому вопросу, является функцией того, где этот заряд dQ является. И что значит «интегрировать по заряду dQ»? Мы знать, как интегрировать по переменной, такой как dx, или по плоскости, такой как dA = dx dy или dA = 2 r dr или dA = r d dr или объем типа dV = dx dy dz. Так что нам нужно будет изменить с этого символического заряда dQ на плотность заряда умноженный на некоторый пространственный дифференциал,
дQ = дА
дQ = дВ
Посмотрите на Пример 23.7 в учебнике Serway и Beichner (стр. 724): Стержень длиной имеет равномерный заряд на единицу длины и полный заряд Q. Вычислить электрическое поле в точке P вдоль оси стержня на расстоянии d от одного конца.
Чему равно электрическое поле в точке P из-за маленького кусочка бесплатно Q находится в позиции x, как показано на рисунке?
Проведем интегрирование от x = d до x = d + так нам нужно изменить это небольшое количество заряда Q на малую длину x,
Е = к (х) / х 2
где
dE = k ( dx) / x 2
dE = k (dx / х 2 )
Как насчет других геометрий?
См. Пример 23.8 на странице 724 текста Сервея и Бейхнера.
Найти электрическое поле, создаваемое кольцом с зарядом : Кольцо радиусом a
имеет однородную плотность заряда с полным зарядом Q. Рассчитайте электрическую
поле вдоль оси кольца в точке P, на расстоянии x от
центр кольца.
Пример 23.8 на странице 724 текста Сервея и Бейхнера.
Найти электрическое поле, создаваемое кольцом с зарядом : Кольцо радиусом a
имеет однородную плотность заряда с полным зарядом Q. Рассчитайте электрическую
поле вдоль оси кольца в точке P, на расстоянии x от
центр кольца.
Плотность заряда
Помните, наше уравнение для электрического поля относится к величина электрического поля. Рассмотрим небольшой кусочек зарядить dq, как показано на схеме. Поскольку этот заряд dq равен там в точке P существует электрическое поле dE в направлении показано. Компонент dEx этого электрического поля вдоль направление оси перпендикулярно плоскости кольца
dE x = dE (x/r)
dE x = [k dq/r 2 ] (x/r)
dE х = [k dq/r 3 ] х
dE x = [k x dq/r 3 ]
dE x = [k x/r 3 ] dq
Обратите внимание, что в этой геометрии после указания радиуса кольца a
и позицию x, полностью определяющую r. г и х сделать не менять как
интегрируем по dq.
г и х сделать не менять как
интегрируем по dq.
[[ Помните, что SQRT() означает «квадратный корень из ()», потому что это проще
чтобы я печатал. ]]
r 3 = (a 2 + x 2 ) 3/2
1/r 3 = 1/(a 2 + х 2 ) 3/2
Помните, х и а равно , а не переменных.
Как насчет компонента E, который перпендикулярен к
это направление? По симметрии этот компонент равен нулю .
Из диаграммы видно, что для каждого элемента заряда dq,
на напротив есть еще один элемент заряда dq сторона кольца, создающая электрическое поле, которое просто отменяет первый — то есть их компоненты перпендикулярно ось симметрии как раз отменяет .
Обратите внимание, что их компоненты вдоль оси не отменяют
ибо они лежат в одном и том же направлении.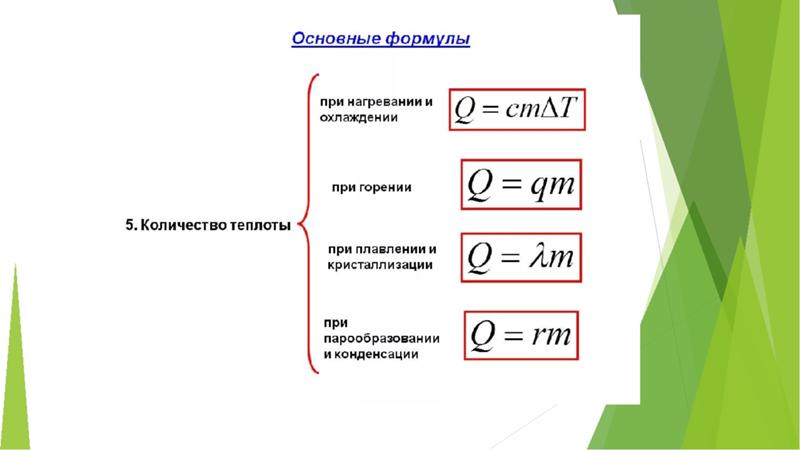 Диаграммы очень
важный. Не начинайте писать уравнения, пока не сделаете
хорошие, четкие, полные схемы!
Диаграммы очень
важный. Не начинайте писать уравнения, пока не сделаете
хорошие, четкие, полные схемы!
Теперь, когда мы рассмотрели электрическое поле из-за кольца заряда, мы можем опираться на него, расширять наши идеи и смотреть на электрические поле из-за диск бесплатно. См. пример 23.9 на стр. 725 учебника Серуэя и Бейхнера.
Диск радиусом R имеет равномерный заряд на единицу площади. Вычислите электрическое поле в точке P, лежащей вдоль центральной оси диска и на расстоянии x от его центра.
Рассмотрим кольцо заряда, как показано здесь. Кольцо имеет радиусом r и толщиной dr и несет заряд dq. Но этот заряд dq как раз пропорционален площади,
дк = [С др]
дк = [ (2 г) др ]
дкв = 2 р др
Вспомните, что мы только что сделали в предыдущем примере. За
заряд Q на кольце радиуса r, мы нашли, что электрическое поле
на расстоянии x от плоскости кольца было
За
заряд Q на кольце радиуса r, мы нашли, что электрическое поле
на расстоянии x от плоскости кольца было
Это именно то, что у нас есть сейчас, за исключением того, что у нас есть заряд dq вместо Q и кольцо имеет радиус r вместо a. Итак, мы могу написать
Будь осторожен; пределы интегрирования важны.
Мы могли бы найти это в таблице интегралов. Но переменная замена по-прежнему довольно прямолинейна и прямолинейна;
Этот результат действителен только для x > 0 и должен быть немного изменен для х < 0.
Электрическое поле | Линии электронного поля | ||
 ; все права защищены
; все права защищенысил — Формула электрического поля $E=F/q$
$\begingroup$
Если следовать формуле $E=F/q$, то получается, что чем больше сила, тем больше и электрическое поле, но если заряд, на который действует сила, больше, электрическое поле как-то уменьшается? Как это понять?
- силы
- электростатика
- электрические поля
- заряд
$\endgroup$
$\begingroup$
Я бы сказал, что вы смотрите на это задом наперед; лучше представить себе, что электрические поля создают силы на зарядах. Для данного электрического поля чем больше заряд, тем больше сила; чтобы увеличить силу, действующую на заряд, необходимо также увеличить электрическое поле; таким образом, для данной силы, чем больше заряд, тем меньше электрическое поле. Это аналогично массе в том смысле, что разные массы (скажем, A больше, чем B), подверженные действию одной и той же силы, будут иметь разные ускорения (B больше, чем A).
$\endgroup$
$\begingroup$
Это отличный пример того, как каузальное понимание физики не является явно очевидным, если вы наивно смотрите на математическое выражение.
То, что вы говорите , является верным, но правильно сформулировано следующим образом: для заданной силы $F$ на заряд $q$ электрическое поле $E$ (в месте расположения заряда) будет увеличиваться по мере уменьшения заряда $q$. Другими словами, это говорит о том, что для создания той же силы при меньшем заряде вам нужно более сильное электрическое поле. Как видите, никакой тайны здесь нет, если понимать так.
Конечно, как вы уже понимаете (как следует из вашего вопроса), электрическое поле, действующее на заряд, не меняется, если вы только меняете пробный заряд, потому что оно определяется внешней конфигурацией зарядов. С физической точки зрения, когда вы меняете только пробный заряд, изменяется только сила, действующая на него. Однако $E\propto 1/q$ говорит вам, что если вы хотите поддерживать постоянную силу на изменяющемся пробном заряде, вам нужно изменить электрическое поле обратно пропорционально значению пробного заряда (через изменение внешней конфигурации зарядов, создающих электрическое поле).
Однако $E\propto 1/q$ говорит вам, что если вы хотите поддерживать постоянную силу на изменяющемся пробном заряде, вам нужно изменить электрическое поле обратно пропорционально значению пробного заряда (через изменение внешней конфигурации зарядов, создающих электрическое поле).
$\endgroup$
$\begingroup$
Если вы, скажем, удвоите заряд $q$, то вы, естественно, также увидите удвоенную силу $F$. Потому что для поля $E$ теперь будет «вдвое больше» заряда для «втягивания».
Но если вы хотите, чтобы сила была одинаковой, вам придется каким-то образом уменьшить напряженность поля. Например, изменив источник, который вызывает поле. В противном случае невозможно изменить заряд , а поддерживать силу постоянной.
Возможно, ваше замешательство вызвано ошибочным предположением, что сила может поддерживаться постоянной при нормальных, неограниченных обстоятельствах. И, таким образом, изменение заряда, казалось бы, меняет поле. Конечно, это математически возможно, но физически не возможно как . Не без того, чтобы вы каким-то образом активно меняли поле. Скорее, это было бы поле, постоянное при таких обстоятельствах, и сила изменялась бы при изменении заряда.
Конечно, это математически возможно, но физически не возможно как . Не без того, чтобы вы каким-то образом активно меняли поле. Скорее, это было бы поле, постоянное при таких обстоятельствах, и сила изменялась бы при изменении заряда.
$\endgroup$
$\begingroup$
В определении электрического поля используется E = F/q, как вы показываете, но вы упускаете остальную часть определения, а именно то, что это отношение F/q в пределе, когда q -> 0. Это сделано для того, чтобы пробный заряд не нарушает распределения заряда, создающего электрическое поле.
$\endgroup$
$\begingroup$
Я думаю, вас смущает то, что означают $F$ и $q$ в уравнении для электрического поля:
$$E = \frac{F}{q} \tag 1$$
где $q$ — тестовый заряд . Испытательный заряд представляет собой заряд очень малой величины, настолько малый, что он не влияет на электрическое поле , но может использоваться для измерения его напряженности.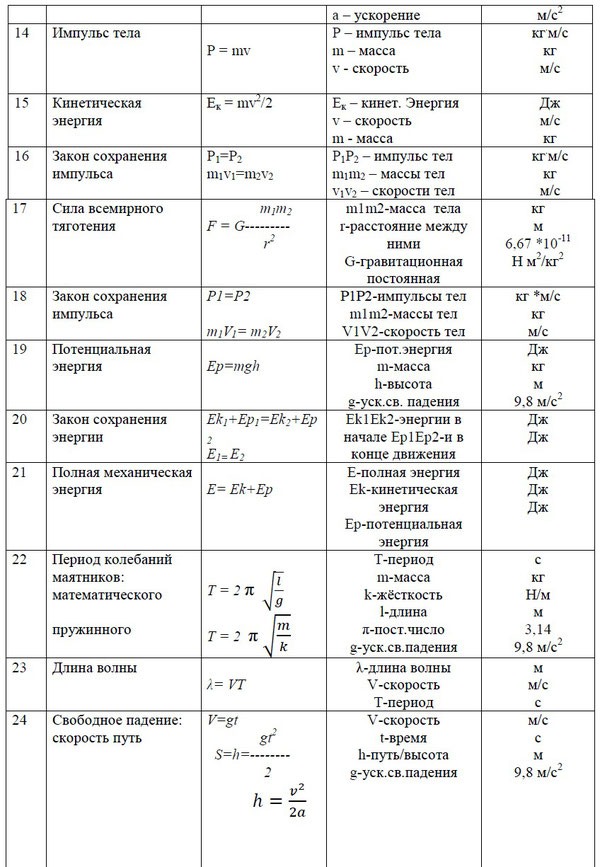

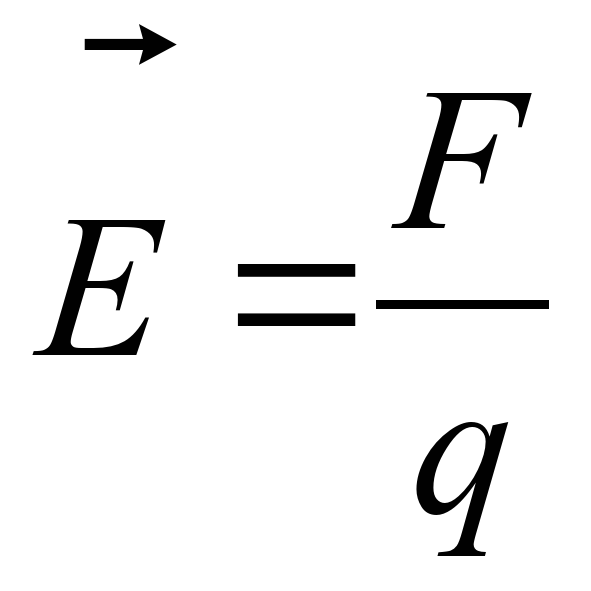
 Каждый РТ можно посещать по два раза, чтобы прорешать оба варианта. Опять же на ЦТ, кроме умения быстро и качественно решать задачи, и знания формул и методов необходимо также уметь правильно спланировать время, распределить силы, а главное правильно заполнить бланк ответов, не перепутав ни номера ответов и задач, ни собственную фамилию. Также в ходе РТ важно привыкнуть к стилю постановки вопросов в задачах, который на ЦТ может показаться неподготовленному человеку очень непривычным.
Каждый РТ можно посещать по два раза, чтобы прорешать оба варианта. Опять же на ЦТ, кроме умения быстро и качественно решать задачи, и знания формул и методов необходимо также уметь правильно спланировать время, распределить силы, а главное правильно заполнить бланк ответов, не перепутав ни номера ответов и задач, ни собственную фамилию. Также в ходе РТ важно привыкнуть к стилю постановки вопросов в задачах, который на ЦТ может показаться неподготовленному человеку очень непривычным. Для этого нужно всего ничего, а именно: посвящать подготовке к ЦТ по физике и математике, изучению теории и решению задач по три-четыре часа каждый день. Дело в том, что ЦТ это экзамен, где мало просто знать физику или математику, нужно еще уметь быстро и без сбоев решать большое количество задач по разным темам и различной сложности. Последнему научиться можно только решив тысячи задач.
Для этого нужно всего ничего, а именно: посвящать подготовке к ЦТ по физике и математике, изучению теории и решению задач по три-четыре часа каждый день. Дело в том, что ЦТ это экзамен, где мало просто знать физику или математику, нужно еще уметь быстро и без сбоев решать большое количество задач по разным темам и различной сложности. Последнему научиться можно только решив тысячи задач. Каждый РТ можно посещать по два раза, чтобы прорешать оба варианта. Опять же на ЦТ, кроме умения быстро и качественно решать задачи, и знания формул и методов необходимо также уметь правильно спланировать время, распределить силы, а главное правильно заполнить бланк ответов, не перепутав ни номера ответов и задач, ни собственную фамилию. Также в ходе РТ важно привыкнуть к стилю постановки вопросов в задачах, который на ЦТ может показаться неподготовленному человеку очень непривычным.
Каждый РТ можно посещать по два раза, чтобы прорешать оба варианта. Опять же на ЦТ, кроме умения быстро и качественно решать задачи, и знания формул и методов необходимо также уметь правильно спланировать время, распределить силы, а главное правильно заполнить бланк ответов, не перепутав ни номера ответов и задач, ни собственную фамилию. Также в ходе РТ важно привыкнуть к стилю постановки вопросов в задачах, который на ЦТ может показаться неподготовленному человеку очень непривычным. кин. энергия молекул одноатомного газа Ek=3/2∙kT
кин. энергия молекул одноатомного газа Ek=3/2∙kT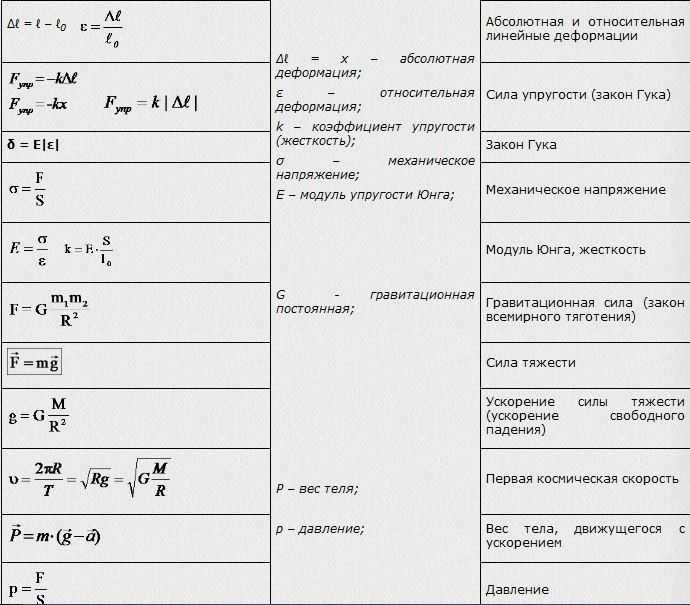 поля точечного заряда E=k∙q/R 2
поля точечного заряда E=k∙q/R 2 контура T=2π ∙√LC
контура T=2π ∙√LC


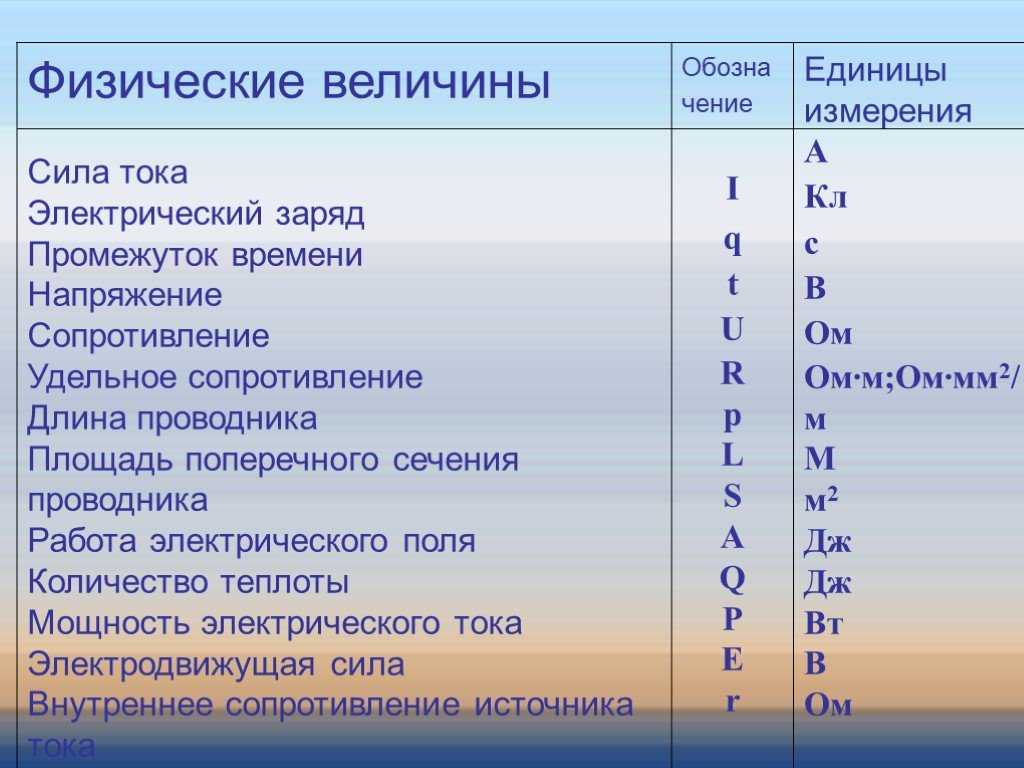

 и длине 1 м имеет электрическую прово-димость, равную 1 См.
и длине 1 м имеет электрическую прово-димость, равную 1 См.

 Следовательно, каждый электрон будет нести больше энергии. Определение того, есть ли влияние на общее число электронов, лежит в будущем.
Следовательно, каждый электрон будет нести больше энергии. Определение того, есть ли влияние на общее число электронов, лежит в будущем. Например, важно отличать кулоновскую силу F от электрического поля E .
Например, важно отличать кулоновскую силу F от электрического поля E . org/details/books/university-physics-volume-2
org/details/books/university-physics-volume-2