Теория бернулли: Ошибка 404. Запрашиваемая страница не найдена

Комбинаторика и теория вероятностей для трейдинга (Часть IV): Логика Бернулли

Содержание

• Введение
• Почему правильное представление данных очень важно для анализа?
• Двойные состояния
• Множественные состояния
• Программная реализация множественных состояний
• Заключение
• Ссылки

Введение

В прошлых статьях цикла я описывал фракталы как инструмент для описания рынка и в частности, для описания ценообразования. Эта модель отлично описывает рынок, что было подтверждено с помощью вычислений и симуляций. Все это затевалось не только ради того, чтобы описать простейшие формы ценообразования, но и для того, чтобы иметь возможность в дальнейшем описывать любые векторные ряды, которые имеют схожий набор параметров что и ценообразование. Ведь действительно, если подумать, а что же такое трейд в общем случае, то окажется, что трейд, это такой же кусочек рынка, который имеет как продолжительность во времени, так и вероятность появления в процессе торговли. Как из цены, так и из трейдов можно составить произвольные кривые, которые в случае с ценой называются ценовой историей, а в случае торговли историей торговли.

В случае с ценой все гораздо понятнее, потому что все члены такого ряда всегда идут четко и друг за другом. Можно, конечно, из цены составить такие ряды, которые будут накладываться друг на друга, но тогда такой анализ абсолютно бесполезен для нас, так как не будет практической пользы от подобного анализа. В случае же с бектестами или историей торгов все обстоит немного иначе. В процессе изучения этих процессов я пришел к однозначному выводу, что к прибыльной и стабильной торговле проложен гораздо более легкий и правильный путь как раз через область анализа торговой истории или бектестов. Будет завершающая статья с описанием одного из таких подходов, но пока для него рановато.

Почему правильное представление данных очень важно для анализа?

Если более глубоко углубиться в поверхностный анализ возможностей описания торговой истории и бектестов языком математики, в первую очередь нужно осознавать для чего нам понадобится такой анализ и что он даст в итоге? Есть ли вообще добавленная стоимость в таком анализе? На самом деле дать четкий ответ сразу невозможно, но он есть и ответ постепенно приводит к простым и работающим решениям, но сначала нам придется углубиться в тернии. Учитывая опыт предыдущих статей, меня сразу интересовали следующие вопросы:

1. Можно ли свести любую стратегию к фрактальному описанию торговли?
2. Если сведение возможно, то для чего оно может пригодиться?
3. Если сведение не всегда возможно, то каковы условия сводимости?
4. Если условия сводимости выполнены, разработка алгоритма сведения
5. Рассмотрение иных вариантов описания стратегии, и обобщение

Сразу отвечу на все эти вопросы. Свести некоторые стратегии к фрактальному описанию возможно, и я разработал этот алгоритм, его я буду описывать дальше. Он пригодится в целом не только для этих целей, ведь он универсальный, но не это главное. А сейчас подумаем и постараемся ответить на вопрос, что же такое история торгов языком случайных чисел и теории вероятностей? Ответ прост: это набор обособленных сущностей или векторов, появление которых на определенном промежутке времени имеет определенную вероятность и коэффициент использования времени. Основной характеристикой каждой такой сущности является вероятность ее появления. Коэффициент использования времени — это просто вспомогательная величина, которая помогает определить, насколько имеющееся время используется для торговли. Можно нарисовать иллюстрацию для того, чтобы лучше понимать, о чем идет речь:

На рисунке есть следующие обозначения:

1. Черная точка – начало трейда
2. Красный треугольник – конец очередного трейда
3. Оранжевый шестиугольник – одновременно и конец предыдущего трейда и начало следующего
4. T[i] – время очередного окна торговли
5. P[i] – прибыль или убыток очередного трейда
6. n – количество трейдов
7. m – количество торговых окон

На рисунке специально изображены 3 графика, для того чтобы показать, что варианты “A” и “B” могут быть сведены к варианту “C”. Теперь разберемся что это за варианты:

1. Вариант “A” – это то, как мы видим произвольную торговлю с использованием всех возможных приемов, мани менеджмента и прочих трюков.
2. Вариант “B” – это то же самое только учитывая, что единовременно может быть открыт лишь 1 ордер на соответствующем счете.
3. Вариант “C” – это то, как мы видим торговлю либо в сервисе сигналов, либо на бектесте.

Очень важно отметить, что вариант “C” максимально информативен и в большинстве случаев мы полагаемся именно на это представление нашей торговли, кроме того, интересно что к данному виду можно свести абсолютно любую стратегию, а все потому, что главной характеристикой любого бектеста, либо торгового сигнала является именно линия эквити. Эта линия отражает реальную прибыль или убытки на текущий момент.

Если проанализировать линию эквити произвольной стратегии, то окажется, что точки открытия и закрытия очередных сделок могут располагаться абсолютно произвольно, если линия эквити остается неизменной. Это говорит нам о том, что ту или иную стратегию торговли можно представить огромным числом различных способов и все эти способы будут эквивалентны друг другу, так как будут эквивалентны их линии эквити. В данной связи не имеет смысла просто так искать все эквивалентные варианты и самое главное зачем их искать?

Если взять стратегию типа “B”, то преобразование ее в тип “C” является крайне простой операцией в том плане, что нам нужно всего лишь склеить воедино временные интервалы в том порядке, что они расположены, тестер и сервис сигналов, собственно, именно это и делает. Другое дело, если мы пытаемся преобразовать тип “A” в тип “C”, тут совсем все иначе. Для того чтобы произвести подобные преобразования, необходимо сначала свести тип “A” к типу “B”, а уже после всего этого производить преобразование в тип “C”. Теперь вы знаете, как работает тестер стратегий и сервис сигналов.

Само по себе данное преобразование не несет какой-то практической ценности для торговли, но может развить понимание глубинных вещей, например можно прийти к тому, что есть следующие типы стратегий:

1. Описываемые двумя состояниями
2. Описываемые несколькими состояниями
3. Описываемые бесконечным количеством состояний

В данной статье я покажу вам примеры описания первых двух типов стратегий. Третий тип стратегий более сложный и подлежит отдельному рассмотрению в рамках другой статьи, я проведу это рассмотрение в свое время, а пока что для того, чтобы понять третий тип стратегии, необходимо разобраться с первыми двумя. Эти два типа помогут разуму созреть до того, чтобы прийти к третьему и последнему, общему типу стратегии.

Двойные состояния

Фракталы, описанные в предыдущих статьях, это не что иное как модель с двумя состояниями. Состояниями в данном случае являются движение вниз и движение вверх. В случае, если мы применяем модель к линии баланса торговли, а не к ценообразованию, то эта модель будет работать точно так же. Данная модель построена на схеме Бернулли. Схема Бернулли описывает простейший фрактал с двумя состояниями:

• P[k] = C(n,k)*Pow(p,k)*Pow(q,n-k)   — формула Бернулли ( P[k] – вероятность выпадения конкретного сочетания )
• p — вероятность выпадения состояния “1” в результате единичного опыта
• q – вероятность выпадения состояния “2” в результате единичного опыта

Эти формулы способны вычислить вероятность того, что по истечении “n” шагов, мы получим кривую баланса или любую другую кривую, в которой будет “k” первых состояний и “n-k” вторых состояний, это не обязательно должны быть профиты сделок. Эти состояния могут символизировать любой вектор параметров, в котором мы видим уникальность. Самое интересное, что сумма всех подобных вероятностей конкретного сочетания должна образовывать полную группу, а это значит, что сумма всех таких вероятностей должна быть равна единице, что символизирует тот факт, что за “n” шагов обязательно должно появиться одно из таких сочетаний:

• Summ(0…k…n)[ P[k] ] = 1

Нас же в данном случае интересует применение данных вещей для описания либо ценообразования, либо бектестов и сигналов. Представим, что наша стратегия состоит из сделок, которые закрываются по равноудаленным стопам, но при этом мы знаем, что невозможно вычислить предполагаемое движение цены в будущем, тогда распределение этих вероятностей будет иметь вот такой вид:

На этих трех рисунках изображены:

1. Распределение вероятностей при случайном блуждании или торговле
2. Распределение вероятностей при прибыльной торговле или восходящем тренде
3. Распределение вероятностей при убыточной торговле или нисходящем тренде

Как видно из этих диаграмм, в зависимости от вероятности шага вверх, вероятности тех или иных сочетаний меняются, и максимально вероятный случай смещается либо влево, либо вправо, как и все остальные вероятности. Такая модель представления бектеста или ценообразования является простейшей и наиболее предпочтительной для анализа. Если для описания ценообразования такой модели может быть достаточно, то для описания торговли, конечно же, нет. На практике мы сталкиваемся с тем, что кривая баланса может содержать самые различные трейды, как по длительности, так и по прибыли. В зависимости от того, какие показатели трейда для нас наиболее важны, мы можем выделить не два, а столько состояний, сколько нам нужно.

Множественные состояния

Теперь давайте разберем наглядный пример. Представим, что по-прежнему нам важна лишь величина прибыли или убытка очередного трейда, но известно, что прибыль или убыток может принимать строго три фиксированных величины, и известны вероятности выпадения каждой такой величины. Если все именно так, то мы можем сказать, что имеем систему с тремя состояниями. Теперь попробуем спросить себя, а можно ли описать все возможные развития событий подобно системе с двумя состояниями? На самом деле можно. Я собираюсь немного усовершенствовать схему Бернулли для того, чтобы она могла работать с системой со сколько угодно состояниями.

Если следовать логике Бернулли, нужно определить счетчики состояний:

• i[0] – количество выпадений первых состояний в цепочке независимых испытаний
• i[1] – количество выпадений вторых состояний в цепочке независимых состояний
• . . .
• i[N] – количество выпадений N – состояния
• N – количество состояний системы
• s – номер состояния

Если по очереди определять количество выпадения определенного состояния, то доступное количество для следующего состояния будет:

• s[i]  = N — Summ(0… k … i — 1) [ s[k] ]

Можно сказать проще. Если мы выбрали количество исходов предыдущего состояния, то на следующее состояние остается исходов меньше ровно на столько, сколько состояний было выбрано на предыдущее состояние. Точно так же, как и в схеме Бернулли, существуют цепочки вероятностей, которые несовместны и имеют одинаковую вероятность. Количество цепочек с одинаковым количеством всех состояний тогда вычислится так:

• A[h](N,i[0]  ,i[1] ,… i[n]) = C(N , i[0]) * C(N-i[0] , i[1]) *…. C(N-Summ(0…k…n-1)[ i[k] ] , i[n])
• С — сочетания
• h – очередной уникальный набор шагов

Ну и соответственно понятно, что вероятности таких наборов можно посчитать точно так же, как в схеме Бернулли. Умножим вероятность одного такого набора на их количество:

• P[k] = A[h](N,i[0]  ,i[1] ,… i[n]) * Pow(p[0], i[0]) * Pow(p[1], i[1]) … * Pow(1- Summ(0…j…N-1)[ p[j] ] , i[1])
• p[j] – вероятность появления определенного состояния

Для наглядности я сделал трехмерные графики, как и в предыдущем примере для двух состояний. Точно так же у нас 30 шагов, но я беру уже три состояния вместо двух:

Конечно же понятно, что объем этого графика будет в точности равен единице, так как каждый столбик символизирует несовместное событие, и все эти несовместные события как раз и образуют полную группу. На графиках две разных стратегии с разными векторами вероятностей. Эти вероятности символизируют шанс выпадения одного из трех состояний.

• S1 – количество выпавших первых состояний
• S2 – количество выпавших вторых состояний
• S3 = 30 – S1 – S2 – количество выпавших третьих состояний

Если вдруг в нашей системе есть четвертое состояние, то изобразить это можно будет только в четырех измерениях, если пять состояний, то соответственно график будет пятимерный и так далее. Для человеческого глаза только 3 измерения доступны, поэтому более сложные системы невозможно будет изобразить графически. Но нужно понимать, что многомерные функции такие же функциональные, как и другие.

Программная реализация множественных состояний

Понятно, что двойные состояния можно представить одномерным массивом данных, а что, если состояний больше? На ум приходит только многомерный массив. Но, насколько я знаю, во всех языках программирования используются максимум двойные массивы. Может быть и есть где-то возможности по созданию трехмерных массивов и массивов с множественным измерениями, но это далеко не самый удобный вариант. Лучше использовать коллекции или кортежи для этих целей:

Здесь как раз та ситуация с “30” шагами. Первый и третий столбики отражают внутреннюю структуру кортежа. Видно, что это просто массив в массиве. Там, где написано к примеру “[31,1]” – это значит, что этот элемент матрицы тоже является матрицей с “31” строкой и одним столбцом. Как раз таки формула Бернулли и вся схема Бернулли является частным случаем именно этой более общей схемы. Если потребовать двух состояний, то кортежи превратятся в одномерные массивы, и мы как раз получим простые сочетания, которые и играют основную роль в формуле Бернулли.

Если посмотреть, что же внутри этих массивов, то получим столбики “2” и “4”. Второй столбик — это количество эквивалентных веток конкретных уникальных наборов состояний, а четвертый — это суммарная вероятность таких веток, ведь их вероятности равны.

Очень наглядным критерием для проверки правильности вычисления подобных кортежей является проверка полной группы событий и общего числа всех уникальных веток. Для этих целей можно соорудить общую функцию, которая просуммирует все элементы этих сложных кортежей вне зависимости от сложности их внутренней структуры. Пример показан на скриншоте выше. Такая функция должна быть обязательно рекуррентной, и вызывать сама себя внутри, тогда она будет универсальной для любого числа состояний и количества шагов. Что касается числа уникальных веток, истинное значение считается так:

• Pow(N,n)

Иначе говоря, количество состояний системы нужно возвести в степень количества шагов, и так мы получим все возможные комбинации уникальных цепочек, состоящих из наших состояний. На рисунке это число выступает в роли переменной “CombTotal”, с ней и сравниваем то, что получилось при суммировании.

Для того чтобы посчитать сами кортежи, нужно использовать похожие функции с такой же рекуррентной структурой:

Видно, что все происходит похоже. Есть всего пара отличий. В каждом уровне обязательно домножение на количество сочетаний по оставшимся свободным шагам. А когда считаем вероятности домножаем на вероятность того состояния, которое сейчас набираем, ну и конечно не забываем домножить на уже собранную вероятность цепи. Просто по очереди набираем все состояния, пока не останется свободных ячеек, а ячейки — это количество наших шагов.

Можно также сделать пример выделения состояний из данных, которые нам известны. Например, известно, что у нас есть торговая статистика, и в этой статистике у каждого ордера сохранена информация о его длительности, объеме торгов и прочая информация, например величина убытка или прибыли. Так как выборка конечна, то и число состояний конечно. Можно, например, определить, сколько вообще вариантов прибыли есть в этой выборке. И каждое уникальное значение профита считать уникальным состоянием. Считаем количество появление всех таких профитов во всей выборке и делим на общее количество всех сделок и получаем вероятность выпадения конкретного состояния. И так делаем для всех состояний. Если потом просуммировать все эти вероятности, то получим единицу. Если так, то все сделано верно. Так же можно сделать, например со временем, сделать классификацию по времени существования ордера. Иначе говоря, состоянием может быть любая уникальная характеристика какого-либо события. В данном случае событием считается трейд, а его параметры это уже как раз характеристики конкретного события. Примеры состояний могут быть такими в нашем случае:

На рисунке пример составления наборов состояний. По правилам состояния должны образовывать полную группу событий, иначе говоря, не должно быть там совместных состояний. Вероятность этих событий можно посчитать, просто разделив количество ордеров в таблице с конкретными состояниями на количество всех ордеров, а в нашем случае это число “7”. Это на примере ордеров, но это не обязательно могут быть ордера, может быть что угодно.

Заключение

В этой статье я старался показать, как можно оценивать выборки данных, как составлять из них новые путем классификации данных и объединения их в наборы состояний, вероятности которых можно посчитать. Что делать с этими данными решать вам. Самым лучшим использованием я считаю множественные выжимки и их оценка, это еще называют кластеризацией выборки. Плюс в том, что кластеризация выборки может служить как отличный фильтр для усиления показателей торговли уже имеющихся систем, а также для получения прибыльной торговли из уже имеющейся, казалось-бы убыточной стратегии — всего-то нужно произвести кластеризацию и найти всеми желаемые прибыльные выборки. А самое главное, подобные механизмы могут являться одной из ступеней обработки данных в масштабируемых торговых системах. Мы будем применять эти механизме на практике, когда перейдем к сборке самоадаптирующейся торговой системы, а пока что это — очередной кирпичик.

Ссылки

• Комбинаторика и теория вероятностей для трейдинга (Часть I): Основы
  
• Комбинаторика и теория вероятностей для трейдинга (Часть II): Универсальный фрактал
  
• Комбинаторика и теория вероятностей для трейдинга (Часть III): Первая математическая модель
  

Якоб Бернулли — увлечение, определившее судьбу

В научной среде фамилия Бернулли более чем хорошо известна, поскольку многие члены семейства посвятили жизнь математике и сделали немало открытий в области физики. С их именами связаны известные уравнения, формулы, тождества.

27 декабря 1654 года появился на свет Якоб Бернулли — известно, что это произошло в городе Базель, этот город и считается родиной математика. Отец его, Николай Бернулли старший, был преуспевающим фармацевтом и поначалу велел сыну изучать в университете родного города богословие. Но мальчику казалось куда более интересным решать уравнения и находить неизвестные переменные в неравенствах. Именно тогда Якоб начал самостоятельно изучать математическую дисциплину.

Ему давались легко не только точные науки, но и иностранные языки, пять из них он знал в совершенстве — итальянский, французский, греческий, латинский и английский. 1671 год принес молодому человеку учёную степень, сделав магистром в области философии.

После получения образования юноша 4 года путешествовал по странам Европы, знакомясь с традициями и обычаями народов, и расширял кругозор. Во Франции он познакомился с идеями Декарта, затем отправился в Италию и лишь после этого вернулся на родину. По возвращении в Базель Якоб непродолжительное время учительствовал, давая частные уроки. С 1677 года начинающий ученый принялся вести дневниковые записи — конспекты, куда записывались идеи и наблюдения научного характера.

Спустя пару лет Якоб вновь отправился странствовать по миру. В 1682 году он посетил Голландию, следом Англию, в которой свёл знакомство с Гуком, Бойлем и Гюйгенсом, а с 1684 года сменил статус холостого юноши на роль отца семейства, выбрав в жёны скромную, миловидную женщину, которая в дальнейшем родила ему двоих детей.

С 1683 года Бернулли ведёт занятия в университете своего родного города, преподает студентам физику, а через тройку лет получает должность профессора физики и математики в Базеле. 1687 становится переломным годом для талантливого учёного, именно тогда он открыл для себя первый мемуар по анализу Лейбница и принялся осваивать новое исчисление. Не все было понятно молодому учёному, и он решился отправить автору послание, где просил разъяснить ему моменты, с пониманием которых возникли трудности. Вот только ответ Лейбница Якоб получил лишь по прошествии трёх лет — по причине, что Лейбниц находился в рабочей командировке в Париже и не смог своевременно ответить молодому последователю. Однако Якоб не терял время зря, пытаясь своими силами разобраться с проблемными местами книги, что ему отлично удалось. Кроме этого, он продолжал изучать дифференциальное и интегральное исчисление, и смог заинтересовать этим брата Иоганна Бернулли. С тех пор они занимались математикой вдвоем.

Когда командированный Лейбниц вернулся из Франции, он вступил в переписку с обоими братьями. Как результат, втроем они два десятилетия стояли во главе математиков Европы, дополняя и развивая новый математический анализ.

1692 изменил жизнь талантливого ученого не в лучшую сторону. В этом году у него обнаружились признаки туберкулёза. Страшная в прошлом болезнь отнимала много сил и спустя 13 лет унесла жизнь гениального математика. В 1705 году 16 августа его не стало. Умер учёный в возрасте 50-ти лет.

Достижения Якоба Бернулли

В 1690 году мир узнал о ярком математике-самоучке, когда Якоб успешно решил задачу Лейбница о форме кривой и опубликовал доказательство. При этом решение было найдено им с помощью нового анализа. Также он вывел и интегрировал дифференциальное уравнение, причём понятие «интеграл» до этого момента не было известно. Именно после открытия старшего Бернулли этот термин оказался в печати. Наряду с развитием математики, талантливый учёный также внёс весомый вклад в аналитическую геометрию, после чего именем математика назвали лемнискату. Ко всему прочему, он не обошел вниманием цепную линию, а вместе с ней логарифмическую спираль, которую завещал начертать на могильной плите. В итоге по неведению на его могиле изобразили спираль Архимеда, перепутав два этих понятия.

Неоценимый вклад в развитие точных наук Якоб Бернулли внёс благодаря открытиям в теории вероятностей и теории чисел, не случайно сохраняющим имя первооткрывателя («числа Бернулли»). Неоценимы заслуги знаменитого ученого в теории рядов — его работы 1689-1704 годов стали настоящим открытием в данном разделе математики.

Любопытную и существенную роль в его научной деятельности сыграла книга Гюйгенса «О расчётах в азартной игре», по которой Якоб изучал теорию вероятностей. До него этот термин не имел чёткой формулировки, а явление называлось «количеством благоприятных случаев».

Якоб Бернулли внес в это определение поправки и дополнения, сформулировав первоначальный вариант закона больших чисел. С этим открытием связана его монография, которая вышла лишь после смерти автора. Когда тяжёлая болезнь подорвала здоровье и силы замечательного математика, он уже не мог опубликовать труд самостоятельно. Напечатал книгу «Искусство предположений» его брат Николай в 1713 году. Темой этого произведения является теория вероятностей, статистика, а также использование этих понятий на практике. Перу Якоба принадлежат и другие труды — по арифметике, геометрии и комбинаторике (где с его именем связано понятие распределения).

Ощутимую пользу принесли открытия Якоба Бернулли в области физики. Многие из страниц записных книжек (конспектов) учёного посвящено заметкам и опытам, на основании которых автор впоследствии издал работы по определению центра качания тел и сопротивлению тел, различных по форме, движущихся в жидкости.

Можно бесконечно восхищаться талантом и работоспособностью блестящего учёного, посвятившего жизнь математическому анализу, который поначалу был всего лишь увлечением. Якоб Бернулли приобщил к занятиям наукой своего младшего брата Иоганна Бернулли, после чего тот также связал свою судьбу с математикой. Вместе с братом они образовали уникальный тандем, к которому на определённом этапе присоединился Лейбниц, и совершили целый ряд открытий. В честь братьев Бернулли был назван кратер на Луне. Об уравнениях Бернулли, теории чисел и теории вероятностей хотя бы понаслышке знает каждый образованный человек. Открытые им формулы изучаются в школах и высших учебных заведениях, а имя до сих пор на слуху благодаря неоценимому вкладу в точные науки.

Схемы Бернулли повторных испытаний — Информио

Аннотация: Рассмотрены на примерах Схемы Бернулли повторных испытаний из теории вероятностей, механизмы ее действия и применения в жизни.

Ключевые слова: Теория вероятностей, схемы Бернулли.

Людей всегда интересовало будущее. Человечество во все времена искало способ его предугадать или спланировать: в разное время разными способами. В современном мире есть теория, которую наука признает и пользуется для планирования и прогнозирования будущего. Речь о теории вероятностей.

Теория вероятностей — это математическая наука, изучающая закономерности в случайных явлениях. На сегодняшний день это полноценная наука, имеющая большое практическое значение.

В жизни мы часто сталкиваемся со случайными явлениями. Чем обусловлена их случайность — нашим незнанием истинных причин происходящего или случайность лежит в основе многих явлений? Споры на эту тему не утихают в самых разных областях науки. Случайным ли образом возникают мутации, насколько зависит историческое развитие от отдельной личности, можно ли считать Вселенную случайным отклонением от законов сохранения? Пуанкаре, призывая разграничить случайность, связанную с неустойчивостью, от случайности, связанной с нашим незнанием, приводил следующий вопрос: «Почему люди находят совершенно естественным молиться о дожде, в то время как они сочли бы смешным просить в молитве о затмении?»

У каждого «случайного» события есть четкая вероятность его наступления. В стабильной системе вероятность наступления событий сохраняется из года в год. То есть с точки зрения человека с ним произошло случайное событие, а с точки зрения системы оно было предопределенно.

Разумный человек должен стремиться мыслить, исходя из законов вероятностей (статистики). Но в жизни о вероятности мало кто думает. Решения принимаются эмоционально. Люди боятся летать самолетами. А между тем, самое опасное в полете на самолете — это дорога в аэропорт на автомобиле. Но попробуй кому-то объяснить, что машина опасней самолета. Вероятность того, что пассажир, севший в самолет погибнет в авиакатастрофе составляет примерно 1/8 000 000. Если пассажир будет садиться каждый день на случайный рейс, ему понадобится 21 000 лет чтобы погибнуть.

Согласно исследованиям, в США в первые 3 месяца после терактов 11 сентября 2001 года погибло еще одна тысяч людей косвенно. Они в страхе перестали летать самолетами и начали передвигаться по стране на автомобилях. А так как это опасней, то количество смертей возросло. Миром правит вероятность и нужно помнить об этом. Они помогут вам взглянуть на мир с точки зрения случая.

Существует мнение, что решающее влияние на возникновение теории вероятностей оказали азартные игры. Действительно, карты, рулетка, игральные кости, различные лотереи издавна привлекали внимание определенных кругов общества.

Возникновение теории вероятностей как науки относится к середине XVII столетия, когда усилиями Паскаля, Ферма, Гюйгенса были введены специфические понятия и доказаны простейшие теоремы о вероятностях случайных событий.

Важный этап в развитие теории вероятностей связан с именем Я. Бернулли. Теорема, которая носит ныне его имя, вскрывает следующую важную особенность вероятностных задач: рассмотрению подлежат лишь те опыты со случайными исходами, которые независимо друг от друга могут быть повторены любое число раз в одинаковых условиях. Для определенности будем говорить о подбрасываниях монеты. Каждое отдельное подбрасывание монеты приводит к непредсказуемому исходу: выпадает либо герб, либо решка.

Если  число гербов, выпадающих при n бросаниях монеты, то непредсказуемой является и частота выпадений герба. Однако с ростом n эта непредсказуемость ослабевает: наблюдаемые значения величины имеют тенденцию группироваться около числа 0,5. Отмеченный принцип устойчивости частот выражает одну из важнейших закономерностей случайных явлений.

Своей знаменитой теоремой Бернулли дал математическое истолкование принципа устойчивости частот и закрепил за теорией вероятностей право называться наукой о математических методах изучения закономерностей случайных явлений.

Вероятность события в жизни не так уж часто считается по формулам, скорее интуитивно. Но проверить, совпадает ли «эмпирический анализ» с математическим,  иногда очень полезно. Выбранная мною тема актуальна, т.е. практически полезная и представляет интерес в научном отношении.

Выбирая данную тему, я руководствовался несколькими правилами: тема очень интересна,  увлекательна, соответствует моей  склонности к изучению «Теории вероятностей», данная тема выполнима, решение ее принесёт реальную пользу (получение новых полезных знаний, умений, навыков, развитие интеллекта, реализация исследовательской потребности). Тема  оригинальна, в ней есть элемент неожиданности, необычности, способности нестандартно смотреть на традиционные предметы и явления.

При практическом применении теории вероятностей часто приходится встречаться с задачами, в которых одно и то же испытание повторяется неоднократно. В результате каждого испытания может появиться или не появиться некоторое событие А. Причем нас интересует не результат каждого отдельного испытания, а общее число появлений события А в результате серии опытов. Например, если производится группа выстрелов по одной и той же цели, нас, как правило, не интересует результат каждого выстрела, а лишь общее число попаданий. В подобных задачах требуется уметь определять вероятность любого заданного числа появлений события в результате серии опытов. Такие задачи и будут рассмотрены. Они решаются весьма просто в случае, когда испытания являются независимыми.

Испытания называются независимыми, если вероятность того или иного исхода каждого из испытаний не зависит от того, какие исходы имели другие испытания. Например, несколько бросаний монеты представляют собой независимые испытания.

Актуальность  темы «Схемы Бернулли повторных испытаний» рассмотрим на примерах из теории вероятностей, механизмы ее действия и применения в жизни, так как очень много процессов в нынешнее время решаются с помощью схем Бернулли.

Я решил проверить классическое определение вероятности.

Определение: «Пусть множество исходов опыта состоит из n равновероятных исходов. Если m из них благоприятствуют событию A, то вероятностью события A называется число Р(А) = m/n.»

Возьмем, к примеру, игру в монету. При бросании может быть два равновероятных исхода: монета может упасть кверху гербом или решкой. Бросая монету один раз нельзя предугадать, какая сторона окажется сверху. Однако, бросив монету 100 раз, можно сделать выводы. Можно заранее сказать, что герб выпадет не 1 и не 2 раза, а больше, но и не 99 и не 98 раз, а меньше. Число выпадений герба будет близко к 50. На самом деле, и на опыте можно в этом убедиться, что это число будет заключено между 40 и 60. Кто и когда впервые проделал опыт с монетой, неизвестно.

 Проведём опыт. Для начала, возьмем в руки монетку, будем ее бросать и записывать результат последовательно в виде строки: О, Р, Р, О, О, Р. Здесь буквами О и Р обозначено выпадение орла или решки. В нашем случае бросание монетки — это испытание, а выпадение орла или решки — событие, то есть возможный исход нашего испытания. В процессе проведения 100 испытаний орел выпал  55 раз, решка — 45. Вероятность выпадения орла в данном случае-0,55; решки – 0,45. Таким образом, я показал, что теория вероятности в данном случае имеет место быть.

Можно ли выиграть в лотерею или рулетку?

Каждый из нас хоть раз в жизни покупал лотерею или играл в азартные игры, но далеко не все использовали заранее спланированную стратегию. Умные игроки давно перестали надеяться на удачу и включили рациональное мышление.

Дело в том, что каждое событие имеет определенное математическое ожидание, как гласят высшая математика и теория вероятности, и, если правильно оценивать ситуацию, то можно обойти неудовлетворительный исход события.

Повторные независимые испытания называются испытаниями Бернулли, если каждое испытание имеет только два возможных исхода и вероятности исходов остаются неизменными для всех испытаний.

Приведу пример практического применения схемы испытаний Бернулли на примере нашего института.  На I курс ТИЖТа в 2016г.  поступило 295 студентов. Требуется найти наиболее вероятное число первокурсников, родившихся в один день, день знаний 1-го сентября, и вероятность этого события.

Решение. В нашем случае р= 1:365  n=295  Используем соотношение для наивероятнейшего числа: m0

295*(1:365)-(364:365)m0295*(1:365)+(1:365)
Учитывая, что m0 целое число, получаем  m0= 1.

Найдем теперь P295(1), используя теорему Пуассона и то, ƛ=295*(1:365)

P295(1)е-10,37

Приведу следующий пример практического применения схемы испытаний Бернулли. Колёсные пары, изготовляемые при массовом производстве, могут отличаться по толщине, но при проверке они классифицируются на годные и дефектные — в зависимости от того, находится ли толщина в предписанных границах. И хотя продукция по многим причинам не может вполне соответствовать схеме Бернулли, эта схема  задает идеальный стандарт для промышленного контроля качества продукции, несмотря даже на то, что этот стандарт никогда не достигается вполне точно. Вагоны подвержены изменениям, и поэтому вероятности не остаются одними и теми же. В режиме эксплуатации вагонов имеется некоторое постоянство, в результате чего длинные серии одинаковых отклонений оказываются более вероятными, чем это было бы при действительной независимости испытаний. Однако с точки зрения контроля качества продукции желательно, чтобы процесс соответствовал схеме Бернулли, и важно то, что в некоторых пределах этого можно добиться. Целью текущего контроля является обнаружение уже на ранней стадии существенных отступлений от идеальной схемы и использование их как указаний на угрожающее нарушение правильности эксплуатации вагонов.

Можем ли мы предугадать с помощью этой теории, что случится с нами через день, два, тысячу? Конечно, нет. Событий, связанных с нами в каждый момент времени, очень много. Только на одну лишь типизацию этих событий не хватит и жизни. А уж их совмещение  и вовсе гиблое дело. С помощью Схемы Бернулли предугадывать можно лишь однотипные события. Например, такое как бросание монеты — это событие из 2 вероятностных результатов. В общем, прикладное применение теории вероятностей связанно с немалым количеством условий и ограничений, а для сложных процессов сопряжено с вычислениями, которые под силу лишь компьютеру.

Но следует помнить, что в жизни есть ещё такое понятие как удача, везение. Это то, что мы говорим — повезло, когда например какой-нибудь человек не учился никогда, никуда не стремился, лежал на диване, играл в компьютер, а теперь, предположим, он выступил в шоу «Минута славы». У него была вероятность 0.001 стать музыкантом, она выпала, ему повезло, такое схождение обстоятельств. То, что мы называем — оказался в нужном месте и в нужное время, когда срабатывают те самые 0.001.

Таким образом, работаем над собой, принимаем решения, которые могут повысить вероятность выполнения наших желаний и стремлений, каждый случай может добавить те заветные 0.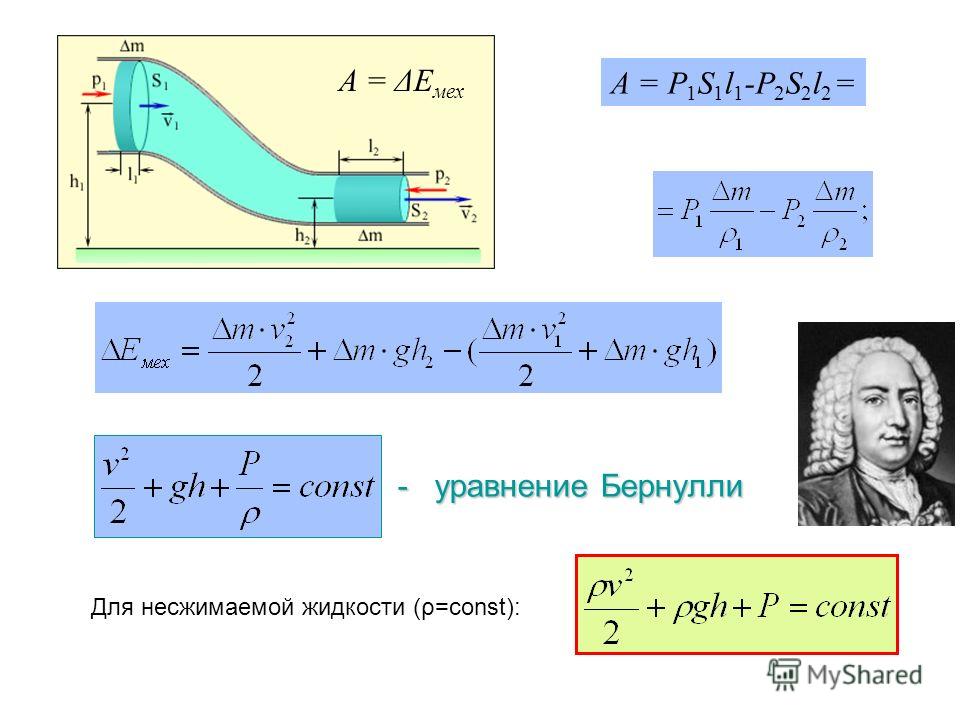 00001, которые сыграют решающую роль в итоге.

В заключение хочется отметить то, что распределение Бернулли является достаточно распространенным и важным распределением, имеющим применение как в теории вероятностей и ее приложениях, так и в математической статистике.

 

Список литературы

1. Журбенко, Л.Н., Никонова, Г.А., Никонова, Н.В.  Дегтярева, О.М. Математика в примерах и задачах: Учеб. пособие / Л.Н. Журбенко, Г.А. Никонова, Н.В. Никонова, О.М. Дегтярева. — М.: ИНФРА-М, 2012. — 372 с.: 60×88 1/16. — (Высшее образование). (обложка) ISBN 978-5-16-003841-4
2. Павлов, С.В. Теория вероятностей и математическая статистика: Учебное пособие / С.В. Павлов. — М.: ИЦ РИОР: ИНФРА-М, 2013. — 186 с.: 70×100 1/32. — (Карманное учебное пособие). (обложка, карм. формат) ISBN 978-5-369-00679-5
3. Балдин, К.В., Башлыков, В.Н.,  Рукосуев, А.В.  Основы теории вероятностей и математической статистики: Учебник / К.В. Балдин, В.Н. Башлыков, А.В. Рукосуев. — М.: Флинта: МПСИ, 2013. — 488 с.: 60×88 1/16. (переплет) ISBN 978-5-9765-0314-4

 

Оригинал работы:

Схемы Бернулли повторных испытаний

Давление

Давление

Уравнение Бернулли можно рассматривать как формулировку принципа сохранения энергии, применимого к текущим жидкостям. Качественное поведение, которое обычно обозначают термином «эффект Бернулли», представляет собой снижение давления жидкости в областях, где скорость потока увеличивается. Это снижение давления при сужении пути потока может показаться нелогичным, но кажется менее таковым, если рассматривать давление как плотность энергии. В высокоскоростном потоке через сужение кинетическая энергия должна увеличиваться за счет энергии давления. Предупреждение об установившемся потоке : Хотя уравнение Бернулли сформулировано в терминах общепризнанных идей, таких как сохранение энергии и идеи давления, кинетической энергии и потенциальной энергии, его применение в приведенной выше форме ограничено случаями установившегося течения. . Для потока через трубу такой поток можно представить как ламинарный поток, что все еще является идеализацией, но если поток в хорошем приближении ламинарный, то можно смоделировать и рассчитать кинетическую энергию потока в любой точке жидкости. Кинетическая энергия на единицу объема в уравнении требует строгих ограничений для применения уравнения Бернулли — в основном это предположение о том, что вся кинетическая энергия жидкости вносит непосредственный вклад в процесс прямого потока жидкости. Это должно сделать очевидным, что существование турбулентности или любого хаотического движения жидкости связано с некоторой кинетической энергией, которая не способствует продвижению жидкости по трубе. Следует также сказать, что хотя закон сохранения энергии применяется всегда, эта форма анализа этой энергии определенно не описывает, как эта энергия распределяется в переходных условиях. Хорошей визуализацией эффекта Бернулли является поток через сужение, но эта аккуратная картина не описывает жидкость, когда вы впервые включаете поток. Другим приближением, используемым в приведенной выше формулировке уравнения Бернулли, является пренебрежение потерями от жидкостного трения. Идеализированный ламинарный поток через трубу можно смоделировать с помощью закона Пуазейля, который включает вязкие потери, приводящие к снижению давления по мере продвижения по трубе. Формулировка уравнения Бернулли, приведенная выше, привела бы к ожиданию того, что давление вернется к значению P 1 миновать сужение, так как радиус возвращается к исходному значению. Этого не происходит из-за потери некоторой энергии активного процесса течения за счет трения в неупорядоченное молекулярное движение (тепловую энергию). Более точное моделирование можно выполнить, объединив уравнение Бернулли с законом Пуазейля. Реальным примером, который может помочь визуализировать процесс, является мониторинг давления потока через суженную трубу. Расчет Бернулли

Индекс Концепции Бернулли

8 Гиперфизика***** Механика ***** Жидкости R Ступица Назад Расчет «реального» давления в сужении трубы выполнить сложно из-за вязких потерь, турбулентности и предположений, которые необходимо сделать о профиле скорости (которые влияют на расчетную кинетическую энергию). Расчет модели здесь предполагает ламинарный поток (отсутствие турбулентности), предполагает, что расстояние от большего диаметра до меньшего достаточно мало, чтобы можно было пренебречь вязкими потерями, и предполагает, что профиль скорости соответствует теоретическому ламинарному потоку. В частности, это предполагает допущение, что эффективная скорость потока составляет половину максимальной скорости и что средняя плотность кинетической энергии равна одной трети максимальной плотности кинетической энергии. Теперь, если вы можете проглотить все эти предположения, вы можете смоделировать* поток в трубе, где объемный расход = см 3 /с, а плотность жидкости равна ρ = гм/см 3 . Для площади входной трубы A 1 = см 2 (радиус r 1 = см) геометрия потока приводит к эффективной скорости жидкости v 1 = см/с. Поскольку уравнение Бернулли включает также потенциальную энергию жидкости, высота впускной трубы определяется как h 1 = см. Если площадь трубки сужена до A 2 =см 2 (радиус r 2 = см), то без дальнейших предположений эффективная скорость жидкости в сужении должна быть v 2 = см/с . Высота суженной трубки указана как h 2 = см. Теперь можно рассчитать плотность кинетической энергии в двух точках трубы и применить уравнение Бернулли для ограничения процесса с целью сохранения энергии, что даст значение давления в сужении. Сначала задайте давление во впускной трубе: Давление на входе = P 1 = кПа = фунт/дюйм 2 = мм рт.ст. = атмосфера Теперь можно рассчитать плотность энергии. Единицей энергии для используемых единиц СГС является эрг. Плотность энергии впускной трубы Плотность кинетической энергии = эрг/см 3 Плотность потенциальной энергии = эрг/см 3 Плотность энергии давления = эрг/см 3 Плотность энергии суженной трубки Плотность кинетической энергии = эрг/см 3 Плотность потенциальной энергии = эрг/см 3 Плотность энергии давления = эрг/см 3 Плотность энергии давления в суженной трубе теперь можно окончательно преобразовать в более традиционные единицы измерения давления, чтобы увидеть влияние суженного потока на давление жидкости: Расчетное давление при сужении = P 2 = кПа = фунт/дюйм 2 = мм рт. ст. = атмосфера Этот расчет может дать некоторое представление об энергии, связанной с потоком жидкости, но его точность всегда сомнительна из-за предположения о ламинарном потоке. Для типичных входных условий плотность энергии, связанная с давлением, будет преобладать на входной стороне; в конце концов, мы живем на дне атмосферного моря, которое дает большое количество энергии давления. Если используется достаточно резкое уменьшение радиуса, чтобы получить давление в сужении, которое меньше атмосферного давления, почти наверняка существует некоторая турбулентность, связанная с потоком в это сужение. Тем не менее, расчет может показать, почему мы можем получить значительную величину всасывания (давление меньше атмосферного) с помощью «аспиратора» на кране высокого давления. Эти устройства состоят из металлической трубки сужающегося радиуса с боковой трубкой в ​​области суженного радиуса для всасывания. *Примечание. Некоторые значения по умолчанию будут введены для некоторых значений, когда вы начнете изучать расчет. Все они могут быть изменены как часть вашего расчета. Индекс Концепции Бернулли  8 Гиперфизика***** Механика ***** Жидкости R Ступица Назад Невращающийся бейсбольный мяч или неподвижный бейсбольный мяч в воздушном потоке демонстрирует симметричный поток. Бейсбольный мяч, брошенный с вращением, будет искривляться, потому что одна сторона мяча испытывает меньшее давление. Это обычно интерпретируется как применение принципа Бернулли и включает вязкость воздуха и пограничный слой воздуха на поверхности шара. Важна шероховатость поверхности мяча и шнурки на мяче! С идеально гладким мячом вы не получите достаточного взаимодействия с воздухом. Есть некоторые трудности с этим изображением изогнутого бейсбольного мяча. Уравнение Бернулли нельзя использовать для предсказания степени искривления мяча; поток воздуха сжимаем, и вы не можете отслеживать изменения плотности, чтобы количественно оценить изменение эффективного давления. Экспериментальная работа Уоттса и Феррера с бейсбольными мячами в аэродинамической трубе предлагает другую модель, в которой особое внимание уделяется вращающемуся пограничному слою воздуха вокруг бейсбольного мяча. Со стороны шара, где пограничный слой движется в том же направлении, что и скорость набегающего потока воздуха, пограничный слой обтекает шар дальше, прежде чем он разделится на турбулентный поток. Со стороны, где пограничный слой противостоит набегающему потоку, он имеет тенденцию к преждевременному отрыву. Это дает чистое отклонение воздушного потока в одном направлении позади мяча и, следовательно, силу реакции третьего закона Ньютона на мяч в противоположном направлении. Это дает эффективную силу в том же направлении, указанном выше. Аналогичные проблемы возникают при обработке вращающегося цилиндра в воздушном потоке, который, как было показано, испытывает подъемную силу. Это является предметом теоремы Кутта-Жуковского. Он также упоминается при обсуждении подъемной силы аэродинамического профиля. Индекс Уравнение Бернулли Концепции Бернулли Ссылка Уоттс и Феррер   Гиперфизика***** Механика 90 ****2 Жидкости 90 ****2 Жидкости R Ступица Назад Воздух в верхней части обычного аэродинамического профиля испытывает сужение линий потока и повышенную скорость воздуха по сравнению с крылом. Это вызывает уменьшение давления на вершину по уравнению Бернулли и обеспечивает подъемную силу. Аэродинамики (см. Истлейк) используют модель Бернулли для корреляции с измерениями давления, сделанными в аэродинамических трубах, и утверждают, что, когда измерения давления производятся в нескольких местах вокруг аэродинамического профиля и суммируются, они разумно согласуются с наблюдаемой подъемной силой. Иллюстрация подъемной силы и угла атаки Бернулли против Ньютона для аэродинамической подъемной силы Терминология аэродинамического профиля Другие апеллируют к модели, основанной на законах Ньютона, и утверждают, что основная подъемная сила возникает в результате угла атаки. Часть модели закона Ньютона части подъемной силы включает в себя прикрепление пограничного слоя воздуха к верхней части крыла с результирующей струей воздуха за крылом. Если крыло сообщает воздуху направленную вниз силу, то по третьему закону Ньютона на крыло действует сила противоположного направления – подъемная сила. В то время как дебаты «Бернулли против Ньютона» продолжаются, позиция Истлейка состоит в том, что они действительно эквивалентны, просто разные подходы к одному и тому же физическому явлению. У НАСА есть хороший сайт по аэродинамике, на котором обсуждаются эти вопросы. Увеличение угла атаки дает большую подъемную силу от направленной вверх составляющей давления на низ крыла. Подъемную силу можно рассматривать как силу реакции третьего закона Ньютона на силу, действующую вниз на воздух со стороны крыла. При слишком большом угле атаки турбулентный поток резко увеличивает сопротивление и останавливает самолет. След пара над крылом помогает визуализировать воздушный поток. Фотография Фрэнка Стармера, используется с разрешения. ИНДЕКС Уравнение Бернулли СПИСОК ЛИТЕРАТУРЫ Eastlake NASA Aerodynamics 1898.898.89898.8 . 44444. Гиперфизика ******* ***** 2 44444 RISAVE ***** 2 Вернуться Принцип Бернулли — Урок — TeachEngineering (8 оценок) Нажмите здесь, чтобы оценить Quick Look Уровень: 11 (9-12) Необходимое время: 30 минут Зависимость урока: Нет предметных областей: Физические науки, физика NGSS Ожидаемые характеристики: HS-PS3-1 Доля: TE Информационный бюллетень Резюме Принцип Бернулли связывает давление жидкости с ее высотой и скоростью. Уравнение Бернулли можно использовать для аппроксимации этих параметров в воде, воздухе или любой жидкости с очень низкой вязкостью. Учащиеся используют соответствующее задание, чтобы узнать о взаимосвязях между компонентами уравнения Бернулли с помощью реальных инженерных примеров и практических задач. Эта учебная программа по инженерному делу соответствует научным стандартам следующего поколения (NGSS). Инженерное подключение Принцип Бернулли имеет широкий спектр применений в инженерной гидродинамике, от проектирования аэрокосмических крыльев до проектирования труб для гидроэлектростанций. Например, в случае гидроэлектростанции, использующей поток воды из горного водохранилища, знание перепада высот от водохранилища в горах до станции в городе помогает инженерам определить, с какой скоростью вода будет течь через турбины, вырабатывающие энергию. растение. Цели обучения После этого урока учащиеся должны уметь: Рассчитать неизвестное состояние жидкости (например, давление жидкости, скорость, плотность или высоту) в одной точке на линии тока, если известны условия в другой точке на той же линии тока. Используйте уравнение Бернулли, чтобы объяснить, что более быстрый поток воздуха вызывает снижение давления, и приведите пример из реальной жизни. Образовательные стандарты Каждый урок или занятие TeachEngineering соотносится с одной или несколькими науками K-12, технологические, инженерные или математические (STEM) образовательные стандарты. Все более 100 000 стандартов K-12 STEM, включенных в TeachEngineering , собираются, поддерживаются и упаковываются сетью стандартов достижений (ASN) , проект Д2Л (www.achievementstandards.org). В ASN стандарты структурированы иерархически: сначала по источнику; напр. по штатам; внутри источника по типу; напр. , естествознание или математика; внутри типа по подтипу, затем по сортам, и т.д. . NGSS: научные стандарты нового поколения — наука Ожидаемая производительность NGSS ГС-ПС3-1. Создайте вычислительную модель для расчета изменения энергии одного компонента в системе, когда известно изменение энергии другого компонента (компонентов) и потоки энергии в систему и из нее. (9-12 классы) Согласны ли вы с таким раскладом? Спасибо за ваш отзыв! Нажмите, чтобы просмотреть другую учебную программу, соответствующую этому ожидаемому результату Этот урок посвящен следующим аспектам трехмерного обучения NGSS: Научная и инженерная практика Ключевые дисциплинарные идеи Сквозные концепции Создать вычислительную модель или симуляцию явления, разработанного устройства, процесса или системы. Соглашение о согласовании: Спасибо за ваш отзыв! Используйте математические представления явлений для описания объяснений. Соглашение о согласовании: Спасибо за ваш отзыв! Энергия — это количественное свойство системы, зависящее от движения и взаимодействия материи и излучения внутри этой системы. Наличие единственной величины, называемой энергией, объясняется тем фактом, что полная энергия системы сохраняется, даже если внутри системы энергия постоянно передается от одного объекта к другому и между ее различными возможными формами. Соглашение о примирении: Спасибо за ваш отзыв! Сохранение энергии означает, что полное изменение энергии в любой системе всегда равно полной энергии, переданной в систему или из нее. Соглашение о согласовании: Спасибо за ваш отзыв! Энергия не может быть создана или уничтожена, но ее можно транспортировать из одного места в другое и передавать между системами. Соглашение о согласовании: Спасибо за ваш отзыв! Математические выражения, которые количественно определяют, как накопленная энергия в системе зависит от ее конфигурации (например, взаимное расположение заряженных частиц, сжатие пружины) и как кинетическая энергия зависит от массы и скорости, позволяют использовать концепцию сохранения энергии. прогнозировать и описывать поведение системы. Соглашение о согласовании: Спасибо за ваш отзыв! Доступность энергии ограничивает то, что может произойти в любой системе. Соглашение о согласовании: Спасибо за ваш отзыв! Модели можно использовать для прогнозирования поведения системы, но эти прогнозы имеют ограниченную точность и надежность из-за допущений и приближений, присущих моделям. Соглашение о согласовании: Спасибо за ваш отзыв! Наука предполагает, что Вселенная представляет собой огромную единую систему, в которой непротиворечивы основные законы. Соглашение о согласовании: Спасибо за ваш отзыв! Общие базовые государственные стандарты — математика Рассуждайте абстрактно и количественно. (Оценки К — 12) Подробнее Посмотреть согласованную учебную программу Согласны ли вы с таким раскладом? Спасибо за ваш отзыв! Модель с математикой. (Оценки К — 12) Подробнее Посмотреть согласованную учебную программу Согласны ли вы с таким раскладом? Спасибо за ваш отзыв! Измените формулы, чтобы выделить интересующую величину, используя те же рассуждения, что и при решении уравнений. (Оценки 9 — 12) Подробнее Посмотреть согласованную учебную программу Согласны ли вы с таким раскладом? Спасибо за ваш отзыв! Решайте линейные уравнения и неравенства с одной переменной, в том числе уравнения с коэффициентами, обозначенными буквами. (Оценки 9 — 12) Подробнее Посмотреть согласованную учебную программу Согласны ли вы с таким раскладом? Спасибо за ваш отзыв! Международная ассоциация преподавателей технологий и инженерии – технология ГОСТ Предложите выравнивание, не указанное выше Какое альтернативное выравнивание вы предлагаете для этого контента? Подписывайся Подпишитесь на нашу рассылку новостей, чтобы получать внутреннюю информацию обо всем, что связано с TeachEngineering, например, о новых функциях сайта, обновлениях учебных программ, выпусках видео и многом другом! PS: Мы никому не передаем личную информацию и электронные письма. Рабочие листы и вложения Рабочий лист по уравнению Бернулли (docx) Рабочий лист по уравнению Бернулли (pdf) Ответы на рабочий лист по уравнению Бернулли (docx) Ответы на рабочий лист по уравнению Бернулли (pdf) Flow Graphics Бернулли (подходит для диапозитивов или раздаточных материалов) (pptx) Потоковая графика Бернулли (подходит для диапозитивов или раздаточных материалов) (pdf) Посетите [www.teachengineering.org/lessons/view/cub_bernoulli_lesson01], чтобы распечатать или загрузить. Больше учебных программ, подобных этому Урок средней школы Принцип Архимеда, закон Паскаля и принцип Бернулли Студенты знакомятся с законом Паскаля, принципом Архимеда и принципом Бернулли. Поставляются основные определения, уравнения, практические задачи и инженерные приложения. Принцип Архимеда, закон Паскаля и принцип Бернулли Урок средней школы Вязкие жидкости Студенты знакомятся со сходствами и различиями в поведении упругих твердых тел и вязких жидкостей. Кроме того, вводятся свойства текучих материалов, такие как вязкость, а также методы, которые инженеры используют для определения этих физических свойств. Вязкие жидкости Урок средней школы Повесть о трениях Учащиеся старших классов узнают, как инженеры математически проектируют дорожки для американских горок, используя подход, согласно которому криволинейная дорожка может быть аппроксимирована последовательностью множества коротких уклонов. Они применяют основное исчисление и теорему о работе-энергии для неконсервативных сил для количественной оценки трения вдоль кривой… Сказка о трениях Урок средней школы Основы Fluid Power Учащиеся узнают об основных понятиях, важных для гидроэнергетики, которая включает в себя как пневматические (газовые), так и гидравлические (жидкостные) системы. Основы гидроэнергетики Предварительные знания алгебра и газовые законы Введение/Мотивация (Обратите внимание, что рисунки 1 и 2 также доступны в виде слайдов PowerPoint в приложении Bernoulli Flow Graphics. Их также можно распечатать в виде диапозитивов или раздаточных материалов для учащихся. ) Вы когда-нибудь задумывались, как самолет может летать? Простой ответ заключается в том, что когда воздух обтекает крыло, самолет выталкивается воздухом с более высоким давлением под крылом по сравнению с более низким давлением над крылом. Но чтобы глубже понять это явление, мы должны обратиться к разделу физики, известному как гидромеханика, и, в частности, к принципу, известному как уравнение Бернулли. Это уравнение может не только предсказать давление воздуха вокруг крыла самолета, но также может быть использовано для определения силы сильного ветра на небоскребе, давления в химическом реакторе или даже скорости воды, вытекающей из шланга в воздухе. твой задний двор. Рис. 1. Простой пример потока в трубе: когда вода теряет высоту от верхнего конца трубы к нижнему, она приобретает скорость. Чтобы найти точное значение любого параметра, мы применяем уравнение Бернулли к двум точкам в любом месте вдоль одной и той же линии тока (обозначенной пунктирной линией). Copyright Copyright © 2009 Карен Кинг. Используется с разрешения. Все права защищены. Уравнение Бернулли утверждает, что для идеальной жидкости (то есть с нулевой вязкостью, постоянной плотностью и установившимся течением) сумма ее кинетической, потенциальной и тепловой энергии не должна изменяться. Это ограничение приводит к предсказуемой зависимости между скоростью (скоростью) жидкости, ее давлением и ее высотой (относительной высотой). В частности, для двух точек на линии тока (воображаемой линии, касательной к направлению потока, как показано на рис. 1) уравнение Бернулли утверждает, что: , где v — скорость жидкости, ρ — плотность жидкости, z — относительная высота, а P — давление. Применение этого уравнения к примеру помогает сделать его более понятным. Рассмотрим водохранилище, расположенное высоко в горах, с трубой, ведущей вниз в город на более низкой высоте. Труба подает воду на гидроэлектростанцию, и мы хотим знать, с какой скоростью вода будет поступать в турбины станции. Рисунок 2 иллюстрирует эту ситуацию. Рис. 2. Пример резервуара. Решение справа от изображения демонстрирует, как использовать уравнение Бернулли, чтобы найти конечную скорость воды, когда она достигает города на более низкой высоте. Copyright Copyright © 2009 Karen King, задача адаптирована из Knight, 2008. Теперь вернемся к тому, как принцип Бернулли применяется к крылу самолета. Когда воздушный поток разделяется вокруг крыла, воздух над крылом движется быстрее, чем воздух под ним, из-за формы крыла. Поскольку скорость верхних слоев воздуха увеличивается, его давление должно уменьшаться для поддержания баланса, как описано в уравнении Бернулли. Это приводит к большему давлению под крылом, чем вверху, что толкает крыло вверх, обеспечивая возможность полета! Предыстория урока и концепции для учителей Уравнение Бернулли представляет собой важное выражение, связывающее давление, высоту и скорость жидкости в одной точке ее течения. Соотношение между этими условиями жидкости вдоль линии тока всегда равно одной и той же константе вдоль этой линии тока в идеализированной системе. Идеализированная система относится к жидкости с постоянной плотностью (несжимаемой) и невязкой. Предположение, что жидкость невязкая, означает, что она не имеет вязкости. Следовательно, некоторые эффекты вязкости, такие как прилипание воды к стенкам ее трубы или емкости, не применяются. Поскольку уравнение Бернулли равно константе во всех точках вдоль линии тока, мы можем приравнять две точки на линии тока. Используя информацию о системе в одной точке, мы можем найти информацию в другой. Согласно эффекту Вентури давление жидкости уменьшается по мере увеличения ее скорости. Уравнение Бернулли переводит это соотношение в математические термины и включает термин для высоты жидкости. Чтобы проиллюстрировать эту взаимосвязь, рассмотрим воду, стекающую по водной горке. В верхней части, где вы загружаетесь, вода движется медленно, толкаясь только водой позади нее. Когда горка падает, вода быстро устремляется вниз, увеличивая скорость по мере падения. Таким образом, на скорость также влияет гравитация через высоту. Когда все эти члены соотносятся и масштабируются для плотности и силы тяжести, мы получаем уравнение Бернулли, где v — скорость жидкости, ρ — плотность жидкости, h — относительная высота, P — давление. Обратите внимание, что константа также имеет единицы измерения давления. Уравнение Бернулли также можно интерпретировать как выражение закона сохранения энергии, которое можно сформулировать как , где KE — кинетическая энергия, PE — потенциальная энергия, а W — работа, выполненная системой. Представьте себе глыбу льда, скользящую по водной горке с некоторой скоростью. Блок имеет кинетическую энергию, равную половине его массы, умноженной на квадрат скорости, или , где KE — кинетическая энергия, а m — масса. Блок также имеет определенную потенциальную энергию, описываемую числом . , где PE — потенциальная энергия, а h — высота. Наконец, над блоком совершается работа силой давления воды за ним (с силой F=PA , где P — давление воды, а A — площадь поверхности льда). который продвигается вперед). Когда блок толкают на расстояние, эквивалентное его собственной ширине, Δx , то работа над блоком равна где V объем. Уравнение сохранения энергии принимает вид . Разделив это уравнение на объем и вспомнив, что плотность ρ Δ равна массе, деленной на объем, получаем , что является уравнением Бернулли. Инженеры могут установить уравнение Бернулли в одной точке равным уравнению Бернулли в любой другой точке на линии тока и найти неизвестные свойства. Учащиеся могут проиллюстрировать эту взаимосвязь, выполнив упражнение «Выстрел под давлением», чтобы найти давление водяного пистолета! Например, инженер-строитель может захотеть узнать, насколько изменяется давление в трубе между верхом здания и землей. Связанные виды деятельности Закрытие урока Уравнение Бернулли имеет широкое применение, от конструкции крыла до потока в трубе. Согласно эффекту Вентури, при увеличении скорости жидкости давление уменьшается и наоборот. Уравнение Бернулли является математическим представлением этого. Уравнение Бернулли можно понять, манипулируя энергией текущей жидкости. Установив уравнение Бернулли равным в двух разных точках вдоль линии тока, можно рассчитать условия жидкости в одной точке, используя информацию из другой точки. Словарь/Определения Принцип Бернулли: в гидродинамике принцип Бернулли утверждает, что для невязкого потока увеличение скорости жидкости происходит одновременно с уменьшением давления или уменьшением потенциальной энергии жидкости. Назван в честь голландско-швейцарского математика Даниэля Бернулли, опубликовавшего свой принцип в книге «Гидродинамика» в 1738 году. Также называется эффектом Бернулли. невязкий поток: поток, в котором можно игнорировать влияние вязкости жидкости. линия тока: Линия, касательная к потоку жидкости в любой момент времени. Эффект Вентури: снижение давления жидкости в результате прохождения жидкости через суженный участок трубы. Когда скорость жидкости увеличивается, ее давление уменьшается, и наоборот. Назван в честь итальянского физика Джованни Баттиста Вентури (1746–1822). Оценка Оценка перед уроком Соответствие: Чтобы помочь учащимся в этом уроке и связанной с ним деятельности, создайте список физических уравнений, которые они уже изучили, таких как кинетическая энергия, потенциальная энергия, работа, уравнения кинематики. В произвольном порядке напишите физические термины на левой стороне доски и соответствующие части уравнений (не по порядку) на правой стороне доски. Попросите учащихся сопоставить правильные стороны вместе. Примеры: Примеры соответствия для оценивания перед уроком. Оценка после внедрения Домашнее задание/самостоятельная практика: Предложите учащимся заполнить Практикум по уравнению Бернулли. Пусть все учащиеся решат первую задачу в классе и вместе проанализируют ответ. Предложите учащимся решить вторую задачу в качестве домашнего задания. Оценка итогов урока Вопрос для обсуждения: В течение следующего урока проведите пятиминутное обсуждение, спросив учащихся, что они узнали из домашнего задания. Дополнительная мультимедийная поддержка Вы можете использовать слайды PowerPoint на Рисунке 1. Простой поток в трубе и Рисунок 2. Пример резервуара с классом, как показано на прилагаемой диаграмме потока Бернулли. См. описания дополнительных реальных применений принципа Бернулли на веб-сайте Science Clarified: http://www.scienceclarified.com/everyday/Real-Life-Chemistry-Vol-3-Physics-Vol-1/Bernoulli-s- Principle-Real-life-applications. html Покажите учащимся интерактивную анимацию принципа Бернулли в виде разреза трубы, форма которой может изменяться с помощью компьютерной мыши, что приводит к изменению давления, площади поперечного сечения и скорости протекающей через нее жидкости. трубы, которые нарисованы под трубой. См. Марк. Веб-сайт Митчелла под названием «Анимированная демонстрация принципа Бернулли» по адресу http://home.earthlink.net/~mmc1919/venturi.html . использованная литература Принцип Бернулли (определение). Последнее обновление: 11 февраля 2010 г. Википедия, бесплатная энциклопедия. По состоянию на 17 февраля 2010 г. http://en.wikipedia.org/w/index.php?title=Bernoulli%27s_principle&oldid=343435891 Найт, Рэндалл. Физика для ученых и инженеров: стратегический подход . Второе издание. Сан-Франциско, Калифорния: Пирсон Аддисон-Уэсли, 2008. . Мансон, Б.Р., Янг, Д.Ф., Окииси, Т.Х. Основы гидромеханики . Пятое издание. Нью-Йорк, штат Нью-Йорк: John Wiley & Sons, Inc., 2006. . Эффект Вентури (определение). Последнее обновление: 12 февраля 2010 г. Википедия, бесплатная энциклопедия. По состоянию на 17 февраля 2010 г. http://en.wikipedia.org/w/index.php?title=Venturi_effect&oldid=343508711 Другая связанная информация Просмотрите центр учебных программ по физике, ориентированных на инженеры NGSS, чтобы найти дополнительную учебную программу по физике и физическим наукам, посвященную инженерии. Авторские права © 2009 Регенты Университета Колорадо Авторы Джеймс Прагер; Карен Кинг; Дениз В. Карлсон Программа поддержки Комплексная программа преподавания и обучения и лаборатория, Инженерный колледж, Колорадский университет в Боулдере Благодарности Содержание этой учебной программы цифровой библиотеки было разработано в рамках гранта Фонда улучшения послесреднего образования (FIPSE), Министерства образования США и Национального научного фонда, грант GK-12 №. 0338326. Однако это содержание не обязательно отражает политику Министерства образования или Национального научного фонда, и вы не должны исходить из того, что оно одобрено федеральным правительством. Последнее изменение: 28 января 2021 г. Гипотеза Бернулли Определение По Джеймс Чен Полная биография Джеймс Чен, CMT — опытный трейдер, инвестиционный консультант и специалист по стратегии глобального рынка. Он является автором книг по техническому анализу и торговле иностранной валютой, опубликованных John Wiley and Sons, а также выступал в качестве приглашенного эксперта на CNBC, BloombergTV, Forbes и Reuters среди других финансовых СМИ. Узнайте о нашем редакционная политика Обновлено 30 ноября 2021 г. Рассмотрено Чарльз Поттерс Рассмотрено Чарльз Поттерс Полная биография Чарльз является признанным на национальном уровне специалистом по рынкам капитала и педагогом с более чем 30-летним опытом разработки программ углубленного обучения для начинающих финансовых специалистов. Чарльз преподавал в ряде учреждений, включая Goldman Sachs, Morgan Stanley, Societe Generale и многих других. Узнайте о нашем Совет финансового контроля Факт проверен Кирстен Рорс Шмитт Факт проверен Кирстен Рорс Шмитт Полная биография Кирстен Рорс Шмитт — опытный профессиональный редактор, писатель, корректор и специалист по проверке фактов. У нее есть опыт в области финансов, инвестиций, недвижимости и всемирной истории. На протяжении всей своей карьеры она писала и редактировала контент для многочисленных потребительских журналов и веб-сайтов, составляла резюме и контент для социальных сетей для владельцев бизнеса, а также создавала материалы для академических кругов и некоммерческих организаций. Кирстен также является основателем и директором Your Best Edit; найдите ее на LinkedIn и Facebook. Узнайте о нашем редакционная политика Что такое Гипотеза Бернулли? Гипотеза Бернулли утверждает, что человек принимает риск не только на основе возможных потерь или выгод, но и на основе полезности, полученной от самого рискованного действия. Основные выводы Гипотеза Бернулли утверждает, что человек принимает риск как на основе возможных потерь или выгод, так и на основе полезности, полученной от самого действия. Гипотеза была предложена математиком Даниэлем Бернулли в попытке решить так называемый петербургский парадокс. Парадокс Санкт-Петербурга был вопросом, который, по сути, спрашивал, почему люди неохотно участвуют в честных играх, где шанс выиграть так же вероятен, как и шанс проиграть. Гипотеза Бернулли также вводит понятие убывающей предельной полезности, получаемой от увеличения количества денег. Понимание гипотезы Бернулли Эта гипотеза была предложена математиком Даниэлем Бернулли в попытке решить то, что было известно как Санкт-Петербургский парадокс. Парадокс Санкт-Петербурга был вопросом, который, по сути, спрашивал, почему люди неохотно участвуют в честных играх, где шанс на победу так же вероятен, как и на проигрыш. Гипотеза Бернулли разрешила парадокс, введя понятие ожидаемой полезности и заявив, что количество полезности от игры является важным фактором, влияющим на то, участвовать или нет. Гипотеза Бернулли также вводит понятие убывающей предельной полезности, получаемой от увеличения количества денег. Чем больше денег у человека, тем меньше пользы он получает от получения большего количества денег. Это сделает человека, который выиграл несколько раундов игры и получил дополнительные деньги, с меньшей вероятностью участвовать в будущем, поскольку фактор полезности больше не присутствует, даже если шансы не изменились. Гипотеза Бернулли в финансах Гипотеза Бернулли может быть применена к финансовому миру при рассмотрении терпимости инвестора к риску. По мере того, как количество денег, которыми располагает человек, растет, он может стать более склонным к риску (несмотря на то, что его способность брать на себя риск увеличивается из-за увеличения его капитала), потому что он испытывает уменьшение предельной полезности с каждым дополнительным заработанным долларом. Поскольку они больше не чувствуют пользы от своих доходов, они больше не хотят играть в рискованные игры. С рациональной точки зрения нет причин прекращать играть в игру, в которой шансы равны. Иными словами, нет причин прекращать инвестировать в более высокие уровни риска и вознаграждения, чтобы максимизировать прибыль. На практике, однако, сумма денег, которую можно выиграть/заработать, в конце концов перестает быть для человека ценностью, поскольку полезность каждого доллара уменьшается по мере того, как у вас их более чем достаточно. Тесно связанная с идеей убывающей предельной отдачи, гипотеза Бернулли, по сути, утверждает, что не следует принимать очень рискованный инвестиционный выбор, если потенциальная отдача не принесет большой пользы или ценности. Можно ожидать, что молодой инвестор, у которого впереди еще годы с самым высоким доходом, примет больший инвестиционный риск, поскольку потенциальная прибыль может быть очень ценной по сравнению с относительным отсутствием богатства у такого человека. С другой стороны, пенсионеру-инвестору, уже имеющему достаточно сбережений в банке, не следует искать высоковолатильные или рискованные инвестиции, поскольку потенциальные выгоды вряд ли будут стоить риска. No related posts. Добавить комментарий Отменить ответ Ваш адрес email не будет опубликован. Обязательные поля помечены * Комментарий * Имя * Email * Сайт