Построение графика функций — презентация онлайн
Похожие презентации:
Использование презентаций PowerPoint на уроках математики при построении графиков функции
Построение графиков функций содержащих знак модуля
Построение графиков функций с помощью сдвигов и деформаций
Построение графиков квадратичной функции, содержащей модуль
Модуль. Графики функций, содержащих переменную под знаком модуля
Применение производной к исследованию функции и построению графика функции
Построение графиков функций со знаком модуля
Исследование функций и построение графиков
Исследование функции. Построение графика
Алгоритм построения графиков функции, аналитическое выражение которых содержит знак абсолютной величины
График функции у = |х|
а) Если х≥0, то |х| = х функция у = х, т.е. график
совпадает с биссектрисой первого координатного угла.
б) Если х<0, то |х| = -х и у = — х. При отрицательных
значениях аргумента х график данной функции – прямая
 е. биссектриса второго координатного угла.
е. биссектриса второго координатного угла.Построить
Далее
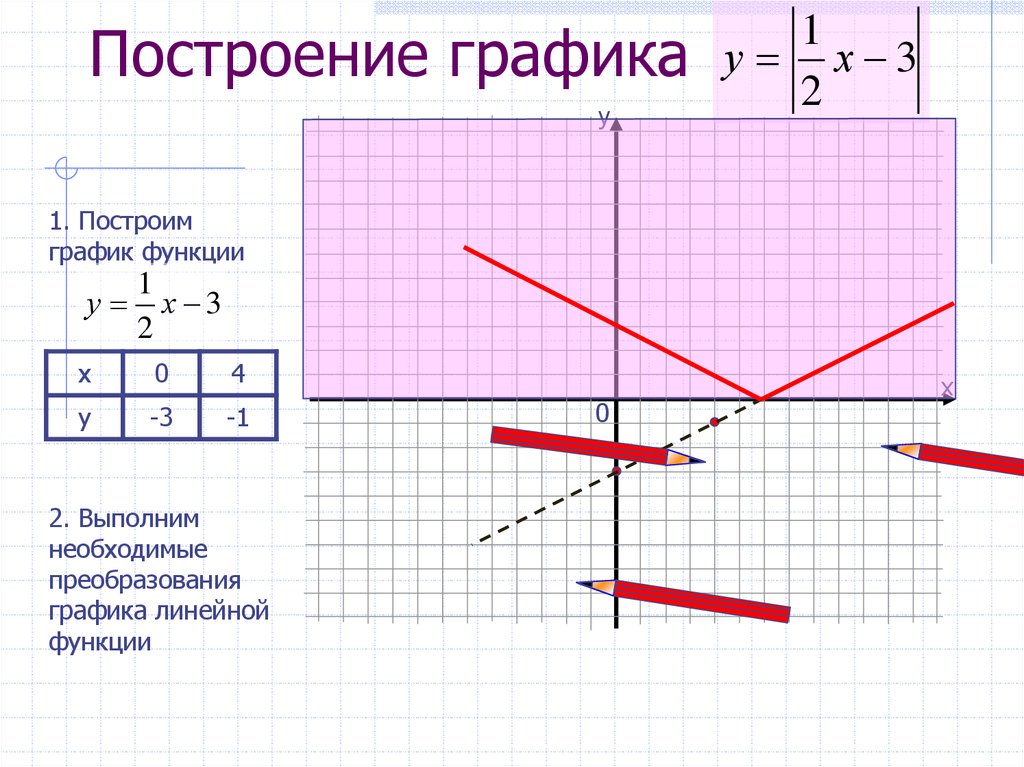
y=
у = |х² — х -6|
1.Построим график функции
у =х² — х -6
Проверь
2.
Участки графика, расположенные в
нижней полуплоскости, отображаем
симметрично относительно оси ОХ.
Для построения графика функции у = |f(х) | достаточно:
1.Построить график функции у = f(х) ;
2. На участках, где график расположен в нижней
полуплоскости, т.е., где
f(х) <0, симметрично отражаем относительно оси абсцисс.
7. График функции у = f |(х)|
Для построения графика функции у = f |(х)| достаточно:1. построить график функции у = f(х) для х>0;
2. Для х<0, симметрично отразить построенную часть
относительно оси ОУ.
Построить график функции у=0,25 х² — |х| -3.
1) Поскольку |х| = х при х≥0, требуемый график совпадает с
параболой у=0,25 х² — х — 3.
Если х<0, то поскольку х² = |х|², |х|=-х
Построить
и требуемый график совпадает с параболой у=0,25 х² + х 3.
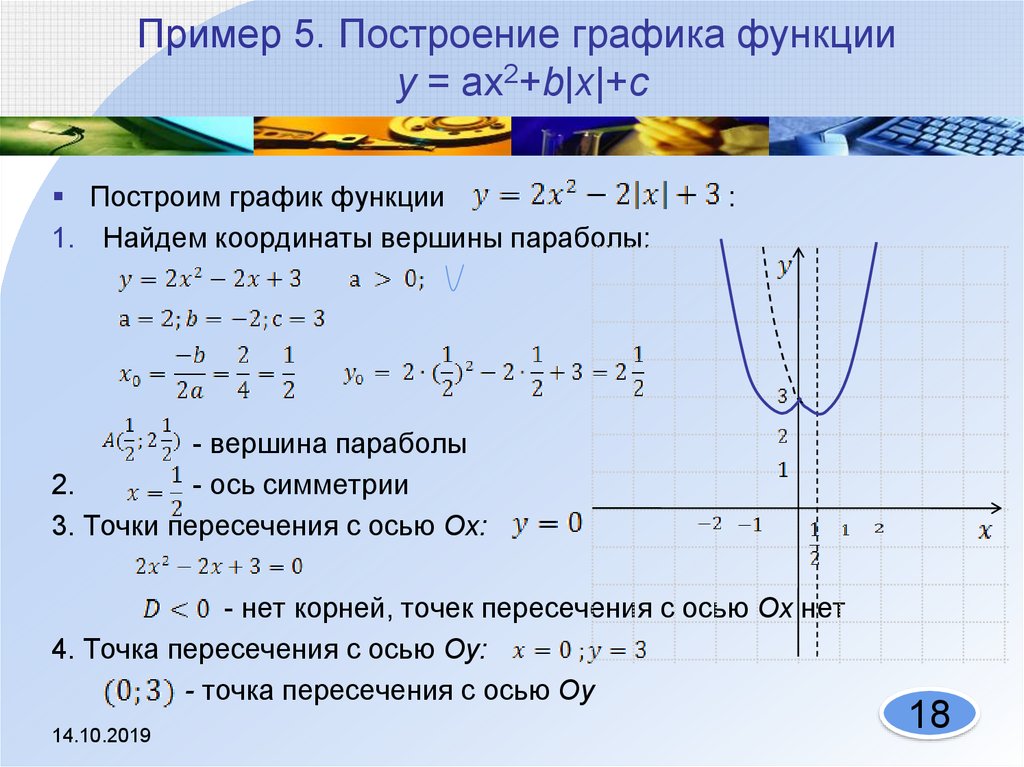
2) Если рассмотрим график у=0,25 х² — х — 3 при х≥0 и
отобразить его относительно оси ОУ мы получим тот
же
самый график.
Найдите все положительные значения к, при
которых прямая у=кх пересекает в одной точке
ломанную, заданную
у условиями:
Х< — 3
9
8
7
6
5
4
3
2
1
Х>3
-3 < x < 3
-7 -6 -5 -4 -3 -2 -1
о
-1
-2
1
-3
-4
-5
-6
2
3
4
5
6
7
1, если х 3
у 2 х 5, х 3
2 х 5, x 3
Построить
1.
у=1,
-3
<
x
<
3
х
2. у=-2х-5, x < -3
3. у=-2х-5, x < 3
Решить систему уравнений
4
у ,
х
у х 1 4.
у
9
8
7
6
5
4
3
2
1
-7 -6 -5 -4 -3 -2 -1
о
-1
-2
1
-3
-4
-5
-6
2
3
4
5
6
7
х
1. у = IхI
2. у = Iх+1I
2. у = Iх+1I – 4
Ответ:
(-1;4), (-4;-1), (4;1).
English Русский Правила
Читать онлайн «Построение графиков функций», Дмитрий Кудрец – Литрес
© Дмитрий Кудрец, 2020
ISBN 978-5-0051-8611-9
Создано в интеллектуальной издательской системе Ridero
Построение графиков функций
Существуют различные способы построения графиков функций. Выбор того или иного способа зависит в первую очередь от уровня подготовленности учащегося, пройденного материала, а также непосредственно от условия поставленной задачи.
Рассмотрим основные способы построения графиков функций:
– построение графика функции по точкам;
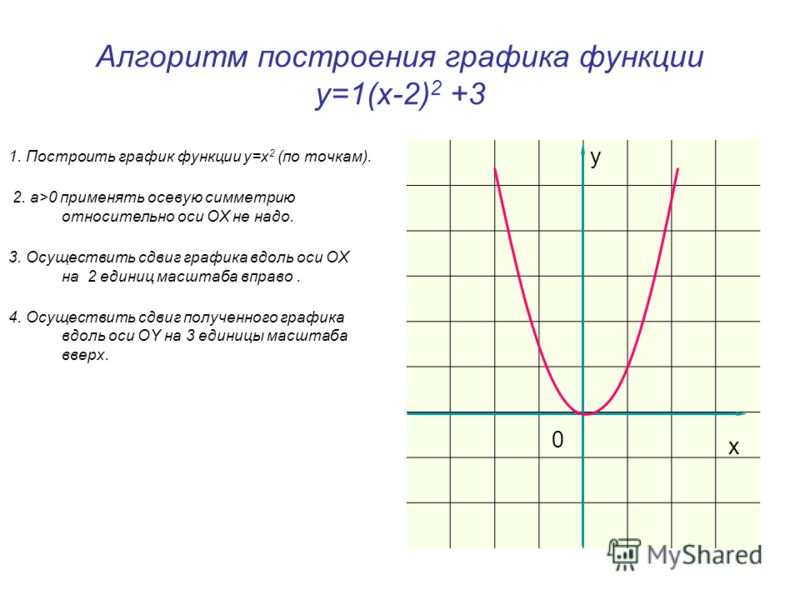
– построение графика функции с помощью преобразования элементарных функций;
– построение путем сложения, умножения, деления элементарных функций;
– построения графика функции путем исследования функции;
– построение графика функции с помощью производной.
При построении графика следует учесть его вид, т.е. тип функции который описывает тот или иной график.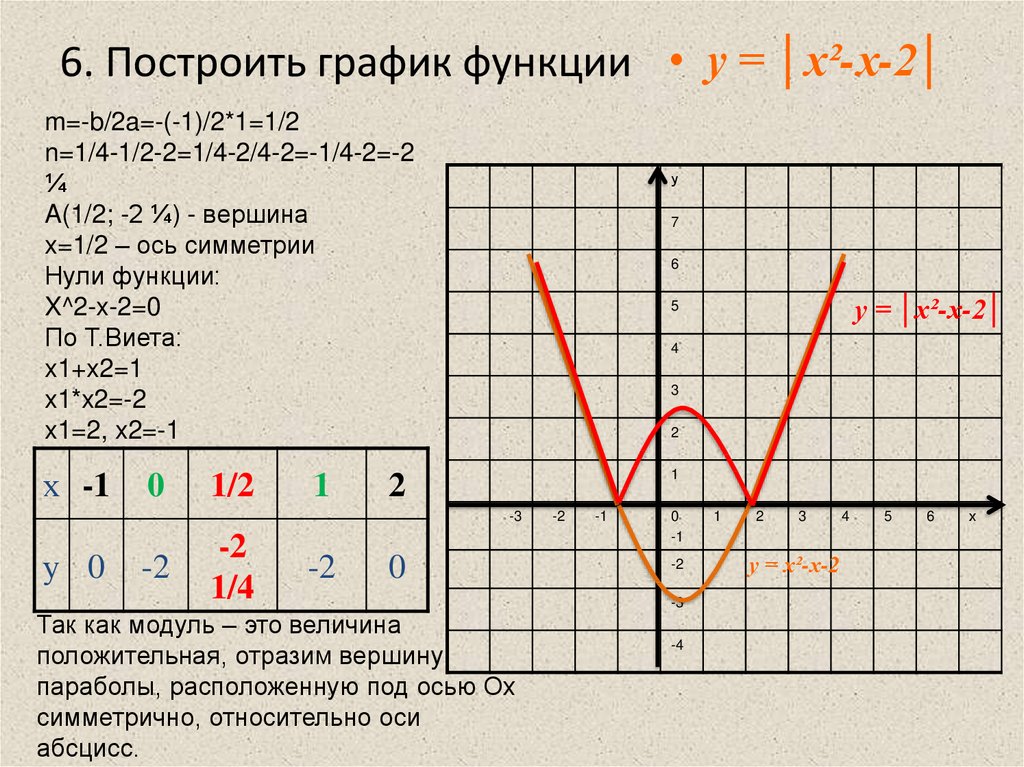
Основными элементарными функциями являются: линейная, степенная, показательная, логарифмическая и тригонометрические функции.
Линейная функция
Линейной называется функция вида f (x) =kx+b, где k, b – действительные числа. k называется угловым коэффициентом прямой, он равен тангенсу угла наклона прямой к оси Ох.
Графиком линейной функции является прямая. Для ее построения на координатной плоскости достаточно указать всего две точки.
В зависимости от значений коэффициентов k и b график может принимать различный вид.
Степенная функция
Степенной называется функция вида f (x) =xn. В зависимости от значения числа n степенная функция может принимать различный вид.
Показательная функция
Показательной называется функция вида f (x) =ax, где a> 0, а≠1.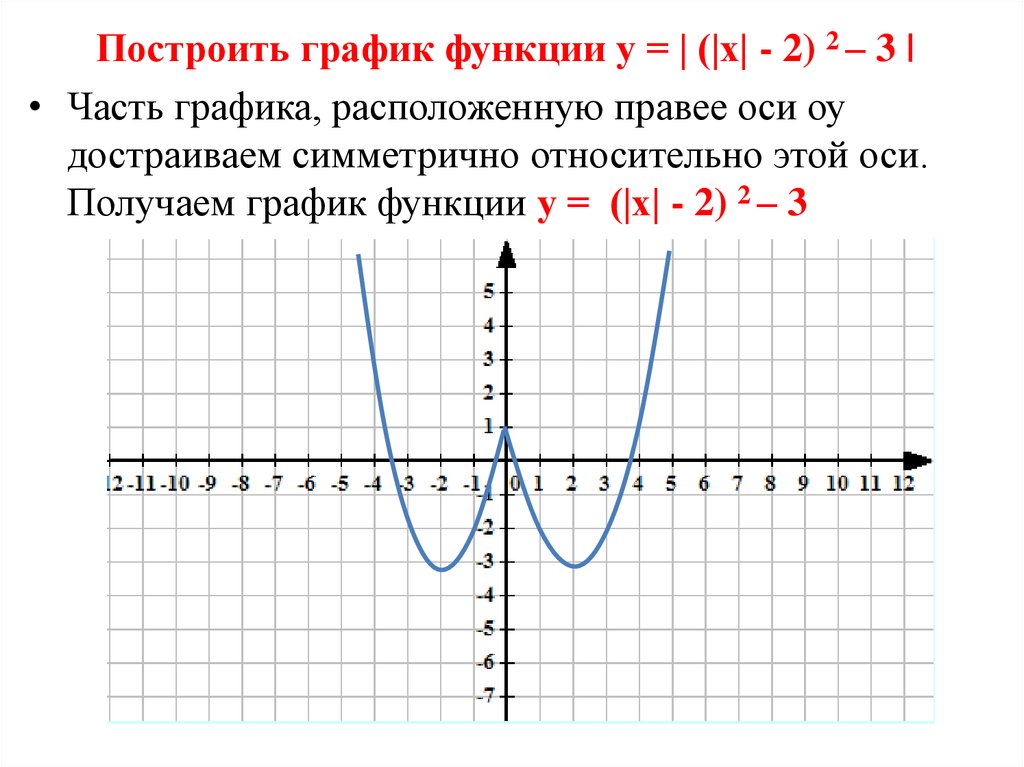 График этой функции проходит через точки с координатами (0;1) и (1; а).
График этой функции проходит через точки с координатами (0;1) и (1; а).
В зависимости от значения числа а, график может иметь вид:
Логарифмическая функция
Логарифмической называется функция вида f (x) =logax, где a> 0, а≠1.
График логарифмической функции не пересекает ось Оу и проходит через точку с координатой (1; а).
В зависимости от значения числа а, график логарифмической функции может иметь различный вид.
Тригонометрические функции
Тригонометрическими называются функции вида f (x) =sinx, f (x) =cosx, f (x) =tgx, f (x) =ctgx.
Построение графика функции по точкам
Построение графика функции по точкам выполняется в следующем порядке:
1. составляется таблица значений аргумента и функции на основе данной формулы;
2. в выбранной системе координат строятся точки, координатами которых являются соответствующие значения переменных, содержащиеся в таблице;
в выбранной системе координат строятся точки, координатами которых являются соответствующие значения переменных, содержащиеся в таблице;
3. полученные точки соединяются плавной линией.
При задании значений аргумента следует учитывать область определения функции.
Пример 1. Построить график функции у=х (6-х), где -1 <х <5.
Решение. Функция у=х (6-х) определена на всем указанном интервале. Составим таблицу значений аргумента и функции:
На координатной плоскости отметим полученные точки и соединим их плавной линией.
Получим график функции у=х (6-х) на интервале -1 <х <5.
При построении графика функции по точкам иногда указывают шаг, т.е. число, через которое выбирается последующее значение аргумента. Чем меньше шаг, тем точнее получается график.
Задание 1. Постойте по точкам график функции…
Пример 2. Постройте график функции у=х2—3, на интервале [– 4; 4] с шагом 1.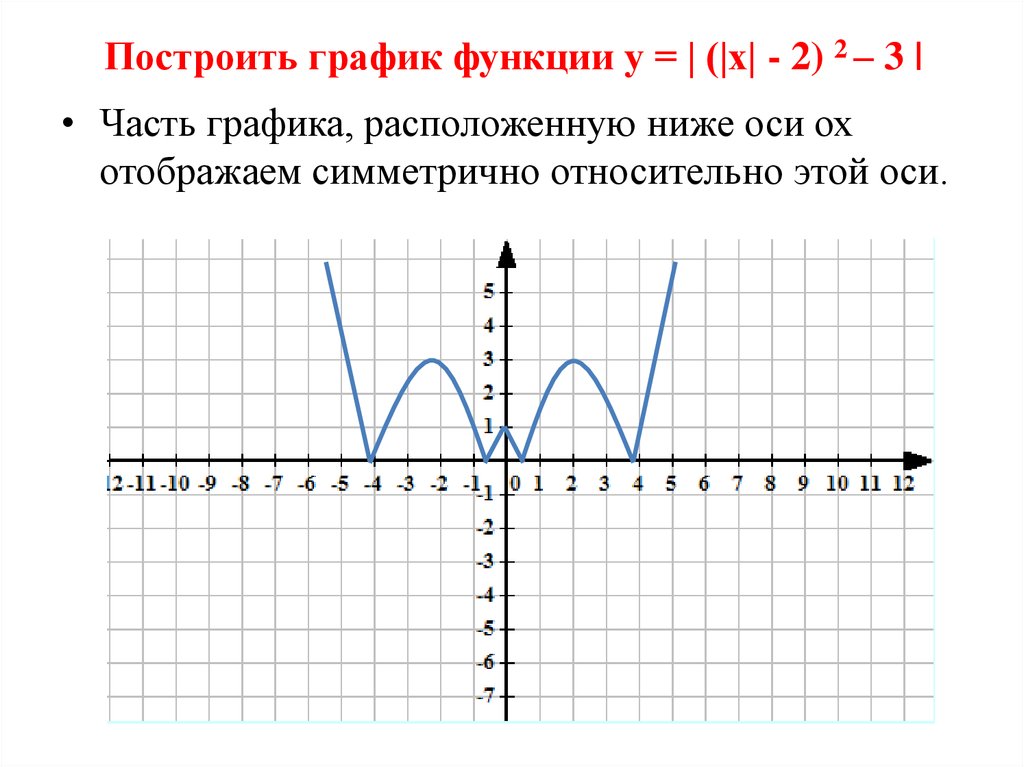
Решение. Функция у=х2—3 определена на всем интервале. Составим таблицу значений. Первое значение аргумента -4. Следующее с учетом шага -4+1=-3 и т. д. пока не получим последнее значение 4.
Графическое представление функции ln(x)
Программное обеспечение для построения графиков онлайн , также известное как графопостроитель , это онлайн-график , который позволяет отображать функции в режиме онлайн. Просто введите выражение в соответствии с x функции, которую нужно построить, используя обычные математические операторы. Построитель кривых особенно подходит для функционального исследования , позволяет получить графическое представление функции из уравнения кривой, его можно использовать для определения вариации, минимума, максимума функции.
Онлайн-плоттер также может рисовать параметрические кривые. и рисовать полярные кривые, а для функций достаточно ввести выражение для представления по параметру t.
и рисовать полярные кривые, а для функций достаточно ввести выражение для представления по параметру t.
В графическом калькуляторе для записи математических функций должны использоваться следующие операторы: 9Для питания
Это программное обеспечение для построения кривых позволяет использовать следующие обычных математических функций :
- абс (абсолютное значение), график абсолютного значения
- арккос (арккосинус), арккосинус участка
- арксинус (арксинус), арксинус графика
- арктангенс (арктангенс), арктангенс графика
- ch (гиперболический косинус), построить гиперболический косинус
- cos (косинус), график косинус
- cosec (косеканс), косеканс участка
- котан (котангенс), котангенс участка
- coth (гиперболический котангенс), построить гиперболический котангенс
- cube_root (кубический корень), построить кубический корень
- опыта (экспоненциальный), экспоненциальный график
- ln (напировский логарифм), построить напьеровский логарифм логарифм
- (логарифм), логарифм графика
- сек (секанс), секущая участка
- ш (гиперболический синус), построить гиперболический синус
- sin (синус), график синуса
- sqrt (квадратный корень), участок квадратный корень
- тангенс (тангенс), участок касательной
- -й (гиперболический тангенс), построить гиперболический тангенс
- абс.
 (абсолютное значение),
график абсолютного значения
(абсолютное значение),
график абсолютного значения - арккос (арккосинус), арккосинус участка
- арксинус (арксинус), арксинус графика
- арктангенс (арктангенс), арктангенс графика
- ch (гиперболический косинус), построить гиперболический косинус
- cos (косинус), график косинус
- cosec (косеканс), косеканс участка
- котан (котангенс), котангенс участка
- coth (гиперболический котангенс), построить гиперболический котангенс
- cube_root (кубический корень), построить кубический корень
- опыта (экспоненциальный), экспоненциальный график
- ln (напировский логарифм), построить напьеровский логарифм логарифм
- (логарифм), логарифм графика
- сек (секанс), секущая участка
- ш (гиперболический синус), построить гиперболический синус
- sin (синус), график синуса
- sqrt (квадратный корень), участок квадратный корень
- тангенс (тангенс), участок касательной
- -й (гиперболический тангенс), построить гиперболический тангенс
- Графические функции онлайн
Этот онлайн-плоттер позволяет вам рисовать несколько кривых одновременно ,
просто введите выражение функции, которую нужно построить, и нажмите «Добавить», графическое представление функции появляется мгновенно, можно повторить операцию для построения других кривых онлайн .
Переменная, которая будет использоваться для представления функций, — «x».
Координаты точек на кривой можно получить с помощью курсора. Для этого нажмите на кривую, чтобы появился этот курсор, а затем перетащите вдоль кривой, чтобы увидеть ее координаты.
Кривые можно удалить из плоттера:
- Чтобы удалить кривую, выберите кривую, затем нажмите кнопку удаления в меню.
- Чтобы удалить все кривые с графика, нажмите кнопку удалить все в меню.
Можно изменить кривую, представленную на графике, выбрав ее, отредактировав ее выражение и затем щелкнув на кнопку редактирования.
онлайн-плоттер имеет несколько опций, позволяющих настроить график.
Чтобы получить доступ к этим параметрам, нажмите кнопку параметров. Затем можно определить границы графов,
чтобы подтвердить эти изменения, необходимо снова нажать кнопку параметров.
- Проведение касательной функции к точке
- График производной функции
Онлайн-плоттер позволяет провести тангенс функции в точке для этого, вы просто рисуете нужную функцию, затем, как только функция нарисована, нажмите на меню, параметры, а затем кнопку касательной, которая появляется на экране, после чего будет нарисована касательная, можно изменить точку касательной, что приводит к перерисовке касательной. Калькулятор позволяет определить уравнение касательной очень просто, с уравнением кривой.
Онлайн-плоттер позволяет вам построить производную функции для этого,
вы просто рисуете нужную функцию, затем после того, как функция нарисована,
нажмите на меню, на параметры, затем на появившуюся производную кнопку,
затем строится производная функции.
9Построитель кривых 0003 также можно использовать для вычисления производной функции и к участок он для этого, вам нужно нарисовать нужную функцию, затем, как только функция будет нарисована, выберите ее, щелкнув по ней, на кривой появится красный курсор. Затем нажмите на меню, на параметры, затем на производную кнопку «выражение», которая появляется на экране, затем строится и вычисляется производная функции. («Выражение» представляет собой выражение, которое необходимо получить и нанести на график).
Плоттер позволяет рисовать параметрическую кривую , для этого
вам просто нужно ввести абсциссу, ординату как функцию от t,
затем нажмите кнопку «Построить параметрическую кривую»,
кривая автоматически отображается с двумя курсорами для отображения нужных точек.
Построитель кривых можно использовать для построения полярной кривой . Для этого просто введите выражение полярной кривой в зависимости от t, затем нажмите кнопку «Построить полярную кривую», кривая автоматически отобразится с двумя курсорами для отображения нужных точек.
Есть возможность двигаться по кривым и получать координаты точки, на которой находится курсор, Для этого необходимо ввести курсор и перемещать его по графику, координаты X и Y отображаются под графиком.
Можно изменить область графика, для этого необходимо зайти в меню, затем нажать на опции, Затем можно изменить пределы графического дисплея.
Графический калькулятор предлагает возможность масштабировать и перемещать область графика. Сделать это,
используйте область в правом нижнем углу графиков.
Сделать это,
используйте область в правом нижнем углу графиков.
- Кнопка + позволяет увеличить масштаб кривых,
- — позволяет уменьшить масштаб кривых,
- Стрелки используются для перемещения кривых,
Можно экспортировать построенные кривые с помощью графического калькулятора , экспорт осуществляется как
изображение в формате PNG. Для этого вам нужно зайти в меню графика, затем в подменю экспорта графиков.
Затем калькулятор отображает построенные кривые в виде изображения, просто щелкните правой кнопкой мыши, чтобы экспортировать изображение,
также возможно скопировать изображение.
Чтобы вернуться к обычному отображению калькулятора, используйте кнопку Выход из режима изображения.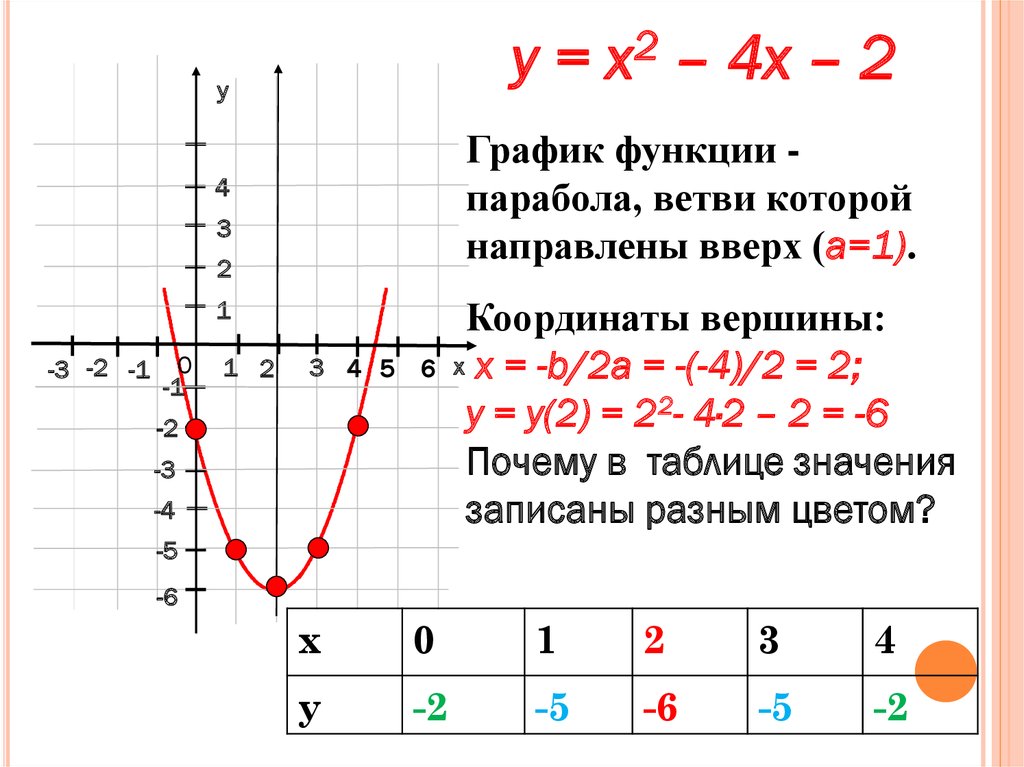
Графический калькулятор и многофункциональный плоттер
Нажмите здесь, чтобы начать Графический калькулятор и многофункциональный плоттер
Графический калькулятор и многофункциональный плоттер с поддержкой стандартных алгебраических функций в декартовой плоскости. Особенности включают быстрое, точное построение графиков и полную поддержку масштабирования и панорамирования с помощью мыши. Кроме того, доступно множество графических инструментов, таких как трассировка функции, поиск корня, поиск производной и т. д.
Помните, что ваше мобильное устройство имеет ограниченную память и вычислительную мощность. Будьте добры к этому! (Держите свою функцию простой…) 9x) и логарифм (ln(x) для натурального логарифма и log(x) для логарифмического основания 10)
 Например, попробуйте sign(sin(x))
Например, попробуйте sign(sin(x))Фактически, вы можете использовать большинство математических функций javascript, в том числе
- потолок: потолок(x) и круглый : круглый(x)
- квадратный корень: sqrt(x)
Вы также можете использовать любые комбинации вышеперечисленных, например, «ln(abs(x)» пары точек на графике и соединить их прямой линией.
Однако, если известно только уравнение функции, то сначала нужно составить таблицу значений.
Мы можем построить график аффинной функции, используя параметры a и b функции. Действительно, если мы знаем точку пересечения (параметр b) и скорость изменения (параметр a), мы можем легко провести линию на декартовой плоскости.
Давайте посмотрим на технику, построив следующее уравнение с использованием параметров a и b: y = 2x − 3. В этом уравнении параметр a равен 2, а параметр b равен -3. Следовательно, мы можем сказать, что скорость изменения равна 2, а точка пересечения равна -3.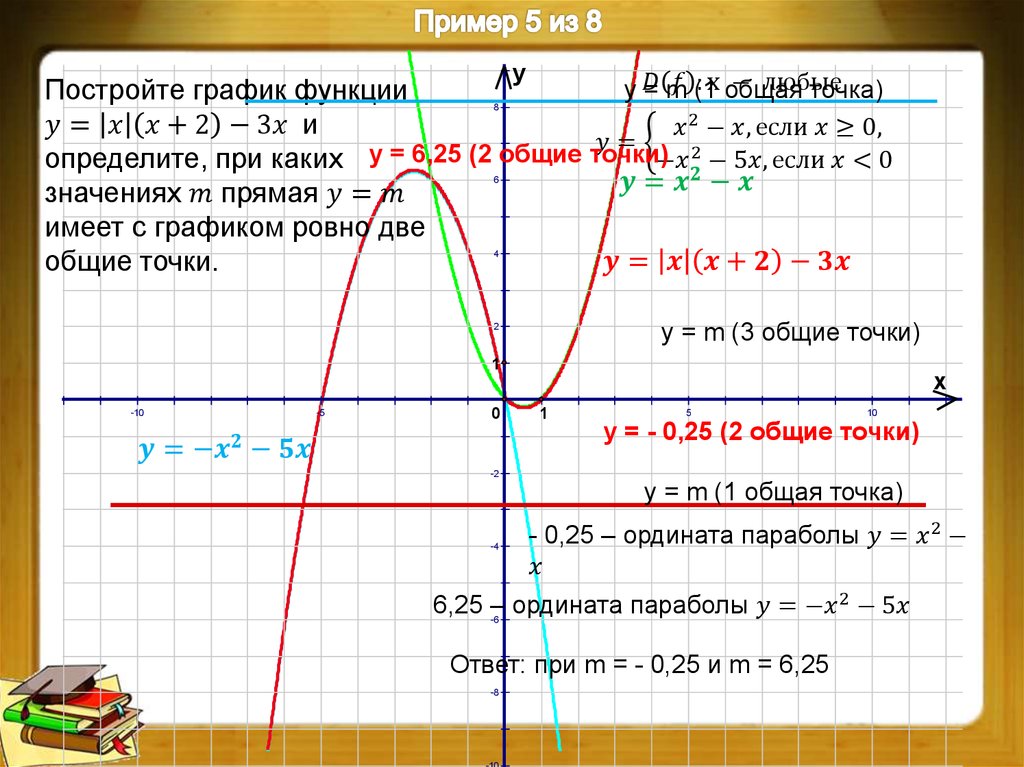

 (абсолютное значение),
график абсолютного значения
(абсолютное значение),
график абсолютного значения