Упорядоченные пары, построение линейных графиков.
 .. Пошаговое решение математических задач
.. Пошаговое решение математических задач8.1 Упорядоченные пары
и y = 2x + 3 представляют отношения между парами переменных. Например, в первом уравнении, если t = 3, то d = 60 * 3 = 180. Понимая, что t — первое, а d — второе, мы можем записать пару (3, 180) для представления t = 3 и d = 180. Пара (8,180) называется упорядоченной парой. Очевидно, (180, 3) отличается от (3, 180), если t — первое число, а d — второе число.
Говорят, что (3, 180) удовлетворяет уравнению или является решением уравнения d=60t. Точно так же (100, 5) удовлетворяет {Iota} = 0,05P, где P = 100 и {Iota} = 0,05 (100) = 5 . Кроме того, (2, 7) удовлетворяет y = 2x + 3, где x = 2 и y=2*2+3=7.
В упорядоченной паре, скажем (x, y), x называется первым компонентом, а y называется вторым компонентом. Чтобы найти упорядоченные пары, удовлетворяющие такому уравнению, как y = 2x + 3, мы можем выбрать любое значение для одной переменной, а затем найти соответствующее значение для другой переменной, подставив его в уравнение.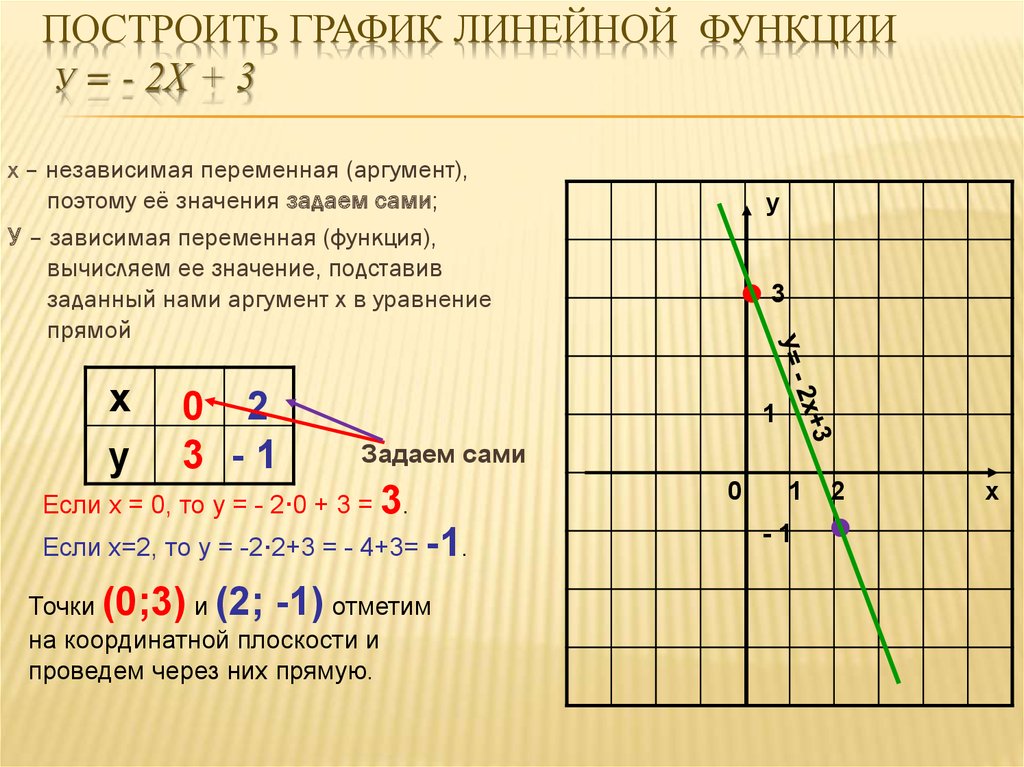
выберите x=1, тогда y=2*1+3=5
выберите x= -2, тогда y=2(-2)+3= -1
выберите x=1/2, тогда y=2 (1/2)+3=4
Все упорядоченные пары (1,5), (-2, -1) и (1/2, 4) удовлетворяют уравнению y = 2x + 3.
Присвоенная переменная к первому компоненту также называется независимой переменной, а переменная, присвоенная второму компоненту, называется зависимой переменной. Таким образом, мы связываем (x, y) с y = 2x + 3, а y «зависит» от значений, присвоенных x.
Мы также можем записать пары в виде таблиц. Выбор значений независимой переменной произволен.
d=60 т
| т | д |
| 5 | 60*5=300 |
| 10 | 60*10=600 |
| 12 | 60*12=720 |
| 15 | 60*15=900 |
{Йота}=0,5P
| P | {Йота} |
| 100 | 0,05*(100)=5 |
| 200 | 0,05(200)=10 |
| 500 | 0,05(500)=25 |
| 1000 | 0,05(1000)=50 |
y=2x+3
| x | г |
| -2 | 2(-2)+3=-1 |
| -1 | 2(-1)+3=1 |
| 0 | 2(0)+3=3 |
| 3 | 2(3)+3=9 |
Другим обозначением, обычно используемым в математике для представления зависимой переменной, является обозначение функции.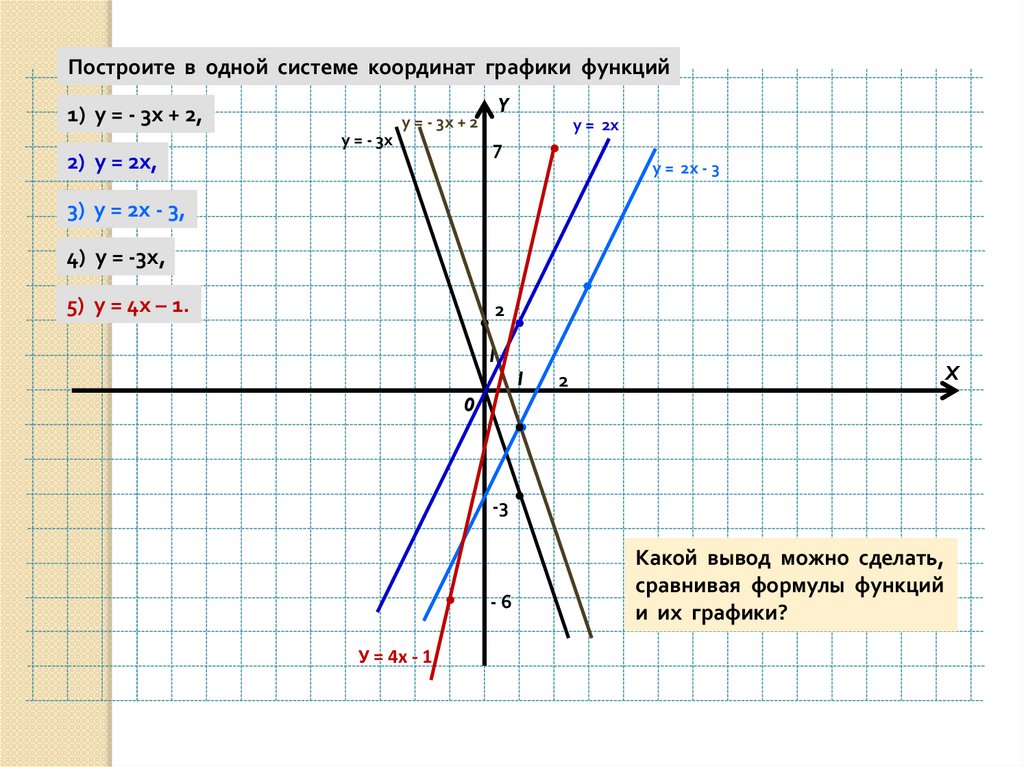
если f(x)=2x-5
то f(1)=2*1-5=-3
f(3)=2*3-5=1
90 906 ж(6) =2*6-5=7и f(-1)=2(-1)-5=-7
(Примечание: f(x) не означает умножение f на x. f(x) — самостоятельная запись.)
Благодаря работам Рене Декарта (1596-1650) мы можем представить упорядоченные пары как точек на плоскости путем построения графика в декартовой системе координат. В этой системе две числовые линии пересекаются под прямым углом и делят плоскость на четыре квадранта. Начало, обозначенное упорядоченной парой (0, 0), является точкой пересечения. Горизонтальная числовая линия называется горизонтальной осью или осью X. Вертикальная числовая линия называется вертикальной осью или осью Y. Точки, лежащие на любой из осей, не находятся ни в одном квадранте. Они просто расположены на оси (см. рис. 8.1).
Другими словами, каждой точке соответствует одна упорядоченная пара действительных чисел, а каждой упорядоченной паре действительных чисел соответствует одна точка.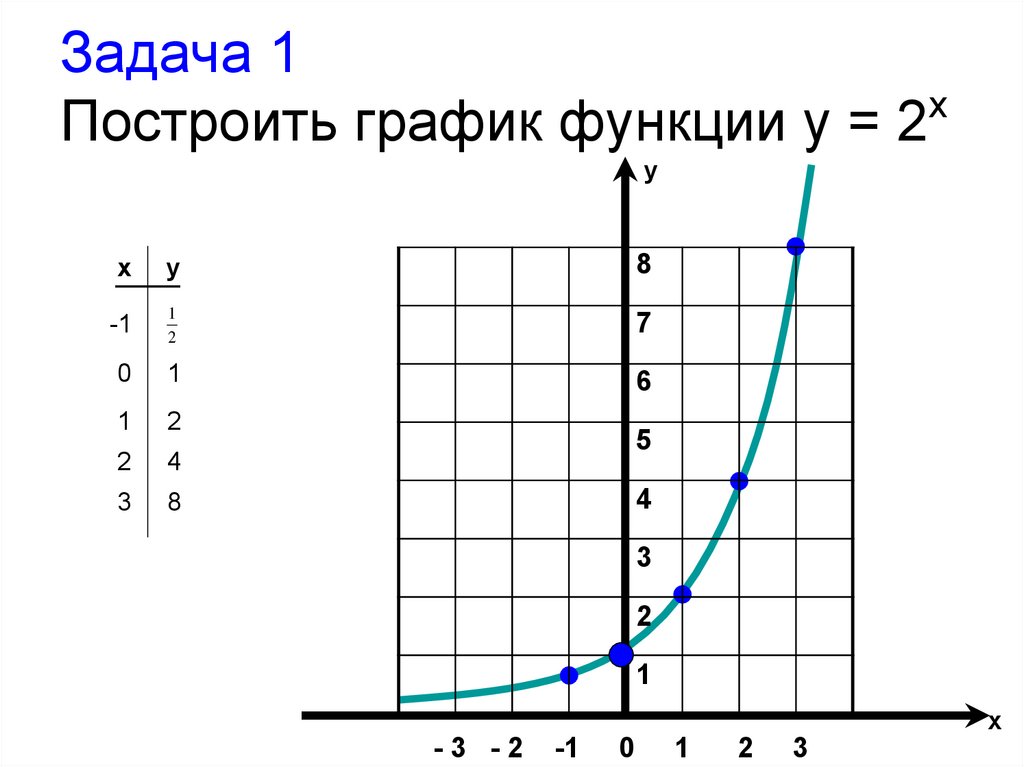 Это важное соотношение является краеугольным камнем декартовой системы координат.
Это важное соотношение является краеугольным камнем декартовой системы координат.
Графики точек A(2, 1), B(-2, 3), C(-3, -2), D(l, -2) и {эпсилон}=(3, 0) показано на рисунке 8.2. (Примечание: упорядоченная пара действительных чисел и соответствующая точка на графике часто используются для обозначения друг друга. Таким образом, упорядоченная пара (2,1) и точка (2,1) взаимозаменяемы.)
Рис. 1 и 2
1.{(-2,1),(0,2),(1,3) , (2, -3)}
2. {(-1,3),(0,1),(1,-1),(2,-3),(3,-5)}
3. Если f(x)=-2x+1, найти f(-1),f(0),f(1),f(2) и f(3).
f(1)=-2(-1)+1=3
f(0)=-2(0)+1=1
f(1)=-2(1)+1=-1
f(2)=-2(2)+1=-3
F (3) =-2 (3) + 1 = -5
8.2 Графические линейные уравнения
Предположим точки. Мы построим график пяти, чтобы попытаться найти закономерность (см. рис. 8.3).
Пять точек на рис. 8.3 лежат на одной прямой. На самом деле они лежат на прямой, и любая упорядоченная пара, удовлетворяющая уравнению y = 2x + 3, также будет лежать на этой прямой.
От чего зависит, будут ли точки, удовлетворяющие уравнению, лежать на прямой? Точки, удовлетворяющие любому уравнению вида
Ax+By=C
будет Лежать на прямой. Уравнение называется линейным уравнением и считается стандартной формой уравнения прямой. Мы можем записать уравнение y = 2x + 3 в стандартной форме -2x + y = 3.
| x | 2х+3=у |
| 0 | 2(0)+3=3 |
| -1 | 2(-1)+3=1 |
| 1/2 | 2(1/2)+3=4 |
| 1 | 2(1)+3=5 |
| -2 | 2(-2)+3=-1 |
Рис. прямой линии, для определения всего графика необходимо всего две точки. (Две точки определяют линию.) Выбор двух точек зависит от выбора любых двух значений x или любых двух значений y.
Примеры
1. Нарисуйте график линейного уравнения x + 3y = 6.
Нарисуйте график линейного уравнения x + 3y = 6.
x=0
0+3y=6
y=2
x=3
3+3y =6
3y=3
y=1
На графике две точки (0, 2) и (3, 1). Возможно, вы выбрали еще два. Избегайте выбора двух точек близко друг к другу.
2. Нарисуйте график линейного уравнения 2x-5y=10
x=5
2*5-5y=10
10-5y=10
-5y=10
y=0
x=0
2*0-5y=10 9090 9
0-5y=10
y=-2
x= -5
2(-5)-5y=10
-10-5y=10
-5y=20
y=-4
Построение графика по трем точкам — хорошая идея, просто чтобы убедиться, что график в правильном положении.
Хотя выбор значений для x или y может быть произвольным, принимая значение x = 0, мы найдем точку на графике, где линия пересекает ось y. Эта точка называется y-перехватом. Точка пересечения с осью X — это точка, которую можно найти, приняв y = 0. Эти две точки обычно легко найти, и они часто используются в качестве двух точек для построения графика линейного уравнения.
Примеры
Нарисуйте следующие линейные уравнения, найдя точки пересечения x и
точек пересечения y.
1. 3y+2x=6
x=0→y=2
y=0→x=3
Посмотрим как наш математический решатель генерирует график этого уравнения и подобных линейных уравнений. Нажмите кнопку «Решить подобное», чтобы увидеть больше примеров.
Решить похожую задачуВведите свою задачу
2. 3y-2x=6
x=0→y=2
y=0→x=-3
y-перехват. В только что приведенных примерах 1 и 2 мы будем говорить, что точка пересечения с осью y равна 2, а не давать координаты (0, 2). Точно так же в примере 1 точка пересечения по оси x равна 3, а в примере 2 точка пересечения по оси x равна -3. Если линия проходит через начало координат, то точка пересечения по оси x и по оси y будет равна 0. В этом случае необходимо использовать какую-то другую точку.
Пример
Нарисуйте следующее линейное уравнение: y — 3x = 0
y-3x=0
x=0→y=0
x=2→y=6
Давайте посмотрите, как наш математический решатель генерирует график этого уравнения и подобных линейных уравнений.
Решите похожую задачуВведите свою задачу
8.3 Формы пересечения наклона и точки-наклона
Плотнику дают набор планов дома, которые требуют крыши 5:12. Что это значит для плотника? Это означает, что он должен построить крышу так, чтобы на каждые 5 дюймов подъема (расстояние по вертикали) приходилось 12 дюймов пробега (расстояние по горизонтали). То есть отношение подъема к пробегу составляет 5/12 (см. рис. 8.4). Стал бы плотник строить крышу так, чтобы на каждые 7 дюймов подъема приходилось 12 дюймов прогона? Конечно. Отношение подъема к бегу будет 7/12 (см. рис. 8.5). 9Рис. 8.5
Для прямой линии отношение подъема к длине называется наклоном линии.
slope=(подъем)/(набег)
График линейного уравнения y=3x-1 показан на рис. 8.6 Как вы думаете, что такое наклон линии?
Рис. 8.6
Чтобы вычислить уклон, найдите любые две точки на линии, затем найдите подъем и уклон, используя эти две точки (см. рис. 8.7а). (Коэффициент подъема
рис. 8.7а). (Коэффициент подъема
Рис. 1=8
х= -1 y=3(-1)-1=-3-1=-4
Теперь, используя P_1(-1, -4) и P_2(3, 8), координаты P_3 равны (3, -4 ), как показано на рисунке 8.7b. P_3 имеет те же координаты x, что и P_2, и те же координаты, что и P_1.
(Примечание. Обозначение P_1 читается как «P sub 1», а 1 называется нижним индексом . Точно так же P_2 читается как «P sub 2», а P_3 читается как «P sub 3».)
Для линии y=3x-1,
наклон=(подъем)/(разгон)=(8-(-4))/(3-(-1))
=12/4=3
Теперь найдите наклон линии y=3x+2. Найдите две точки на линии и рассчитайте отношение, подъем/пробег
Например,
x=0 y=3*0+2=0+2=2
x=1 y=3*1+2= 3+2=5
Таким образом, P_1(0, 2), P_2(1, 5) и P_3(1, 2) показаны на рис. 8.8.
Обратите внимание, что две линии y = 3x — 1 и y = 3x + 2 имеют одинаковый наклон, равный 3. (См. рис. 8.9..) Это означает, что прямые параллельны. Все прямые с одинаковым наклоном параллельны. Все линии на рис. 8.9 имеют наклон 3 и параллельны.
Все прямые с одинаковым наклоном параллельны. Все линии на рис. 8.9 имеют наклон 3 и параллельны.
Используя индексную запись, мы можем вывести формулу для наклона любая линия. Пусть P_1(x_1,y_1) и P_2(x_2, y_2) — две точки на прямой. Тогда P_3(x_2, y_1) находится под прямым углом, как показано на рисунке 8.10, и можно вычислить наклон.
наклон=(подъем)/(бег)=(y_2-y_1)/(x_2-x_1) 92=6
-6+3y_2=6
3y_2=12
y_2=4
(x_1,y_1)=(0,2) и x_2, y_2)=(-3,4)
наклон= (y_2-y_1)/(x_2-x_1)=(4-2)/(-3-0)=2/(-3)=-(2/3)
2. Предположим, что порядок точек в пример 1 изменен. То есть (x_1,y_1)=(-3,4) и (x_2,y_2) = (0, 2). Будет ли это влиять на наклон?
slope=(y_2-y_1)/(x_2-x_1)=(2-4)/(0-(-3))=-2/(3)=-(2/3)
Изменение порядка точки не имеют значения при расчете наклона. И числитель, и знаменатель меняют знак, поэтому дробь имеет одинаковое значение. В примере 1 2/-3=-(2/3), а в примере 2 -2/3=-(2/3). Важной процедурой является то, что координаты должны вычитаться в одном и том же порядке как в числителе, так и в знаменатель.
В общем случае
slope=(y_2-y_1)/(x_2-x_1)=(y_1-y_2)/(x_1-x_2)
Отрицательный наклон для линии 2x + 3y = 6 означает, что линия наклоны (или уклоны) вниз вправо (см. рис. 8.11). Все линии с отрицательным наклоном наклонены вниз вправо, а все линии с положительным наклоном наклонены вверх вправо.
slope=-2/3=-(2/3)
Рис. 5). Начните с точки (4, 5) и найдите другую точку на линии, используя наклон как (подъем)/(спуск)=3/4.
Четыре единицы вправо (бег) и три единицы вверх (подъем) от (4, 5) дадут еще одну точку на линии. Из (4, 5) вы могли переместиться на 4 единицы влево и на 3 единицы вниз или на 8 единиц вправо, а затем на 6 единиц вверх. Просто двигайтесь так, чтобы отношение подъема к бегу было 3 к 4, и вы найдете вторую точку на графике. (Для отрицательного наклона двигайтесь либо вправо, а затем вниз, либо влево, а затем вверх.)
Решите уравнение 2x+3y=6 относительно y.
2x+3y=6
3y=-2x+6
(3y)/3=(-2x+6)/3
y=(-2x)/3+6/3
y=-(2/3x)+ 2
Обратите внимание, что коэффициент x,-(2/3) совпадает с наклоном линии.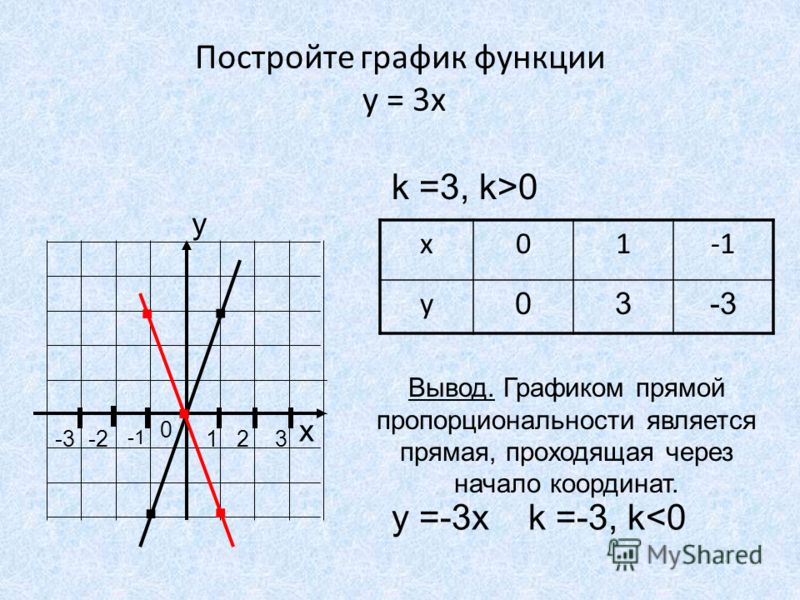 Кроме того, для линий, обсуждавшихся ранее, y = 3x-1 и y = 3x + 2, наклон каждой линии был равен 3, что является коэффициентом x. Если линейное уравнение решается относительно y, всегда ли коэффициент при x будет наклоном? Это важный вопрос, и ответ на него можно найти в следующем обсуждении.
Кроме того, для линий, обсуждавшихся ранее, y = 3x-1 и y = 3x + 2, наклон каждой линии был равен 3, что является коэффициентом x. Если линейное уравнение решается относительно y, всегда ли коэффициент при x будет наклоном? Это важный вопрос, и ответ на него можно найти в следующем обсуждении.
Предположим, что уравнение решено относительно y и y=mx+b. Пусть (x_1,y_1) и (x_2,y_2) — две точки на прямой. (x_1!=y_1) Тогда
y_1=mx_1+b and y_2=mx_2+b
slope=(y_2-y_1)/(x_2-x_1)=((mx_2+b)-(mx _1+б)) /(x_2-x_1)
=(mx_2+b-mx_1-b)/(x_2-x_1)=(mx_2-mx_1)/(x_2-x_1)
=
Наклон m, коэффициент x , в виде y = mx + b
Для прямой y = mx + b пусть x=0. Тогда y=m*0+b=b и y = b является точкой пересечения с осью y. Поскольку m — наклон, а b — точка пересечения с осью y, мы приходим к следующему определению.
y = mx + b называется формой наклона и пересечения для уравнения прямой; m — наклон, а b — точка пересечения с осью y.
Найдите наклон (м) и точку пересечения по оси y b каждой из следующих линий, переписав уравнение в форме наклона и точки пересечения. Затем начертите линию.
1. 2x+3y=3
3y=-2x+3
y=(-2x+3)/3
y=-(2 /3x)+1
м=-(2/3 )
y-отрезок = 1.
2. x-2y=6
x=6+2y
x-6=2y
(x-6)/2=y
1/2x-3=y 9 0909
m=1/2 b=-3
3 . -4x+2y=7
2y=4x+7
y=(4x+7)/2
y=2x+7/2
m=2 b=7/2
Если линия должна иметь определенный наклон и проходить через определенную точку, уравнение, представляющее линию, можно найти, как показано на следующем рисунке.
Пусть линия имеет наклон § и проходит через точку (1, 5). Если (x, y) представляет точку на линии, то наклон, рассчитанный с использованием (1, 5) и (x, y), должен составлять 2/3. то есть
(y-5)/(x-1)=2/3
В другой форме:
y-5=2/3(x-1)
фиксированная точка (x_1,y_1) может быть представлена в виде строка
; m — наклон, а (x_1,y_1) — фиксированная точка.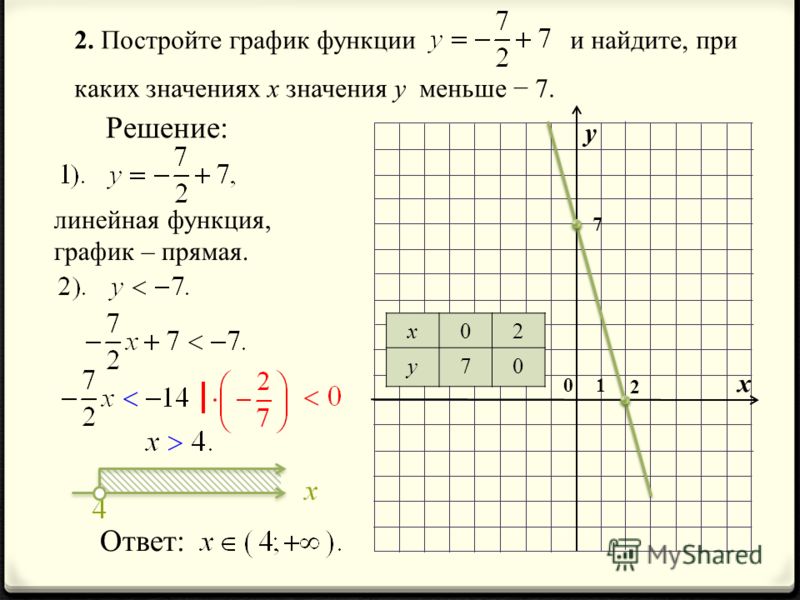
Примеры
1. Найдите уравнение прямой, имеющей наклон m=3/4 и проходящей через точку (4,5).
y-y_1=m(x-x_1)
y-5=3/4(x-4) (уравнение в форме точка-наклон)
или y-5=3/4x-3
y=3/4x+2 (уравнение в форме наклона-отрезка)
или 4y=3x+8
-3x+4y=8 (уравнение в стандартной форме, Ax+By=C)
2 . Найдите уравнение прямой, проходящей через две точки (- 1, -3) и (5, -2).
m=(y_2-y_1)/(x_2-x_1)=(-2-(-3))/(5-(-1))=(-2+3)/(5+1)=1/ 6Найдите m, используя формулу для наклона .
Используя форму точка-наклон (любая точка (-1, -3 или (5, -2) даст тот же результат)
y-(-2)=1/6(x-5)
y+ 2=1/6(x-5) (уравнение в форме точка-наклон)
или y+2=1/6x-5/6
y=1/6x-17/6 (уравнение в
или 6y=x-17
17=x-6y (уравнение в стандартной форме, Ax+By=C)
Любая из трех основных форм для уравнения линии приемлема В любом случае, если ответ дан в форме, отличной от вашей, вы должны быть в состоянии признать уравнения эквивалентными. 0909
0909
Давайте посмотрим, как наш математический решатель создает графики прямых линий и посмотрим на различные наклоны линий. Нажмите кнопку «Решить подобное», чтобы увидеть больше примеров.
Решите похожую задачуВведите свою задачу
8.4 Горизонтальные и вертикальные линии
Рассмотрите уравнение y = 3. Если x = 5, чему равно y? Если х = -2, чему равно у? Если х=0, чему равно у? В каждом случае y = 3. Все точки (5, 3), (-2, 3) и (0,3) удовлетворяют условию y = 3. x может иметь любое значение, но y должен быть x. Чтобы подчеркнуть этот факт, уравнение y = 3 можно записать как 0x + y = 3 или y = 0x + 3. График уравнения y = 3 представляет собой горизонтальную линию, и каждая координата y равна 3 (см. рис. 8.12). .)
Рис. 8.12
Каков наклон линии y = 3? Записав уравнение в форме y = 0x + 3, наклон равен 0. Кроме того, по формуле для наклона, используя (-2, 3) и (5, 3), наклон действительно равен 0:
slope = m=(y_2-y_1)/(x_2-x_1)=(3-3)/(5-(2))=0/7=0
Каковы графики уравнений y = -2 и y = 3 /2? Обе являются горизонтальными линиями с наклоном 0. На самом деле любое уравнение вида y = b (или y = 0x + b) является горизонтальной линией с наклоном 0 (см. рис. 8.13). Теперь рассмотрим уравнение x = 2. Если y = 4, чему равно x? Если у = -3, что такое х? Если у = 0, то чему равен х? В каждом случае x = 2. Все точки (2, 4), (2, -3) и (2, 0) удовлетворяют условию x = 2. y может иметь любое значение, но x должно быть равно 2. Мы можно записать x = 2 в виде 0y + x = 2 или x = 0y + 2. График уравнения x = 2 представляет собой вертикальную линию, и каждая координата x равна 2 (см. рис. 8.14).
На самом деле любое уравнение вида y = b (или y = 0x + b) является горизонтальной линией с наклоном 0 (см. рис. 8.13). Теперь рассмотрим уравнение x = 2. Если y = 4, чему равно x? Если у = -3, что такое х? Если у = 0, то чему равен х? В каждом случае x = 2. Все точки (2, 4), (2, -3) и (2, 0) удовлетворяют условию x = 2. y может иметь любое значение, но x должно быть равно 2. Мы можно записать x = 2 в виде 0y + x = 2 или x = 0y + 2. График уравнения x = 2 представляет собой вертикальную линию, и каждая координата x равна 2 (см. рис. 8.14).
Каков наклон линии x = 2? Чтобы ответить на этот вопрос, воспользуемся формулой наклона и двумя точками (2, 4) и (2, -3):
slope = m=(y_2-y_1)/(x_2-x_1)=(4-( -3))/(2-2)=7/0 undefined
Наклон не определен, потому что 0 не может быть знаменателем. Это справедливо для любой вертикальной линии. Графики уравнений вида x = a представляют собой вертикальные линии без наклона (или с неопределенным наклоном). Обратите внимание на то различие, что горизонтальные линии ((y = b)) имеют нулевой наклон, а вертикальные линии (x = a)) не имеют наклона. И уравнения для горизонтальных линий ((y = b)) и уравнения для вертикальных линий (x=a)) являются частными случаями общего линейного уравнения в стандартной форме, Ax + By = C, обсуждаемого в разделе 8.2. 9Рисунок 8.14
И уравнения для горизонтальных линий ((y = b)) и уравнения для вертикальных линий (x=a)) являются частными случаями общего линейного уравнения в стандартной форме, Ax + By = C, обсуждаемого в разделе 8.2. 9Рисунок 8.14
Примеры
Следуя линейным уравнениям, найдите наклон линии, если он существует, и начертите линию.
1. 2y=5
y=5/2
m=0
2. x +6=0
x=-6
без наклона
3. x+y= 0
y=-x
m=-1
8,5 Расстояние между двумя точками
Каково расстояние между двумя точками P_1(2, 3) и P_2(6, 3)? Каково расстояние между точками P_3 (-1, -4) и P_4 (-1, 1)? (См. рис. 8.15.)
расстояние (от P_1 до P_2)=6-2=4?
Это верно, так как точки P_1 и P_2 лежат на горизонтальной линии и имеют одинаковую координату y. Вы нашли
расстояние (от P_3 до P_4)=1-(-4)=5?
Это верно, так как точки P_3 и P_4 лежат на одной вертикальной линии и имеют одинаковую координату x.
Для расстояния от P_1 до P_2 почему бы не взять
расстояние (от P_1 до P_2) = 2-6=-4?
Причина в том, что термин расстояние означает положительное число. Как можно гарантировать положительное число после вычитания координат? Ответ состоит в том, чтобы взять абсолютное значение разности координат. Расстояние между двумя точками обозначается d.
Для P_1(x_1,y_1) и P_2(x_2,y_1) на горизонтальной линии,
Для P_1(x_1,y_1) и P_2(x_1,y_2) на вертикальной линии, 9090 9
Примеры
1. Найдите расстояние d между двумя точками (5, 7) и (-3, 7). Поскольку точки лежат на горизонтальной линии (они имеют одинаковую координату y),
или
2. Найдите расстояние d между двумя точками (2, 8) и 2,-(1/2 ). Поскольку точки находятся на вертикальной линии (они имеют одинаковую x:координату),
или
Что делать, если точки не лежат на вертикальной или горизонтальной прямой? Действительно, это более общий случай.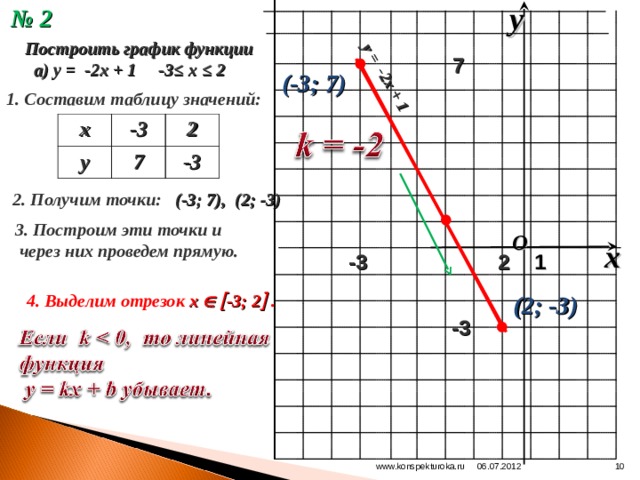 Нам нужна теорема Пифагора. Сформулированная здесь теорема Пифагора будет более подробно обсуждаться в разделе 10.6.
Нам нужна теорема Пифагора. Сформулированная здесь теорема Пифагора будет более подробно обсуждаться в разделе 10.6.
Теорема Пифагора: В прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов двух сторон.
Чтобы найти расстояние между двумя точками P_1(-1, 2) и P_2(5, 4), примените теорему Пифагора и вычислите длину гипотенузы, как показано на рис. 8.16. 92)
=корень(1/16+1)
=корень(1/16+16/16)
=корень(17/16)
9090 6 3. Покажите, что треугольник, определяемый точками A(- 2, 1), B(3,4) и C(1, -4) — равнобедренный треугольник. У равнобедренного треугольника две равные стороны.Решение:
Длина отрезка – это расстояние между точками A и B. Обозначим это расстояние через . Таким образом, чтобы показать, что треугольник ABC равнобедренный, нам нужно показать, что = или что = . Если ни одно из этих соотношений не верно, то треугольник не имеет двух равных сторон и не является равнобедренным.