Алгебра. Учебник для 6-8 классов
Алгебра. Учебник для 6-8 классов
ОглавлениеГЛАВА ПЕРВАЯ АЛГЕБРАИЧЕСКИЕ ВЫРАЖЕНИЯ. § 2. Алгебраические выражения. § 3. Допустимые значения букв. § 4. Порядок действий. § 5. Основные законы сложения и умножения. § 6. Краткие исторические сведения. ГЛАВА ВТОРАЯ. РАЦИОНАЛЬНЫЕ ЧИСЛА. § 7. Положительные и отрицательные числа. § 8. Числовая ось. § 9. Противоположные числа. § 10. Абсолютная величина числа. § 11. Сравнение рациональных чисел. § 12. Сложение рациональных чисел. § 13. Сложение нескольких чисел. § 14. Законы сложения. § 15. Вычитание рациональных чисел. § 16. Алгебраическая сумма. § 17. Умножение. § 18. Умножение нескольких чисел. § 19. Законы умножения. § 20. Деление. § 21. Свойства деления. § 22. Возведение в степень. § 23. Порядок выполнения действий. § 24. Уравнения. § 25. Решение задач с помощью уравнений. § 26. Графики. § 27. Краткие исторические сведения. (Из истории отрицательных чисел.) ГЛАВА ТРЕТЬЯ. ДЕЙСТВИЯ НАД ЦЕЛЫМИ АЛГЕБРАИЧЕСКИМИ ВЫРАЖЕНИЯМИ.  § 28. Одночлен и многочлен. § 29. Тождества и тождественные преобразования. § 30. Коэффициент. § 31. Расположенные многочлены. § 32. Приведение подобных членов. § 33. Сложение одночленов и многочленов. § 34. Противоположные многочлены. § 35. Вычитание одночленов и многочленов § 36. Умножение одночленов. § 37. Умножение многочлена на одночлен. § 38. Умножение многочленов. § 39. Умножение расположенных многочленов. § 40. Возведение одночленов в степень. § 41. Формулы сокращённого умножения. § 42. Общие замечания о делении целых алгебраических выражений. § 43. Деление одночленов. § 44. Деление многочлена на одночлен § 45. Примеры решения уравнений. ГЛАВА ЧЕТВЁРТАЯ. УРАВНЕНИЯ ПЕРВОЙ СТЕПЕНИ С ОДНИМ НЕИЗВЕСТНЫМ. § 48. Два основных свойства уравнений. § 49. Уравнения, содержащие неизвестное в обеих частях. § 50. Уравнение первой степени с одним неизвестным. § 51. Общие указания к решению уравнений.  § 52. Решение задач с помощью уравнений. § 53. Краткие исторические сведения. (Из истории уравнений.) ГЛАВА ПЯТАЯ. РАЗЛОЖЕНИЕ МНОГОЧЛЕНОВ НА МНОЖИТЕЛИ. § 54. Понятие о разложении на множители. § 55. Вынесение за скобки общего множителя. § 56. Способ группировки. § 57. Применение формул сокращённого умножения. § 58. Применение нескольких способов. § 59. Деление многочленов при помощи разложения на множители. ГЛАВА ШЕСТАЯ. АЛГЕБРАИЧЕСКИЕ ДРОБИ. § 60. Понятие об алгебраической дроби. § 61. Основное свойство дроби и сокращение дробей. § 62. Перемена знака у членов дроби. § 63. Целая отрицательная и нулевая степени числа. § 64. Приведение дробей к общему знаменателю. § 65. Сложение дробей. § 66. Вычитание дробей. § 67. Умножение дробей. § 68. Деление дробей. § 69. Возведение дроби в натуральную степень. § 70. Дробные уравнения. § 71. Примеры решения уравнений с буквенными коэффициентами. ГЛАВА СЕДЬМАЯ.  КООРДИНАТЫ И ПРОСТЕЙШИЕ ГРАФИКИ. КООРДИНАТЫ И ПРОСТЕЙШИЕ ГРАФИКИ.§ 72. Координаты точки на плоскости. § 73. Прямо пропорциональная зависимость. § 74. График прямо пропорциональной зависимости. § 75. Линейная зависимость. § 76. Обратно пропорциональная зависимость. ГЛАВА ВОСЬМАЯ. СИСТЕМА УРАВНЕНИЙ ПЕРВОЙ СТЕПЕНИ С ДВУМЯ НЕИЗВЕСТНЫМИ. § 77. Уравнение первой степени с двумя неизвестными. § 78. Система двух уравнений первой степени с двумя неизвестными. § 80. Решение систем уравнений. § 81. Графическое решение системы двух уравнений. § 82. Решение задач. § 83. Уравнение с тремя неизвестными. § 84. Система трёх уравнений с тремя неизвестными. ГЛАВА ДЕВЯТАЯ. СЧЁТНАЯ (ЛОГАРИФМИЧЕСКАЯ) ЛИНЕЙКА. § 85. Равномерные и неравномерные шкалы. § 86. Устройство счётной (логарифмической) линейки. § 87. Основная шкала. § 88. Умножение и деление с помощью счётной линейки. ГЛАВА ДЕСЯТАЯ. КВАДРАТНЫЙ КОРЕНЬ. § 89. Построение графика зависимости y = x^2 § 90.  (1/3) (1/3)§ 130. Примеры графического решения уравнений и систем уравнений. |
№ | Этап урока | Время | Содержание этапа | Деятельность учителя | Деятельность учащихся | УУД |
1 | Самоопределение к деятельности, организационный момент | 1 | Создать благоприятный настрой на работу | Сообщают о готовности к уроку | Личностные: положительное отношение к урокам математики | |
2 | Актуализация знаний | 7 | Актуализировать опорные знания | — Для проведения сегодняшнего урока нам потребуется вспомнить формулы сокращённого умножения а именно формулу квадрата суммы и квадрата разности, а также вспомнить уже изученные свойства квадратичной функции. Оценим свою работу. Откройте ваши файлы «оценочный лист» (Приложение №2) и поставьте напротив №1 оценку: 13-14 баллов – «5», 10-12 баллов – «4», 7-9 баллов – «3» | Фронтально работают с учителем, отвечают на поставленные вопросы | Познавательные: анализ, сопоставление Регулятивные: оценка своей деятельности |
3 | Целеполагание, планирование деятельности | 5 | Обеспечить принятие ими задач урока | — Какая была тема прошлого урока? (Квадратичная функция y=аx2) — Что мы делали на прошлом уроке? (Строили график квадратичной функции, определяли точки пересечения параболы с осями координат, определяли промежутки возрастания убывания функции) По наводящим вопросам учителя составляют план урока: 1) повторить правила + (уже выполнили, можно отметить) 2) Решить примеры на выделение полного квадрата 3) Построить график функции y=ax2+bx+c и сравнить с графиком функции y=ax2 4) Самостоятельно построить на координатной плоскости 2 графика функций и найти их точку пересечения 5) проверить | Определяют цель и задачи урока, расставляют их по порядку | Регулятивные: целеполагание, планирование Коммуникативные: умение полно и точно выражать свои мысли Личностные: смысловообразование |
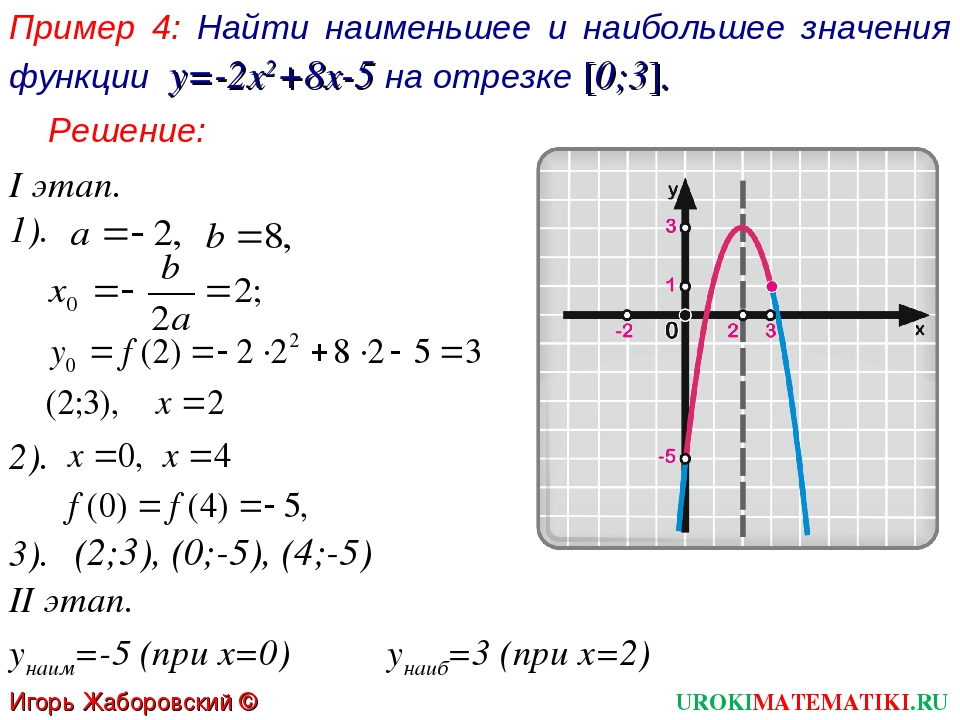
4 | Включение нового знания в систему знаний | 17 | Отработка навыка построения графика функции | 1. Выделите полный квадрат 4x2+4x-5 – 2 пункт плана: Для этого даю вам 3 минуты, затем проверим. (взаимопроверка – учащиеся проверяют решение одноклассников выставляют оценку в оценочный лист напротив №2) 2.Самостоятельная работа у доски, фронтальная работа с классом 2.1. Построение графика функции y=ax2+bx+c и сравнение с графиком функции y=ax2 (пункт 3): — Построим график функции y=x2-2x+3; — Построим график функции y=x2; — Для сравнения графиков преобразуем формулу x2-2x+3, используя метод выделения полного квадрата; — Сравниваем коэффициенты xo, yo преобразованной функции y=x2-2x+3 с координатами вершины параболы. Делаем вывод о взаимосвязи коэффициентов xo, yoс перемещением графика функции y=x2 | Познавательные: выполнение действий по алгоритму Регулятивные: контроль, оценка Коммуникативные: учет разных мнений, достижение договоренностей и согласование общего решения Личностные: следование в поведении моральным нормам и этическим требованиям | |
5 | Физкультминутка | 2 | ||||
6 | Самостоятельная работа | 8 | — У нас остался последний пункт – проверить, как вы усвоили новый материал. построить на координатной плоскости 2 графика функций и найти их точку пересечения y=(x-2)2-1 и y=-2x+2 – «3»; y=(x-2)2+1 и y=(x-4)2-3 – «4»; y=x2-6x+11 и y=x2-8x+17 – «5». Решив пример и проверив свое решение, выставите оценку в оценочный лист напротив №3 | Самостоятельно выбирают и решают пример по действиям, проверяют по эталону | Познавательные: анализ, применение правила Регулятивные: контроль, оценка Коммуникативные: самопроверка выполненной работы | |
7 | Подведение итогов урока, рефлексия | 3 | Учащиеся дают качественную оценку своей работы на уроке | — Какая была цель урока? — Посмотрите на план урока, все запланированные шаги выполнены? — Что осталось сделать? — Оцените себя – поставив итоговую оценку за урок в оценочный лист (выставляют оценки и делают выводы – сравнивают оценки №1, №2, №3, что получилось, что нет, над чем надо поработать еще) | Проставляют результат работы на листе оценки | Регулятивные: самооценка своей деятельности Коммуникативные: умение оформлять свои мысли в устной форме Личностные: адекватное понимание причин успеха/неуспеха в учебной деятельности |
8 | Постановка домашнего задания | 2 | Откройте дневник, запишите домашнее задание:
| Записывают домашнее задание | Личностные: самоопределение | |
АНГЛИЙСКИЙ SAT-ПАСПОРТ К ПРОДВИНУТОЙ МАТЕМАТИКЕ-Множественный выбор
20 видеоРЕКЛАМА
Ab Padhai каро бина объявления ке
Khareedo DN Про и дехо сари видео бина киси объявление ки рукаават ке!
Обновлено: 27-06-2022
Текст Решение
A
B
C
D
C3 Правильный ответ
30003
Ответить
Пошаговое решение от экспертов, которое поможет вам в разрешении сомнений и получении отличных оценок на экзаменах.
Расшифровка
Привет всем, поэтому вопрос в том, если квадратное уравнение X квадрат + bx + c и C являются отрицательными константами, то какая из следующих криптографических функций подходит, так что если X квадрат + bx + c и которая меньше нуля и C меньше нуля, затем найдите, что коэффициент квадрата x отрицателен, тогда парабола, очевидно, будет примерно такой, как эта, в порядке, обращенном к загрузке, из-за ее отрицательного значения она будет указывать вниз, и последние параметры, поэтому вариант и вариант видят, что наш третий вариант вполне похожи и выглядят так, что элементы интерпретации являются вариантом этого варианта в этом варианте
Варианты Baljeet и обращены вверх, наши эти два варианта теперь я иду в гонку, хорошо, теперь давайте посмотрим, заметили ли вы сейчас разницу в опции, чтобы увидеть, что y-пересечение в этом варианте является положительным, а y-пересечение в этом варианте отрицательное значение для расчета ветра это я буду только для значения для оси 0 а другое отрицательное или положительное 1 80 х равно нулю тогда я буду теперь видеть значение С не меньше нулевого сезона 2 12 2012 будет отрицательным, поэтому вариант третьего пересечения отрицательный, и он также указывает вниз, сорбция усыновления будет подходящей 12 Физика сначала мы увидели, что сотрудничество процесса транзакции, где отрицательно
калькулятор, который все отключают, наш третий вариант будет наиболее подходящим, все было понятно, большое спасибо
Похожие видео
Если f(x)=ax2+bx+c
— квадратичная функция такая, что f(1)=8,f(2)=11
и f(−3)=6
найти f (х)
с помощью определителей. Также найдите f(0).
Также найдите f(0).
График функции y=f(x). Тогда что из следующего может представлять собой график функции y=|f(x)|
График квадратичного полинома f(x)=ax2+bx+c показан ниже. Что из следующего верно? |β−α|>2 9(2)+bx+c, где a,b,c в R и a!=0, так что f(x)=f(2-x) для всех действительных чисел x. Сумма корней f(x) равна
6008490
Для какого из следующих графиков квадратного выражения f(x)=ax2+bx+c произведение abc отрицательно
110287316
Предположим, что квадратичная функция f(x)=ax2+bx+c неотрицательна на интервале [-1,1] . Тогда площадь под графиком f на интервале [-1,1] и по оси X определяется формулой
118622941
На рисунке выше показан график квадратичной функции f с точкой минимума в (1,−2). Если f(5)=f(c), то какие из следующих значений могут быть значениями c?
167970376
Если f(x)=ax2+bx+c,a≠0 и все a, b и c отрицательны, какой может быть график f(x)?
195770974
Для функции f(x)=ax2+bx+c,a≠0 сумма корней равна произведению корней .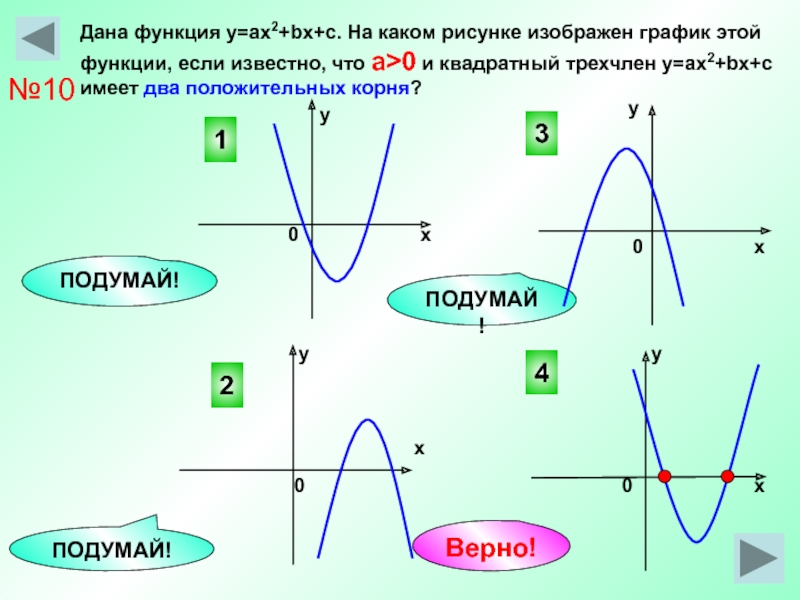 Что может быть f(x) ?
Что может быть f(x) ?
195770978
Текст Решение
Функция f:R→R, определяемая формулой f(x)=ax2+bx+c,(a≠0), называется ____ функцией.
201224013
Определить квадратичную функцию (f), определяемую выражением f(x)=ax2+bx+c. Если f(0)=6,f(2)=11,f(-3)=6
277385460
Предположим, что квадратичная функция f(x)=ax2+bx+c неотрицательна на интервале [ -1,1]. Тогда площадь под графиком f на интервале [-1,1] и по оси X определяется формулой
644012224
Найдите производную w.r.to x0094 1ax2+bx+c(где |a|+|b|+|c|≠0)
644425933
Для какого из следующих графиков квадратного выражения f(x)=ax2+bx+c произведение abc отрицательное
645832724
Квадратные функции: краткий обзор
Мы знаем, что такое квадратные уравнения. Теперь мы собираемся изобразить их на графике. Вот как мы катимся. Всякий раз, когда мы узнаем, что такое лотерейные номера Mega Millions, мы также наносим их на график. То же самое касается результатов баскетбольных матчей, результатов выборов и кассовых сборов за первые выходные. У нас могут быть проблемы.
У нас могут быть проблемы.
Чтобы получить функции, нарисуем квадратные уравнения вида
y = ax 2 + bx + c .
Это гарантирует, что у нас будет только одно значение y для каждого значения x .
Пример задачи
Нарисуйте уравнение y = x 2 .
Это простейшее квадратное уравнение. Это тоже отношение, так что мы уже знаем, как изобразить его на графике. Возможно, мы забыли об этом, но знание где-то там.
Сначала мы делаем таблицу значений, чтобы мы могли изобразить некоторые точки, а затем мы видим фигуру, которую мы получаем, и соединяем точки. Вот выборка точек:
Теперь давайте изобразим их на графике:
Это образует своего рода U-образную форму, вот как мы соединяем точки:
Единственный корень многочлена x 2 равно x = 0. Таким образом, 0 — это единственное значение x , которое мы можем подставить в уравнение 9. 0110 y = x 2 если мы хотим получить 0 вместо y . Неслучайно единственная точка на графике y = x 2 с координатой y -0 — это точка (0, 0).
0110 y = x 2 если мы хотим получить 0 вместо y . Неслучайно единственная точка на графике y = x 2 с координатой y -0 — это точка (0, 0).
И снова появление вечно популярного 0. Этот парень в последнее время повсюду. Должно быть, он продвигает новый фильм.
Давайте сделаем несколько более интересных, хотя и более сложных примеров. Конечно, мы могли бы просто изобразить их на калькуляторе, но мы хотели бы понять, почему мы получаем именно такие изображения. Так что, если у вас нет одного из тех калькуляторов, которые постоянно болтают о том, как они «попали туда», давайте продолжим и сделаем работу сами.
Иногда нас просят набросать график. Не напрягайтесь; никакие баллы не будут сняты за менее чем идеально прямые линии или полное отсутствие художественных способностей. Идея состоит в том, чтобы нарисовать грубую форму графика и обозначить пару простых значений, но не беспокоиться о точности. Сохраните высочайшую точность для практики стрельбы из лука.
Сохраните высочайшую точность для практики стрельбы из лука.
Пример задачи
Не используя калькулятор, нарисуйте график функции y = x 2 + 1.
Честно говоря, когда мы строим график y = x 2 + 1, мы получаем график y = x 2 . Единственное значение, которое нам нужно обозначить на эскизе, это y = 1.
Примеры, которые мы делали до сих пор, были довольно простыми, но теперь мы перейдем к некоторым примерам, которые прямо противоположны. Графики в наших предыдущих примерах выглядели как график x 2 немного сдвинулся вверх или вниз. Однако для построения общих квадратных уравнений нам нужно действовать по-другому.
Сначала нам нужно несколько новых определений, так что расслабьтесь и освободите немного места…
График любого квадратного уравнения представляет собой параболу . Парабола будет выглядеть как перевернутая U:
. .. или перевернутая U:
.. или перевернутая U:
Места, где парабола пересекает ось x позвонил в x — пересекает , как и в линейных уравнениях. Место, где парабола пересекает ось y , является точкой пересечения y . Самая низкая или самая высокая точка параболы, в зависимости от того, в какую сторону она раскрывается, называется вершиной параболы. Это не вихрь, так что не нужно беспокоиться о том, что вас поглотит крутящаяся спираль, похожая на торнадо… если только вы не живете в Канзасе.
Чтобы нарисовать график общего квадратного уравнения, нам нужно знать три вещи.
- Пересечения
- Вершина
- Открыт ли график вверх («U») или вниз (перевернутая «U»)
Давайте рассмотрим пример, чтобы увидеть, как найти все эти вещи, и как собрать их вместе в графике. Это будет приятная, расслабляющая прогулка. Вы даже можете делать это сидя; вот как это расслабляет.
Пример задачи
Нарисуйте график y = x 2 + 3 x + 2.
Нам нужно найти точки пересечения, вершину и направление параболы вверх или вниз. Мы также должны выяснить, до какого числа он будет открыт, на случай, если нам понадобится пробежаться поздно ночью.
1. Где парабола пересекает оси?
Во-первых, где парабола пересекает ось x ? Точка пересечения x — это точка формы (что-то, 0).
Таким образом, x пересечений нашего графика будут происходить при любых значениях x сделать y нулем; другими словами, в корнях многочлена x 2 + 3 x + 2. Чтобы найти корни, мы факторизируем полином, приравниваем его к нулю и находим x .
x 2 + 3 x + 2 = 0
( x + 2) ( x + 1) = 0
x = -2, x = -1
9000 2
9000 2 9000 2 9000 2 . Это корни многочлена, и в качестве бонуса они также являются х — точки пересечения параболы. Не проблема, что они оба отрицательные. Это график равных возможностей.
Это корни многочлена, и в качестве бонуса они также являются х — точки пересечения параболы. Не проблема, что они оба отрицательные. Это график равных возможностей.
Теперь мы знаем, что точки (-2, 0) и (-1, 0) находятся на графике:
Где парабола пересекает ось y ? Чтобы найти y -intercept, мы подставим 0 вместо x и посмотрим, что получится. В этом случае мы находим:
y = (0) 2 + 3(0) + 2 = 2
Таким образом, точка пересечения y равна 2. У нас также есть точка (0, 2) на графике:
Теперь у нас есть две точки. Если бы это была НФЛ, это было бы безопасно.
2. Что такое вершина?
Вершина параболы находится на полпути между корнями, по крайней мере, когда корни существуют. Через мгновение мы будем беспокоиться о том, что происходит, когда они этого не делают. Ну, вы можете беспокоиться об этом сейчас, но, пожалуйста, держите это при себе, пока мы не доберемся до этого. Нет ничего хорошего в том, чтобы тем временем портить его всем остальным.
Нет ничего хорошего в том, чтобы тем временем портить его всем остальным.
Для этой параболы вершина возникает, когда x находится на полпути между -2 и -1 или на . Мы находим значение
Хорошо. Точка тоже на нашей параболе.
3. График открывается вверх или вниз?
Вы когда-нибудь пытались толкнуть «тянущую» дверь? Потому что мы, гм, нет. Важно знать, как открываются вещи. Парабола ничем не отличается.
Когда x находится за пределами x -пересекает, чем дальше x получается с нуля, чем больше y получается, и он даже не принимает гормоны роста. Когда х = 5, у = 42; когда х = 100, у = 10302. Мы можем представить, что если бы мы нанесли на график больше точек, то увидели бы, что график открывается вверх.
Соединяя все части вместе, мы соединяем наши точки в форме буквы «U», вот так:
Теперь, когда мы прошли пример задачи, и вам это так понравилось, что ваш рот приобрел форму параболы, открывающейся вверх, давайте поговорим немного больше о подзадачах, связанных с построением графика квадратного уравнения формы у = ах 2 + бх + в.
1. Поиск перехватов.
Здесь есть два шага: найти точки пересечения x и найти точки пересечения y . Это похоже на охоту за пасхальными яйцами снова и снова. x -перехваты — это значения x , которые делают y нулевыми. Другими словами, решения квадратного уравнения
0 = ах 2 + бх + с .
Это может включать использование квадратичной формулы. Поскольку не все квадратные уравнения имеют решения, на графике может не быть x -пересечений. Это может выглядеть, например, так:
y -значение, которое мы получим, если подставим x = 0 в уравнение . Когда мы это сделаем, мы найдем
a (0) 2 + б (0) + в = в .
Таким образом, точка пересечения y равна y = c . Парабола всегда будет иметь точку пересечения и , поскольку c всегда будет некоторым числом (возможно, 0). Приятно осознавать, что со всем этим x -перехватом, мы все еще можем полагаться на c и y -intercept. Они останутся с нами, несмотря ни на что.
Приятно осознавать, что со всем этим x -перехватом, мы все еще можем полагаться на c и y -intercept. Они останутся с нами, несмотря ни на что.
2. Нахождение вершины.
Когда парабола имеет x точек пересечения, вершина оказывается на полпути между ними. Число на полпути между двумя числами также известно как их среднее. Точно так же, как вы находитесь на полпути между возрастом вашего старшего брата и младшей сестры, что делает вас совершенно средним. Подождите…
Среднее между 4 и 10 равно , что является числом на полпути между 4 и 10. Если мы используем квадратичную формулу для нахождения x -перехватов, мы получим значения
.
Число посередине между этими двумя значениями равно
Это означает, что вершина находится в .
Но подождите, что происходит, когда квадратичная формула не дает нам никаких решений? Достаточно скрытно, вершина все еще будет в .

 Перейдите по ссылке и выполните задание: https://app.wizer.me/preview/77D0DL. (Приложение №1)
Перейдите по ссылке и выполните задание: https://app.wizer.me/preview/77D0DL. (Приложение №1)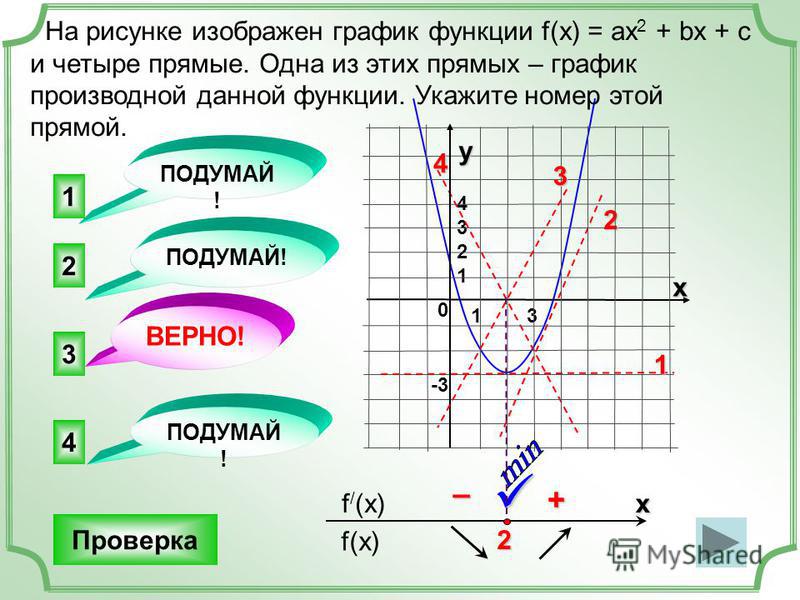 Самостоятельная работа
Самостоятельная работа  Для этого выберите пример, который сможете решить:
Для этого выберите пример, который сможете решить: