График двух переменных онлайн. Квадратичная и кубическая функции
В золотой век информационных технологий мало кто будет покупать миллиметровку и тратить часы для рисования функции или произвольного набора данных, да и зачем заниматься столь муторной работой, когда можно построить график функции онлайн. Кроме того, подсчитать миллионы значений выражения для правильного отображения практически нереально и сложно, да и несмотря на все усилия получится ломаная линия, а не кривая. Потому компьютер в данном случае – незаменимый помощник.
Что такое график функций
Функция – это правило, по которому каждому элементу одного множества ставится в соответствие некоторый элемент другого множества, например, выражение y = 2x + 1 устанавливает связь между множествами всех значений x и всех значений y, следовательно, это функция. Соответственно, графиком функции будет называться множество точек, координаты которых удовлетворяют заданному выражению.
На рисунке мы видим график функции y = x . Это прямая и у каждой ее точки есть свои координаты на оси X и на оси Y . Исходя из определения, если мы подставим координату X некоторой точки в данное уравнение, то получим координату этой точки на оси Y .
Это прямая и у каждой ее точки есть свои координаты на оси X и на оси Y . Исходя из определения, если мы подставим координату X некоторой точки в данное уравнение, то получим координату этой точки на оси Y .
Сервисы для построения графиков функций онлайн
Рассмотрим несколько популярных и лучших по сервисов, позволяющих быстро начертить график функции.
Открывает список самый обычный сервис, позволяющий построить график функции по уравнению онлайн. Umath содержит только необходимые инструменты, такие как масштабирование, передвижение по координатной плоскости и просмотр координаты точки на которую указывает мышь.
Инструкция:
- Введите ваше уравнение в поле после знака «=».
- Нажмите кнопку «Построить график» .
Как видите все предельно просто и доступно, синтаксис написания сложных математических функций: с модулем, тригонометрических, показательных — приведен прямо под графиком. Также при необходимости можно задать уравнение параметрическим методом или строить графики в полярной системе координат.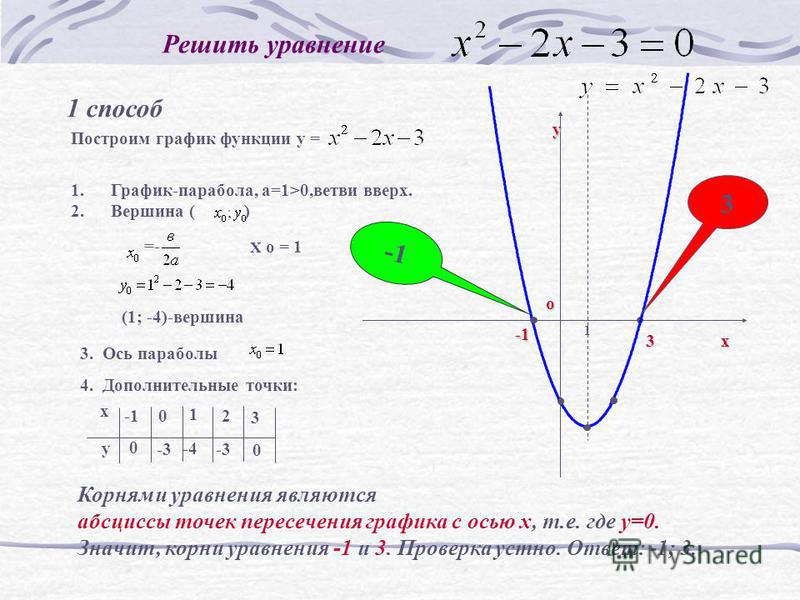
В Yotx есть все функции предыдущего сервиса, но при этом он содержит такие интересные нововведения как создание интервала отображения функции, возможность строить график по табличным данным, а также выводить таблицу с целыми решениями.
Инструкция:
- Выберите необходимый способ задания графика.
- Введите уравнение.
- Задайте интервал.
- Нажмите кнопку «Построить» .
Для тех, кому лень разбираться, как записать те или иные функции, на этой позиции представлен сервис с возможностью выбирать из списка нужную одним кликом мыши.
Инструкция:
- Найдите в списке необходимую вам функцию.
- Щелкните на нее левой кнопкой мыши
- При необходимости введите коэффициенты в поле «Функция:» .
- Нажмите кнопку «Построить» .
В плане визуализации есть возможность менять цвет графика, а также скрывать его или вовсе удалять.
Desmos безусловно – самый навороченный сервис для построения уравнений онлайн.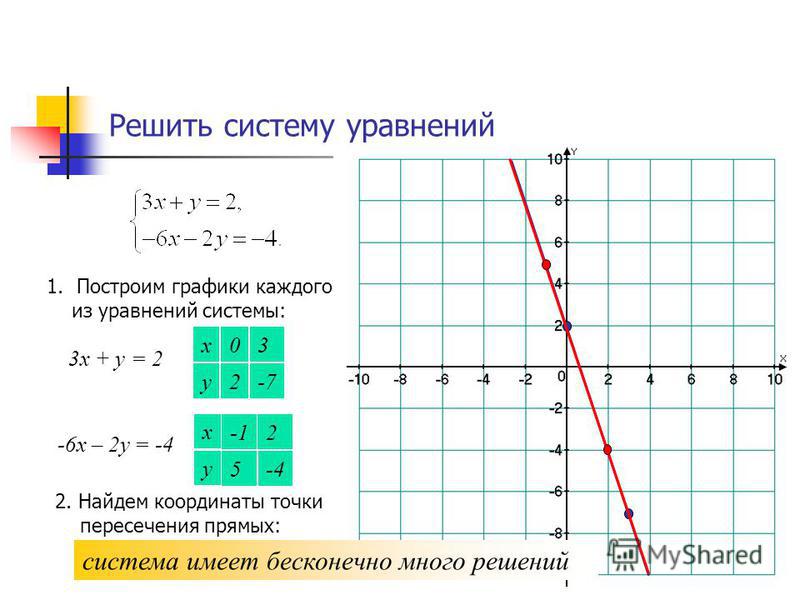 Передвигая курсор с зажатой левой клавишей мыши по графику можно подробно посмотреть все решения уравнения с точностью до 0,001. Встроенная клавиатура позволяет быстро писать степени и дроби. Самым важным плюсом является возможность записывать уравнение в любом состоянии, не приводя к виду: y = f(x).
Передвигая курсор с зажатой левой клавишей мыши по графику можно подробно посмотреть все решения уравнения с точностью до 0,001. Встроенная клавиатура позволяет быстро писать степени и дроби. Самым важным плюсом является возможность записывать уравнение в любом состоянии, не приводя к виду: y = f(x).
Инструкция:
- В левом столбце кликните правой кнопкой мыши по свободной строке.
- В нижнем левом углу нажмите на значок клавиатуры.
- На появившейся панели наберите нужное уравнение (для написания названий функций перейдите в раздел «A B C»).
- График строится в реальном времени.
Визуализация просто идеальная, адаптивная, видно, что над приложением работали дизайнеры. Из плюсов можно отметить огромное обилие возможностей, для освоения которых можно посмотреть примеры в меню в верхнем левом углу.
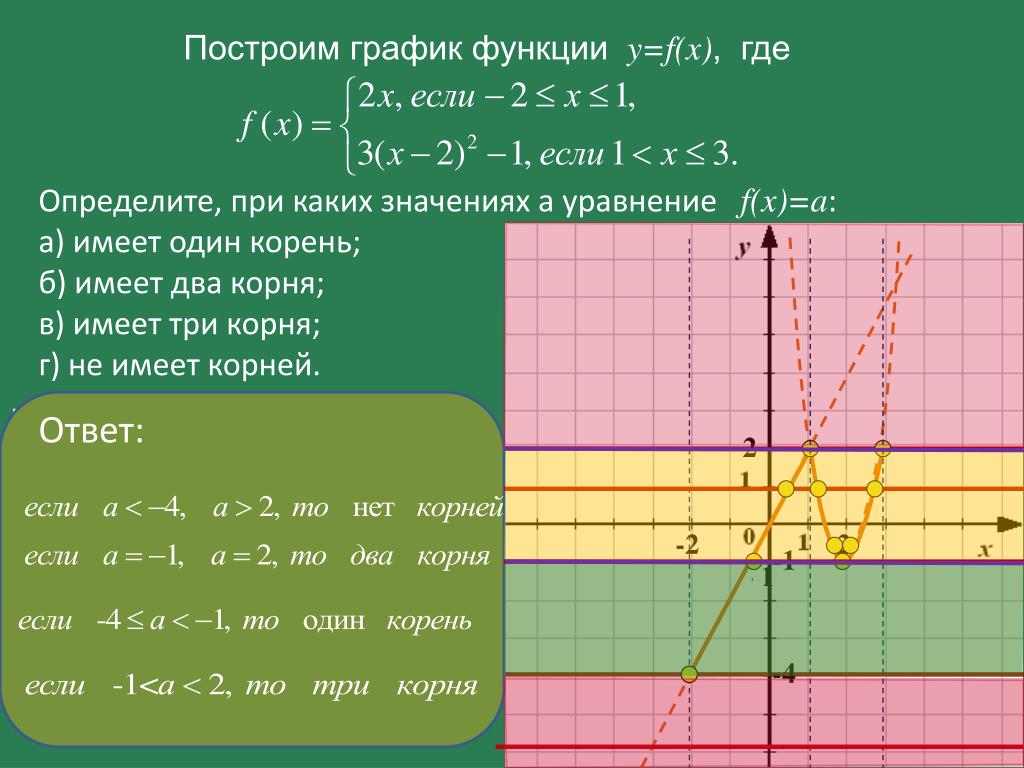
Сайтов для построения графиков функций великое множество, однако каждый волен выбирать для себя исходя из требуемого функционала и личных предпочтений. 2 называется квадратичной функцией. Графиком квадратичной функции является парабола. Общий вид параболы представлен на рисунке ниже.
2 называется квадратичной функцией. Графиком квадратичной функции является парабола. Общий вид параболы представлен на рисунке ниже.
Квадратичная функция
Рис 1. Общий вид параболы
Как видно из графика, он симметричен относительно оси Оу. Ось Оу называется осью симметрии параболы. Это значит, что если провести на графике прямую параллельную оси Ох выше это оси. То она пересечет параболу в двух точках. Расстояние от этих точек до оси Оу будет одинаковым.
Ось симметрии разделяет график параболы как бы на две части. Эти части называются ветвями параболы. А точка параболы которая лежит на оси симметрии называется вершиной параболы. То есть ось симметрии проходит через вершину параболы. Координаты этой точки (0;0).
Основные свойства квадратичной функции
1. При х =0, у=0, и у>0 при х0
2. Минимальное значение квадратичная функция достигает в своей вершине. Ymin при x=0; Следует также заметить, что максимального значения у функции не существует.
3. Функция убывает на промежутке (-∞;0] и возрастает на промежутке }
2.7. Графики функций двух переменных
MatLab предлагает различные способы визуализации функций двух переменных: построение трехмерных графиков и линий уровня, параметрически заданных линий и поверхностей.
Задание 8. Построить график функции z (x, y) =
Методика выполнения:
1. Для построения графика функции двух переменных область определения следует разбить прямоугольной сеткой. Удобно использовать два двумерных массива x и y для хранения информации о координатах узлов. Для построения сетки следует использовать команду
>>
[X, Y]
= meshgrid (0:0.2:1,0:0.2:1) – команду вывода результата
не подавлять.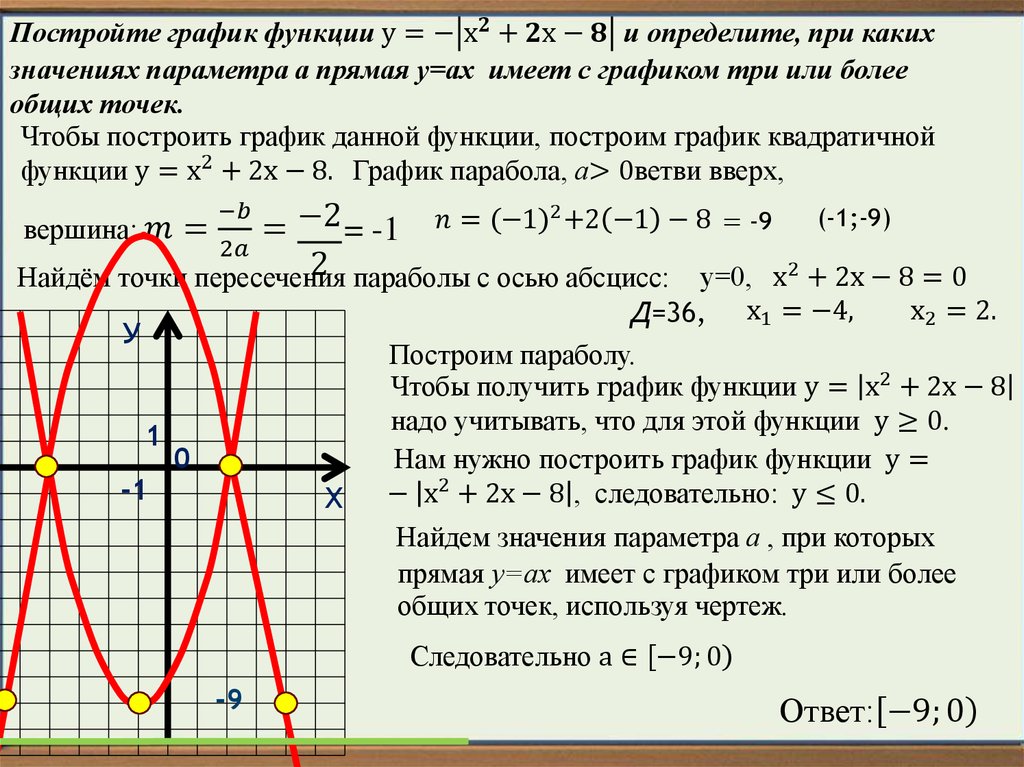 2
– команду вывода результата не подавлять.
2
– команду вывода результата не подавлять.
3. Построить график функции командой
>> mesh (X, Y, Z)
4. Для более точного построения следует выбрать меньший шаг сетки. Выберите шаг сетки 0,05 и снова постройте график функции z (x, y).
Изучение цветовых эффектов производите на примере графика, полученного при выполнении самостоятельной работы. Используя новую команду, копируйте заново этапы построения сетки и вычисления функции и изменяйте команду вывода графика.
1. Команда surf строит каркасную поверхность графика функции и заливает каждую клетку поверхности определенным цветом, причем в пределах каждой клетки цвет постоянный:
>> surf (X, Y, Z)
2. Команда shading убирает каркасные линии:
>> shading (X, Y, Z)
3. Команда shading integr плавно заливает поверхность цветом,
зависящим от значений функции.
Команда shading integr плавно заливает поверхность цветом,
зависящим от значений функции.
4. Вернуться к первоначальному виду графика, определенному командой mesh, можно при помощи shading faceted.
5. Сделать каркасную поверхность прозрачной можно командой hidden of.
6. Убрать невидимую часть поверхности можно командой hidden on.
7. В MatLab можно вывести рядом с графиком столбик, устанавливающий соответствие между цветом и значением функции (colorbar).
Задание 9. Постройте при помощи surf график поверхности, заданной в задании 8, и дополните его информацией о цвете:
>> surf (X,Y,Z)
>> colorbar
8. Чтобы сделать вывод о значении функции в той или иной точке плоскости xy, следует использовать команду meshc
или surfc. Эти команды размещают на плоскости xy линии уровня функции (линии постоянства
функции).
Эти команды размещают на плоскости xy линии уровня функции (линии постоянства
функции).9. MatLab позволяет строить поверхности, состоящие из линий уровня. Для задания из самостоятельной работы вместо команды построения графика введите следующие команды:
>> levels = (0:0.01:0.5)
>> contour3 (X, Y, Z, levels)
>> colorbar
Установка цветовой палитры
Простым, но эффективным способом цветового оформления графика является установка цветовой палитры при помощи функции colormap.
Пример (примените к графику из самостоятельной работы):
>> surfc (X, Y, Z)
>> colorbar
>> colormap (autumn)
>> title (‘График функции z (x, y)’)
>> xlabel (‘x’)
>> ylabel (‘y’)
>> zlable (‘z’)
Таблица
2. 2
2
Исчисление II. Функции нескольких переменных
Онлайн-заметки Пола
Главная
/
Исчисление II
/
Трехмерное пространство
/ Функции нескольких переменных
Показать мобильное уведомление Показать все примечания Скрыть все примечания
Мобильное уведомление
Похоже, вы используете устройство с «узкой» шириной экрана ( т. е. вы, вероятно, используете мобильный телефон). Из-за характера математики на этом сайте лучше всего просматривать в ландшафтном режиме. Если ваше устройство не находится в ландшафтном режиме, многие уравнения будут отображаться сбоку вашего устройства (должна быть возможность прокрутки, чтобы увидеть их), а некоторые пункты меню будут обрезаны из-за узкой ширины экрана.
Раздел 12.5: Функции нескольких переменных 92}-4\).
Это эллиптический параболоид и пример квадратичной поверхности. Мы видели несколько из них в предыдущем разделе. Квадратичные поверхности мы будем довольно часто встречать позже в Calculus III.
Еще один распространенный граф, который мы будем часто встречать в этом курсе, — это граф плоскости. У нас есть соглашение о графическом отображении плоскостей, которое немного облегчит их графическое представление и, надеюсь, визуализацию.
Напомним, что уравнение плоскости задается
\[ax + by + cz = d\]
или если мы решим это для \(z\), мы можем записать это в терминах обозначения функций. Это дает,
\[f\left( {x,y} \right) = Ax + By + D\]
Чтобы нарисовать плоскость, мы обычно находим точки пересечения с тремя осями, а затем рисуем треугольник, соединяющий эти три точки. Этот треугольник будет частью плоскости, и он даст нам довольно приличное представление о том, как должна выглядеть сама плоскость. Например, давайте изобразим плоскость, заданную
Этот треугольник будет частью плоскости, и он даст нам довольно приличное представление о том, как должна выглядеть сама плоскость. Например, давайте изобразим плоскость, заданную
\[f\влево( {x,y} \right) = 12 — 3x — 4y\]
Для построения графика, возможно, было бы проще записать это как
. \[z = 12 — 3x — 4y\hspace{0.25in} \Rightarrow \hspace{0.25in}\,\,\,\,\,3x + 4y + z = 12\]
Теперь каждая из точек пересечения с тремя главными осями координат определяется тем фактом, что две координаты равны нулю. Например, пересечение с осью \(z\) определяется как \(x = y = 0\). Итак, три точки пересечения равны 9.0004
\[\ begin{align*}& x — {\mbox{axis:}}\left({4,0,0} \right)\\ & y — {\mbox{axis:}}\left({0 ,3,0} \right)\\ & z — {\mbox{ось:}}\left({0,0,12} \right)\hspace{0,25 дюйма}\end{align*}\]
Вот график самолета.
Теперь, чтобы расширить это, графики функций вида \(w = f\left( {x,y,z} \right)\) будут четырехмерными поверхностями. Конечно, мы не можем их изобразить в виде графика, но указать на это не помешает.
Далее мы хотим поговорить об областях определения функций более чем одной переменной. Напомним, что домены функций одной переменной \(y = f\left( x \right)\) состояли из всех значений \(x\), которые мы могли подставить в функцию и получить обратно действительное число. Теперь, если задуматься, это означает, что область определения функции одной переменной представляет собой интервал (или интервалы) значений от числовой прямой или одномерного пространства.
Область определения функций двух переменных, \(z = f\left( {x,y} \right)\), являются областями из двумерного пространства и состоят из всех пар координат, \(\left( {x ,y} \right)\), чтобы мы могли подключиться к функции и получить действительное число. 92}} \справа)\)
Показать все решения Скрыть все решения
a \(f\left( {x,y} \right) = \sqrt {x + y} \) Показать решение
В этом случае мы знаем, что не можем извлечь квадратный корень из отрицательного числа, поэтому это означает, что мы должны потребовать,
\[х + у \ge 0\]
Вот набросок графика этого региона.
b \(f\left( {x,y} \right) = \sqrt x + \sqrt y \) Показать решение 92} > 16\]
Итак, областью определения этой функции является множество точек, лежащих полностью вне сферы радиуса 4 с центром в начале координат.
Следующая тема, которую мы должны рассмотреть, это кривых уровня или кривых контура . Кривые уровня функции \(z = f\left( {x,y} \right)\) — это двумерные кривые, которые мы получаем, полагая \(z = k\), где \(k\) — любое число. Итак, уравнения кривых уровня имеют вид \(f\left( {x,y} \right) = k\). Обратите внимание, что иногда уравнение будет иметь вид \(f\left( {x,y,z} \right) = 0\), и в этих случаях уравнения кривых уровня будут \(f\left( {x, у,к} \справа) = 0\).
Вероятно, вы уже видели кривые уровня (или контурные кривые, называйте их как хотите) раньше. Если вы когда-либо видели карту высот участка земли, то это не что иное, как контурные кривые для функции, которая дает высоту земли в этом районе.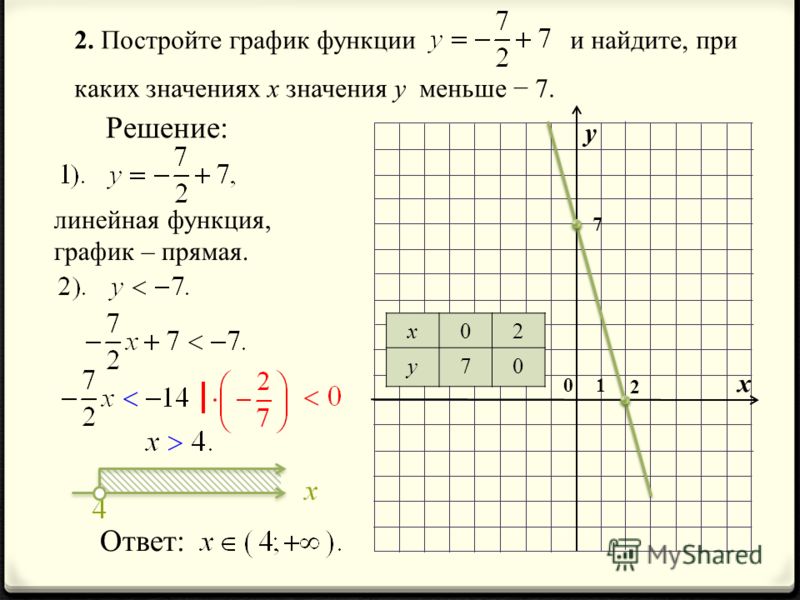 2}} \). Нарисуйте несколько из них.
92}} \]
2}} \). Нарисуйте несколько из них.
92}} \]
Вспомним из раздела Quadric Surfaces, что это верхняя часть «конуса» (или поверхности в форме песочных часов).
Обратите внимание, что для данной проблемы это не требовалось. Это было сделано для практики определения поверхности, и это может пригодиться в будущем.
Теперь о настоящей проблеме. Кривые уровня (или контурные кривые) для этой поверхности задаются уравнением и находятся при подстановке \(z = k\). В нашем примере это 9.2}\]
где \(k\) — любое число. Итак, в этом случае кривые уровня представляют собой окружности радиуса \(k\) с центром в начале координат.
Мы можем изобразить их одним из двух способов. Мы можем отобразить их либо на самой поверхности, либо отобразить их в двухмерной системе координат. Вот каждый график для некоторых значений \(k\).
Обратите внимание, что мы можем думать о контурах с точки зрения пересечения поверхности, которая задается \(z = f\left( {x,y} \right)\) и плоскости \(z = k\).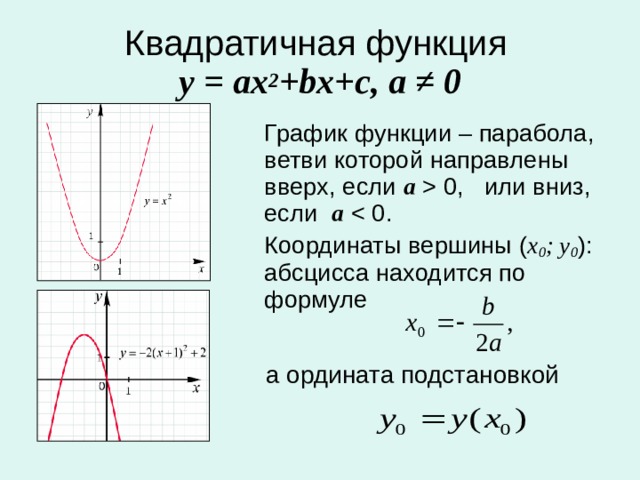 Контур будет представлять собой пересечение поверхности и плоскости.
Контур будет представлять собой пересечение поверхности и плоскости.
Для функций вида \(f\left( {x,y,z} \right)\) мы иногда будем рассматривать поверхностей уровня . Уравнения поверхностей уровня задаются формулой \(f\left({x,y,z} \right) = k\), где \(k\) — любое число.
Последняя тема в этом разделе посвящена трассировкам . В чем-то они похожи на контуры. Как отмечалось выше, мы можем думать о контурах как о пересечении поверхности, заданной \(z = f\left({x,y} \right)\), и плоскости \(z = k\). Следы поверхностей — это кривые, которые представляют собой пересечение поверхности и плоскости, задаваемой \(x = a\) или \(y = b\). 92}\]
, и это будет отображено на плоскости, заданной \(x = 1\).
Ниже приведены два графика. График слева представляет собой график, показывающий пересечение поверхности и плоскости, заданной \(x = 1\). Справа график поверхности и трасса, которую мы ищем в этой части.
Для \(y = 2\) мы сделаем почти то же самое, что и в первой части. 2}\]
2}\]
и вот эскизы для этого дела.
Калькулятор точечной диаграммы | Maker, Examples, Definition, Correlation
В век данных создатель точечных диаграмм бесценен, помогая вам понять мир . Как всегда, Omni прикрывает вашу спину; мы создали средство для создания точечных диаграмм, которое поможет вам визуализировать любой имеющийся у вас набор данных.
Мы покажем вам, как находить корреляции, как читать точечный график и как создавать свои собственные. Давайте освоим навыки, необходимые для понимания мира, в котором мы живем, и сдадим следующий экзамен по математике.
Что такое точечная диаграмма? Переосмысление определения точечной диаграммы
Перво-наперво; что такое точечная диаграмма? Этот простой. Это набор из 90 100 точек, представленных в двумерном пространстве 90 101 . Другими словами: это самый простой способ объективно визуализировать данные. Поскольку точечный график обычно двухмерный (он может быть и трехмерным, но встречается реже), он удобен для выявления корреляций между двумя факторами.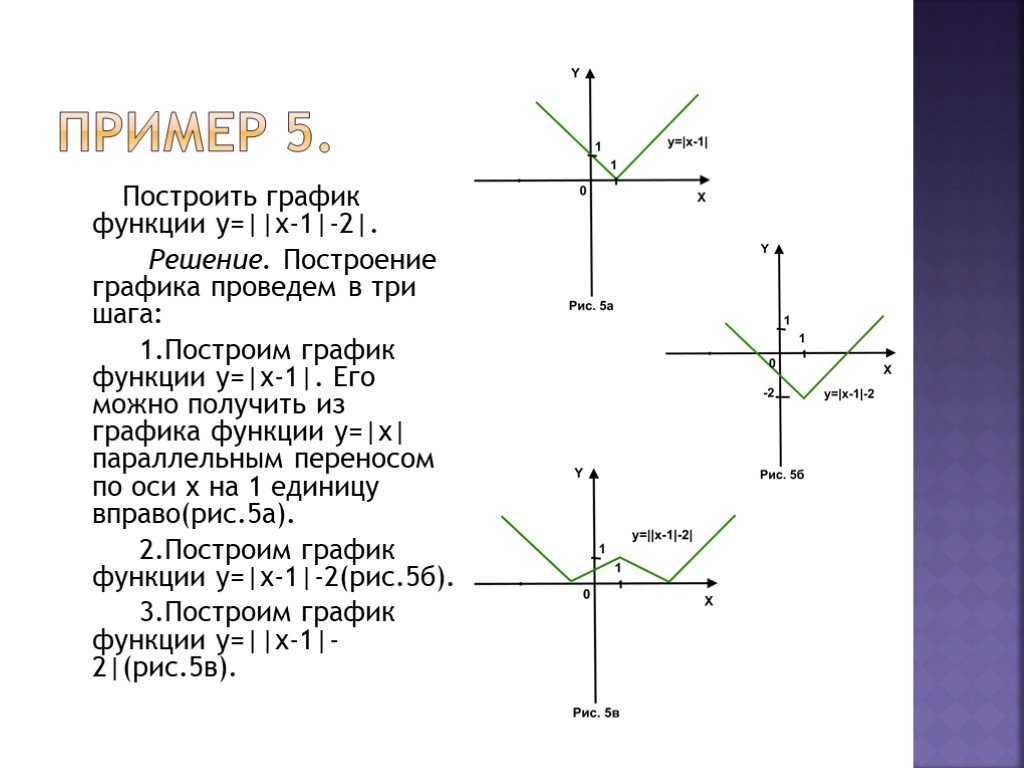
Например, если мы запишем деньги, которые у нас есть в разные дни в течение месяца, мы увидим что-то вроде этого:
Время (день)=[1,8,13,15,22,23]\footnotesize \mathrm{Время\ \scriptsize{(день)}\normalsize{}}=[1,8,13,15,22 ,23] Время (день) = [1,8,13,15,22,23]
И:
Деньги (доллары) = [100,75,60,65,53,44]\footnotesize \mathrm{ Money\ \scriptsize{(доллары)}\normalsize{}}=[100, 75, 60, 65, 53, 44]Money (доллары)=[100,75,60,65,53,44]
, что выглядит как просто какие-то скучные, бесполезные данные. Однако, если вы создадите точечный график с данными, вы сможете увидеть гораздо больше, чем вы думали. Вам не нужно много знать о том, как читать точечный график до понимаю, что со временем мои деньги уменьшаются (надеюсь, потому что мы купили хорошие вещи).
Вы не только можете увидеть это быстрее на этом примере диаграммы разброса , но вы можете сразу увидеть, что единственный момент, когда мы заработали деньги, был выбросом, а не частью реального тренда. Мы вернемся к этому примеру диаграммы рассеяния позже, когда будем говорить о коэффициентах корреляции, линейной регрессии и узнаем больше о том, как читать диаграмму рассеяния.
Мы вернемся к этому примеру диаграммы рассеяния позже, когда будем говорить о коэффициентах корреляции, линейной регрессии и узнаем больше о том, как читать диаграмму рассеяния.
Пока все, что вам нужно понять, это сколько легче обнаружить тренды, выбросы и получить представление о лежащей в их основе взаимосвязи между переменными, используя диаграмму рассеяния. И помните, это пример с 6 точками данных, в реальных наборах данных вы можете легко иметь сотни точек или больше, так что удачи в понимании чего-либо, глядя только на необработанные числа.
Итак, теперь мы понимаем, что такое точечный график, а также какое значение они имеют. Пришло время создать точечную диаграмму самостоятельно. Нет, не вручную, это много лишней работы; мы будем использовать Калькулятор точечной диаграммы Omni .
Как построить точечную диаграмму с помощью калькулятора точечной диаграммы Omni?
Как сделать точечный график? Использование калькулятора точечной диаграммы Omni очень просто . Вам просто нужно взять свои данные, решить, какая переменная будет X-переменной, а какая Y-переменной, и просто ввести точки данных в поля калькулятора. Если вы не хотите анализировать свои данные , порядок ввода переменных не имеет большого значения.
Вам просто нужно взять свои данные, решить, какая переменная будет X-переменной, а какая Y-переменной, и просто ввести точки данных в поля калькулятора. Если вы не хотите анализировать свои данные , порядок ввода переменных не имеет большого значения.
Просто помните, что график точечной диаграммы обновляется с каждым новым вводом (вам нужно ввести полную пару x-y), но он начинает показывать значения только после второго ввода, так как бесполезно создавать точечную диаграмму целиком. данных, если честно. Теперь, когда вы ввели все свои данные, калькулятор точечной диаграммы покажет вам ваше облако точек данных. Это было несложно , не так ли?
Возможно, вы задаетесь вопросом, стоит ли вам научиться создавать точечный график вручную, и мы возражаем против этого. Гораздо важнее ответьте на вопросы, которые следуют после вы делаете точечную диаграмму: что это значит? Я не умею читать точечную диаграмму. Какую информацию он мне показывает?
Какую информацию он мне показывает?
Не волнуйтесь. Мы говорили вам, что поддерживает Omni , и мы это делаем. Давайте посмотрим на некоторые примеры точечных диаграмм и узнаем, как интерпретировать результаты нашего создателя точечных диаграмм.
Как читать точечную диаграмму? Примеры
Мы должны быть с вами честны; если вы действительно хотите научиться читать точечный график в самый эффективный способ, вам нужно будет выучить математику . Но прежде чем мы это сделаем, мы можем многое узнать о данных, просто взглянув на них и подумав о них. Давайте покажем вам на этом примере точечной диаграммы. Считайте, что это более реалистичная версия первого примера точечной диаграммы, который мы видели.
Здесь у нас есть 30 переменных, которые, кажется, не имеют никакой связи, но, если мы нанесем их на график, то ясно увидим, что имеем дело с линейной диаграммой рассеяния с некоторым шумом. Этот шум мы называем любым отклонением от основного тренда. Мы можем определить эту тенденцию математически, но, как люди, у нас есть развился, чтобы хорошо определять закономерности и отношения, иногда слишком хорошо, поэтому мы можем многое сделать без формального анализа.
Мы можем определить эту тенденцию математически, но, как люди, у нас есть развился, чтобы хорошо определять закономерности и отношения, иногда слишком хорошо, поэтому мы можем многое сделать без формального анализа.
Важными вещами, которые необходимо освоить при обучении чтению точечной диаграммы, являются выбор переменных , выявление тенденций и знание разницы между корреляцией и причинно-следственной связью . Выбор переменных прост, но сложен. Как мы уже говорили, это важно только для математического анализа данных. Тем не менее, в общем, вы хотите иметь независимую переменную на оси x и зависимую на оси y.
Самый быстрый способ определить, что есть что, это подумать о причинно-следственной ситуации. В такой ситуации «причина» является независимой переменной и, следовательно, идет по оси x. «Эффект» идет по оси Y , потому что это зависимая переменная. Это не жесткое правило, и все может выглядеть по-разному в зависимости от того, как вы планируете эксперимент или что вы хотите выяснить, но это хорошая отправная точка.
Определение трендов — самая простая часть, потому что это часть того, что определяет нас как людей . Просто взглянув на данные на точечной диаграмме, корреляция должна быть очевидной. Если это не так, вам нужно будет провести корреляционный анализ точечной диаграммы , который немного сложнее и также имеет много общего с последней частью: корреляция против причинно-следственной связи.
Диаграмма корреляции рассеяния и линейная диаграмма рассеяния
Таким образом, корреляция между двумя переменными определяется математически и измеряет, насколько сильно связаны две переменные (или более) . Одно из самых больших заблуждений состоит в том, что сильная корреляция означает, что одна переменная вызывает другую, но это неверно . Иногда есть промежуточная переменная, которая действует как причинная связь между обеими переменными, а иногда причинно-следственная связь вообще отсутствует.
Веб-комикс от XKCD Важно помнить, что, как и большинство математических инструментов, корреляция ничего не говорит нам о реальных связях; это просто говорит о том, как одинаково изменяются две переменные. Если вы разработали разумный эксперимент, справедливо предположить что сильно коррелированные переменные как-то связаны. Однако нельзя быть уверенным в том, какая связь или тип связи существует, просто взглянув на точечную диаграмму или значения корреляции.
Если вы разработали разумный эксперимент, справедливо предположить что сильно коррелированные переменные как-то связаны. Однако нельзя быть уверенным в том, какая связь или тип связи существует, просто взглянув на точечную диаграмму или значения корреляции.
Но предположим, что вы воспользовались средством создания точечной диаграммы и получили то, что кажется линейной точечной диаграммой . Что это значит? Откуда я знаю, что это на самом деле линейный график рассеяния, а не какой-то другой тип? Простой! Ну не так просто, но хоть легко, если у вас есть подходящие инструменты . Позвольте мне кратко провести вас через процесс.
- Убедитесь визуально, что это выглядит как линия. Чем больше у вас очков, тем лучше.
- Анализ точечной диаграммы: с помощью калькулятора линии регрессии методом наименьших квадратов вы можете получить нужные вам математические параметры.
- Убедитесь, что ошибки наклона и точки пересечения малы.

- Убедитесь, что коэффициент корреляции Пирсона близок к максимальному значению 1.
Если все эти тесты положительны, вы можете быть уверены, что у вас есть линейная диаграмма рассеяния . Это отличная новость, потому что вы можете использовать наш калькулятор превышения пробега, чтобы узнать больше о линии тренда, или 90 100, вы можете предсказать 90 101 других пар значений, используя наш калькулятор линейной интерполяции.
В противном случае вам потребуется расширить поиск до других типов корреляции. Удобно, что у нас есть необходимые инструменты для вас в Omni! (Как мы уже говорили, у нас есть ваша спина!) Вот несколько примеров:
- График экспоненциального рассеяния: используйте калькулятор экспоненциальной регрессии; и
- График квадратичного рассеяния: используйте калькулятор квадратичной регрессии.
Однако иногда вам может быть интересно узнать больше о вашем наборе данных , но вас не интересует, как каждая точка данных связана друг с другом, особенно если у вас есть набор одномерных точек.

