Построить график функции y 2 х. Как построить график функции
«Преобразование функций» — Качелями. Сдвиг по оси y вверх. Включи полную громкость – увеличишь a (амплитуду) колебаний воздуха. Сдвиг по оси x влево. Задачи урока. 3 балла. Музыкой. Постройте график функции и определите D(f), E(f) и T: Сжатие по оси x. Сдвиг по оси y вниз. Добавь красного цвета в палитру – уменьшишь k (частоту) электромагнитных колебаний.
«Функции нескольких переменных» — Производные высших порядков. Функцию двух переменных можно изобразить графически. Дифференциальное и интегральное исчисления. Внутренние и граничные точки. Определение предела функции 2-х переменных. Курс математического анализа. Берман. Предел функции 2-х переменных. График функции. Теорема. Ограниченная область.
«Понятие функции» — Способы построение графиков квадратичной функции. Изучение разных способов задания функции – важный методический прием. Особенности изучения квадратичной функции. Генетическая трактовка понятия «функция».
Функции и графики в школьном курсе математики. Представление о линейной функции выделяется при построении графика некоторой линейной функции.
«Тема Функция» — Анализ. Нужно выяснить не то, что ученик не знает, а то, что он знает. Заложение основ для успешной сдачи ЕГЭ и поступление в ВУЗы. Синтез. Если ученики работают по-разному, то и учитель должен с ними работать по-разному. Аналогия. Обобщение. Распределение заданий ЕГЭ по основным блокам содержания школьного курса математики.
«Преобразование графиков функций» — Повторить виды преобразований графиков. Сопоставить каждому графику функцию. Симметрия. Цель урока: Построение графиков сложных функций. Рассмотрим примеры преобразований, объясним каждый вид преобразования. Преобразование графиков функций. Растяжение. Закрепить построение графиков функций с использованием преобразований графиков элементарных функций.
«Графики функций» — Функция вида. Область значений функции – все значения зависимой переменной у. Графиком функции является парабола.
План построения квадратичной функции.
1. Область определения функции (D (y )).
2. Графиком данной функции является парабола, ветви которой направлены вверх (вниз), т.к. а = __ > 0 (а = __
3. Координаты вершины параболы.
4. Уравнение оси симметрии.
5. Точка пересечения графика с осью OY .
6. Нули функции.
7. Таблица значений функции.
8. График.
Пример построения графика функции y = x 2 – 4 x + 3
1. D (y ) = (- ∞; + ∞).
2. Графиком данной функции является парабола, ветви которой направлены вверх, т. к. а = 1 > 0.
3. Координаты вершины параболы:
x
0
= —
,
y
0
= 2
2
— 4·2 + 3 = 4 – 8 + 3 = — 1.
4. Уравнение оси симметрии x = 2.
5. Точка пересечения с осью OY (0; 3).
6. Нули функции:
x 2 – 4 x + 3 = 0 D = (- 4) 2 – 4 ·1·3 = 16 -12 = 4 = 2 2
x 1 = = 1 x 2 = = 3
7. Составим таблицу значений функции:
0
1
2
3
3
0
— 1
0
8. Построим график
Свойства функции:
1. Множество значений функции (E (y )).
2. Промежутки знакопостоянства функции (y >0, y
3. Промежутки монотонности функции (возрастает, убывает).
4. Точки максимума и минимума функции.
Свойства функции y = x 2 – 4 x + 3.
1. E (y ) = [-1; + ∞).
2. y
Разберем как строить график с модулем.
Найдем точки при переходе которых знак модулей меняется.
Каждое выражения, которое под модулем приравниваем к 0.
У нас их два x-3 и x+3.
x-3=0 и x+3=0
x=3 и x=-3
У нас числовая прямая разделится на три интервала (-∞;-3)U(-3;3)U(3;+∞). На каждом интервале нужно определить знак под модульных выражений.
1. Это сделать очень просто, рассмотрим первый интервал (-∞;-3). Возьмем с этого отрезка любое значение, например, -4 и подставим в каждое под модульное уравнение вместо значения х.
х=-4
x-3=-4-3=-7 и x+3=-4+3=-1
У обоих выражений знаки отрицательный, значит перед знаком модуля в уравнении ставим минус, а вместо знака модуля ставим скобки и получим искомое уравнение на интервале (-∞;-3).
y=— (x-3)-(— (x+3))=-х+3+х+3=6
На интервале (-∞;-3) получился график линейной функции (прямой) у=6
2. Рассмотрим второй интервал (-3;3). Найдем как будет выглядеть уравнение графика на этом отрезке. Возьмем любое число от -3 до 3, например, 0. Подставим вместо значения х значение 0.
х=0
x-3=0-3=-3 и x+3=0+3=3
У первого выражения x-3 знак отрицательный получился, а у второго выражения x+3 положительный.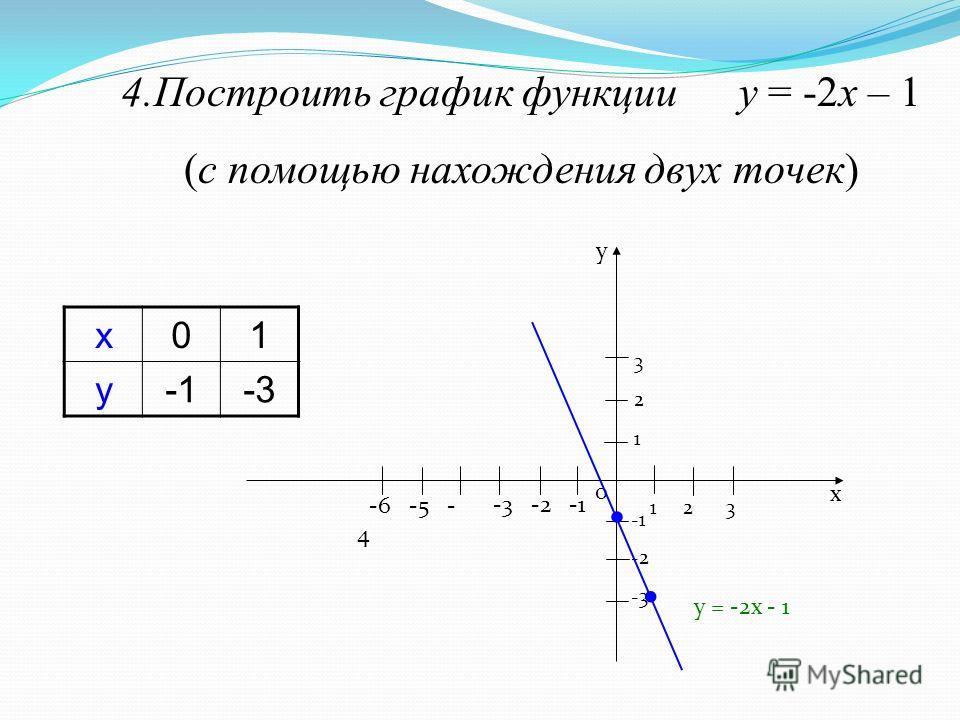
Следовательно, перед выражением x-3 запишем знак минус, а перед вторым выражением знак плюс.
y=— (x-3)-(+ (x+3))=-х+3-х-3=-2x
На интервале (-3;3) получился график линейной функции (прямой) у=-2х
3.Рассмотрим третий интервал (3;+∞). Возьмем с этого отрезка любое значение, например 5, и подставим в каждое под модульное уравнение вместо значения х.
х=5
x-3=5-3=2 и x+3=5+3=8
У обоих выражений знаки получились положительными, значит перед знаком модуля в уравнении ставим плюс, а вместо знака модуля ставим скобки и получим искомое уравнение на интервале (3;+∞).
y=+ (x-3)-(+ (x+3))=х-3-х-3=-6
На интервале (3;+∞) получился график линейной функции (прямой) у=-6
4. Теперь подведем итог.Постоим график y=|x-3|-|x+3|.
На интервале (-∞;-3) строим график линейной функции (прямой) у=6.
На интервале (-3;3) строим график линейной функции (прямой) у=-2х.
Чтобы построить график у=-2х подберем несколько точек.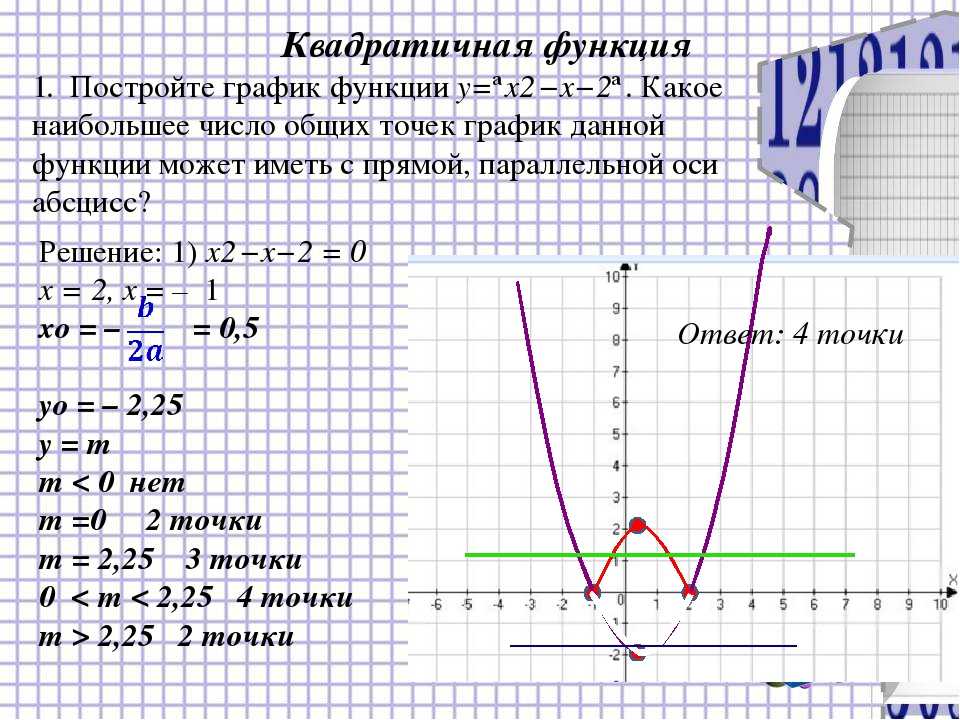
x=-3 y=-2*(-3)=6 получилась точка (-3;6)
x=0 y=-2*0=0 получилась точка (0;0)
x=3 y=-2*(3)=-6 получилась точка (3;-6)
На интервале (3;+∞) строим график линейной функции (прямой) у=-6.
Прямая y=kx при любом значении k всегда будет проходить через точку (0;0). Поэтому мы можем изменить только наклон данной прямой y=kx, а за наклон у нас отвечает коэффициент k.
Если k будет любое положительное число, то будет одно пересечение прямой y=kx с графиком y=|x-3|-|x+3|. Этот вариант нам подходит.
Если k будет принимать значение (-2;0), то пересечений прямой y=kx с графиком y=|x-3|-|x+3| будет три.Этот вариант нам не подходит.
Если k=-2, решений будет множество [-2;2], потому что прямая y=kx будет совпадать с графиком y=|x-3|-|x+3| на данном участке. Этот вариант нам не подходит.
Если k будет меньше -2, то прямая y=kx с графиком y=|x-3|-|x+3| будет иметь одно пересечение.Этот вариант нам подходит.
Если k=0, то пересечений прямой y=kx с графиком y=|x-3|-|x+3| также будет одно.Этот вариант нам подходит.
Ответ: при k принадлежащей интервалу (-∞;-2)U}
«Как построить график функции F(x+l)+m»
Дата публикации: .
Дополнительные материалы
Уважаемые пользователи, не забывайте оставлять свои комментарии, отзывы, пожелания! Все материалы проверены антивирусной программой.
Скачать:Как построить график функции f(x+l)+m (PPTX)
Обучающие пособия и тренажеры в интернет-магазине «Интеграл» для 8 класса
Комбинаторика и теория вероятностей
Уравнения и неравенства
Ребята, на двух последних уроках мы разбирали, как правильно строить графики с помощью операции параллельного переноса.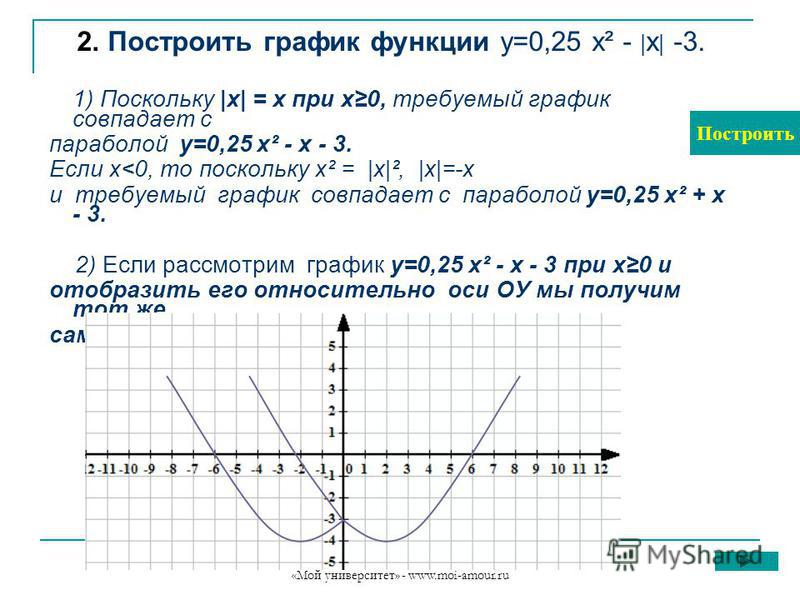
2) так как к $x$ прибавляется положительное число, то надо сдвинуть график параболы на 3 единицы влево.
3) поскольку от нашей функции отнимается число 2, следует воспользоваться приемом построения графиков функций $y=f(x)+m$.
И сместить график функции, полученный в пункте два, на две единицы вниз.
Строим наши графики.
Нам пришлось построить целых три графика, согласитесь, это неудобно и скучно. Можно ли упростить данную операцию?
Давайте внимательно посмотрим на графики, получившиеся в итоге. Что бросается в глаза? Были построены три совершенно одинаковых параболы, отличающиеся координатой вершины. Значит, нам надо обратить особое внимание на вершину: какая координата получилась по $х$ в итоге? Очевидно, что это координата равна $-3$. Как раз та величина, на которую сместили всю параболу влево, совпала с координатой вершины по $х$. А какая координата по $y$ получилась у вершины? Очевидно, что -2. Именно то число, на которое сместили график исходной параболы вниз.
2$. Мы получили два способа построения графиков функций $y=f(x+l)+m$.
Опишем оба алгоритма.
Алгоритм 1 построения графика функции $y=f(x+l)+m$.
1. Построить график функции $y=f(x)$.
2. Перенести построенный график на $l$ единиц влево, если $l>0$ или на $l$ единиц вправо, если $l
3. Перенести полученный во втором пункте график на $m$ единиц вверх, если $m>0$ или на $m$ единиц вниз, если $m
Алгоритм 2 построения графика функции $y=f(x+l)+m$.
1. Перейти к вспомогательной системе координат, построив две прямые $x=-l$ и $y=m$. Точка пересечения этих прямых – начало координат новой системы.
2. В новой вспомогательной системе построить график функции $y=f(x)$.
Каким алгоритмом пользоваться – ваш выбор. Второй – более быстрый метод, что может быть важным при решении многих задач. Выиграть время и решить больше задач всегда полезно!
Пример 3.
Построить график функции: $y=\frac{3}{x+2}-3$.
Решение.
Воспользуемся вторым алгоритмом.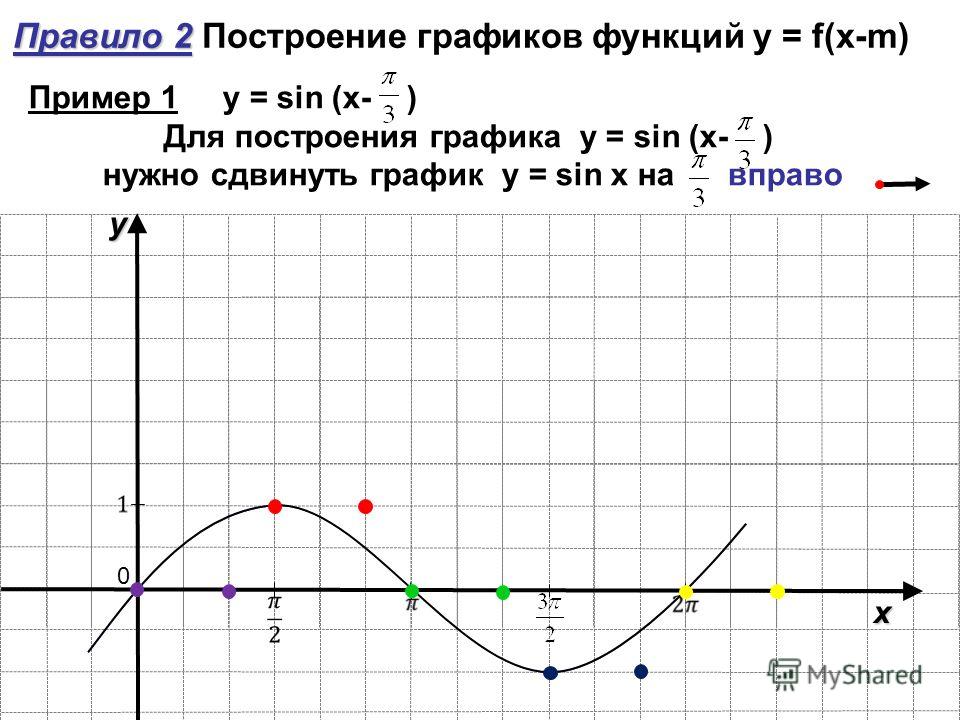
2+2$.
2. Построить график функции: $y=-\frac{4}{x-1}-2$.
3. Построить график функции: $y=\sqrt{x+2}-3$.
| 1 | Оценка с использованием заданного значения | квадратный корень из 50 | |
| 2 | Оценка с использованием заданного значения | квадратный корень из 45 | |
| 3 | Оценить | 5+5 | |
| 4 | Оценить | 7*7 | |
| 5 | Найти простую факторизацию | 24 | |
| 6 | Преобразование в смешанный номер | 52/6 | |
| 7 | Преобразование в смешанный номер | 93/8 | |
| 8 | Преобразование в смешанный номер | 34/5 | |
| 9 | График | у=х+1 | |
| 10 | Оценка с использованием заданного значения | квадратный корень из 128 | |
| 11 | Найдите площадь поверхности | сфера (3) | |
| 12 | Оценить | 54-6÷2+6 | |
| 13 | График | г=-2x | |
| 14 | Оценить | 8*8 | |
| 15 | Преобразование в десятичное число | 5/9 | |
| 16 | Оценка с использованием заданного значения | квадратный корень из 180 | |
| 17 | График | у=2 | |
| 18 | Преобразование в смешанный номер | 7/8 | |
| 19 | Оценить | 9*9 | |
| 20 | Решите для C | С=5/9*(Ф-32) | |
| 21 | Упростить | 1/3+1 1/12 | |
| 22 | График | у=х+4 | |
| 23 | График | г=-3 | |
| 24 | График | х+у=3 | |
| 25 | График | х=5 | |
| 26 | Оценить | 6*6 | |
| 27 | Оценить | 2*2 | |
| 28 | Оценить | 4*4 | |
| 29 | Оценить | 1/2+(2/3)÷(3/4)-(4/5*5/6) | |
| 30 | Оценить | 1/3+13/12 | |
| 31 | Оценка | 5*5 | |
| 32 | Решить для d | 2д=5в(о)-вр | |
| 33 | Преобразование в смешанный номер | 3/7 | |
| 34 | График | г=-2 | |
| 35 | Найдите склон | у=6 | |
| 36 | Преобразование в проценты | 9 | |
| 37 | График | у=2х+2 | |
| 38 | 92+5х+6=0|||
| 41 | Преобразование в смешанный номер | 1/6 | |
| 42 | Преобразование в десятичное число | 9% | |
| 43 | Найти n | 12н-24=14н+28 | |
| 44 | Оценить | 16*4 | |
| 45 | Упростить | кубический корень из 125 | |
| 46 | Преобразование в упрощенную дробь | 43% | |
| 47 | График | х=1 | |
| 48 | График | у=6 | |
| 49 | График | г=-7 | |
| 50 | График | у=4х+2 | |
| 51 | Найдите склон | у=7 | |
| 52 | График | у=3х+4 | |
| 53 | График | у=х+5 | |
| 54 | График | 92-9=0||
| 58 | Оценка с использованием заданного значения | квадратный корень из 192 | |
| 59 | Оценка с использованием заданного значения | квадратный корень из 25/36 | |
| 60 | Найти простую факторизацию | 14 | |
| 61 | Преобразование в смешанный номер | 7/10 | |
| 62 | Решите для | (-5а)/2=75 | |
| 63 | Упростить | х | |
| 64 | Оценить | 6*4 | |
| 65 | Оценить | 6+6 | |
| 66 | Оценить | -3-5 | |
| 67 | Оценить | -2-2 | |
| 68 | Упростить | квадратный корень из 1 | |
| 69 | Упростить | квадратный корень из 4 | |
| 70 | Найди обратное | 1/3 | |
| 71 | Преобразование в смешанный номер | 20. 11. | |
| 72 | Преобразование в смешанный номер | 7/9 | |
| 73 | Найти LCM | 11, 13, 5, 15, 14 | , , , , |
| 76 | График | 3x+4y=12 | |
| 77 | График | 3x-2y=6 | |
| 78 | График | у=-х-2 | |
| 79 | График | у=3х+7 | |
| 80 | Определить, является ли многочлен | 2x+2 | |
| 81 | График | у=2х-6 | |
| 82 | График | у=2х-7 | |
| 83 | График | у=2х-2 | |
| 84 | График | у=-2х+1 | |
| 85 | График | у=-3х+4 | |
| 86 | График | у=-3х+2 | |
| 87 | График | у=х-4 | |
| 88 | Оценить | (4/3)÷(7/2) | |
| 89 | График | 2x-3y=6 | |
| 90 | График | х+2у=4 | |
| 91 | График | х=7 | |
| 92 | График | х-у=5 | |
| 93 | Решение с использованием свойства квадратного корня 92-2x-3=0 | ||
| 95 | Найдите площадь поверхности | конус (12)(9) | |
| 96 | Преобразование в смешанный номер | 3/10 | |
| 97 | Преобразование в смешанный номер | 7/20 | 92)
Mathscene — Функции 1 — Урок 1
Mathscene — Функции 1 — Урок 1| 2007 Расмус Эф и Джанн Сак | Функции я | Распечатать |
Урок 1
Функции и графики
Пример 1
У нас есть уравнение у = 2х + 4,
Сначала мы делаем таблицу из
values вычисляют значения y из выбранных нами значений x.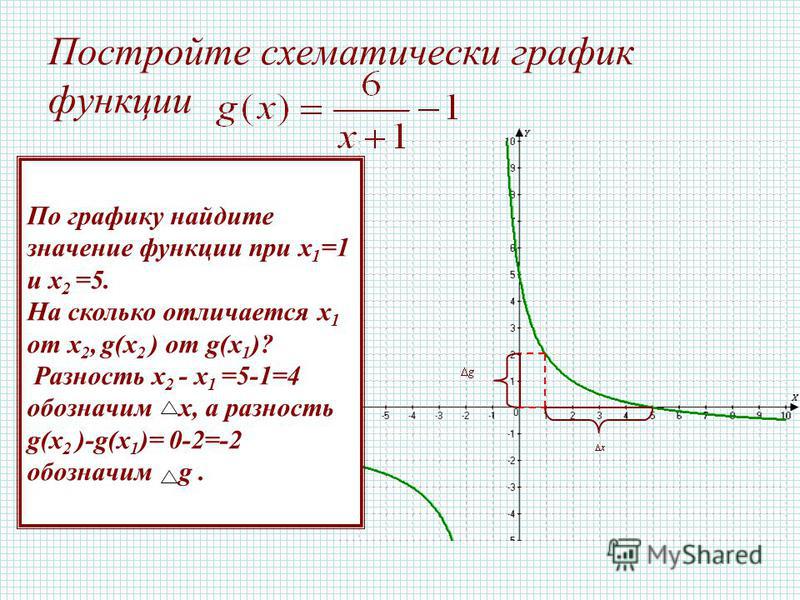
Когда мы строим
эти точки в системе координат мы видим, что они лежат на прямой линии. Мы присоединяемся
точки вместе.
|
Это очень легко сделать
с помощью графического калькулятора.
Если у нас есть Casio, мы выбираем TABLE в меню.
Затем мы пишем 2x + 4 в Откроется меню функций таблицы. Y1 = 2x + 4 теперь на экране 909:25
Теперь нам нужно решить, какой x значения, которые мы хотим использовать. Для этого мы выбираем ДИАПАЗОН, нажав F5. Следующее появляется экран:
Мы решили начать с −2 и заканчиваются на 2. Шаг говорит нам, на какие шаги мы хотим поднять x. В нашем В этом случае мы оставим его равным 1 и нажмем EXE.
Следующий набор действий выполняет это:
Это возвращает нас к предыдущий экран, где мы выбираем TABLE, нажав F6. Затем таблица значений появляется. 909:25
Мы можем построить график, выбрав G-CON ( F5 ).
Также можно использовать в программе EXCEL составить таблицу значений и нарисовать график. В EXCEL вводим
числа −2 и −1 в ячейках A2
и A3 (см. таблицу EXCEL выше), мы можем автоматически заполнить остальную часть столбца
A, заблокировав A2 и A3, а затем скопировав их.
Формула в B2 = 2A2 + 4, что равно
скопировано вниз.
Мы можем построить график, блокировка чисел в двух столбцах, затем нажатие кнопки построения графика (1). Мы выбираем xy-разброс (2) и затем выберите один из подключенных графиков (3), прежде чем нажать «Готово» (4). Затем мы можем внести любые изменения во внешний вид графика, указав наведите курсор мыши на элемент, который мы хотим изменить, и нажмите правую кнопку мыши. 909:25
Теперь давайте посмотрим еще кое-что Примеры.
Пример 2
Составьте таблицу значений и нарисуйте следующее графики
| График у = х | ||
| х | г. = х | |
| -2 | -2 | |
| -1 | -1 | |
| 0 | 0 | |
| 1 | 1 | |
| 2 | 2 | |
| График у = 2 | ||
| х | г. = 2 | |
| -2 | 2 | |
| -1 | 2 | |
| 0 | 2 | |
| 1 | 2 | |
| 2 | 2 | |
| График у = х 2 | ||
| х | г. = 2 | |
| -2 | 4 | |
| -1 | 1 | |
| 0 | 0 | |
| 1 | 1 | |
| 2 | 4 | |
| График у = 2 x | ||
| х | г. = 2 х | |
| -2 | ||
| -1 | ||
| 0 | 1 | |
| 1 | 2 | |
| 2 | 4 | |
Теперь мы рассмотрим еще несколько примеров, которые нельзя относиться одинаково. В этих примерах формула не записывается как y =….. и поэтому мы не можем использовать табличную функцию в нашем калькулятор. 909:25
Пример 3
х = 2
Единственным условием здесь является то, что x принимает значение
2. Когда мы составляем таблицу значений, мы всегда должны иметь x равным 2. y может принимать
любое значение, мы выбрали −2, −1, 0, 1 или 2. Здесь вы можете увидеть наши
таблица значений.
| График х = 2 | ||
| х = 2 | г | |
| 2 | -2 | |
| 2 | -1 | |
| 2 | 0 | |
| 2 | 1 | |
| 2 | 2 | |
Результат — вертикальная линия, проходящая через точку 2 по оси х.
Пример 4
Далее рассмотрим отношение y 2 = х.
Когда мы решим это уравнение относительно y, мы получим два
ответы.
Другими словами, есть два значения y для каждого х, который мы выбираем. Также мы ограничены выбором только положительных значений для x как мы не можем извлечь квадратный корень из отрицательного числа. Ниже Вы можете увидеть таблицу значений и график.
| График у = х | ||
| х | г | |
| -1 | Нет в наличии | |
| 0 | 0 | |
| 1 | 1 | |
| 2 | 2 | |
| 3 | 3 | |
Пример 5
Теперь посмотрим на уравнение x 2 + у 2 = 4.
Нахождение у:
х 2 + у 2 = 4
г 2 = 4 — х 2
Снова мы получаем два значения y для каждого значения x, которое мы выбрали. Мы также находим, что мы не можем выбрать любые значения x вне интервала [−2, 2], потому что тогда мы получим отрицательное число под квадратный корень.
Таблица значений и график показаны ниже. 909:25
График | ||
| х | ||
| -2 | 0 | |
| -1 | 3 | |
| 0 | 2 | |
| 1 | 3 | |
| 2 | 0 | |
Когда мы наносим точки, мы видим, что все они лгут. на окружности с центром в начале координат (0, 0) . Радиус круга
составляет 2 единицы.
Этот результат легко понять, потому что х 2 + у 2 = 4 на самом деле является правилом Пифагора для прямоугольного треугольника с гипотенузой длины 2, а другие стороны длины x и y. Эти примеры показывают, что некоторые уравнения, которые дают правило, связывающее x и y, имеют только одно значение y для каждого x которые мы выбираем, и некоторые уравнения имеют более одного y для каждого x. 909:25
Уравнения, связывающие один y с одним x, очень важные в науках и называются ФУНКЦИЯМИ. Мы говорим, что у функция от x и написать y = f(x) . Мы читаем это как y равно f от x
Когда мы смотрим на графики уравнений, которые функций мы видим, что вертикальные линии никогда не пересекают график более одного раза.Мы видим это, если посмотрим на графики в примеры, с которыми мы уже работали.
Красная вертикальная линия пересекает графики 2, 3 и 4 в
два или более места, показывающие нам, что это не графики функций. 909:25
В примере 1 любую вертикальную линию мы draw разрезает график только один раз. Это график функции с уравнением y = х 2 .
А также записать это уравнение как y = x 2 мы можем записать это как f(x) = x 2 где y = f(x) .Мы используем f(x) вместо y, чтобы показать, что значение у зависит от значения х является функцией от х.
В этом примере, если мы выберем x = 2, мы можем вычислить y по формуле y = 2 2 = 4.
На функциональном языке мы говорим, что f от 2 равно 4.
Используя обозначение функции, мы можем написать f(2) = 2 2 = 4.
Пример 6
| Учитывая функцию | Находить f(0), f(1) и f(3) |
Ставим значения 0, 1 и 3 в уравнение вместо x и выработать значение функции (значение y) в каждом случае.
| Это невозможно |
Мы можем вставлять не только цифры, но и буквы.