Построить график функции y sin x 3: Mathway | Популярные задачи

Mathway | Популярные задачи

1	Найти точное значение	sin(30)
2	Найти точное значение	sin(45)
3	Найти точное значение	sin(30 град. )
4	Найти точное значение	sin(60 град. )
5	Найти точное значение	tan(30 град. )
6	Найти точное значение	arcsin(-1)
7	Найти точное значение	sin(pi/6)
8	Найти точное значение	cos(pi/4)
9	Найти точное значение	sin(45 град. )
10	Найти точное значение	sin(pi/3)
11	Найти точное значение	arctan(-1)
12	Найти точное значение	cos(45 град. )
13	Найти точное значение	cos(30 град. )
14	Найти точное значение	tan(60)
15	Найти точное значение	csc(45 град. )
16	Найти точное значение	tan(60 град. )
17	Найти точное значение	sec(30 град. )
18	Найти точное значение	cos(60 град. )
19	Найти точное значение	cos(150)
20	Найти точное значение	sin(60)
21	Найти точное значение	cos(pi/2)
22	Найти точное значение	tan(45 град. )
23	Найти точное значение	arctan(- квадратный корень из 3)
24	Найти точное значение	csc(60 град. )
25	Найти точное значение	sec(45 град. )
26	Найти точное значение	csc(30 град. )
27	Найти точное значение	sin(0)
28	Найти точное значение	sin(120)
29	Найти точное значение	cos(90)
30	Преобразовать из радианов в градусы	pi/3
31	Найти точное значение	tan(30)
32	Преобразовать из градусов в радианы	45
33	Найти точное значение	cos(45)
34	Упростить	sin(theta)^2+cos(theta)^2
35	Преобразовать из радианов в градусы	pi/6
36	Найти точное значение	cot(30 град. )
37	Найти точное значение	arccos(-1)
38	Найти точное значение	arctan(0)
39	Найти точное значение	cot(60 град. )
40	Преобразовать из градусов в радианы	30
41	Преобразовать из радианов в градусы	(2pi)/3
42	Найти точное значение	sin((5pi)/3)
43	Найти точное значение	sin((3pi)/4)
44	Найти точное значение	tan(pi/2)
45	Найти точное значение	sin(300)
46	Найти точное значение	cos(30)
47	Найти точное значение	cos(60)
48	Найти точное значение	cos(0)
49	Найти точное значение	cos(135)
50	Найти точное значение	cos((5pi)/3)
51	Найти точное значение	cos(210)
52	Найти точное значение	sec(60 град. )
53	Найти точное значение	sin(300 град. )
54	Преобразовать из градусов в радианы	135
55	Преобразовать из градусов в радианы	150
56	Преобразовать из радианов в градусы	(5pi)/6
57	Преобразовать из радианов в градусы	(5pi)/3
58	Преобразовать из градусов в радианы	89 град.
59	Преобразовать из градусов в радианы	60
60	Найти точное значение	sin(135 град. )
61	Найти точное значение	sin(150)
62	Найти точное значение	sin(240 град. )
63	Найти точное значение	cot(45 град. )
64	Преобразовать из радианов в градусы	(5pi)/4
65	Найти точное значение	sin(225)
66	Найти точное значение	sin(240)
67	Найти точное значение	cos(150 град. )
68	Найти точное значение	tan(45)
69	Вычислить	sin(30 град. )
70	Найти точное значение	sec(0)
71	Найти точное значение	cos((5pi)/6)
72	Найти точное значение	csc(30)
73	Найти точное значение	arcsin(( квадратный корень из 2)/2)
74	Найти точное значение	tan((5pi)/3)
75	Найти точное значение	tan(0)
76	Вычислить	sin(60 град. )
77	Найти точное значение	arctan(-( квадратный корень из 3)/3)
78	Преобразовать из радианов в градусы	(3pi)/4
79	Найти точное значение	sin((7pi)/4)
80	Найти точное значение	arcsin(-1/2)
81	Найти точное значение	sin((4pi)/3)
82	Найти точное значение	csc(45)
83	Упростить	arctan( квадратный корень из 3)
84	Найти точное значение	sin(135)
85	Найти точное значение	sin(105)
86	Найти точное значение	sin(150 град. )
87	Найти точное значение	sin((2pi)/3)
88	Найти точное значение	tan((2pi)/3)
89	Преобразовать из радианов в градусы	pi/4
90	Найти точное значение	sin(pi/2)
91	Найти точное значение	sec(45)
92	Найти точное значение	cos((5pi)/4)
93	Найти точное значение	cos((7pi)/6)
94	Найти точное значение	arcsin(0)
95	Найти точное значение	sin(120 град. )
96	Найти точное значение	tan((7pi)/6)
97	Найти точное значение	cos(270)
98	Найти точное значение	sin((7pi)/6)
99	Найти точное значение	arcsin(-( квадратный корень из 2)/2)
100	Преобразовать из градусов в радианы	88 град.

Свойства функции y = sin x и ее график

Похожие презентации:

Элементы комбинаторики ( 9-11 классы)

Применение производной в науке и в жизни

Проект по математике «Математика вокруг нас. Узоры и орнаменты на посуде»

Знакомство детей с математическими знаками и монетами

Тренажёр по математике «Собираем урожай». Счет в пределах 10

Методы обработки экспериментальных данных

Лекция 6. Корреляционный и регрессионный анализ

Решение задач обязательной части ОГЭ по геометрии

Дифференциальные уравнения

Подготовка к ЕГЭ по математике. Базовый уровень Сложные задачи

y
— 2π
-π
0
π
2π
x
1

2. Свойства функции

1.D(y)
2.E(y)
3. Четность функции
4. Периодичность функции
5.Нули функции
6. Наибольшее значение
7. Наименьшее значение
8. Положительные значения
9. Отрицательные значения
10. Возрастание функции
11. Убывание функции
2

3. y = sin x

y
y = sin x
1
D (y)
x
0
xЄR
-1
— 3π/2
-π
— π/2
0
π/2
π
3π/2
2π
3
x

4. y = sin x

y
y = sin x
E (y)
1
0
[ -1; 1]
y
x
-1
1
— 3π/2
-π
— π/2
0
π/2
π
3π/2
2π
-1
4
x

5.

y = sin xy
y = sin x
1
Четность функции
Функция нечетна, т.к. sin(-x)=-sin x,
график симметричен относительно
(0;0)
0
x
-1
y
1
— 3π/2
-π
— π/2
0
π/2
π
3π/2
2π
-1
5
x

6. y = sin x

y
y = sin x
1
Периодичность функции
0
Период функции Т=2π,
sin(x+2π)=sin x
x
-1
y
1
— 3π/2
-π
— π/2
0
π/2
π
3π/2
2π
-1
6
x

7. y = sin x

y
y = sin x
1
Нули функции sin x = 0
при x = πk
0
y
x
-1
1
— 3π/2
-π
— π/2
0
π/2
π
3π/2
2π
-1
7
x

8. y = sin x

y
1
y = sin x
0
Наибольшее значение sin x = 1
при х= π/2+2πk
y
x
-1
х= π/2
1
— 3π/2
-π
— π/2
0
π/2
π
3π/2
2π
-1
8
x

9. y = sin x

y
y = sin x
1
Наименьшее значение sin x = -1
при х= -π/2+2πk
0
y
x
-1
х= 3π/2
1
— 3π/2
-π
— π/2
0
π/2
π
3π/2
x
2π
-1
9

10.

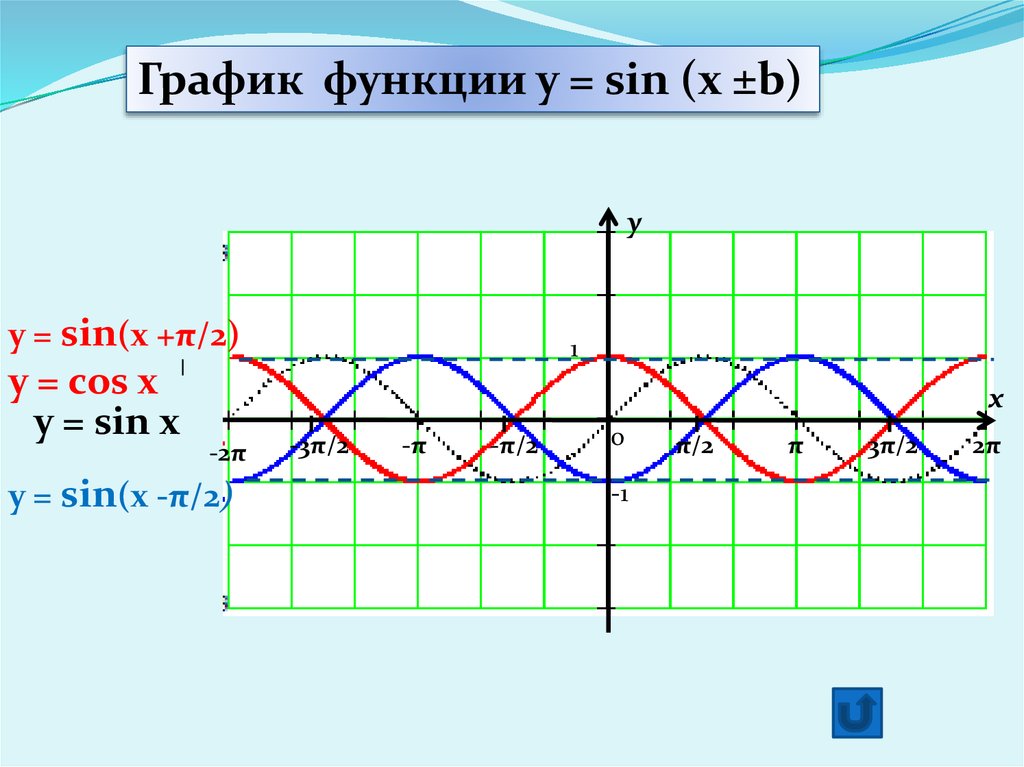y = sin на отрезкеПостроение графика функции
y = sin на отрезке
y
0, 2
3
4
6
sin(π/6)=0,5
x
sin(π/4) 0,7
y
sin(π/3) 0,866
1
— 3π/2
-π
— π/2
0
6 4 3
π/2
π
3π/2
2π
-1
10
x
График функции на отрезке
;
y
у = sin x
x
y
— 3π/2
-π
— π/2
0
π/2
π
x
3π/2
11

12. y = sin x

y
y = sin x
x
y
1
— 3π/2
-π
— π/2
0
π/2
π
3π/2
2π
-1
12
x

13. y = sin x

График функции y=sin x называется синусоида
y
1
-2π
— 3π/2
-π
— π/2
0
π/2
π
3π/2
2π
5π/2 x
-1
13

14. y = sin x

Промежутки знакопостоянства
y
y = sin x
+
+
Положительные значения sin x>0
на отрезке (2πk; π+2πk), k
x
y
1
— 3π/2
-π
— π/2
0
π/2
π
3π/2
2π
-1
14
x

15.

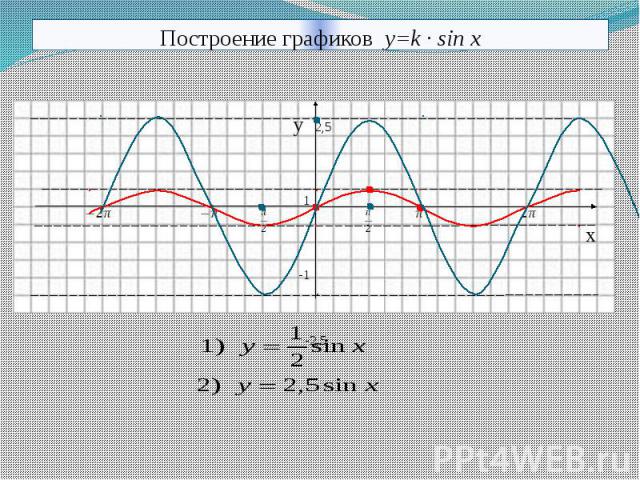y = sin x.
y
Промежутки знакопостоянства
y = sin x
Отрицательные значения sin x<0
–
на отрезке (π+2πk; 2π+2πk). k
x
–
y
1
— 3π/2
-π
— π/2
0
π/2
π
3π/2
2π
-1
15
x

16. y = sin x

Промежутки возрастания
y
y = sin x
Функция возрастает
на отрезке [-π/2+2πk; π/2+2πk]
x
y
1
— 3π/2
-π
— π/2
0
π/2
π
3π/2
x
2π
-1
16

17. y = sin x

Промежутки убывания
y
y = sin x
Функция убывает
на отрезке [π/2+2πk; 3π/2+2πk]
x
y
1
— 3π/2
-π
— π/2
0
π/2
π
3π/2
2π
-1
17
x
Задача
Сравнить числа
Так как
= 3,14,
< 2 < 3 <
sin 2
2
и
1,57
sin 3
, то
2
Из графика видно, что на отрезке ;
2
функция у=sinх убывает.
Ответ: sin 2 > sin 3.
18
Преобразование графика
y = sinx
4,5
Построить график
функции
у=sinх+3
y = sinx + 3
4
3,5
3
3
2,5
2
1,5
y = sinx
1
+
Сдвиг вдоль оси ординат
0,5
вверх
0
2
-0,5
-1
-1,5
1,5
Построить график
функции
у=sinх-3
1
0,5
0
-0,5
-1
-2
-2,5
-3
—
y = sinx — 3
-1,5
-3
-3,5
вниз
-4
-4,5
19
Сдвиг вдоль оси абсцисс
Построить график функции
у=sin(х — 4 )
1,5
+
y = sin x
1
y = sin(x —
0,5
4
)
π/
0
Сдвиг влево
-0,5
-1
-1,5
Построить
график функции
у=sin(х+ )
—
4
1,5
y = sinx
1
y = sin(x +
4
)
0,5
0
-0,5
—
-1
Сдвиг вправо
-1,5
20
Сжатие и растяжение к оси абсцисс
Построить график
функции у= 3 sinх
K >1
растяжение
У = 3 sin x
3,5
3
2,5
2
1,5
1
0,5
0
-0,5
-1
-1,5
-2
-2,5
-3
-3,5
1,5
Построить график 1
функции у=1/ 3 sinх0,5
у = 1/3 sin x
0
0< K <1
сжатие
-0,5
-1
-1,5
21
Сжатие и растяжение к оси ординат
Построить график
функции
у = sin2х
1,5
У =sin 2х
1
0,5
0
K >1
-0,5
сжатие
Построить
график функции
у = sin х
2
-1
-1,5
У = sin
y
1,5
х
2
1
0,5
0
x
0
-0,5
0< K <1
растяжение
-1
-1,5
— π/2
π/2
π
3π/2
2
π
22

English     Русский Правила

график y = sin (x/3)

график y = sin (x/3) | mathtestpreparation. com

вернуться к математический вопрос и ответ

График y = A sin Bx обладает свойством

(1). амплитуда = |А|

(2). период = 2pi/B

Для y = sin(x/3),

, поскольку A = 1, поэтому его амплитуда равна |1|

, так как B = 1/3, поэтому его период = 2pi/B = 2pi &divide 1/3 = 2pi &times 3 = 6pi

Таким образом, его амплитуда равна 1, а период равен 6pi

Найти пять точек за один период

один период равен 6pi, половина периода равна 3pi, четверть периода равна 3pi/2

разделить пять точек поровну в периоде [0, 6pi]

, поэтому пять точек по оси x:

х ₁ = 0

х ₂ = 3pi/2

х ₃ = 3 пи

x ₄ = 3pi + 3pi/2 = 6pi/2 + 3pi/2 = 9pi/2

x ₅ = 9pi/2 + 3pi/2 = 12pi/2 = 6pi

, поэтому пять точек в плоскости xy: (0, ?), (3pi/2, ?), (3pi, ?), (9pi/2, ?), (6pi, ?)

Теперь найдем значения функции y = sin(x/3) в пяти точках

, когда x = 0, y = sin(x/3) = sin[(1/3) × 0] = sin(0) = 0, поэтому точка равна (0, 0)

, когда x = 3pi/2, y = sin(x/3) = sin[(1/3) &times 3pi/2] = sin(pi/2) = 1, поэтому точка равна (3pi/2, 1)

, когда x = 3pi, y = sin(x/3) = sin[(1/3) &times 3pi] = sin(pi) = 0, поэтому точка равна (3pi, 0)

, когда x = 9pi/2, y = sin(x/3) = sin[(1/3) &times 9pi/2] = sin(3pi/2) = -1, поэтому точка равна (9pi/2, — 1)

, когда x = 6pi, y = sin(x/3) = sin[(1/3) &times 6pi] = sin(2pi) = 0, поэтому точка равна (6pi, 0)

Пять точек: (0, 0), (3pi/2, 1), (3pi, 0), (9pi/2, -1), (6pi, 0)

Нарисуйте график y = sin(x/3) на основе пяти точек

Значения функции синуса для специальных углов:

грех(0) = 0

sin(pi/2) = 1

грех (пи) = 0

sin(3pi/2) = -1

sin(2pi) = 0

Анализ графика:

х = 0, у = 0.

x = 3 pi — его полупериод, в этот момент его значение y равно 0.

x = (3/2)pi — его четвертьпериод, в этот момент его значение y равно 1, что является максимальным.

x = (9/2)pi — это его три четверти периода, в этот момент его значение y равно -1, что является минимальным.

x = 6 pi является конечной точкой одного периода, в этой точке его значение y равно 0,

Кривая y = sin (x/3) непрерывна,

его второй период от x = 6 pi до x = 6 pi + 6 pi = 12 pi,

его третий период от 12 пи до 12 пи + 6 пи = 18 пи,

его четвертый период от 18 pi до 18 pi + 6 pi = 24 pi и так далее.

Графический синус

Прежде всего, мы дадим вам несколько новых терминов. Надеюсь, вы принесли свою рукавицу ловца.

Ваша базовая синусоидальная функция имеет следующую форму:

Период триггерной функции представляет собой горизонтальную длину одного полного цикла.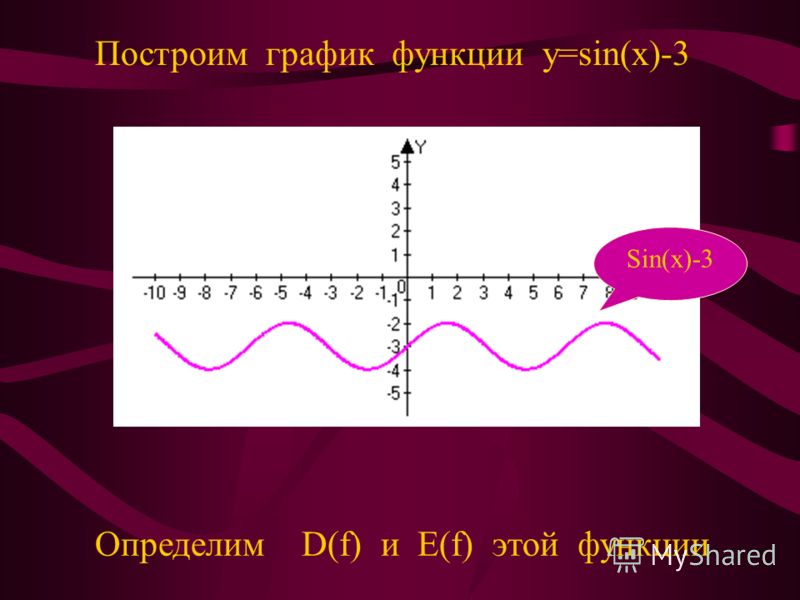 Например, приведенный выше график начинает повторять свою форму через 2π единиц по оси x , поэтому его период равен 2π.

В общем, для y = a sin( bx ) , период равен

Средняя линия функции в значительной степени именно то, на что это похоже: горизонтальная линия, проходящая через «середину» нашей триггерной функции. Это будет прямо между максимальным и минимальным значениями графика. Поскольку это горизонтальная линия, она всегда будет выглядеть как y = (что-то).

Для функций вида y = a sin( bx ), как на графике выше, средняя линия всегда представляет собой ось x , также известную как линия y = 0. Чуть позже мы увидим, что произойдет, когда эта линия переместится.

Амплитуда триггерной функции — это ее «высота» или расстояние по вертикали между средней линией и максимальным или минимальным значением. По сути, это то, насколько высокими становятся «волны» функции.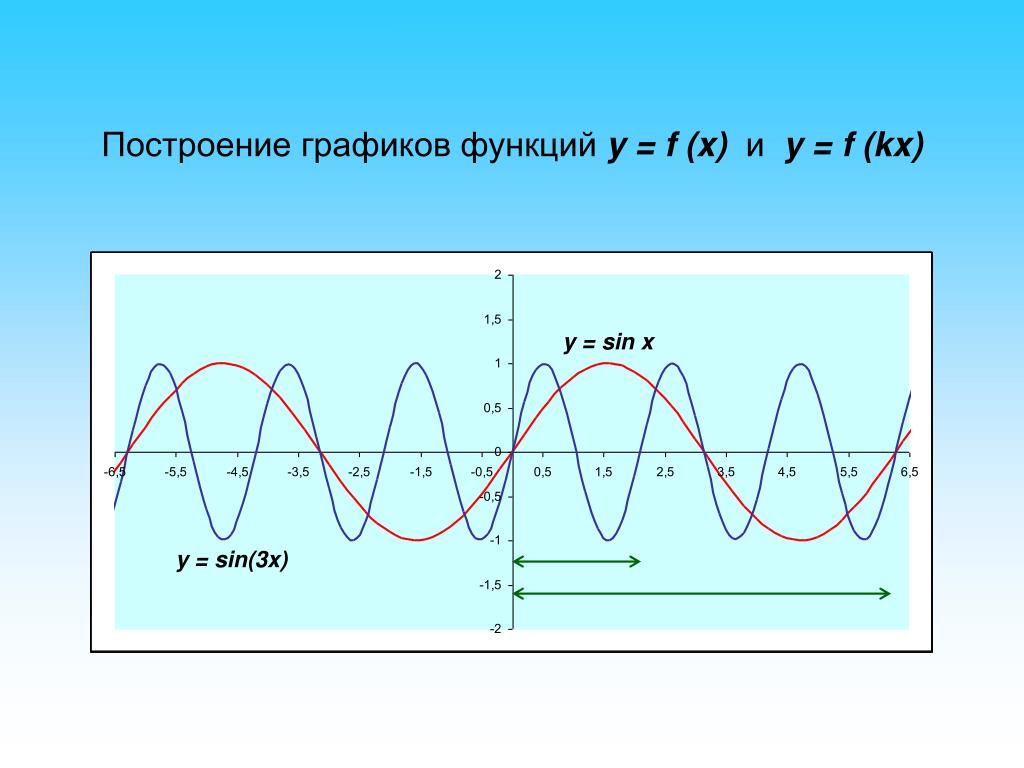 График выше имеет пики при y = 1 и y = -1, поэтому его амплитуда равна всего 1. | и |. Также важно отметить, что если a < 0, график переворачивается (инвертируется).

Разговоры дешевы, так что теперь давайте посмотрим на них в действии.

Пример задачи

Как выглядит график y = sin x ?

Амплитуда (максимальное значение) y = sin x равна |1| = 1. Период (время, необходимое для одного полного цикла) y = sin x равен ^2π ⁄ ₁ = 2π. Средняя линия y = sin x является осью x . Построим график у = sin х.

Как и в случае с любым графиком, он помогает построить график значений x и y . Включите пять ключевых углов, используя период 2π, и пять ключевых точек, полученных из этих углов.

График x против y дает нам:

Пример задачи

График y = 3 sin x.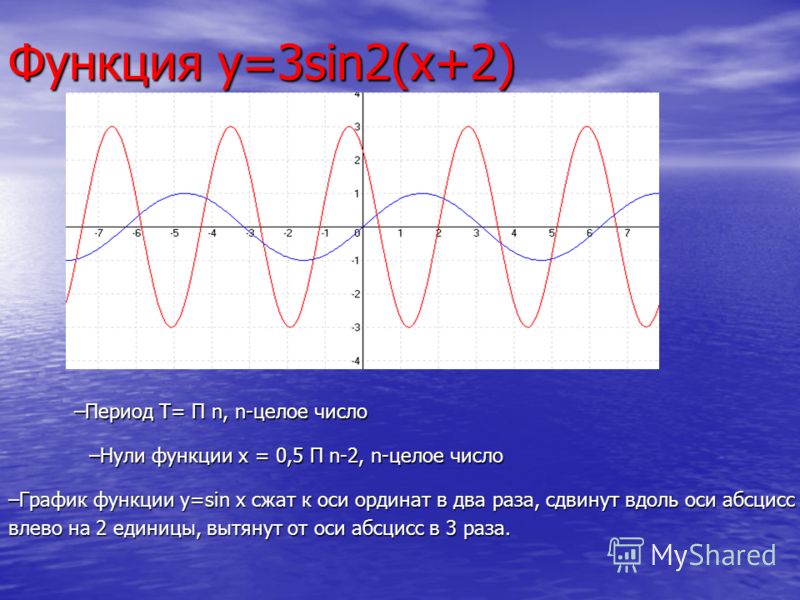

На этот раз наша амплитуда равна |3| = 3. Наш период по-прежнему ^2π ⁄ ₁ = 2π, а наша средняя линия по-прежнему y = 0.

Давайте составим нашу таблицу.

Применим период 2π к пяти ключевым углам и амплитуду 3 к пяти ключевым точкам.

Расставьте точки.

Пример задачи

Укажите амплитуду и период у = 4 грех х. Затем постройте график функции.

Из y = a sin( bx ) мы получаем амплитуду |4| = 4, а период ^2π ⁄ ₁ = 2π.

Теперь нарисуйте это.

Начните со стола.

При построении этого графика мы просто будем следовать той же схеме, чтобы расширить график до 2π.

До сих пор все графики, которые мы рассматривали, имели ось x в качестве средней линии. Мы бросали в тебя софтболы. Иногда в высшей лиге графики равны переведено на или перемещено вверх или вниз по оси x .