| 1 | Найти точное значение | sin(30) | |
| 2 | Найти точное значение | sin(45) | |
| 3 | Найти точное значение | sin(30 град. ) | |
| 4 | Найти точное значение | sin(60 град. ) | |
| 5 | Найти точное значение | tan(30 град. ) | |
| 6 | Найти точное значение | arcsin(-1) | |
| 7 | Найти точное значение | sin(pi/6) | |
| 8 | cos(pi/4) | ||
| 9 | Найти точное значение | sin(45 град. ) | |
| 10 | Найти точное значение | sin(pi/3) | |
| 11 | Найти точное значение | arctan(-1) | |
| 12 | Найти точное значение | cos(45 град. ) | |
| 13 | Найти точное значение | cos(30 град. ) | |
| 14 | Найти точное значение | tan(60) | |
| 15 | Найти точное значение | csc(45 град. ) | |
| 16 | Найти точное значение | tan(60 град. ) | |
| 17 | Найти точное значение | sec(30 град. ) | |
| 18 | Найти точное значение | cos(60 град. ) | |
| 19 | Найти точное значение | cos(150) | |
| 20 | Найти точное значение | sin(60) | |
| 21 | Найти точное значение | cos(pi/2) | |
| 22 | Найти точное значение | tan(45 град. ) | |
| 23 | Найти точное значение | arctan(- квадратный корень из 3) | |
| 24 | Найти точное значение | csc(60 град. ) | |
| 25 | Найти точное значение | sec(45 град. ) | |
| 26 | Найти точное значение | csc(30 град. ) | |
| 27 | Найти точное значение | sin(0) | |
| 28 | Найти точное значение | sin(120) | |
| 29 | Найти точное значение | cos(90) | |
| 30 | Преобразовать из радианов в градусы | pi/3 | |
| 31 | Найти точное значение | tan(30) | |
| 32 | Преобразовать из градусов в радианы | 45 | |
| 33 | Найти точное значение | cos(45) | |
| 34 | Упростить | sin(theta)^2+cos(theta)^2 | |
| 35 | Преобразовать из радианов в градусы | pi/6 | |
| 36 | Найти точное значение | cot(30 град. ) | |
| 37 | Найти точное значение | arccos(-1) | |
| 38 | Найти точное значение | arctan(0) | |
| 39 | Найти точное значение | cot(60 град. ) | |
| 40 | Преобразовать из градусов в радианы | 30 | |
| 41 | Преобразовать из радианов в градусы | (2pi)/3 | |
| 42 | Найти точное значение | sin((5pi)/3) | |
| 43 | Найти точное значение | sin((3pi)/4) | |
| 44 | Найти точное значение | tan(pi/2) | |
| 45 | Найти точное значение | sin(300) | |
| 46 | Найти точное значение | cos(30) | |
| 47 | Найти точное значение | cos(60) | |
| 48 | Найти точное значение | cos(0) | |
| 49 | Найти точное значение | cos(135) | |
| 50 | Найти точное значение | cos((5pi)/3) | |
| 51 | Найти точное значение | cos(210) | |
| 52 | Найти точное значение | sec(60 град. ) | |
| 53 | Найти точное значение | sin(300 град. ) | |
| 54 | Преобразовать из градусов в радианы | 135 | |
| 55 | Преобразовать из градусов в радианы | 150 | |
| 56 | Преобразовать из радианов в градусы | (5pi)/6 | |
| 57 | Преобразовать из радианов в градусы | (5pi)/3 | |
| 58 | Преобразовать из градусов в радианы | 89 град. | |
| 59 | Преобразовать из градусов в радианы | 60 | |
| 60 | Найти точное значение | sin(135 град. ) | |
| 61 | Найти точное значение | sin(150) | |
| 62 | Найти точное значение | sin(240 град. ) | |
| 63 | Найти точное значение | cot(45 град. ) | |
| 64 | Преобразовать из радианов в градусы | (5pi)/4 | |
| 65 | Найти точное значение | sin(225) | |
| 66 | Найти точное значение | sin(240) | |
| 67 | Найти точное значение | cos(150 град. ) | |
| 68 | Найти точное значение | tan(45) | |
| 69 | Вычислить | sin(30 град. ) | |
| 70 | Найти точное значение | sec(0) | |
| 71 | Найти точное значение | cos((5pi)/6) | |
| 72 | Найти точное значение | csc(30) | |
| 73 | Найти точное значение | arcsin(( квадратный корень из 2)/2) | |
| 74 | Найти точное значение | tan((5pi)/3) | |
| 75 | Найти точное значение | tan(0) | |
| 76 | Вычислить | sin(60 град. ) | |
| 77 | Найти точное значение | arctan(-( квадратный корень из 3)/3) | |
| 78 | Преобразовать из радианов в градусы | (3pi)/4 | |
| 79 | Найти точное значение | sin((7pi)/4) | |
| 80 | Найти точное значение | arcsin(-1/2) | |
| 81 | Найти точное значение | sin((4pi)/3) | |
| 82 | Найти точное значение | csc(45) | |
| 83 | Упростить | arctan( квадратный корень из 3) | |
| 84 | Найти точное значение | sin(135) | |
| 85 | Найти точное значение | sin(105) | |
| 86 | Найти точное значение | sin(150 град. ) | |
| 87 | Найти точное значение | sin((2pi)/3) | |
| 88 | Найти точное значение | tan((2pi)/3) | |
| 89 | Преобразовать из радианов в градусы | pi/4 | |
| 90 | Найти точное значение | sin(pi/2) | |
| 91 | Найти точное значение | sec(45) | |
| 92 | Найти точное значение | cos((5pi)/4) | |
| 93 | Найти точное значение | cos((7pi)/6) | |
| 94 | Найти точное значение | arcsin(0) | |
| 95 | Найти точное значение | sin(120 град. ) | |
| 96 | Найти точное значение | tan((7pi)/6) | |
| 97 | Найти точное значение | cos(270) | |
| 98 | Найти точное значение | sin((7pi)/6) | |
| 99 | Найти точное значение | arcsin(-( квадратный корень из 2)/2) | |
| 100 | Преобразовать из градусов в радианы | 88 град. |
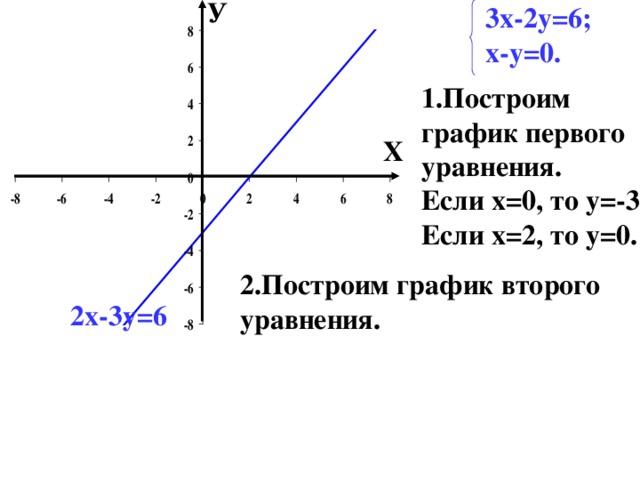
Креативный урок алгебры в 9-м классе по теме «Графики уравнений, содержащих символ модуля»
Санников Юрий Григорьевич,преподаватель математикиГБОУ СОШ № 539 Кировского рна,г.
СанктПетербург[email protected]Креативный урок алгебры в 9м классе по теме «Графики уравнений, содержащих символ модуля»
Аннотация. В статье рассматривается тренинг креативного мышления в обучении математике. В статье приведена разработка урока по теме «Графики уравнений, содержащих символ модуля». Вводится понятие графика уравнения, и построение графиков уравнений,содержащих символ модуля. В процессе работы выявляется связь алгебры и геометрии. Рассматривается применение этой темы к решению уравнений с параметром, содержащих символ модуля.Ключевые слова: график уравнения, модуль, параметр, творчество, гипотеза, эксперимент.
Тема урока:Графики уравнений, содержащих символ модуля.Предмет:алгебра.Тип урока:комбинированный.
Рис. 1. Блоксхема урокаБЛОК ЭКСПЕРИМЕНТОВ.БЛОК МОТИВАЦИИБЛОК ТВОРЧЕСКОГО РАЗОГРЕВАТЕОРЕТИЧЕСКИЙ БЛОК 1ТЕОРЕТИЧЕСКИЙ БЛОК 2БЛОК ЭКСПЕРИМЕНТОВ2.ТЕОРЕТИЧЕСКИЙ БЛОК 3ЭКСПЕРИМЕНТ 1ЭКСПЕРИМЕНТ2БЛОК ПОСТАНОВКИ ТВОРЧЕСКИХ ЗАДАЧБЛОК РЕЗЮМЕЭКСПЕРИМЕНТ 3
Продолжительность занятия:90 минут.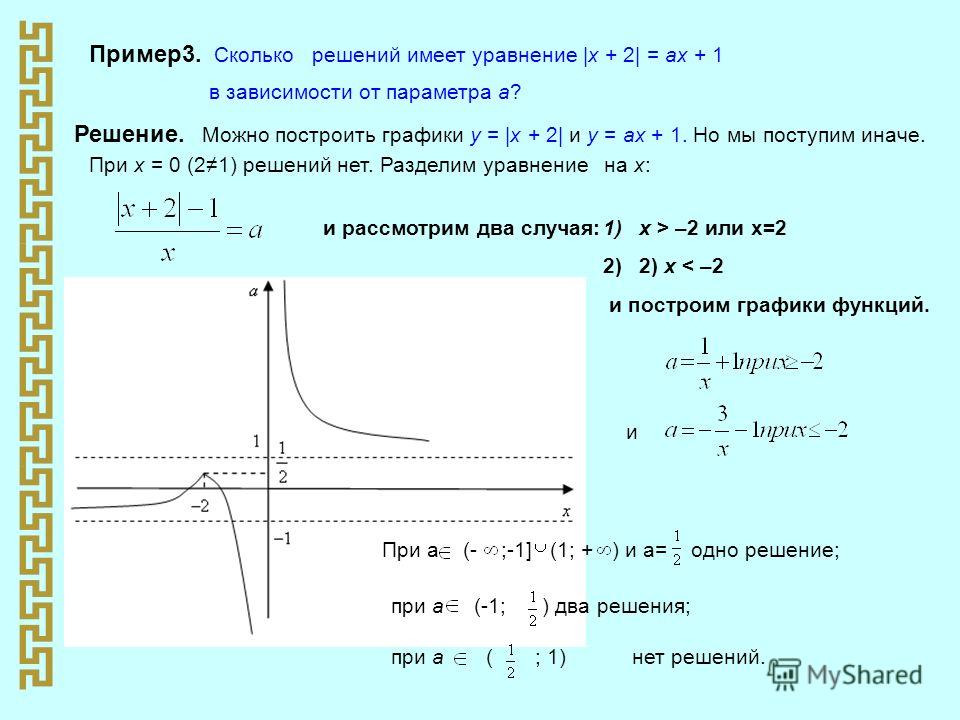
Главная дидактическая цель урока:выявление области приложения темы «График уравнения»в алгебре и в её связи с геометрией, формирование знаний по данной теме при решении стандартных и нестандартных алгебраических задач. Развитие у учащихся навыков исследовательской работы.Цели урока: 1.Формирование умений распознавать стандартные задачи в различных формулировках.2.Формирование способности к интеграции знаний изразличных тем курса математики.3.Содействовать развитию логического мышления учащихся, умение выделять главное, обобщать.4.Формирование исследовательской, креативной работы учащихся.5.Воспитание графической культуры учащихся.6.Совершенствование коммуникативной культуры учащихся.Оборудование: доска, мультимедийное оборудование, раздаточный дидактический материал для учащихся.
План урока
1.Блок мотивации. Изучая темы «Графики функций» и «Векторы», мы обнаруживаем тесную связь геометрии и алгебры, и, естественно, возникает вопрос –нельзя ли геометрические фигуры такие как квадрат, прямоугольник, ромб, треугольник задавать алгебраическими уравнениями и иследовать свойства этих фигур алгебраическими методами.
Выявлению этой связи между геометрией и алгеброй и будет посвящёнурок. Мы введём новое понятие «График уравнения»и рассмотрим графики уравнений в алгебраических и графических задачах.(3 мин.)
2.Блок творческого разогрева. Повторение определения функции и графика функции. Обсуждение необходимости введения понятия «График уравнения».Устная работа (20 мин.)Актуализация знаний учащихся: повторение, анализ, обобщение.Работа учащихся вследующих режимах: диалог, обсуждение, самостоятельная деятельность.Материалы для проведения устной работы оформлены на доске.
Повторение определения функции и графика функции.На доскепредставлены следующие чертежи (Рис. 2).Каждый ученик получает раздаточный материал с этими чертежами.Обсуждение:1)На каких чертежах представлены графики функций? Почему?2)Графики каких функций представлены на этих чертежах?3)На каких чертежах графики не задают функции? Почему?Обсуждается необходимость введения понятияграфика уравнения.Определение: Графиком уравнения (ݔǢݕ)=0называют множество точек координатной плоскости ݔ0ݕ, координаты которых удовлетворяют заданному уравнению.
Рис. 2.
3.Теоретический блок 1. Изображение множества точек, координаты которых удовлетворяют заданным условиям. Ведущие идеи: симметрия, сдвиг графика уравнения(Рис. 3).
Рис. 3.
Обсуждается наилучший способ построения графика этого уравнения.
01ݕݔ01ݕݔ01ݕݔ01ݕݔ01ݕݔ01ݕݔ01ݕݔ01ݕݔ−201ݕݔ
Изобразите на координатной плоскости множество точек, координаты которых удовлетворяют условию:|ݔ|+|ݕ|=4Варианты:1.Решить задачу “в лоб”: раскрыть модули в четырёх случаях:I.{ݔ≥0ݕ≥0, ݕ=−ݔ+4II.{ݔ≤0ݕ≥0ǡ ݕ=ݔ+4III.{ݔ≤0ݕ≤0ǡ ݕ=−ݔ−4 IV.{ݔ≥0ݕ≤0, ݕ=ݔ−42.Если ݕ≥0ǡто ݕ=4−|ݔ|Если ݕ
3.Замечаем, что переменные ݔиݕвходят в уравнение симметрично.Так как |−ݔ|=|ݔ|и|−ݕ|=|ݕ|, то график уравнения должен быть симметричным как относительно оси ܺ, так и относительно оси ܻǤРис. 4Строим график в первой четверти при условии, что {ݔ≥0ݕ≥0ݕ=−ݔ+4И симметрично отображаем его как относительнооси ܺ, так и относительно оси ܻǤВопрос: какую геометрическую фигуру описывает уравнение |ݔ|+|ݕ|=4?Задание: найти площадь этого квадратаи его сторону: =12∙82=32ǡܽ=√42+42=4√2Творческое задание: Начертить график уравнения |ݔ|+|ݕ|=ǡгде
>0и записать формулы для его площади и стороны.
=12∙(2)2=22ǡܽ=√2+2=√2
Рис. 5
4.Блок экспериментов.
Эксперимент. Преобразоватьуравнение |ݔ|+|ݕ|=ǡгде
>0ǡкоторое описывает квадрат так, чтобыуравнение задавало ромб.Гипотеза: уравнение должно иметь вид:݉|ݔ|+݊|ݕ|=ǡгде
>0ǡ݉≠݊.После обсуждения учащиеся получают задание на два варианта:Построить графики уравнений:1вариант: 2|ݔ|+|ݕ|=4 2вариант: |ݔ|+2|ݕ|=401ݕݔ−444−401ݕݔ−−
Рис. 6 Рис. 7
5.Теоретический блок 2. Построение графика уравнения вида: |ݔ+ܽ|+|ݕ+ܾ|=Задание: построить график уравнения |ݔ−2|+|ݕ+2|=41.Повторяется вопрос о построении графика функции ݕ=(ݔ+ܽ).Выдаются дидактические материалы. Учитель работает удоски.
Рис. 8.01ݕݔ4−4−2201ݕݔ4−42−201ݕݔ01ݕݔ01ݕݔ01ݕݔ201ݕݔ201ݕݔ201ݕݔ−201ݕݔ−201ݕݔ−2ݕ=(ݔ)ݕ=(ݔ−2)ݕ=(ݔ+2)Гипотеза:график уравнения |ݔ−2|+|ݕ+2|=4получается из графика уравнения |ݔ|+|ݕ|=4в результате сдвига на две единицы вправо вдоль оси ܺи на две единицы в отрицательном направлении вдоль оси ܻǤГрафик уравнения будет представлять собой квадрат, центр симметрии которого находится в точке (2Ǣ−2)ǤОсями симметрии квадрата будут прямые ݔ=2иݕ=−2Ǥ
Рис.
9.
Выполняется непосредственная проверка гипотезы. Раскрываются модули в четырёх случаях:
I.{ݔ≥2ݕ≥−2, ݕ=−ݔ+4II.{ݔ≤2ݕ≥−2ǡ ݕ=ݔIII.{ݔ≤2ݕ≤−2ǡ ݕ=−ݔ−4 IV.{ݔ≥2ݕ≤−2, ݕ=ݔ−8
6.Блок экспериментов 2. Эксперимент 1.Построить график уравнения: |ݕ−ݔ|+|ݕ+ݔ|=6Рассматриваем четыре случая:
I.{ݕ≥ݔݕ≥−ݔ, ݕ−ݔ+ݕ+ݔ=6ǡ
ݕ=3II.{ݕ≥ݔݕ≤−ݔǡ ݕ−ݔ−ݕ−ݔ=6ǡݔ=−3 III.{ݕ≤ݔݕ≤−ݔ, −ݕ+ݔ−ݕ−ݔ=6ǡݕ=−3IV.{ݕ≤ݔݕ≥−ݔǡ −ݕ+ݔ+ݕ+ݔ=6ǡݔ=3График уравнения представляет собой квадрат центром симметрии которого является точка (0Ǣ0)ǡсторона которого ܽ=6ǡа площадь =36. Рис. 10.
Эксперимент 2.Построить график уравнения: |ݕ−ݔ|+|ݕ+ݔ|=ǡ
где>0Ǥ
Найти его сторону и площадь.
Рис. 11.ܽ=ǡ
=201ݕݔ−66−2−22201ݕݔ−33−3301ݕݔ−22−22Эксперимент 3.Творческое задание: изменить уравнение|ݕ−ݔ|+|ݕ+ݔ|=8так, чтобы оно описывало прямоугольник.Учащиеся предлагают свои варианты. После чего сроят график уравнения:|ݕ−2ݔ|+|ݕ+2ݔ|=8
I.{ݕ≥ݔݕ≥−ݔ, ݕ−2ݔ+ݕ+2ݔ=8ǡ
ݕ=4II.{ݕ≥ݔݕ≤−ݔǡ ݕ−2ݔ−ݕ−2ݔ=8ǡݔ=−2 III.{ݕ≤ݔݕ≤−ݔ, −ݕ+2ݔ−ݕ−2ݔ=8ǡݕ=−4IV.
{ݕ≤ݔݕ≥−ݔǡ −ݕ+2ݔ+ݕ+2ݔ=2ǡݔ=2
Рис. 12
7.Теоретический блок 3. Методика применения полученных знаний и навыков при решении уравнений некоторых типов с модулем и параметром.Задание: Решить уравнение |−|+|++|=При решении уравнений и неравенств с одним неизвестным, содержащих параметр, удобно проводить исследование на координатнопараметрической плоскости ݔܽǤ(Значение параметра ܽбудем откладывать по вертикальной оси, а значение неизвестного ݔпо горизонтальной оси).
Построим на плоскости ݔܽграфик данного уравнения.Для этого построим прямые ܽ=ݔи ܽ=−ݔ−1, которые разобьют плоскость на 4 части.I.{ܽ≥ݔܽ≥−ݔ−1, ܽ−ݔ+ܽ+ݔ+1=3ǡ
ܽ=1II.{ܽ≥ݔܽ≤−ݔ−1ǡ ܽ−ݔ−ܽ−ݔ−1=3ǡݔ=−2 III.{ܽ≤ݔܽ≤−ݔ−1, −ݕ+2ݔ−ݕ−2ݔ=8ǡݕ=−4IV.{ܽ≤ݔܽ≥−ݔ−1ǡ −ݕ+2ݔ+ݕ+2ݔ=2ǡݔ=2
Рис. 1301ݕݔ−22−44ܽ1−2−2101ܽݔ
1)Если ܽ−2ǡто корней нет;2)Если ܽ=−2ǡторешением уравнения является отрезок [−2Ǣ1];3)Если −21ǡто корней нет; Ответ: 1) Если ܽ∈(−∞Ǣ−2)∪(1ǣ+∞), то уравнение корней не имеет;2) Если ܽ=−2 или ܽ=1, то решением является отрезок [−2Ǣ1];3) Если −2
Рис.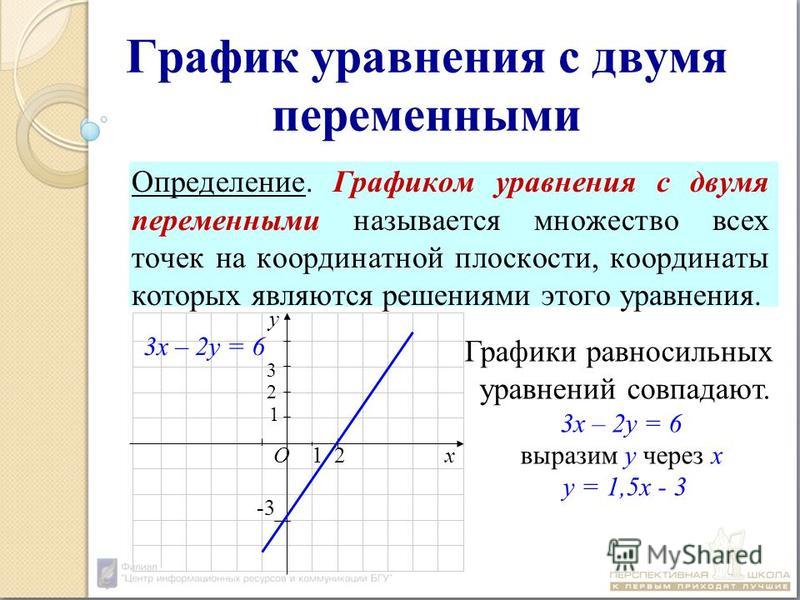
14.
При решении задания 4 допускается совместное творчество.2)Творческая часть (допускается совместное творчество)(Рис. 15).
Рис. 15.
Учащиеся должныпостроить графики этих уравнений и убедиться в том, что одно уравнение описывает параллелограмм, а второе–треугольник.Учащимся предлагается поэкспериментировать с этими уравнениями, меняя коэффициенты при неизвестных, и понаблюдать как это влияет на геометрию получаемых геометрических фигур.Результаты этой самостоятельной работы учащиеся смогут продемонстрировать на следующем уроке.ǤБлок резюме.1.Учащиеся формулируют главные выводы урока:Дано определение графика уравнения в сравнении с определениемграфика функции.Научились строить графики уравнений, содержащих символ модуля.Установили связь геометрии с алгеброй: различные геометрические фигуры могут быть заданы алгебраическими уравнениями. В частности, были построены квадрат, ромб и прямоугольник.ПОСТРОИТЬ ГРАФИКИ УРАВНЕНИЙ:1.|ݔ+3|+|ݕ−1|=42.|ݔ|−|ݕ|=43.|ݔ+3|−|ݕ−1|=4
РЕШИТЬ УРАВНЕНИЕ4.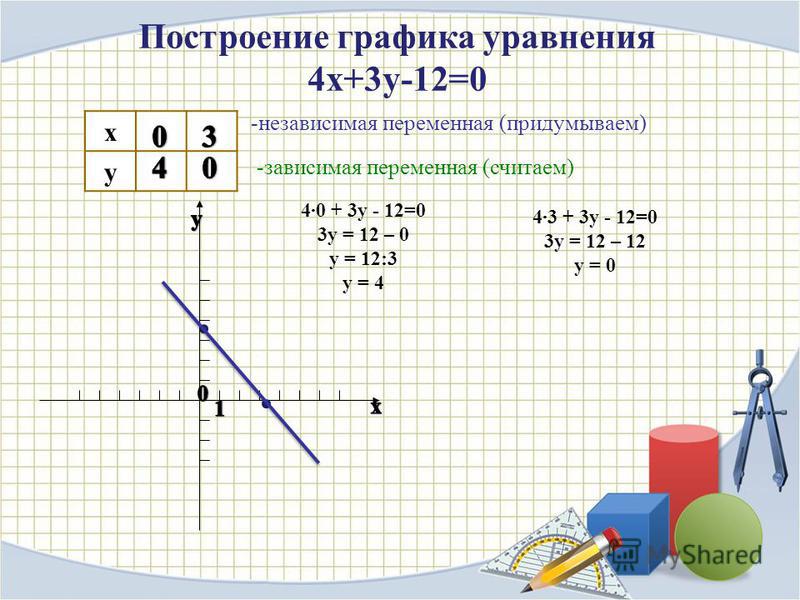
|ܽ−ݔ+2|+|ܽ+ݔ−2|=6 ПОСТРОИТЬ ГРАФИКИ УРАВНЕНИЙ:5.|ݕ−ݔ|+|ݔ|=46.1−|ݔ+1|=|ݕ−|ݔ+1||7.Найти формулы площади, длин диагоналей и сторону ромба, заданного уравнением: ݉|ݔ|+݊|ݕ|=ǡгде
>0ǡ݉≠݊.Познакомились графическим методом решения уравнений с модулем и параметром, с использованием навыков полученных при построении графиков уравнений. 2.Оценивание работы учащихся: самооценка, взаимооценка, оценка работы учащихся учителем.3.Выяснение мнения учащихся об уроке.
Ссылки на источники1.А.Г.Мордкович, Н.П.Николаев Алгебра 9. Учебник для учащихся общеобразовательных учреждений. –М.:Мнемозина, 2013.2.И.Ф. Шарыгин.Факультативный курс по математике 10. –М. «Просвещение», 1989.3.В.Г. Болтянский, Ю.В. Сидоров, М.И Шабунин. Лекции и задачи по элементарной математике. Издательство “Наука”, М. 1974.
Как построить уравнение в Excel без данных (с помощью простых шагов)
Microsoft Excel — мощное программное обеспечение. Мы можем выполнять многочисленные операции с нашими наборами данных, используя инструменты и функции Excel.
Существует множество функций Excel по умолчанию , которые мы можем использовать для создания формул. Многие образовательные учреждения и коммерческие компании используют файлы Excel для хранения ценных данных. Иногда мы вставляем диаграммы или графики, потому что они лучше отражают результаты опроса. Опять же, мы выполняем математические задачи с уравнениями на листе Excel. Построение диаграммы без предварительного набора данных может показаться сложной задачей. Эта статья покажет вам пошаговые процедуры для График и Уравнение в Excel без данных .
Скачать практическую рабочую тетрадь
Пошаговые процедуры для построения графика уравнения в Excel без данных
ШАГ 1: Введите уравнение
ШАГ 2: Примените формулу для расчета
ШАГ 3: Графическое уравнение
ШАГ 4: Ввод данных
Окончательный результат
Вывод
Статьи по Теме
Загрузить рабочую тетрадь
Загрузите следующую рабочую тетрадь, чтобы попрактиковаться самостоятельно.
Пошаговые процедуры построения графика уравнения в Excel без данных
Вы можете использовать любое математическое уравнение по своему желанию. В этом примере мы будем использовать простое линейное уравнение: y = mx + c . Это уравнение будет возвращать прямые линии при построении графика. Здесь x является независимой переменной, тогда как переменная y зависит от x . И с — это константа, известная как точка пересечения и . Наконец, м — это уклон, также известный как уклон прямой линии. Итак, мы нарисуем уравнение, не имея заранее набора данных. Поэтому внимательно выполните следующие шаги, чтобы выполнить задачу.
ШАГ 1: Введите уравнение
На первом шаге мы введем уравнение.
- Для этой цели введите m , x , c и y в диапазоне ячеек B4:E4 соответственно.
- См. изображение ниже для четкого понимания.
Подробнее: Как построить график линейного уравнения в Excel (с помощью простых шагов)
ШАГ 2. Применение формулы для расчета
Однако нам нужно создать простую формулу для вычисления переменной y . Здесь мы создадим эту формулу. Следовательно, следуйте процессу выполнения задачи.
- Теперь в ячейке E5 введите формулу:
=(B5*C5)+D5
- Затем нажмите Введите .
- На данный момент он вернет 0 , так как мы еще не ввели значения ячеек.
Подробнее: Как получить уравнение Y на графике Excel (6 способов)
ШАГ 3: Уравнение графика
Это самый важный шаг. На этом шаге мы вставим график.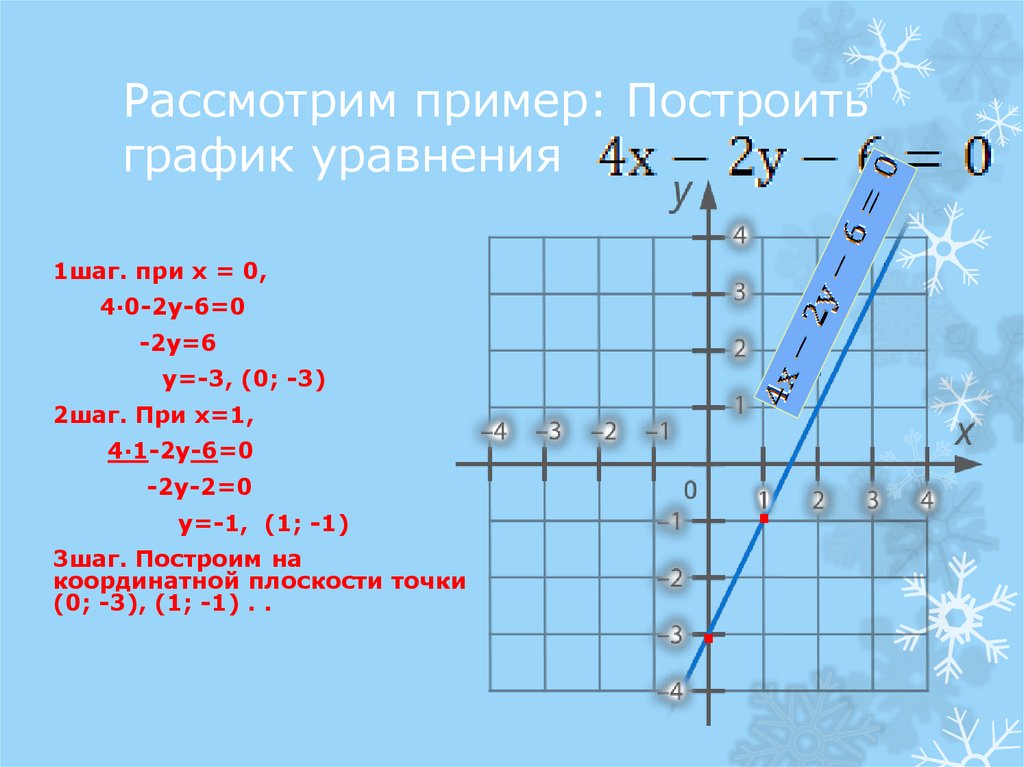
Итак, изучите процесс выполнения операции.
- Сначала выберите диапазон C4:C9 .
- Затем нажмите и удерживайте клавишу Ctrl.
- После этого выберите диапазон E4:E9 .
- Следующий рисунок прояснит это для вас.
- Затем перейдите на вкладку Вставка.
- Там нажмите Рекомендуемые графики .
- В результате появится диалоговое окно Insert Chart .
- Перейдите на вкладку All Chart.
- Затем нажмите X Y (Scatter) .
- Следовательно, выберите Scatter with Smooth Lines and Markers .
- После этого нажмите OK .
- Таким образом, вы получите график.
- Но поскольку у нас есть пустой набор данных, вы пока не увидите графиков.
Подробнее: Как показать уравнение в диаграмме Excel (с помощью простых шагов)
ШАГ 4: Ввод данных
Мы также покажем, как вводить данные после того, как закончим вставку графика.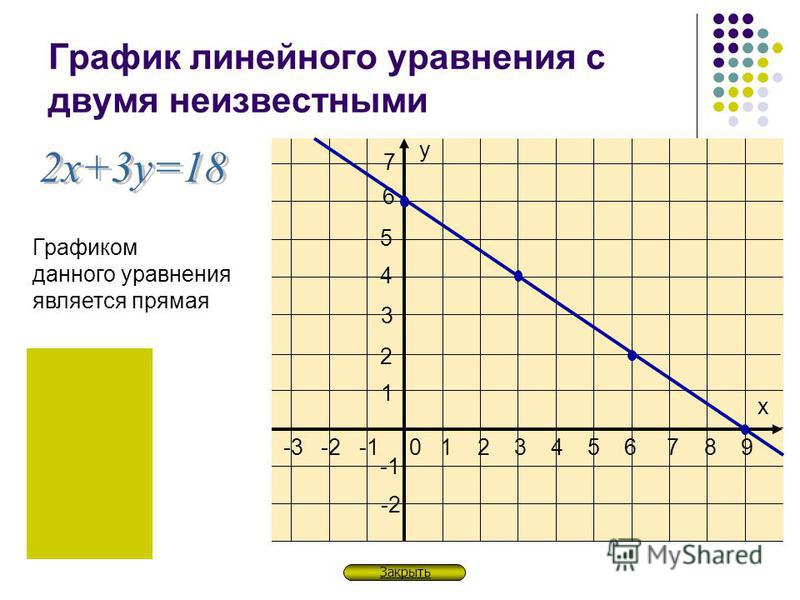
- Прежде всего, поместите значение м как 2 для всех случаев.
- Затем введите нужные значения для независимой переменной x .
- Аналогичным образом вставьте значение c как 5 .
- Наконец, примените инструмент Автозаполнение для получения результатов диапазона Е5:Е9 .
- Следовательно, он вернет точные выходные данные для переменной y.
- Посмотрите на приведенный ниже набор данных, чтобы лучше понять.
Подробнее: Как создать уравнение на основе точек данных в Excel
Конечный результат
В результате вы автоматически увидите линейный график, как показано ниже. Таким образом, мы можем построить уравнение, не имея набора данных. Это применимо к любому уравнению.
Заключение
Отныне вы сможете График и Уравнение в Excel без данных следуя вышеописанным процедурам.
Продолжайте использовать их и дайте нам знать, если у вас есть другие способы выполнить задачу. Следите за веб-сайтом ExcelDemy , чтобы узнать больше подобных статей. Не забудьте оставить комментарии, предложения или вопросы, если они у вас есть, в разделе комментариев ниже.
Связанные статьи
- Как найти неизвестное значение на графике Excel (4 простых способа)
- Найти уравнение линии в Excel (с помощью быстрых шагов)
- Как отобразить уравнение линии в диаграмме Excel (2 простых способа)
- Определение концентрации белка по стандартной кривой в Excel
- Как построить график двух уравнений в Excel (с помощью простых шагов)
- Расчет неизвестной концентрации по стандартной кривой в Excel
Как построить линейное уравнение в Matplotlib с примерами кода
Как построить линейное уравнение в Matplotlib с примерами кода
На этом занятии мы попробуем решить головоломку «Как построить линейное уравнение в Matplotlib», используя компьютерный язык.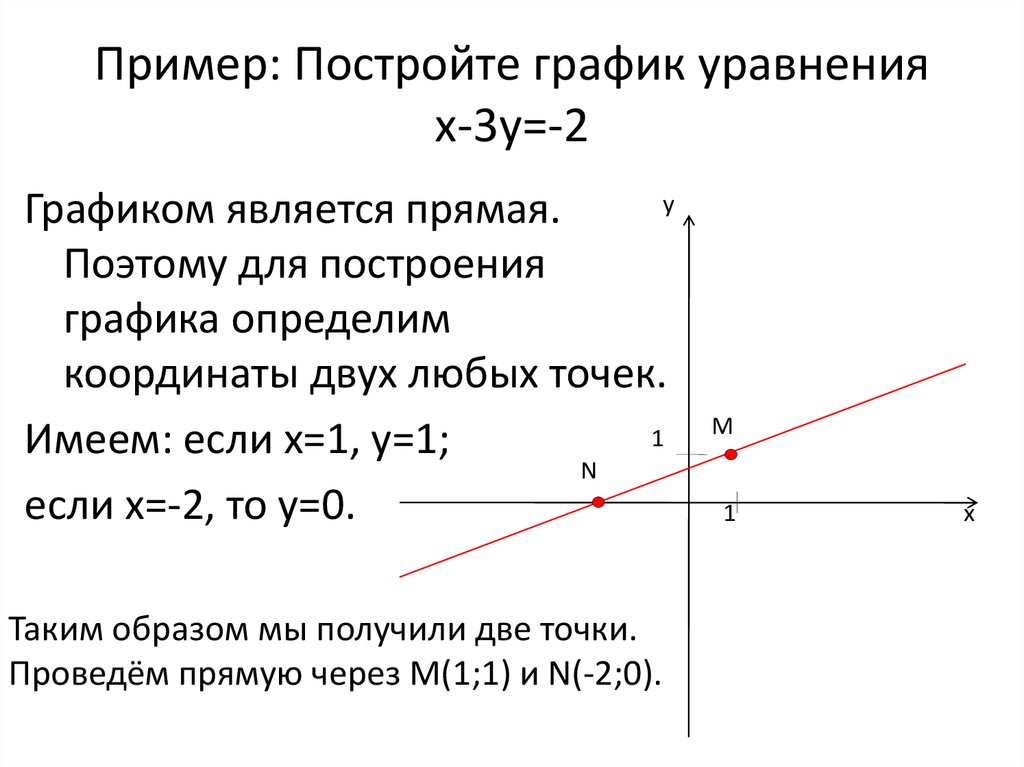
Следующий код служит для иллюстрации этого момента.
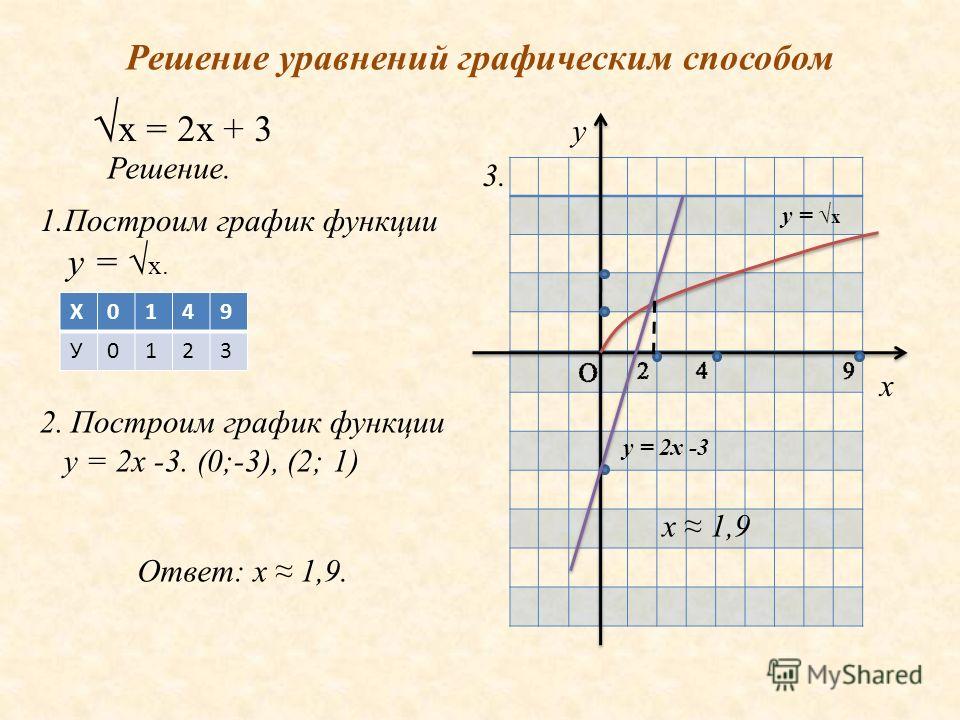
импортировать matplotlib.pyplot как plt
импортировать numpy как np
х = np.linspace (-5,5,100)
у = 2*х+1
plt.plot(x, y, '-r', label='y=2x+1')
plt.title('График y=2x+1')
plt.xlabel('x', цвет='#1C2833')
plt.ylabel('у', цвет='#1C2833')
plt.legend(loc='верхний левый')
plt.grid()
plt.show() Нам удалось исправить код проблемы How To Plot A Linear Equation In Matplotlib, рассмотрев несколько различных примеров.
Как построить уравнение в Python matplotlib?
Для построения уравнений мы будем использовать два модуля Matplotlib. pyplot и Numpy. Настройка графиков.
Как нарисовать линейную линию в matplotlib?
Вы можете построить вертикальную линию в matplotlib python, либо используя функцию plot() и задав вектор тех же значений, что и список значений оси Y, либо используя функцию axvline() из matplotlib. pyplot, который принимает только постоянное значение x. Вы также можете использовать функцию vlines() библиотеки matplotlib.
10-Aug-2021
Как построить линейную функцию в Python?
как построить линейное уравнение в matplotlib
- импортировать matplotlib. pyplot как плт.
- импортировать numpy как np.
- х = нп. linspace(-5,5,100)
- у = 2*х+1.
- пл. график (х, у, ‘-r’, метка = ‘у = 2x + 1’)
- пл. title(‘График y=2x+1’)
- пл. xlabel(‘x’, цвет=’#1C2833′)
- пл. ylabel(‘y’, цвет=’#1C2833′)
Как построить линию между двумя точками в matplotlib?
Используйте matplotlib. сюжет. plot() для рисования линии между двумя точками
- point1 = [1, 2]
- точка2 = [3, 4]
- x_values = [point1[0], point2[0]] собрать значения x.
- y_values = [point1[1], point2[1]] собрать значения y.
- пл. график (x_values, y_values)
Как построить вертикальную линию в Python matplotlib?
Создание одной вертикальной линии
- x: положение по оси X для построения линии. Принимает целые числа.
- xmin и xmax: скаляр, необязательный, по умолчанию: 0/1. Он строит линию в заданном диапазоне.
- color: цвет линии, принимает строку. например ‘р’ или ‘б’ .
- стиль линии: определяет тип линии, принимает строку. например ‘-‘, ‘-‘, ‘-.
Принимает целые числа.Как построить прямую вертикальную линию в Python?
Чтобы построить вертикальную линию с помощью pyplot, вы можете использовать функцию axvline(). В этом синтаксисе: x — это координата оси x. Это точка, из которой линия будет генерироваться по вертикали. ymin — нижняя часть графика; ymax — вершина графика.06 февраля 2020 г.
Как построить линейный график?
Чтобы построить линейный график, расположите собранные данные в числовом порядке от меньшего к большему или наоборот. Затем нарисуйте числовую линию, которая включает все числа в ваших данных, двигаясь слева направо. Отметьте «X» над числом каждый раз, когда это конкретное число встречается в вашем наборе данных.