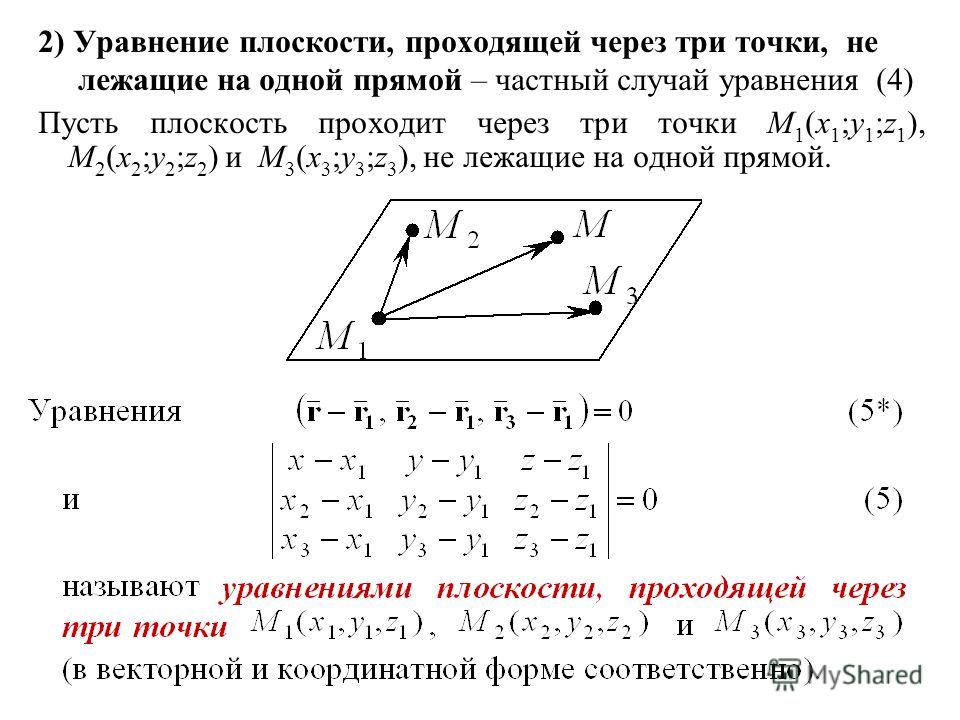
Уравнение плоскости по координатам трех точек
Любая плоскость может быть проведена через три точки, не принадлежащие одной прямой. Автоматический сервис находит уравнение плоскости, которая проходит через эти три точки.
x-xay-yaz-zaxb-xayb-yazb-zaxc-xayc-yazc-za=0.
Чтобы решить уравнение плоскости по трем точкам онлайн, выполните простые действия:
- впишите значения точек A, B, C в соответствующие пустые поля;
- для получения решения воспользуйтесь кнопкой «Рассчитать».
Zaochnik предоставляет пошаговые вычисления и точный ответ бесплатно.
Как найти уравнение плоскости по координатам трех принадлежащих ей точек с помощью онлайн-калькулятора
Рассмотрим пример, наглядно демонстрирующий работу с онлайн-калькулятором. Пусть нужно найти уравнение плоскости, проходящей через три известные точки. Для этого в онлайн-калькуляторе просто зададим эти точки:
Важно: точки не должны принадлежать одной прямой!
Зададим точки произвольно и нажмем «Рассчитать»:
После этого калькулятор выдаст ответ с подробными выкладками решения:
Материалы, которые помогут вам лучше разобраться в теме:
- Уравнение плоскости, виды уравнения плоскости
- Общее уравнение плоскости : описание, примеры, решение задач
- Нормальное уравнение плоскости: описание, примеры, решение задач
- Уравнение плоскости в отрезках: описание, примеры, решение задач
- Уравнение плоскости, проходящей через заданную точку перпендикулярно к заданной прямой
- Прямоугольная система координат на плоскости и в пространстве
Ответ:
Решение
Ответ:
- list» :key=»`error-${eIdx}`» v-html=»e»/>
Похожие калькуляторы:
- Длина отрезка. Расстояние между точками
- Середина отрезка
- Каноническое уравнение прямой проходящей через две точки
- Расстояние от точки до прямой на плоскости
- Уравнение плоскости (координаты вектора нормали и точки)
- Точка пересечения прямых (с угловыми коэффициентами)
- Расстояние от точки до прямой в пространстве
- Расстояние от точки до плоскости
- Расстояние между плоскостями
- Угол между плоскостями
- Угол между прямой и плоскостью
Уравнение плоскости онлайн по 3 точкам
Построить плоскость по уравнению онлайн понадобится:
- студентам университетов при выполнении заданий по математическим дисциплинам;
- школьникам, которые готовятся к поступлению в технические ВУЗы и участникам олимпиад;
- преподавателям, проверяющим работы учащихся и составляющим задачи;
- инженерам для облегчения процесса расчетов.

Цель сервиса – помощь в самостоятельных вычислениях учащимся. Автоматическая формула ускоряет получение ответа на задачу, позволяет избежать ошибок и не требует многократной перепроверки одних и тех же действий. Онлайн-калькулятор позволяет осуществлять подготовку к занятиям с усвоением непонятого ранее материала, запоминать и применять готовые алгоритмы решений.
Если возникла необходимость заказать услуги опытных преподавателей по решению уравнений или заданий на другие темы, обратитесь к консультанту. Мы гарантируем оперативный ответ и выгодное предложение.
Понравился калькулятор? Поделись с друзьями!
Уравнение плоскости, проходящей через данную прямую параллельно другой прямой онлайн
С помощю этого онлайн калькулятора можно построить уравнение плоскости, проходящей через прямую L1 параллельно другой прямой L2 (прямые L1 и L2 не параллельны). Дается подробное решение с пояснениями. Для построения уравнения плоскости задайте вид уравнения прямых (канонический или параметрический) введите коэффициенты уравнений прямых в ячейки и нажимайте на кнопку «Решить».
Для построения уравнения плоскости задайте вид уравнения прямых (канонический или параметрический) введите коэффициенты уравнений прямых в ячейки и нажимайте на кнопку «Решить».
Очистить все ячейки?
Инструкция ввода данных. Числа вводятся в виде целых чисел (примеры: 487, 5, -7623 и т.д.), десятичных чисел (напр. 67., 102.54 и т.д.) или дробей. Дробь нужно набирать в виде a/b, где a и b (b>0) целые или десятичные числа. Примеры 45/5, 6.6/76.4, -7/6.7 и т.д.
Уравнение плоскости, проходящей через данную прямую параллельно другой прямой − теория, примеры и решения
Пусть задана декартова прямоугольная система координат Oxyz и пусть в этой системе координат заданы прямые
Задача заключается в построении уравнения плоскости α, проходящей через прямую L1 параллельно прямой L2(Рис.1).
Решение. Уравнение прямой L1 проходит через точку M1(x1, y1, z1) и имеет направляющий вектор q1={m1, p1, l1}. Уравнение прямой L2 проходит через точку M2(x2, y2, z2) и имеет направляющий вектор q2={m2, p2, l2}.
Уравнение прямой L2 проходит через точку M2(x2, y2, z2) и имеет направляющий вектор q2={m2, p2, l2}.
Прамая L1 должна лежать на искомой плоскости α, следовательно точка M1 должна нежать на плоскости α.
Уравнение плоскости можно записать формулой
| Ax+By+Cz+D=0. | (3) |
и поскольку M1(x1, y1, z1) принадлежит этой плоскости, то справедливо следующее равенство:
| Ax1+By1+Cz1+D=0. | (4) |
Для того, чтобы плоскость α проходила через прямую L1, нормальный вектор плоскости n={A, B, C} должен быть ортогональным направляющему вектору q1 прямой L1, т. е. скалярное произведение этих векторов должен быть равным нулю:
е. скалярное произведение этих векторов должен быть равным нулю:
| Am1+Bp1+Cl1=0 | (5) |
Для того, чтобы плоскость α была параллельна прямой L2, нормальный вектор плоскости n={A, B, C} должен быть ортогональным направляющему вектору q2 прямой L2, т.е. скалярное произведение этих векторов должен быть равным нулю:
| Am2+Bp2+Cl2=0 | (6) |
Таким образом мы должны решить систему трех уравнений с четыремя неизвестными (4)−(6). Представим систему линейных уравнений (4)−(6) в матричном виде:
Решив однородную систему линейных уравнений (7) найдем частное решение. (как решить систему линейных уравнений посмотрите на странице метод Гаусса онлайн).
Пример 1.Найти уравнение плоскости α, проходящей через прямую L1:
паралленьно другой прямой L2 :
Решение. Прямая L1 проходит через точку M1(x1, y1, z1)=M1(1, 1, 5) и имеет направляющий вектор
Прямая L2 проходит через точку M2(x2, y2, z2)=M2(1, 1, −2) и имеет направляющий вектор
Поскольку плоскость проходит через прямую L1 , то она проходит также через точку M1(x
 Тогда уравнение плоскости должна удовлетворять условию:
Тогда уравнение плоскости должна удовлетворять условию:а условие параллельности прямой L1 и искомой плоскости α представляется следующим равенством:
Так как плоскость α должна быть параллельной прямой L2, то должна выполнятся условие:
Таким образом мы должны решить систему трех уравнений с четыремя неизвестными (10)−(12). Подставим значения m1, p1, l1, m2, p2, l2, x1, y1, z1 в (10),(11) и (12):
Представим эти уравнения в матричном виде:
Решим систему линейных уравнений (16) отностительно A, B, C, D:
Так как искомая плоскость проходит через точку M1 и имеет нормальный вектор n={A, B, C}={−13/24,1/6,−1/8} то она может быть представлена формулой:
| Ax+By+Cz+D=0 | (18) |
Подставляя значения A,B,C,D в (17), получим:
Уравнение плоскости можно представить более упрощенном виде, умножив на число −24:
| 13x−4y+3z−24=0 | (19) |
Ответ: Уравнение плоскости, проходящей через прямую (1) параллельно прямой (2) имеет вид (19).
——————
Пример 2. Найти уравнение плоскости α, проходящей через прямую L1:
и паралленьной другой прямой L2
Решение. Прямая L1 проходит через точку M1(x1, y1, z1)=M1( −2, 0, 1) и имеет направляющий вектор
| q1={m1, p1, l1}={5, −8, 3} |
Прямая L2 проходит через точку M2(x2, y2, z2)=M2(1, 1,−2) и имеет направляющий вектор
| q2={m2, p2, l2}={1, 1, 1} |
Поскольку плоскость проходит через прямую L1 , то она проходит также через точку M1(x1, y1, z1)=M1(−2, 0, 1) и нормальный вектор плоскости n={A, B, C} перпендикулярна направляющему вектору q1={m1, p1, l1}={5, −8, 3} прямой L1. Тогда уравнение плоскости должна удовлетворять условию:
Тогда уравнение плоскости должна удовлетворять условию:
| Ax1+By1+Cz1+D=0 | (22) |
а условие параллельности прямой L1 и искомой плоскости α представляется следующим равенством:
Так как плоскость α должна быть параллельной прямой L2, то должна выполнятся условие:
Таким образом мы должны решить систему трех уравнений с четыремя неизвестными (22)−(24). Подставим значения m1, p1, l1, m2, p2, l2, x1, y1, z1 в (22),(23) и (24):
| A(−2)+B·0+C·1+D=0, | (25) |
| A·5+B(−8)+C·3=0, | (26) |
| A·1+B·1+C·1=0, | (27) |
Представим эти уравнения в матричном виде:
Решим систему линейных уравнений (28) отностительно A, B, C, D:
Так как искомая плоскость проходит через точку M1 и имеет нормальный вектор n={A, B, C}={11/35,2/35,−13/35} то она может быть представлена формулой:
| Ax+By+Cz+D=0 | (30) |
Подставляя значения A,B,C,D в (30), получим:
Уравнение плоскости можно представить более упрощенном виде, умножив на число 35:
| 11x+2y−13z+35=0 | (32) |
Ответ: Уравнение плоскости, проходящей через прямую (1) параллельно прямой (2) имеет вид (32).
Касательная плоскость к поверхности онлайн
Графиком функции 2-х переменных z = f(x,y) является поверхность, проектирующаяся на плоскость XOY в область определения функции D.Рассмотрим поверхность σ, заданную уравнением z = f(x,y), где f(x,y) – дифференцируемая функция, и пусть M0(x0,y0,z0) – фиксированная точка на поверхности σ, т.е. z0 = f(x0,y0). Назначение. Онлайн-калькулятор предназначен для нахождения уравнения касательной плоскости и нормали к поверхности. Решение оформляется в формате Word. Если необходимо найти уравнение касательной к кривой (y = f(x)), то необходимо использовать данный сервис.
- Решение онлайн
- Видеоинструкция
z = f(x,y)
в точке M0(;)Функция задана в неявном виде f(x,y,z)
F(x,y,z) =
в точке M(;;)Дополнительно находить уравнение нормали
Правила ввода функций:
Правила ввода функций:
- Все переменные выражаются через x,y,z
Касательной плоскостью к поверхности σ в её точке М0 называется плоскость, в которой лежат касательные ко всем кривым, проведённым на поверхности σ через точку М0.
Уравнение касательной плоскости к поверхности, заданной уравнением z = f(x,y), в точке M0(x0,y0,z0) имеет вид:
z – z0 = f’x(x0,y0)(x – x0) + f’y(x0,y0)(y – y0)
Вектор называется вектором нормали к поверхности σ в точке М0. Вектор нормали перпендикулярен касательной плоскости.
Нормалью к поверхности σ в точке М0 называется прямая, проходящая через эту точку и имеющая направление вектора N.
Канонические уравнения нормали к поверхности, заданной уравнением z = f(x,y), в точке M0(x0,y0,z0), где z0 = f(x0,y0), имеют вид:
Пример №1. Поверхность задана уравнением x3+5y. Найти уравнение касательной плоскости к поверхности в точке M0(0;1). 3+5*y:
3+5*y:
f'x(x,y) = (x3+5•y)'x = 3•x2
f’x(x,y) = (x3+5•y)’y = 5
В точке М0(0,1) значения частных производных:
f'x(0;1) = 0
f'y(0;1) = 5
Пользуясь формулой, получаем уравнение касательной плоскости к поверхности в точке М0: z - 5 = 0(x - 0) + 5(y - 1) или -5•y+z = 0
Пример №2. Поверхность задана неявным образом y2-1/2*x3-8z. Найти уравнение касательной плоскости к поверхности в точке M0(1;0;1).
Решение. Находим частные производные функции. Поскольку функция задана в неявном виде, то производные ищем по формуле:
Для нашей функции:
Тогда:
В точке М0(1,0,1) значения частных производных:
f'x(1;0;1) = -3/16
f'y(1;0;1) = 0
Пользуясь формулой, получаем уравнение касательной плоскости к поверхности в точке М0: z - 1 = -3/16(x - 1) + 0(y - 0) или 3/16•x+z-19/16 = 0
Пример. Поверхность σ задана уравнением z= y/x + xy – 5x3. Найти уравнение касательной плоскости и нормали к поверхности σ в точке М0(x0, y0, z0), принадлежащей ей, если x0 = –1, y0 = 2.
Поверхность σ задана уравнением z= y/x + xy – 5x3. Найти уравнение касательной плоскости и нормали к поверхности σ в точке М0(x0, y0, z0), принадлежащей ей, если x0 = –1, y0 = 2.
Найдем частные производные функции z= f(x, y) = y/x + xy – 5x3:
fx’(x, y) = (y/x + xy – 5x3)’x = – y/x2 + y – 15x2;
fy’ (x, y) = (y/x + xy – 5x3)’y = 1/x + x.
Точка М0(x0, y0, z0) принадлежит поверхности σ, поэтому можно вычислить z0, подставив заданные x0 = –1 и y0 = 2 в уравнение поверхности:
z= y/x + xy – 5x3
z0 = 2/(-1) + (–1) 2 – 5 (–1)3 = 1.
В точке М0(–1, 2, 1) значения частных производных:
fx’(М0) = –1/(-1)2 + 2 – 15(–1)2 = –15; fy’(М0) = 1/(-1) – 1 = –2.
Пользуясь формулой (5) получаем уравнение касательной плоскости к поверхности σ в точке М0:
z – 1= –15(x + 1) – 2(y – 2) z – 1= –15x – 15 – 2y +4 15x + 2y + z + 10 = 0.
Пользуясь формулой (6) получаем канонические уравнения нормали к поверхности σ в точке М0: .
Ответы: уравнение касательной плоскости: 15x + 2y + z + 10 = 0; уравнения нормали: .
Пример №1. Дана функция z=f(x,y) и две точки А(х0, y0) и В(х1,y1). Требуется: 1) вычислить значение z1 функции в точке В; 2) вычислить приближенное значение z1 функции в точке В исходя из значения z0 функции в точке А, заменив приращение функции при переходе от точки А к точке В дифференциалом; 3) составить уравнение касательной плоскости к поверхности z = f(x,y) в точке C(x0,y0,z0). 2:
2:
f’x(x,y) = (x2+3•x•y•+y2)’x = 2•x+3•y3
f’x(x,y) = (x2+3•x•y•+y2)’y = 9•x•y2
В точке М0(1,2) значения частных производных:
f’x(1;2) = 26
f’y(1;2) = 36
Пользуясь формулой, получаем уравнение касательной плоскости к поверхности в точке М0:
z — 25 = 26(x — 1) + 36(y — 2)
или
-26•x-36•y+z+73 = 0
Пример №2. Написать уравнения касательной плоскости и нормали к эллиптическому параболоиду z = 2x2 + y2 в точке (1;-1;3).
Скачать решение
общее, через три точки, нормальное
- Плоскость, общее уравнение плоскости
- Уравнение плоскости, проходящей через три точки
- Нормальное уравнение плоскости. Расстояние от точки до плоскости
Чтобы получить общее уравнение плоскости, разберём плоскость, проходящую через заданную точку.
Пусть в пространстве есть три уже известные нам оси координат — Ox, Oy и Oz. Подержим лист бумаги так, чтобы он оставался плоским. Плоскостью будет сам лист и его продолжение во всех направлениях.
Пусть P произвольная плоскость в пространстве. Всякий перпендикулярный ей вектор называется вектором нормали к этой плоскости. Естественно, речь идёт о ненулевом векторе.
Если известна какая-нибудь точка плоскости P и какой-нибудь вектор нормали к ней, то этими двумя условиями плоскость в пространстве вполне определена (через заданную точку можно провести единственную плоскость, перпендикулярную данному вектору). Общее уравнение плоскости будет иметь вид:
Итак, условия, которыми задаётся уравнение плоскости, есть. Чтобы получить само уравнение плоскости, имеющее
приведённый выше вид, возьмём на плоскости P произвольную точку M с переменными координатами x, y, z. Эта точка
принадлежит плоскости только в том случае, когда вектор перпендикулярен вектору (рис. 1). Для этого, согласно условию перпендикулярности векторов, необходимо и достаточно, чтобы скалярное
произведение этих векторов было равно нулю, то есть
Эта точка
принадлежит плоскости только в том случае, когда вектор перпендикулярен вектору (рис. 1). Для этого, согласно условию перпендикулярности векторов, необходимо и достаточно, чтобы скалярное
произведение этих векторов было равно нулю, то есть
.
Вектор задан по условию. Координаты вектора найдём по формуле :
.
Теперь, используя формулу скалярного произведения векторов , выразим скалярное произведение в координатной форме:
. (1)
Так как точка M(x; y; z) выбрана на плоскости произвольно, то последнему уравнению удовлетворяют координаты любой точки, лежащей на плоскости P. Для точки N, не лежащей на заданной плоскости, , т.е. равенство (1) нарушается.
Перед решением задач может пригодиться урок о декартовой системе координат.
Также хорошо бы владеть материалом о скалярном произведении векторов.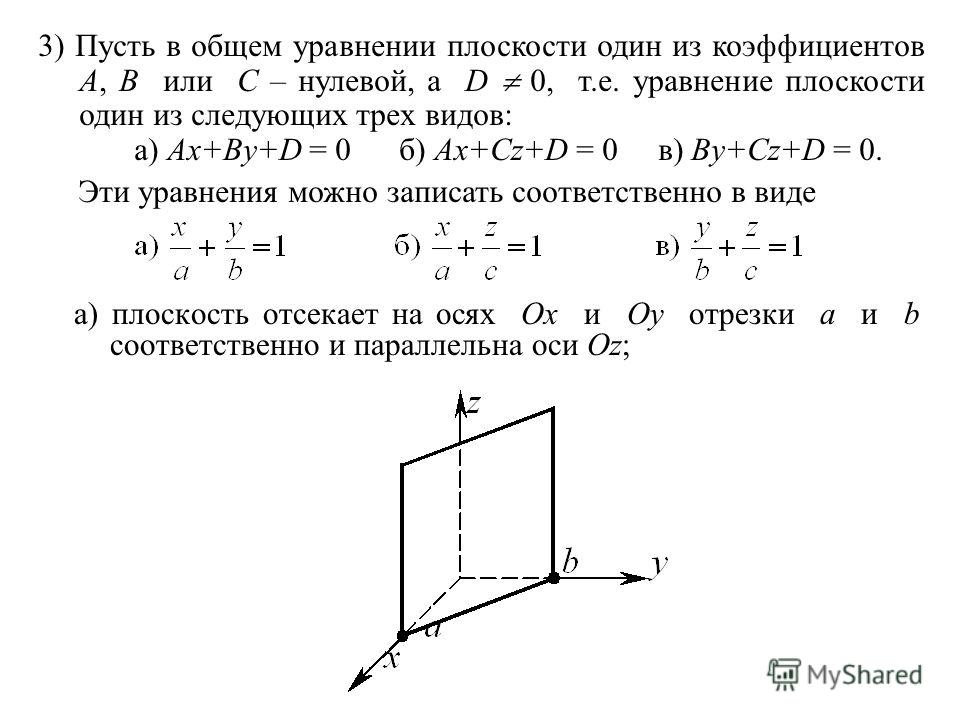
Пример 1. Составить уравнение плоскости, проходящей через точку и перпендикулярной вектору .
Решение. Используем формулу (1), еще раз посмотрим на неё:
.
В этой формуле числа A, B и C координаты вектора , а числа x0, y0 и z0 — координаты точки .
Вычисления очень простые: подставляем эти числа в формулу и получаем
.
Умножаем всё, что нужно умножить и складываем просто числа (которые без букв). Результат:
.
Требуемое уравнение плоскости в этом примере оказалось выражено общим уравнением первой степени относительно переменных координат x, y, z произвольной точки плоскости.
Итак, уравнение вида
(2)
называется общим уравнением плоскости.
Пример 2. Построить в прямоугольной декартовой системе координат плоскость, заданную уравнением .
Решение. Для построения плоскости необходимо и достаточно знать какие-либо три её точки, не лежащие на одной прямой, например, точки пересечения плоскости с осями координат.
Как найти эти точки? Чтобы найти точку пересечения с осью Oz, нужно в уравнение, данное в условии задачи, вместо икс и игрека подставить нули: x = y = 0. Поэтому получаем z = 6. Таким образом, заданная плоскость пересекает ось Oz в точке A(0; 0; 6).
Точно так же находим точку пересечения плоскости с осью Oy. При x = z = 0 получаем y = −3, то есть точку B(0; −3; 0).
И, наконец, находим точку пересечения нашей плоскости с осью Ox. При y = z = 0
получим x = 2, то есть точку C(2; 0; 0).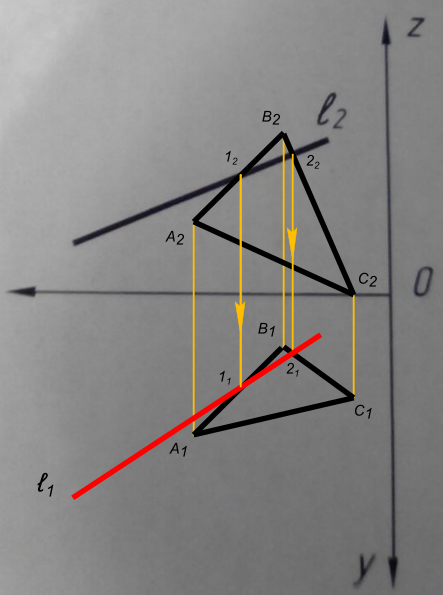 По трём полученным в нашем решении точкам A(0; 0; 6), B(0; −3; 0) и C(2; 0; 0)
строим заданную плоскость.
По трём полученным в нашем решении точкам A(0; 0; 6), B(0; −3; 0) и C(2; 0; 0)
строим заданную плоскость.
Решения типичных задач, которые бывают на контрольных работах — в пособии «Задачи на плоскость: параллельность, перпендикулярность, пересечение трёх плоскостей в одной точке».
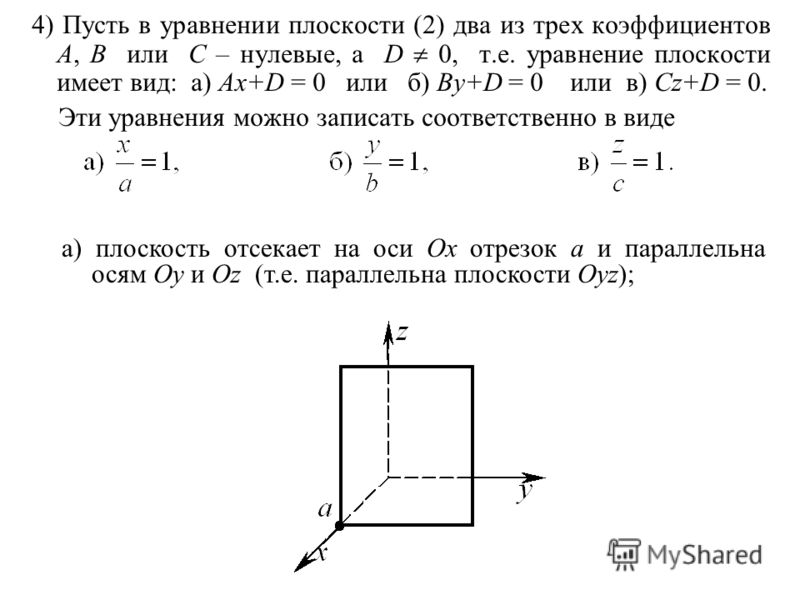
Рассмотрим теперь частные случаи общего уравнения плоскости. Это случаи, когда те или иные коэффициенты уравнения (2) обращаются в нуль.
1. При D = 0 уравнение определяет плоскость, проходящую через начало координат, так как координаты точки 0(0; 0; 0) удовлетворяют этому уравнению.
2. При A = 0 уравнение
определяет плоскость, параллельную оси Ox, поскольку вектор нормали
этой плоскости перпендикулярен оси Ox (его проекция на ось Ox равна нулю).
Аналогично, при B = 0 плоскость параллельная оси Oy, а при C = 0 плоскость
параллельна оси Oz.
3. При A = D = 0 уравнение определяет плоскость, проходящую через ось Ox, поскольку она параллельна оси Ox (A = 0) и проходит через начало координат (D = 0). Аналогично, плоскость проходит через ось Oy, а плоскость через ось Oz.
4. При A = B = 0 уравнение определяет плоскость, параллельную координатной плоскости xOy, поскольку она параллельна осям Ox (A = 0) и Oy (B = 0). Аналогично, плоскость параллельна плоскости yOz, а плоскость — плоскости xOz.
5. При A = B = D = 0 уравнение
(или z = 0) определяет координатную плоскость xOy, так как она параллельна плоскости xOy (A = B = 0)
и проходит через начало координат (D = 0). Аналогично, уравнение y = 0 в пространстве
определяет координатную плоскость xOz, а уравнение x = 0 — координатную плоскость yOz.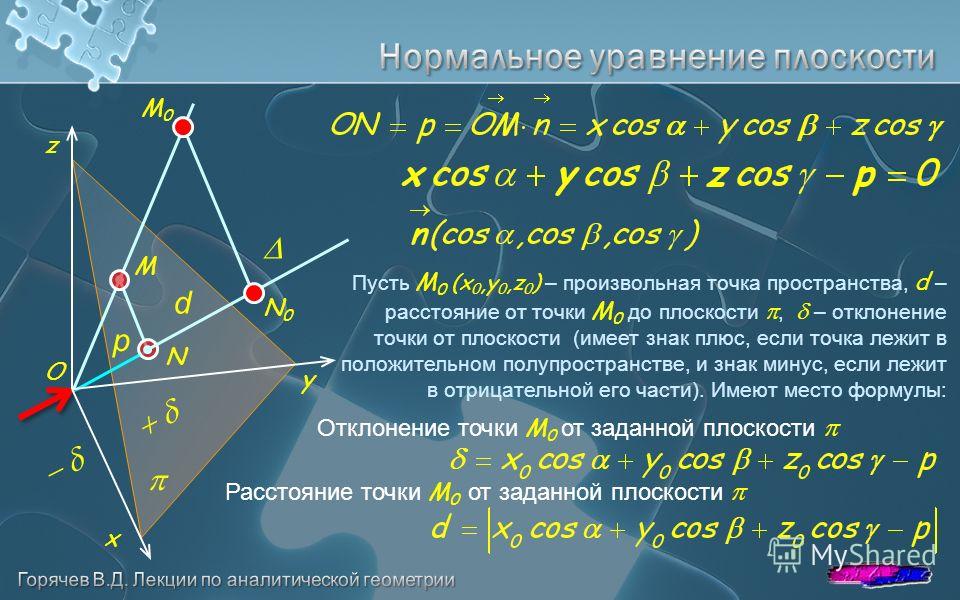
Пример 3. Составить уравнение плоскости P, проходящей через ось Oy и точку .
Решение. Итак, плоскость проходит через ось Oy. Поэтому в её уравнении y = 0 и это уравнение имеет вид . Для определения коэффициентов A и C воспользуемся тем, что точка принадлежит плоскости P.
Поэтому среди её координат есть такие, которые можно подставить в уравнению плоскости, которое мы уже вывели (). Смотрим ещё раз на координаты точки:
M0(2; −4; 3).
Среди них x = 2, z = 3. Подставляем их в уравнение общего вида и получаем уравнение для нашего частного случая:
2A + 3C = 0.
Оставляем 2A в левой части уравнения, переносим 3C в правую часть и получаем
A = −1,5C.
Подставив найденное значение A в уравнение , получим
или .
Это и есть уравнение, требуемое в условии примера.
Решить задачу на уравнения плоскости самостоятельно, а затем посмотреть решение
Пример 4. Определить плоскость (или плоскости, если больше одной) относительно координатных осей или координатных плоскостей, если плоскость (плоскости) задана уравнением .
Посмотреть правильное решение и ответ.
Решения типичных задач, которые бывают на контрольных работах — в пособии «Задачи на плоскость: параллельность, перпендикулярность, пересечение трёх плоскостей в одной точке».
Нет времени вникать в решение? Можно заказать работу!
К началу страницы
Пройти тест по теме Прямая и плоскость
Как уже упоминалось, необходимым и достаточным условием для построения плоскости, кроме одной точки и вектора нормали, являются также три точки, не лежащие на одной прямой.
Пусть даны три различные точки ,
и ,
не лежащие на одной прямой. Так как указанные три точки не лежат на одной прямой, векторы и
не коллинеарны, а поэтому
любая точка плоскости
лежит в одной плоскости с точками , и
тогда и только тогда, когда векторы
, и
компланарны, т.е. тогда и только тогда,
когда смешанное произведение этих векторов равно нулю.
Так как указанные три точки не лежат на одной прямой, векторы и
не коллинеарны, а поэтому
любая точка плоскости
лежит в одной плоскости с точками , и
тогда и только тогда, когда векторы
, и
компланарны, т.е. тогда и только тогда,
когда смешанное произведение этих векторов равно нулю.
Используя выражение смешанного произведения в координатах, получим уравнение плоскости
(3)
После раскрытия определителя это уравнение становится уравнением вида (2), т.е. общим уравнением плоскости.
Пример 5. Составить уравнение плоскости, проходящей через три данные точки, не лежащие на одной прямой:
, ,
и определить частный случай общего уравнения прямой, если такой имеет место.
Решение. По формуле (3) имеем:
Раскрываем определитель по первой строке:
Получили общее уравнение плоскости
или после деления на -2:
.
Это уравнение, в котором A = 0, т.е. оно определяет плоскость, параллельную оси Ox.
Решения типичных задач, которые бывают на контрольных работах — в пособии «Задачи на плоскость: параллельность, перпендикулярность, пересечение трёх плоскостей в одной точке».
Нормальным уравнением плоскости называется её уравнение, записанное в виде
,
где — направляющие косинусы нормали плоскости, — расстояние от начала координат до плоскости.
Нормалью к плоскости называется вектор, направление которого совпадает с направлением прямой, проведённой через начало координат перпендикулярно данной плоскости. (Есть полная аналогия с нормалью к прямой на плоскости, с той лишь разницей, что нормальное уравнение прямой существует в двух измерениях, а нормальное уравнение плоскости — в трёх).
Пусть M — какая угодно точка пространства. Для нахождения
отклонения
точки M от плоскости следует в левую часть нормального уравнения плоскости
подставить на место x, y и z подставить координаты
этой точки.
Для нахождения
отклонения
точки M от плоскости следует в левую часть нормального уравнения плоскости
подставить на место x, y и z подставить координаты
этой точки.
Это правило позволяет найти и расстояние от точки M до плоскости: расстояние равно модулю отклонения, т.е.
,
так как расстояние не может быть отрицательным числом.
Общее уравнение плоскости
приводится к нормальному виду почленным умножением на нормирующий множитель, определяемый формулой
.
Знак нормирующего множителя берётся противоположным знаку свободного члена в общем уравнении плоскости.
Пример 6. Привести уравнение плоскости к нормальному виду.
Решение. Вычислим нормирующий множитель:
.
Знак нормирующего множителя положительный, то есть, противоположен знаку
свободного члена в общем уравнении плоскости.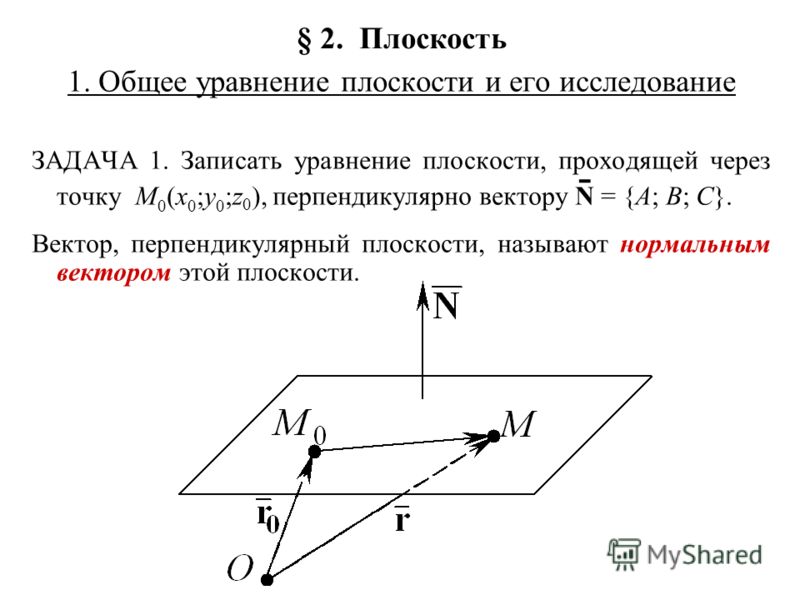 Умножим общее уравнение почленно на нормирующий
множитель и получим требуемое в условии примера нормальное уравнение плоскости:
Умножим общее уравнение почленно на нормирующий
множитель и получим требуемое в условии примера нормальное уравнение плоскости:
.
Пример 7. Вычислить величину отклонения и расстояния от точки до прямой, если точка задана координатами (-2; -4; 3), а плоскость задана общим уравнением .
Решение. Сначала приведём уравнение плоскости к нормальному виду. Вычислим нормирующий множитель:
.
Знак нормирующего множителя отрицательный, то есть, противоположен знаку свободного члена в общем уравнении плоскости. Умножим общее уравнение почленно на нормирующий множитель и получим нормальное уравнение плоскости:
.
Вычислим отклонение точки от плоскости:
Найдём теперь расстояние от точки до плоскости как модуль отклонения:
| Назад | Листать | Вперёд>>> |
Нет времени вникать в решение? Можно заказать работу!
К началу страницы
Пройти тест по теме Прямая и плоскость
Всё по теме «Прямая и плоскость»
- Плоскость
- Уравнения плоскости, взаимное расположение плоскостей
- Прямая в пространстве
- Уравнения прямой в пространстве
- Задачи на плоскость и прямую в пространстве
- Задачи на плоскость: параллельность, перпендикулярность, пересечение трёх плоскостей в одной точке
- Прямая на плоскости
- Уравнение прямой с угловым коэффициентом
- Общее уравнение прямой на плоскости
- Уравнение прямой в отрезках
- Каноническое уравнение прямой на плоскости
- Параметрические уравнения прямой на плоскости
- Нормальное уравнение прямой на плоскости, расстояние от точки до прямой
- Угол между двумя прямыми
Плоскость — презентация онлайн
Похожие презентации:
Элементы комбинаторики ( 9-11 классы)
Применение производной в науке и в жизни
Проект по математике «Математика вокруг нас. Узоры и орнаменты на посуде»
Узоры и орнаменты на посуде»
Знакомство детей с математическими знаками и монетами
Тренажёр по математике «Собираем урожай». Счет в пределах 10
Методы обработки экспериментальных данных
Лекция 6. Корреляционный и регрессионный анализ
Решение задач обязательной части ОГЭ по геометрии
Дифференциальные уравнения
Подготовка к ЕГЭ по математике. Базовый уровень Сложные задачи
Плоскость
Дисциплина Математика 1
Лекция 5
2016-17 учебный год
План Лекции
1. Основные уравнения плоскости
2. Построение плоскости
3. Взаимное расположение
плоскостей
4. Расстояние от точки до плоскости
3. 1. Плоскость
Основные уравнения плоскости1. Уравнение плоскости, проходящей через заданную
точку M 0 ( x0 ; y0 ; z0 ) перпендикулярно
заданному вектору N A; B; C
N A; B; C
A( x x0 ) B( y y0 ) C ( z z0 ) 0
2. Общее уравнение плоскости
M 0 ( x0 ; y0 ; z0 )
Ax By Cz D 0
N A; B; C
Z
— вектор нормали
c
3.
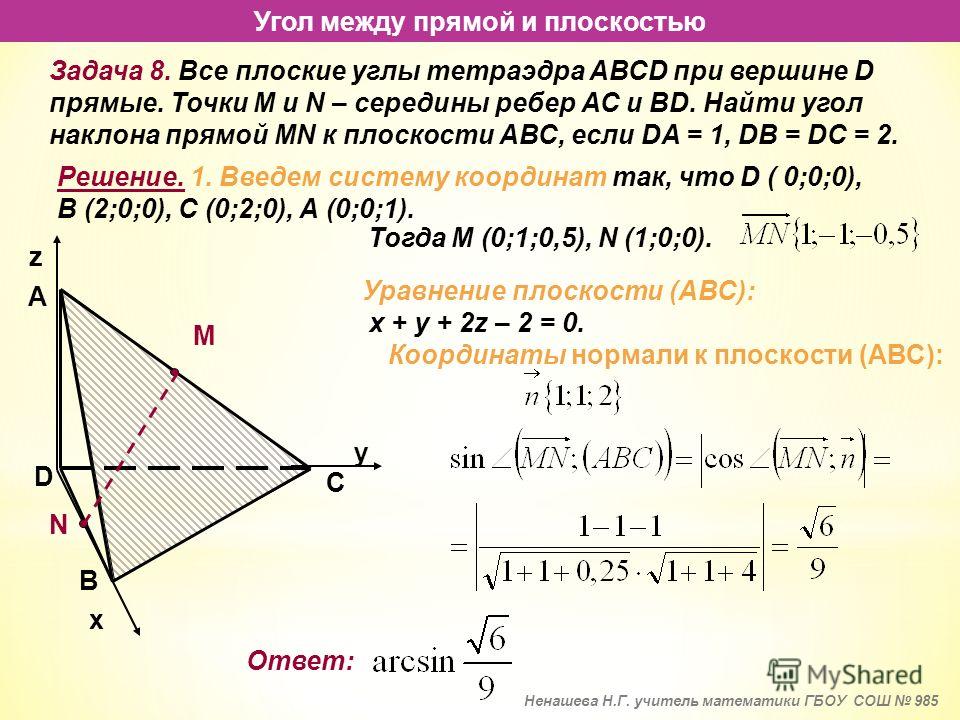 Уравнение плоскости « в отрезках»
Уравнение плоскости « в отрезках»x y z
1
a b c
Y
a
X
b
4. Уравнения плоскости
4. Уравнение плоскости, проходящей через тризаданные точки M 1 ( x1 ; y1 ; z1 ) , M 2 ( x2 ; y2 ; z2 ) и M 3 ( x3 ; y3 ; z3 )
N A; B; C
M ( x; y; z )
M 2 ( x2 ; y 2 ; z 2 )
M 1 ( x1 ; y1 ; z1 )
M 3 ( x3 ; y3 ; z3 )
Условие компланарности векторов
x x1
y y1
z z1
x2 x1
y2 y1
z 2 z1 0
x3 x1
y3 y1
z3 z1
M 1M x x1 ; y y1 ; z z1
M 1M 2 x2 x1 ; y2 y1 ; z 2 z1
M1M 3 x3 x1; y3 y1 ; z3 z1
( M 1M M 1M 2 M 1M 3 ) 0
5. Построение плоскостей
1. Построить плоскость3x 4 y 6 z 12 0
Находим координаты точек пересечения плоскости с осями координат.
Z
x
0
0
4
y
0
3
0
z
2
0
0
2
3 Y
4
X
Можно привести уравнение плоскости к уравнению «в отрезках»
1) Переносим вправо свободный член уравнения
3x 4 y 6 z 12
2) Делим на 12, чтобы получить единицу в правой части
3) Убираем коэффициенты из числителей
x y z
1
4 3 2
3x 4 y 6 z
1
12 12 12
Числа, стоящие в знаменателях, являются длинами отрезков, которые
плоскость отсекает на осях координат
6.
 Построение плоскостей2. Построить плоскость
Построение плоскостей2. Построить плоскость3x 5 y 10 0
В уравнении отсутствует переменная z.
Находим точки пересечения плоскости с осями OX и OY.
X
0
10/3
y
-2
0
Соединяем точки прямой линией и получаем
след плоскости на плоскости XOY.
Теперь из точек пересечения проводим
прямые, параллельные оси OZ.
Аналогично строятся все плоскости,
в уравнении которых отсутствует одна
переменная
Z
Z
3
2
Z
Y
-2
10/3
X
X
2
Y
7
2 x 7 z 14 0
X
3 y 2z 6
Y
7. Построение плоскостей
3z 8 03. Построить плоскость
В уравнении отсутствуют две переменные x и y. Такая плоскость
проходит параллельно и оси OX , и оси OY, т.е. она проходит
параллельно координатной плоскости XOY через точку z=8/3 на оси OZ.
Z
8/3
Y
Аналогично строятся плоскости,
в уравнениях которых отсутствуют
две переменные
0
X
Z
4x 9 0
5y 3 0
Z
Y
X
9/4
0
X
0
3/5
Y
Таким образом, если в уравнении плоскости
отсутствует одна переменная, то плоскость проходит
параллельно той оси координат, переменной которой
нет в уравнении.

Если в уравнении плоскости отсутствует свободный
член, то плоскость проходит через начало координат.
Если в уравнении плоскости отсутствуют две
переменные, то плоскость проходит параллельно
координатной плоскости, переменных которой нет в
уравнении.
Уравнения координатных плоскостей
— уравнение плоскости YOZ
x 0
— уравнение плоскости XOZ
y 0
— уравнение плоскости XOY
z 0
9. Взаимное расположение плоскостей
1. Условие параллельности плоскостейN 1 || N 2
A1 B1 C1
A2 B2 C 2
N1 A1 ; B1 ; C1
N 2 A2 ; B2 ; C2
2. Условие перпендикулярности плоскостей
N1
N2
( N1 N 2 ) 0
A1 A2 B1 B2 C1 C 2 0
N1
N2
3. Косинус угла между плоскостями
Угол между плоскостями – это угол между векторами
нормалей этих плоскостей
cos cos( N1 , N 2 )
A1 A2 B1 B2 C1 C 2
A12 B12 C12 A22 B22 C 22
10. Расстояние от точки до плоскости
Расстояние от точки M 1 ( x1 ; y1 ; z1 ) до плоскостиAx By Cz D 0 находится по формуле
d
| Ax1 By1 Cz1 D |
M 1 ( x1 ; y1 ; z1 )
d
A2 B 2 C 2
Расстояние – это длина перпендикуляра, опущенного из точки на плоскость
Правило: для нахождения расстояния от точки до плоскости нужно
координаты точки подставить в левую часть уравнения плоскости,
разделить на длину вектора нормали плоскости и полученное значение
взять по абсолютной величине.

!
Расстояние – величина всегда положительная
Задание на СРС
1. Построение произвольных плоскостей. [1]
2. Точка пересечения трех плоскостей (конспект).
Задание на СРСП
1. ИДЗ – 3.1. [1. стр.97].
Глоссарий
№
1
2
3
4
5
На русском языке
Плоскость
Общее уравнение
Параметрическое
Каноническое
Нормаль
На казахском языке
Жазықтық
Жалпы теңдеу
Параметрлік
Канондық
Нормаль
На английском языке
Plane
General equation
Parameter
Canon
Normal vector
Литература:
Основная
А.П. Рябушко. Индивидуальные задания по высшей математике, т.1.- Мн.: Выш. Школа, 2011.
Данко П.Е., Попов А.Г. Высшая математика в упражнениях и задачах: Учебное пособие для втузов.
— М.: Оникс, 2007.
Дополнительная
Буганова С.Н. Математика для технических специальностей с применением прикладных программ.
— Алматы: КазГАСА, 2015, с.108.
Сыдыкова Д.К. «Курс Математики- I», Модуль I, II для дистанционного обучения.
 Электронный
Электронныйучебник.-Алматы: КазГАСА, 2012.
www.studentlibrary.ru
http://sferaznaniy.ru/vysshaya-matematika.
English Русский Правила
Уравнение плоскости 11 класс онлайн-подготовка на Ростелеком Лицей
Введение
На этом уроке мы поговорим о плоскостях. Начнем с очередной планиметрической аналогии. Помните, мы выводили уравнение прямой на плоскости? Оно имело вид . Мы использовали это уравнения для решения различных задач, например для вычисления угла между прямыми, нахождения расстояния от точки до прямой и т. д. Выведем аналогичное уравнение для плоскости в пространстве.
Уравнение плоскости
Выведем уравнение плоскости, проходящей через точку и перпендикулярной вектору . (См. Рис. 1.)
Рис. 1. Исходные данные
Оказывается, этого достаточно, чтобы задать плоскость. Действительно, раз вектор перпендикулярен плоскости, это равносильно тому, что он перпендикулярен двум пересекающимся прямым данной плоскости. Если рассмотреть такие две прямые, проходящие через точку , они однозначно задают плоскость по следствию из аксиомы.
Если рассмотреть такие две прямые, проходящие через точку , они однозначно задают плоскость по следствию из аксиомы.
Как задать уравнение плоскости? Вообще, что такое уравнение плоскости? Уравнение плоскости – это уравнение, которому удовлетворяют координаты всех точек этой плоскости и только они.
Пусть – произвольная точка пространства, отличная от . Эта точка лежит в нашей плоскости тогда и только тогда, когда векторы и перпендикулярны. А это в свою очередь означает, что скалярное произведение этих векторов равно нулю. (См. Рис. 2.)
Рис. 2.
Запишем координаты вектора : . Тогда скалярное произведение . Домножим всё на и раскроем скобки. Получим:
Обозначая через , приходим к общему (стандартному) виду уравнения плоскости:
Обратите внимание, что для каждой плоскости существует такой набор коэффициентов (и он не один, с точностью до домножения на число), который задает ее уравнение (а значит, и саму плоскость). Кстати, верно и обратное утверждение: любое уравнение такого вида задает плоскость. Действительно, по первым трем коэффициентам можно однозначно определить вектор, перпендикулярный плоскости, а коэффициент помогает установить необходимую точку из плоскости.
Действительно, по первым трем коэффициентам можно однозначно определить вектор, перпендикулярный плоскости, а коэффициент помогает установить необходимую точку из плоскости.
Уравнение плоскости в пространстве напоминает уравнение прямой на плоскости – только добавилась еще одна переменная (из-за трёхмерности пространства). Обратите внимание, что в данном уравнении – координаты произвольной точки пространства и уравнение обращается в верное равенство тогда и только тогда, когда точка лежит в плоскости .
Также отметим, что коэффициенты при переменных в данном равенстве – это просто координаты вектора, перпендикулярного нашей плоскости. И это полезно запомнить: теперь, зная координаты вектора, перпендикулярного плоскости, и одной точки, лежащей в плоскости, мы легко можем построить ее уравнение.
Но верно и обратное утверждение: если дано уравнение плоскости, то легко можно выписать координаты вектора, ей перпендикулярного. Кстати, такой вектор называют нормальным или вектором нормали к плоскости.
Но ведь таких векторов бесконечно много. Конечно, но и уравнений плоскости бесконечно много – мы же можем домножить его на любую константу. Это и позволит получить любой нормальный вектор, коллинеарный исходному.
Примеры
Пример 1. Дан единичный куб . Написать уравнение плоскости, проходящей через точку перпендикулярно прямой . Система координат задана. (См. Рис. 3.)
Рис. 3. Иллюстрация к задаче
Решение:
Найдем координаты интересующих нас вершин: , , .
Значит, . Стандартное уравнение плоскости имеет вид: . Но ведь коэффициенты при переменных в данном равенстве – это просто координаты вектора, перпендикулярного нашей плоскости, то есть координаты вектора .
Таким образом, уравнение плоскости имеет вид .
Мы знаем, что эта плоскость проходит через точку . Подставляя эти координаты в найденное уравнение плоскости, мы можем найти . Имеем:
Получаем, что уравнение плоскости имеет вид .
Ответ: .
Пример 2. Пусть даны точки , , . Написать уравнение плоскости .
Решение:
Будем искать уравнение плоскости в виде .
Подставив координаты точек , и в уравнение, имеем систему:
Итого, имеем: . Поделив на , имеем ответ:
Ответ: .
Заодно мы нашли координаты нормального вектора: .
Расстояние от точки до плоскости. Пример
Даны плоскость и точка , не лежащая в этой плоскости. Найдите расстояние от точки до плоскости. (См. Рис. 4.)
Рис. 4. Иллюстрация к примеру
Решение:
Будем считать, что уравнение плоскости известно: (имеется в виду, что нам известны все коэффициенты этого уравнения: ).
По определению, искомое расстояние – это длина перпендикуляра , где – проекция точки на данную плоскость. (См. Рис. 5.)
Рис. 5. – искомое расстояние
Заметим, что , где – нормальный вектор к плоскости . При этом известно, что .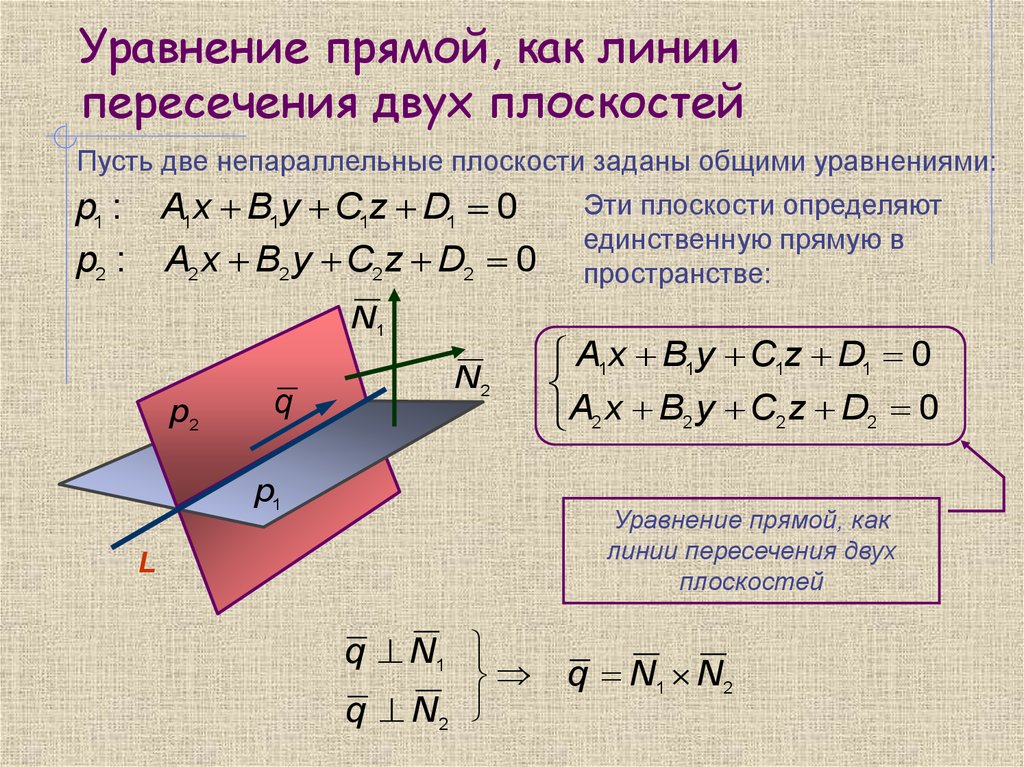 Но если два вектора коллинеарны, то их координаты пропорциональны: .
Но если два вектора коллинеарны, то их координаты пропорциональны: .
Теперь, зная координаты точки , найдем координаты точки – конца нашего искомого вектора. Так как координаты вектора вычисляются с помощью вычитания координат начала из координат конца, то координаты конца вектора соответственно равны сумме координат начала и координат вектора. Значит, координаты точки : .
Точка принадлежит плоскости , следовательно, ее координаты удовлетворяют уравнению плоскости. Подставляя найденные координаты точки в уравнение плоскости , находим неизвестный коэффициент :
И наконец, найдем искомую длину вектора :
Сокращая это выражение на , приходим к окончательной формуле:
Обратите внимание, что, хотя «вывод» формулы занял у нас изрядное время, повторять его при решении задач не придется. Достаточно будет просто применить формулу. Так что внимательно ознакомимся с этой формулой и поймём, что именно в нее нужно подставить. Во-первых, числа .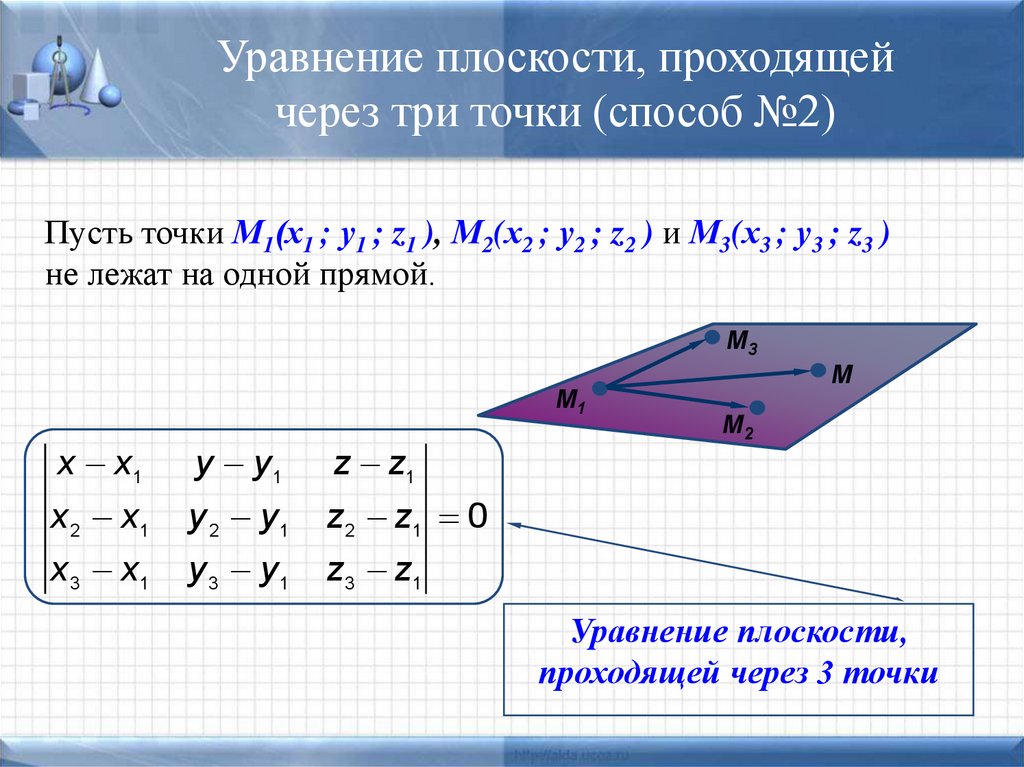 Они берутся из уравнения плоскости, так что первым делом нам надо будет вывести само уравнение плоскости, зная координаты точек , и . И, во-вторых, это – координаты точки М. Они нам даны, так что тут ничего дополнительно считать не надо.
Они берутся из уравнения плоскости, так что первым делом нам надо будет вывести само уравнение плоскости, зная координаты точек , и . И, во-вторых, это – координаты точки М. Они нам даны, так что тут ничего дополнительно считать не надо.
Пример
В правильной четырехугольной призме сторона основания равна , а высота – . Точка – середина ребра . Найти расстояние от точки до плоскости . (См. Рис. 6.)
Рис. 6. Иллюстрация к примеру
Решение:
Введем систему координат. (См. Рис. 7.)
Рис. 7. Введенная система координат
1. Найдем координаты точек , , , , :
, , , ,
2. Найдем уравнение плоскости . Общий вид уравнения плоскости: . Подставим в него координаты точек , , :
Итак, уравнение плоскости имеет вид:
.
Разделим всё на и домножим на . Получим:
.
3. Вычислим расстояние от точки до плоскости по формуле:
Ответ:.
Заключение
На этом уроке мы узнали, как выглядит уравнение плоскости в пространстве: . Выяснили, что оно похоже на уравнение прямой на плоскости. Также мы выяснили, что соответствующие коэффициенты , , – это координаты нормального вектора. Кроме того, мы обнаружили, что уравнение плоскости часто применяется при нахождении расстояния от точки до плоскости, и записали формулу для нахождения этого расстояния: .
Выяснили, что оно похоже на уравнение прямой на плоскости. Также мы выяснили, что соответствующие коэффициенты , , – это координаты нормального вектора. Кроме того, мы обнаружили, что уравнение плоскости часто применяется при нахождении расстояния от точки до плоскости, и записали формулу для нахождения этого расстояния: .
Список литературы
- Атанасян Л.С. и др. Геометрия. Учебник для 10-11 классов. 18-е изд. — М.: Просвещение, 2009. — 255 с.
- А.В. Погорелов. Геометрия 11 класс. – М.: Просвещение, 2002.
- В.Ф. Бутузов, Ю.А. Глазков. Рабочая тетрадь по геометрии 11 класс.
Дополнительные рекомендованные ссылки на ресурсы сети Интернет
- Cleverstudents.ru (Источник).
- Mathematics.ru (Источник).
- Function-x.ru (Источник).
Домашнее задание
- Составьте уравнение плоскости, зная, что точка служит основанием перпендикуляра, проведенного из начала координат к этой плоскости.

- Составьте уравнение плоскости, проходящей через точки , и .
- В единичном кубе найдите расстояние от точки до плоскости .
Нахождение уравнений нормальной и соприкасающейся плоскостей — Krista King Math
Пошаговое руководство по нахождению уравнения нормальной плоскости и уравнения соприкасающейся плоскости
Пример
Найти уравнения нормальная и соприкасающаяся плоскости векторной функции в точке ???P(1,1,0)???.
???r(t)=\cos{t}\жирный i+\sin{t}\жирный j+t\жирный k???
Нам нужно найти следующие значения в следующем порядке:
Уравнение нормальной плоскости ???r'(t)_1(x-x_0)+r'(t)_2(y-y_0 )+r'(t)_3(z-z_0)=0??? используя 92}???
???N(t)=\frac{T'(t)}{\left|T'(t)\right|}???
???B(t)=T(t)\times{N(t)}???
Поиск ???t???
Начнем с определения значения ???t???. Так как коэффициент при ???\bold k??? ???т??? мы можем просто взять значение ???z??? от точки координат и сказать, что ???t=0???.
Нахождение ???r'(t)=\langle r'(t)_1,r'(t)_2,r'(t)_3\rangle???
Теперь мы можем перейти к уравнению нормальной плоскости. Наш первый шаг — найти производную вектор-функции. Чтобы взять производную векторной функции, мы игнорируем ???\bold i???, ???\bold j??? и ???\жирный k??? и просто взять производную каждого из коэффициентов.
???r(t)=\cos{t}\жирный i+\sin{t}\жирный j+t\жирный k???
???r'(t)=-\sin{t}\bold i+\cos{t}\bold j+\bold k???
???r'(t)=\left\langle-\sin{t},\cos{t},1\right\rangle???
Поскольку ???t=0???, производная становится равной
???r'(0)=\left\langle-\sin{0},\cos{0},1\right\rangle? ??
???r'(0)=\влево\langle0,1,1\вправо\rangle???
???r'(0)=0\жирный i+1\жирный j+1\жирный k???
???r'(0)=\жирный j+\жирный k???
Нахождение уравнения нормальной плоскости 92{x}=1???, мы можем сказать
???\left|r'(t)\right|=\sqrt{1+1}???
???\влево|r'(t)\вправо|=\sqrt{2}???
Так как нет ???т??? переменная в правой части, оценивающая величину производной при ???t=0??? не меняет своего значения, поэтому
???\left|r'(0)\right|=\sqrt{2}???
Нахождение ???T(t)=\frac{r'(t)}{\left|r'(t)\right|}???
Следовательно, мы можем сказать, что единичный касательный вектор равен
???T(t)=\frac{r'(t)}{\left|r'(t)\right|}???
???T(t)=\frac{-\sin{t}\bold i+\cos{t}\bold j+\bold k}{\sqrt2}???
???T(t)=-\frac{1}{\sqrt2}\sin{t}\bold i+\frac{1}{\sqrt2}\cos{t}\bold j+\frac{1} {\ sqrt2} \ полужирный k???
???T(t)=\frac{\sqrt2}{\sqrt2}\left(-\frac{1}{\sqrt2}\sin{t}\bold i+\frac{1}{\sqrt2} \cos{t}\жирный j+\frac{1}{\sqrt2}\жирный k\право)???
???T(t)=-\frac{\sqrt2}{2}\sin{t}\bold i+\frac{\sqrt2}{2}\cos{t}\bold j+\frac{\sqrt2 {2}\жирный к???
???T(t)=\left\langle-\frac{\sqrt2}{2}\sin{t},\frac{\sqrt2}{2}\cos{t},\frac{\sqrt2 {2}\право\угол???
Поскольку ???t=0???, мы получаем
???T(0)=\left\langle-\frac{\sqrt2}{2}\sin{0},\frac{\sqrt2 {2}\cos{0},\frac{\sqrt2}{2}\right\rangle???
???T(0)=\left\langle0,\frac{\sqrt2}{2},\frac{\sqrt2}{2}\right\rangle???
???T(0)=\frac{\sqrt2}{2}\bold j+\frac{\sqrt2}{2}\bold k???
Нахождение ???T'(t)=\langle T'(t)_1,T'(t)_2,T'(t)_3\rangle???
Наш следующий шаг — найти единичный вектор нормали ???N(t)???, но так как
???N(t)=\frac{T'(t)}{\left|T ‘(т)\право|}???
нам нужно найти производную единичного касательного вектора ???T'(t)??? и сначала его величина, чтобы мы могли подставить их в формулу для единичного вектора нормали.
???T(t)=-\frac{\sqrt2}{2}\sin{t}\bold i+\frac{\sqrt2}{2}\cos{t}\bold j+\frac{\sqrt2 {2}\жирный к???
???T'(t)=-\frac{\sqrt2}{2}\cos{t}\bold i-\frac{\sqrt2}{2}\sin{t}\bold j+0\ смелый к???
???T'(t)=-\frac{\sqrt2}{2}\cos{t}\bold i-\frac{\sqrt2}{2}\sin{t}\bold j???
???T'(t)=\left\langle-\frac{\sqrt2}{2}\cos{t},-\frac{\sqrt2}{2}\sin{t},0\right \ rangle??? 92{х}=1??? чтобы получить
???\left|T'(t)\right|=\sqrt{\frac12(1)}???
???\влево|T'(t)\вправо|=\sqrt{\frac12}???
???\влево|T'(t)\вправо|=\frac{\sqrt1}{\sqrt2}???
???\влево|T'(t)\вправо|=\frac{1}{\sqrt2}???
???\влево|T'(t)\вправо|=\frac{1}{\sqrt2}\cdot\frac{\sqrt2}{\sqrt2}???
???\влево|T'(t)\вправо|=\frac{\sqrt2}{2}???
Так как нет ???т??? переменная в правой части, оценивающая величину производной при ???t=0??? не меняет своего значения, поэтому
???\влево|T'(0)\вправо|=\frac{\sqrt2}{2}???
Нахождение ???N(t)=\frac{T'(t)}{\left|T'(t)\right|}???
Следовательно, мы можем сказать, что единичный вектор нормали равен
???N(t)=\frac{T'(t)}{\left|T'(t)\right|}???
???N(t)=\frac{-\frac{\sqrt2}{2}\cos{t}\bold i-\frac{\sqrt2}{2}\sin{t}\bold j} {\ гидроразрыва {\ sqrt2} {2}}???
???N(t)=\frac{-1\cos{t}\bold i-1\sin{t}\bold j}{1}???
???N(t)=-\cos{t}\bold i-\sin{t}\bold j???
???N(t)=\langle-\cos{t},-\sin{t},0\rangle???
Поскольку ???t=0???, мы получаем
???N(0)=\langle-\cos{0},-\sin{0},0\rangle???
???N(0)=\langle-1,0,0\rangle???
???N(0)=-\жирный i???
Нахождение ???B(t)=T(t)\times{N(t)}???
Теперь, когда у нас есть единичный тангенс и единичный вектор нормали, мы можем найти единичный вектор бинормалей.
???B(t)=T(t)\times{N(t)}???
???B(t)=\begin{vmatrix}\bold i & \bold j & \bold k\\-\frac{\sqrt2}{2}\sin{t} & \frac{\sqrt2} {2}\cos{t} & \frac{\sqrt2}{2}\\-\cos{t} & -\sin{t} & 0\end{vmatrix}???
???B(t)=\begin{vmatrix}\frac{\sqrt2}{2}\cos{t} & \frac{\sqrt2}{2}\\-\sin{t} & 0\ end{vmatrix}\bold i-\begin{vmatrix}-\frac{\sqrt2}{2}\sin{t} & \frac{\sqrt2}{2}\\-\cos{t} & 0\end {vmatrix}\жирный шрифт j+\begin{vmatrix}-\frac{\sqrt2}{2}\sin{t} & \frac{\sqrt2}{2}\cos{t}\\-\cos{t} & -\sin{t}\end{vmatrix}\жирный k???
???B(t)=\left[\left(\frac{\sqrt2}{2}\cos{t}\right)(0)-(-\sin{t})\left(\frac {\ sqrt2} {2} \ справа) \ справа] \ полужирным шрифтом i???
???-\left[\left(-\frac{\sqrt2}{2}\sin{t}\right)(0)-(-\cos{t})\left(\frac{\sqrt2 {2}\справа)\справа]\жирный j??? 92{х}=1??? чтобы получить
???B(t)=\frac{\sqrt2}{2}\sin{t}\bold i-\frac{\sqrt2}{2}\cos{t}\bold j+\left( \frac{\sqrt2}{2}(1)\right)\жирный k???
???B(t)=\frac{\sqrt2}{2}\sin{t}\bold i-\frac{\sqrt2}{2}\cos{t}\bold j+\frac{\sqrt2 {2}\жирный к???
???B(t)=\left\langle\frac{\sqrt2}{2}\sin{t},-\frac{\sqrt2}{2}\cos{t},\frac{\sqrt2 {2}\право\угол???
Поскольку ???t=0???, мы получаем
???B(0)=\left\langle\frac{\sqrt2}{2}\sin{0},-\frac{\sqrt2 {2}\cos{0},\frac{\sqrt2}{2}\right\rangle???
???B(0)=\left\langle0,-\frac{\sqrt2}{2},\frac{\sqrt2}{2}\right\rangle???
???B(0)=-\frac{\sqrt2}{2}\bold j+\frac{\sqrt2}{2}\bold k???
Нахождение уравнения соприкасающейся плоскости
Подстановка значений единичного вектора бинормалей и точки ???P(1,1,0)??? к формуле уравнения соприкасающейся плоскости получаем
???B(t)_1(x-x_0)+B(t)_2(y-y_0)+B(t)_3(z-z_0) =0???
???0(x-1)-\frac{\sqrt2}{2}(y-1)+\frac{\sqrt2}{2}(z-0)=0???
???-\frac{\sqrt2}{2}y+\frac{\sqrt2}{2}+\frac{\sqrt2}{2}z=0???
???-\frac{\sqrt2}{2}y+\frac{\sqrt2}{2}z=-\frac{\sqrt2}{2}???
???-1y+1z=-1???
???-y+z=-1???
???y=1+z???
Итак, уравнение соприкасающейся плоскости ???y=1+z???.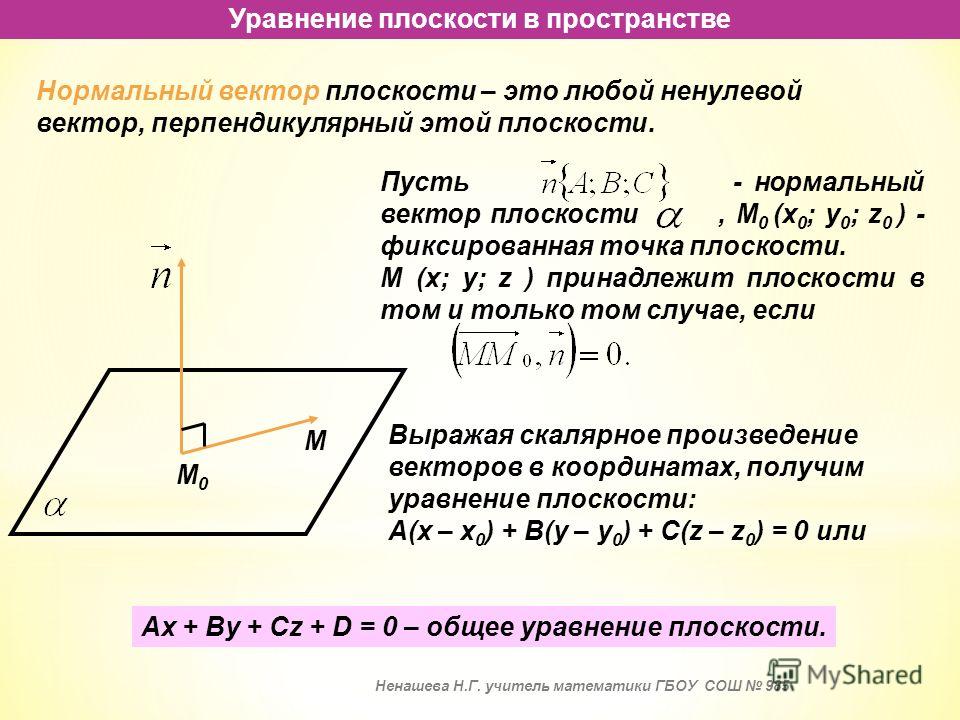
Получите доступ к полному курсу Calculus 3
Определение класса плоскости здания
12.02.2021
0 комментариев
ОБНОВЛЕНИЕ: см. новый калькулятор среднего уклона самолета, ссылка на который приведена ниже.
За последние несколько месяцев у меня было несколько клиентов, которые задавали мне вопросы, касающиеся расчетов уровня земли, чаще всего связанных с определением того, считается ли конкретный этаж этажом выше уровня земли или цокольным этажом. Вот краткое изложение того, как сделать расчет и последствия.
Плоскость среднего уклона
Глава 2 IBC определяет плоскость уклона (часто называемую синонимом плоскости среднего уклона) следующим образом:
Эталонная плоскость, представляющая среднее значение готового уровня земли, примыкающего к зданию у наружных стен.
Таким образом, если у вас есть абсолютно ровная площадка, отметка, на которой готовый уровень земли примыкает к внешним стенам здания, является вашей уклонной плоскостью. Если ваш участок имеет наклон, вам необходимо взять несколько высот, где готовый уровень земли примыкает к зданию, и усреднить их, чтобы определить плоскость уклона.
Если ваш участок имеет наклон, вам необходимо взять несколько высот, где готовый уровень земли примыкает к зданию, и усреднить их, чтобы определить плоскость уклона.
Самый частый вопрос, который я получаю по этому поводу: сколько точек высоты вам нужно в среднем для этого?
Во-первых, IBC не дает никаких конкретных требований или инструкций для ответа на этот вопрос. В вашей местной юрисдикции потенциально могут быть некоторые указания о том, как они хотят видеть выполнение расчета, но, по моему опыту, в большинстве случаев этого нет.
Как правило, я советую клиентам основывать количество точек высот на уклоне участка. Если у вас относительно ровная площадка, небольшое количество точек отметки даст вам точную отметку плоскости уклона. Вам может понадобиться только одна точка отметки на грань здания. С другой стороны, если у вас участок неправильной формы с большим уклоном, вам потребуется много точек высот. Однажды я работал над зданием, которое было построено на склоне крутого холма — там мы измеряли высоту через каждые 10 футов в некоторых местах. Если вы сомневаетесь, большее количество точек высоты в вашем расчете приведет к более точному измерению.
Если вы сомневаетесь, большее количество точек высоты в вашем расчете приведет к более точному измерению.
Простой расчет плоскости уклона участка с равномерным уклоном.
В приведенном выше простом примере измерение плоскости уклона представляет собой просто среднее значение отметок в конце каждого сегмента стены (например, для восточной стены (280+270)/2 = 275 футов). Однако при более сильном уклоне, особенно при неравномерном уклоне, вам потребуется выполнить дополнительные измерения, как показано в примере ниже.
Сложный расчет плоскости уклона с неравномерным уклоном.
Еще один распространенный вопрос: что делать, если мой участок имеет уклон перпендикулярно наружным стенам?
К счастью, определение плоскости уклона конкретно касается этого: линия участка или, если линия участка находится на расстоянии более 6 футов от здания, между зданием и точкой на расстоянии 6 футов от здания. Итак, вы ищете самую низкую точку на высоте в пределах 6 футов от внешней стены (или меньше, если линия участка ближе). |
Последствия — определение этажа выше плоскости уровня
Почему расчет плоскости уровня имеет значение? В моих проектах это всегда всплывает, когда клиент пытается определить, является ли тот или иной этаж на самом деле этажом выше уровня земли или цокольным этажом.
Глава 2 IBC определяет «Этаж выше уровня земли» как:
Любой этаж, у которого чистая поверхность пола полностью выше уровня земли, или в котором чистая поверхность пола находится выше уровня земли:
- Более 6 футов (1829 мм) над уровнем земли; или
- Более 12 футов (3658 мм) над чистым уровнем земли в любой точке.
В прошлом это определение вызывало некоторую путаницу, поэтому вот пошаговая разбивка:
- Находится ли поверхность пола рассматриваемого этажа полностью над отметкой уровня земли?
- Находится ли поверхность пола выше рассматриваемого этажа на высоте более 6 футов над уровнем земли?
- Находится ли поверхность пола выше рассматриваемого этажа на высоте более 12 футов над любым из измерений уклона в любой точке вдоль наружных стен здания?
Если вы ответили утвердительно на любой из трех вышеприведенных вопросов, данный этаж считается этажом выше уровня земли.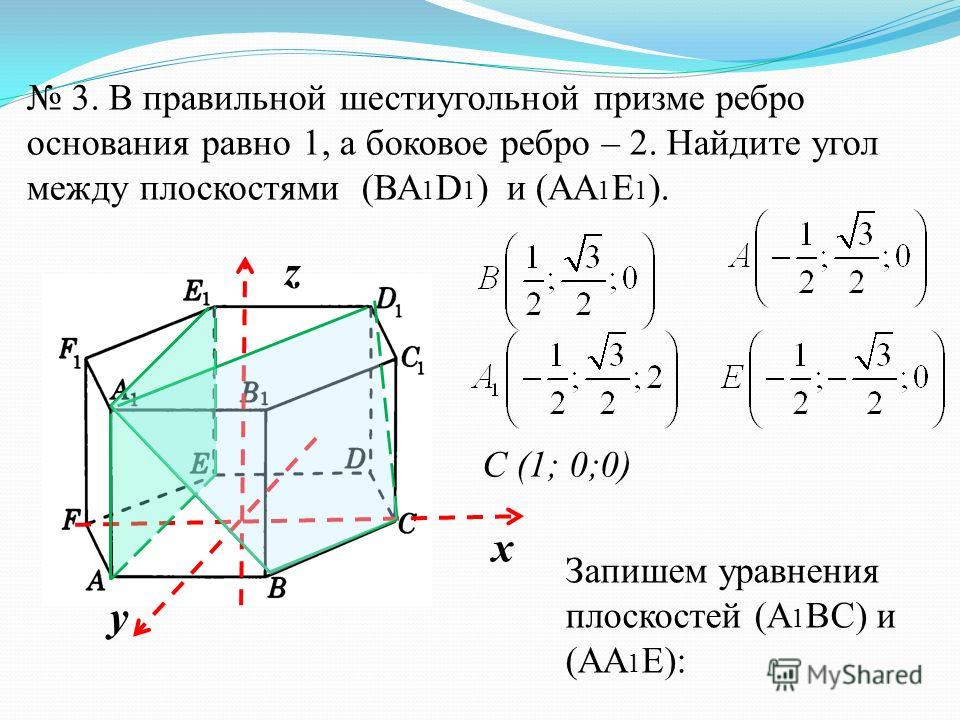
Существует множество кодовых требований, которые различаются между этажом и подвалом, но наиболее распространенным из них является соблюдение допустимого количества этажей в зависимости от занятости и типа конструкции. В этом году у меня был проект, в котором поверхность пола на уровне выше была на 5 футов 10 дюймов выше уровня земли, едва проходя как подвал. 2+ дюйма больше, и здание было бы на один этаж выше, что привело бы к требованиям к более прочному типу конструкции, более высоким номинальным значениям шахты и значительным дополнительным затратам.
Если ваша ситуация настолько близка, я предлагаю включить в пакет разрешений план, на котором четко показаны высотные отметки вокруг здания и показан ваш расчет плоскости уклона. Это позволяет рецензентам плана легко следовать вашей логике и, надеюсь, согласиться с вашим подходом (помните, что нет никаких конкретных инструкций или требований IBC относительно того, как выполнять расчеты).
Новый калькулятор среднего уклона
Если вам нужно выполнить расчет уклона или вам интересно, считается ли конкретный этаж этажом выше уровня, проверьте этот новый калькулятор по ссылке ниже!
* Указывает требуемое полеИмя * Первый Последний | Электронная почта * |
Go To The The Calculator
.
У вас был проект, требующий подробного расчета плоскости уклона? Были ли у вас случаи, когда рецензент плана или должностное лицо по коду не соглашались с вашим расчетом? Дайте мне знать в поле для комментариев!
0 комментариев
Авторское право © 1999 — 1728 программных систем |
Как рассчитать вес и балансировку: пошаговое руководство
Обучение вычислению веса и баланса является одним из самых фундаментальных предполетных навыков, которым учится пилот. В учебном самолете это простой и простой расчет, который со временем станет второй натурой.
По мере того, как вы переходите на более крупный самолет, вес и балансировка могут стать более сложными. Ваша цель должна состоять в том, чтобы практиковать его, пока он не укоренится, и расчет веса и баланса для каждого полета не должен обсуждаться.
К счастью, вес и баланс не требуют сумасшедших математических навыков или часов тяжелой работы. Вместо этого это простой расчет, который вы научитесь вычислять за несколько минут.
Вот пошаговое руководство, как сделать это на любом самолете. Существует также новая технология, такая как ForeFlight, которая упрощает эти расчеты.
Зачем рассчитывать вес и балансировку?
Легко сказать, что перед каждым полетом вы должны выполнять взвешивание и балансировку, потому что так говорит ваш летный инструктор, но почему они так говорят?
Каждый компонент проблемы веса и балансировки является критическим ограничением самолета. Немногие аспекты производительности или безопасности важнее, чем знание того, что ваш полет находится в пределах допустимых норм.
Правила прямо не требуют, чтобы вы вычисляли свой вес и равновесие перед каждым полетом, однако это подразумевается. Правила предусматривают, что вы рассчитываете взлетную и посадочную дистанции и управляете самолетом в соответствии с AFM.
Если вы не знаете свой вес и равновесие, вы не можете соблюдать это правило. (14 CFR часть 91.9)
Вес
Все мы знаем, что самолеты рассчитаны только на определенный вес. Какие бы ограничения ни были напечатаны в Главе 2 вашего POH/AFM, они будут вашим руководством. Наиболее важным числом является максимальная взлетная масса.
Превышая максимальный вес, вы попадаете в сферу летчика-испытателя. Вот лишь некоторые из отрицательных летных характеристик, которые вы можете ожидать.
- Более высокая скорость взлета с более длинными разбегами
- Более длинные посадочные пробеги
- Снижение производительности, в том числе более низкие крейсерские скорости и медленные наборы высоты
- Более высокие скорости сваливания
- Превышены ограничения на шасси и тормоза
- На конструкцию самолета возлагается большая нагрузка, чем она была рассчитана
Баланс
или ваш самолет не находится в равновесии, все о поиске загруженного самолета центра тяжести или CG. Получив это, вы можете сравнить его с диаграммами или таблицами, которые предоставляет вам производитель, чтобы убедиться, что оно находится в допустимых пределах.
Получив это, вы можете сравнить его с диаграммами или таблицами, которые предоставляет вам производитель, чтобы убедиться, что оно находится в допустимых пределах.
ЦТ не может быть слишком далеко вперед или слишком далеко назад. Любая ситуация сделает самолет опасным и потенциально нестабильным.
ЦТ, расположенный впереди переднего предела, приведет к тому, что самолет будет иметь тенденцию к снижению носа. Если нагрузка достаточно серьезная, ход руля высоты может не создавать достаточной силы, чтобы позволить самолету расширяться или вращаться.
Тенденция к опусканию носа увеличивает скорость сваливания самолета и значительно замедляет крейсерский полет.
Если ЦТ расположен слишком далеко от кормы, самолет будет иметь тенденцию задирать нос. Обычно это самая опасная ситуация. Самолет будет иметь заметно более высокую крейсерскую скорость, но будет значительно менее устойчив.
Если самолет начнет тангаж и замедление, как в сценарии сваливания, пилот может оказаться не в состоянии опустить нос, уменьшить угол атаки и восстановиться.
Запредельный ЦТ, направленный назад, связан с неустранимыми срывами и вращением.
Условия веса и балансировки
Стандартный пустой вес — Вес планера, двигателей и стационарно установленных приспособлений и жидкостей (включая непригодное топливо и полное моторное масло)
Базовый вес пустого — Стандартный вес пустого плюс любые аксессуары, которые могут быть установлены на вашем самолете
Лицензионный вес пустого — Более старый термин, чем «стандартный вес пустого», который не включает моторное масло
Максимальный вес рампы — Общий вес загруженного самолета публикуется только для некоторых самолетов. Это будет на несколько фунтов тяжелее максимального взлетного веса, потому что предполагается, что вы сожжете немного на руление и разбег.
Максимальный взлетный вес — Максимальный вес, с которым вы можете взлететь.
Максимальный вес приземления — Максимальный вес, с которым вы можете приземлиться. Это не всегда публикуется, или оно может быть опубликовано как равное взлетному весу. Более крупные самолеты имеют посадочную массу намного меньше взлетной, поскольку они рассчитаны на сжигание сотен (или тысяч) фунтов топлива во время полета.
Это не всегда публикуется, или оно может быть опубликовано как равное взлетному весу. Более крупные самолеты имеют посадочную массу намного меньше взлетной, поскольку они рассчитаны на сжигание сотен (или тысяч) фунтов топлива во время полета.
Максимальный вес без топлива — Вес загруженного самолета всем, кроме топлива. Опубликовано только для некоторых самолетов. Это показатель нагрузки для уменьшения нагрузки на крылья.
Полезная нагрузка — общий термин, обозначающий максимальный вес, который самолет может нести, чтобы оплатить счет — пассажиров или груза.
Полезная загрузка — Общий термин для обозначения того, что может нести самолет, что пилот загружает на борт: пилота, пассажиров, груз и топливо. Его можно найти, взяв максимальный взлетный вес и вычтя из него базовый вес пустого самолета.
Datum — Выбранная производителем контрольная точка, от которой измеряются все рычаги. Где это неважно, но обычно он находится на кончике кок винта или брандмауэре двигателя.
Где это неважно, но обычно он находится на кончике кок винта или брандмауэре двигателя.
Рукав — Расстояние, измеренное до или после исходной точки. Каждое место, где пилот может загрузить объект, будет иметь расстояние до руки, указанное в POH/AFM. Если рука расположена перед базой данных, это будет отрицательное число.
Станция — Место в самолете, где можно что-то загрузить. Примеры станций включают передние сиденья, задние сиденья, основное багажное отделение, носовое багажное отделение, топливные баки и т. д.
Центр тяжести — Центр тяжести, измеренный в дюймах позади исходной точки. Самолет будет иметь минимальное и максимальное положение ЦТ для каждого доступного веса.
Момент — Измерение силы, с которой предмет действует на самолет. Объект массой 100 фунтов производит больше силы, чем дальше он находится от точки отсчета. Другими словами, 100-фунтовая сумка повлияет на ваше компьютерное местоположение тем сильнее, чем дальше в самолете она находится. Моменты измеряются в дюйм-фунтах.
Моменты измеряются в дюйм-фунтах.
Индекс момента — Моменты обычно представляют собой длинные числа, поэтому многие POH/AFM индексируют их для упрощения математики. Это просто означает, что они делят их либо на 100, либо на 1000. Таким образом, 123 456,0 дюймо-фунтов становятся 1 234,56 или 123,456.
Три метода расчета веса и баланса
Часто говорят, что существует три метода или способа расчета веса и баланса, но это не совсем так. Все эти «методы» основаны на расчете веса и баланса с помощью простой математической формулы.
Лучше сказать, что ваш POH или AFM предоставит вам один или несколько из этих трех способов выполнения работы. Вы будете либо использовать числа для выполнения математических операций, либо находить числа на графике, либо находить числа в таблице.
Метод расчета
В какой-то степени все расчеты веса и баланса сводятся к математической формуле для веса и баланса.
Вес x Рука = Моменты
Вычисление веса и баланса одним лишь расчетом просто означает, что вы делаете математику для всего — все числа заполняются строка за строкой. Другие методы просто облегчают вам жизнь, быстро предоставляя вам часть этой информации.
Другие методы просто облегчают вам жизнь, быстро предоставляя вам часть этой информации.
Понимание метода расчета важно, поскольку он является основой для других методов. Если вы можете вычислить вес самолета и сбалансировать его таким образом, вы все равно сможете это вычислить.
Хотите узнать больше о навигационных плоттерах? Перейдите по этой ссылке, чтобы узнать больше!
Продолжение статьи ниже.
Графический метод
Если ваш POH или AFM включает графики, вы получите как минимум два.
Первый покажет, сколько моментов производит предмет на каждой станции. Таким образом, каждая станция самолета (передние сиденья, задние сиденья, топливо, багаж и т. д.) будет иметь свою линию на графике. На дне будет вес, а на боку моменты.
После того, как вы подсчитали все элементы самолета, просто добавьте общий вес и общий момент. Второй график покажет вам допустимые пределы CG, используя эти два числа.
Табличный метод
Таблицы аналогичны графикам, только они содержат таблицы чисел для каждой станции и аналогичную таблицу для пределов ЦТ.
Как и в графическом методе, единственными математическими вычислениями должны быть подсчеты столбца веса и момента.
Таблицы могут потребовать, чтобы вы немного округлили числа, поскольку каждый предмет будет указан для четного веса. Например, если ваши передние пассажиры в сумме весят 345 фунтов, вы можете использовать линию 350 фунтов. В качестве альтернативы вы можете использовать предоставленную руку и прибегнуть к методу расчета, чтобы получить более точное число.
Определение веса и центровки методом расчета
Шаг 1. Составьте таблицу
Вес и балансировка начинаются с пустой таблицы, которую вы можете заполнить для каждого рейса. Многие школы и FBO предоставляют вам лист планирования, но его легко сделать самостоятельно.
В первом столбце будут «веса», во втором — «плечо», а в третьем — «моменты». Чтобы напомнить себе, вы можете написать формулу веса и баланса вверху.
Вес x Рычаг = Моменты
Обычные позиции будут следующими. Список будет зависеть от доступных станций для загрузки в вашем самолете. В первой строке всегда будет вес пустого самолета.
Список будет зависеть от доступных станций для загрузки в вашем самолете. В первой строке всегда будет вес пустого самолета.
| Вес x | Рычаг = | Моменты | |
| Вес пустого | ? | ? | ? |
| Пилот + второй пилот | ? | ? | ? |
| Задние пассажиры | ? | ? | ? |
| Топливо — основные баки | ? | ? | ? |
| Топливо — дополнительные баки | ? | ? | ? |
| Место для багажа 1 | ? | ? | ? |
| Место для багажа 2 | ? | ? | ? |
| Итого | ? | ? | ? |
Шаг 2. Определите массу и момент пустого самолета
Вы не сможете оформить документы, пока не узнаете, на каком самолете вы будете летать. Единственным официальным источником информации о массе пустого, центровке и моменте самолета является официальная запись, найденная в POH/AFM этого конкретного самолета. Не используйте образец информации, найденный в Интернете или в вашем личном PIM.
Единственным официальным источником информации о массе пустого, центровке и моменте самолета является официальная запись, найденная в POH/AFM этого конкретного самолета. Не используйте образец информации, найденный в Интернете или в вашем личном PIM.
Официальная запись относится к последнему разу, когда механик физически взвешивал самолет. Он должен быть подписан A&P и относиться к конкретному самолету.
Из этой формы вам нужен пустой вес и суммарные моменты. Добавьте их в первую строку таблицы.
| Weight x | Arm = | Moments | |
| Empty weight | 2,100 | 78.3 | 164,430 |
| Pilot + Copilot | ? | ? | ? |
| Задние пассажиры | ? | ? | ? |
| Топливо — основные баки | ? | ? | ? |
| Топливо — дополнительные баки | ? | ? | ? |
| Место для багажа 1 | ? | ? | ? |
| Место для багажа 2 | ? | ? | ? |
| Итого | ? | ? | ? |
Шаг 3.
 Взвесьте снаряжение и пассажиров
Взвесьте снаряжение и пассажировЗаполните все пункты в столбце веса. Оценки недостаточно хороши для маленького самолета — вы должны использовать точные цифры. Не бойтесь спрашивать пассажиров, сколько они весят. У многих ПФ есть шкала, которую вы можете использовать, если они не знают. Не забудьте включить тяжелые куртки и ботинки, если сейчас зима!
Вы должны знать, сколько галлонов топлива вмещает ваш самолет, но сколько он весит? Avgas весит 6 фунтов на галлон, так что умножьте галлоны на 6. (Если ваш самолет сжигает Jet-A, у вас будет таблица, в которой указано, сколько он весит при различных температурах — обычно это чуть более 7 фунтов на галлон. .)
Не забудьте включить в самолет все, что не закреплено болтами. Обычно пропущенными предметами являются летные сумки, брошенные на задние сиденья, или запасные части, масло и различные вещи, хранящиеся в багажном отделении.
| Weight x | Arm = | Moments | |
| Empty weight | 2,100 | 78. 3 3 | 164,430 |
| Pilot + Copilot | 340 | ? | ? |
| Задние пассажиры | 350 | ? | ? |
| Топливо — основные баки | 450 | ? | ? |
| Топливо — дополнительные баки | 0 | ? | ? |
| Место для багажа 1 | 80 | ? | ? |
| Багажное отделение 2 | 0 | ? | ? |
| Итого | ? | 903:30 ?? |
Шаг 4. Найдите рычаг для каждой станции
Далее вам нужно узнать рычаг для каждого веса в вашем списке. Это взято из главы 6 вашего POH/AFM. Заполните свою таблицу.
| Weight x | Arm = | Moments | |
| Empty weight | 2,100 | 78.3 | 164,430 |
| Pilot + Copilot | 340 | 85.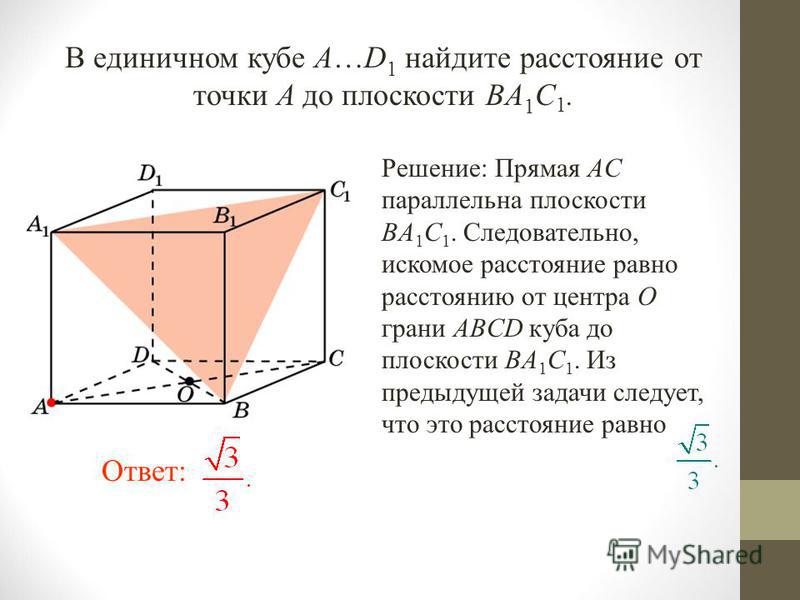 0 0 | ? |
| Задние пассажиры | 350 | 121.0 | ? |
| Топливо — основные баки | 450 | 75,0 | ? |
| Топливо — дополнительные баки | 0 | – | ? |
| Место для багажа 1 | 80 | 150.0 | ? |
| Место для багажа 2 | 0 | – | ? |
| Всего | ? | ? | ? |
Шаг 5. Найдите момент для каждой позиции строки
Выполните умножение для каждой строки, чтобы найти момент.
| Weight x | Arm = | Moments | |
| Empty weight | 2,100 | 78.3 | 164,430 |
| Pilot + Copilot | 340 | 85.0 | 28,900 |
| Rear passengers | 350 | 121. 0 0 | 42,350 |
| Fuel — main tanks | 450 | 75.0 | 33,750 |
| Fuel — aux tanks | 0 | – | 0 |
| Baggage area 1 | 80 | 150.0 | 12,000 |
| Baggage area 2 | 0 | – | 0 |
| Total | ? | ? | ? |
Шаг 6 – Найдите общий вес
Сложите столбец веса. Ваш общий вес меньше максимального взлетного веса вашего самолета?
Если вы превысили максимальный взлетный вес, перепроверьте свои цифры. Возможно, вам придется оставить некоторые предметы (или людей!) позади. Или вы можете подумать о том, чтобы уйти с меньшим количеством топлива, если это безопасно.
| Вес x | Рычаг = | Moments | |
| Empty weight | 2,100 | 78. 3 3 | 164,430 |
| Pilot + Copilot | 340 | 85.0 | 28,900 |
| Rear passengers | 350 | 121.0 | 42,350 |
| Топливо — основные баки | 450 | 75,0 | 33 750 |
| Топливо — дополнительные баки | 3 9 3 0 9 03 39 | ||
| Baggage area 1 | 80 | 150.0 | 12,000 |
| Baggage area 2 | 0 | – | 0 |
| Total | 3,320 | ? | ? |
Шаг 7 – Найдите общий момент и центр тяжести
Ваш POH/AFM предоставит способ определить, находится ли самолет в равновесии. Это даст ответ, используя общие моменты, общее плечо (CG) или и то, и другое.
Добавьте столбец момента. Этого будет достаточно, если у вас есть диаграмма в вашем POH/AFM для загруженных моментов. Не забудьте исправить его на соответствующий индекс, который соответствует информации в вашем POH. Возможно, вам придется разделить на 100 или 1000.
Не забудьте исправить его на соответствующий индекс, который соответствует информации в вашем POH. Возможно, вам придется разделить на 100 или 1000.
| Вес x | ARM = | Моменты | ||||
| EMPE | 2,100 | 78,3 | 164330 49333333333333333333330 гг. | 340 | 85.0 | 28,900 |
| Rear passengers | 350 | 121.0 | 42,350 | |||
| Fuel — main tanks | 450 | 75.0 | 33,750 | |||
| Fuel — aux tanks | 0 | – | 0 | |||
| Baggage area 1 | 80 | 150.0 | 12,000 | |||
| Baggage area 2 | 0 | – | 0 | |||
| Итого | 3 320 | ? | 281 430 |
Если вам нужно вычислить центр тяжести, возьмите общий момент (не индексированный) и разделите на общий вес. Распространенной ошибкой является сложение всех рук, но это не даст полезного числа. Вместо этого вам нужно рассчитать его на основе веса и сил в самолете, которые представлены моментами и весом.
Распространенной ошибкой является сложение всех рук, но это не даст полезного числа. Вместо этого вам нужно рассчитать его на основе веса и сил в самолете, которые представлены моментами и весом.
| Вес x | Arm = | Moments | |
| Empty weight | 2,100 | 78.3 | 164,430 |
| Pilot + Copilot | 340 | 85.0 | 28,900 |
| Rear passengers | 350 | 121.0 | 42 350 |
| Топливо — основные баки | 450 | 75,0 | 33 750 |
| Топливные — 30 9 3909 39 | – | 0 | |
| Baggage area 1 | 80 | 150.0 | 12,000 |
| Baggage area 2 | 0 | – | 0 |
| Total | 3,320 | CG = 84.8 * | 281,430 |
*ЦТ = Моменты/Вес = 281,430/3,320 = 84,8
Помните – Вес и балансировка перед каждым полетом , вам нужно принять меры, чтобы исправить это до отъезда.
 Проблемы с весом обычно решаются уменьшением количества топлива в самолете, в то время как вы можете исправить проблемы с ЦТ, перемещая груз внутри самолета.
Проблемы с весом обычно решаются уменьшением количества топлива в самолете, в то время как вы можете исправить проблемы с ЦТ, перемещая груз внутри самолета.После того, как вы научитесь рассчитывать вес и центровку для обычных тренировочных полетов, попрактикуйтесь в длительном путешествии с пассажирами и сумками. Вы можете быть удивлены, насколько легко перегрузить или опасно загрузить небольшой самолет АОН!
Для дальнейшего чтения вес и балансировка рассматриваются в главе 10 Справочника пилотов по авиационным знаниям FAA.
Калькулятор наклонной плоскости
Вы, наверное, даже не думали, что пандусы — это машины: наш калькулятор наклонной плоскости поможет вам быстро, но всесторонне изучить формулы и уравнения для наклонной плоскости, даже учитывая трение .
Что вы найдете в нашем калькуляторе наклонной плоскости?
- Что такое наклонная плоскость?
- Силы на наклонной плоскости: сила трения и составляющие силы тяжести;
- Как найти ускорение на рампе;
- Физика наклонного самолета: как найти время снижения и конечную скорость;
- Поведение тел, вращающихся по наклонной плоскости.

Что такое наклонная плоскость: физика пандусов
Наклонная плоскость — это именно то, что следует из названия: плоская поверхность , расположенная под определенным углом по отношению к горизонтальной плоскости . Наклонные плоскости или пандусы появляются повсюду: поскольку они дают механическое преимущество , они используются, когда вам нужно поднять или опустить тяжелый предмет (слишком тяжелый, чтобы поднимать его вертикально) или помочь уменьшить усилия при подъеме по лестнице или небольшим препятствиям. .
🙋 Рампы широко распространены не только в пространстве, но и во времени. Большинство археологов сходятся во мнении, что только так древние египтяне могли строить свои колоссальные пирамиды.
Наклонная плоскость характеризуется высотой и длиной , которые вместе определяют угол наклона . Если вам нужна математика, вот уравнение для расчета угла наклона пандуса:
sin(θ)=HL\sin{(\theta)} = \frac{H}{L}sin(θ) =LH
Где:
- HHH высота ;
- LLL — длина ; и
- θ\thetaθ — угол наклонной плоскости .

Уравнения для наклонной плоскости
На наклонной плоскости вес объекта разложим на две составляющие , пропорции которых зависят от угла наклона: вычислим их с помощью следующих характеристических уравнений для наклонная плоскость:
F∥=m⋅g⋅sin(θ)F⊥=m⋅g⋅cos(θ)\begin{align*} F_{\parallel}&=m\cdot g\cdot\sin{(\ theta)}\\ F _ {\ perp} & = m \ cdot g \ cdot \ cos {(\ theta)} \end{align*}F∥F⊥=m⋅g⋅sin(θ)=m⋅g⋅cos(θ)
Где:
- F∥F_{\parallel}F∥ — **компонент гравитационной силы, параллельный поверхности самолета;
- F⊥F_{\perp}F⊥ — составляющая гравитационной силы, перпендикулярная поверхности ;
- ммм это масса кузова ; и
- ггг ускорение свободного падения .
Эти формулы взяты из тригонометрии. Если вы вычислите векторную сумму двух компонентов, вы найдете значение гравитационная сила , действующая на тело.
Если вы добавите к задаче трение , вы немного усложните ситуацию. Если тело движется вниз (по пандусу), сила трения указывает вверх (против направления движения). Запомните формулу трения:
Ff=f⋅m⋅gcos(θ)F_{\text{f}} = f\cdot m\cdot g\cos{(\theta)}Ff=f⋅m⋅ gcos(θ)
Чтобы вычислить силу трения наклонной плоскости, мы должны рассмотреть перпендикулярную составляющую силы тяжести .
При вычислении общей силы , действующей на объект, скользящий вниз по наклонной плоскости, мы вычисляем сумму сил , параллельных поверхности . Перпендикулярные силы не мешают непосредственно движению (но подразумеваются в расчетах силы трения на наклонной плоскости). Суммарная сила:
F=F∥−Ff=m⋅g(sin(θ)−f⋅cos(θ))\begin{align*} F& = F_{\parallel} -F_{\text{f}}\\ &= m\cdot g \left(\sin{(\theta)} — f\cdot\cos{(\theta)}\right) \end{align*} F=F∥−Ff=m⋅g(sin(θ)−f⋅cos(θ))
🙋 Если пандус недостаточно наклонен, сила трения может быть достаточно высокой, чтобы превзойти параллельную составляющую силы тяжести: в этом случае тело не будет двигаться!
Движение по наклонной плоскости: формула для ускорения на наклонной плоскости, время спуска и конечная скорость
Зная результирующую силу, действующую на тело, можно применить второй закон Ньютона для вычисления ускорения на наклонной плоскости . При отсутствии других сил, действующих на тело, ускорение вычисляем как: 92 — + 2\cdot L\cdot a} — v_0\right)}{a}\\
v_t & = v_0+a\cdot t
\end{align*}tvt=a(v02−+2⋅L⋅a
При отсутствии других сил, действующих на тело, ускорение вычисляем как: 92 — + 2\cdot L\cdot a} — v_0\right)}{a}\\
v_t & = v_0+a\cdot t
\end{align*}tvt=a(v02−+2⋅L⋅a
−v0)=v0+a⋅t
Где:
- ttt — время;
- v0v_0v0 — это начальная скорость , а vtv_tvt — конечная скорость в момент времени ttt; и
- ааа ускорение по наклонной плоскости.
Скатывание с наклонной плоскости: физика пандусов и круглых объектов
Уравнения, которые мы видели в предыдущем абзаце, справедливы для скользящих объектов , как куб . Наш калькулятор наклонной плоскости позволяет рассчитать ускорение, время, конечную скорость (и многое другое) для объектов , катящихся по пандусу .
Анализ движения был бы слишком сложен, чтобы делать его таким же образом: мы прибегнем к закону сохранения энергии , чтобы найти ускорение на наклонной плоскости. Формула, учитывающая крутящего момента и вращательной энергии , выглядит так:
Формула, учитывающая крутящего момента и вращательной энергии , выглядит так:
Где:
- III — момент инерции массы ; и
- ррр радиус (расстояние между центром тела качения и поверхностью плоскости).
Вы найдете множество вариантов тел в первой переменной нашего калькулятора наклонной плоскости.
Калькулятор касательной плоскости — поиск уравнения (пошагово)
Онлайн-калькулятор касательной плоскости поможет вам эффективно определить касательную плоскость в заданной точке кривой. Более того, он может точно обрабатывать математические функции с 2 и 3 переменными и обеспечивает пошаговое решение. Возможность быстро вычислить касательную плоскость с помощью этого калькулятора, не выполняя все шаги дифференциального исчисления, значительно экономит время.
Кроме того, вы также получите теоретическую основу и найдете несколько решенных примеров в качестве бонуса.
Что такое касательная плоскость?
Как известно, производная \(\frac{dy}{dx}\) функции \(f(x)\) в определенной точке представляет собой касательную в этой точке. Вы можете рассчитать касательную к поверхности с помощью нашего Калькулятора касательной. Точно так же частная производная \(frac{∂y}{∂x}\) функции \(f(x)\) в конкретной точке представляет касательную плоскость в этой точке. В какой-то момент он будет содержать все касательные линии, которые касаются кривизны рассматриваемой функции в этой точке, как показано на рисунке ниже.
Условие касательной плоскости:Функция, образующая поверхность, должна быть дифференцируемой в точке, чтобы эта плоскость могла там существовать.
Уравнение касательной плоскости: Пусть S — поверхность, определяемая дифференцируемой функцией \(z = f(x,y) \), которая включает 2 переменные, и пусть \(P_o = (x_o, y_o)\) быть точкой в области определения f. Тогда уравнение касательной плоскости к S в точке Po задается следующим образом: $$
Тогда уравнение касательной плоскости к S в точке Po задается следующим образом: $$
Аналогично, общее уравнение касательной плоскости в точке \(P_o=(x_o, y_o, z_o)\) к поверхности S, определяемой математической функцией \(z = f(x,y,z)\), которая включает 3 переменных приведено ниже:
$$z = f(x_o, y_o, z_o) + f_x(x_o, y_o, z_o)(x − x_o) + f_y(x_o, y_o, z_o)(y − y_o) + f_z(x_o) , y_o, z_o)(z − z_o)$$
Вам необходимо выполнить следующие шаги, чтобы найти уравнение касательной плоскости к поверхности, заданной функцией. Этот калькулятор касательной плоскости также дает аналогичное решение за долю времени.
Проверка предварительных требований:Убедитесь, что у вас есть математическая функция поверхности и координаты точки на этой поверхности, где вы хотите вычислить уравнение.
Решение частных дифференциалов: Частичное дифференцирование математической функции рассматриваемой поверхности.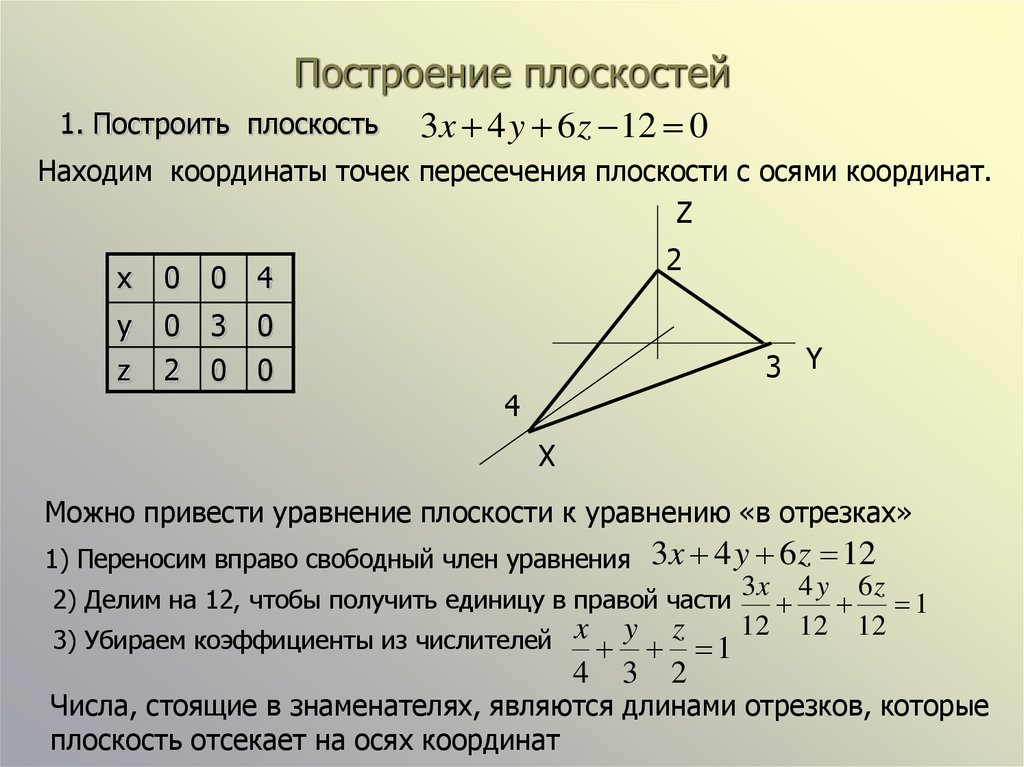 Подробные расчеты можно увидеть из примеров, показанных в следующем разделе.
Подробные расчеты можно увидеть из примеров, показанных в следующем разделе.
Рассчитайте значение частично дифференцированной функции в заданных точках для нахождения уравнения касательной плоскости, как показано в следующих примерах.
Решаемые примеры:Следующие примеры наглядно иллюстрируют, как можно определить желаемое уравнение, используя вышеупомянутые шаги.
Наш калькулятор касательной плоскости также следует той же процедуре, что и в этих примерах, и вы можете получить точно такой же результат за считанные секунды.
Пример-1: 92\) имеем:
$fx(x,y) = 2x$$
$$fy(x,y) = 2y$$
Итак, уравнение касательной плоскости в точке \((1, 2,5)\):
$$2(1)(x−1)+2(2)(y−2)−z+5 = 0$$
$$= 2x+4y−z−5=0 $$
Пример-2:
Найти уравнение касательной плоскости к поверхности, заданной функцией \(f(x,y)=sin(2x)cos(3y)\) в точке \( (π/3,π/4)\).
Решение:
Сначала вычислим \(fx(x,y)\) и \(fy(x,y)\), затем вычислим требуемое уравнение касательной плоскости, используя общее уравнение \ (z=f(x_o,y_o)+fx(x_o,y_o)(x-x_o)+fy(x_o,y_o)(y-y_o)\) с \(xo = \frac{π}{3}\) и \(yo = \frac{π}{4}\):
$$f_x(x,y) = 2cos(2x)cos(3y)$$
$$f_y(x,y) = −3sin(2x)sin(3y)$$
$$f(\frac{π {3}, \ frac {π} {4}) = sin (2 (\ frac {π} {3})) cos (3 (\ frac {π} {4})) = (\ frac {\ sqrt {3}}{2})(\frac{-\sqrt{2}}{2}) = \frac{-\sqrt{6}}{2}$$
$$f_x(\frac{π}{ 3},\frac{π}{4}) = 2cos(2(\frac{π}{3}))cos(3(\frac{π}{4})) = 2(\frac{-1} {2})( \frac{-√2}{2}) = \frac{\sqrt{2}}{2}$$
$$f_y(\frac{π}{3},\frac{π} {4}) = 2\sqrt{2} — 3sin(2(\frac{π}{3}))sin(3(\frac{π}{4})) = -3(3\sqrt{2} )(2\sqrt{2}) = −36\sqrt{4}$$
Теперь подставим эти значения в общее уравнение: 92$$
Тогда наша поверхность является поверхностью уровня \(w = 36\). Следовательно, нормаль к поверхности равна:
$$∇w = (2x, 4y, 6z)$$
В точке P имеем \(∇w|P = (2, 8, 18)\). Используя точечную нормальную форму, уравнение касательной плоскости имеет вид:
Используя точечную нормальную форму, уравнение касательной плоскости имеет вид:
$$2(x − 1) + 8(y − 2) + 18(z − 3) = 0, \text { или эквивалентно} 2x + 8y + 18z = 72$$
С помощью этого онлайн-калькулятора можно эффективно и быстро рассчитать уравнение касательной плоскости, выполнив следующие шаги:
Вы можете переключаться между расчетом с 2 переменными и расчетом с 3 переменными, нажимая соответствующие вкладки в верхней части полей ввода.
Ввод:- Сначала введите нужную математическую функцию в поле ввода под названием «Введите функцию».
- Затем просто введите координаты в зависимости от количества переменных в функции.
Калькулятор определяет уравнение касательной плоскости, касающейся поверхности (образованной заданной математической функцией) в координатных точках. Он также предоставляет пошаговое решение, предполагающее дифференциацию всех соответствующих деталей.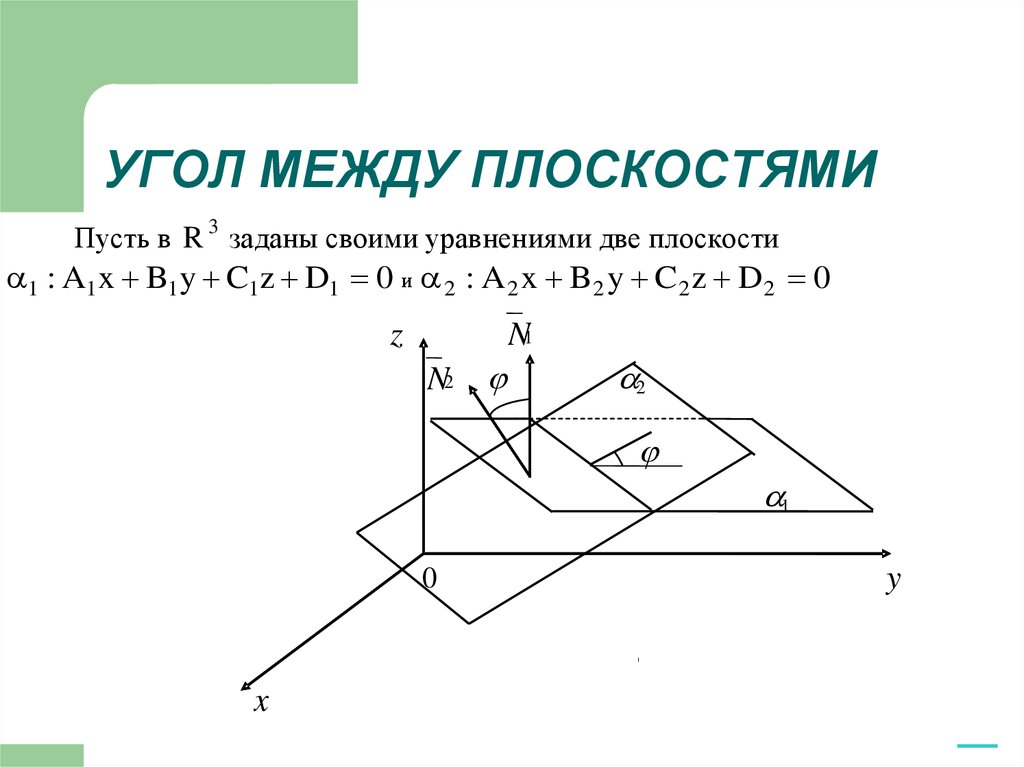
Частичное дифференцирование в основном используется для определения уравнения, управляющего плоскостью. Этот калькулятор касательной плоскости основан на той же математической концепции и дает точные результаты за считанные секунды.
Касательная плоскость лежит в двумерном или трехмерном пространстве?Касательные линии лежат в двумерном пространстве, но касательные плоскости представляют собой комбинацию всех касательных линий, касающихся поверхности в определенной точке, следовательно, они лежат в трехмерном пространстве.
В чем разница между касательным вектором и касательной плоскостью? Касательный вектор — это отдельная линия, которая едва касается поверхности (определяемой математической функцией) в точке, тогда как касательная плоскость представляет собой комбинацию всех касательных векторов, касающихся поверхности в определенной точке.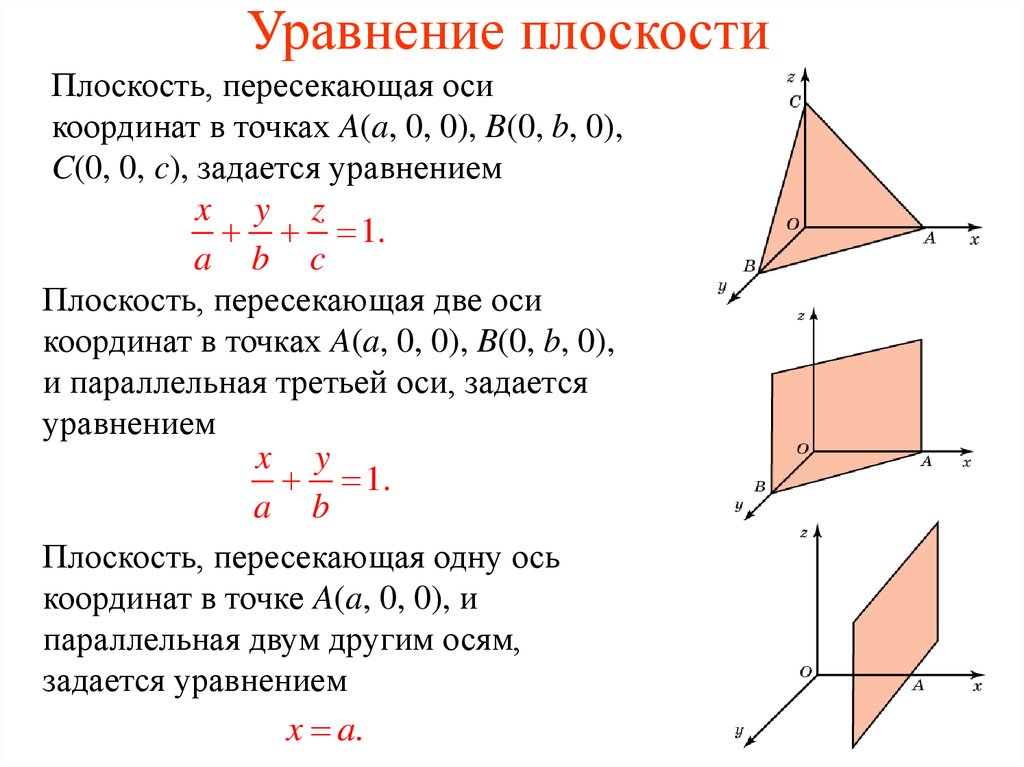



 (2015 МДС)
(2015 МДС) 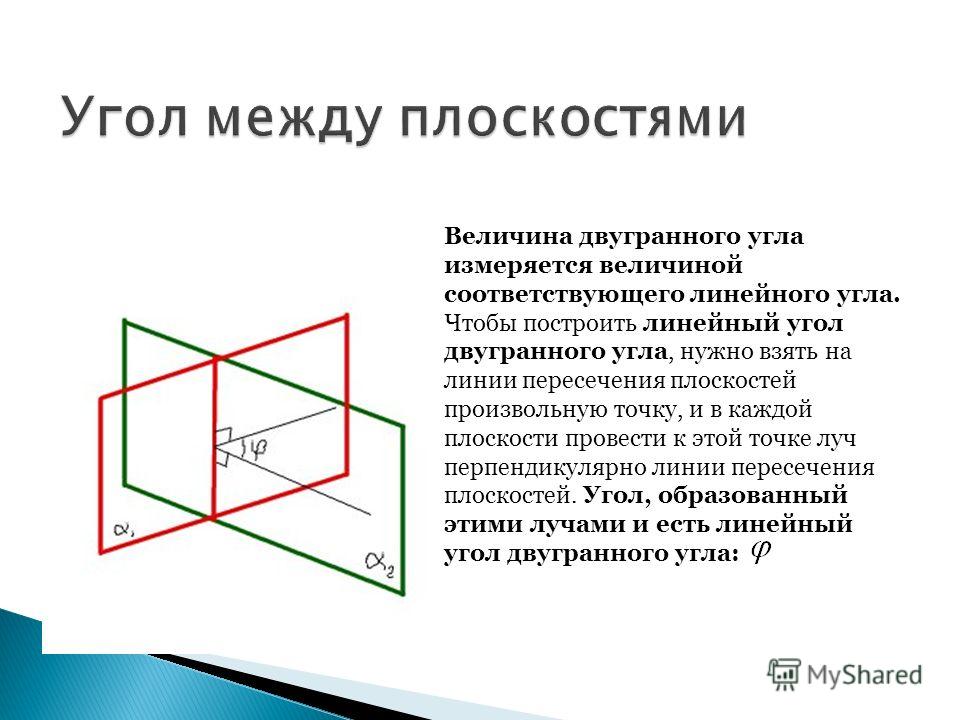

 5 * скорость плоскости
5 * скорость плоскости