Умножение матриц Excel — voxt.ru
Что такое умножение матриц в Excel?
В excel у нас есть встроенная функция для умножения матриц, и это функция MMULT, она принимает два массива в качестве аргумента и возвращает произведение двух массивов, учитывая, что оба массива должны иметь одинаковое количество строк и одинаковое количество столбцов.
Объяснение
Умножение матриц — одна из полезных функций Excel, предназначенных для выполнения математических операций. Это помогает получить произведение двух матриц. Матрицы, которые нужно умножить, имеют определенное количество строк и столбцов для представления данных. Размер полученной матрицы берется из количества строк первого массива и количества столбцов второго массива. Есть условие умножения матриц; количество столбцов в первой матрице должно быть равно количеству строк во второй матрице.
Для выполнения матричного умножения используется предопределенная функция MMULT, представленная в программном обеспечении Excel. Умножение матриц в Excel сокращает время, затрачиваемое на вычисление произведения матриц вручную.
Умножение матриц в Excel сокращает время, затрачиваемое на вычисление произведения матриц вручную.
В общем, умножение матриц выполняется двумя способами. Простое скалярное умножение выполняется с использованием основных арифметических операций, а расширенное умножение матриц управляется с помощью функции массива в Excel.
Формула Excel, используемая для умножения, вводится двумя способами, включая ручной ввод функции MMULT после знака равенства или выбор библиотеки функций Math and Trig, представленной на вкладке «Формулы». Математическая функция MMULT помогает вернуть результат умножения двух массивов. Это одна из предопределенных функций Excel, используемых в рабочих таблицах для выполнения расчетов за короткое время.
Синтаксис
Требуемый синтаксис, которому следует следовать при умножении матриц, таков:
- Параметры: Array1 и Array2 — два параметра, необходимые для умножения.
- Правило: Столбцы массива array1 должны быть равны строкам array2, а размер продукта равен количеству строк в array1 и количеству столбцов в array2.

- Возврат: Функция MMULT генерирует числа в матрице продукта. Он вводится как формула или функция рабочего листа в вычислениях Excel.
Рассматривать,
Тогда произведение A * B выглядит следующим образом.
Как сделать умножение матриц в Excel? (с примерами)
Умножение матриц в Excel имеет некоторое приложение в реальном времени. Есть два способа выполнить матричное умножение. Ниже приведены несколько примеров умножения матриц Excel.
Вы можете скачать этот шаблон Excel для умножения матриц здесь — Шаблон для умножения матриц в Excel
Пример №1 — Умножение матрицы на скалярное число.
- Шаг 1: В первую очередь необходимо ввести данные в массив.
- Шаг 2: Выберите скалярное значение, которое мы собираемся умножить на массив, т.е. 3
- Шаг 3: Оцените строки и столбцы результирующего массива.
 Здесь результирующий массив будет размером 3 x 3.
Здесь результирующий массив будет размером 3 x 3. - Шаг 4: Выберите диапазон ячеек, равный размеру результирующего массива, чтобы разместить результат, и введите обычную формулу умножения.
- Шаг 5: После ввода формулы нажмите Ctrl + Shift + Enter. И результат будет, как показано на нижеприведенном рисунке.
Пример # 2 — Матричное умножение двух отдельных массивов
- Шаг 1: В первую очередь необходимо ввести данные в массив А размером 3 × 3.
- Шаг 2: Введите данные во второй массив под названием B размером 3 × 3.
- Шаг 3: Нам нужно убедиться, что столбцы первого массива имеют такой же размер, как и строки второго массива.
- Шаг 4: Оцените строки и столбцы результирующего массива.
- Шаг 5: Выберите диапазон ячеек, равный размеру результирующего массива, чтобы разместить результат, и введите формулу умножения MMULT.

Введите значения, чтобы вычислить произведение A и B.
После ввода формулы нажмите Ctrl + Shift + Enter чтобы получить результат. Результаты получаются путем умножения двух массивов следующим образом, а размер результирующего массива составляет 3×3.
Пример # 3
Умножение матриц между массивами с одной строкой и одним столбцом. Рассмотрим элементы матриц как
Матрица A имеет размер 1 × 3, а матрица B — 3 × 1. Размер изделия А * Б [AB] матрица 1 × 1. Итак, введите в ячейку формулу умножения матриц.
Нажмите Enter, чтобы получить результат.
Пример # 4 — Умножение матриц между массивами с одним столбцом и одной строкой
Матрица A имеет размер 3 × 1, а матрица B — 1 × 3. Размер изделия А * Б [AB] матрица 3 × 3.
Итак, ответ будет такой:
Пример # 5 — Определение квадрата матрицы с помощью MMULT в Excel
Квадрат матрицы A определяется умножением A на A.
Результирующая матрица получается как
То, что нужно запомнить
- Чтобы выполнить матричное умножение, количество столбцов, представленных в массиве 1, и количество строк, представленных в массиве 2, равны.
- Изменить часть массива сложно, так как массив представляет собой группу элементов.
- При выполнении умножения массива следует использовать CTRL + SHIFT + ENTER для создания всех элементов результирующей матрицы. В противном случае производится только один элемент.
- Элементы массива не должны быть нулевыми, а текст не должен использоваться в матрицах, чтобы избежать ошибок.
- Размер массива товаров равен строкам первого массива и столбцам второго массива.
- Умножение A * B не равно умножению B * A в матричном умножении.
- Умножение матрицы на единичную матрицу приводит к той же матрице (т.е. [A]*[Unit matrix]знак равно[A])
УЗНАТЬ БОЛЬШЕ >>
Post Views: 529
Похожие записи
Прокрутить вверхТри способа умножения матриц в Excel
Дата публикации Jul 2, 2019
Часть-2 изФастай «Из фондов»наконец-то вышел. Я не помню, когда в последний раз я был так взволнован по поводу MOOC. Как только курс был обнародован, я начал копаться в нем, чтобы углубить свое понимание глубокого обучения и основополагающих концепций.
Я не помню, когда в последний раз я был так взволнован по поводу MOOC. Как только курс был обнародован, я начал копаться в нем, чтобы углубить свое понимание глубокого обучения и основополагающих концепций.
На этот раз я решил последовать совету Джереми и Рэйчел и написать блоги. Эта конкретная статья объясняетразличные методы умножения матриц,что Джереми реализует в Уроке-8. Я буду использоватьМайкрософт Эксельдля иллюстрации.
Итак, начнем!
Умножение матриц
Отличное и интерактивное место для понимания умножения матриц, на которое ссылается Джереми, доступно по адресу:
matrixmultiplication.xyzПо сути, как видно из изображения, мы берем транспонирование второй матрицы, умножаем и складываем элементы вместе, чтобы получить результат. Как пример, самый первый пункт15в результирующей матрице происходит от1*2 + 6*2 + 1*1 = 2 + 12 + 1 = 15,
Хотя это объяснение визуально приятно, по моему скромному мнению, его трудно преобразовать в код. Так что давайте использовать Excel и понимать матричное умножение по-другому!
Так что давайте использовать Excel и понимать матричное умножение по-другому!
Умножение матриц в EXCEL
Рассмотрим две матрицыа такжеВразмера4x3а также3x4,
Примечание: я буду использовать жирный шрифта такжеВсослаться на матрицы в этой статье. Обычная практика — ссылаться на векторы и матрицы, используя жирный шрифт.
Из изображения, которое мы видели раньше, если вы помните, мы взяли транспонированиеВи умноженные строкис колоннамиВчтобы получить результирующую матрицу. Скорее, давайте пропустим этот шаг, сделав транспонирование на этот раз, и сразу умножим строки и столбцы.
Поэтому строка 0 изумножается на столбец 0Впоэлементные и результирующие поэлементные продукты добавляются для получения первого элемента в результирующей матрицеСв положении[0][0],
Вот как это выглядит в Excel:
C [0] [0] = 1 * 1 + 10 * 5 + 100 * 9 = 1 + 50 + 900 = 951Точно так же мы получаемC[0][3]поэлементно умножая строку 0 изи кол 3 изB. В Excel это выглядит так:
В Excel это выглядит так:
И, наконец, мы следуем тому же процессу, чтобы пройти каждый пустой ящик вСчтобы получить окончательный результат.
C [3] [3] = 4 * 4 + 40 * 8 + 400 * 12 = 16 + 320 + 4800 = 5136Вот и мы! Вот так мы делаем матричное умножение! Это было легко, не так ли? Мы теперь не только поняли умножение матриц, но и внедрили его в Excel! Как это круто?
Я лично считаю, что теперь вы готовы работать с некоторыми правилами, связанными с умножением матрицMatMul):
- Позволять
ar,acбыть количеством строк и столбцов вA.Точно так же, пустьbr, bcбыть количеством строк и столбцов вB.Тогда для выполнения умножения матриц необходимо, чтобыac == br, Зачем? Итак, как вы видели в Excel, мы умножили строки и столбцы поэлементно, а затем добавили промежуточные продукты, чтобы получить конечный результат. Если есть несоответствие в размерах, и один вектор длиннее другого, мы больше не можем выполнять поэлементное умножение!
Если есть несоответствие в размерах, и один вектор длиннее другого, мы больше не можем выполнять поэлементное умножение! - Размеры результирующей матрицы всегда будут
ar,bc, То есть количество строк исходит оти количество столбцов исходит отB.
Способ 1: использование 3-х циклов FOR
Вот еще один отказ от ответственности, при реализации умножения матриц в Excel, мы не только поняли это, но и повторили первый метод Джереми, который использовал 3 цикла FOR. Вот как это выглядит в коде:
def matmul1(a,b):
ar,ac = a.shape
br,bc = b.shape
assert ac==br
c = torch.zeros(ar, bc)
for i in range(ar):
for j in range(bc):
for k in range(ac): #or br
c[i,j] += a[i,k]*b[k,j]
return c
Надеюсь, теперь вы сможете лучше понять это. Если нет, то сейчас самое время сделать паузу, поэкспериментировать с кодом и посмотреть, что на самом деле происходит. Я обещаю вам, это так же, как наша версия Excel!
Хорошо, я предполагаю, что вы потратили некоторое время на размышления о коде, поэтому давайте обсудим это!
- Почему первые две петли в
range(ar)а такжеrange(bc)? Ну, как вы помните изПравило-2наша результирующая матрица будет иметь размерыar,bc, И из Excel мы увидели, что мы пересекаем каждый элементСследовательно, один за другим, чтобы пройтиarстроки иbcстолбцы нам нужно 2 цикла вrange(ar)а такжеrange(bc), - Итак, почему третий цикл FOR в
range(ac) #or br? Ну изПравило-1, мы знаем этоac==brтак что на самом деле не имеет значения, ставим ли мыrange(ac)илиrange(br)в третьем цикле. По сути, именно здесь отдельные элементы умножаются вместе и добавляются. Из нашего предыдущего примера Excel, для
По сути, именно здесь отдельные элементы умножаются вместе и добавляются. Из нашего предыдущего примера Excel, дляC[0][0]это где шагC[0][0] = 1*1 + 10*5 + 100*9 = 1 + 50 + 900 = 951произойдет, и, наконец, мы перейдем к следующей коробке. Количество предметов, которые умножаются и складываются вместе, равноac or br,
Это действительно так! Это метод-1 для вас! Вот песня, чтобы помнить Матричное Умножение. (Я узнал об этом первым из fast.ai, оригинальный автор неизвестен)
Надеюсь, теперь вы понимаете, как две матрицы умножаются друг на друга. Если не,Вотэто еще один учебник Хан Академии
Метод 2: Использование поэлементного умножения
Так что до сих пор мы разбираем каждую позицию в результирующей матрицеC,найти отдельные элементы, а затем суммировать их вместе. Если вы помните, что-то вродеC[0][0] = 1*1 + 10*5 + 100*9 = 1 + 50 + 900 = 951, Конечно, должен быть другой путь? Что если вместо того, чтобы делать отдельные продукты, а затем суммировать их, мы умножаем векторы за один раз, чтобы получить результирующий вектор, и суммируем полученный вектор, чтобы получить конечный элемент?
m = tensor([1, 2, 3])
n = tensor([10, 10, 10])
m*n>>tensor([10, 20, 30])
До сих пор мы находили отдельные продукты10, 20, 30и сложить их вместе10 + 20 + 30 = 60, Но, действительно, все это можно заменить на:
m = tensor([1, 2, 3])
n = tensor([10, 10, 10])
(m*n).sum()>>tensor(60)
Если вы помните, самый внутренний цикл вrange(ac) #or brнаходил отдельные продукты и добавлял их. Ну, мы можем заменить этот цикл, чтобы выполнить векторное поэлементное произведение и положить.sum()в конце концов, и PyTorch / NumPy имеют возможность выполнять поэлементные операции для нас!
Вот как это выглядит в Excel:
C [0] [0] = сумма (A [строка 0] * B [столбец 0])Точно так же мы получаемC[0][3]путем умножения вектора в строке 0с вектором на цв 3Ви суммируя полученный вектор.
И, наконец, мы следуем тому же процессу, чтобы пройти каждый пустой ящик вСчтобы получить окончательный результат.
C [3] [3] = сумма (A [строка 3] * B [столбец 3])Обратите внимание, как это отличается отМетод-1? На этот раз мы просто говорим Excel или PyTorch: умножьте строку 0с col 0 изВи суммируем полученный вектор, чтобы дать нам ответ. Вместо того чтобы делать
Вместо того чтобы делать1*1 + 10*5 + 100*9, Например, дляC[0][0]этот метод умножает Vector на строку 0tensor([1,10,100])с вектором в столбце 0 изВtensor{[1,5,9])чтобы получить промежуточный продукт Векторtensor([1,50,900])и суммирует это, чтобы дать результат в положенииC[0][0]какtensor(951),
В коде это выглядит так:
def matmul2(a,b):
ar,ac = a.shape
br,bc = b.shape
assert ac==br
c = torch.zeros(ar,bc)
for i in range(ar):
for j in range(bc):
c[i,j] = (a[i,:]*b[:,j]).sum()
return c
Таким образом, мы просто анализируем каждую позициюC,используя две петли FOR и введите соответствующий результат в этой позиции. Еслиi,jпредставляют строки и столбцы вСэто выглядит примерно так …
i:0,j:0
a:tensor([ 1, 10, 100]),b:tensor([1, 5, 9])
tensor([[951., 0., 0., 0.],
[ 0., 0., 0., 0.],
[ 0., 0., 0., 0.],
[ 0., 0., 0., 0.]])
---
i:0,j:1
a:tensor([ 1, 10, 100]),b:tensor([ 2, 6, 10])
tensor([[ 951., 1062., 0., 0.],
[ 0., 0., 0., 0.],
[ 0., 0., 0., 0.],
[ 0., 0., 0., 0.]])
---
i:0,j:2
a:tensor([ 1, 10, 100]),b:tensor([ 3, 7, 11])
tensor([[ 951., 1062., 1173., 0.],
[ 0., 0., 0., 0.],
[ 0., 0., 0., 0.],
[ 0., 0., 0., 0.]])
---
i:0,j:3
a:tensor([ 1, 10, 100]),b:tensor([ 4, 8, 12])
tensor([[ 951., 1062., 1173., 1284.],
[ 0., 0., 0., 0.],
[ 0., 0., 0., 0.],
[ 0., 0., 0., 0.]])
---
i:1,j:0
a:tensor([ 2, 20, 200]),b:tensor([1, 5, 9])
tensor([[ 951., 1062., 1173., 1284.],
[1902., 0., 0., 0.],
[ 0., 0., 0., 0.],
[ 0., 0., 0., 0.]])
И так далее .. пока мы не получим полную матрицуС,
tensor([[ 951., 1062., 1173., 1284.],
[1902., 2124., 2346., 2568.],
[2853., 3186., 3519., 3852.],
[3804., 4248., 4692., 5136.]])
Метод 3: вещание
Заметили общую тему здесь? Каждый раз мы должны умножить каждый рядс каждым столбцомВполучитьС, Вы замечаете повторение? Мы умножаем один и тот же вектор строки вbcраз! И мы повторяем этот процессarраз!
Есть ли способ умножить вектор строкисо всеми столбцамиВполучить соответствующий ряд вC?Да, есть! Войдите в трансляцию …
Примечание: я не буду объяснять вещание, Джереми делает это очень хорошоВот,
Вместо этого давайте посмотрим, что это за волшебный кусок кода
for i in range(ar):
c[i] = (a[i,:].unsqueeze(-1).expand_as(b)*b).sum(dim=0)
Как обычно, давайте повторим в Excel! Это сделает вещи действительно легкими. Давайте сделаем это поэтапно.
Шаг 1)Выберите i-й рядa[i,:], Мы выбираем строку 0 в качестве примера.
Шаг 2)Возьмите егоТранспонированиеa[i,:].unsqueeze(-1)
Шаг 3)Развернуть матрицу столбца какВa[i,:].unsqueeze(-1).expand_as(b)
Шаг-4)Элемент мудрый умножить наВa[i,:].unsqueeze(-1).expand_as(b)*b
Шаг-5)Суммируйте по строкам, чтобы получить строку 0 C
Суммируйте по измерению боковой строки, чтобы получить строку 0 CПолный процесс вещания для каждого рядавыглядит примерно так:
Вещание в целомЯ надеюсь, что теперь вы получитевещания!Итак, давайте посмотрим, как это выглядит в коде ..
def matmul3(a,b):
ar,ac = a.shape
br,bc = b.shape
assert ac==br
c = torch.zeros(ar,bc)
for i in range(ar):
c[i] = (a[i,:].unsqueeze(-1).expand_as(b)*b).sum(dim=0)
print(f"i:{i}")
print(c)
return c
Вывод выглядит так:
i:0
tensor([[ 951., 1062., 1173., 1284.],
[ 0., 0., 0., 0.],
[ 0., 0., 0., 0.],
[ 0., 0., 0., 0.]])
i:1
tensor([[ 951., 1062., 1173., 1284.],
[1902., 2124., 2346., 2568.],
[ 0., 0., 0., 0.],
[ 0., 0., 0., 0.]])
i:2
tensor([[ 951., 1062., 1173., 1284.],
[1902., 2124., 2346., 2568.],
[2853., 3186., 3519., 3852.],
[ 0., 0., 0., 0.]])
i:3
tensor([[ 951., 1062., 1173., 1284.],
[1902., 2124., 2346., 2568.],
[2853., 3186., 3519., 3852.],
[3804., 4248., 4692., 5136.]])
Это именно то, как мы ожидаем, что это будет так же, как нашиВерсия Excel!
Вот и все! Мы успешно рассмотрели три метода умножения матриц, включая вещание.
Google лист для вышеупомянутой иллюстрации можно найтиВот, Спасибо за чтение! Если у вас есть какие-либо вопросы, пожалуйста, не стесняйтесь обращаться ко мне по адресуhttps://linkedin. com/in/aroraaman/,
com/in/aroraaman/,
Оригинальная статья
Как перемножать матрицы в эксель : Радиосхема.ру
В этой статье рассмотрены операции умножения матриц с помощью функции МУМНОЖ() или англ.MMULT и с помощью других формул, а также свойства ассоциативности и дистрибутивности операции умножения матриц. Примеры решены в MS EXCEL.
Операция умножения двух матриц А и В определена только для случаев, когда число столбцов матрицы А равно числу строк матрицы В.
Произведение матрицы А порядка P x N и матрицы В порядка N x Q — это такая матрица С порядка P x Q, у которой каждый элемент равен сумме произведений элементов i-ой строки матрицы А на соответствующие элементы j-ого столбца матрицы В , то есть:
Для умножения матриц в MS EXCEL существует специальная функция МУМНОЖ() , которую нужно вводить как формулу массива .
Рассмотрим сначала умножение квадратных матриц 2 х 2.
Разместим матрицы в диапазонах А8:В9 и D8:E9 (см. файл примера ).
файл примера ).
Результат, также матрицу 2 х 2, будем вводить в диапазон H8:I9 .
- выделите указанный диапазон H8:I9
- поставьте курсор в Строку формул (или нажмите клавишу F2 )
- введите формулу =МУМНОЖ(A8:B9;D8:E9)
- нажмите CTRL+SHIFT+ENTER
Выделенный диапазон заполнится элементами матрицы. В принципе можно выделить заведомо б о льший диапазон, в этом случае лишние ячейки будут заполнены ошибкой #Н/Д.
Удалить отдельный элемент матрицы А*В не удастся — только все элементы сразу (выделите весь диапазон и нажмите клавишу DEL ).
Чтобы изменить значения аргументов функции (например, поменять матрицы местами), выделите любую ячейку матрицы, нажмите F2 , исправьте формулу и нажмите CTRL+SHIFT+ENTER .
Альтернативной формулой для перемножения матриц является формула массива =СУММПРОИЗВ($A8:$B8;ТРАНСП(D$8:D$9)) . Введите формулу в верхнюю левую ячейку диапазона и нажмите CTRL+SHIFT+ENTER . Затем скопируйте ее вниз и вправо на нужное количество ячеек.
Введите формулу в верхнюю левую ячейку диапазона и нажмите CTRL+SHIFT+ENTER . Затем скопируйте ее вниз и вправо на нужное количество ячеек.
Если попытаться перемножить матрицы неподходящей размерности (когда число столбцов матрицы А НЕ равно числу строк матрицы В), то функция МУМНОЖ() вернет ошибку #ЗНАЧ!
В файле примера также продемонстрированы свойства ассоциативности и дистрибутивности операции умножения матриц.
Функция МУМУЛЬ возвращает матричное произведение двух массивов. Результатом является массив с таким же числом строк, что и массив1, и с таким же числом столбцов, что и массив2.
Примечание: Если у вас есть текущая версия Microsoft 365,вы можете просто ввести формулу в левую верхнюю ячейку диапазона вывода и нажать ввод, чтобы подтвердить формулу как формулу динамического массива. Иначе формулу необходимо вводить с использованием прежней версии массива, выбрав диапазон вывода, введя формулу в левой верхней ячейке диапазона и нажав клавиши CTRL+SHIFT+ВВОД для подтверждения. Excel автоматически вставляет фигурные скобки в начале и конце формулы. Дополнительные сведения о формулах массива см. в статье Использование формул массива: рекомендации и примеры.
Excel автоматически вставляет фигурные скобки в начале и конце формулы. Дополнительные сведения о формулах массива см. в статье Использование формул массива: рекомендации и примеры.
Синтаксис
Аргументы функции МУМНОЖ описаны ниже.
массив1, массив2 Обязательный. Перемножаемые массивы.
Замечания
Число столбцов в массиве1 должно быть таким же, как и число строк в массиве 2, и оба массива должны содержать только числа.
Массив1 и массив2 могут быть заданы как диапазоны ячеок, константы массива или ссылки.
Функция МУМНОЖ возвращает значение ошибки #ЗНАЧ! в следующих случаях, указанных ниже.
Если какая-либо ячейка пуста или содержит текст.
Число столбцов в массиве1 отличается от числа строк в массиве «массив2».
Массив a, который является произведением двух массивов b и c, определяется следующим образом:
где i — номер строки, а j — номер столбца.
Примеры
Чтобы указанные выше формулы вычислялись правильно, нужно вводить их в виде формул массивов. После ввода формулы нажмите ввод, если у вас есть текущая Microsoft 365 подписка; в противном случае нажмите CTRL+SHIFT+ВВОД. Если формула не будет введена как формула массива, возвращается единственный результат.
После ввода формулы нажмите ввод, если у вас есть текущая Microsoft 365 подписка; в противном случае нажмите CTRL+SHIFT+ВВОД. Если формула не будет введена как формула массива, возвращается единственный результат.
Дополнительные сведения
Вы всегда можете задать вопрос специалисту Excel Tech Community, попросить помощи в сообществе Answers community, а также предложить новую функцию или улучшение на веб-сайте Excel User Voice.Программа Microsoft Office Excel позволяет выполнять операции с матрицами с помощью встроенных функций и формул. Рассмотрим основные операции над матрицами:
- умножение и деление матрицы на число;
- сложение, вычитание и умножение матриц;
- транспонирование матрицы;
- нахождение обратной матрицы;
- вычисление определителя.
Введем условные обозначения. Матрица А размерностью i x j — это прямоугольная таблица чисел, состоящая из i строк и j столбцов, аij — элемент матрицы.
Умножение и деление матрицы на число в Excel
Способ 1
Рассмотрим матрицу А размерностью 3х4. Умножим эту матрицу на число k. При умножении матрицы на число получается матрица такой же размерности, что и исходная, при этом каждый элемент матрицы А умножается на число k.
Введем элементы матрицы в диапазон В3:Е5, а число k — в ячейку Н4. В диапазоне К3:N5 вычислим матрицу В, полученную при умножении матрицы А на число k: В=А*k. Для этого введем формулу =B3*$H$4 в ячейку K3, где В3 — элемент а11 матрицы А.
Примечание: адрес ячейки H4 вводим как абсолютную ссылку, чтобы при копировании формулы ссылка не менялась.
С помощью маркера автозаполнения копируем формулу ячейки К3 вниз и вправо на весь диапазон матрицы В.
Таким образом, мы умножили матрицу А в Excel и получим матрицу В.
Для деления матрицы А на число k в ячейку K3 введем формулу =B3/$H$4 и скопируем её на весь диапазон матрицы В.
Способ 2
Этот способ отличается тем, что результат умножения/деления матрицы на число сам является массивом. В этом случае нельзя удалить элемент массива.
Для деления матрицы на число этим способом выделяем диапазон, в котором будет вычислен результат, вводим знак «=», выделяем диапазон, содержащий исходную матрицу А, нажимаем на клавиатуре знак умножить (*) и выделяем ячейку с числом k. После ввода формулы нажимаем сочетание клавиш Ctrl+Shift+Enter, чтобы значениями заполнился весь диапазон.
Для выполнения деления в данном примере в диапазон вводим формулу =B3:E5/h5, т.е. знак «*» меняем на «/».
Сложение и вычитание матриц в Excel
Способ 1
Следует отметить, что складывать и вычитать можно матрицы одинаковой размерности (одинаковое количество строк и столбцов у каждой из матриц). Причем каждый элемент результирующей матрицы С будет равен сумме соответствующих элементов матриц А и В, т.е. сij = аij + bij.
Рассмотрим матрицы А и В размерностью 3х4. Вычислим сумму этих матриц. Для этого в ячейку N3 введем формулу =B3+h4, где B3 и h4 – первые элементы матриц А и В соответственно. При этом формула содержит относительные ссылки (В3 и H3), чтобы при копировании формулы на весь диапазон матрицы С они могли измениться.
С помощью маркера автозаполнения скопируем формулу из ячейки N3 вниз и вправо на весь диапазон матрицы С.
Для вычитания матрицы В из матрицы А (С=А — В) в ячейку N3 введем формулу =B3 — h4 и скопируем её на весь диапазон матрицы С.
Способ 2
Этот способ отличается тем, что результат сложения/вычитания матриц сам является массивом. В этом случае нельзя удалить элемент массива.
Для деления матрицы на число этим способом выделяем диапазон, в котором будет вычислен результат, вводим знак «=», выделяем диапазон, содержащий первую матрицу А, нажимаем на клавиатуре знак сложения (+) и выделяем вторую матрицу В. После ввода формулы нажимаем сочетание клавиш Ctrl+Shift+Enter, чтобы значениями заполнился весь диапазон.
Умножение матриц в Excel
Следует отметить, что умножать матрицы можно только в том случае, если количество столбцов первой матрицы А равно количеству строк второй матрицы В.
Рассмотрим матрицы А размерностью 3х4 и В размерностью 4х2. При умножении этих матриц получится матрица С размерностью 3х2.
Вычислим произведение этих матриц С=А*В с помощью встроенной функции =МУМНОЖ(). Для этого выделим диапазон L3:M5 — в нём будут располагаться элементы матрицы С, полученной в результате умножения. На вкладке Формулы выберем Вставить функцию.
В диалоговом окне Вставка функции выберем Категория Математические — функция МУМНОЖ — ОК.
В диалоговом окне Аргументы функции выберем диапазоны, содержащие матрицы А и В. Для этого напротив массива1 щёлкнем по красной стрелке.
Выделим диапазон, содержащий элементы матрицы А (имя диапазона появится в строке аргументов), и щелкнем по красной стрелке.
Для массива2 выполним те же действия. Щёлкнем по стрелке напротив массива2.
Выделим диапазон, содержащий элементы матрицы В, и щелкнем по красной стрелке.
В диалоговом окне рядом со строками ввода диапазонов матриц появятся элементы матриц, а внизу — элементы матрицы С. После ввода значений нажимаем на клавиатуре сочетание клавиш Shift+Ctrl и щелкаем левой кнопкой мыши по кнопке ОК.
ВАЖНО. Если просто нажать ОК, то программа вычислит значение только первой ячейки диапазона матрицы С.
Мы получим результат умножения матриц А и В.
Мы можем изменить значения ячеек матриц А и В, значения матрицы С поменяются автоматически.
Транспонирование матрицы в Excel
Транспонирование матрицы — операция над матрицей, при которой столбцы заменяются строками с соответствующими номерами. Обозначим транспонированную матрицу А Т .
Пусть дана матрица А размерностью 3х4, с помощью функции =ТРАНСП() вычислим транспонированную матрицу А Т , причем размерность этой матрицы будет 4х3.
Выделим диапазон Н3:J6, в который будут введены значения транспонированной матрицы.
На вкладке Формулы выберем Вставить функцию, выберем категорию Ссылки и массивы — функция ТРАНСП — ОК.
В диалоговом окне Аргументы функции указываем диапазон массива В3:Е5, содержащего элементы матрицы А. Нажимаем на клавиатуре сочетание клавиш Shift+Ctrl и щелкаем левой кнопкой мыши по кнопке ОК.
ВАЖНО. Если просто нажать ОК, то программа вычислит значение только первой ячейки диапазона матрицы А Т .
Нажмите для увеличения
Мы получили транспонированную матрицу.
Нахождение обратной матрицы в Excel
Матрица А -1 называется обратной для матрицы А, если А?А -1 =А -1 ?А=Е, где Е — единичная матрица. Следует отметить, что обратную матрицу можно найти только для квадратной матрицы (одинаковое количество строк и столбцов).
Пусть дана матрица А размерностью 3х3, найдем для неё обратную матрицу с помощью функции =МОБР().
Для этого выделим диапазон G3:I5, который будет содержать элементы обратной матрицы, на вкладке Формулы выберем Вставить функцию.
В диалоговом окне Вставка функции выберем категорию Математические — функция МОБР — ОК.
В диалоговом окне Аргументы функции указываем диапазон массива В3:D5, содержащего элементы матрицы А. Нажимаем на клавиатуре сочетание клавиш Shift+Ctrl и щелкаем левой кнопкой мыши по кнопке ОК.
ВАЖНО. Если просто нажать ОК, то программа вычислит значение только первой ячейки диапазона матрицы А -1 .
Нажмите для увеличения
Мы получили обратную матрицу.
Нахождение определителя матрицы в Excel
Определитель матрицы — это число, которое является важной характеристикой квадратной матрицы.
Как найти определить матрицы в Excel
Пусть дана матрица А размерностью 3х3, вычислим для неё определитель с помощью функции =МОПРЕД().
Для этого выделим ячейку Н4, в ней будет вычислен определитель матрицы, на вкладке Формулы выберем Вставить функцию.
В диалоговом окне Вставка функции выберем категорию Математические — функция МОПРЕД — ОК.
В диалоговом окне Аргументы функции указываем диапазон массива В3:D5, содержащего элементы матрицы А. Нажимаем ОК.
Нажмите для увеличения
Мы вычислили определитель матрицы А.
В заключение обратим внимание на важный момент. Он касается тех операций над матрицами, для которых мы использовали встроенные в программу функции, а в результате получали новую матрицу (умножение матриц, нахождение обратной и транспонированной матриц). В матрице, которая получилась в результате операции, нельзя удалить часть элементов. Т.е. если мы выделим, например, один элемент матрицы и нажмём Del, то программа выдаст предупреждение: Нельзя изменять часть массива.
Нажмите для увеличения
Мы можем удалить только все элементы этой матрицы.
Видеоурок
Кратко об авторе:
Шамарина Татьяна Николаевна — учитель физики, информатики и ИКТ, МКОУ «СОШ», с. Саволенка Юхновского района Калужской области. Автор и преподаватель дистанционных курсов по основам компьютерной грамотности, офисным программам. Автор статей, видеоуроков и разработок.
Спасибо за Вашу оценку. Если хотите, чтобы Ваше имя
стало известно автору, войдите на сайт как пользователь
и нажмите Спасибо еще раз. Ваше имя появится на этой стрнице.
Под матрицей подразумевается набор ячеек, расположенных непосредственно друг возле друга и которые образуют вместе прямоугольник. Не требуется особых навыков, чтобы выполнять различные действия с матрицей, достаточно тех же, какие используются во время работы с классическим диапазоном.
Каждая матрица имеет свой адрес, записывающийся аналогичным диапазону способом. Первая составная часть – первая ячейка диапазона (расположенная в верхнем левом углу), а второй – последняя ячейка, которая находится в нижнем правом углу.
Формулы массива
В подавляющем количестве задач при работе с массивами (а матрицы и являются таковыми) используются формулы соответствующего типа. Базовое их отличие от обычных заключается в том, что последние выводят всего одно значение. Для применения формулы массива необходимо осуществить несколько действий:
- Выделить набор ячеек, где будут выводиться значения.

- Непосредственно введение формулы.
- Нажатие последовательности клавиш Ctrl + Shift + Ввод.
После осуществления этих простых действий в поле ввода отображается формула массива. Ее можно отличить от обычной по фигурным скобкам.
Для редактирования, удаления формул массива, надо выделить требуемый диапазон и сделать то, что нужно. Чтобы редактировать матрицу, нужно использовать ту же комбинацию, что и для ее создания. При этом нет возможности редактировать отдельный элемент массива.
Что можно делать с матрицами
В целом, есть огромное количество действий, применение которых возможно для матриц. Давайте каждое из них рассмотрим более подробно.
Транспонирование
Многие люди не понимают значения этого термина. Представьте, что вам нужно поменять строки и колонки местами. Вот это действие и называется транспонированием.
Перед тем, как это осуществить, необходимо выделить отдельную область, которая имеет такое же количество строчек, сколько столбцов есть у исходной матрицы и такое же количество столбцов. Чтобы более наглядно понять, как это работает, посмотрите на этот скриншот.
Чтобы более наглядно понять, как это работает, посмотрите на этот скриншот.
Далее есть несколько методов, как можно осуществить транспонирование.
Первый способ следующий. Для начала нужно выделить матрицу, после чего скопировать ее. Далее выделяется диапазон ячеек, куда должен быть вставлен транспонированный диапазон. Далее открывается окно «Специальная вставка».
Там есть множество операций, но нам нужно найти радиокнопку «Транспонировать». После совершения этого действия нужно подтвердить его нажатием клавиши ОК.
Есть еще один способ, с помощью которого можно транспонировать матрицу. Сперва надо выделить ячейку, расположенную в верхнем левом углу диапазона, отведенного под транспонированную матрицу. Далее открывается диалоговое окно с функциями, где есть функция ТРАНСП . Ниже в примере вы более подробно узнаете, как это сделать. В качестве параметра функции используется диапазон, соответствующий изначальной матрице.
После нажатия кнопки ОК сначала будет показано, что вы допустили ошибку. Ничего в этом страшного нет. Все потому, что вставленная нами функция не определена, как формула массива. Поэтому нам нужно совершить такие действия:
Ничего в этом страшного нет. Все потому, что вставленная нами функция не определена, как формула массива. Поэтому нам нужно совершить такие действия:
- Выделить набор ячеек, отведенных под транспонированную матрицу.
- Нажать клавишу F2.
- Нажать на горячие клавиши Ctrl + Shift + Enter.
Главное достоинство метода заключается в способности транспонированной матрицы сразу корректировать содержащуюся в ней информацию, как только вносятся данные в изначальную. Поэтому рекомендуется использовать именно данный способ.
Сложение
Эта операция возможна лишь применительно к тем диапазонам, количество элементов которых такое же самое. Проще говоря, у каждой из матриц, с которыми пользователь собирается работать, должны быть одинаковые размеры. И приводим скриншот для наглядности.
В матрице, которая должна получиться, нужно выделить первую ячейку и ввести такую формулу.
=Первый элемент первой матрицы + Первый элемент второй матрицы
Далее подтверждаем ввод формулы с помощью клавиши Enter и используем автозаполнение (квадратик в правом нижнем углу), чтобы скопировать все значения на новую матрицу.
Умножение
Предположим, у нас есть такая таблица, которую следует умножить на 12.
Догадливый читатель может легко понять, что метод очень похож на предыдущий. То есть, каждая из ячеек матрицы 1 должна умножаться на 12, чтобы в итоговой матрице каждая ячейка содержала значение, умноженное на этот коэффициент.
При этом важно указывать абсолютные ссылки на ячейки.
Итого, получится такая формула.
=A1*$E$3
Дальше методика аналогична предыдущей. Нужно это значение растянуть на необходимое количество ячеек.
Предположим, что необходимо перемножить матрицы между собой. Но есть лишь одно условие, при котором это возможно. Надо, чтобы количество столбцов и строк у двух диапазонов было зеркально одинаковое. То есть, сколько столбцов, столько и строк.
Чтобы было более удобно, нами выделен диапазон с результирующей матрицей. Надо переместить курсор на ячейку в верхнем левом углу и ввести такую формулу =МУМНОЖ(А9:С13;Е9:h21). Не стоит забыть нажать Ctrl + Shift + Enter.
Не стоит забыть нажать Ctrl + Shift + Enter.
Обратная матрица
Если наш диапазон имеет квадратную форму (то есть, количество ячеек по горизонтали и вертикали одинаковое), то тогда получится найти обратную матрицу, если в этом есть такая необходимость. Ее величина будет аналогичной исходной. Для этого используется функция МОБР .
Для начала следует выделить первую ячейку матрицы, в какую будет вставляться обратная. Туда вводится формула =МОБР(A1:A4) . В аргументе указывается диапазон, для какого нам надо создать обратную матрицу. Осталось только нажать Ctrl + Shift + Enter, и готово.
Поиск определителя матрицы
Под определителем подразумевается число, находящееся матрицы квадратной формы. Чтобы осуществить поиск определителя матрицы, существует функция – МОПРЕД .
Для начала ставится курсор в какой-угодно ячейке. Далее мы вводим =МОПРЕД(A1:D4)
Несколько примеров
Давайте для наглядности рассмотрим некоторые примеры операций, которые можно осуществлять с матрицами в Excel.
Умножение и деление
Метод 1
Предположим, у нас есть матрица A, имеющая три ячейки в высоту и четыре – в ширину. Также есть число k, которое записывается в другой ячейке. После выполнения операции умножения матрицы на число появится диапазон значений, имеющий аналогичные размеры, но каждая ее часть умножается на k.
Диапазон B3:E5 – это исходная матрица, которая будет умножаться на число k, которое в свою очередь расположено в ячейке h5. Результирующая матрица будет находиться в диапазоне K3:N5. Исходная матрица будет называться A, а результирующая – B. Последняя образуется путем умножения матрицы А на число k.
Далее вводится =B3*$H$4 в ячейку K3, где В3 — элемент A11 матрицы А.
Не стоит забывать о том, ячейку h5, где указано число k необходимо вводить в формулу с помощью абсолютной ссылки. Иначе значение будет изменяться при копировании массива, и результирующая матрица потеряет работоспособность.
Далее маркер автозаполнения (тот самый квадратик в правом нижнем углу) используется для того, чтобы скопировать значение, полученное в ячейке K3, во все другие ячейки этого диапазона.
Вот у нас и получилось умножить матрицу A на определенное число и получить на выходе матрицу B.
Деление осуществляется аналогичным образом. Только вводить нужно формулу деления. В нашем случае это =B3/$H$4.
Метод 2
Итак, основное отличие этого метода в том, в качетве результата выдается массив данных, поэтому нужно применить формулу массива, чтобы заполнить весь набор ячеек.
Необходимо выделить результирующий диапазон, ввести знак равно (=), выделить набор ячеек, с соответствующими первой матрице размерами, нажать на звездочку. Далее выделяем ячейку с числом k. Ну и чтобы подтвердить свои действия, надо нажать на вышеуказанную комбинацию клавиш. Ура, весь диапазон заполняется.
Деление осуществляется аналогичным образом, только знак * нужно заменить на /.
Сложение и вычитание
Давайте опишем несколько практических примеров использования методов сложения и вычитания на практике.
Метод 1
Не стоит забывать, что возможно сложение лишь тех матриц, размеры которых одинаковые. В результирующем диапазоне все ячейки заполняются значением, являющим собой сумму аналогичных ячеек исходных матриц.
В результирующем диапазоне все ячейки заполняются значением, являющим собой сумму аналогичных ячеек исходных матриц.
Предположим, у нас есть две матрицы, имеющие размеры 3х4. Чтобы вычислить сумму, следет в ячейку N3 вставить такую формулу:
Тут каждый элемент являет собой первую ячейку матриц, которые мы собрались складывать. Важно, чтобы ссылки были относительными, поскольку если использовать абсолютные, не будут отображаться правильные данные.
Далее, аналогично умножению, с помощью маркера автозаполнения распространяем формулу на все ячейки результирующей матрицы.
Вычитание осуществляется аналогично, за тем лишь исключением, что используется знак вычитания (-), а не сложения.
Метод 2
Аналогично методу сложения и вычитание двух матриц, этот способ подразумевает использование формулы массива. Следовательно, в качестве ее результата будет выдаваться сразу набор значений. Поэтому нельзя редактировать или удалять какие-то элементы.
Сперва надо выделить диапазон, отделенный под результирующую матрицу, а потом нажать на «=». Затем надо указать первый параметр формулы в виде диапазона матрицы А, нажать на знак + и записать второй параметр в виде диапазона, соответствующему матрице B. Подтверждаем свои действия нажатием комбинации Ctrl + Shift + Enter. Все, теперь вся результирующая матрица заполнена значениями.
Затем надо указать первый параметр формулы в виде диапазона матрицы А, нажать на знак + и записать второй параметр в виде диапазона, соответствующему матрице B. Подтверждаем свои действия нажатием комбинации Ctrl + Shift + Enter. Все, теперь вся результирующая матрица заполнена значениями.
Пример транспонирования матрицы
Допустим, нам надо создать матрицу АТ из матрицы А, которая у нас есть изначально методом транспонирования. Последняя имеет, уже по традиции, размеры 3х4. Для этого будем использовать функцию =ТРАНСП() .
Выделяем диапазон для ячеек матрицы АТ.
Для этого надо перейти на вкладку «Формулы», где выбрать опцию «Вставить функцию», там найти категорию «Ссылки и массивы» и найти функцию ТРАНСП . После этого свои действия подтверждаются кнопкой ОК.
Далее переходим в окно «Аргументы функции», где вводится диапазон B3:E5, который повторяет матрицу А. Далее надо нажать Shift + Ctrl, после чего кликнуть «ОК».
Важно .
Нужно не лениться нажимать эти горячие клавиши, потому что в ином случае будет рассчитано только значение первой ячейки диапазона матрицы АТ.
В результате, у нас получается такая транспонированная таблица, которая изменяет свои значения вслед за исходной.
Поиск обратной матрицы
Предположим, у нас есть матрица А, которая имеет размеры 3х3 ячеек. Мы знаем, что для поиска обратной матрицы необходимо использовать функцию =МОБР() .
Теперь опишем, как это делать на практике. Сначала необходимо выделить диапазон G3:I5 (там будет располагаться обратная матрица). Необходимо найти на вкладке «Формулы» пункт «Вставить функцию».
Откроется диалог «Вставка функции», где нужно выбрать категорию «Математические». И там в перечне будет функция МОБР . После того, как мы ее выберем, нужно нажать на клавишу ОК . Далее появляется диалоговое окно «Аргументы функции», в котором записываем диапазон B3:D5, который соответствует матрице А. Далее действия аналогичные транспонированию. Нужно нажать на комбинацию клавиш Shift + Ctrl и нажать ОК.
Далее действия аналогичные транспонированию. Нужно нажать на комбинацию клавиш Shift + Ctrl и нажать ОК.
Выводы
Мы разобрали некоторые примеры, как можно работать с матрицами в Excel, а также описали теорию. Оказывается, что это не так страшно, как может показаться на первый взгляд, не так ли? Это только звучит непонятно, но на деле с матрицами среднестатистическому пользователю приходится иметь дело каждый день. Они могут использоваться почти для любой таблицы, где есть сравнительно небольшое количество данных. И теперь вы знаете, как можно себе упростить жизнь в работе с ними.
Как перемножать матрицы в эксель
Как перемножить матрицы в excel
Умножение матриц в EXCEL
В этой статье рассмотрены операции умножения матриц с помощью функции МУМНОЖ() или англ.MMULT и с помощью других формул, а также свойства ассоциативности и дистрибутивности операции умножения матриц. Примеры решены в MS EXCEL.
Операция умножения двух матриц А и В определена только для случаев, когда число столбцов матрицы А равно числу строк матрицы В.
Произведение матрицы А порядка P x N и матрицы В порядка N x Q — это такая матрица С порядка P x Q, у которой каждый элемент равен сумме произведений элементов i-ой строки матрицы А на соответствующие элементы j-ого столбца матрицы В , то есть:
Для умножения матриц в MS EXCEL существует специальная функция МУМНОЖ() , которую нужно вводить как формулу массива .
Рассмотрим сначала умножение квадратных матриц 2 х 2.
Разместим матрицы в диапазонах А8:В9 и D8:E9 (см. файл примера ).
Результат, также матрицу 2 х 2, будем вводить в диапазон H8:I9 .
- выделите указанный диапазон H8:I9
- поставьте курсор в Строку формул (или нажмите клавишу F2 )
- введите формулу =МУМНОЖ(A8:B9;D8:E9)
- нажмите CTRL+SHIFT+ENTER
Выделенный диапазон заполнится элементами матрицы. В принципе можно выделить заведомо б о льший диапазон, в этом случае лишние ячейки будут заполнены ошибкой #Н/Д.
В принципе можно выделить заведомо б о льший диапазон, в этом случае лишние ячейки будут заполнены ошибкой #Н/Д.
Удалить отдельный элемент матрицы А*В не удастся — только все элементы сразу (выделите весь диапазон и нажмите клавишу DEL ).
Чтобы изменить значения аргументов функции (например, поменять матрицы местами), выделите любую ячейку матрицы, нажмите F2 , исправьте формулу и нажмите CTRL+SHIFT+ENTER .
Альтернативной формулой для перемножения матриц является формула массива =СУММПРОИЗВ($A8:$B8;ТРАНСП(D$8:D$9)) . Введите формулу в верхнюю левую ячейку диапазона и нажмите CTRL+SHIFT+ENTER . Затем скопируйте ее вниз и вправо на нужное количество ячеек.
Если попытаться перемножить матрицы неподходящей размерности (когда число столбцов матрицы А НЕ равно числу строк матрицы В), то функция МУМНОЖ() вернет ошибку #ЗНАЧ!
В файле примера также продемонстрированы свойства ассоциативности и дистрибутивности операции умножения матриц.
Перемножение одной матрицы на другую в Microsoft Excel
Одной из частых операций, которую выполняют при работе с матрицами, является перемножение одной из них на другую. Программа Excel является мощным табличным процессором, который предназначен, в том числе и для работы над матрицами. Поэтому у него имеются инструменты, которые позволяют перемножить их между собой. Давайте узнаем, как это можно выполнить различными способами.
Процедура перемножения матриц
Сразу нужно сказать, что перемножить между собой можно далеко не все матрицы, а только те, которые соответствуют определенному условию: число столбцов одной матрицы должно быть равным числу строк другой и наоборот. Кроме того, исключается наличие в составе матриц пустых элементов. В этом случае тоже выполнить требуемую операцию не получится.
Способов перемножить матрицы в Экселе все-таки не так уж и много — всего два. И оба они связаны с применением встроенных функций Excel. Разберем в деталях каждый из данных вариантов.
Способ 1: функция МУМНОЖ
Наиболее простым и популярным вариантом среди пользователей является применение функции МУМНОЖ. Оператор МУМНОЖ относится к математической группе функций. Как раз его непосредственной задачей и является нахождение произведения двух матричных массивов. Синтаксис МУМНОЖ имеет такой вид:
Таким образом этот оператор имеет два аргумента, которые представляют собой ссылки на диапазоны двух перемножаемых матриц.
Теперь давайте посмотрим, как используется функция МУМНОЖ на конкретном примере. Имеется две матрицы, число строк одной из которых, соответствует количеству столбцов в другой и наоборот. Нам нужно перемножить два этих элемента.
- Выделяем диапазон, где будет отображаться результат умножения, начиная с его верхней левой ячейки. Размер данного диапазона должен соответствовать числу строк у первой матрицы и числу столбцов у второй. Клацаем по пиктограмме «Вставить функцию».
Способ 2: использование составной формулы
Кроме того, существует ещё один способ умножения двух матриц. Он более сложный, чем предыдущий, но тоже заслуживает упоминания, как альтернативный вариант. Данный способ предполагает использование составной формулы массива, которая будет состоять из функции СУММПРОИЗВ и вложенного в неё в качестве аргумента оператора ТРАНСП.
Он более сложный, чем предыдущий, но тоже заслуживает упоминания, как альтернативный вариант. Данный способ предполагает использование составной формулы массива, которая будет состоять из функции СУММПРОИЗВ и вложенного в неё в качестве аргумента оператора ТРАНСП.
- На этот раз выделяем на листе только левый верхний элемент массива пустых ячеек, который рассчитываем использовать для вывода результата. Щелкаем по значку «Вставить функцию».
В качестве аргументов из группы «Массив» используется ссылка на конкретный диапазон, который нужно перемножить. Всего может быть использовано от двух до 255 таких аргументов. Но в нашем случае, так как мы имеем дело с двумя матрицами, нам понадобится как раз два аргумента.
То есть, единственным аргументом данного оператора является ссылка на тот массив, который следует «перевернуть». Вернее, в нашем случае даже не на весь массив, а только на его первый столбец.
Как видим, несмотря на то, что был получен равнозначный результат, использовать функцию для умножения матриц МУМНОЖ значительно проще, чем применять для этих же целей составную формулу из операторов СУММПРОИЗВ и ТРАНСП. Но все-таки данный альтернативный вариант тоже нельзя оставить без внимания при изучении всех возможностей перемножения матриц в Microsoft Excel.
Мы рады, что смогли помочь Вам в решении проблемы.
Помимо этой статьи, на сайте еще 12345 инструкций.
Добавьте сайт Lumpics.ru в закладки (CTRL+D) и мы точно еще пригодимся вам.
Отблагодарите автора, поделитесь статьей в социальных сетях.
Опишите, что у вас не получилось. Наши специалисты постараются ответить максимально быстро.
Как перемножить матрицы в excel
Работа с матрицами и их преобразование.
Матрица представляет собой таблицу с числовыми значениями, которая состоит из n – строк и m – столбцов.
Сложение матриц
Матрицы можно сложить двумя способами:
1. Для сложения двух матриц выбираем, пустую ячейку, и воспользуемся пунктом меню – «вставка» — «функция».
В появившемся окне выбираем функцию «СУММ» и нажимаем кнопку «ок».
Появляется окно с шаблоном для заполнения. В пустых полях указываем первые ячейки матриц. Нажимаем кнопку «ок» и получаем в исходной ячейке результат. Затем за правый нижний угол растягиваем исходную ячейку в размер складываемых матриц и получаем сумму двух матриц(рис.5).
Рис.5 Сложение матриц при помощи стандартной функции
2. Для сложения двух матриц выбираем любую свободную ячейку, в которую записываем формулу для сложения. Формула представляет собой сумму двух первых ячеек матриц. Затем выделяем ячейку с формулой, и за Для сложения матриц выбираем пустую ячейку и воспользуемся пунктом меню – «вставка» — «функция».
В появившемся окне выбираем функцию «СУММ» и нажимаем кнопку «ок».
Появляется окно с шаблоном для заполнения. В пустых полях указываем первые ячейки матриц. Нажимаем кнопку «ок» и получаем в исходной ячейке результат. Затем за правый нижний угол растягиваем исходную ячейку в размер складываемых матриц и получаем сумму двух матриц (рис.6).
Рис.6 Сложение матриц
Перемножение матриц
Для перемножения матриц необходимо выделить точное количество ячеек, как и в перемножаемых матрицах.
Затем выбираем пункт меню – «вставка» — «функция».
В появившемся окне выбираем функцию «МУМНОЖ» и нажимаем кнопку «ок».
В появившемся окне с шаблоном заполняем поля путём выделения ячеек, в которых находится матрица. После введения матриц необходимо нажать, Ctrl + Sift + Enter и в указанной матрице мы получаем результат (рис.7).
Рис.7 Перемножение матриц
Транспонирование матриц
Для транспонирования матрицы необходимо выделить массив и скопировать его в буфер обмена. Затем войти в пункт меню «Правка» – «Специальная вставка». Предварительно указав свободную ячейку. После чего появится окно, в котором необходимо поставить флажок напротив
Затем войти в пункт меню «Правка» – «Специальная вставка». Предварительно указав свободную ячейку. После чего появится окно, в котором необходимо поставить флажок напротив
пункта транспонировать и нажать кнопку «ок». В результате чего мы получаем транспонированную матрицу (рис.8).
Рис.8 Транспонирование матриц
Аналогично функции «МУМНОЖ» используются функции «МОПРЕД» (нахождение определителя матрици) и «МОБР» (нахождение обратной матрици).
Как перемножить матрицы в excel
Перемножение одной матрицы на другую в Microsoft Excel
Одной из частых операций, которую выполняют при работе с матрицами, является перемножение одной из них на другую. Программа Excel является мощным табличным процессором, который предназначен, в том числе и для работы над матрицами. Поэтому у него имеются инструменты, которые позволяют перемножить их между собой. Давайте узнаем, как это можно выполнить различными способами.
Процедура перемножения матриц
Сразу нужно сказать, что перемножить между собой можно далеко не все матрицы, а только те, которые соответствуют определенному условию: число столбцов одной матрицы должно быть равным числу строк другой и наоборот. Кроме того, исключается наличие в составе матриц пустых элементов. В этом случае тоже выполнить требуемую операцию не получится.
Кроме того, исключается наличие в составе матриц пустых элементов. В этом случае тоже выполнить требуемую операцию не получится.
Способов перемножить матрицы в Экселе все-таки не так уж и много — всего два. И оба они связаны с применением встроенных функций Excel. Разберем в деталях каждый из данных вариантов.
Способ 1: функция МУМНОЖ
Наиболее простым и популярным вариантом среди пользователей является применение функции МУМНОЖ. Оператор МУМНОЖ относится к математической группе функций. Как раз его непосредственной задачей и является нахождение произведения двух матричных массивов. Синтаксис МУМНОЖ имеет такой вид:
Таким образом этот оператор имеет два аргумента, которые представляют собой ссылки на диапазоны двух перемножаемых матриц.
Теперь давайте посмотрим, как используется функция МУМНОЖ на конкретном примере. Имеется две матрицы, число строк одной из которых, соответствует количеству столбцов в другой и наоборот. Нам нужно перемножить два этих элемента.
Нам нужно перемножить два этих элемента.
- Выделяем диапазон, где будет отображаться результат умножения, начиная с его верхней левой ячейки. Размер данного диапазона должен соответствовать числу строк у первой матрицы и числу столбцов у второй. Клацаем по пиктограмме «Вставить функцию».
Способ 2: использование составной формулы
Кроме того, существует ещё один способ умножения двух матриц. Он более сложный, чем предыдущий, но тоже заслуживает упоминания, как альтернативный вариант. Данный способ предполагает использование составной формулы массива, которая будет состоять из функции СУММПРОИЗВ и вложенного в неё в качестве аргумента оператора ТРАНСП.
- На этот раз выделяем на листе только левый верхний элемент массива пустых ячеек, который рассчитываем использовать для вывода результата. Щелкаем по значку «Вставить функцию».
В качестве аргументов из группы «Массив» используется ссылка на конкретный диапазон, который нужно перемножить. Всего может быть использовано от двух до 255 таких аргументов. Но в нашем случае, так как мы имеем дело с двумя матрицами, нам понадобится как раз два аргумента.
Всего может быть использовано от двух до 255 таких аргументов. Но в нашем случае, так как мы имеем дело с двумя матрицами, нам понадобится как раз два аргумента.
То есть, единственным аргументом данного оператора является ссылка на тот массив, который следует «перевернуть». Вернее, в нашем случае даже не на весь массив, а только на его первый столбец.
Как видим, несмотря на то, что был получен равнозначный результат, использовать функцию для умножения матриц МУМНОЖ значительно проще, чем применять для этих же целей составную формулу из операторов СУММПРОИЗВ и ТРАНСП. Но все-таки данный альтернативный вариант тоже нельзя оставить без внимания при изучении всех возможностей перемножения матриц в Microsoft Excel.
Мы рады, что смогли помочь Вам в решении проблемы.
Помимо этой статьи, на сайте еще 12560 инструкций.
Добавьте сайт Lumpics.ru в закладки (CTRL+D) и мы точно еще пригодимся вам.
Отблагодарите автора, поделитесь статьей в социальных сетях.
Опишите, что у вас не получилось. Наши специалисты постараются ответить максимально быстро.
Умножение матриц в EXCEL
В этой статье рассмотрены операции умножения матриц с помощью функции МУМНОЖ() или англ.MMULT и с помощью других формул, а также свойства ассоциативности и дистрибутивности операции умножения матриц. Примеры решены в MS EXCEL.
Операция умножения двух матриц А и В определена только для случаев, когда число столбцов матрицы А равно числу строк матрицы В.
Произведение матрицы А порядка P x N и матрицы В порядка N x Q — это такая матрица С порядка P x Q, у которой каждый элемент равен сумме произведений элементов i-ой строки матрицы А на соответствующие элементы j-ого столбца матрицы В , то есть:
Для умножения матриц в MS EXCEL существует специальная функция МУМНОЖ() , которую нужно вводить как формулу массива .
Рассмотрим сначала умножение квадратных матриц 2 х 2.
Разместим матрицы в диапазонах А8:В9 и D8:E9 (см. файл примера ).
Результат, также матрицу 2 х 2, будем вводить в диапазон H8:I9 .
- выделите указанный диапазон H8:I9
- поставьте курсор в Строку формул (или нажмите клавишу F2 )
- введите формулу =МУМНОЖ(A8:B9;D8:E9)
- нажмите CTRL+SHIFT+ENTER
Выделенный диапазон заполнится элементами матрицы. В принципе можно выделить заведомо б о льший диапазон, в этом случае лишние ячейки будут заполнены ошибкой #Н/Д.
Удалить отдельный элемент матрицы А*В не удастся — только все элементы сразу (выделите весь диапазон и нажмите клавишу DEL ).
Чтобы изменить значения аргументов функции (например, поменять матрицы местами), выделите любую ячейку матрицы, нажмите F2 , исправьте формулу и нажмите CTRL+SHIFT+ENTER .
Альтернативной формулой для перемножения матриц является формула массива =СУММПРОИЗВ($A8:$B8;ТРАНСП(D$8:D$9)) . Введите формулу в верхнюю левую ячейку диапазона и нажмите CTRL+SHIFT+ENTER . Затем скопируйте ее вниз и вправо на нужное количество ячеек.
Если попытаться перемножить матрицы неподходящей размерности (когда число столбцов матрицы А НЕ равно числу строк матрицы В), то функция МУМНОЖ() вернет ошибку #ЗНАЧ!
В файле примера также продемонстрированы свойства ассоциативности и дистрибутивности операции умножения матриц.
Как перемножить матрицы в excel
В этой статье рассмотрены операции умножения матриц с помощью функции МУМНОЖ() или англ.MMULT и с помощью других формул, а также свойства ассоциативности и дистрибутивности операции умножения матриц. Примеры решены в MS EXCEL.
Операция умножения двух матриц А и В определена только для случаев, когда число столбцов матрицы А равно числу строк матрицы В.
Произведение матрицы А порядка P x N и матрицы В порядка N x Q — это такая матрица С порядка P x Q, у которой каждый элемент равен сумме произведений элементов i-ой строки матрицы А на соответствующие элементы j-ого столбца матрицы В , то есть:
Для умножения матриц в MS EXCEL существует специальная функция МУМНОЖ() , которую нужно вводить как формулу массива .
Рассмотрим сначала умножение квадратных матриц 2 х 2.
Разместим матрицы в диапазонах А8:В9 и D8:E9 (см. файл примера ).
Результат, также матрицу 2 х 2, будем вводить в диапазон H8:I9 .
- выделите указанный диапазон H8:I9
- поставьте курсор в Строку формул (или нажмите клавишу F2 )
- введите формулу =МУМНОЖ(A8:B9;D8:E9)
- нажмите CTRL+SHIFT+ENTER
Выделенный диапазон заполнится элементами матрицы. В принципе можно выделить заведомо б о льший диапазон, в этом случае лишние ячейки будут заполнены ошибкой #Н/Д.
Удалить отдельный элемент матрицы А*В не удастся — только все элементы сразу (выделите весь диапазон и нажмите клавишу DEL ).
Чтобы изменить значения аргументов функции (например, поменять матрицы местами), выделите любую ячейку матрицы, нажмите F2 , исправьте формулу и нажмите CTRL+SHIFT+ENTER .
Альтернативной формулой для перемножения матриц является формула массива =СУММПРОИЗВ($A8:$B8;ТРАНСП(D$8:D$9)) . Введите формулу в верхнюю левую ячейку диапазона и нажмите CTRL+SHIFT+ENTER . Затем скопируйте ее вниз и вправо на нужное количество ячеек.
Если попытаться перемножить матрицы неподходящей размерности (когда число столбцов матрицы А НЕ равно числу строк матрицы В), то функция МУМНОЖ() вернет ошибку #ЗНАЧ!
В файле примера также продемонстрированы свойства ассоциативности и дистрибутивности операции умножения матриц.
Перемножение одной матрицы на другую в Microsoft Excel
Одной из частых операций, которую выполняют при работе с матрицами, является перемножение одной из них на другую. Программа Excel является мощным табличным процессором, который предназначен, в том числе и для работы над матрицами. Поэтому у него имеются инструменты, которые позволяют перемножить их между собой. Давайте узнаем, как это можно выполнить различными способами.
Процедура перемножения матриц
Сразу нужно сказать, что перемножить между собой можно далеко не все матрицы, а только те, которые соответствуют определенному условию: число столбцов одной матрицы должно быть равным числу строк другой и наоборот. Кроме того, исключается наличие в составе матриц пустых элементов. В этом случае тоже выполнить требуемую операцию не получится.
Способов перемножить матрицы в Экселе все-таки не так уж и много — всего два. И оба они связаны с применением встроенных функций Excel. Разберем в деталях каждый из данных вариантов.
Способ 1: функция МУМНОЖ
Наиболее простым и популярным вариантом среди пользователей является применение функции МУМНОЖ. Оператор МУМНОЖ относится к математической группе функций. Как раз его непосредственной задачей и является нахождение произведения двух матричных массивов. Синтаксис МУМНОЖ имеет такой вид:
Таким образом этот оператор имеет два аргумента, которые представляют собой ссылки на диапазоны двух перемножаемых матриц.
Теперь давайте посмотрим, как используется функция МУМНОЖ на конкретном примере. Имеется две матрицы, число строк одной из которых, соответствует количеству столбцов в другой и наоборот. Нам нужно перемножить два этих элемента.
- Выделяем диапазон, где будет отображаться результат умножения, начиная с его верхней левой ячейки. Размер данного диапазона должен соответствовать числу строк у первой матрицы и числу столбцов у второй. Клацаем по пиктограмме «Вставить функцию».
Способ 2: использование составной формулы
Кроме того, существует ещё один способ умножения двух матриц. Он более сложный, чем предыдущий, но тоже заслуживает упоминания, как альтернативный вариант. Данный способ предполагает использование составной формулы массива, которая будет состоять из функции СУММПРОИЗВ и вложенного в неё в качестве аргумента оператора ТРАНСП.
- На этот раз выделяем на листе только левый верхний элемент массива пустых ячеек, который рассчитываем использовать для вывода результата.
 Щелкаем по значку «Вставить функцию».
Щелкаем по значку «Вставить функцию».В качестве аргументов из группы «Массив» используется ссылка на конкретный диапазон, который нужно перемножить. Всего может быть использовано от двух до 255 таких аргументов. Но в нашем случае, так как мы имеем дело с двумя матрицами, нам понадобится как раз два аргумента.
То есть, единственным аргументом данного оператора является ссылка на тот массив, который следует «перевернуть». Вернее, в нашем случае даже не на весь массив, а только на его первый столбец.
Как видим, несмотря на то, что был получен равнозначный результат, использовать функцию для умножения матриц МУМНОЖ значительно проще, чем применять для этих же целей составную формулу из операторов СУММПРОИЗВ и ТРАНСП. Но все-таки данный альтернативный вариант тоже нельзя оставить без внимания при изучении всех возможностей перемножения матриц в Microsoft Excel.
Мы рады, что смогли помочь Вам в решении проблемы.
Помимо этой статьи, на сайте еще 12345 инструкций.
Добавьте сайт Lumpics.ru в закладки (CTRL+D) и мы точно еще пригодимся вам.
Отблагодарите автора, поделитесь статьей в социальных сетях.
Опишите, что у вас не получилось. Наши специалисты постараются ответить максимально быстро.
Как перемножить матрицы в excel
Работа с матрицами и их преобразование.
Матрица представляет собой таблицу с числовыми значениями, которая состоит из n – строк и m – столбцов.
Сложение матриц
Матрицы можно сложить двумя способами:
1. Для сложения двух матриц выбираем, пустую ячейку, и воспользуемся пунктом меню – «вставка» — «функция».
В появившемся окне выбираем функцию «СУММ» и нажимаем кнопку «ок».
Появляется окно с шаблоном для заполнения. В пустых полях указываем первые ячейки матриц. Нажимаем кнопку «ок» и получаем в исходной ячейке результат. Затем за правый нижний угол растягиваем исходную ячейку в размер складываемых матриц и получаем сумму двух матриц(рис. 5).
5).
Рис.5 Сложение матриц при помощи стандартной функции
2. Для сложения двух матриц выбираем любую свободную ячейку, в которую записываем формулу для сложения. Формула представляет собой сумму двух первых ячеек матриц. Затем выделяем ячейку с формулой, и за Для сложения матриц выбираем пустую ячейку и воспользуемся пунктом меню – «вставка» — «функция».
В появившемся окне выбираем функцию «СУММ» и нажимаем кнопку «ок».
Появляется окно с шаблоном для заполнения. В пустых полях указываем первые ячейки матриц. Нажимаем кнопку «ок» и получаем в исходной ячейке результат. Затем за правый нижний угол растягиваем исходную ячейку в размер складываемых матриц и получаем сумму двух матриц (рис.6).
Рис.6 Сложение матриц
Перемножение матриц
Для перемножения матриц необходимо выделить точное количество ячеек, как и в перемножаемых матрицах.
Затем выбираем пункт меню – «вставка» — «функция».
В появившемся окне выбираем функцию «МУМНОЖ» и нажимаем кнопку «ок».
В появившемся окне с шаблоном заполняем поля путём выделения ячеек, в которых находится матрица. После введения матриц необходимо нажать, Ctrl + Sift + Enter и в указанной матрице мы получаем результат (рис.7).
Рис.7 Перемножение матриц
Транспонирование матриц
Для транспонирования матрицы необходимо выделить массив и скопировать его в буфер обмена. Затем войти в пункт меню «Правка» – «Специальная вставка». Предварительно указав свободную ячейку. После чего появится окно, в котором необходимо поставить флажок напротив
пункта транспонировать и нажать кнопку «ок». В результате чего мы получаем транспонированную матрицу (рис.8).
Рис.8 Транспонирование матриц
Аналогично функции «МУМНОЖ» используются функции «МОПРЕД» (нахождение определителя матрици) и «МОБР» (нахождение обратной матрици).
Функции для работы с матрицами в Excel
В программе Excel с матрицей можно работать как с диапазоном. То есть совокупностью смежных ячеек, занимающих прямоугольную область.
Адрес матрицы – левая верхняя и правая нижняя ячейка диапазона, указанные черед двоеточие.
Формулы массива
Построение матрицы средствами Excel в большинстве случаев требует использование формулы массива. Основное их отличие – результатом становится не одно значение, а массив данных (диапазон чисел).
Порядок применения формулы массива:
- Выделить диапазон, где должен появиться результат действия формулы.
- Ввести формулу (как и положено, со знака «=»).
- Нажать сочетание кнопок Ctrl + Shift + Ввод.
В строке формул отобразится формула массива в фигурных скобках.
Чтобы изменить или удалить формулу массива, нужно выделить весь диапазон и выполнить соответствующие действия. Для введения изменений применяется та же комбинация (Ctrl + Shift + Enter). Часть массива изменить невозможно.
Часть массива изменить невозможно.
Решение матриц в Excel
С матрицами в Excel выполняются такие операции, как: транспонирование, сложение, умножение на число / матрицу; нахождение обратной матрицы и ее определителя.
Транспонирование
Транспонировать матрицу – поменять строки и столбцы местами.
Сначала отметим пустой диапазон, куда будем транспонировать матрицу. В исходной матрице 4 строки – в диапазоне для транспонирования должно быть 4 столбца. 5 колонок – это пять строк в пустой области.
- 1 способ. Выделить исходную матрицу. Нажать «копировать». Выделить пустой диапазон. «Развернуть» клавишу «Вставить». Открыть меню «Специальной вставки». Отметить операцию «Транспонировать». Закрыть диалоговое окно нажатием кнопки ОК.
- 2 способ. Выделить ячейку в левом верхнем углу пустого диапазона. Вызвать «Мастер функций». Функция ТРАНСП. Аргумент – диапазон с исходной матрицей.
Нажимаем ОК. Пока функция выдает ошибку. Выделяем весь диапазон, куда нужно транспонировать матрицу. Нажимаем кнопку F2 (переходим в режим редактирования формулы). Нажимаем сочетание клавиш Ctrl + Shift + Enter.
Нажимаем кнопку F2 (переходим в режим редактирования формулы). Нажимаем сочетание клавиш Ctrl + Shift + Enter.
Преимущество второго способа: при внесении изменений в исходную матрицу автоматически меняется транспонированная матрица.
Сложение
Складывать можно матрицы с одинаковым количеством элементов. Число строк и столбцов первого диапазона должно равняться числу строк и столбцов второго диапазона.
В первой ячейке результирующей матрицы нужно ввести формулу вида: = первый элемент первой матрицы + первый элемент второй: (=B2+h3). Нажать Enter и растянуть формулу на весь диапазон.
Умножение матриц в Excel
Чтобы умножить матрицу на число, нужно каждый ее элемент умножить на это число. Формула в Excel: =A1*$E$3 (ссылка на ячейку с числом должна быть абсолютной).
Умножим матрицу на матрицу разных диапазонов. Найти произведение матриц можно только в том случае, если число столбцов первой матрицы равняется числу строк второй.
В результирующей матрице количество строк равняется числу строк первой матрицы, а количество колонок – числу столбцов второй.
Для удобства выделяем диапазон, куда будут помещены результаты умножения. Делаем активной первую ячейку результирующего поля. Вводим формулу: =МУМНОЖ(A9:C13;E9:h21). Вводим как формулу массива.
Обратная матрица в Excel
Ее имеет смысл находить, если мы имеем дело с квадратной матрицей (количество строк и столбцов одинаковое).
Размерность обратной матрицы соответствует размеру исходной. Функция Excel – МОБР.
Выделяем первую ячейку пока пустого диапазона для обратной матрицы. Вводим формулу «=МОБР(A1:D4)» как функцию массива. Единственный аргумент – диапазон с исходной матрицей. Мы получили обратную матрицу в Excel:
Нахождение определителя матрицы
Это одно единственное число, которое находится для квадратной матрицы. Используемая функция – МОПРЕД.
Ставим курсор в любой ячейке открытого листа. Вводим формулу: =МОПРЕД(A1:D4).
Вводим формулу: =МОПРЕД(A1:D4).
Таким образом, мы произвели действия с матрицами с помощью встроенных возможностей Excel.
Как записать матрицу в excel
Содержание
- Умножение и деление матрицы на число в Excel
- Способ 1
- Способ 2
- Сложение и вычитание матриц в Excel
- Способ 1
- Способ 2
- Умножение матриц в Excel
- Транспонирование матрицы в Excel
- Нахождение обратной матрицы в Excel
- Нахождение определителя матрицы в Excel
- Как найти определить матрицы в Excel
- Видеоурок
- Формулы массива
- Решение матриц в Excel
- Транспонирование
- Сложение
- Умножение матриц в Excel
- Обратная матрица в Excel
- Нахождение определителя матрицы
- Вращение фигур в трехмерном пространстве (3D Rotation) в MS EXCEL
- Трансформация фигур в двухмерном пространстве (2D Transformation) в MS EXCEL
- Вычисление определителя матрицы в MS EXCEL
- Вычисление обратной матрицы в MS EXCEL
- Умножение матриц в MS EXCEL
- Транспонирование матриц в MS EXCEL
- Сложение и вычитание матриц, умножение матриц на число в MS EXCEL
Программа Microsoft Office Excel позволяет выполнять операции с матрицами с помощью встроенных функций и формул. Рассмотрим основные операции над матрицами:
Рассмотрим основные операции над матрицами:
- умножение и деление матрицы на число;
- сложение, вычитание и умножение матриц;
- транспонирование матрицы;
- нахождение обратной матрицы;
- вычисление определителя.
Введем условные обозначения. Матрица А размерностью i x j — это прямоугольная таблица чисел, состоящая из i строк и j столбцов, аij — элемент матрицы.
Умножение и деление матрицы на число в Excel
Способ 1
Рассмотрим матрицу А размерностью 3х4. Умножим эту матрицу на число k. При умножении матрицы на число получается матрица такой же размерности, что и исходная, при этом каждый элемент матрицы А умножается на число k.
Введем элементы матрицы в диапазон В3:Е5, а число k — в ячейку Н4. В диапазоне К3:N5 вычислим матрицу В, полученную при умножении матрицы А на число k: В=А*k. Для этого введем формулу =B3*$H$4 в ячейку K3, где В3 — элемент а11 матрицы А.
В диапазоне К3:N5 вычислим матрицу В, полученную при умножении матрицы А на число k: В=А*k. Для этого введем формулу =B3*$H$4 в ячейку K3, где В3 — элемент а11 матрицы А.
Примечание: адрес ячейки H4 вводим как абсолютную ссылку, чтобы при копировании формулы ссылка не менялась.
С помощью маркера автозаполнения копируем формулу ячейки К3 вниз и вправо на весь диапазон матрицы В.
Таким образом, мы умножили матрицу А в Excel и получим матрицу В.
Для деления матрицы А на число k в ячейку K3 введем формулу =B3/$H$4 и скопируем её на весь диапазон матрицы В.
Способ 2
Этот способ отличается тем, что результат умножения/деления матрицы на число сам является массивом. В этом случае нельзя удалить элемент массива.
Для деления матрицы на число этим способом выделяем диапазон, в котором будет вычислен результат, вводим знак «=», выделяем диапазон, содержащий исходную матрицу А, нажимаем на клавиатуре знак умножить (*) и выделяем ячейку с числом k. После ввода формулы нажимаем сочетание клавиш Ctrl+Shift+Enter, чтобы значениями заполнился весь диапазон.
Для выполнения деления в данном примере в диапазон вводим формулу =B3:E5/h5, т.е. знак «*» меняем на «/».
Сложение и вычитание матриц в Excel
Способ 1
Следует отметить, что складывать и вычитать можно матрицы одинаковой размерности (одинаковое количество строк и столбцов у каждой из матриц). Причем каждый элемент результирующей матрицы С будет равен сумме соответствующих элементов матриц А и В, т. е. сij = аij + bij.
е. сij = аij + bij.
Рассмотрим матрицы А и В размерностью 3х4. Вычислим сумму этих матриц. Для этого в ячейку N3 введем формулу =B3+h4, где B3 и h4 – первые элементы матриц А и В соответственно. При этом формула содержит относительные ссылки (В3 и H3), чтобы при копировании формулы на весь диапазон матрицы С они могли измениться.
С помощью маркера автозаполнения скопируем формулу из ячейки N3 вниз и вправо на весь диапазон матрицы С.
Для вычитания матрицы В из матрицы А (С=А — В) в ячейку N3 введем формулу =B3 — h4 и скопируем её на весь диапазон матрицы С.
Способ 2
Этот способ отличается тем, что результат сложения/вычитания матриц сам является массивом. В этом случае нельзя удалить элемент массива.
Для деления матрицы на число этим способом выделяем диапазон, в котором будет вычислен результат, вводим знак «=», выделяем диапазон, содержащий первую матрицу А, нажимаем на клавиатуре знак сложения (+) и выделяем вторую матрицу В. После ввода формулы нажимаем сочетание клавиш Ctrl+Shift+Enter, чтобы значениями заполнился весь диапазон.
Умножение матриц в Excel
Следует отметить, что умножать матрицы можно только в том случае, если количество столбцов первой матрицы А равно количеству строк второй матрицы В.
Рассмотрим матрицы А размерностью 3х4 и В размерностью 4х2. При умножении этих матриц получится матрица С размерностью 3х2.
Вычислим произведение этих матриц С=А*В с помощью встроенной функции =МУМНОЖ(). Для этого выделим диапазон L3:M5 — в нём будут располагаться элементы матрицы С, полученной в результате умножения. На вкладке Формулы выберем Вставить функцию.
В диалоговом окне Вставка функции выберем Категория Математические — функция МУМНОЖ — ОК.
В диалоговом окне Аргументы функции выберем диапазоны, содержащие матрицы А и В. Для этого напротив массива1 щёлкнем по красной стрелке.
Выделим диапазон, содержащий элементы матрицы А (имя диапазона появится в строке аргументов), и щелкнем по красной стрелке.
Для массива2 выполним те же действия. Щёлкнем по стрелке напротив массива2.
Щёлкнем по стрелке напротив массива2.
Выделим диапазон, содержащий элементы матрицы В, и щелкнем по красной стрелке.
В диалоговом окне рядом со строками ввода диапазонов матриц появятся элементы матриц, а внизу — элементы матрицы С. После ввода значений нажимаем на клавиатуре сочетание клавиш Shift+Ctrl и щелкаем левой кнопкой мыши по кнопке ОК.
ВАЖНО. Если просто нажать ОК, то программа вычислит значение только первой ячейки диапазона матрицы С.
Мы получим результат умножения матриц А и В.
Мы можем изменить значения ячеек матриц А и В, значения матрицы С поменяются автоматически.
Транспонирование матрицы в Excel
Транспонирование матрицы — операция над матрицей, при которой столбцы заменяются строками с соответствующими номерами. Обозначим транспонированную матрицу А Т .
Обозначим транспонированную матрицу А Т .
Пусть дана матрица А размерностью 3х4, с помощью функции =ТРАНСП() вычислим транспонированную матрицу А Т , причем размерность этой матрицы будет 4х3.
Выделим диапазон Н3:J6, в который будут введены значения транспонированной матрицы.
На вкладке Формулы выберем Вставить функцию, выберем категорию Ссылки и массивы — функция ТРАНСП — ОК.
В диалоговом окне Аргументы функции указываем диапазон массива В3:Е5, содержащего элементы матрицы А. Нажимаем на клавиатуре сочетание клавиш Shift+Ctrl и щелкаем левой кнопкой мыши по кнопке ОК.
ВАЖНО. Если просто нажать ОК, то программа вычислит значение только первой ячейки диапазона матрицы А Т .
Если просто нажать ОК, то программа вычислит значение только первой ячейки диапазона матрицы А Т .
Нажмите для увеличения
Мы получили транспонированную матрицу.
Нахождение обратной матрицы в Excel
Матрица А -1 называется обратной для матрицы А, если АА -1 =А -1 А=Е, где Е — единичная матрица. Следует отметить, что обратную матрицу можно найти только для квадратной матрицы (одинаковое количество строк и столбцов).
Пусть дана матрица А размерностью 3х3, найдем для неё обратную матрицу с помощью функции =МОБР().
Для этого выделим диапазон G3:I5, который будет содержать элементы обратной матрицы, на вкладке Формулы выберем Вставить функцию.
В диалоговом окне Вставка функции выберем категорию Математические — функция МОБР — ОК.
В диалоговом окне Аргументы функции указываем диапазон массива В3:D5, содержащего элементы матрицы А. Нажимаем на клавиатуре сочетание клавиш Shift+Ctrl и щелкаем левой кнопкой мыши по кнопке ОК.
ВАЖНО. Если просто нажать ОК, то программа вычислит значение только первой ячейки диапазона матрицы А -1 .
Нажмите для увеличения
Мы получили обратную матрицу.
Нахождение определителя матрицы в Excel
Определитель матрицы — это число, которое является важной характеристикой квадратной матрицы.
Как найти определить матрицы в Excel
Пусть дана матрица А размерностью 3х3, вычислим для неё определитель с помощью функции =МОПРЕД().
Для этого выделим ячейку Н4, в ней будет вычислен определитель матрицы, на вкладке Формулы выберем Вставить функцию.
В диалоговом окне Вставка функции выберем категорию Математические — функция МОПРЕД — ОК.
В диалоговом окне Аргументы функции указываем диапазон массива В3:D5, содержащего элементы матрицы А. Нажимаем ОК.
Нажмите для увеличения
Мы вычислили определитель матрицы А.
В заключение обратим внимание на важный момент. Он касается тех операций над матрицами, для которых мы использовали встроенные в программу функции, а в результате получали новую матрицу (умножение матриц, нахождение обратной и транспонированной матриц). В матрице, которая получилась в результате операции, нельзя удалить часть элементов. Т.е. если мы выделим, например, один элемент матрицы и нажмём Del, то программа выдаст предупреждение: Нельзя изменять часть массива.
Т.е. если мы выделим, например, один элемент матрицы и нажмём Del, то программа выдаст предупреждение: Нельзя изменять часть массива.
Нажмите для увеличения
Мы можем удалить только все элементы этой матрицы.
Видеоурок
Кратко об авторе:
Шамарина Татьяна Николаевна — учитель физики, информатики и ИКТ, МКОУ «СОШ», с. Саволенка Юхновского района Калужской области. Автор и преподаватель дистанционных курсов по основам компьютерной грамотности, офисным программам. Автор статей, видеоуроков и разработок.
Спасибо за Вашу оценку. Если хотите, чтобы Ваше имя
стало известно автору, войдите на сайт как пользователь
и нажмите Спасибо еще раз. Ваше имя появится на этой стрнице.
Есть мнение?
Оставьте комментарий
Понравился материал?
Хотите прочитать позже?
Сохраните на своей стене и
поделитесь с друзьями
Вы можете разместить на своём сайте анонс статьи со ссылкой на её полный текст
В программе Excel с матрицей можно работать как с диапазоном. То есть совокупностью смежных ячеек, занимающих прямоугольную область.
То есть совокупностью смежных ячеек, занимающих прямоугольную область.
Адрес матрицы – левая верхняя и правая нижняя ячейка диапазона, указанные черед двоеточие.
Формулы массива
Построение матрицы средствами Excel в большинстве случаев требует использование формулы массива. Основное их отличие – результатом становится не одно значение, а массив данных (диапазон чисел).
Порядок применения формулы массива:
- Выделить диапазон, где должен появиться результат действия формулы.
- Ввести формулу (как и положено, со знака «=»).
- Нажать сочетание кнопок Ctrl + Shift + Ввод.
В строке формул отобразится формула массива в фигурных скобках.
Чтобы изменить или удалить формулу массива, нужно выделить весь диапазон и выполнить соответствующие действия. Для введения изменений применяется та же комбинация (Ctrl + Shift + Enter). Часть массива изменить невозможно.
Решение матриц в Excel
С матрицами в Excel выполняются такие операции, как: транспонирование, сложение, умножение на число / матрицу; нахождение обратной матрицы и ее определителя.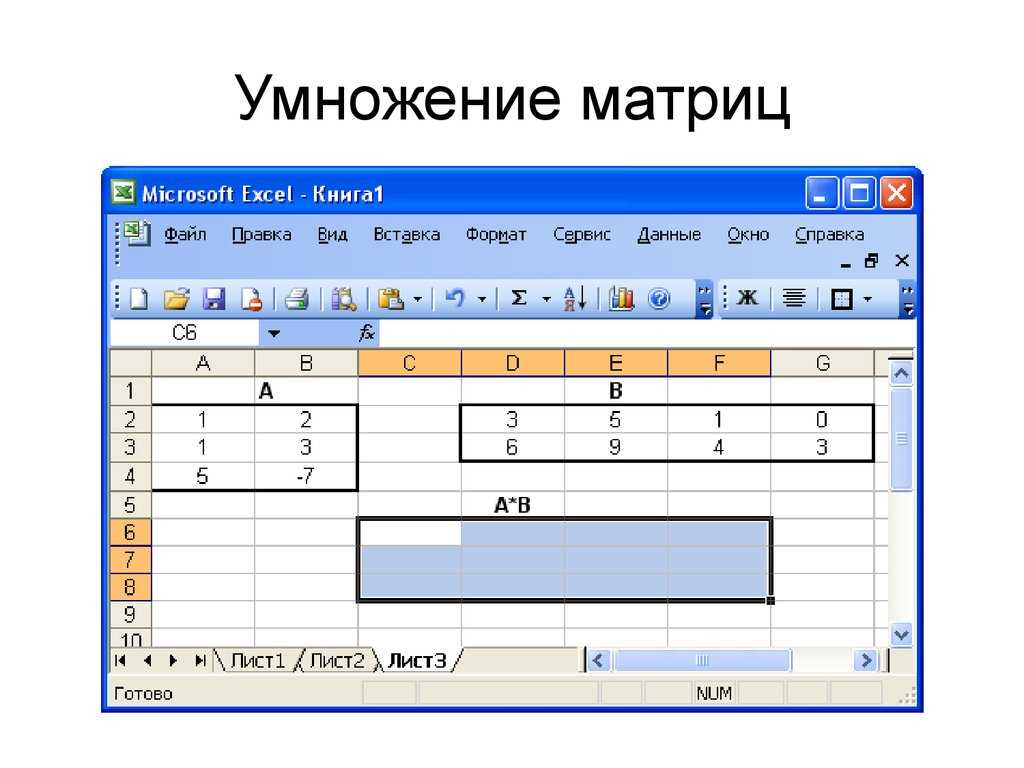
Транспонирование
Транспонировать матрицу – поменять строки и столбцы местами.
Сначала отметим пустой диапазон, куда будем транспонировать матрицу. В исходной матрице 4 строки – в диапазоне для транспонирования должно быть 4 столбца. 5 колонок – это пять строк в пустой области.
- 1 способ. Выделить исходную матрицу. Нажать «копировать». Выделить пустой диапазон. «Развернуть» клавишу «Вставить». Открыть меню «Специальной вставки». Отметить операцию «Транспонировать». Закрыть диалоговое окно нажатием кнопки ОК.
- 2 способ. Выделить ячейку в левом верхнем углу пустого диапазона. Вызвать «Мастер функций». Функция ТРАНСП. Аргумент – диапазон с исходной матрицей.
Нажимаем ОК. Пока функция выдает ошибку. Выделяем весь диапазон, куда нужно транспонировать матрицу. Нажимаем кнопку F2 (переходим в режим редактирования формулы). Нажимаем сочетание клавиш Ctrl + Shift + Enter.
Преимущество второго способа: при внесении изменений в исходную матрицу автоматически меняется транспонированная матрица.
Сложение
Складывать можно матрицы с одинаковым количеством элементов. Число строк и столбцов первого диапазона должно равняться числу строк и столбцов второго диапазона.
В первой ячейке результирующей матрицы нужно ввести формулу вида: = первый элемент первой матрицы + первый элемент второй: (=B2+h3). Нажать Enter и растянуть формулу на весь диапазон.
Умножение матриц в Excel
Чтобы умножить матрицу на число, нужно каждый ее элемент умножить на это число. Формула в Excel: =A1*$E$3 (ссылка на ячейку с числом должна быть абсолютной).
Умножим матрицу на матрицу разных диапазонов. Найти произведение матриц можно только в том случае, если число столбцов первой матрицы равняется числу строк второй.
В результирующей матрице количество строк равняется числу строк первой матрицы, а количество колонок – числу столбцов второй.
Для удобства выделяем диапазон, куда будут помещены результаты умножения. Делаем активной первую ячейку результирующего поля. Вводим формулу: =МУМНОЖ(A9:C13;E9:h21). Вводим как формулу массива.
Делаем активной первую ячейку результирующего поля. Вводим формулу: =МУМНОЖ(A9:C13;E9:h21). Вводим как формулу массива.
Обратная матрица в Excel
Ее имеет смысл находить, если мы имеем дело с квадратной матрицей (количество строк и столбцов одинаковое).
Размерность обратной матрицы соответствует размеру исходной. Функция Excel – МОБР.
Выделяем первую ячейку пока пустого диапазона для обратной матрицы. Вводим формулу «=МОБР(A1:D4)» как функцию массива. Единственный аргумент – диапазон с исходной матрицей. Мы получили обратную матрицу в Excel:
Нахождение определителя матрицы
Это одно единственное число, которое находится для квадратной матрицы. Используемая функция – МОПРЕД.
Ставим курсор в любой ячейке открытого листа. Вводим формулу: =МОПРЕД(A1:D4).
Таким образом, мы произвели действия с матрицами с помощью встроенных возможностей Excel.
Работа с матрицами в Excel: сложение и умножение матриц, вычисление определителя, транспонирование и нахождение обратной матрицы.
Вращение фигур в трехмерном пространстве (3D Rotation) в MS EXCEL
Научимся вращать в MS EXCEL трехмерные фигуры вокруг координатных осей Х, Y, Z, а также поворачивать плоскости вокруг произвольно заданной оси. Для этого используем соответствующие матрицы вращения. Также покажем, что проекция фигуры на плоскость, построенная с помощью диаграммы типа Точечная, может служить альтернативой диаграмме типа Поверхность.
Трансформация фигур в двухмерном пространстве (2D Transformation) в MS EXCEL
Трансформация (преобразование) геометрической фигуры означает ее изменение по определенным правилам. Например, вращение, смещение или изменение масштаба некого прямоугольника на плоскости. Правила, по которым происходит изменение, будем записывать в матричном виде. Используем произведение матриц для применения к фигуре сразу нескольких преобразований. Также используем однородную систему координат (Homogenous Coordinates). Здесь рассмотрим трансформацию в двумерном пространстве с использованием MS EXCEL.
Вычисление определителя матрицы в MS EXCEL
Вычислим определитель (детерминант) матрицы с помощью функции МОПРЕД() или англ. MDETERM, разложением по строке/столбцу (для 3 х 3) и по определению (до 6 порядка).
Вычисление обратной матрицы в MS EXCEL
Для вычисления обратной матрицы в MS EXCEL существует специальная функция МОБР() или англ. MINVERSE .
Умножение матриц в MS EXCEL
В этой статье рассмотрены операции умножения матриц с помощью функции МУМНОЖ() или англ.MMULT и с помощью других формул, а также свойства ассоциативности и дистрибутивности операции умножения матриц. Примеры решены в MS EXCEL.
Транспонирование матриц в MS EXCEL
Транспонирование матрицы — это операция над матрицей, при которой ее строки и столбцы меняются местами. Для этой операции в MS EXCEL существует специальная функция ТРАНСП() или англ. TRANSPOSE.
Сложение и вычитание матриц, умножение матриц на число в MS EXCEL
В этой статье рассмотрены операции сложения и вычитания над матрицами одного порядка, а также операции умножения матрицы на число. Примеры решены в MS EXCEL.
Примеры решены в MS EXCEL.
МУМНОЖ Функция Excel для умножения матриц
Поскольку рабочий лист по сути является гигантской матрицей, неудивительно, что умножение матриц в Excel очень просто — нам просто нужно использовать функцию МУМНОЖ.
Содержание
- Умножение матриц с функцией МУМНОЖ Excel
- Правила умножения матриц
- Примеры умножения матриц в Excel
- Умножение матриц как функция массива (все версии Excel)
- Умножение матриц как функция динамического массива (только Excel 365)
- Другие примеры МУМНОЖ в Excel
- МУМНОЖ Ошибки Excel (Почему МУМНОЖ не работает в Excel?)
- МУМНОЖ #ЗНАЧ! Ошибка
- ММУЛЬМ Возвращает одно значение
- МММУЛЬТ Возвращает слишком много значений
- МММУЛЬМ #Н/Д! Ошибка
- Пределы умножения матриц в Excel
Умножение матриц с помощью функции МУМНОЖ Excel
Вы можете умножать матрицы в Excel благодаря функции МУМНОЖ. это 9Функция массива 0039 возвращает произведение двух матриц, введенных на листе.
это 9Функция массива 0039 возвращает произведение двух матриц, введенных на листе.
Синтаксис этой функции:
МУМНОЖ(массив1,массив2)
где массив1 и массив2 — это массивы или матрицы, которые нужно перемножить.
Результатом функции МУМНОЖ является массив с количеством строк, таким же, как у массива1, и количеством столбцов, таким же, как у массива2.
Если вы используете Excel 365, МУМНОЖ — это функция динамического массива. Это означает, что вы можете ввести формулу с помощью МУМНОЖ в одну ячейку, и Excel автоматически расширит диапазон, чтобы он соответствовал результату функции.
Если вы НЕ используете Excel 365, МУМНОЖ необходимо ввести как функцию массива, выбрав соответствующее количество ячеек для результирующего массива и нажав CTRL+SHIFT+ENTER.
Правила умножения матриц
Чтобы эффективно выполнять умножение матриц в Excel, в первую очередь полезно помнить, как работает умножение матриц. Итак, допустим, у нас есть две матрицы, A и B, как показано ниже:
Итак, допустим, у нас есть две матрицы, A и B, как показано ниже:
Произведение этих двух матриц (назовем его C) находится путем умножения записей в первой строке столбца A на записи в первом столбце B и суммируя их вместе. Это также известно как скалярный продукт. Это единственное значение становится записью в первой строке и первом столбце матрицы C.
Продолжаем делать это до тех пор, пока не найдем скалярное произведение для каждой комбинации строки и столбца.
Поскольку мы умножаем строки матрицы A на столбцы матрицы B, результирующая матрица C будет иметь размер 2 x 2. Или, в более общем случае, матричное произведение имеет такое же количество строк, что и матрица A, и такое же количество столбцов, как у матрицы B .
Из-за того, как работает умножение матриц, также важно помнить, что мы можем умножать только две матрицы, если количество строк в B совпадает с количеством столбцов в A.
Понятно?
Если нет, ничего страшного. Надеюсь, несколько примеров прояснят ситуацию. 🙂
Надеюсь, несколько примеров прояснят ситуацию. 🙂
Примеры умножения матриц в Excel
Умножение матриц как функция массива (все версии Excel)
Давайте возьмем матрицы сверху и найдем произведение, используя умножение матриц в Excel с помощью функции МУМНОЖ:
Во-первых, давайте найти C, продукт AB.
Поскольку МУМНОЖ является функцией массива, она будет возвращать значения более чем в одну ячейку.
Мы знаем, что результатом будет матрица 2×2, потому что первая матрица, A, имеет две строки, а вторая матрица, B, имеет два столбца.
Итак, если мы работали в Excel 365 или любой предыдущей версии Excel, мы выбираем область на листе 2 ячейки в ширину и 2 ячейки в высоту:
Затем, когда область все еще выделена, введите формулу массива и выберите аргументы (я присвоил имена матрицам A и B):
Наконец, нажмите CTRL+SHIFT+ENTER (поскольку это формула массива), чтобы вернуть результирующее матричное произведение:
Умножение матриц как функция динамического массива (только Excel 365) необходимо выбрать правильное количество возвращаемых ячеек или нажать CTRL+SHIFT+ENTER.
 Просто введите формулу массива в самую верхнюю левую ячейку массива, и Excel динамически заполнит все полученные значения:
Просто введите формулу массива в самую верхнюю левую ячейку массива, и Excel динамически заполнит все полученные значения:Другие примеры MMULT в Excel
Что, если вместо вычисления матрицы C путем умножения матрицы A на B мы вычислим другую матрицу D, умножив матрицу B на A?
Поскольку первая матрица B имеет 3 строки, а вторая матрица A имеет 3 столбца, матрица D будет иметь 3 строки и 3 столбца. Итак, мы начнем с выбора 3 ячейки в ширину и высоту :
Затем введите формулу для МУМНОЖ, выбрав B как массив1 и A как массив2…
… и нажмите CTRL+SHIFT+ENTER чтобы получить матрицу D:
Функция МУМНОЖ также работает для умножения матрицы (A) на массив (x). Конечно, остается в силе правило, согласно которому количество строк в x должно совпадать с количеством столбцов в A.
Результатом является массив F с 1 столбцом и таким же количеством строк, как у A:
МУМНОЖ Ошибки Excel (Почему МУМНОЖ не работает в Excel?)
Существует несколько способов получения ошибок в Excel с помощью функции МУМНОЖ:
МУМНОЖ #ЗНАЧ! Ошибка
А #ЗНАЧ! ошибка возникает, когда количество столбцов в массиве 1 (A ниже) не совпадает с количеством строк в array2 (x ниже).
Чтобы исправить это, потребуется, чтобы массив x имел три строки, поэтому, вероятно, это означает, что одно из значений массива x отсутствует.
Если вы не используете Excel 365 и МУМНОЖ не вводится как формула массива путем нажатия CTRL+SHIFT+ВВОД, также будет возвращено #ЗНАЧ! ошибка в одной ячейке:
Наконец, #ЗНАЧ! Ошибка также возникает, если какой-либо из элементов массива1 или массива2 не содержит чисел.
МУЛЬТИ возвращает одно значение
Если вы не используете Excel 365 и ММУЛЬТИ возвращает одно значение, это связано с тем, что для результирующего массива была выбрана только одна ячейка. В более ранних версиях Excel пользователь мог выбрать подходящее количество ячеек, в которые Excel возвращает результат. Если выбрана одна ячейка, МУМУЛЬТ выполнит умножение матриц и вернет первое значение в результирующем массиве в эту ячейку.
Такое поведение также возможно в Excel 365, если для результата выбрана одна ячейка, а функция МУМНОЖ введена как формула массива путем нажатия CTRL+SHIFT+ВВОД.
ММУЛЬТИ возвращает слишком много значений
Хотя это и не всегда является ошибкой, ММУЛЬТИ может возвращать неожиданные результаты, когда область вывода для функции больше требуемой.
Добавление дополнительных столбцов приводит к дублированию результатов:
МУЛЬТИ #Н/Д! Ошибка
Добавление дополнительных строк в массив MMULT приводит к ошибке #N/A! ошибка, которая будет отображаться, хотя она отображается только в дополнительной ячейке:
Пределы умножения матриц в Excel
В текущих версиях Excel нет программных ограничений на размер матрицы, которую можно умножить. По сути, вы можете умножать матрицы любого размера, если на вашем компьютере достаточно оперативной памяти.
Однако, если вы все еще используете Excel 2003 или более раннюю версию, вы будете ограничены выводом 5046 ячеек при использовании функции МУМНОЖ (примерно матрица 71 × 71).
Даже если вы используете более новые версии Excel, есть одно предостережение: вы не можете создать массив, который заполнит весь столбец рабочего листа. Поскольку на листе в Microsoft Excel 2007 и более поздних версиях 1 048 576 строк, я предполагаю, что это ограничение на умножение матриц в Excel.
Поскольку на листе в Microsoft Excel 2007 и более поздних версиях 1 048 576 строк, я предполагаю, что это ограничение на умножение матриц в Excel.
В этой статье службы поддержки Microsoft содержится полезная информация об ограничениях Excel при работе с массивами.
Умножение матриц в Excel (5 примеров)
Матрица — важный инструмент, ежедневно используемый в статистике и научных исследованиях. Электронные таблицы Excel сами по себе представляют собой очень большие матрицы, содержащие 1 048 576 строк и 16 384 столбца. Неудивительно, что Excel предоставляет несколько полезных инструментов для матричных операций. В этой статье мы сосредоточимся на 9Умножение матрицы 0045 в Excel с разными примерами разных сценариев.
Скачать практическую рабочую тетрадь
Как выполнить умножение матриц?
5 подходящих примеров для умножения матриц в Excel
1. Матричное умножение двух массивов
2. Умножьте один столбец на один массив строк
Умножьте один столбец на один массив строк
3. Умножение массива одной строки и одного столбца в Excel
4. Вычислить квадрат матрицы из умножения матриц
5. Умножение матрицы на скаляр.
Ошибки при умножении матриц в Excel
Ограничение умножения матриц в Excel
Вывод
Статьи по Теме
Загрузить рабочую тетрадь
Вы можете загрузить книгу, содержащую все примеры, использованные в этой статье, из поля ниже.
Как выполнять умножение матриц?
Во-первых, давайте сосредоточимся на том, как на самом деле работает умножение матриц. Если есть две матрицы размерности i x j и j x k каждый элемент первой строки будет умножен на элементы их соответствующих входных номеров из первого столбца второй матрицы. Затем все добавленные результаты будут указывать значение элемента первой строки и первого столбца результирующей матрицы, взяв номер строки из первой матрицы и номер столбца из второй. Это будет продолжаться i x k раз и приведет к матрице i x k .
Это будет продолжаться i x k раз и приведет к матрице i x k .
Давайте возьмем пример, где мы добавляем две матрицы A и B.
Каждая запись из первой строки матрицы A будет умножаться на соответствующие записи из первого столбца матрицы B. Тогда результат даст нам значение 1×1 умноженной матрицы, скажем, C. В этом примере это будет 1 *4+2*6+3*8=40.
Тот же процесс повторяется для 1-й строки из A и 2-го столбца из B, 2-й строки из A и 1-го столбца из B, 2-й строки из A и 2-го столбца из B.
Наконец, результат будет выглядеть примерно так.
Это произведение матрицы А и В.
5 подходящих экземпляров для умножения матриц в Excel
Excel имеет встроенную функцию МУМНОЖ для умножения матриц. Эта функция принимает в качестве аргументов два массива. Мы можем использовать матрицы в качестве массивов аргументов в этой функции, чтобы получить желаемый результат.
1. Матричное умножение двух массивов
Возьмем две отдельные матрицы A и B. В Excel мы будем рассматривать их как массивы для умножения матриц.
Шаги:
- Сначала выберите ячейки, в которые вы хотите поместить свою матрицу.
- Затем запишите следующую формулу.
=МУМНОЖ(B5:D7,B10:D12)
- Теперь на клавиатуре нажмите Ctr+Shift+Enter . Вы получите результат матрицы AxB.
Вы можете сделать то же самое для матрицы BxA, введя матрицу B в качестве первого и матрицу A в качестве второго аргумента ММУЛЬМ функция.
Подробнее: Как умножить 3 матрицы в Excel (2 простых метода)
2. Умножение одного столбца на массив одной строки
Возьмем следующий набор данных с матрицами, содержащими только один столбец и одну строку.
Перемноженная матрица AxB будет результатом умножения матриц с одним столбцом и одной строкой.
Шаги:
- Сначала выберите диапазон ячеек для перемножаемой матрицы.
- Затем запишите следующую формулу.
=МУМНОЖ(B5:B7,B10:D10)
- Наконец, нажмите Ctrl+Shift+Enter на клавиатуре. У вас получится результирующая матрица.
Подробнее: Как умножить несколько ячеек в Excel (4 метода)
Аналогичные показания
- Как умножать столбцы в Excel (9Полезные и простые способы)
- Умножение двух столбцов в Excel (5 самых простых способов)
- Как использовать функцию умножения в Excel (с 3 альтернативными методами)
- Если ячейка содержит значение, умножьте его с помощью формулы Excel (3 примера)
3.
 Умножение массива одной строки и одного столбца в Excel
Умножение массива одной строки и одного столбца в ExcelДля того же набора данных, который использовался в предыдущем методе, матричное умножение BxA будет означать умножение матриц из одной строки и одного столбца.
Шаги:
- Сначала выберите ячейку. Это умножение даст только одно значение, поэтому выберите здесь одну ячейку.
- Затем введите следующую формулу.
=МУМНОЖ(B10:D10,B5:B7)
- Теперь нажмите Ctrl+Shift+Enter на клавиатуре. Вы получите желаемый результат.
Подробнее: Формула умножения в Excel (6 быстрых подходов)
4. Вычисление площади матрицы путем умножения матриц
Вернемся к матрицам на примерах, использованных в первом примере. Здесь мы воспользуемся умножением матриц, чтобы определить квадраты матриц A и B.
Шаги:
- Выберите диапазон ячеек для вашей квадратной матрицы.

- Теперь запишите следующую формулу.
=МУМНОЖ(B5:D7,B5:D7)
- Теперь нажмите Ctrl+Shift+Enter на клавиатуре. У вас получится квадрат матрицы А.
Можно заменить диапазон матрицы A на диапазон матрицы B (B10:D12) и получить квадрат матрицы B тоже.
Подробнее: Что такое формула умножения в Excel для нескольких ячеек? (3 направления)
Аналогичные показания
- Как умножить столбец на число в Excel (4 простых метода)
- Умножение на проценты в Excel (4 простых способа)
- Как умножить столбец в Excel на константу (4 простых способа)
- Умножение двух столбцов, а затем суммирование в Excel
5. Умножение матрицы на скаляр
Когда матрица умножается только на число, все элементы матрицы умножаются на это число. Это также может быть достигнуто в Excel.
Это также может быть достигнуто в Excel.
Для демонстрации я использую здесь матрицу A и умножаю ее на 7.
Шаги:
- Выберите диапазон ячеек для перемножаемой матрицы.
- Затем введите в поле следующую формулу.
=B5:D7*G7
- Нажмите Ctrl+Shift+Enter на клавиатуре.
Подробнее: Как умножать в Excel: столбцы, ячейки, строки и числа
Ошибки при умножении матриц в Excel
Существует несколько ошибок, с которыми вы можете столкнуться при выполнении умножения матриц в Excel.
Из них #ЦЕННОСТЬ! Ошибка может возникнуть, если количество столбцов в первом массиве и количество строк во втором массиве не совпадают.
Вы получите ту же ошибку, если в ячейке массива есть хотя бы одно нечисловое значение.
Если вы выберете больше значений, чем выглядит ваша предполагаемая матрица умножения, вы получите ошибку #N/A , но только в дополнительных выбранных вами ячейках.
Подробнее: Как делить и умножать в одной формуле Excel (4 способа)
Ограничение умножения матриц в Excel
Если вы используете Excel 2003 или более раннюю версию, существует ограничение на умножение матриц размером 71×71. Но для более поздних версий вы можете выполнять операцию столько, сколько позволяет электронная таблица, ограничиваясь только оперативной памятью вашей системы.
Заключение
Это были разные ситуации, в которых вы можете выполнять умножение матриц в Excel. Надеюсь, вы нашли эту статью полезной и информативной. Если у вас есть какие-либо вопросы или предложения для нас, сообщите нам об этом ниже.
Дополнительные руководства, подобные этим, см. на веб-сайте Exceldemy. com .
com .
Связанные статьи
- Как составить таблицу умножения в Excel (4 метода)
- Умножение одной ячейки на несколько ячеек в Excel (4 способа)
- Как рассчитать ковариационную матрицу в Excel (с помощью простых шагов)
- Создание тренировочной матрицы в Excel (3 простых метода)
- Как создать матрицу прослеживаемости в Excel
- Создание корреляционной матрицы в Excel (2 удобных подхода)
ММУЛЬТ в Excel | Примеры выполнения умножения матриц в Excel
Excel MMULT ( Содержание)
- Что такое функция МУМНОЖ в Excel?
- Примеры MMULT в Excel
С математической точки зрения явление умножения двух матриц друг на друга называется умножением матриц. Однако умножение двух матриц имеет определенные правила. Поскольку произведение матриц дается путем умножения элементов каждой строки первой матрицы на элементы каждого столбца второй матрицы, становится обязательным, чтобы количество столбцов первой матрицы было равно количеству строк второй. матрица.
матрица.
Что такое функция МУМНОЖ в Excel?
В Excel у нас есть функция под названием «MMUL», функция массива, которая является частью множества формул в функции «Математика и тригонометрия», которую можно найти в разделе «Формулы». MMULT можно использовать для получения произведения двух массивов матриц в Excel, в котором количество строк из первой матрицы равно количеству столбцов из второй матрицы.
Синтаксис:
Ниже приведен синтаксис функции МУМНОЖ в Excel.
Аргументы:
- array1 — Обязательный аргумент для функции, указывающей первый массив матриц, который вы хотите умножить.
- array2 — Обязательный аргумент для функции, указывающей второй массив матриц, который вы хотите умножить.
Запятая разделяет оба этих аргумента в функции МУМНОЖ. Это означает, что после того, как вы ввели первый массив в формулу, вы должны упомянуть запятую («,»), прежде чем добавлять второй аргумент массива.
Как уже упоминалось в начале, МУМУЛЬТИМЕТР является функцией массива. Таким образом, при его выполнении вам нужно одновременно нажать кнопку Ctrl + Shift + Enter вместо прямого нажатия клавиши Enter на клавиатуре.
Примеры MMULT в Excel
Давайте рассмотрим несколько примеров на практике.
Вы можете скачать этот шаблон MMULT Excel здесь — Шаблон MMULT Excel
Пример №1 — Использование MMULT для умножения двух матриц
Предположим, у нас есть две матрицы с двумя строками, тремя столбцами и тремя строками и двумя столбцами соответственно, как показано ниже.
После того, как мы перейдем к произведению этих двух матриц, они в лучшем случае могут дать две строки и два столбца (это потому, что у нас есть две строки в первой матрице и два столбца во второй матрице). Следовательно, наша результирующая матрица будет матрицей 2X2. Мы будем хранить то же самое в ячейках, варьирующихся от A6: B8, как показано ниже:
Шаг 1: Выберите все ячейки (A7:B8) из результирующей матрицы, чтобы сразу применить формулу.
Шаг 2: Внутри активной ячейки (ячейка A7) начните ввод формулы для умножения матриц. Используйте =МУМНОЖ( в ячейке, чтобы инициировать формулу.
Шаг 3: Используйте ячейки первой матрицы, т. е. от A2 до C3, в качестве первого аргумента массива в формуле для умножения матриц. Поставьте запятую (» ,») после установки первого массива в формуле.
Шаг 4: Используйте ячейки второй матрицы, т. е. от E2 до F4, в качестве аргумента второго массива по формуле для умножения матриц. Закройте скобки, чтобы завершить эту формулу.
Шаг 5: Теперь формула готова. Но не нажимайте кнопку Enter напрямую. Помните, что функция МУМНОЖ является функцией массива. Вместо нажатия Enter используйте Ctrl + Shift + Enter , чтобы получить вывод этой формулы.
Вы получите результат умножения/произведения двух матриц в ячейках A7:B8, как показано ниже:
Обратите внимание на фигурные открывающие и закрывающие скобки, в которые заключена формула для MMULT. Эти фигурные скобки указывают на то, что введенная нами формула является формулой массива или применяется к массивам.
Эти фигурные скобки указывают на то, что введенная нами формула является формулой массива или применяется к массивам.
Как работает формула? Давайте посмотрим ниже:
Умножение матриц похоже на то, что каждый элемент каждой строки из первой матрицы умножается на каждый элемент каждого столбца из другой матрицы. Затем мы суммируем все значения по элементам, чтобы получить одно значение. Первая строка для первой матрицы — это 2, 6, 3, а первый столбец второй матрицы имеет значения 2, 7, 4. Продолжая поэлементное умножение, мы получим —
(2*2) = 4, (6*7) = 42 и (3*4) = 12 в результате умножения. Теперь мы сложим эти три значения вместе, чтобы получить первый элемент результирующей матрицы.
4 + 42 + 12 = 58.
Таким образом, первый элемент результирующей матрицы будет равен 58.
Пример 2. Использование MMULT для умножения двух матриц
Предположим, у нас есть две матрицы с тремя строками, как показано ниже. и три столбца:
Мы будем использовать MMULT, чтобы получить произведение этих двух матриц и получить из него новую матрицу, называемую результирующей матрицей, которую можно сохранить в A7: C9. .
.
Поскольку у нас есть три строки в первом столбце и такое же количество столбцов во второй матрице, результирующая матрица будет матрицей с тремя строками и тремя столбцами.
Шаг 1: Выберите все ячейки в A7:C9 в Resultant Matrix и введите формулу для МУМНОЖ в ячейке A7.
Шаг 2: Используйте первую матрицу в качестве первого аргумента функции МУМНОЖ, которая распределена по ячейкам A2:C4. Используйте запятую, чтобы отделить первый аргумент от второго.
Шаг 3: Используйте вторую матрицу в качестве аргумента второго массива в функции МУМНОЖ, которая распределена по E2:G4. Завершите формулу, добавив закрывающую скобку.
Шаг 4: Теперь нажмите Ctrl + Shift + Enter , чтобы получить вывод этой формулы массива вместо нажатия клавиши Enter. Вы получите вывод, как показано ниже:
Вот как мы можем использовать функцию МУМНОЖ, чтобы получить умножение матриц для двух массивов матриц. Давайте подведем итоги, вспомнив некоторые моменты:
Давайте подведем итоги, вспомнив некоторые моменты:
Что нужно помнить
- Поскольку функция МУМНОЖ возвращает значение массива, его необходимо вводить как формулу массива. Чтобы это произошло, вы должны использовать кнопку Ctrl + Shift + Enter вместо нажатия кнопки во время выполнения формулы МУМНОЖ.
- Вы получите #ЗНАЧ! ошибка, если количество строк из первой матрицы и столбца из второй матрицы не совпадают. Кроме того, если какая-либо из ячеек пуста или в ней хранятся текстовые значения для какой-либо матрицы, мы получим ту же ошибку.
- Мы можем получить ошибку #Н/Д, если мы выбрали ячейки в результирующей матрице, которые не являются ее частью.
Рекомендуемые статьи
Это руководство по MMULT в Excel. Здесь мы обсуждаем, как использовать MMULT в Excel вместе с практическими примерами и загружаемым шаблоном Excel. Вы также можете ознакомиться с другими нашими рекомендуемыми статьями —
- Excel Match Multiple Criteria
- Матрица в Excel
- Обратная матрица в Excel
- Матрица корреляции Excel
Умножение матриц в Excel — замена MMULT на Power Query
В моем последнем сообщении с благодарностью я предположил, что умножение матриц не является сильной стороной Excel. После этого поста я получил классное решение Power Query от Имке Фельдманн, автора ThedBIccountant.com, которое выполняет умножение матриц с помощью Power Query.
После этого поста я получил классное решение Power Query от Имке Фельдманн, автора ThedBIccountant.com, которое выполняет умножение матриц с помощью Power Query.
Итак, сегодня я решил поделиться с вами своей версией умножения матриц с использованием Power Query. Я с нетерпением жду ваших комментариев.
Прежде чем мы начнем, если вы настаиваете на использовании Excel для умножения матриц, давайте объясним, почему вам следует рассмотреть параметр Power Query вместо формулы массива MMULT в Excel.
Функция МУМНОЖ в Excel требует ручного выбора новых размеров матрицы A*B всякий раз, когда одна из ваших матриц A или B меняет свои размеры.
Например, если A является матрицей 3×2 и B — матрица 2×4. A*B должна быть матрицей 3×4. (Если вы забыли определение умножения матриц, перейдите сюда).
Теперь представьте, что матрица A увеличивается на одну строку, поэтому она становится матрицей 4×2, что должно сделать A*B матрицей 4×4. В результате, если вы используете MMULT , вы должны вручную выбрать новый диапазон функции массива и нажать CTRL+Shift+Enter, чтобы вызвать его.
Использование MMULT может стать утомительным и повторяющимся ручным трудом, если матрица A постоянно расширяется новыми строками, или матрица B расширяется новыми столбцами. Я не завидую аналитикам данных, которым необходимо каждый раз обновлять свои рабочие книги необходимыми чреватыми ошибками ручными действиями.
К счастью для нас, у нас есть технология Power Query в Excel и Power BI. С помощью Power Query вы можете автоматизировать умножение матриц без необходимости выполнять ручные корректировки при изменении размеров.
Загрузите эту книгу, чтобы увидеть версию Power Query для умножения матриц в действии.
В этой общей книге у нас есть матрица A и матрица B в виде двух именованных диапазонов MatrixA и MatrixB . В частности, диапазон B6:G9 определяется как диапазон имен MatrixA , а диапазон I6:K11 os определяется как MatrixB .
Теперь, используя приведенное ниже выражение Power Query M, вы можете выполнить матричное умножение A*B .
(В общей книге вы получаете все, чтобы начать перемножать матрицы, поэтому, если вы не являетесь экспертом по Power Query, вы можете пропустить этот блок кода).
лет
MatrixA = Excel.CurrentWorkbook(){[Name="MatrixA"]}[Содержание],
MatrixB = Excel.CurrentWorkbook(){[Name="MatrixB"]}[Содержание],
RowIndices = List.Numbers(0,Table. RowCount(MatrixA)),
ColumnIndices = List.Numbers(0,Table.ColumnCount(MatrixB)),
#"Преобразовано в таблицу" = Таблица.ИзСписка(
RowIndices, Splitter.SplitByNothing(), null, null, ExtraValues.Error),
#"Переименованные столбцы" = Table.RenameColumns(#"Преобразованы в таблицу",
{{"Столбец1", "Строка"}}),
#"Добавленный пользовательский" = Table.AddColumn(#"Переименованные столбцы", "Пользовательский",
каждый индекс столбца),
#"Переименованные столбцы1" = Table.RenameColumns(#"Добавлено пользовательское",
{{"Пользовательский", "Столбец"}}),
#"Расширенный пользовательский" = Table.ExpandListColumn(#"Переименованные столбцы1", "Столбец"),
#"Добавленный пользовательский1" = Table.AddColumn(#"Расширенный пользовательский", "Данные строки",
каждый Record.FieldValues(MatrixA{[Row]})),
MatrixBColumns = Table.ToColumns(MatrixB),
#"Добавлен пользовательский2" = Table.AddColumn(#"Добавлен пользовательский1", "Данные столбца",
каждый MatrixBColumns{[Столбец]}),
fnMatrixProduct = (список1, список2) =>
Список.
RowCount(MatrixA)),
ColumnIndices = List.Numbers(0,Table.ColumnCount(MatrixB)),
#"Преобразовано в таблицу" = Таблица.ИзСписка(
RowIndices, Splitter.SplitByNothing(), null, null, ExtraValues.Error),
#"Переименованные столбцы" = Table.RenameColumns(#"Преобразованы в таблицу",
{{"Столбец1", "Строка"}}),
#"Добавленный пользовательский" = Table.AddColumn(#"Переименованные столбцы", "Пользовательский",
каждый индекс столбца),
#"Переименованные столбцы1" = Table.RenameColumns(#"Добавлено пользовательское",
{{"Пользовательский", "Столбец"}}),
#"Расширенный пользовательский" = Table.ExpandListColumn(#"Переименованные столбцы1", "Столбец"),
#"Добавленный пользовательский1" = Table.AddColumn(#"Расширенный пользовательский", "Данные строки",
каждый Record.FieldValues(MatrixA{[Row]})),
MatrixBColumns = Table.ToColumns(MatrixB),
#"Добавлен пользовательский2" = Table.AddColumn(#"Добавлен пользовательский1", "Данные столбца",
каждый MatrixBColumns{[Столбец]}),
fnMatrixProduct = (список1, список2) =>
Список. Сумма(
Список.Создать(
()=>[A=список1,B=список2, индекс=0],
каждый [Индекс] < List.Count([A]),
каждый [A=[A],B=[B],индекс =[индекс]+1],
каждый [A]{[Индекс]}*[B]{[Индекс]}
)
),
#"Добавлено Custom3" = Table.AddColumn(#"Добавлено Custom2",
«Пользовательский», каждый fnMatrixProduct([Данные строки],[Данные столбца])),
#"Удаленные столбцы" = Table.RemoveColumns(#"Добавлено Custom3",
{"Данные строки", "Данные столбца"}),
#"Сводная колонка" = Table.Pivot(Table.TransformColumnTypes(#"Удаленные колонки",
{{"Столбец", введите текст}}, "en-US"),
List.Distinct(Table.TransformColumnTypes(#"Удаленные столбцы",
{{"Столбец", введите текст}}, "en-US")[Столбец]), "Столбец", "Пользовательский")
в
# "Поворотная колонна"
Сумма(
Список.Создать(
()=>[A=список1,B=список2, индекс=0],
каждый [Индекс] < List.Count([A]),
каждый [A=[A],B=[B],индекс =[индекс]+1],
каждый [A]{[Индекс]}*[B]{[Индекс]}
)
),
#"Добавлено Custom3" = Table.AddColumn(#"Добавлено Custom2",
«Пользовательский», каждый fnMatrixProduct([Данные строки],[Данные столбца])),
#"Удаленные столбцы" = Table.RemoveColumns(#"Добавлено Custom3",
{"Данные строки", "Данные столбца"}),
#"Сводная колонка" = Table.Pivot(Table.TransformColumnTypes(#"Удаленные колонки",
{{"Столбец", введите текст}}, "en-US"),
List.Distinct(Table.TransformColumnTypes(#"Удаленные столбцы",
{{"Столбец", введите текст}}, "en-US")[Столбец]), "Столбец", "Пользовательский")
в
# "Поворотная колонна" Вы можете увидеть результат, который представляет собой матрицу A*B в общей книге. Чтобы обновить расчет, щелкните Данные -> Обновить Все или просто обновите запрос MatrixAB на панели Запросы рабочей книги.
Примечание. Всякий раз, когда одна из матриц изменяется по значению или измерению, при обновлении рабочей книги будет загружаться результат.
Если вы опытный пользователь Power Query и хотите узнать, как работает приведенное выше выражение, сообщите мне об этом.
В этом посте я сосредоточусь только на основном преобразовании, которое использует функцию List.Generate , чтобы выполнить вычисление основного матричного умножения отдельной ячейки в матрице A*B .
В приведенном выше выражении M мы используем функцию fnMatrixProduct , которая использует List.Generate для перебора заданной строки из 9 столбца и B и вычислить одну ячейку в A*B .
fnMatrixProduct = (список1, список2) =>
Список.Сумма(
List.Generate(()=>[A=list1,B=list2, Index=0],
каждый [Индекс] < List. Count([A]),
каждый [A=[A],B=[B],индекс =[индекс]+1],
each [A]{[Index]}*[B]{[Index]})),
Count([A]),
каждый [A=[A],B=[B],индекс =[индекс]+1],
each [A]{[Index]}*[B]{[Index]})), Поскольку Power Query использует функциональный язык для преобразования, он не предназначен для выполнения итераций цикла, ну, по крайней мере, не напрямую. Итак, мы используем List.Generate для перебора двух входных списков и создания нового списка, элементы которого являются произведением элементов во входных списках.
Функция List.Generate состоит из 4 аргументов (подробнее здесь):
| Аргумент | Описание |
|---|---|
| начало | Функция, предоставляющая начальное значение |
| состояние | Условие, управляющее последовательностью генерации |
| следующий | Функция, которая генерирует следующее значение для итерации |
| Трансформатор | Функция преобразования для применения к каждому элементу в списке |
Давайте объясним, как мы реализовали здесь каждый аргумент:
List.Generate( ()=>[A=список1,B=список2, индекс=0], каждый [Индекс] < List.Count([A]), каждый [A=[A],B=[B],индекс =[индекс]+1], каждый [A]{[Index]}*[B]{[Index]}) ),
Часть 1: «Начало» аргумент
()=>[A=list1,B=list2, Index=0],
Этот аргумент содержит запись (пары ключ-значение, которые используются для определения состояния во время генерации списка). Запись используется в качестве начального состояния для нашего цикла, и к ней можно получить доступ и изменить ее на каждом этапе итерации. Назначаем ключ A со значением список1 и ключ B со значением список2 . Последнее поле в записи используется для текущего индекса.
Часть 2: «Условие» аргумент
каждый [Индекс] < List.Count([A]),
Эта часть содержит условие, которое должно выполняться на каждой итерации. Когда условие не выполняется, генерация нового списка останавливается. С Индекс начинается с нуля, мы должны прекратить генерировать список, когда индекс равен одному из размеров списков.
С Индекс начинается с нуля, мы должны прекратить генерировать список, когда индекс равен одному из размеров списков.
Часть 3: «Следующий» аргумент
каждый [A=[A],B=[B],Index =[Index]+1],
Этот аргумент определяет изменения, которые мы должны выполнить в записи, до следующей итерации. В нашем случае мы сохраняем ключи A и B с исходными списками ввода и увеличиваем индекс на 1.
Часть 4: «преобразователь» аргумент
каждый [A]{[Index]}*[B ]{[Индекс]}) Этот аргумент содержит основной этап расчета. Он определяет арифметическую операцию, которую мы выполняем, когда генерируем k-й элемент в новом списке. Мы читаем k-е значения в каждом списке и умножаем их. Результат сохраняется как новый элемент в списке.
Результатом List.Generate является список продуктов. Теперь нам просто нужно применить ∑ часть формулы выше, и для этого мы можем использовать функцию List. Sum .
Sum .
fnMatrixProduct = (список1, список2) => Список.Сумма( List.Generate(...),
На сегодня это все. В моем следующем сообщении в блоге я могу пойти дальше и объяснить остальную часть запроса. Но никаких обещаний 🙂
Я завершаю эту запись в блоге, я буду рад услышать ваши отзывы и узнать больше о ваших сценариях использования матричного умножения в Excel. Я уверен, что новая методика намного лучше, чем классическая формула массива MMULT.
Обновление: 06.06.2016 : Оказывается, приведенный выше запрос относительно медленный. Я получил более быстрые версии от Билла Шиша и Имке Фельдманн. Я обновил более быстрый запрос здесь и новую запись в блоге с пошаговыми инструкциями.
Enjoy,
Gil
Три способа умножения матриц в Excel — Фастай часть-2, урок-8 | by Aman Arora
Наконец-то вышла вторая часть fastai «From the Foundations» . Я не помню, когда в последний раз я был так взволнован МООК. Как только курс был выпущен для широкой публики, я начал копаться в нем, чтобы углубить свое понимание глубокого обучения и лежащих в его основе концепций.
Как только курс был выпущен для широкой публики, я начал копаться в нем, чтобы углубить свое понимание глубокого обучения и лежащих в его основе концепций.
На этот раз я решил последовать совету Джереми и Рэйчел и вести блоги. Эта конкретная статья объясняет различных методов умножения матриц, , которые Джереми реализует в Уроке-8. Я буду использовать Microsoft Excel для иллюстрации.
Итак, приступим!
Умножение матриц
Отличное интерактивное место для понимания умножения матриц, на которое ссылается Джереми, доступно по адресу:
matrixmultiplication.xyz По сути, как видно из изображения, мы берем транспонированную вторую матрицу, умножаем и складываем элементы вместе, чтобы получить результат. Например, самый первый элемент 15 в результирующей матрице получается из 1*2 + 6*2 + 1*1 = 2 + 12 + 1 = 15 .
Хотя это объяснение визуально приятно, по моему скромному мнению, его трудно преобразовать в код. Итак, давайте использовать Excel и понять умножение матриц по-другому!
Итак, давайте использовать Excel и понять умножение матриц по-другому!
Умножение матриц в EXCEL
Рассмотрим две матрицы A и B размером 4x3 и 3x4 .
Примечание. Я буду использовать жирные обозначения A и B для обозначения матриц в этой статье. Общепринятой практикой является выделение векторов и матриц жирным шрифтом.
Из изображения, которое мы видели раньше, если вы помните, мы транспонировали B и умножили строки A на столбцы B , чтобы получить результирующую матрицу. Скорее, давайте на этот раз пропустим этот шаг транспонирования и сразу умножим строки и столбцы.
Таким образом, строка 0 матрицы A умножается на столбец 0 матрицы B поэлементно, и результирующие поэлементные произведения добавляются, чтобы получить первый элемент результирующей матрицы C в позиции [0][0] .
Вот как это выглядит в Excel:
C[0][0] = 1*1 + 10*5 + 100*9 = 1 + 50 + 900 = 951 Аналогично получаем C[0][ 3] путем поэлементного умножения строки 0 A и столбца 3 B. В excel это выглядит так:
И, наконец, мы следуем тому же процессу, чтобы пройти каждый пустой блок в C , чтобы получить окончательный результат .
C[3][3] = 4*4 + 40*8 + 400*12 = 16 + 320 + 4800 = 5136Вот так! Вот как мы делаем матричное умножение! Это было легко, не так ли? Теперь мы не только поняли принцип умножения матриц, но и реализовали его в Excel! Как это круто?
Я лично считаю, что теперь вы готовы обращаться с некоторыми правилами, связанными с умножением матриц (или короче MatMul ):
- Пусть
ar,acбудет количеством строк и столбцов в A. Аналогично, пустьbr, bcбудет количеством строк и столбцов в B. Тогда для выполнить умножение матриц необходимо, чтобы
Тогда для выполнить умножение матриц необходимо, чтобы ac == br. Почему? Ну, как вы видели в Excel, мы умножали строки и столбцы поэлементно, а затем добавляли промежуточные продукты, чтобы получить окончательный результат. Если есть несоответствие размеров, и один вектор длиннее другого, мы больше не можем выполнять поэлементное умножение! - Размеры результирующей матрицы всегда будут
ar,bc. То есть количество строк происходит от A , а количество столбцов происходит от B.
Метод 1: использование 3 циклов FOR
Вот еще один отказ от ответственности, при реализации матричного умножения в Excel мы не только понял это, но мы также воспроизвели первый метод Джереми, который использовал 3 цикла FOR. Вот как это выглядит в коде:
def matmul1(a,b):
ar,ac = a.shape
br,bc = b.shape
assert ac==br
c = torch.zeros(ar, bc)
для i в диапазоне (ar):
для j в диапазоне (bc) :
для k в диапазоне (ac): #or br
c[i,j] += a[i,k]*b[k,j]
return c
Надеюсь, теперь вы можете понять это лучше. Если нет, то самое время сделать паузу, поэкспериментировать с кодом и посмотреть, что на самом деле происходит. Я обещаю вам, это то же самое, что и наша версия Excel!
Если нет, то самое время сделать паузу, поэкспериментировать с кодом и посмотреть, что на самом деле происходит. Я обещаю вам, это то же самое, что и наша версия Excel!
Хорошо, я предполагаю, что вы потратили некоторое время на обдумывание кода, так что давайте его обсудим!
- Почему первые две петли в диапазоне
(ar)и диапазоне(bc)? Ну, как вы помните из Rule-2 , наша результирующая матрица будет иметь размерыar,bc. А из Excel мы увидели, что мы обходим каждый элемент C один за другим, поэтому для обходаarстрок иbcстолбцов нам нужно 2 цикла FOR вrange(ar)иrange(bc). - Итак, почему третий цикл FOR в диапазоне
(ac) #or br? Что ж, из Rule-1 мы знаем, чтоac==br, поэтому на самом деле не имеет значения, поместим ли мыrange(ac)илиrange(br)в третий цикл. По сути, это то место, где отдельные элементы умножаются и складываются. Из нашего предыдущего примера Excel для
По сути, это то место, где отдельные элементы умножаются и складываются. Из нашего предыдущего примера Excel для C[0][0]шагC[0][0] = 1*1 + 10*5 + 100*9 = 1 + 50 + 900 = 951произойдет, и, наконец, мы перейдем к следующему блоку. Количество элементов, которые умножаются и складываются вместе, равно 9.0287 ак или бр .
Вот это да! Это метод-1 для вас! Вот песня на память о Matrix Multiplication. (Я узнал об этом впервые из fast.ai, автор оригинала неизвестен)
Надеюсь, теперь вы понимаете, как две матрицы перемножаются друг с другом. Если нет, вот еще один учебник от Академии Хана.
Способ 2: Использование поэлементного умножения
Итак, до сих пор мы анализировали каждую позицию в результирующей матрице C, нахождение отдельных поэлементных произведений и последующее их суммирование. Если вы помните, что-то вроде C[0][0] = 1*1 + 10*5 + 100*9 = 1 + 50 + 900 = 951 . Конечно, должен быть другой путь? Что, если вместо того, чтобы делать отдельные произведения, а затем суммировать их, мы умножаем векторы за один раз, чтобы получить результирующий вектор и суммировать результирующий вектор, чтобы получить конечный элемент?
m = тензор([1, 2, 3])
n = тензор([10, 10, 10])
m*n>>tensor([10, 20, 30])
До сих пор мы находили отдельные продукты 10, 20, 30 и складывали их вместе 10 + 20 + 30 = 60 . Но, действительно, все это можно заменить на:
Но, действительно, все это можно заменить на:
m = tensor([1, 2, 3])
n = tensor([10, 10, 10])
(m*n).sum()>> tensor(60)
Если вы помните, самый внутренний цикл в range(ac) #or br находил отдельные продукты и добавлял их. Что ж, мы можем заменить этот цикл на векторное поэлементное произведение и поставить .sum() в конце концов, и PyTorch/NumPy могут выполнять за нас поэлементные операции!
Вот как это выглядит в Excel:
C[0][0] = sum(A[row 0] * B[col 0]) Точно так же мы получаем C[0][3] , умножая вектор в строке 0 A с вектором в столбце 3 B и суммированием полученного вектора.
И, наконец, мы следуем тому же процессу, чтобы пройти каждый пустой блок в C , чтобы получить окончательный результат.
C[3][3] = сумма(A[строка 3] * B[столбец 3]) Обратите внимание, чем это отличается от Method-1 ? На этот раз мы просто говорим Excel или PyTorch, чтобы они умножили строку 0 из A на столбец 0 из B и просуммировали полученный вектор, чтобы дать нам ответ. Вместо
Вместо 1*1 + 10*5 + 100*9 . Например, для C[0][0] этот метод умножает вектор в строке 0 A tensor([1,10,100]) на вектор в столбце 0 B тензор{[1,5,9]) для получения промежуточного продукта Vector тензор([1,50,900]) и суммирует его, чтобы получить результат в позиции C[0][0] как тензор(951) .
В коде это выглядит так:
def matmul2(a,b):
ar,ac = a.shape
br,bc = b.shape
assert ac==br
c = torch.zeros(ar, bc)
для i в диапазоне (ar):
для j в диапазоне (bc):
c[i,j] = (a[i,:]*b[:,j]).sum()
return c
Итак, мы просто анализируем каждую позицию C, , используя два цикла FOR, и введите соответствующий результат в этой позиции. Если i,j представляют позицию строки и столбца в C , это выглядит примерно так..
i:0,j:0
a:tensor([ 1, 10, 100]),b:tensor([ 1, 5, 9])
тензор([[951., 0., 0., 0.],
[ 0., 0., 0., 0.],
[ 0., 0., 0. , 0.],
[ 0., 0., 0., 0.]])
---
i:0,j:1
a:tensor([ 1, 10, 100]),b:tensor ([ 2, 6, 10])
тензор([[ 951., 1062., 0., 0.],
[0., 0., 0., 0.],
[0., 0., 0., 0.],
[0., 0., 0., 0.]])
---
i:0,j:2
a:tensor([ 1, 10, 100]),b:tensor([ 3, 7, 11])
tensor([[ 951., 1062., 1173., 0. ],
[0., 0., 0., 0.],
[0., 0., 0., 0.],
[0., 0., 0., 0.]])
- --
i:0,j:3
a:tensor([ 1, 10, 100]),b:tensor([ 4, 8, 12])
tensor([[ 951., 1062., 1173., 1284.],
[0., 0., 0., 0.],
[0., 0., 0., 0.],
[ 0., 0., 0., 0.]])
---
i:1,j:0
a:tensor([ 2, 20, 200]),b:tensor([1, 5 , 9])
тензор([[ 951., 1062., 1173., 1284.],
[1902., 0., 0., 0.],
[0., 0., 0., 0. ],
[ 0., 0., 0., 0.]])
И так далее.. пока не получим полную матрицу C .
тензор([[ 951., 1062., 1173., 1284.],
[1902., 2124., 2346., 2568.],
[2853., 3186., 3519., 3852.],
[3804., 4248., 4692., 5136.]])
Метод-3: Трансляция
Заметили здесь общую тему? Каждый раз мы должны умножать каждую строку A на каждый столбец B , чтобы получить C . Вы замечаете повторение? Мы умножаем один и тот же вектор строки в A bc раз! И мы повторяем этот процесс или раз!
Есть ли способ умножить вектор-строку A на все столбцы B , чтобы получить соответствующую строку в C? Да, есть! Введите трансляцию…
Примечание: я не буду объяснять трансляцию, Джереми отлично с ней справляется.
Вместо этого давайте посмотрим, что представляет собой этот волшебный фрагмент кода
для i в диапазоне (ar):
c[i] = (a[i,:].unsqueeze(-1).expand_as(b)*b) .sum(dim=0)
Как обычно, реплицируем в Excel! Это действительно упростит задачу. Давайте сделаем это по шагам.
Давайте сделаем это по шагам.
Шаг-1) Выберите i-ю строку A a[i,:] . Мы выбираем строку 0 в качестве примера.
Шаг 2) Взять ее Транспонировать a[i,:].unsqueeze(-1)
Шаг 3) Расширить матрица столбцов как B a[i,:].unsqueeze(-1).expand_as(b)
Шаг 4) Поэлементно умножить на B a[i, :].unsqueeze(-1).expand_as(b)*b
Шаг 5) Суммировать по строкам, чтобы получить строку 0 C
Суммируйте размер боковой строки, чтобы получить строку 0 CПолный процесс трансляции для каждой строки A выглядит примерно так:
Трансляция в целом Я надеюсь, что к настоящему времени вы получили Трансляция ! Итак, давайте посмотрим, как это выглядит в коде. .zeros(ar,bc)
.zeros(ar,bc)
для i в диапазоне (ar):
c[i] = (a[i,:].unsqueeze(-1).expand_as(b)*b).sum(dim=0)
print(f"i:{i}")
print(c)
return c
Вывод выглядит так:
i:0
tensor([[ 951., 1062., 1173., 1284.],
[0., 0., 0., 0.],
[0., 0., 0., 0.],
[0., 0., 0., 0.]])
i:1
тензор([[ 951., 1062., 1173., 1284.],
[1902., 2124., 2346., 2568.],
[0., 0., 0., 0.],
[ 0., 0., 0., 0.]])
i:2
тензор([[ 951., 1062., 1173., 1284.],
[1902., 2124., 2346., 2568.] ,
[2853., 3186., 3519., 3852.],
[ 0., 0., 0., 0.]])
i:3
тензор([[ 951., 1062., 1173., 1284 .],
[1902., 2124., 2346., 2568.],
[2853., 3186., 3519., 3852.],
[3804., 4248., 4692., 5136.]])
Это именно то, что мы ожидаем, и такое же, как наша версия Excel !
Вот и все! Мы успешно рассмотрели три метода матричного умножения, включая широковещательную передачу.
Лист Google для иллюстрации выше можно найти здесь . Спасибо за чтение! Если у вас есть какие-либо вопросы, пожалуйста, не стесняйтесь обращаться ко мне по адресу https://linkedin.com/in/aroraaman/.
Спасибо за чтение! Если у вас есть какие-либо вопросы, пожалуйста, не стесняйтесь обращаться ко мне по адресу https://linkedin.com/in/aroraaman/.
| Дата | да |
| Прибавление (вычитание) дней к дате | |
| Объединение дат | |
| Преобразование даты в число | |
| Преобразование даты в текст | |
| От имени месяца до номера | |
| Создание диапазона дат из дат | |
| Номер дня года | |
| Название месяца с даты | |
| Первый день месяца | |
| Добавление (вычитание) недель к дате | |
| Если функции с датами | |
| Максимальная дата | |
| Количество дней между датами | |
| Количество дней в месяце | |
| Количество недель между датами | |
| Количество лет между датами | |
| Разбить дату и время на отдельные ячейки | |
| Обратный отсчет оставшихся дней | |
| Вставка дат | |
| Генератор случайных дат | |
| Использование динамических диапазонов — значения с начала года | |
| Прибавление (вычитание) лет к дате | |
| Примеры формул даты | |
| Извлечение дня из даты | |
| Получить название дня из даты | |
| Подсчет оставшихся дней в месяце/годе | |
| Подсчет оставшихся рабочих дней в месяце/годе | |
| Получить последний день месяца | |
| Последний рабочий день месяца/года | |
| Количество рабочих/рабочих дней в месяце | |
| Сокращения для рабочих дней | |
| Автоматическое заполнение дат | |
| Количество месяцев между датами | |
| Четверть с даты | |
| Годы службы | |
| Изменить формат даты | |
| Сравнение дат | |
| Время | да |
| Добавить (вычесть) часы ко времени | |
| Добавить (вычесть) минуты ко времени | |
| Добавить (вычесть) секунды ко времени | |
| Суммарное время (общее время) | |
| Разница во времени | |
| Изменить формат времени | |
| Преобразование минут в часы | |
| Преобразование времени в десятичное число | |
| Преобразование времени в часы | |
| Преобразование времени в минуты | |
| Преобразование времени в секунды | |
| Военное время | |
| Время раунда до ближайших 15 минут | |
| Калькулятор сверхурочной работы | |
| Количество часов между интервалами | |
| Преобразование секунд в минуты, часы или время | |
| Подсчет отработанных часов | |
| Разница во времени | |
| Формат времени — Показать минуты секунды | |
| Текст | да |
| Добавление запятых в ячейки | |
| Получить первое слово из текста | |
| Заглавная первая буква | |
| Очистка и форматирование номеров телефонов | |
| Удалить лишние пробелы в конце/в начале | |
| Добавить пробелы в ячейку | |
| Присвоение числового значения тексту | |
| Объединение ячеек с запятой | |
| Объединить имя и фамилию | |
| Преобразование текстовой строки в дату | |
| Преобразование текста в число | |
| Извлечение текста из ячейки | |
| Получить последнее слово | |
| Удаление ненужных символов | |
| Извлечение текста до или после символа | |
| Как разделить текстовую строку по пробелу, запятой и другим параметрам | |
| Удаление специальных символов | |
| Удалить первые символы слева | |
| Замена нескольких значений | |
| Переключение имен и фамилий с запятыми | |
| Удалить определенный текст из ячейки | |
| Извлечение текста между символами (например, скобки) | |
| Добавление ведущих нулей к числу | |
| Удалить разрывы строк из текста | |
| Удалить все цифры из текста | |
| Обратный текст | |
| Удалить нечисловые символы | |
| Удалить последний символ(ы) справа | |
| Отдельные имена и фамилии | |
| Отдельный текст и цифры | |
| Круглый | да |
| Круглые формулы | |
| Округлить цену до ближайшего доллара или цента | |
| Округлить до ближайших 10, 100 или 1000 | |
| Округлить до ближайших 5 или 0,5 | |
| Круглые проценты | |
| Округление до значащих цифр | |
| Подсчет | да |
| Подсчет пустых и непустых ячеек | |
| Подсчет ячеек между двумя числами | |
| Количество ячеек не равно | |
| Подсчет, если ячейки находятся в диапазоне | |
| Подсчет количества слов, появляющихся в ячейке | |
| Подсчет слов в ячейке | |
| Подсчет определенных символов в столбце | |
| Подсчет общего количества символов в столбце | |
| Подсчет ячеек, равных одному из двух результатов | |
| Подсчет ячеек, не содержащих | |
| Подсчет ячеек, содержащих определенный текст | |
| Подсчет уникальных значений в диапазоне | |
| Countif — Несколько критериев | |
| Подсчет общего количества ячеек в диапазоне | |
| Подсчет ячеек с любым текстом | |
| Подсчет всех ячеек в таблице | |
| Поиск | да |
| Двумерная ВПР | |
| ВПР Простой пример | |
| ВПР — несколько совпадений | |
| Поиск с учетом регистра | |
| ВПР с учетом регистра | |
| Сумма, если - ВПР | |
| Поиск с учетом регистра | |
| ВПР с учетом регистра | |
| Поиск дубликатов с функцией ВПР или ПОИСКПОЗ | |
| ИНДЕКС СООТВЕТСТВИЕ | |
| Поиск — возврат адреса ячейки (не значение) | |
| Поиск последнего значения в столбце или строке | |
| Обратный ВПР (справа налево) | |
| Сегмент оценки риска с функцией ВПР | |
| Сумма с функцией ВПР | |
| ВПР И НЕПРЯМАЯ | |
| ВПР Объединение | |
| ВПР содержит (частичное совпадение) | |
| 17 причин, почему XLOOKUP не работает | |
| Двойной (вложенный) XLOOKUP — динамические столбцы | |
| ЕСЛИОШИБКА (& IFNA) XLOOKUP | |
Поиск мин. /макс. значения /макс. значения | |
| Вложенная функция ВПР | |
| 11 лучших альтернатив ВПР (обновлено в 2022 году!) | |
| ВПР – Ссылка на динамическую колонку | |
| ВПР – Исправить ошибку № Н/Д | |
| ВПР – Несколько листов одновременно | |
| Комбинированный ВПР и ГПР | |
| ВПР И ПОИСКПОЗ Комбинированный | |
| ВПР между рабочими листами или электронными таблицами | |
| ВПР Повторяющиеся значения | |
| Буквенные оценки ВПР | |
| ВПР Возврат нескольких столбцов | |
| ВПР Возвращает 0? Вернуть пустой вместо | |
| ВПР без ошибки #Н/Д | |
| XLOOKUP Несколько листов одновременно | |
| XLOOKUP между рабочими листами или электронными таблицами | |
| XLOOKUP по дате | |
| XLOOKUP Повторяющиеся значения | |
| XLOOKUP Множественные критерии | |
| XLOOKUP Вернуть несколько столбцов | |
| XLOOKUP Возвращает 0? Вернуть пустой вместо | |
| XLOOKUP Текст | |
| XLOOKUP с ЕСЛИ | |
| XLOOKUP с оператором If | |
| Разное | да |
| Сортировка нескольких столбцов | |
| Использовать значение ячейки в формуле | |
| Процентное изменение между числами | |
| Процентная разбивка | |
| Значения рангов | |
| Добавить пробелы в ячейку | |
| Формула CAGR | |
| Среднее время | |
| Десятичная часть числа | |
| Целая часть числа | |
| Сравнение элементов в списке | |
| Обработка ошибок NA() | |
| Получить имя листа | |
| Подстановочные знаки | |
| Гиперссылка на текущую папку | |
| Формула сложных процентов | |
| Увеличение в процентах | |
| Создание случайных групп | |
| Сортировка с использованием малых и больших функций | |
| Альтернативы энергонезависимой функции | |
| Уменьшение числа на процент | |
| Расчет процентной дисперсии | |
| Калькулятор маржи прибыли | |
| Преобразование номера столбца в букву | |
| Получить полный адрес именованного диапазона | |
| Вставить имя файла | |
| Путь вставки | |
| Функции широты/долготы | |
| Замена отрицательных значений | |
| Диапазон обратного списка | |
| Преобразование названия штата в аббревиатуру | |
| Создание динамических гиперссылок | |
| Пользовательский список сортировки с формулой | |
| Проверка данных — пользовательские формулы | |
| Динамический справочник листа (КОСВЕННЫЙ) | |
| Справочная ячейка в другом листе или книге | |
| Получить значение ячейки по адресу | |
| Получить имя листа | |
| Увеличение ссылки на ячейку | |
| Список имен листов | |
| Список пропущенных номеров в последовательности | |
| Адрес возврата максимального значения в диапазоне | |
| Поиск по ключевым словам | |
| Выбрать каждую вторую (или каждую n-ю) строку | |
| Основы | да |
Основы ссылок на ячейки — A1, R1C1, 3d и т. д. д. | |
| Сложение (сумма) всего столбца или строки | |
| В формулы динамического массива | |
| Преобразования | да |
| Преобразование часовых поясов | |
| Преобразование градусов Цельсия в градусы Фаренгейта | |
| Преобразование фунтов в килограммы | |
| Преобразование времени в время Unix | |
| Преобразование футов в метры | |
| Преобразование сантиметров в дюймы | |
| Преобразование километров в мили | |
| Преобразование дюймов в футы | |
| Преобразование даты в юлианский формат | |
| Преобразование буквы столбца в число | |
| Тесты | да |
| Проверить, содержит ли диапазон какой-либо текст | |
| Проверить, является ли какая-либо ячейка в диапазоне номером | |
| Проверить, содержит ли ячейка конкретное значение | |
| Проверить, содержит ли ячейка любое число | |
| Проверить, содержит ли ячейка определенный номер | |
| Проверить, является ли ячейка числом или текстом | |
| Если | да |
| Процентиль Если | |
| Промежуточный итог Если | |
| Суммарное произведение Если | |
| Большой, если и Маленький, если | |
| Медиана Если | |
| Объединить, если | |
| Максимум Если | |
| Ранг | |
| ТЕКСТОВОЕ СОЕДИНЕНИЕ Если | |
| Сумма | да |
| Сумма, если - начинается с / заканчивается на | |
| Сумма, если - месяц или год до даты | |
| Сумма, если - по годам | |
| Сумма, если - пусто/не пусто | |
| Сумма, если - Горизонтальная сумма | |
| Количество/сумма If - Цвет ячейки | |
| НЕПРЯМАЯ Сумма | |
| Сумма если - по нескольким листам | |
| Сумма, если - по месяцам | |
| Сумма, если - ячейки не равны | |
| Сумма, если не пусто | |
| Сумма между значениями | |
| Сумма, если - номер недели | |
| Сумма Текст | |
| Сумма, если - по категориям или группам | |
| Сумма, если - ячейка содержит определенный текст (подстановочные знаки) | |
| Сумма if - Date Rnage | |
| Сумма, если - даты равны | |
| Сумма, если - День недели | |
| Сумма, если больше | |
| Сумма, если меньше | |
| В среднем | да |
| Средние ненулевые значения | |
| Среднее значение, если не пусто | |
| Среднее — игнорировать 0 | |
| Среднее — игнорировать ошибки | |
| Математика | да |
| Таблица умножения | |
| Кубические корни | |
| Энные корни | |
| Квадратные цифры | |
| Квадратные корни | |
| Расчеты | да |
| Рассчитать отношение | |
| Рассчитать возраст | |
| УБИТЬ | |
| Расчет платежей по кредиту | |
| Формула среднего балла | |
| Расчет НДС | |
| Как оценивать формулы | |
| Найти | да |
| Поиск числа в столбце/рабочей книге | |
| Поиск наиболее частых номеров | |
| Поиск наименьших n значений | |
| Найти n-е вхождение символа в текст | |
| Поиск и извлечение числа из строки | |
| Поиск самой ранней или самой поздней даты на основе критериев | |
| Найти первую ячейку с любым значением | |
| Найти последнюю строку | |
| Найти последнюю строку с данными | |
| Поиск недостающих значений | |
| Поиск наибольших n значений | |
| Самый частый номер | |
| Условное форматирование | да |
| Условный формат — дата и время | |
| Условный формат — выделение пустых ячеек | |
| Новые функции | |
| XLOOKUP | Заменяет VLOOKUP, HLOOKUP и INDEX/MATCH |
| Логический | да |
| И | Проверяет выполнение всех условий. ИСТИНА/ЛОЖЬ ИСТИНА/ЛОЖЬ |
| IF | Если условие выполнено, сделать что-то, если нет, сделать что-то еще. |
| ЕСЛИОШИБКА | Если результатом является ошибка, сделайте что-нибудь еще. |
| NOT | Изменяет TRUE на FALSE и FALSE на TRUE. |
| ИЛИ | Проверяет выполнение каких-либо условий. ИСТИНА/ЛОЖЬ |
| XOR | Проверяет, выполняется ли одно и только одно условие. ИСТИНА/ЛОЖЬ |
| Поиск и ссылка | да |
| ЛОЖЬ | Логическое значение: ЛОЖЬ. |
| ИСТИНА | Логическое значение: ИСТИНА. |
| АДРЕС | Возвращает адрес ячейки в виде текста. |
| ОБЛАСТИ | Возвращает количество областей в ссылке. |
| ВЫБОР | Выбирает значение из списка на основе его номера позиции. |
| СТОЛБЦ | Возвращает номер столбца ссылки на ячейку. |
| СТОЛБЦЫ | Возвращает количество столбцов в массиве. |
| HLOOKUP | Поиск значения в первой строке и возврат значения. |
| ГИПЕРССЫЛКА | Создает интерактивную ссылку. |
| ИНДЕКС | Возвращает значение на основе номеров столбца и строки. |
| НЕПРЯМАЯ | Создает ссылку на ячейку из текста. |
| ПРОСМОТР | Поиск значений по горизонтали или по вертикали. |
| ПОИСКПОЗ | Ищет значение в списке и возвращает его позицию. |
| СМЕЩЕНИЕ | Создает смещение привязки от начальной точки. |
| ROW | Возвращает номер строки ссылки на ячейку. |
| ROWS | Возвращает количество строк в массиве. |
| ТРАНСП | Меняет ориентацию диапазона ячеек. |
| ВПР | Поиск значения в первом столбце и возврат значения. |
| Дата и время | да |
| ДАТА | Возвращает дату из года, месяца и дня. |
| DATEDIF | Количество дней, месяцев или лет между двумя датами. |
| DATEVALUE | Преобразует дату, сохраненную в виде текста, в действительную дату |
| ДЕНЬ | Возвращает день в виде числа (1-31). |
| ДНЕЙ | Возвращает количество дней между двумя датами. |
| DAYS360 | Возвращает количество дней между двумя датами в 360-дневном году. |
| EDATE | Возвращает дату, отстоящую от начальной даты на n месяцев. |
| КОНМЕСЯЦ | Возвращает последний день месяца, за n месяцев до даты. |
| ЧАС | Возвращает час в виде числа (0-23). |
| МИНУТЫ | Возвращает минуты в виде числа (0-59). |
| МЕСЯЦ | Возвращает месяц в виде числа (1-12). |
| ЧИСТРАБДНИ | Количество рабочих дней между двумя датами. |
| NETWORKDAYS.INTL | Рабочие дни между двумя датами, настраиваемые выходные. |
| СЕЙЧАС | Возвращает текущую дату и время. |
| СЕКУНД | Возвращает секунды в виде числа (0-59) |
| ВРЕМЯ | Возвращает время из часов, минут и секунд. |
| TIMEVALUE | Преобразует время, сохраненное в виде текста, в допустимое время. |
| СЕГОДНЯ | Возвращает текущую дату. |
| ДЕНЬ НЕД | Возвращает день недели в виде числа (1-7). |
| WEEKNUM | Возвращает номер недели в году (1-52). |
| РАБДЕНЬ | Дата n рабочих дней от даты. |
| WORKDAY.INTL | Дата n рабочих дней от даты, настраиваемые выходные. |
| ГОД | Возвращает год. |
| YEARFRAC | Возвращает долю года между двумя датами. |
| Машиностроение | да |
| ПРЕОБРАЗОВАТЬ | Преобразовать число из одной единицы в другую. |
| Финансы | да |
| FV | Расчет будущей стоимости. |
| PV | Вычисляет текущую стоимость. |
| КПЕР | Вычисляет общее количество периодов платежей. |
| PMT | Расчет суммы платежа. |
| СТАВКА | Расчет процентной ставки. |
| NPV | Расчет чистой приведенной стоимости. |
| IRR | Внутренняя норма доходности для набора периодических КФ. |
| XIRR | Внутренняя норма доходности для набора непериодических КФ. |
| ЦЕНА | Рассчитывает цену облигации. |
| ДОХОД | Рассчитывает доходность облигации. |
| INTRATE | Процентная ставка полностью инвестированной ценной бумаги. |
| Информация | да |
| CELL | Возвращает информацию о ячейке. |
| ERROR.TYPE | Возвращает значение, представляющее ошибку ячейки. |
| IПУСТО | Проверить, пуста ли ячейка. ИСТИНА/ЛОЖЬ |
| ISERR | Проверяет, является ли значение ячейки ошибкой, игнорирует #N/A. ИСТИНА/ЛОЖЬ |
| ЕОШИБКА | Проверить, является ли значение ячейки ошибкой. ИСТИНА/ЛОЖЬ |
| ISEVEN | Проверка четности значения ячейки. ИСТИНА/ЛОЖЬ |
| ISFORMULA | Проверить, является ли ячейка формулой. ИСТИНА/ЛОЖЬ |
| НЕЛОГИЧНОСТЬ | Проверка логичности ячейки (ИСТИНА или ЛОЖЬ). ИСТИНА/ЛОЖЬ |
| ИСНА | Проверить, является ли значение ячейки #N/A. ИСТИНА/ЛОЖЬ |
| ISNONTEXT | Проверить, не является ли ячейка текстом (пустые ячейки не являются текстом). ИСТИНА/ЛОЖЬ ИСТИНА/ЛОЖЬ |
| ISNUMBER | Проверить, является ли ячейка числом. ИСТИНА/ЛОЖЬ |
| ISODD | Проверить, является ли значение ячейки нечетным. ИСТИНА/ЛОЖЬ |
| ISREF | Проверить, является ли значение ячейки ссылкой. ИСТИНА/ЛОЖЬ |
| ISTEXT | Проверить, является ли ячейка текстовой. ИСТИНА/ЛОЖЬ |
| N | Преобразует значение в число. |
| NA | Возвращает ошибку: #N/A. |
| TYPE | Возвращает тип значения в ячейке. |
| Математика | да |
| ABS | Вычисляет абсолютное значение числа. |
| АГРЕГАТ | Определение и выполнение вычислений для базы данных или списка. |
| ПОТОЛОК | Округляет число до ближайшего указанного кратного. |
| COS | Возвращает косинус угла. |
| ГРАДУСЫ | Преобразует радианы в градусы. |
| DSUM | Суммирует записи базы данных, соответствующие определенным критериям. |
| ЧЕТНЫЙ | Округляет до ближайшего четного целого числа. |
| EXP | Вычисляет экспоненциальное значение для заданного числа. |
| ФАКТ | Возвращает факториал. |
| ПОЛ | Округляет число в меньшую сторону до ближайшего указанного кратного. |
| НОД | Возвращает наибольший общий делитель. |
| INT | Округляет число в меньшую сторону до ближайшего целого числа. |
| LCM | Возвращает наименьшее общее кратное. |
| LN | Возвращает натуральный логарифм числа. |
| LOG | Возвращает логарифм числа по указанному основанию. |
| LOG10 | Возвращает логарифм числа по основанию 10. |
| MOD | Возвращает остаток после деления. |
| ОКРУГЛ | Округляет число до указанного кратного. |
| НЕЧЕТНОЕ | Округляет до ближайшего нечетного целого числа. |
| PI | Значение PI. |
| POWER | Вычисляет число, возведенное в степень. |
| ПРОИЗВЕД | Умножает массив чисел. |
| ЧАСТНОЕ | Возвращает целочисленный результат деления. |
| РАДИАНЫ | Преобразует угол в радианы. |
| RAND | Вычисляет случайное число от 0 до 1. |
| СЛУЧМЕЖДУ | Вычисляет случайное число между двумя числами. |
| ОКРУГЛ | Округляет число до указанного количества цифр. |
| ОКРУГЛ ВНИЗ | Округляет число в меньшую сторону (к нулю). |
| ОКРУГЛВВЕРХ | Округляет число в большую сторону (от нуля). |
| ЗНАК | Возвращает знак числа. |
| SIN | Возвращает синус угла. |
| SQRT | Вычисляет квадратный корень числа. |
| ПРОМЕЖУТОЧНЫЙ ИТОГ | Возвращает сводную статистику для серии данных. |
| СУММ | Складывает числа. |
| СУММЕСЛИ | Суммирует числа, соответствующие критерию. |
| СУММЕСЛИМН | Суммирует числа, соответствующие нескольким критериям. |
| СУММПРОИЗВ | Умножает массивы чисел и суммирует полученный массив. |
| TAN | Возвращает тангенс угла. |
| TRUNC | Усекает число до определенного количества цифр. |
| Статистика | да |
| СРЕДНЕЕ | Средние числа. |
| СРЗНАЧA | Средние числа. Включает текст и FALSE = 0, TRUE = 1. |
| СРЗНАЧЕСЛИ | Усредняет числа, соответствующие критерию. |
| СРЗНАЧЕСЛИМН | Усредняет числа, соответствующие нескольким критериям. |
| КОРРЕЛ | Вычисляет корреляцию двух рядов. |
| COUNT | Подсчет ячеек, содержащих числа. |
| COUNTA | Подсчет непустых ячеек. |
| COUNTBLANK | Подсчет пустых ячеек. |
| СЧЁТЕСЛИ | Подсчитывает ячейки, соответствующие критерию. |
| СЧЁТЕСЛИМН | Подсчитывает ячейки, соответствующие нескольким критериям. |
| ПРОГНОЗ | Прогноз будущих значений y на основе линейной линии тренда. |
| ЧАСТОТА | Подсчитывает значения, попадающие в указанные диапазоны. |
| РОСТ | Вычисляет значения Y на основе экспоненциального роста. |
| INTERCEPT | Вычисляет точку пересечения Y для линии наилучшего соответствия. |
| НАИБОЛЬШИЙ | Возвращает k-е наибольшее значение. |
| ЛИНЕЙНАЯ | Возвращает статистику по линии тренда. |
| MAX | Возвращает наибольшее число. |
| МЕДИАНА | Возвращает медианное число. |
| МИН | Возвращает наименьшее число. |
| РЕЖИМ | Возвращает наиболее распространенный номер. |
| ПРОЦЕНТИЛЬ | Возвращает k-й процентиль. |
| PERCENTILE.INC | Возвращает k-й процентиль. Где k включительно. |
| PERCENTILE.EXC | Возвращает k-й процентиль. Где k является исключительным. |
| КВАРТИЛЬ | Возвращает указанное значение квартиля. |
| QUARTILE.INC | Возвращает указанное значение квартиля. включительно. |
| QUARTILE.EXC | Возвращает указанное значение квартиля. Эксклюзив. |
| RANK | Ранг числа в серии. |
RANK. AVG AVG | Ранг числа в серии. Средние. |
| RANK.EQ | Ранг числа в серии. Высший ранг. |
| НАКЛОН | Вычисляет наклон на основе линейной регрессии. |
| МАЛЕНЬКИЙ | Возвращает k-е наименьшее значение. |
| СТАНДОТКЛОН | Вычисляет стандартное отклонение. |
| STDEV.P | Вычисляет стандартное отклонение для всего населения. |
| СТАНДОТКЛОН.С | Вычисляет стандартное отклонение образца. |
| STDEVP | Вычисляет SD всего населения |
| TREND | Вычисляет значения Y на основе линии тренда. |
| Текст | да |
| CHAR | Возвращает символ, заданный кодом. |
| CLEAN | Удаляет все непечатаемые символы. |
| CODE | Возвращает цифровой код символа. |
| СЦЕПИТЬ | Объединяет текст. |
| ДОЛЛАР | Преобразует число в текст в денежном формате. |
| EXACT | Проверить, равны ли ячейки. Деликатный случай. ИСТИНА/ЛОЖЬ |
| НАЙТИ | Находит положение текста в ячейке. С учетом регистра. |
| LEFT | Обрезает текст на несколько символов слева. |
| LEN | Подсчитывает количество символов в тексте. |
| LOWER | Преобразует текст в нижний регистр. |
| MID | Извлекает текст из середины ячейки. |
| PROPER | Преобразует текст в правильный регистр. |
| REPLACE | Заменяет текст в зависимости от его местоположения. |
| ПОВТОР | Повтор текста несколько раз. |
| RIGHT | Усекает текст на несколько символов справа. |
| ПОИСК | Находит положение текста в ячейке. Регистр не учитывается. |


 Здесь результирующий массив будет размером 3 x 3.
Здесь результирующий массив будет размером 3 x 3.
 Если есть несоответствие в размерах, и один вектор длиннее другого, мы больше не можем выполнять поэлементное умножение!
Если есть несоответствие в размерах, и один вектор длиннее другого, мы больше не можем выполнять поэлементное умножение! По сути, именно здесь отдельные элементы умножаются вместе и добавляются. Из нашего предыдущего примера Excel, для
По сути, именно здесь отдельные элементы умножаются вместе и добавляются. Из нашего предыдущего примера Excel, для sum()>>tensor(60)
sum()>>tensor(60) ],
],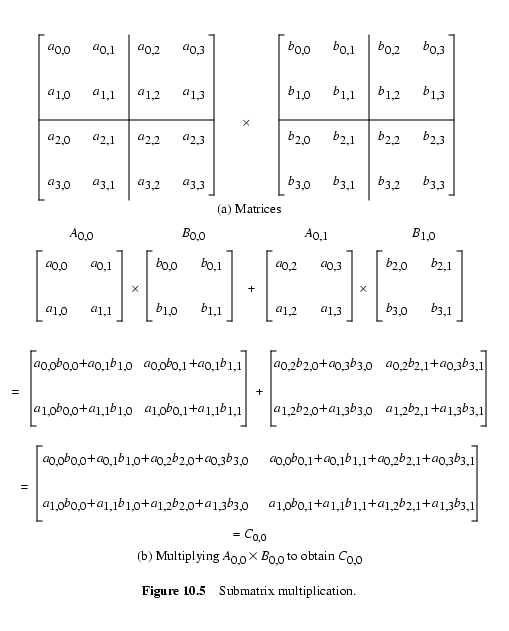 , 1062., 1173., 1284.],
, 1062., 1173., 1284.], expand_as(b)*b).sum(dim=0)
expand_as(b)*b).sum(dim=0)
 Нужно не лениться нажимать эти горячие клавиши, потому что в ином случае будет рассчитано только значение первой ячейки диапазона матрицы АТ.
Нужно не лениться нажимать эти горячие клавиши, потому что в ином случае будет рассчитано только значение первой ячейки диапазона матрицы АТ.