Линейные уравнения и функции: функции и их графики. Учебное пособие
Функция, функция, какая у тебя функция? Вы личный тренер, известный шпион, дверной косяк или что-то совсем другое? Мы думаем, что это последний.
Функция принимает некоторые входные данные, обычно называемые x , в уравнение f ( x ). Затем x проходит через уравнение, и в конце мы получаем результат, обычно известный как 9.0009 и . Обратите внимание, что y и f ( x ) на самом деле одно и то же. Может быть, и — знаменитый шпион?
Мы называем x независимой переменной , а y — зависимой переменной . Так что у x хорошая работа, а y все еще живет дома. Все возможные значения x- являются доменом , а все возможные значения y- являются диапазоном .
Пример задачи
Найдите область значений и диапазон значений y = 3 x – 4, где 0 ≤ x < 4.
– 4, ничего не говоря, мы бы сказали, что домен – это все действительные числа. Это исключает воображаемые, фальшивые, бредовые и позерские числа.
В этом случае, однако, мы не можем выбрать любое x , которое нам нравится под солнцем. В задаче сказано, что 0 ≤ x < 4. Это означает, что наш домен ограничен всеми действительными числами от 0 до 4, включая 0, но не 4 (из-за линии под голодным ртом Pacman).
Теперь диапазон. Диапазон — все возможные значения и . В нашем уравнении y = 3 x – 4 значения y- – это то, что мы получаем, когда подставляем известные нам значения x-. Давайте составим таблицу, чтобы зафиксировать диапазон.
Диапазон этой функции -4 ≤ y < 8. Обратите внимание, что y меньше 8, потому что x не может равняться 4, поэтому y никогда не может точно равняться 8.
В этом случае диапазон прост; мы могли бы посмотреть наименьшее и наибольшее значения x , и они дают нам наименьшее и наибольшее значения y .
Что, если бы у нас было что-то вроде y = — x 2 , где -2 < x < 2?
Вот, если мы просто подключим х = -2 и 2, мы получаем y = -4 для них обоих. Однако мы знаем, что y не всегда находится на уровне -4. Мы должны проверить x = 0, чтобы обнаружить, что там y = 0, что дает нам диапазон -4 < y < 0. Каждый раз, когда график может наклониться или опуститься, проверьте различные числа, чтобы найти правильный диапазон.
Теперь давайте на секунду поговорим о графических функциях. На самом деле, давайте поговорим и построим график одновременно. Только не просите нас тоже жевать жвачку.
Пример задачи
График y = 3 x – 4, где 0 ≤ x < 4.
О, это снова вы. Вы собираетесь повторять вещь , не так ли?
Это нормально, потому что это означает, что мы уже проделали большую часть работы. Нам известен домен и диапазон, и мы подключили несколько точек.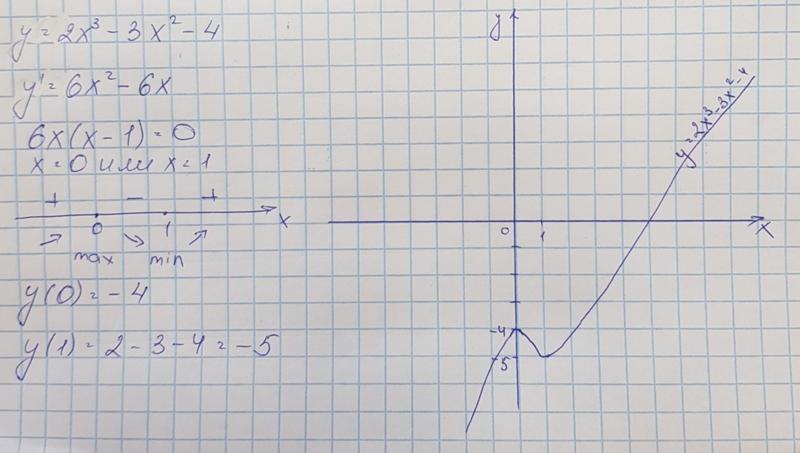
Начните с построения координатной плоскости . x -ось лежит на спине, лежа, а y -ось стоит по стойке смирно. Они встречаются посередине в точке происхождения . Не пытайтесь слишком сильно визуализировать это; на самом деле это не так больно, как кажется. Мы надеемся.
Мы используем числа на осях, чтобы нанести точки и провести линию. Делаем упорядоченных пар , которые выглядят так: ( x , y ). И x всегда вызывает дробовик, поэтому y никогда не будет первым.
Начиная с исходной точки, (0, 0), положительные значения x перемещаются вправо, а положительные значения y перемещаются вверх. Переместите оба числа вместе, чтобы построить каждую точку из нашей таблицы.
Видишь, как красиво они выстроились? Почему они не могли так красиво выглядеть на своих школьных фотографиях? Что ж, давайте проведем через них линию, пока они сидят на месте.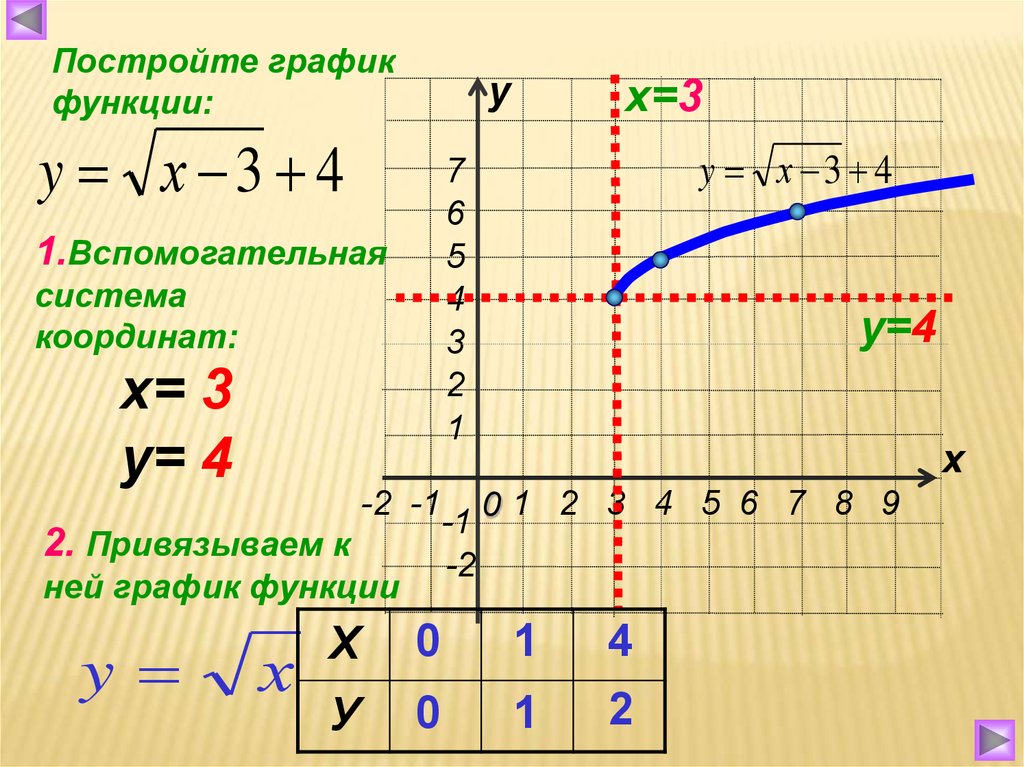
Здесь у нас ограниченная область, поэтому мы рисуем только линию, где функция действительно существует. Несуществующие линии на удивление легко рисовать, так что следите за ними.
Вертикальность
В функциях есть кое-что очень важное. На самом деле, это настолько важно, что мы поместим его в отдельную строку:
На каждые x приходится только одно y . Другими словами, каждый вход имеет только один выход. Один x входит, один y выходит.
Если уравнение нарушает этот принцип, оно не является функцией. К счастью, нам не нужно подключаться и проверять каждое значение x-, чтобы увидеть, есть ли среди них общие 9.0009 г- значение . Это было бы утомительно и ужасно. Вместо этого мы можем использовать тест вертикальной линии . Какое имя, а?
Возьмем, к примеру, эти графики. Тест именно на то, на что он похож: рисование вертикальных линий поверх графика. Если любая вертикальная линия может пройти через график более одного раза, то уравнение , а не является функцией.
Видишь? Мы можем с первого взгляда сказать, что является функцией, а что нет. И обратите внимание, что на втором графике в середине те же y- для двух разных значений x- (например, y = 0). Это полностью разрешено. Мы просто не можем иметь одно и то же значение x- для более чем одного значения y-, как на первом и третьем графиках.
С этого момента мы будем иметь дело с линейными уравнениями, которые легко классифицировать как линейные функции (о-о, название упало). Это вертикальная линия? Если нет, то да, Вирджиния, это функция.
Нарисовать грубый набросок графика функции \\[y = 3x\\]?
Последняя обновленная дата: 13 марта 2023 г.
•
Общее представление: 228,6K
•
Просмотры сегодня: 2,10K
Ответ
Проверено
228,6K+ виды
Hint: 52525.6K+. график «х» против «у». Мы даем случайные значения для «x» и находим значение «y».
Мы можем указать все действительные числа для значения «x». Таким образом, у нас будут координатные точки (x, y). Следовательно, мы можем построить график, используя значения. Мы также можем нарисовать график, используя метод перехвата. Но здесь у нас есть функция, проходящая через начало координат. Поэтому мы используем таблицы для построения графика.
Полное пошаговое решение:
Дано \[y = 3x\].
Давайте зададим значения для «x» и найдем значение «y».
Положим \[x = 1\]в \[y = 3x\] и получим,
Таким образом, у нас есть координатные точки \[(1,3)\] .
Подставляем \[x = — 1\]в \[y = 3x\] имеем,
\[y = 3 \times ( — 1) = — 3\]
Таким образом имеем координатную точку \[( — 1, — 3)\].
Положим \[x = 2\]в \[y = 3x\] и получим,
\[y = 3 \times (2) = 6\]
Таким образом, у нас есть координатные точки \[(2,6)\] .
Положим \[x = — 2\]в \[y = 3x\] и получим,
\[y = 3 \times ( — 2) = — 6\]
Таким образом, мы получим координатную точку \[( — 2, — 6)\].
Положим \[x = 3\]в \[y = 3x\] и получим,
\[y = 3 \times 3 = 9\]
Таким образом, у нас есть координатные точки \[(3,9)\].
Положим \[x = — 3\] в \[y = 3x\] и получим
\[y = 3 \times \left( { — 3} \right) = — 9\]
Таким образом, у нас есть координатные точки \[( — 3, — 9)\].
Таким образом, мы имеем,
| \[x\] | \[1\] | \[ — 1\] | \[2\] | \[ — 2\] | \[3\] | \[ — 3\] |
| \[у\] | \ [3\]\[ — 3\] | \[6\] | \[ — 6\] | \[9\] | \[ — 9\] |
3 9’0 Нарисуем график для этих координат,
Ось X = 1uint = 1 единица
Ось Y = 1 единица = 2 единицы
Примечание: Мы видим, что данная кривая является параболой. График показывает отношение между двумя переменными величинами, он содержит две оси, перпендикулярные друг другу, а именно ось x и ось y. Каждая переменная измеряется по одной из осей.