Решение Ященко ОГЭ 2023 Вариант №6 (36 вариантов) Математика
Решение заданий варианта №6 из сборника ОГЭ 2023 по математике И.В. Ященко 36 типовых вариантов ФИПИ школе. ГДЗ решебник для 9 класса. Ответы с решением. Полный разбор всех заданий.
ЧАСТЬ 1
Задание 1-5.
На рисунке изображён план двухкомнатной квартиры в многоэтажном жилом доме. В правой части рисунка даны обозначения двери и окна, а также указано, что длина стороны клетки на плане соответствует 0,4 м. Вход в квартиру находится в прихожей. Справа от входа в квартиру располагаются кухня и санузел, а также одна из лоджий, в которую можно попасть из кухни. В эту же лоджию можно пройти и из гостиной. Наименьшую площадь имеет кладовая. В квартире есть ещё одна лоджия, куда можно попасть из прихожей, пройдя через спальню.
Задание 6.
Найдите значение выражения 5,5 – 13,5·0,6. {6}}.
{6}}.
Задание 9.
Решите уравнение х2 – 15 = 2х.
Если уравнение имеет более одного корня, в ответ запишите меньший из корней.
Задание 10.
Родительский комитет закупил 20 пазлов для подарков детям в связи с окончанием учебного года, из них 8 с машинами и 12 с видами городов. Подарки распределяются случайным образом между 20 детьми, среди которых есть Вася. Найдите вероятность того, что Васе достанется пазл с машиной.
Задание 11.
Установите соответствие между графиками функций и формулами, которые их задают.
ФОРМУЛЫ
1) y=-\frac{4}{x}
2) y=\frac{1}{4x}
3) y=\frac{4}{x}
ГРАФИКИ
В таблице под каждой буквой укажите соответствующий номер.
Задание 12.
Мощность постоянного тока (в ваттах) вычисляется по формуле P = I2R, где I – сила тока (в амперах), R – сопротивление (в омах). Пользуясь этой формулой, найдите R (в омах), если Р = 180 Вт и I = 6 А.
Пользуясь этой формулой, найдите R (в омах), если Р = 180 Вт и I = 6 А.
Задание 13.
Укажите решение неравенства 4x – x2 < 0.
1) (–∞; 0) ∪ (4; +∞)
2) (0; +∞)
3) (0; 4)
4) (4; +∞)
Задание 14.
В ходе бета-распада радиоактивного изотопа А каждые 9 минут половина его атомов без потери массы преобразуются в атомы стабильного изотопа Б. В начальный момент масса изотопа А составляла 640 мг. Найдите массу образовавшегося изотопа Б через 45 минут. Ответ дайте в миллиграммах.
Задание 15.
Косинус острого угла A треугольника ABC равен \frac{2\sqrt{6}}{5}. Найдите sin A.
Задание 16.
Радиус окружности, описанной около квадрата, равен 24√2. Найдите радиус окружности, вписанный в этот квадрат.
Задание 17.
Диагональ BD параллелограмма ABCD образует с его сторонами углы, равные 65° и 80°. {2}-y=11 \end{cases}.
{2}-y=11 \end{cases}.
Задание 21.
Баржа прошла по течению реки 48 км и, повернув обратно, прошла ещё 42 км, затратив на весь путь 5 часов. Найдите собственную скорость баржи, если скорость течения реки равна 5 км/ч.
Задание 22.
Постройте график функции y = x2 – 3|x| – x и определите, при каких значениях m прямая y = m имеет с графиком не менее двух, но не более трёх общих точек.
Задание 23.
Катеты прямоугольного треугольника равны 10 и 24. Найдите высоту, проведённую к гипотенузе.
Задание 24.
Окружности с центрами в точках R и S не имеют общих точек, ни одна из них не лежит внутри другой, а их радиусы относятся как с : d. Докажите, что внутренняя общая касательная к этим окружностям делит отрезок, соединяющий их центры, в отношении с : d.
Задание 25.
Основания трапеции относятся как 1:5. Через точку пересечения диагоналей проведена прямая, параллельная основаниям. В каком отношении эта прямая делит площадь трапеции?
Источник варианта: Сборник ОГЭ 2023 по математике. Типовые экзаменационные варианты. 36 вариантов. Под редакцией И.В. Ященко.
Есть три секунды времени? Для меня важно твоё мнение!
Насколько понятно решение?
Средняя оценка: 5 / 5. Количество оценок: 5
Оценок пока нет. Поставь оценку первым.
Расскажи, что не так? Я исправлю в ближайшее время!
В отзыве оставь любой контакт для связи, если хочешь, что бы я тебе ответил.
- Запись опубликована:09.11.2022
- Рубрика записи+ Типовые экзаменационные варианты ОГЭ
- Автор записи:Andrei Maniakin
Видео с вопросами: Определение графика функции синуса
Стенограмма видео
Что из следующего является графиком 𝑦 равно sin 𝑥?
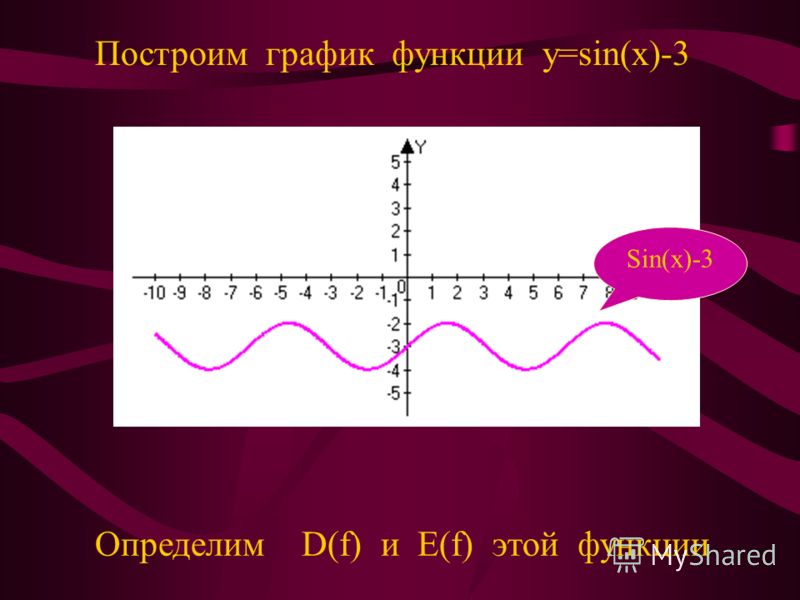
Давайте начнем с напоминания о некоторых важных характеристиках синусоидального графика.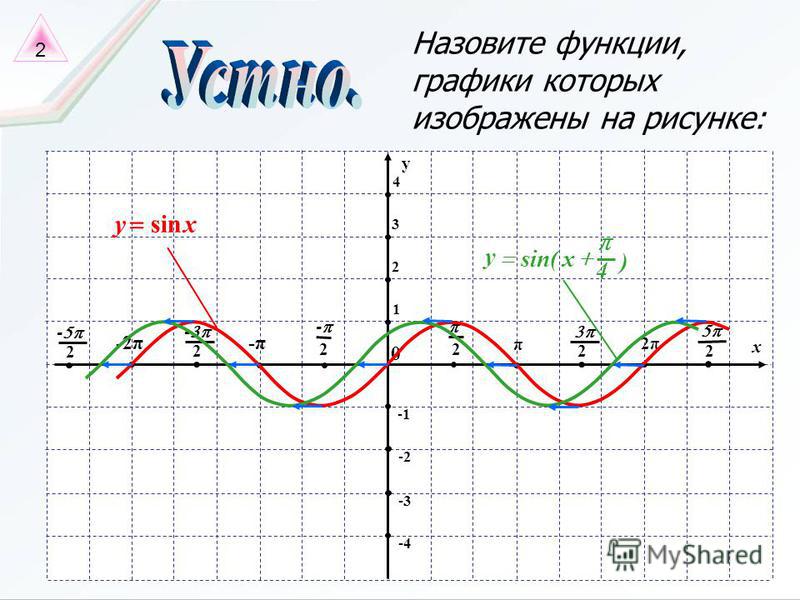 Во-первых, он периодический с периодом 360 градусов или два 𝜋 радиана. Таким образом, один и тот же шаблон повторяется после каждого интервала в 360 градусов. Мы знаем, что будем работать в градусах в этом вопросе, потому что, глядя на пять графиков, мы видим, что значения на оси 𝑥 являются целыми числами, кратными 9.0. Во-вторых, диапазон функции синуса — это замкнутый интервал от отрицательной единицы до единицы. Функция непрерывно колеблется между минимальным отрицательным значением и максимальным положительным значением.
Во-первых, он периодический с периодом 360 градусов или два 𝜋 радиана. Таким образом, один и тот же шаблон повторяется после каждого интервала в 360 градусов. Мы знаем, что будем работать в градусах в этом вопросе, потому что, глядя на пять графиков, мы видим, что значения на оси 𝑥 являются целыми числами, кратными 9.0. Во-вторых, диапазон функции синуса — это замкнутый интервал от отрицательной единицы до единицы. Функция непрерывно колеблется между минимальным отрицательным значением и максимальным положительным значением.
Далее, все корни синуса являются целыми числами, кратными 180 градусам. Таким образом, график функции синуса пересекает ось 𝑥 в каждом целом кратном 180 градусов. В частности, 𝑥 равно нулю является корнем синуса. Итак, граф проходит через начало координат, или, другими словами, 𝑦-перехват графа равен нулю. Теперь мы можем использовать эти свойства, чтобы определить, какой из пяти приведенных графиков представляет 𝑦 равно sin 𝑥. График (A) имеет период где-то между 90 и 135 градусов.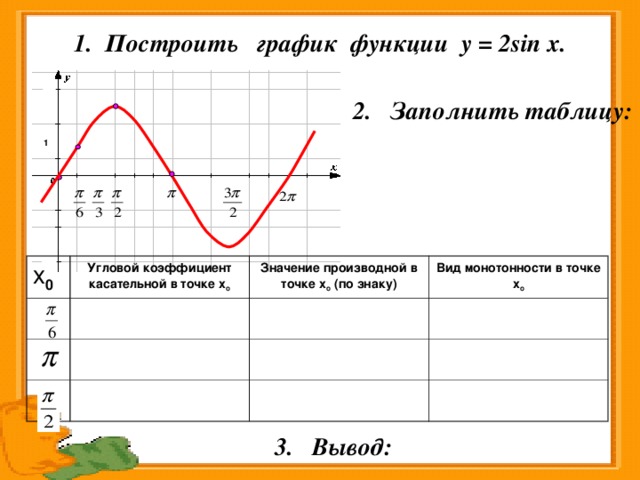
График (D) имеет правильный 𝑦-перехват, но имеет период 180 градусов. Так что это тоже не правильный график. График (D) может представлять горизонтальное растяжение синусоидальной функции с масштабным коэффициентом, равным половине. Глядя на график (C), мы видим, что этот график полностью расположен выше и на оси 𝑥. Диапазон этого графика от нуля до двух, а не отрицательный от одного до одного. Итак, мы можем исключить график (C). У нас остались графики (B) и (E), которые имеют одинаковую форму. И мы видим, что они оба имеют правильный диапазон отрицательного отношения один к одному. Каждый график также имеет период 360 градусов. Давайте тогда рассмотрим корни каждой функции. График (B) пересекает ось 𝑥 в точках нуля, 180 градусов, 360 градусов и минус 180 градусов, минус 360 градусов. Это целые числа, кратные 180 градусам.