Поверхность второго порядка | это… Что такое Поверхность второго порядка?
Поверхность второго порядка — геометрическое место точек, декартовы прямоугольные координаты которых удовлетворяют уравнению вида
в котором по крайней мере один из коэффициентов , , , , , отличен от нуля.
Содержание
|
Типы поверхностей второго порядка
Цилиндрические поверхности
Поверхность называется цилиндрической поверхностью с образующей , если для любой точки этой поверхности прямая, проходящая через эту точку параллельно образующей , целиком принадлежит поверхности .
Теорема (об уравнении цилиндрической поверхности).
Если в некоторой декартовой прямоугольной системе координат поверхность имеет уравнение , то — цилиндрическая поверхность с образующей, параллельной оси .
Кривая, задаваемая уравнением в плоскости , называется направляющей цилиндрической поверхности.
Если направляющая цилиндрической поверхности задаётся кривой второго порядка, то такая поверхность называется цилиндрической поверхностью второго порядка.
| Эллиптический цилиндр: | Параболический цилиндр: | Гиперболический цилиндр: |
|---|---|---|
| Пара совпавших прямых: | Пара совпавших плоскостей: | Пара пересекающихся плоскостей: |
Конические поверхности
Коническая поверхность.
Основная статья: Коническая поверхность
Поверхность называется конической поверхностью с вершиной в точке , если для любой точки этой поверхности прямая, проходящая через и , целиком принадлежит этой поверхности.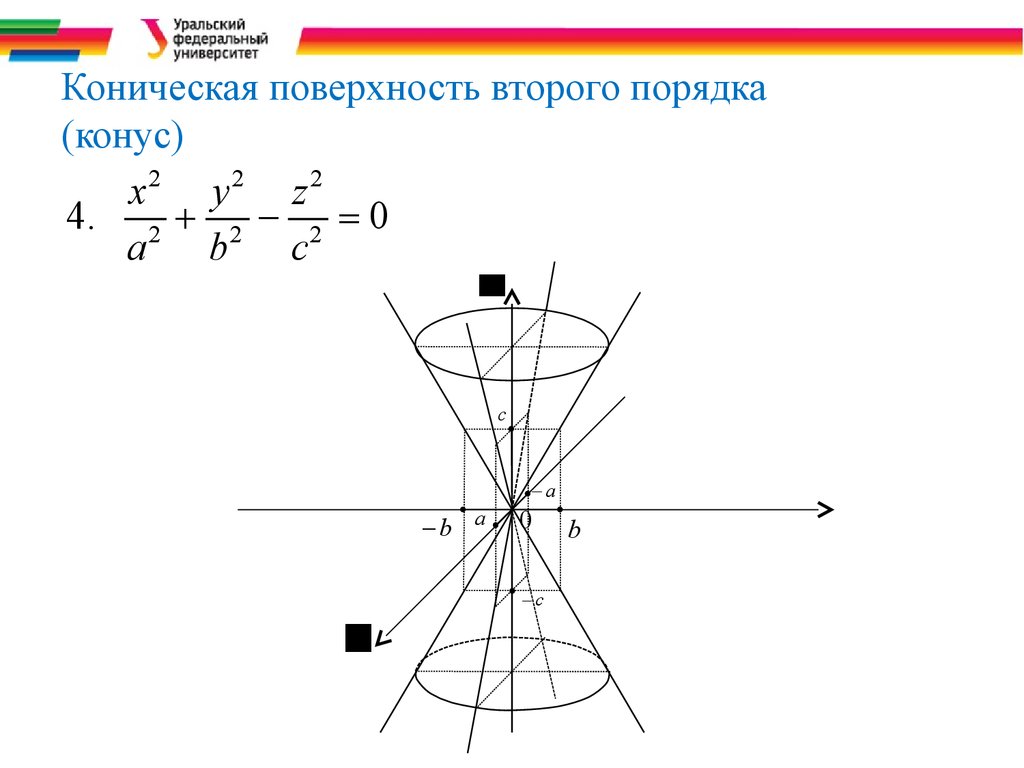
Функция называется однородной порядка , если выполняется следующее:
Теорема (об уравнении конической поверхности).
Если в некоторой декартовой прямоугольной системе координат поверхность задана уравнением , где — однородная функция, то — коническая поверхность с вершиной в начале координат.
Если поверхность задана функцией , являющейся однородным алгебраическим многочленом второго порядка, то называется конической поверхностью второго порядка.
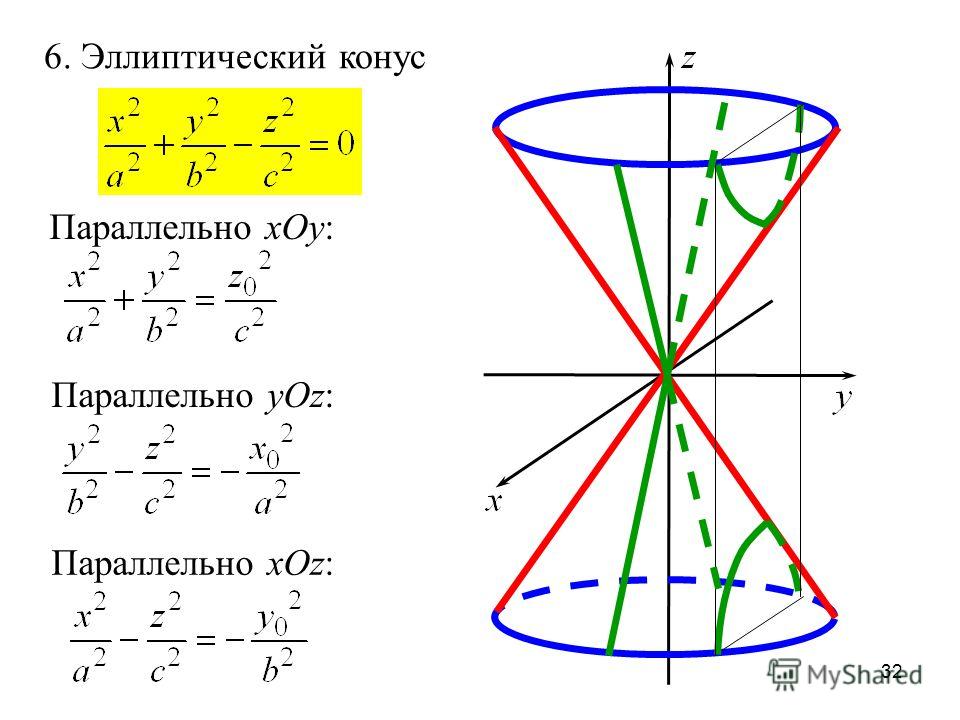
- Каноническое уравнение конуса второго порядка имеет вид:
Поверхности вращения
Поверхность называется поверхностью вращения вокруг оси , если для любой точки этой поверхности окружность, проходящая через эту точку в плоскости с центром в и радиусом , целиком принадлежит этой поверхности.
Теорема (об уравнении поверхности вращения).
Если в некоторой декартовой прямоугольной системе координат поверхность задана уравнением , то — поверхность вращения вокруг оси .
| Эллипсоид: | Однополостной гиперболоид: | Двуполостной гиперболоид: | Эллиптический параболоид: |
|---|---|---|---|
В случае, если , перечисленные выше поверхности являются поверхностями вращения.
Эллиптический параболоид
Уравнение эллиптического параболоида:
Если то эллиптический параболоид представляет собой поверхность вращения, образованную вращением параболы вокруг вертикальной оси, проходящей через вершину и фокус данной параболы.
При сечении эллиптический параболоида плоскостью поверхность порождает эллипс.
При сечении эллиптический параболоида плоскостью или поверхность порождает параболу.
Гиперболический параболоид
Гиперболический параболоид.
Уравнение гиперболического параболоида:
При сечении гиперболического параболоида плоскостью поверхность порождает гиперболу.
При сечении гиперболического параболоида плоскостью или поверхность порождает параболу.
Ввиду геометрической схожести гиперболический параболоид часто называют «седлом».
Центральные поверхности
Если центр поверхности второго порядка существует и единственен, то его координаты можно найти решив систему уравнений:
Литература
- В. А. Ильин, Э. Г. Позняк. Аналитическая геометрия.. — М.: ФИЗМАТЛИТ, 2002. — 240 с.
- П. С. Александров. Курс аналитической геометрии и линейной алгебры.. — М.: ФИЗМАТЛИТ, 1979. — 511 с.
- Шаль. Исторический обзор происхождения и развития геометрических методов. Гл. 5, § 46-54. М., 1883.
См. также
- Квадрика
- Поверхность вращения
- Цилиндрическая поверхность
- Гиперболоид
- Параболоид
- Эллипсоид
Высшая математика Т1
Высшая математика Т1
ОглавлениеПРЕДИСЛОВИЕ§ 1. Определители второго порядка 2.1. Определители третьего порядка. 2.2. Определители n-го порядка. §3. Матрицы 4.1 Система из n линейных уравнений с n неизвестными. 4.2. Формула Крамера 4.4 Правило решения системы линейных уравнений Системы линейных уравнений: 4.5 Примеры приложения правил Системы линейных уравнений: 4.6 Обоснование правил 4.7. Метод решения системы путем исключения неизвестных 4.8. Нахождение ранга матрицы 5.1. Понятие вектора 5.2. Проекция вектора 5.3. Свойства проекций векторов 5.4 Скалярное произведение векторов 5.5. Прямоугольная система координат 6.1. n-мерное пространство 6.2 Скалярное произведение в действительном пространстве 6.3 Скалярное произведение в комплексном пространстве 6.4. Неравенства Буняковского 6.5. Неравенство Минковского § 7. Отрезок.  Деление отрезка в данном отношении Деление отрезка в данном отношении§ 8. Прямая линия 9.1. Уравнение плоскости в нормальном виде 9.2. Уравнение плоскости в общем виде 9.3. Уравнение плоскости в отрезках 9.4. Уравнение плоскости, роходящей через точку 9.5. Уравнение плоскости, проходящей через три точки 9.6 Угол между двумя плоскостями 9.7. Расстояние от точки до плоскости 10.1 Уравнение прямой в каноническом виде 10.2 Расположение двух плоскостей 11.1. Двумерная система координат 11.2. Трехмерная система координат 12.1. Два определения векторного произведения 12.2. Геометрический смысл определителя второго порядка 12.3. Свойства векторного произведения § 13. Смешанное (векторно-скалярное) произведение § 14. Линейно независимая система векторов § 15. Линейные операторы § 16. Базисы в Rn § 17. Ортогональные базисы в Rn § 18. Инвариантные свойства скалярного и векторного произведений § 19. Преобразование прямоугольных координат в плоскости § 20.  Линейные подпространства в Rn Линейные подпространства в Rn§ 21. Теоремы фредгольмова типа § 23. Квадратичная форма в двухмерном пространстве § 24. Кривая второго порядка Эллипс Гипербола Парабола 24.3 Классификация кривых второго порядка § 25. Поверхность второго порядка в трехмерном пространстве Эллипсоид Однополостный гиперболоид Двуполостный гиперболоид Эллиптический и гиперболический параболоиды Конус второго порядка Цилиндры второго порядка Линейчатые поверхности § 26. Общая теория поверхности второго порядка в трехмерном пространстве § 27. Плоскость в Rn. Общие положения 27.2. Плоскость в Rn 27.3. Уравнение плоскости в нормальном виде 27.4. Уравнение плоскости в векторной форме 27.5. Геометрическая интерпретация уравнений 27.6. Уравнение плоскости, проходящей через n точек 27.7. Условия ортогональности и параллельности плоскостей 27.8. Уравнение плоскости, проходящей через точку 27. 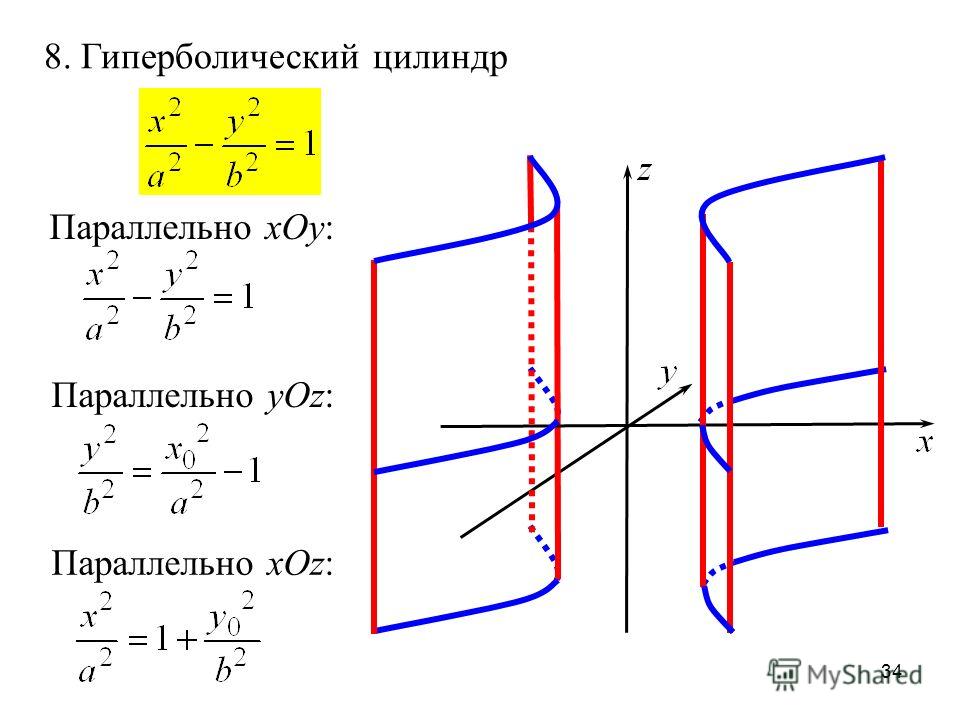 9. Прямая в пространстве Rn 9. Прямая в пространстве Rn27.10. Расположение (n-1) плоскостей 27.11. Расстояние от точки до плоскости 27.12. Различные задачи § 28. Линейное программирование 28.2. Транспортная задача 28.3.Общая задача линейного программирования 28.4. Векторно-матричная форма задачи линейного программирования 28.5. Симплекс-метод 28.7. Выбор разрешающего элемента 28.8. Условия существования базиса |
Поверхности второго порядка | Semantic Scholar
- DOI:10.1007/978-3-319-11773-7_35
- Идентификатор корпуса: 123736353
@inproceedings{Krivoshapko2015TheSO,
title={Поверхности второго порядка},
author={Сергей Н. Кривошапко и Вячеслав Н. Иванов},
год = {2015}
} - Кривошапко С., Иванов В.Н.
- Опубликовано в 2015 г.

- Математика
Поверхности второго порядка задаются алгебраическими уравнениями второго порядка относительно декартовых координат. Поверхности второго порядка называются также квадратичными поверхностями или квадриками.
View Via Publisher
Дизайн квадратичный пластырь и кубический участок поверхности
- R. M. Amer, M. A. ABD
Математика, компьютерная наука
- 2013
. описано использование программ Mathematica для расчета уравнений участка поверхности.
Динамическая эволюция природных образований на орбитах точек либрации в многочастичном режиме
- А. Эритье, К. Хауэлл
Физика, геология
- 2014
Использование различных нелинейных поверхностей отклика для математического описания типа комбинированной токсичности
Статья, характеризующая проблему комбинированного типа
действие смеси токсических веществ с помощью нелинейных функций отклика и показывает, что квадратичная модель в полной мере отражает эти общие характеристики, но интерпретация комбинированных видов токсичности на основе изоболограмм, полученных по модели quadRatic, более сложна.
Естественные образования в треугольной точке Земля–Луна в возмущенных ограниченных задачах
- Ф. Салазар, О. Винтер, Э. Макао, Х. Масдемонт, Г. Гомес à base d’Algèbres Géométriques Conforme
- Stéphane Breuils, Vincent Nozick, L. Fuchs
Philosophy
- 2019
Les Algebres Geometriques constituent un outil intuitif et performant pour representer et manipuler des objets geometriques ainsi que pour calculer les пересечения entre plusieurs objets…
Области нулевого дрейфа и стратегии управления для удержания спутников в формации вокруг треугольной точки либрации в ограниченном сценарии Солнце-Земля-Луна
- Ф. Салазар, О. Винтер, Э. Макао, Дж. Масдемон, Г. Гомес
Физика
- 2015
Новый метод объективной идентификации трехмерных аномалий потенциальной завихренности0019
- 2022
Аннотация. Анализ потенциальной завихренности (PV) играет центральную роль в изучении динамики атмосферы и, в частности, в изучении жизненного цикла погодных систем. Трехмерные (3-D)…
Трехмерные (3-D)…
О маятниках, полимерах и роботах: Вычислительная механика с ограничениями
- Ф. Веселый
Биология
- 2013
- 2.6.1 Определите цилиндр как тип трехмерной поверхности.
- 2.6.2 Знать основные свойства эллипсоидов, параболоидов и гиперболоидов.
- 2.6.3 Используйте трассировки, чтобы нарисовать пересечения поверхностей квадрика с координатными плоскостями.
- x2+z2=25×2+z2=25
- z=2×2-yz=2×2-y
- у=синху=синкс
- Переменная yy может принимать любое значение без ограничений. Следовательно, линии, управляющие этой поверхностью, параллельны и -ось. Пересечение этой поверхности с плоскостью xz образует окружность с центром в начале координат и радиусом 55 (см. следующий рисунок).
Рисунок 2,77 График уравнения x2+z2=25×2+z2=25 представляет собой цилиндр радиусом 55 с центром на оси y .

- В этом случае уравнение содержит все три переменные —x,y,—x,y и z—z— поэтому ни одна из переменных не может изменяться произвольно. Самый простой способ визуализировать эту поверхность — использовать компьютерную графическую утилиту (см. следующий рисунок).
Рисунок 2,78
- В этом уравнении переменная z может принимать любое значение без ограничений. Следовательно, линии, составляющие эту поверхность, параллельны оси z . Пересечение этой поверхности с плоскостью xy очерчивает кривую y=sinxy=sinx (см. следующий рисунок).
Рисунок 2,79 График уравнения y=sinxy=sinx образован набором прямых, параллельных оси z , проходящей через кривую y=sinxy=sinx в xy -самолет.
- 16×2+9y2+16z2=14416×2+9y2+16z2=144
- 9×2-18x+4y2+16y-36z+25=09×2-18x+4y2+16y-36z+25=0
- Члены x, y, x, y и zz возводятся в квадрат и все положительны, так что это, вероятно, эллипсоид. Однако давайте приведем уравнение к стандартной форме для эллипсоида, чтобы быть уверенным. У нас есть
16×2+9y2+16z2=144,16×2+9y2+16z2=144.
Деление на 144 даетx29+y216+z29=1.x29+y216+z29=1.
Итак, на самом деле это эллипсоид с центром в начале координат. - Сначала заметим, что член zz возводится только в первую степень, так что это либо эллиптический параболоид, либо гиперболический параболоид. Мы также отмечаем, что есть члены xx и члены yy, которые не возведены в квадрат, поэтому эта квадратичная поверхность не имеет центра в начале координат. Нам нужно заполнить квадрат, чтобы представить это уравнение в одной из стандартных форм. У нас есть
9×2-18x+4y2+16y-36z+25=09×2-18x+4y2+16y+25=36z9(x2-2x)+4(y2+4y)+25=36z9(x2-2x+1-1)+ 4(y2+4y+4−4)+25=36z9(x−1)2−9+4(y+2)2−16+25=36z9(x−1)2+4(y+2)2 =36z(x−1)24+(y−2)29=z,9×2−18x+4y2+16y−36z+25=09×2−18x+4y2+16y+25=36z9(x2−2x)+4(y2 +4y)+25=36z9(x2−2x+1−1)+4(y2+4y+4−4)+25=36z9(x−1)2−9+4(y+2)2−16+ 25=36z9(x−1)2+4(y+2)2=36z(x−1)24+(y−2)29=z.

Это эллиптический параболоид с центром в точке (1,2,0).(1,2,0). - Укажите имя поверхности квадрика.
- Определить ось симметрии поверхности квадрата.
- x24+y29-z212=1×24+y29-z212=1
- x24-y29-z212=1×24-y29-z212=1
- x24+y29+z212=1×24+y29+z212=1
- z=4×2+3y2z=4×2+3y2
- z=4×2-y2z=4×2-y2
- 4×2+y2-z2=04×2+y2-z2=0
- Укажите имя поверхности квадрика.
- Какое из уравнений: 16×2+9y2+36z2=3600,9×2+36y2+16z2=3600,16×2+9y2+36z2=3600,9×2+36y2+16z2=3600 или 36×2+9y2+16z2=360036×2+9y2+16z2 =3600 — соответствует графику?
- Использование б. записать уравнение поверхности квадрата в стандартной форме.
- Укажите имя поверхности квадрика.
- Какое из уравнений — 36z=9×2+y2,9×2+4y2=36z или −36z=−81×2+4y236z=9×2+y2,9×2+4y2=36z или −36z=−81×2+4y2 — соответствует графику выше?
- Использование б. записать уравнение поверхности квадрата в стандартной форме.
- Используйте метод заполнения квадрата, чтобы записать уравнение в стандартной форме.

- Определите поверхность.
- Решите систему, состоящую из уравнений поверхностей, чтобы найти уравнения кривой пересечения. ( Подсказка: Найдите xx и yy через z.)z.)
- Используйте систему компьютерной алгебры (CAS) для визуализации кривой пересечения на сфере x2+y2+z2=4.
 x2+y2+z2=4.
x2+y2+z2=4. - Роговица глаза аппроксимируется в виде вытянутого сфероида с осью, являющейся глазом, где а=8,7 мм и с=9,6 мм, а=8,7 мм и с=9,6 мм. Напишите уравнение сфероида, моделирующего роговицу, и зарисуйте поверхность.
- Приведите два примера объектов вытянутой сфероидальной формы.
- Напишите уравнение в стандартной форме эллипсоида, представляющего форму Земли. Предположим, что центр Земли находится в начале координат и что след, образованный плоскостью z=0z=0, соответствует экватору.
- Нарисуйте график.
- Найдите уравнение кривой пересечения поверхности с плоскостью z=1000z=1000, параллельной плоскости xy .
 Кривая пересечения называется параллелью .
Кривая пересечения называется параллелью . - Найдите уравнение кривой пересечения поверхности с плоскостью x+y=0x+y=0, проходящей через ось z . Кривая пересечения называется меридианом .
- Напишите уравнение вытянутого сфероида с центром в начале координат, которое описывает форму одного из магнитов.
- Напишите уравнения вытянутых сфероидов, которые моделируют форму жужжащих трюковых магнитов. Используйте CAS для создания графиков.

- 7 Движение точек под действием масс потенциал можно вычислить простыми методами. Однако, если траектории ограничены механическими ограничениями, такими как струны, рельсы и т. д.
2.6 Квадратичные поверхности. Расчет, том 3
Цели обучения
Мы изучали векторы и векторные операции в трехмерном пространстве и разработали уравнения для описания линий, плоскостей и сфер. В этом разделе мы используем наши знания о плоскостях и сферах, которые являются примерами трехмерных фигур, называемых 9. 0133 поверхностей , чтобы исследовать множество других поверхностей, которые можно изобразить в виде графика в трехмерной системе координат.
0133 поверхностей , чтобы исследовать множество других поверхностей, которые можно изобразить в виде графика в трехмерной системе координат.
Идентификация цилиндров
Первая поверхность, которую мы рассмотрим, это цилиндр. Хотя большинство людей сразу же думают о полой трубке или соломинке из-под газировки, когда слышат слово , цилиндр , здесь мы используем широкое математическое значение этого термина. Как мы видели, цилиндрические поверхности не обязательно должны быть круглыми. Прямоугольный нагревательный канал представляет собой цилиндр, как и свернутый коврик для йоги, поперечное сечение которого имеет форму спирали.
В двумерной координатной плоскости уравнение x2+y2=9×2+y2=9 описывает окружность с центром в начале координат и радиусом 3,3. В трехмерном пространстве это же уравнение представляет собой поверхность. Представьте себе копии круга, наложенные друг на друга с центром на оси z (рис. 2.75), образуя полую трубку. Затем мы можем построить цилиндр из набора линий, параллельных оси z , проходящих через окружность x2+y2=9×2+y2=9 в плоскости xy , как показано на рисунке. Таким образом, любую кривую в одной из координатных плоскостей можно расширить до поверхности.
2.75), образуя полую трубку. Затем мы можем построить цилиндр из набора линий, параллельных оси z , проходящих через окружность x2+y2=9×2+y2=9 в плоскости xy , как показано на рисунке. Таким образом, любую кривую в одной из координатных плоскостей можно расширить до поверхности.
Рисунок 2,75 В трехмерном пространстве график уравнения x2+y2=9×2+y2=9 представляет собой цилиндр радиусом 33 с центром на оси z . Это продолжается бесконечно в положительном и отрицательном направлениях.
Определение
Набор линий, параллельных данной линии, проходящей через данную кривую, называется цилиндрической поверхностью или цилиндром. Параллельные линии называются линейками.
Из этого определения видно, что у нас все еще есть цилиндр в трехмерном пространстве, даже если кривая не является окружностью. Любая кривая может образовывать цилиндр, а линии, составляющие цилиндр, могут быть параллельны любой заданной прямой (рис. 2.76).
2.76).
Рисунок 2,76 В трехмерном пространстве график уравнения z=x3z=x3 представляет собой цилиндр или цилиндрическую поверхность с линиями, параллельными оси y .
Пример 2,55
Графики цилиндрических поверхностей
Нарисуйте графики следующих цилиндрических поверхностей.
Решение
Контрольно-пропускной пункт 2,52
Нарисуйте или используйте графический инструмент для просмотра графика цилиндрической поверхности, определяемой уравнением z=y2.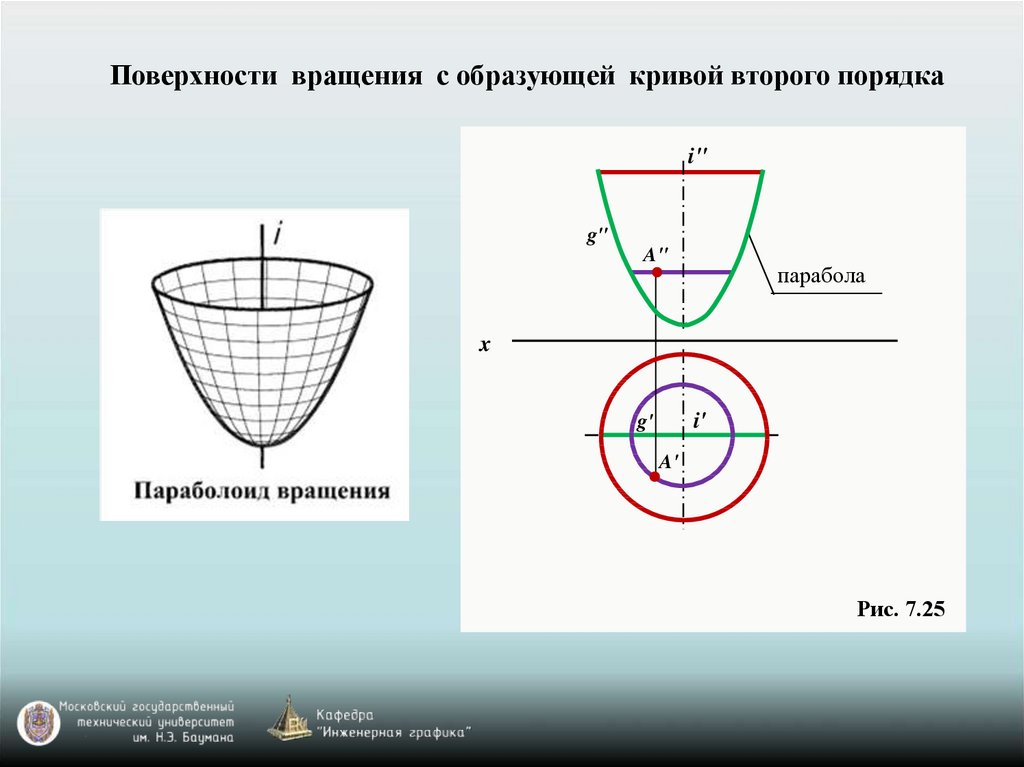 z=y2.
z=y2.
При рисовании поверхностей мы видели, что полезно рисовать пересечение поверхности с плоскостью, параллельной одной из координатных плоскостей. Эти кривые называются трассами. Мы можем видеть их на графике цилиндра на рис. 2.80.
Определение
Трассы поверхности — это поперечные сечения, созданные при пересечении поверхностью плоскости, параллельной одной из координатных плоскостей.
Рисунок 2,80 (a) Это один из видов графика уравнения z=sinx.z=sinx. (b) Чтобы найти трассу графика в плоскости xz , установите y=0.y=0. Трассировка представляет собой просто двумерную синусоиду.
Трассировки полезны при создании эскизов цилиндрических поверхностей. Однако для трехмерного цилиндра полезен только один набор трасс. Обратите внимание на рис. 2.80, что кривая графика z=sinxz=sinx в плоскости xz полезна при построении графика. След в 9Однако 0133 xy -плоскость представляет собой просто ряд параллельных линий, а след в плоскости yz — это просто одна линия.
Цилиндрические поверхности образованы набором параллельных линий. Однако не все поверхности в трех измерениях конструируются так просто. Теперь мы исследуем более сложные поверхности, и трассировки являются важным инструментом в этом исследовании.
Квадратные поверхности
Мы узнали о трехмерных поверхностях, описываемых уравнениями первого порядка; это самолеты. Некоторые другие распространенные типы поверхностей можно описать уравнениями второго порядка. Мы можем рассматривать эти поверхности как трехмерные расширения конических сечений, которые мы обсуждали ранее: эллипса, параболы и гиперболы. Мы называем эти графы квадратичными поверхностями.
Определение
Квадратичные поверхности представляют собой графики уравнений, которые могут быть выражены в виде Fyz+Gx+Hy+Jz+K=0.
Когда квадратичная поверхность пересекает координатную плоскость, трасса представляет собой коническое сечение.
Эллипсоид — это поверхность, описываемая уравнением вида x2a2+y2b2+z2c2=1. x2a2+y2b2+z2c2=1. Установите x=0x=0, чтобы увидеть след эллипсоида в плоскости yz . Чтобы увидеть следы в xy — и xz -плоскости, установите z=0z=0 и y=0,y=0 соответственно. Заметьте, что если a=b,a=b, трасса в плоскости xy представляет собой окружность. Аналогично, если a=c,a=c, то след в плоскости xz представляет собой окружность, а если b=c,b=c, то след в плоскости yz представляет собой окружность. Таким образом, сфера — это эллипсоид с a=b=c.a=b=c.
x2a2+y2b2+z2c2=1. Установите x=0x=0, чтобы увидеть след эллипсоида в плоскости yz . Чтобы увидеть следы в xy — и xz -плоскости, установите z=0z=0 и y=0,y=0 соответственно. Заметьте, что если a=b,a=b, трасса в плоскости xy представляет собой окружность. Аналогично, если a=c,a=c, то след в плоскости xz представляет собой окружность, а если b=c,b=c, то след в плоскости yz представляет собой окружность. Таким образом, сфера — это эллипсоид с a=b=c.a=b=c.
Пример 2,56
Эскиз эллипсоида
Эскиз эллипсоида x222+y232+z252=1.x222+y232+z252=1.
Решение
Начните с наброска трасс. Чтобы найти трассу в плоскости xy , установите z=0:z=0:x222+y232=1×222+y232=1 (см. рис. 2. 81). Чтобы найти другие трассы, сначала установите y=0y=0, а затем установите x=0.x=0.
81). Чтобы найти другие трассы, сначала установите y=0y=0, а затем установите x=0.x=0.
Рисунок 2,81 (a) Этот график представляет собой след уравнения x222+y232+z252=1×222+y232+z252=1 в плоскости xy , когда мы установили z=0.z=0. (b) Когда мы устанавливаем y=0,y=0, мы получаем след эллипсоида в плоскости xz , который является эллипсом. (c) Когда мы устанавливаем x=0,x=0, мы получаем след эллипсоида в yz -плоскость, она же эллипс.
Теперь, когда мы знаем, как выглядят следы этого твердого тела, мы можем нарисовать поверхность в трех измерениях (рис. 2.82).
Рисунок 2,82 (а) Следы обеспечивают основу для поверхности. (b) Центр этого эллипсоида является началом координат.
След эллипсоида представляет собой эллипс в каждой из координатных плоскостей. Однако это не обязательно должно иметь место для всех поверхностей квадрики. Многие квадратичные поверхности имеют следы, которые представляют собой различные виды конических сечений, и это обычно указывается в названии поверхности. Например, если поверхность может быть описана уравнением вида x2a2+y2b2=zc,x2a2+y2b2=zc, то мы называем эту поверхность эллиптическим параболоидом. След в xy -плоскость представляет собой эллипс, а трассы в xz -плоскости и yz -плоскости представляют собой параболы (рис. 2.83). Другие эллиптические параболоиды могут иметь другую ориентацию, просто заменив переменные местами, чтобы получить другую переменную в линейном члене уравнения x2a2+z2c2=ybx2a2+z2c2=yb или y2b2+z2c2=xa.y2b2+z2c2=xa.
Например, если поверхность может быть описана уравнением вида x2a2+y2b2=zc,x2a2+y2b2=zc, то мы называем эту поверхность эллиптическим параболоидом. След в xy -плоскость представляет собой эллипс, а трассы в xz -плоскости и yz -плоскости представляют собой параболы (рис. 2.83). Другие эллиптические параболоиды могут иметь другую ориентацию, просто заменив переменные местами, чтобы получить другую переменную в линейном члене уравнения x2a2+z2c2=ybx2a2+z2c2=yb или y2b2+z2c2=xa.y2b2+z2c2=xa.
Рисунок 2,83 Эта квадратичная поверхность называется эллиптическим параболоидом .
Пример 2,57
Идентификация следов четырехугольных поверхностей
Опишите следы эллиптического параболоида x2+y222=z5.x2+y222=z5.
Решение
Чтобы найти трассу в плоскости xy , установите z=0:z=0:x2+y222=0. x2+y222=0. След в плоскости z=0z=0 — это просто одна точка, начало координат. Поскольку одна точка не говорит нам, какова форма, мы можем двигаться вверх по оси z к произвольной плоскости, чтобы найти форму других следов фигуры.
x2+y222=0. След в плоскости z=0z=0 — это просто одна точка, начало координат. Поскольку одна точка не говорит нам, какова форма, мы можем двигаться вверх по оси z к произвольной плоскости, чтобы найти форму других следов фигуры.
Трасса в плоскости z=5z=5 представляет собой график уравнения x2+y222=1,x2+y222=1, представляющий собой эллипс. В xz — плоскость, уравнение принимает вид z=5×2.z=5×2. След представляет собой параболу в этой плоскости и в любой плоскости с уравнением y=b.y=b.
В плоскостях, параллельных плоскости yz , следы также являются параболами, как мы можем видеть на следующем рисунке.
Рисунок 2,84 (а) Параболоид x2+y222=z5.x2+y222=z5. (б) След в плоскости z=5.z=5. (в) След в плоскости xz . (г) След в плоскости yz .
Контрольно-пропускной пункт 2,53
Однослойный гиперболоид — это любая поверхность, которая может быть описана уравнением вида x2a2+y2b2−z2c2=1.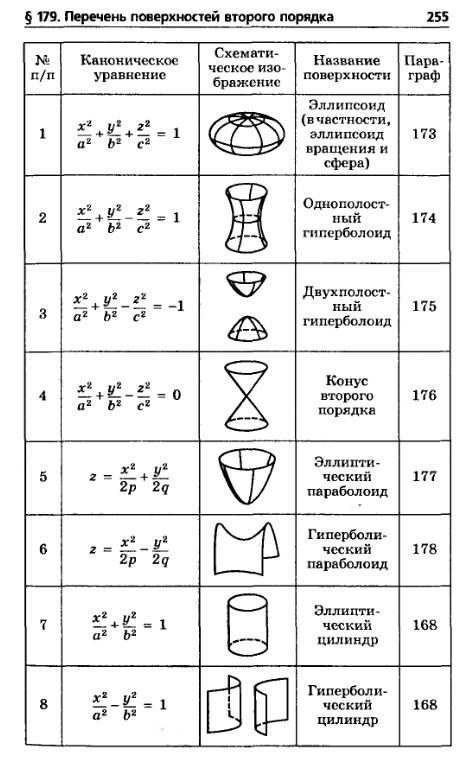 x2a2+y2b2−z2c2=1. Опишите следы гиперболоида одного листа, заданного уравнением x232+y222−z252=1.x232+y222−z252=1.
x2a2+y2b2−z2c2=1. Опишите следы гиперболоида одного листа, заданного уравнением x232+y222−z252=1.x232+y222−z252=1.
Гиперболоиды из одного листа обладают интересными свойствами. Например, их можно построить с помощью прямых линий, как в скульптуре на рис. 2.85(а). На самом деле градирни для атомных электростанций часто строят в форме гиперболоида. Строители могут использовать в конструкции прямые стальные балки, что делает башни очень прочными при использовании относительно небольшого количества материала (рис. 2.85(b)).
Рисунок 2,85 (а) Скульптура в форме гиперболоида может быть построена из прямых линий. (b) Градирни для атомных электростанций часто строят в форме гиперболоида.
Пример 2,58
Вступительное слово: определение фокуса параболического отражателя
Энергия, падающая на поверхность параболического отражателя, концентрируется в фокусе отражателя (рис. 2.86). Если поверхность параболического отражателя описывается уравнением x2100+y2100=z4,x2100+y2100=z4, где находится фокус отражателя?
Рисунок
2,86
Энергия отражается от параболического отражателя и собирается в фокусе. (кредит: модификация CGP Grey, Wikimedia Commons)
(кредит: модификация CGP Grey, Wikimedia Commons)
Решение
Поскольку z является переменной первой степени, ось отражателя соответствует оси z . Коэффициенты при x2x2 и y2y2 равны, поэтому поперечное сечение параболоида, перпендикулярное оси z , представляет собой окружность. Мы можем рассмотреть след в xz -плоскость или yz -плоскость; результат тот же. При y=0,y=0 трасса представляет собой параболу, расходящуюся вдоль оси z , со стандартным уравнением x2=4pz,x2=4pz, где pp — фокусное расстояние параболы. В этом случае это уравнение принимает вид x2=100·z4=4pzx2=100·z4=4pz или 25=4p.25=4p. Таким образом, p составляет 6,256,25 м, что говорит нам о том, что фокус параболоида находится на расстоянии 6,256,25 м вверх по оси от вершины. Поскольку вершина этой поверхности является началом координат, точка фокуса равна (0,0,6,25).(0,0,6,25).
Поскольку вершина этой поверхности является началом координат, точка фокуса равна (0,0,6,25).(0,0,6,25).
Семнадцать стандартных квадратичных поверхностей могут быть получены из общего уравнения
Ax2+By2+Cz2+Dxy+Exz+Fyz+Gx+Hy+Jz+K=0.Ax2+By2+Cz2+Dxy+Exz+Fyz+Gx+Hy+Jz+K=0.
На следующих рисунках представлены наиболее важные из них.
На следующих двух рисунках «ось» квадратичной поверхности может быть или не быть осью симметрии. Однако все следы на поверхности, образованной любой плоскостью, перпендикулярной «оси», будут иметь один и тот же тип конического сечения.
Рисунок 2,87 Характеристики обычных квадратичных поверхностей: эллипсоид, гиперболоид из одного листа, гиперболоид из двух листов.
Рисунок 2,88 Характеристики обычных квадратичных поверхностей: эллиптический конус, эллиптический параболоид, гиперболический параболоид.
Пример 2,59
Определение уравнений квадратных поверхностей
Определение поверхностей, представленных данными уравнениями.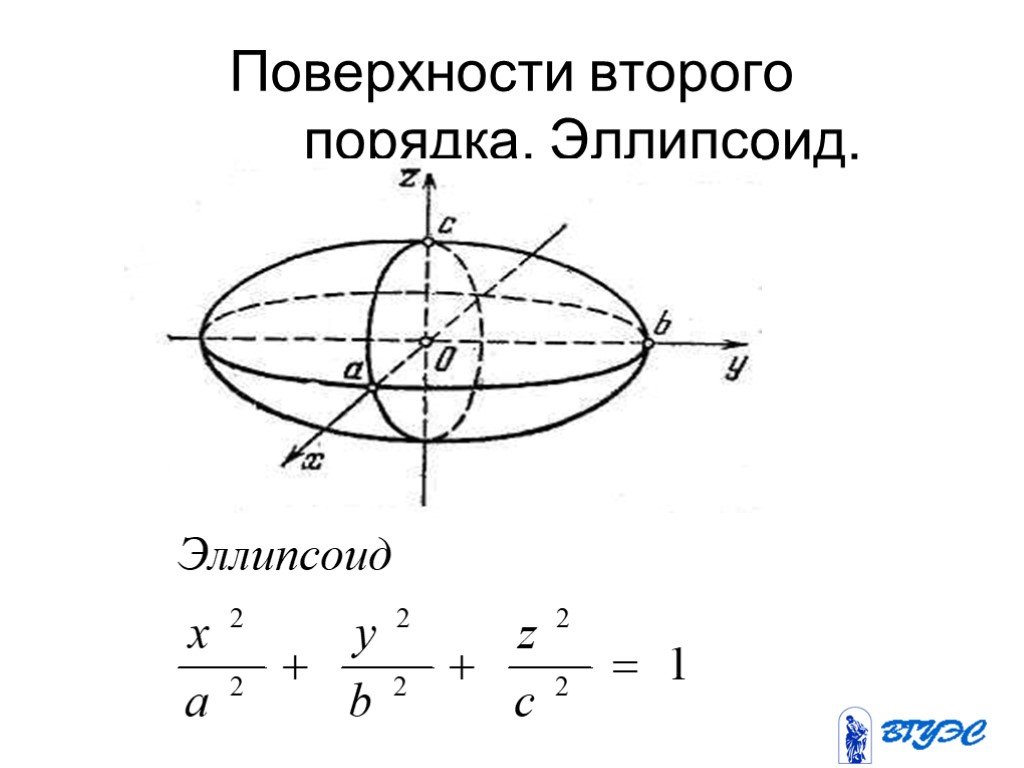
Решение
Контрольно-пропускной пункт 2,54
Определите поверхность, представленную уравнением 9×2+y2-z2+2z-10=0,9×2+y2-z2+2z-10=0.
Раздел 2.6 Упражнения
Для следующих упражнений нарисуйте и опишите цилиндрическую поверхность данного уравнения.
303.
[Т] x2+z2=1×2+z2=1
304.
[Т] х2+у2=9х2+у2=9
305.
[Т] z=cos(π2+x)z=cos(π2+x)
306.
[Т] z=exz=ex
307.
[Т] z=9-y2z=9-y2
308.
[Т] z=ln(x)z=ln(x)
Для следующих упражнений дан график квадратичной поверхности.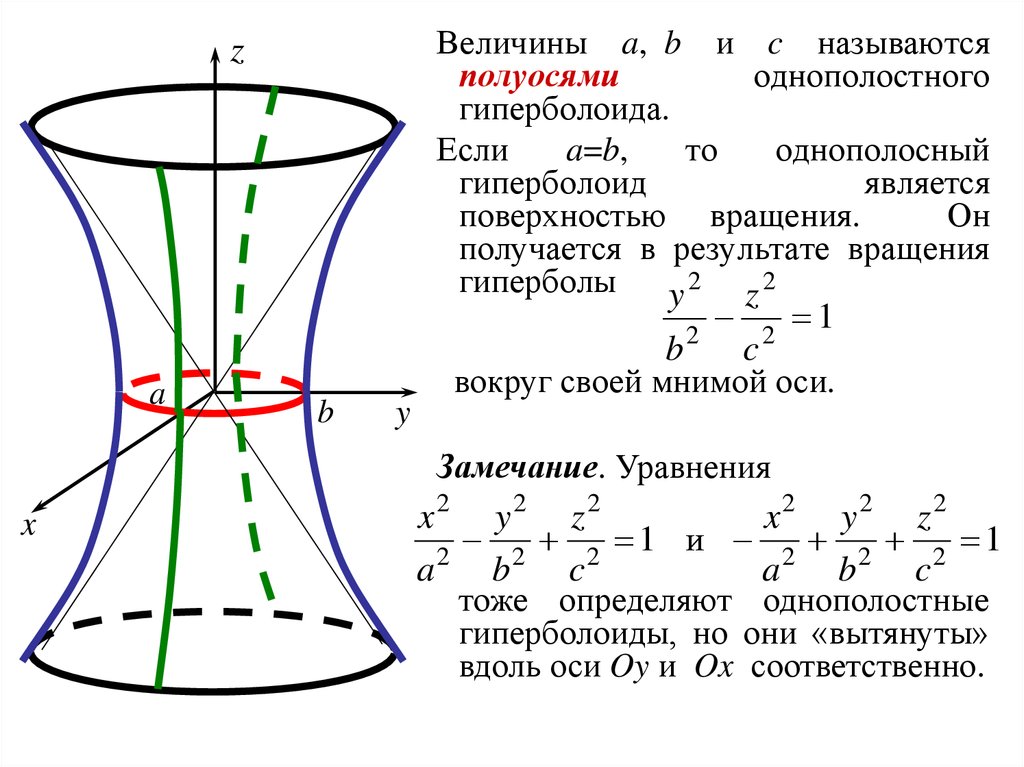
309.
310.
311.
312.
Для следующих упражнений сопоставьте заданную квадратную поверхность с соответствующим уравнением в стандартной форме.
313.
Гиперболоид из двух листов
314.
Эллипсоид
315.
Эллиптический параболоид
316.
Гиперболический параболоид
317.
Гиперболоид из одного листа
318.
Эллиптический конус
Для следующих упражнений перепишите данное уравнение поверхности квадрата в стандартной форме. Определите поверхность.
319.
−x2+36y2+36z2=9−x2+36y2+36z2=9
320.
−4×2+25y2+z2=100−4×2+25y2+z2=100
321.
−3×2+5y2−z2=10−3×2+5y2−z2=10
322.
3×2-y2-6z2=183×2-y2-6z2=18
323.
5y=x2−z25y=x2−z2
324.
8×2-5y2-10z=08×2-5y2-10z=0
325.
x2+5y2+3z2-15=0x2+5y2+3z2-15=0
326.
63×2+7y2+9z2−63=063×2+7y2+9z2−63=0
327.
х2+5у2-8г2=0х2+5у2-8г2=0
328.
5×2−4y2+20z2=05×2−4y2+20z2=0
329.
6x=3y2+2z26x=3y2+2z2
330.
49y=x2+7z249y=x2+7z2
Для следующих упражнений найдите след заданной поверхности квадрата в заданной плоскости координат и зарисуйте его.
331.
[T] x2+z2+4y=0,z=0x2+z2+4y=0,z=0
332.
[T] x2+z2+4y=0,x=0x2+z2+4y=0,x=0
333.
[Т] −4×2+25y2+z2=100,x=0−4×2+25y2+z2=100,x=0
334.
[T] −4×2+25y2+z2=100,y=0−4×2+25y2+z2=100,y=0
335.
[T] x2+y24+z2100=1,x=0x2+y24+z2100=1,x=0
336.
[Т] x2-y-z2=1,y=0x2-y-z2=1,y=0
337.
Используйте график заданной поверхности квадрата, чтобы ответить на вопросы.
338.
Используйте график заданной поверхности квадрата, чтобы ответить на вопросы.
Для следующих упражнений дается уравнение поверхности квадрата.
339.
x2+2z2+6x−8z+1=0x2+2z2+6x−8z+1=0
340.
4×2-y2+z2-8x+2y+2z+3=04×2-y2+z2-8x+2y+2z+3=0
341.
x2+4y2-4z2-6x-16y-16z+5=0x2+4y2-4z2-6x-16y-16z+5=0
342.
х2+z2-4у+4=0x2+z2-4у+4=0
343.
x2+y24−z23+6x+9=0x2+y24−z23+6x+9=0
344.
x2-y2+z2-12z+2x+37=0x2-y2+z2-12z+2x+37=0
345.
Напишите стандартную форму уравнения эллипсоида с центром в начале координат, проходящего через точки A(2,0,0),B(0,0,1),A(2,0,0),B(0 ,0,1) и С(12,11,12).С(12,11,12).
346.
Напишите стандартную форму уравнения эллипсоида с центром в точке P(1,1,0)P(1,1,0), проходящего через точки A(6,1,0),B(4,2, 0)А(6,1,0),В(4,2,0) и С(1,2,1). С(1,2,1).
С(1,2,1).
347.
Определить точки пересечения эллиптического конуса x2−y2−z2=0x2−y2−z2=0 с прямой уравнения симметрии x−12=y+13=z.x−12=y+13=z.
348.
Определить точки пересечения параболического гиперболоида z=3×2−2y2z=3×2−2y2 с линией параметрических уравнений x=3t,y=2t,z=19t,x=3t,y=2t,z=19t, где t∈ℝ.t∈ℝ.
349.
Найдите уравнение поверхности квадрата с точками P(x,y,z)P(x,y,z), равноудаленными от точки Q(0,−1,0)Q(0,−1,0) и плоскость уравнения y=1.y=1. Определите поверхность.
350.
Найдите уравнение поверхности квадрата с точками P(x,y,z)P(x,y,z), равноудаленными от точки Q(0,2,0)Q(0,2,0) и плоскости уравнения y=−2.y=−2. Определите поверхность.
351.
Если поверхность параболического отражателя описывается уравнением 400z=x2+y2,400z=x2+y2, найдите фокус отражателя.
352.
Рассмотрим параболический отражатель, описываемый уравнением z=20×2+20y2.z=20×2+20y2. Найдите его фокус.
353.
Покажите, что квадратичная поверхность x2+y2+z2+2xy+2xz+2yz+x+y+z=0x2+y2+z2+2xy+2xz+2yz+x+y+z=0 сводится к двум параллельным плоскостям.
354.
Покажите, что квадратичная поверхность x2+y2+z2−2xy−2xz+2yz−1=0x2+y2+z2−2xy−2xz+2yz−1=0 сводится к двум пересекающимся параллельным плоскостям.
355.
[T] Пересечение цилиндра (x−1)2+y2=1(x−1)2+y2=1 и сферы x2+y2+z2=4×2+y2+z2=4 называется Кривая Вивиани .
356.
Гиперболоид из одного листа 25×2+25y2−z2=2525×2+25y2−z2=25 и эллиптического конуса −25×2+75y2+z2=0−25×2+75y2+z2=0 представлены на следующем рисунке вместе с кривыми их пересечения. Определите кривые пересечения и найдите их уравнения ( Подсказка: Найдите и из системы, состоящей из уравнений поверхностей.)
357.
[T] Используйте CAS для создания пересечения между цилиндром 9×2+4y2=189×2+4y2=18 и эллипсоидом 36×2+16y2+9z2=144,36×2+16y2+9z2=144 и найдите уравнения пересечения кривые.
358.
[T] Сфероид – это эллипсоид с двумя равными полуосями. Например, уравнение сфероида с осью z в качестве оси симметрии имеет вид x2a2+y2a2+z2c2=1,x2a2+y2a2+z2c2=1, где aa и cc — положительные действительные числа. Сфероид называется сплющенный , если c
Сфероид называется сплющенный , если c
359.
[T] В картографии Земля изображается сплюснутым сфероидом, а не сферой. Радиусы на экваторе и полюсах примерно равны 39633963 миль и 39503950 миль соответственно.
360.
[T] Набор жужжащих трюковых магнитов (или «яиц гремучей змеи») включает в себя два сверкающих, полированных, сверхсильных магнита в форме сфероида, хорошо известных для детских развлечений. Каждый магнит имеет длину 1,6251,625 дюйма и ширину в середине 0,50,5 дюйма. Подбрасывая их в воздух, они издают жужжащий звук, притягивая друг друга.

 для вузов: В 3 т. / Я. С. Бугров, С. М. Никольский; Под ред. В. А. Садовничего. — 6-е изд., стереотип. — М.: Дрофа, 2004. — (Высшее образование: Современный учебник).
для вузов: В 3 т. / Я. С. Бугров, С. М. Никольский; Под ред. В. А. Садовничего. — 6-е изд., стереотип. — М.: Дрофа, 2004. — (Высшее образование: Современный учебник).