Правила деления на 4: § Признак делимости на 2, 4 и 8

правило и примеры нахождения частного двух чисел без остатка

Математика

12.11.21

7 мин.

При упрощении выражений необходимо знать некоторые особенности или правила с примерами. Признаки делимости на 4 вызывают сложности у учеников в 5 классе. Для изучения этой темы специалисты предлагают использовать научный подход, который основан на психофизиологических особенностях работы головного мозга. Он включает ознакомление с основными элементами теории и алгоритмом.

Оглавление:

• Классификация деления
• Признаки делимости на 4
• Пример реализации

Общие сведения

Деление — арифметическая операция, позволяющая найти один из множителей при их произведении. Иными словами, деление является обратным действием относительно умножения. Записывается оно следующим образом: U/T=V. Далее следует подробно разобрать каждый из элементов операции:

1. U — делимое (исходная величина, представляющая целое или дробное число).
2. T — делитель (значение, показывающее количество равных частей, на которые требуется разделить первоначальное значение).
3. V — результат операции.

Если провести аналогию с умножением, то компоненты можно назвать по-другому: U — произведение, T и V — I и II множители соответственно. Следует отметить, что операция деления проверяется при помощи произведения.

Например, нужно поделить 12 на 4. Записывать действие необходимо в виде математического числового выражения, т. е. 12/4. Результат эквивалентен значению 3. Чтобы проверить правильность нахождения частного, необходимо осуществить произведение «4*3».

По таблице Пифагора результат равен числу 12. Так выглядит доказательство того, что деление — обратная операция умножению. Можно придумать любой пример для закрепления материала. Следует помнить, что теория должна всегда подтверждаться практикой.

Классификация деления

Следует отметить, что деление бывает двух видов: целочисленным и с остатком. Первое осуществляется без остатка, и его результатом всегда является целое число. Об этом говорят, что исходное значение кратно делителю.

Если величина не делится нацело на определенное число, то образуется дробь. Последняя бывает обыкновенной или десятичной. При сокращении выражений следует подбирать делитель только для целочисленной операции. Например, для дроби 24/32 общим делителем является 8, поскольку 8*3=24 и 8*4=32. Математическая запись имеет такой вид: 24/32=(8*3)/(8*4)=(8/8)*(¾)=¾.

Специалисты рекомендуют всегда подбирать делитель, чтобы при сокращении получалось целая величина.

Если этого принципа не придерживаться, то вычисления существенно усложняться. Далее необходимо разобрать критерии деления числа на четверку, поскольку эта тема является очень сложной для некоторых учеников.

Признаки делимости на 4

Для деления искомого числа на четверку нацело специалисты разработали специальный алгоритм. Он позволяет быстро определить, какое число делится на 4. Он имеет следующий вид:

1. Проверить величину на четность. Если число — четное, то нужно перейти ко второму пункту.
2. Отсеять две последние цифры.
3. Значение, полученное во втором пункте, должно нацело делиться на четверку.

Исходя из методики, можно сформулировать такое свойство, позволяющее узнать, делится ли исходное значение на 4: величина на четверку делится в том случае, когда является четной и число, образованное разрядами десятков и единиц, можно поделить на это значение без остатка.

Пример реализации

Для реализации методики необходимо доказать кратность числа 213 четверке. Это осуществляется таким образом:

1. Записать величину: 213.
2. Проверить ее на четность: 213 — нечетное значение.
3. Вывод: число 213 на четверку нацело поделить невозможно.

Далее необходимо разобрать другой пример деления 212 на 4. Проверка кратности осуществляется следующим образом:

1. Записать число: 212.
2. Проверить на четность: 212 — четное, т. к. последний разряд заканчивается на двойку.
3. Число, образованное из двух последних цифр: 12.
4. Вывод: 212 можно без остатка поделить на 4, поскольку значение является четным, а две последние элементы разрядной сетки делятся на четверку.

Если выполнить операцию «212/4» при помощи калькулятора, то можно получить целочисленное значение, которое равно 53. Чтобы понять принцип действия алгоритма, нужно придумать любое число, и попытаться поделить его на четверку. Например, нужно разделить 4325624 на 4. Для этого требуется сначала выяснить кратность искомого числа четырем.

Решать задачу нужно таким образом:

1. Записать величину: 4325624.
2. Определить четность: четное, поскольку заканчивается на 4.
3. Взять последние 2 цифры: 24. Они делятся на 4, поскольку 4*6=24.

Далее требуется на калькуляторе или в столбик осуществить операцию деления, результатом которой будет число «1081406».

Таким образом, чтобы поделить любое числовое значение на четверку нужно проверить его четность, а также целочисленное деление на искомый делитель величины, образованной двумя последними цифрами.

Не успеваете написать работу?

Заполните форму и узнайте стоимость

Вид работыПоиск информацииДипломнаяВКРМагистерскаяРефератОтчет по практикеВопросыКурсовая теорияКурсовая практикаДругоеКонтрольная работаРезюмеБизнес-планДиплом MBAЭссеЗащитная речьДиссертацияТестыЗадачиДиплом техническийПлан к дипломуКонцепция к дипломуПакет для защитыСтатьиЧасть дипломаМагистерская диссертацияКандидатская диссертация

Контактные данные — строго конфиденциальны!

Указывайте телефон без ошибок! — потребуется для входа в личный кабинет.

* Нажимая на кнопку, вы даёте согласие на обработку персональных данных и соглашаетесь с политикой конфиденциальности

Подтверждение

Ваша заявка принята.

Ей присвоен номер 0000.
Просьба при ответах не изменять тему письма и присвоенный заявке номер.
В ближайшее время мы свяжемся с Вами.

Ошибка оформления заказа

Кажется вы неправильно указали свой EMAIL, без которого мы не сможем ответить вам.
Пожалуйста проверте заполнение формы и при необходимости скорректируйте данные.

Признак делимости на 4: примеры, доказательство

Приступим к рассмотрению темы «Признак делимости на 4». Приведем здесь формулировку признака, проведем его доказательство, рассмотрим основные примеры задач. В конце раздела мы собрали сведения о подходах, которые можно применять в тех случаях, когда нам нужно доказать делимость чисел на 4, заданных буквенным выражением.

Признак делимости на 4, примеры

Мы можем пойти простым путем и поделить однозначное натуральное число на 4 для того, чтобы проверить, делится ли это число на 4 без остатка. Так же можно поступить с двузначными, трехзначными и проч. числами.  Однако, чем больше становятся числа, тем сложнее проводить с ними действия с целью проверки делимости их на 4.

Гораздо проще становится использовать признак делимости на 4. Он предполагает проведение проверки делимости одной или двух последних цифр целого числа на 4. Что это значит? Это значит, что некоторое число a делится на 4 в том случае, если одна или две крайние правые цифры в записи числа a делятся на 4. Если число, составленное из двух крайних правых цифр в записи числа a не делятся на 4 без остатка, то и число a не делится на 4 без остатка.

Пример 1

Какие из чисел 98 028, 7 612 и 999 888 777 делятся на 4?

Решение

Крайние правые цифры чисел − 98 028, 7 612 составляют числа 28 и 12, которые делятся на 4 без остатка. Это значит, что и целые числа − 98 028, 7 612​​​​​​ ​делятся на 4 без остатка.

Последние две цифры в записи числа 999 888 777 образуют число 77, которое не делится на 4 без остатка. Это значит, что и исходное число на 4 без остатка не делится.

Ответ: −98 028 и 7 612.

Если предпоследней цифрой в записи числа является 0, то нам необходимо этот ноль отбросить и смотреть на оставшуюся крайнюю правую цифру в записи. Получается, что две цифры 01 мы заменяем 1. И уже по одной оставшейся цифре мы делаем вывод о том, делится ли исходное число на 4.

Пример 2

Делится ли числа 75 003 и −88 108 на 4?

Решение

Две последние цифры числа 75 003 — видим 03. Если отбросить ноль, то у нас остается цифра 3, которая на 4 без остатка не делится. Это значит, что исходное число 75 003 на 4 без остатка не делится.

Теперь возьмем две последние цифры числа −88 108. Это 08, из которых мы должны оставить лишь последнюю цифру 8. 8 делится на 4 без остатка.

Это значит, что и исходное число −88 108 мы можем поделить на 4 без остатка.

Ответ: 75 003 не делится на 4, а −88 108 – делится.

Числа, у которых в конце записи идет сразу два нуля, также делятся на 4 без остатка. Например, 100 делится на 4, получается 25. Доказать правдивость этого утверждения нам позволяет правило умножения числа на 100.

Представим произвольно выбранное многозначное число a, запись которого справа заканчивается двумя нулями, как произведение a1·100, где число a1 получается из числа a, если в его записи справа отбросить два нуля. Например, 486700=4867·100.

Произведение a1·100 содержит множитель 100, который делится на 4. Это значит, что все приведенное произведение делится на 4.

Доказательство признака делимости на 4

Представим любое натуральное число a в виде равенства a=a1·100+a0, в котором число a1 – это число a, из записи которого убрали две последние цифры, а число a0 – это две крайние правые цифры из записи числа a. Если использовать конкретные натуральные числа, то равенство будет иметь вид undefined. Для одно- и двузначных чисел

a=a0.

Определение 1

Теперь обратимся к свойствам делимости: 

• деление модуля числа a на модуль числа b необходимо и достаточно для того, чтобы целое число a делилось на целое число b;
• если в равенстве a=s+t все члены, кроме одного делятся на некоторое целое число b, то и этот оставшийся член делится на число b.

Теперь, освежив в памяти необходимые свойства делимости, переформулируем доказательство признака делимости на 4 в виде необходимого и достаточного условия делимости на 4.

Теорема 1

Деление двух последних цифр в записи числа a на 4 – это необходимое и достаточное условие для делимости целого числа a на 4.

Доказательство 1

Если предположить, что a=0, то теорема в доказательстве не нуждается. Для всех остальных целых чисел a мы будем использовать модуль числа a, который является числом положительным:a=a1·100+a0

С учетом того, что произведение a1·100всегда делится на 4, а также с учетом свойств делимости, которые мы привели выше, мы можем сделать следующее утверждение: если число a делится на 4, то и модуль числа a делится на 4, тогда из равенства a=a1·100+a0 следует, что a0 делится на 4. Так мы доказали необходимость.

Из равенства a=a1·100+a0 следует, что модуль a делится на 4. Это значит, что и само число a делится на 4. Так мы доказали достаточность.

Другие случаи делимости на 4

Рассмотрим случаи, когда нам нужно установить делимость на 4 целого числа, заданного некоторым выражением, значение которого надо вычислить. Для этого мы можем пойти следующим путем:

• представить исходное выражение в виде  произведения нескольких множителей, один из которых будет делиться на 4;
• сделать вывод на основании свойства делимости о том, что все исходное выражение делится на
  4.

Помочь в решении задачи часто помогает формула бинома Ньютона.

Пример 3

Делится ли на 4 значение выражения 9n-12n+7 при некотором натуральном n?

Решение

Мы можем представить 9 в виде суммы 8+1. Это дает нам возможность применить формулу бинома Ньютона:

9n-12n+7=8+1n-12n+7==Cn0·8n+Cn1·8n-1·1+…+Cnn-2·82·1n-2+Cnn-1·8·1n-1+Cnn·1n—12n+7==8n+Cn1·8n-1·1+.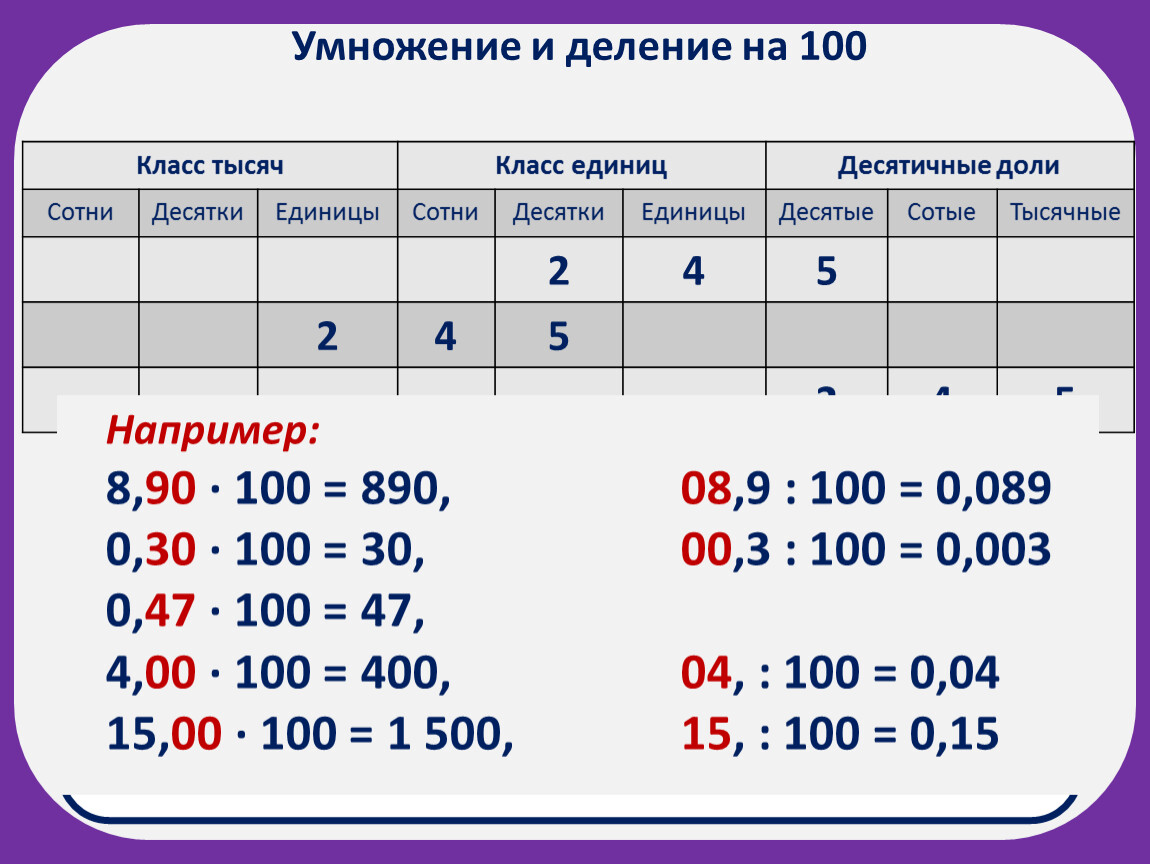 ..+Cnn-2·82+n·8+1—12n+7==8n+Cn1·8n-1·1+…+Cnn-2·82-4n+8==4·2·8n-1+2·Cn1·8n-2+…+2·Cnn-2·81-n+2

Произведение, которое мы получили в ходе преобразований, содержит множитель 4, а выражение в скобках представляет собой натуральное число. Это значит, что это произведение можно разделить на 4 без остатка.

Мы можем утверждать, что исходное выражение 9n-12n+7 делится на 4 при любом натуральном n.

Ответ: Да.

Также мы можем применить к решению задачи метод математической индукции. Чтобы не отвлекать ваше внимание на второстепенные детали разбора решения, возьмем прежний пример.

Пример 4

Докажите, что 9n-12n+7 делится на 4 при любом натуральном n.

Решение

Начнем с установления того, что при значении n=1 значение выражения 9n-12n+7
можно будет разделить на 4 без остатка.

Получаем: 91-12·1+7=4. 4 делится на 4 без остатка.

Теперь мы можем предположить, что при значении n=k значение выражения
9n-12n+7 будет делиться на 4. Фактически, мы будем работать с выражением 9k-12k+7, которое должно делиться на 4.

Нам необходимо доказать, что 9n-12n+7 при n=k+1будет делиться на 4 с учетом того, что 9k-12k+7​​​​​ делится на 4:

9k+1-12(k+1)+7=9·9k-12k-5=9·9k-12k+7+96k-68==9·9k-12k+7+4·24k-17

Мы получили сумму, в которой первое слагаемое 9·9k-12k+7 делится на 4 в связи с нашим предположением о том, что 9k-12k+7 делится на 4, а второе слагаемое 4·24k-17 содержит множитель 4, в связи с чем также делится на 4. Это значит, что вся сумма делится на 4.

Ответ: мы доказали, что 9n-12n+7 делится на 4 при любом натуральном значении n методом математической индукции.

Мы можем использовать еще один подход для того, чтобы доказать делимость некоторого выражения на 4. Этот подход предполагает:

• доказательство факта того, что значение данного выражения с переменной n делится на 4 при n=4·m, n=4·m+1, n=4·m+2 и n=4·m+3, где m – целое число;
• вывод о доказанности делимости данного выражения на 4 для любого целого числа n.

Пример 5

Докажите, что значение выражения n·n2+1·n+3·n2+4 при любом целом nделится на 4.

Решение

Если предположить, что n=4·m, получаем:

 4m·4m2+1·4m+3·4m2+4=4m·16m2+1·4m+3·4·4m2+1

Полученное произведение содержит множитель 4, все остальные множители представлены целыми числами. Это дает нам основание предполагать, что все произведение делится на 4.

Если предположить, что n=4·m+1, получаем:

4m+1·4m+12+1·4m+1+3·4m+12+4==(4m·1)+4m+12+1·4m+1·4m+12+4

И опять в произведении, которое мы получили в ходе преобразований,
содержится множитель 4.

Это значит, что выражение делится на 4.

Если предположить, что n=4·m+2, то:

4m+2·4m+22+1·4m+2+3·4m+22+4==2·2m+1·16m2+16m+5·(4m+5)·8·(2m2+2m+1)

Здесь в произведении мы получили множитель 8, который можно без остатка поделить на 4. Это значит, что все произведение делится на 4.

Если предположить, что n=4·m+3, получаем:

4m+3·4m+32+1·4m+3+3·4m+32+4==4m+3·2·8m2+12m+5·2·2m+3·16m2+24m+13==4·4m+3·8m2+12m+5·16m2+24m+13

Произведение содержит множитель 4, значит делится на 4 без остатка.

Ответ: мы доказали, что исходное выражение делится на 4 при любом n.

Правило делимости на 4 — Методы, примеры также известен как тест на делимость на 4. Правило делимости на 4 помогает узнать, делится ли число на 4 или нет без выполнения деления. Первые четыре целых числа, которые делятся на 4, — это 0, 4, 8, 12 и 16. Все они кратны 4, и каждое кратное 4 полностью делится на 4.

1.	Что такое правило делимости на 4?
2.	Правило делимости на 4 для больших чисел
3.	Правило делимости на 4 и 6
4.	Признак делимости на 4 и 8
5.	Часто задаваемые вопросы о правиле делимости числа 4

Что такое правило делимости на 4?

Согласно правилу делимости на 4, целое число считается делящимся на 4, если оно удовлетворяет одному из двух условий:

• Если последние две цифры данного числа — нули. Это означает, что число имеет нули в разряде десятков и разряде единиц. Например, в числе 300 последние две цифры 00, следовательно, 300 делится на 4.
• Если последние две цифры данного числа образуют число, которое точно делится на 4. Например, в 316 последние две цифры образуют число 16, которое делится на 4. Следовательно, 316 делится на 4.

Правило делимости на 4 с примерами

Правило делимости на 4 можно понять с помощью следующих примеров.

Пример: Проверить делимость следующих чисел на 4.

а.) 1124

б.) 1171

в.) 1300

г.) 500 9 0005

Решение:

а. ) В 1124 последние две цифры в данном числе образуют число 24, которое делится на 4 (24 ÷ 4 = 6)
Таким образом, 1124 делится на 4. Это можно проверить следующим образом: 1124 ÷ 4 = 281

b.) В 1171 последние две цифры в данном числе образуют число 71, которое не делится полностью на 4 (71÷4 = 17 — частное, а 3 — остаток)
Таким образом, 1171 не делится на 4.

в.) В числе 1300 последние две цифры в данном числе — нули. Это означает, что 1300 полностью делится на 4.
1300 ÷ 4 = 325
Таким образом, 1300 делится на 4.

г) В числе 500 последние две цифры данного числа — нули. Это означает, что 500 полностью делится на 4.
500 ÷ 4 = 125
Таким образом, 500 делится на 4.

Правила делимости помогают решать задачи без процесса деления.

Правило делимости на 4 для больших чисел

Правило делимости на 4 гласит, что если число имеет два нуля в конце или две последние цифры образуют число, которое точно делится на 4, то данное число также делится на 4. Следовательно, для любых больших чисел мы проверяем последние две цифры и применяем правило делимости на 4 и можем узнать, делится ли большое число на 4 или нет.

Пример 1: в 238900 последние две цифры в разряде десятков и разряде единиц равны нулю. Это означает, что 238900 делится на 4.
238900 ÷ 4 = 59725
Таким образом, 238900 делится на 4.

Пример 2: В числе 148936 две последние цифры десятков и единиц образуют число 36, которое делится на 4 (36 ÷ 4 = 9).
148936 ÷ 4 = 37234
Таким образом, 148936 делится на 4.

Правило делимости на 4 и 6

Правила делимости на 4 и 6 совершенно разные. В правиле делимости 4, если последние две цифры являются нулями или число, образованное двумя последними цифрами, точно делится на 4, то мы можем сказать, что число делится на 4. Однако, согласно правилу делимости 6 , говорят, что число делится на 6 только в том случае, если оно делится и на 2, и на 3. В тесте на делимость 4 мы проверяем две последние цифры, а в тесте на делимость 6 мы проверяем, все ли число делится на 2 и 3 или нет. Например, давайте проверим, если 936 делится на 6. Поскольку последняя цифра числа 936 четное число, можно сказать, что 936 делится на 2. Теперь проверим его делимость на 3. Сумма цифр равна 9 + 3 + 6 = 18, что делится на 3. Это означает, что 936 тоже делится на 3. Следовательно, можно сказать, что число 936 полностью делится на 6.

Признак делимости на 4 и 8

Признаки делимости 4 и 8 немного похожи. В тесте на делимость 4 мы проверяем две последние цифры, если последние две цифры — нули или число, образованное двумя последними цифрами числа, точно делится на 4, то исходное число также делится на 4. В тесте тест делимости 8, мы проверяем последние три цифры, если последние три цифры нули или число, образованное последними тремя цифрами числа, точно делится на 8, то исходное число также делится на 8. Например, пусть мы проверим, делится ли 61816 на 8. Если мы проверим последние 3 цифры, они образуют число 816, которое делится на 8. Следовательно, можно сказать, что 61816 делится на 8.

☛ Похожие темы

• Правило делимости на 3
• Правило делимости числа 5
• Правило делимости числа 6
• Правило делимости числа 7
• Правило делимости числа 8
• Правило делимости числа 9
• Правило делимости числа 11
• Правило делимости числа 13

 

Правило делимости на 4 примера

1. Пример 1: Узнать, делятся ли данные числа на 4 или нет, используя признак делимости на 4.

   а.) 380
   б.) 549
   в) 740

   Решение:

   а) В числе 380 последние две цифры образуют число 80, которое делится на 4. Следовательно, 380 делится на 4 (380 ÷ 4 = 95).

   б) В числе 549 последние две цифры образуют число 49, которое не делится на 4. Следовательно, 549 не делится на 4.

   в) В числе 740 последние две цифры образуют число 40, которое делится на 4. Следовательно, 740 делится на 4 (740 ÷ 4 = 185).

2. Пример 2: Определите, делится ли наименьшее 6-значное число на 4 или нет, используя правило делимости на 4.

   Решение: последние две цифры наименьшего шестизначного числа — два нуля.
   (100000 ÷ 4 = 25000)

3. Пример 3: Проверить, делится ли заданное большое число 434788 на 4, используя правило делимости на 4.

   Решение: В 434788 последние две цифры образуют число 88, а 88 делится на 4 точно, следовательно, число 434788 делится на 4.
   (434788 ÷ 4 = 108697)

перейти к слайду перейти к слайду перейти к слайду

Отличное обучение в старшей школе с использованием простых подсказок

Увлекаясь зубрежкой, вы, скорее всего, забудете понятия. С Cuemath вы будете учиться визуально и будете удивлены результатами.

Записаться на бесплатный пробный урок

Практические вопросы по правилу делимости 4

 

перейти к слайдуперейти к слайду

Часто задаваемые вопросы о правиле делимости числа 4

Что такое правило делимости на 4?

Правило делимости числа 4 гласит, что число считается делящимся на 4, если две последние цифры числа равны нулю или образуют число, которое делится на 4. Например, 2300 делится на 4, потому что два нуля в конце числа. Точно так же 488 также делится на 4, потому что последние две цифры 88 делятся на 4.

Используя правило делимости на 4, проверьте, делится ли 14540 на 4.

Сначала нам нужно проверить, делится ли число, состоящее из двух последних цифр заданного числа, на 4 или нет. В данном числе 14540 число, образованное двумя последними цифрами, равно 40, а 40 делится на 4. Таким образом, 14540 делится на 4.

Каково правило делимости 4 и 8?

Правила делимости на 4 и 8 немного похожи. В правиле делимости на 4 мы ориентируемся на две последние цифры числа. Если последние две цифры нули или число, образованное двумя последними цифрами числа, точно делится на 4, то можно сказать, что данное число также делится на 4. Например, 800, 900 и 348 делятся на 4, поскольку они удовлетворяют условию правила делимости на 4.

В правиле делимости на 8 мы фокусируемся на трех последних цифрах числа. Если последние три цифры — нули или число, образованное последними тремя цифрами числа, точно делится на 8, то мы можем сказать, что исходное число также делится на 8. Например, 8000, 9000 и 3896 делятся. на 8, поскольку они удовлетворяют условию правила делимости на 8.

Как узнать, делится ли большое число на 4?

Согласно правилу делимости на 4 любое большое число делится на 4 точно, если число, состоящее из цифр, стоящих на десятках и единицах, делится на 4 точно. Например, число 2 146 484 делится на 4 точно, потому что число 84 (последние две цифры) делится на 4.

Используя правило делимости 4, проверьте, делится ли 19500 на 4. нули в конце или две последние цифры образуют число, которое точно делится на 4, тогда это число также делится на 4.

Какие числа делятся на 4?

Согласно правилу делимости на 4, если последние две цифры данного числа равны нулю или образуют число, которое полностью делится на 4, то говорят, что данное число делится на 4. Например, 412, 532, 700 и т. д. — это несколько чисел, которые делятся на 4, потому что они удовлетворяют критерию делимости на 4.

Скачать БЕСПЛАТНЫЕ учебные материалы

Рабочий лист правил делимости

Правила деления в математике

Предоставление учащимся инструментов для решения деления с помощью этих ярлыков не только делает деление менее сложным, но и превращает его в забавную головоломку. Для многих наличие четкого набора правил и структуры помогает прояснить концепцию и помогает учащимся решать уравнения и манипулировать выражениями. Возможность проверки делимости может помочь во многих математических настройках, таких как возможность проверить решение, уменьшить дроби или проверить правильность расчета.

Каковы правила разделения?

Приступая к разделу о делении, обязательно поделитесь этими правилами с классом и обсудите их во время выступления по математике:

ДЕЛИМОСТЬ НА 2

Число, которое делится на 2, называется четным. Когда последняя цифра в числе равна 0 или даже четной, то есть 2, 4, 6 или 8, то число делится на 2. Например, 20 оканчивается на 0, поэтому оно делится на 2. Число 936 заканчивается в 6, а 6 четно. Значит, 936 делится на 2,9.0005

ДЕЛИМОСТЬ НА 3

Число делится на 3, если сумма цифр делится на 3. Чтобы использовать этот прием, учащиеся должны уметь делить, но проверка меньших чисел менее сложна, чем проверка больших. . Например, если вы спросите учащихся, делится ли 168 на 3, они должны ответить следующим образом:

1 + 6 + 8 = 15

15/3 = 5

Следовательно, 168 делится на 3.

ДЕЛИМОСТЬ НА 4

Если последние две цифры числа делятся на 4, то делится и все число. Например, в 1012 12 делится на 4. Однако в 1013 13 не делится. Следовательно, 1012 делится на 4, а 1013 — нет.

ДЕЛИМОСТЬ НА 5

Когда последняя цифра числа 0 или 5, число можно разделить на 5 без остатка. Таким образом, 5, 10, 15, 20, 25 и так далее можно разделить на 5. Учащиеся могут посмотреть на большие числа и сразу сказать, можно ли их поровну разделить на пять частей.

ДЕЛИМОСТЬ НА 6

Числа, которые делятся на 6, также могут делиться на как на 3, так и на 2. Учащиеся должны проверить число с обоими правилами для 3 и 2. Если число проходит оба теста, его можно разделить на 6. Если он провалит хотя бы один тест, он не сможет. Например:

308 оканчивается на четную цифру, поэтому оно делится на 2. Однако 3 + 0 + 8 = 11, что не может делиться на 3 без остатка. Таким образом, 308 не делится на 6.

ДЕЛИМОСТЬ НА 8

Большое число делится на 8, если последние три цифры также делятся на 8 или равны 000. В числе 7120 120 можно разделить на 8 без остатка, поэтому 7120 также делится на 8.

ДЕЛИМОСТЬ НА 9

Правило делимости 9 такое же, как и 3. Если сумма цифр числа делится на 9, так же как и весь номер. Например:

В числе 549 5 + 4 + 9 = 18

18/9 = 2

Итак, 549 делится на 9.

ДЕЛИМОСТЬ НА 10

Если последняя цифра 0, число может быть разделить поровну на 10.

Почему правила помогают и как их использовать

Эти правила позволяют учащимся рассматривать большие числа в менее сложном контексте. Правила делимости также позволяют им многое узнать о числе, просто взглянув на его цифры. Таким образом, вы должны поощрять учащихся использовать все правила при изучении числа.