ПРИЗНАКИ ДЕЛИМОСТИ — ФОРМУЛЫ по МАТЕМАТИКЕ
Признак делимости на 2Число делится на 2 тогда и только тогда, когда его последняя цифра делится на 2, то есть является чётной.Признак делимости на 3
Число делится на 3 тогда и только тогда, когда сумма его цифр делится на 3.Признак делимости на 4
Число делится на 4 тогда и только тогда, когда число из двух последних его цифр нули или делится на 4.
Признак делимости на 5
Число делится на 5 тогда и только тогда, когда последняя цифра делится на 5 (то есть равна 0 или 5).
Признак делимости на 6
Число делится на 6 тогда и только тогда, когда оно делится на 2 и на 3.
Признак делимости на 7
Число делится на 7 тогда и только тогда, когда результат вычитания удвоенной последней цифры из этого числа без последней цифры делится на 7 (например, 259 делится на 7, так как 25 — (2 · 9) = 7 делится на 7).
Признак делимости на 8
Число делится на 8 тогда и только тогда, когда три его последние цифры — нули или образуют число, которое делится на 8.
Признак делимости на 9
Число делится на 9 тогда и только тогда, когда сумма его цифр делится на 9.
Признак делимости на 10
Число делится на 10 тогда и только тогда, когда оно оканчивается на ноль.
Признак делимости на 11
Число делится на 11 тогда и только тогда, когда сумма цифр с чередующимися знаками делится на 11 (то есть 182919 делится на 11, так как 1 — 8 + 2 — 9 + 1 — 9 = -22 делится на 11) — следствие факта, что все числа вида 10n при делении на 11 дают в остатке (-1)n.
Признак делимости на 12
Число делится на 12 тогда и только тогда, когда оно делится на 3 и на 4.
Признак делимости на 13
Число делится на 13 тогда и только тогда, когда число его десятков, сложенное с учетверённым числом единиц, кратно 13 (например, 845 делится на 13, так как 84 + (4 · 5) = 104 делится на 13).
Признак делимости на 14
Число делится на 14 тогда и только тогда, когда оно делится на 2 и на 7.
Признак делимости на 15
Число делится на 15 тогда и только тогда, когда оно делится на 3 и на 5.
Признак делимости на 17
Число делится на 17 тогда и только тогда, когда число его десятков, сложенное с увеличенным в 12 раз числом единиц, кратно 17 (например, 29053→2905+36=2941→294+12=306→30+72=102→10+24=34. Поскольку 34 делится на 17, то и 29053 делится на 17). Признак не всегда удобен, но имеет определенное значение в математике. Есть способ немного попроще – Число делится на 17 тогда и только тогда, когда разность между числом его десятков и упятеренным числом единиц, кратно 17(например, 32952→3295-10=3285→328-25=303→30-15=15. поскольку 15 не делится на 17, то и 32952 не делится на 17)
Признак делимости на 18
Число делится на 18 тогда и только тогда, когда оно делится на 2 и на 9.
Признак делимости на 19
Число делится на 19 тогда и только тогда, когда число его десятков, сложенное с удвоенным числом единиц, кратно 19 (например, 646 делится на 19, так как 64 + (6 · 2) = 76 делится на 19).
Признак делимости на 20
Число делится на 20 тогда и только тогда, когда оно делится на 4 и на 5
Признак делимости на 21
Число делится на 21 тогда и только тогда, когда оно делится на 7 и на 3
Признак делимости на 22
Число делится на 22 тогда и только тогда, когда оно делится на 2 и на 11
Признак делимости на 23
Число делится на 23 тогда и только тогда, когда число его сотен, сложенное с утроенным числом десятков, кратно 23 (например, 28842 делится на 23, так как 288 + (3 * 42) = 414 продолжаем 4 + (3 * 14) = 46 очевидно делится на 23).
Признак делимости на 24
Число делится на 24 тогда и только тогда, когда оно делится на 3 и на 8
Признак делимости на 25
Число делится на 25 тогда и только тогда, когда две его последние цифры делятся на 25 (то есть образуют 00, 25, 50 или 75).
Признак делимости на 26
Число делится на 26 тогда и только тогда, когда оно делится на 2 и на 13
Признак делимости на 28
Число делится на 28 тогда и только тогда, когда оно делится на 4 и на 7
Признак делимости на 30
Число делится на 30 тогда и только тогда, когда оно делится на 10 и на 3
Признак делимости на 34
Число делится на 34 тогда и только тогда, когда оно делится на 2 и на 17
Признак делимости на 35
Число делится на 35 тогда и только тогда, когда оно делится на 5 и на 7
Признак делимости на 36
Число делится на 36 тогда и только тогда, когда оно делится на 4 и на 9
Признак делимости на 38
Число делится на 38 тогда и только тогда, когда оно делится на 2 и на 19
Признак делимости на 39
Число делится на 39 тогда и только тогда, когда оно делится на 3 и на 13
Признак делимости на 40
Число делится на 40 тогда и только тогда, когда оно делится на 5 и на 8
Признак делимости на 42
Число делится на 42 тогда и только тогда, когда оно делится на 6 и на 7
Признак делимости на 44
Число делится на 44 тогда и только тогда, когда оно делится на 4 и на 11
Признак делимости на 45
Число делится на 45 тогда и только тогда, когда оно делится на 5 и на 9
Признак делимости на 99
Разобьем число на группы по 2 цифры справа налево (в самой левой группе может быть одна цифра) и найдем сумму этих групп, считая их двузначными числами. Эта сумма делится на 99 тогда и только тогда, когда само число делится на 99.
Призннак делимости на 101
Разобьем число на группы по 2 цифры справа налево (в самой левой группе может быть одна цифра) и найдем сумму этих групп с переменными знаками, считая их двузначными числами. Эта сумма делится на 101 тогда и только тогда, когда само число делится на 101. Например, 590547 делится на 101, так как 59-05+47=101 делится на 101).
Признак делимости на 2n
Число делится на n-ю степень двойки тогда и только тогда, когда число, образованное его последними n цифрами, делится на ту же степень.
Признак делимости на 5n
Число делится на n-ю степень пятёрки тогда и только тогда, когда число, образованное его последними n цифрами, делится на ту же степень.
Признак делимости на 10n-1
Разобьем число на группы по n цифр справа налево (в самой левой группе может быть от 1 до n цифр) и найдем сумму этих групп, считая их n-значными числами. Эта сумма делится на 10n — 1 тогда и только тогда, когда само число делится на 10n — 1.
Признак делимости на 10n
Число делится на n-ю степень десятки тогда и только тогда, когда n его последних цифр — нули.
Признак делимости на 10
Разобьем число на группы по n цифр справа налево (в самой левой группе может быть от 1 до n цифр) и найдем сумму этих групп с переменными знаками, считая их n-числами. Эта сумма делится на 10n + 1 тогда и только тогда, когда само число делится на 10n + 1.
Признаки делимости на 2,3,4,5,6,7,8 и 9. Примеры решения задач.
Что такое делимость?
«Делимость» означает, что при делении одного числа на другое результатом должно быть целое число с нулевым остатком. Под признаком делимости понимают правило, позволяющие быстро определить, является ли число кратным заданному числу.
Пример:
\(6:3 =2; \) \(6\) делится на \(3\), так как результат \(2\) — целое число, а остаток равен \(0\).
\(7:3=2,333…\) \(7\) не делится на \(3\) так как результат \(2,333…\) не является целым числом.
Признаки делимости чисел от \(1\) до \(10\).
Признак делимости на \(1\)
Каждое целое число делится на \(1\)
Признак делимости на \(2\)Последняя цифра должна быть четной — \(0,2,4,6,8\).
Пример : \(3456\) делится на \(2\) так как последняя цифра \(6\) — четное число.
\(343423\) не делится на \(2\), так как последняя цифра \(3\) нечетная.
Все четные числа делятся на \(2\).
Признак делимости на \(3\)
Сумма цифр в данном числе должна быть кратна \(3\). Это простой способ найти числа кратные \(3\).
\(3789\) делится на \(3\), так как сумма \(3+7+8+9=27\) делится на \(3\).
\(43266737\) не делится на \(3\) – сумма цифр \(4+3+2+6+6+7+3+7=38\) не делится на \(3\).
Признак делимости на \(4\)
Число, образованное последними двумя цифрами в данном числе, должно быть кратно \(4\).
Пример: \(23746228\) делится на \(4\) если \(28\) делится на \(4\).
\(674235642\) не делится на \(4\), так как \(4\) не кратно \(42\).
Признаки делимости на \(5\)
Последняя цифра должна быть \(0\) или \(5\).
Пример: \(42340\) делится на \(5\) так как \(0\) — последняя цифра.
\(672234\) не делится на \(5\) так как \(4\) последняя цифра.
Признак делимости на \(6\)
Число должно быть кратным \(2\) и \(3\).
\(7563894\) делится на \(6\) — последняя цифра \(4\) делится на \(2\) и сумма цифр \(7+5+6+3+8+9+4=42\) делится на \(3\).
\(567423\) не делится на \(6\) — последняя цифра \(3\), поэтому не делится на \(2\). Даже не нужно проверять на \(3\).
Признаки делимости на \(7\)
Дважды умноженная последняя цифра отнимается от оставшихся цифр в данном числе, результат должен быть кратным \(7\).
- \(343\) делится на 7 так как \(34-(2*3)=28\), \(28\) делится на \(7\).
2. \(345343\) \(3\) — последняя цифра. Вычитаем \(2*3\) из \(34534\).
\(34534-(2*3)=34528\) число слишком большое.
\(3452-(2*8)-3436\) число слишком большое.
\(343-(2*6)=331\) повторяем снова
\(33-(2*1)=31,31\)не делится на \(7\).\(345343\) не делится на \(7\).
Признак делимости на \(8\)
Число, образованное последними тремя цифрами в данном числе, должно быть кратно \(8\).
Пример:\(234568:8-568\) делится на \(8\).
\(4568742\)не делится на \(8\) , так как \(8\) не кратно \(742\)
Признак делимости на \(9\)
Сумма цифр в данном числе должна быть кратна \(9\).
\(456786:9 -\) если сумма \( 4+5+6+7+8+6=36\) делится на \(9\).
\(87956:9-\) сумма \(8+7+9+5+6=25\)не делится на 9.
Признак делимости на \(10\)
Последняя цифра должна быть \(0\).
Пример: \(456780\) делится на \(10\) — если последняя цифра равна \(0\).
\(78521\) не делится на \(10\) – последняя цифра \(1\).
Если число \(S\) делится на два числа \(a\) и \(b\), где \(a,b\) — простые числа , то \(S\) делится на \(a*b\), где \(a\) и \(b\) простые числа.
\(24\) делится на \(2\) и \(3\) и следовательно и на \(6\).
\(36\) делится на \(2 \) и \(4\), но не делится на \(8\), так как \(4\) не простое число.
Если число \(N\) делится на другое число \(M\), то \(N\) также делится на множители \(M\).
Например:
- \(72:12=6\)
- \(72\) также делится на \(2,3,4,6\) так как \(12\) кратно \(2,3,4,6\).
Больше уроков и заданий по математике вместе с преподавателями нашей онлайн-школы «Альфа». Запишитесь на пробное занятие уже сейчас!
Запишитесь на бесплатное тестирование знаний!
Признаки делимости чисел / Блог :: Бингоскул
Признаки делимости натуральных чисел
Признаки делимости от 2 до 19 и 24, 25, 36 с примерами

Признаки делимости на 2
- На 2 делятся все четные натуральные числа или последняя цифра должна быть четной — 0, 2, 4, 6, 8.
- Например: 24, 48, 94, 172, 1670, 67838.
Признаки делимости на 3
- На 3 делятся все натуральные числа, сумма цифр которых кратна 3.
- Например: 16734, сумма цифр = 1+6+7+3+4=21; 21 : 3 = 7 — делится на 3
Признаки делимости на 4
- На 4 делятся все натуральные числа, две последние цифры которых составляют нули или число, кратное 4.
- Например: 1024 делится на 4, так как 24 делится на 4
Признаки делимости на 5
- На 5 делятся все натуральные числа, оканчивающиеся на 5 или 0.
- Например: 125 делится на 5, поскольку последняя цифра 5
Признаки делимости на 6
- На 6 делятся те натуральные числа, которые делятся на 2 и на 3 одновременно (все четные числа, которые делятся на 3).
- Например: 126 делится 6, так как 126 — четное и сумма = 1 + 2 + 6 = 9 кратна 3
Признаки делимости на 7
- На 7 делятся те натуральные числа, у которых результат вычитания удвоенной последней цифры из этого числа без последней цифры делится на 7
- Например: 17948 делится на 7, 1794 — (2 · 8) = 1778 большое число, 177 — (8 · 2) = 161 повторяем снова, 16 — (1 · 2) = 14
Признаки делимости на 8
- Числа делятся на 8, если три его последние цифры делятся на 8.
- Например: 1568 делится на 8 — 568 кратно 8
Признаки делимости на 9
- На 9 делятся те натуральные числа, сумма цифр которых кратна 9.
- Например: 1179 — сумма =1 + 1 + 7 + 9 = 18, делится на 9
Признаки делимости на 10
- На 10 делятся все натуральные числа, оканчивающиеся на 0.
- Например: 1570 — делится на 10, последняя цифра 0
Признаки делимости на 11
- На 11 делятся только те натуральные числа, у которых сумма цифр, занимающих четные места, равна сумме цифр, занимающих нечетные места
- Например: 105787 делится на 11 — сумма 1 + 5 + 8 = 14 равна 0 + 7 + 7 = 14;
Признаки делимости на 12
- Число делится на 12 тогда и только тогда, когда она делится на 3 и на 4 одновременно.
- Например: 168 — делится на 3 и 4, следовательно делится на 12
Признаки делимости на 13
- Число делится на 13 тогда и только тогда, когда число его десятков, сложенное с учетверённым числом единиц, кратно 13.
- Например: 221 делится на 13: 22 + 1· 4 = 26 кратно 13
Признаки делимости на 14
- Число делится на 14 тогда и только тогда, когда оно делится на 2 и на 7.
Признаки делимости на 15
- Число делится на 15 тогда и только тогда, когда оно делится на 3 и на 5.
Признаки делимости на 16
- Число делится не 16 только тогда, когда 4 последние цифры делятся на 16
- Например: 24576 делится 16, так как 4576:16 = 286
Признаки делимости на 17
- Число делится на 17, если разность числа кроме последней цифры справа и последней цифры умноженную на пять кратно 17.
- Например: 272 делится на 17, 27 — 2 · 5 = 17 кратно 17
Признаки делимости на 18
- На 18 делятся те натуральные числа, которые четные и сумма цифр делится на 9.
- Например: 5508 — сумма = 5 + 5 + 0 + 8 = 18 кратна 9 и четное число, следовательно делится на 18
Признаки делимости на 19
- Число делится на 19 тогда и только тогда, когда число его десятков, сложенное с удвоенным числом единиц, кратно 19
- Например: 646 — 64 + (6 · 2) = 76 делится на 19
Признаки делимости на 24
- Число, делится на 24, если сумма всех цифр данного числа делится на 3 и последние три цифры данного числа делится на 8.
- Например: 1512 делится на 24 — сумма 1 + 5 + 1 + 2 = 9 кратна 3 и 512 : 8 = 64
Признаки делимости на 25
- На 25 делятся числа, если две последние цифры делятся на 25.
- Например: 650 — 50 : 25 = 2; 1475 — 75: 25 = 3
Признаки делимости на 36
- Число делится на 36, если 2-е последние цифры делятся на 4 и сумма цифр кратна 9.
- Например: 1620 — 20 : 4 = 5 и сумма 1 + 6 + 2 + 0 = 9 кратно 9; 4860 — 60 : 4 = 15 и 4 + 8 + 6 + 0 = 18 кратно 9
Смотри также: Основные формулы по математике
Решай с разбором:
Признаки делимости чисел | umath.ru
Содержание
- Таблица признаков делимости чисел
- Доказательство признаков делимости чисел
- Признаки делимости по последним цифрам [2, 4, 5, 8, 10, 25]
- Признаки делимости по сумме цифр [3, 9, 11]
- Признаки делимости по сумме граней [7, 11, 13, 37]
Признаки делимости — особенности чисел, которые помогают быстро определить, делится ли данное число на другое. Знание этих признаков необходимо при решении многих арифметических задач. Кроме того, умение пользоваться признаками делимости часто пригождается при решении задач ЕГЭ, особенно задания С6.
Таблица признаков делимости чисел
*Грани числа – числа, полученные при разбиении исходного числа на двузначные или трёхзначные числа, взятые справа налево. Например, разбиение числа 1234567 на двузначные грани выглядит так: 1|23|45|67, а на трёхзначные так: 1|234|567.
Признаки делимости чисел и их доказательство
Пусть натуральное число имеет десятичную запись
![\[\overline{a_{n} a_{n-1}\ldots a_{2}a_{1}a_0} = 10^n a_n + 10^{n-1} a_{n-1} + \ldots + 10^2 a_2 + 10a_1 + a_0, \]](/800/600/https/umath.ru/wp-content/ql-cache/quicklatex.com-7e9a7f061f406ad941705ff3e6bab3e7_l3.png)
где  — цифры этого числа,
— цифры этого числа, 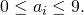
Разобьём признаки делимости на три группы. Доказательства признаков делимости в каждой группе основаны на одной и той же идее.
Признаки делимости по последним цифрам
Доказательство этих признаков основано на одной и той же идее. Приведём её на примере признака делимости на 25.Распишем число так:
![\[\overline{a_{n} a_{n-1}\ldots a_{2}a_{1}a_0} = \overline{a_{n} a_{n-1}\ldots 00} + \overline{a_{1} a_{0}} = 100\overline{a_{n} a_{n-1}\ldots a_{2}} + \overline{a_{1} a_{0}}.\]](/800/600/https/umath.ru/wp-content/ql-cache/quicklatex.com-00cb18db9c91d88c7af15afd1d06af19_l3.png)
Число 100 делится на 25, поэтому если число 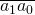 делится на 25, то и
делится на 25, то и  делится на 25. Заметим, что обратное утверждение тоже верно.
делится на 25. Заметим, что обратное утверждение тоже верно.
Признаки делимости по сумме цифр
| Если | то  делится на делится на |
Сумма цифр числа  делится на 3 или 9 делится на 3 или 9 | 3 или 9 соответственно |
Знакочередующаяся сумма цифр числа  делится на 11 делится на 11 | 11 |
Докажем признаки делимости на 3 и 9.
![\[\overline{a_{n} a_{n-1}\ldots a_{2}a_{1}a_0}=10^n a_n+ 10^{n-1} a_{n-1} + \ldots + 10^2 a_2 + 10a_1 + a_0=\]](/800/600/https/umath.ru/wp-content/ql-cache/quicklatex.com-a4e8c7b2a31e4231d2881fa2d7b96be3_l3.png)
![\[=\left(\underbrace{99\ldots 9}_n a_n + \underbrace{99\ldots 9}_{n-1} a_{n-1} + \ldots + 99a_2+9a_1\right) + \]](/800/600/https/umath.ru/wp-content/ql-cache/quicklatex.com-ab2663f6c70f51fa2f15a8e69f5f3591_l3.png)
![\[+\left(a_n + a_{n-1} + \ldots + a_2 + a_1 + a_0\right)=\]](/800/600/https/umath.ru/wp-content/ql-cache/quicklatex.com-bbe72011b3dc2c6c9a60fbc4e75b8b1c_l3.png)
![\[=9\cdot\left(\underbrace{11\ldots 1}_n a_n + \underbrace{11\ldots 1}_{n-1} a_{n-1} + \ldots + 11a_2+a_1\right) + \]](/800/600/https/umath.ru/wp-content/ql-cache/quicklatex.com-634d2871f0e9bfd2863e8705e1853838_l3.png)
![\[+\left(a_n + a_{n-1} + \ldots + a_2 + a_1 + a_0\right).\]](/800/600/https/umath.ru/wp-content/ql-cache/quicklatex.com-16e386367c1cf413fffa04a297fafab4_l3.png)
Выражение под первыми скобками делится на 9. Поэтому число  делится на 3 или 9 тогда и только тогда, когда число
делится на 3 или 9 тогда и только тогда, когда число 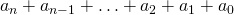 делится на 3 или 9 соответственно.
делится на 3 или 9 соответственно.
Признаки делимости по сумме граней
Введём такое определение:
Определение.
Двузначные грани числа — это числа, которые получены разбиением исходного числа на двузначные числа. Например, разбиение числа 123456789 на двузначные грани выглядит так: 1|23|45|67|89 (разбиение числа начинается с его конца). Числа 1, 23, 45, 67, 89 являются двузначными гранями числа 123456789.
Трёхзначные грани числа — это числа, полученные разбиением исходного числа на трёхзначные числа. Например, разбиение числа 1234567890 на трёхзначные грани выглядит так: 1|234|567|890. Числа 1, 234, 567, 890 являются трёхзначными гранями числа 1234567890.
Перейдём к признакам делимости.
| Если | то  делится на делится на |
| Сумма двузначных граней делится на 11 | 11 |
| Сумма трёхзначных граней делится на 37 | 37 |
| Знакочередующаяся сумма трёхзначных граней делится на 7, 11, 13 | 7, 11, 13 соответственно |
Докажем признак делимости на 11 по сумме двузначных граней
![\[\overline{a_n a_{n-1}\ldots a_2a_1a_0}= \overline{a_1a_0}+100 \overline{a_3a_2} + 10000\overline{a_6a_5}+\ldots=\]](/800/600/https/umath.ru/wp-content/ql-cache/quicklatex.com-2d67eb52bf7faa520b46fc4b7372061f_l3.png)
![\[=\left(99\overline{a_3a_2} + 9999\overline{a_6a_5} + \ldots \right) + \left(\overline{a_1a_0} + \overline{a_3a_2} + \overline{a_6a_5} + \ldots\right). \]](/800/600/https/umath.ru/wp-content/ql-cache/quicklatex.com-e62b3687210278547459c04eef412d56_l3.png)
В левых скобках все числа делятся на 11, поэтому число  делится на 11 тогда и только тогда, когда сумма его двузначных граней делится на 11.
делится на 11 тогда и только тогда, когда сумма его двузначных граней делится на 11.
Остальные признаки доказываются аналогично.
Признаки делимости правило и примеры
Число, которое делится на 2 называется четным, а если не делится — нечетным.
Число делится на 2, если его последняя цифра оканчивается на нуль или чётная.
Пример
Число 7774 делится на 2, так как последняя цифра 4 — чётная.
Число 7775 не делится на 2, так как последняя цифра 5 — нечётная.
На 3 делятся только те числа, у которых сумма всех цифр делится на 3.
Пример
777 делится на 3, так как 7+7+7=21, а 21 делится на 3.
Число делится на 4 в том случае, если две последние его цифры нули или делятся на 4.
Пример
788 делится на 4, так как последние его цифры 88 делятся на 4.
700 делится на 4, так как последние его цифры нули.
Число делится на 5, если последняя цифра которых оканчивается на 0 или 5.
Пример
775 делится на 5, так как последняя цифра равна 5.
Число делится на 6, если оно делится как на 2, так и на 3.
Пример
786 делится на 6, так как оно делится и на 2 и на 3 одновременно.
Число делится на 7, когда знакочередующаяся сумма трехзначных граней числа делится на 7.
Пример
147700259 делится на 7, так как 147-700+259=-294, а 294 делится на 7.
Число делится на 7, когда утроенное число десятков, сложенное с числом единиц делится на 7.
Пример
189 делится на 7, так как 18*3+9=63 делится на 7.
Число делится на 7, когда разность числа десятков и удвоенного числа единиц, взятая по модулю, делится на 7.
Пример
539 делится на 7, так как 53-9*2=35 делится на 7.
Число делится на 8, если три последние цифры его нули или делятся на 8.
Пример
7000 делится на 8, так как три нуля в конце.
7648 делится на 8, так как последние его цифры делятся на 8.
На 9 делятся только те числа, у которых сумма цифр делится на 9.
Пример
774 делится на 9, так как 7+7+4=18, а 18 делится на 9.
На 11 делятся только те числа, у которых сумма цифр с чередующимися знаками по модулю делится на 11
Пример
Число 292919 делится на 11, так как 2-9+2-9+1-9=-22 делится на 11.
Число делится на 12, если оно делится как на 3, так и на 4.
Пример
924 делится на 12, так как оно делится и на 3 и на 4 одновременно.
Число делится на 13, если число десятков, сложенное с учетверенным числом единиц, делится 13.
Пример
572 делится 13, так как 72-4*5=52 делится на 13.
На 25 делятся те числа, у которых две последние цифры нули или образуют число, которое делится на 25 (т. е. числа, которые оканчиваются на 00, 25, 50, 75).
Пример
7775 делится на 25, так как оканчивается на 75
На 10 делятся только те числа, последняя цифра которых оканчивается на нуль, на 100 делятся только те числа, у которых две последние цифры нули, на 1000 — только те, у которых три последние цифры нули.
Пример
777 000 делится на 10,100,1000.
| ПОЛЕЗНЫЕ ССЫЛКИ: БОНУСЫ ИНЖЕНЕРАМ!: МЫ В СОЦ.СЕТЯХ: | Навигация по справочнику TehTab.ru:  главная страница / / Техническая информация / / Математический справочник / / Математика для самых маленьких. Детский сад — 7 класс. / / Признаки делимости на 2, 3, 4, 5, 6, 8, 9, 10 без остатка. + Признаки делимости на 11,13,25,36. главная страница / / Техническая информация / / Математический справочник / / Математика для самых маленьких. Детский сад — 7 класс. / / Признаки делимости на 2, 3, 4, 5, 6, 8, 9, 10 без остатка. + Признаки делимости на 11,13,25,36.
| |
Признаки делимости
При решении задач ЕГЭ базового и профильного уровня необходимо знать признаки делимости. Многие признаки делимости чисел нацело вы знаете из начального курса математики. Поэтому такая простая информация могла легко забыться. Сегодня мы с вами повторим основные признаки делимости и решим некоторые задачи.
Признаки делимости
Говорят, что целое число a делится на натуральное число b, если существует такое целое число c, что выполняется равенство a = bc. В этом случае число b называют делителем числа a, а число a — кратным числу b.
Если числа делится на b, то пишут  .
.
Пример.
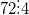 так как
так как 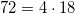
Свойства делимости чисел
Простые числа и составные числа.
Простые и составные числа
Число p  называется простым, если оно делится только на себя и на единицу.
называется простым, если оно делится только на себя и на единицу.
Составными числами называются целые числа, имеющие больше двух различных делителей.
Пример.
Число 17 простое. Делители 17: 1, 17.
Число 9 составное. Делители 9: 1, 3, 9.
Единица не является ни простым, ни составным числом.
Два числа, наибольший делитель которых, равен 1, называются взаимно простыми.
Признаки делимости
Признак делимости на 2
Число делится на 2 тогда и только тогда, когда последняя цифра в записи числа есть число, которое делится на 2 (последняя цифра – образует четное число).

Например, число 124 делится на 2, так как 4 — четное число.
Признак делимости на 4
Число делится на 4 тогда и только тогда, когда последние две цифры числа дают число, которое делится на 4.
Пример: 132 делится на 4, потому что последние две цифры «3» и «2» образуют число 32, которое делится на 4.
Признак делимости на 8
Число делится на 8 тогда и только тогда, когда последние три цифры в записи числа образуют число, которое делится на 8.
Пример, число 2192 делится на 8, поскольку последние три цифры «1», «9» и «2» образуют число 192, которое делится на 8. При рассмотрении задач надо иметь в виду, что число делящееся на 8, в свою очередь должно делится и на 4 и на 2 одновременно.
Признак делимости на 3
Число делится на 3 тогда и только тогда, когда сумма чисел, образованных цифрами в записи числа, делится на 3.
Пример: число 153 делится на 3, так как сумма чисел 1+3+5=9 делится на 3.
Признак делимости на 9
Число делится на 9 тогда и только тогда, когда сумма чисел, образованных цифрами в записи числа, делится на 9.
Пример: число 198 делится на 9, поскольку сумма чисел 1+9+8=18 делится на 9.
Признак делимости на 5
Число делится на 5 тогда и только тогда, когда последняя цифра в записи числа образует число, которое делится на 5 (последняя цифра 0 или 5).
Пример, число 165 делится на 5, так как заканчивается на 5.
Признак делимости на 25
Число делится на 25 тогда и только тогда, когда последние две цифры в записи числа, образуют число, которое делится на 25.
Пример: число 125 делится на 25, так как последние две цифра «2» и «5» образуют число 25, которое делится на 25.
Следует помнить, что цифры не могут суммироваться, делиться и т.д. Цифры это такие значки, которыми записываются числа. И веса у них самих по себе не более чем у любого другого значка, как у смайлика. Но, если мы цифрой запишем число, то с числом мы уже можем проводить любые операции. Числа могут быть однозначные и двузначные, их бесконечное количество, но цифр для их записи всего 10. Не путайте понятия числа и цифры, не портите отношения с проверяющими ваши работы математиками.
Признак делимости на 11
Число делится на 11 тогда и только тогда, когда разность суммы чисел, стоящих на нечетных местах в записи числа, и суммы чисел, стоящих на четных местах в записи числа, делится на 11. А также если сумма чисел стоящих на четных местах, делится на сумму чисел, стоящих на нечетных местах.
Пример 1.
123456789 делится на 3, так как 1 + 2 + 3 + 4 + 5 + 6 + 7 + 8 + 9 = 45, а 45 делится на 3.
Пример 2.
1452 делится на 11, так как (1 + 5) – (4 + 2) делится на 11. Или 1+5=4+2.
Деление с остатком
Пусть a и b ≠ 0 – два целых числа. Разделить число a на число b с остатком – это значит найти такие числа c и d, что выполнены следующие условия:
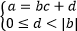
От деления на b могут быть только остатки: 0, 1, 2, 3…, |b|-1.
Пример 1.
19 : 7 = 2 (ост. 5)
19 = 7 ∙ 2 + 5
Пример 2.
22 : (-3) = -7 (ост. 1).
22 = -3 ∙ (-7) + 1
Пример 3.
-22 : 3 = -8 (ост. 2)
-22 = 3 ∙ (-8) + 2
Теоремы
1) Сумма чисел a и b даёт тот же остаток при делении на число m, что и сумма остатков чисел a и b при делении на число m.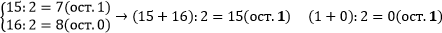
2) Произведение чисел a и b даёт тот же остаток при делении на число m, что и произведение остатков чисел a и b при делении на число m.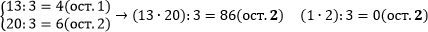
Теперь рассмотрим конкретные задания из ЕГЭ на делимость
Задание №1
Найдите четырёхзначное число, которое делится на 33 и состоит только из цифр 1 и 2. В ответе укажите наименьшее из таких чисел.
Решение:
Если число делится на 33 то оно делиться на 11 и 3. Число делится на 11, если сумма цифр стоящих на четных позициях будет равна сумме цифр на нечетных позициях. Число делится на 3, если сумма цифр делится на 3.
Значит стоит чередовать 1 и 2 по 2 раза, причем если сложим 2 двойки и 2 единицы получим 6, значит, число будет делиться на 3. Получим число 1122.
Ответ: 1122
Задание №2
Найдите трёхзначное число, состоящее только из чётных цифр и кратное 9. В ответе укажите наименьшее из таких чисел.
Решение:
Если число должно делиться на 9, то и сумма цифр должна делиться на 9, наименьшее 9, но его нельзя представить как сумму 3 чётных цифр, рассмотрим 18, первой цифрой поставим 2 ( минимальное четное число), тогда на остальные 2 остается только 8 и 8, получим число 288.
Ответ: 288
Задание №3
Найдите трёхзначное число, которое при делении на 5 и 7 даёт равные ненулевые остатки, а вторая цифра этого числа равна сумме первой и третьей цифр. В ответе укажите какое-нибудь одно такое число.
Решение:
Число не должно оканчиваться на 0 или 5, так как в этом случае остаток от деления на 5 равен 0. Пусть вторая цифра в числе будет 4, тогда первая и третья цифры могут быть 1 и 3, получаем число 143. Проверяем:
1) 143:5=28 (Остаток 3)
2) 143:7=20 (Остаток 3)
Остатки равны, соответственно условие выполнено.
Аналогичными рассуждениями можно найти и другие числа: 176; 352; 561.
Ответ: 176
Задание №4
Найдите трёхзначное число, сумма цифр которого равна 7, если известно, что число содержит цифру 1, и квадрат этого числа делится на 25. В ответе укажите какое-нибудь одно такое число.
Решение:
Если квадрат числа делится на 25, то само число должно делиться на 5. Признак делимости на 5: число делиться на 5, если его последняя цифра 0 или 5. У нас трехзначное число, пусть последняя цифра будет 5, а первая 1, вторая цифра должна быть такой, чтобы сумма цифр была равна 7. Сумма цифр уже 6, то есть вторая цифра должна быть равна 1. Получим число 115.
Аналогичными рассуждениями можно получить числа 160 и 610.
Ответ: 115
Задание №5
Найдите четырёхзначное число, кратное 9, но не кратное 6, произведение цифр которого равно 1960. В ответе укажите какое-нибудь одно такое число.
Решение:
Чтобы число делилось на 9, но не делилось на 6, оно должно быть нечетным.
Разложим 1960 на простые множители: 1960=2*2*2*5*7*7=8*5*7*7
Эти цифры обозначают числа, которые в сумме дают 27, значит число будет делиться на 9. Составим из этих цифр нечетное число, например: 7785.
Аналогичными рассуждениями (простой перестановкой цифр) можно получить другие числа.
Ответ: 7785
Задание №6
Сумма четырёх последовательных трёхзначных чисел равна 458. Найдите третье число.
Решение:
Все 4 числа приблизительно равны между собой, поэтому разделив 458 на 4 получаем 114 с остатком 2. Начинаем подбирать числа от 114.
114+115+116+117=462, это больше 458, начинаем считать от 113.
113+114+115+116=458, получили необходимую сумму. Третье число в данной последовательности равно 115.
Можно было решить альтернативно.
Пусть первое число равно n. Тогда следующие числа n+1, n+2, n+3.
Составим и решим уравнение:
n+n+1+n+2+n+3=458
4n=452
n=113
Тогда третье число 115.
Ответ: 115
Задание №7
Найдите трёхзначное число, у которого сумма цифр, стоящих на нечетных местах, кратна 5, а само число кратно 9. В ответе запишите наименьшее такое число.
Решение:
Так как число должно быть наименьшим, то будет подбирать цифры так, чтобы оно начиналось с минимальной цифры (1 и далее), и аналогично будем подбирать для всех разрядов.
Нечетные места это 1 и 3, чтобы сумма цифр на нечетных местах была кратна 5, она должна быть равна, 5, 10 или 15. Пусть она будет равна 5, в сумме 5 составляют числа 1 и 4. Тогда чтобы число делилось на 9 сумма цифр должна делиться на 9, то есть в нашем случае сумма цифр должна равняться 9. То есть, на 2 месте должна стоять цифра 4. Получим число 144.
Ответ: 144
Задание №8
Найдите трёхзначное число, делящееся на 9, если известно, что его цифры являются последовательными членами возрастающей арифметической прогрессии. В ответе укажите какое-нибудь одно такое число.
Решение:
Чтобы число делилось на 9, необходимо чтобы сумма его цифр делилась на 9. А, учитывая, что его цифры должны являться членами возрастающей арифметической прогрессии, каждая цифра должна отличаться от предыдущей на одно и то же число.
Если разность прогрессии равна 1, получаем a, a+1, a+2. Сумма равна 3a+3.
3a+3=9,тогда a=2, а число 234
3a+3=18,тогда a=5, а число 567
Если разность прогрессии равна 2, получаем a, a+2, a+4. Сумма равна 3a+6.
3a+6=9,тогда a=1, а число 135
3a+6=18,тогда a=4, а число 468
3a+6=27, тогда а=7, но следующие члены уже больше 10, не подходит.
Если разность прогрессии равна 3, получаем a, a+3, a+6. Сумма равна 3a+9.
3a+9=9,тогда a=0, не подходит
3a+9=18,тогда a=3, а число 369
3a+9=27,тогда a=6, но следующие члены уже больше 10, не подходит.
Если разность прогрессии равна 4, получаем a, a+4, a+8. Сумма равна 3a+12.
3a+12=18,тогда a=6, но следующие члены уже больше 10, не подходит.
Ответ: 234 или 567, или 135, или 468, или 369.
Задание №9
Найдите четырёхзначное число, которое состоит только из цифр 0 и 2 и делится на 12.
Решение:
Чтобы число делилось на 12, оно должно делиться на 3 и 4. На 3 число делится, если сумма цифр делится на 3. А на 4 делится, если 2 последние цифры нули или образуют число, которое делится на 4.
Чтобы число делилось на 3, в нем должно быть три двойки (чтобы в сумме давали 6). Значит 0 только один, последние 2 цифры должны быть 20, чтобы полученное число делилось на 4. То есть получаем число 2220.
Ответ: 2220
Итак, мы подробно рассмотрели делимость чисел, признаки делимости чисел и поучились применять полученные знания в задании №19 базового уровня егэ по математике.
Читайте еще наши статьи: таблица кубов натуральных чисел от 1 до 100.
Правила делимости (тесты)
Легко проверить, можно ли точно разделить одно число на другое
делится на
«Делится на» означает «при делении одного числа на другое получается целое число»
Примеры:
14 делится на 7, потому что 14 ÷ 7 = 2 ровно
15 — это , а не , делимое на 7, потому что 15 ÷ 7 = 2 1 7 (результат , а не целое число)
0 это , делимое на 7, потому что 0 ÷ 7 = 0 ровно (0 — целое число)
«Может быть разделено на» и «может быть разделено на» означает одно и то же.
Правила делимости
Эти правила позволяют вам проверить, делится ли одно число на другое, без необходимости выполнять слишком много вычислений!
Пример: делится ли 723 на 3?
Можно попробовать разделить 723 на 3
Или используйте правило «3»: 7 + 2 + 3 = 12 и 12 ÷ 3 = 4 точно Да
Примечание. Ноль делится на любого числа (кроме самого себя), поэтому мы получаем «да» на все эти тесты.
1
Любое целое число (не дробное) делится на 1
2
Последняя цифра четная (0,2,4,6,8)
12 8 Есть
12 9 Нет
3
Сумма цифр делится на 3
381 (3 + 8 + 1 = 12 и 12 ÷ 3 = 4) Да
217 (2 + 1 + 7 = 10 и 10 ÷ 3 = 3 1 / 3 ) №
Это правило можно повторить при необходимости:
99996 (9 + 9 + 9 + 9 + 6 = 42, затем 4 + 2 = 6) Да
4
Последние 2 цифры делятся на 4
13 12 равно (12 ÷ 4 = 3) Да
70 19 не является (19 ÷ 4 = 4 3 / 4 ) Нет
Быстрая проверка (полезная для маленьких чисел) состоит в том, чтобы уменьшить число вдвое, и результатом будет целое число.
12/2 = 6, 6/2 = 3, 3 — целое число. Есть
30/2 = 15, 15/2 = 7,5, что не является целым числом. №
5
Последняя цифра 0 или 5
17 5 Есть
80 9 Нет
6
Четно и делится на 3 (соответствует как правилу 2, так и правилу 3 выше)
114 (четно, и 1 + 1 + 4 = 6 и 6 ÷ 3 = 2) Да
308 (четно, но 3 + 0 + 8 = 11 и 11 ÷ 3 = 3 2 / 3 ) Нет
7
Удвойте последнюю цифру и вычтите ее из числа, образованного другими цифрами.Результат должен делиться на 7. (Мы можем снова применить это правило к этому ответу)
672 (Двойное 2 равно 4, 67−4 = 63 и 63 ÷ 7 = 9) Да
105 (Двойная 5 равна 10, 10−10 = 0, а 0 делится на 7) Да
905 (Двойное 5 равно 10, 90-10 = 80 и 80 ÷ 7 = 11 3 / 7 ) №
8
Последние три цифры делятся на 8
109 816 (816 ÷ 8 = 102) Есть
216 302 (302 ÷ 8 = 37 3 / 4 ) №
Быстрая проверка — это трижды уменьшить вдвое, и результат останется целым числом:
816/2 = 408, 408/2 = 204, 204/2 = 102 Да
302/2 = 151, 151/2 = 75.5 №
9
Сумма цифр делится на 9
(Примечание: это правило можно повторить при необходимости)
1629 (1 + 6 + 2 + 9 = 18, и снова 1 + 8 = 9) Да
2013 (2 + 0 + 1 + 3 = 6) №
10
Число заканчивается на 0
22 0 Есть
22 1 №
11
Сложить и вычесть цифры поочередно (добавить цифру, вычесть следующую цифру, добавить следующую цифру и т. Д.).Затем проверьте, делится ли этот ответ на 11.
1 3 6 4 (+ 1-3 + 6-4 = 0 ) Есть
9 1 3 (+ 9−1 + 3 = 11 ) Есть
3 7 2 9 (+ 3−7 + 2−9 = −11 ) Да
9 8 7 (+ 9-8 + 7 = 8 ) №
12
Число делится на 3 и 4 (он проходит как правило 3, так и правило 4 выше)
648
( По 3? 6 + 4 + 8 = 18 и 18 ÷ 3 = 6 Да)
(По 4? 48 ÷ 4 = 12 Да)
Оба пройдены, поэтому Да
524
( По 3? 5 + 2 + 4 = 11, 11 ÷ 3 = 3 2 / 3 Нет)
(Нет необходимости проверять по 4) Нет
Есть еще много всего! Существуют не только тесты на делимость для больших чисел, но и другие тесты для чисел, которые мы показали.
Факторы, которые могут быть полезны
Факторы— это числа, которые вы умножаете, чтобы получить другое число:
Это может быть полезно, потому что:
Когда одно число делится на другое число …
… тогда это , также делимое на каждый из множителей этого числа.
Пример: если число делится на 6, оно также делится на 2 и 3
Пример: если число делится на 12, оно также делится на 2, 3, 4 и 6.
Еще одно правило для 11
- Вычтите последнюю цифру из числа, образованного другими цифрами.
- Если это число делится на 11, то и исходное число тоже.
При необходимости можно повторить,
Пример: 286
28-6 равно 22, из которых делится на на 11, поэтому 286 делится на 11
Пример: 14641
- 1464-1 это 1463
- 146-3 это 143
- 14-3 равно 11, из которых делится на , поэтому 14641 делится на 11
правил делимости | Helping With Math
Правила делимости помогают нам определить, делится ли число в точности на другие числа (т. Е. Нет остатка).
Правила — это ярлыки, позволяющие определить, делятся ли числа точно, без выполнения вычислений деления. Некоторые из этих правил вместе с примерами проиллюстрированы ниже:
Делимо на 2?
Правило: если оно заканчивается на 0, 2, 4, 6 или 8

| Число | Делимо? | Почему? |
| 456 | Да | Последняя цифра 6 |
| 68 | Да | Последняя цифра 8 |
| 25 | Нет | Последняя цифра 5 ( не a 2,4,6, или 8) |
| 207 | Нет | Последняя цифра 7 ( не a 2,4,6 или 8) |
Вернуться ко всем правилам делимости
Делится на 3?
Правило: Если сумма цифр кратна 3

| Число | Делимо? | Почему? |
| 405 | Да | 4 + 0 + 5 = 9 (9 кратно 3) |
| 381 | Да | 3 + 8 + 1 = 12 (12 кратно 3) |
| 928 | Нет | 9 + 2 + 8 = 19 (19 равно , а не , кратно 3) |
| 4,616 | Нет | 4 + 6 + 1 + 6 = 17 (17 — , а не , кратное 3) |
| Помощник: Кратное 3 включает… |
| 3 6 9 12 15 18 21 24 27 30 33 36 39 42 45 |
Вернуться к Все правила делимости
Делимо на 4?
Правило: если последние две цифры кратны 4
(или если последние две цифры равны 00)

| Число | Делимо? | Почему? |
| 348 | Да | 48 кратно 4 |
| 27 616 | Да | 16 кратно 4 |
| 8,514 | Нет | 14 равно не кратно 4 |
| 722 | Нет | 22 — это , а не , кратное 4 |
| 1,200 | Да | Последние две цифры — 00 200 кратно 4 |
| Помощник: число, кратное 4, включает… |
| 4 8 12 16 20 24 28 32 36 40 44 48 52 56 60 |
Вернуться ко всем правилам делимости
Делимо на 5?
Правило: если оно заканчивается на 5 или 0

| Число | Делимо? | Почему? |
| 3,425 | Да | Последняя цифра 5 |
| 750 | Да | Последняя цифра 0 |
| 8,551 | Нет | Последняя цифра 1 ( не a 0 или 5) |
| 394 | Нет | Последняя цифра 4 (, а не a 0 или 5) |
Вернуться ко всем правилам делимости
Делимо на 6?
Правило: делится ли оно на 2 и на 3

| Число | Делимо? | Почему? |
| 5,106 | Да | Последняя цифра — 2 (кратно 2) и… 5 + 1 + 0 + 6 = 12 (12 кратно 3) |
| 636 | Да | Последняя цифра — 6 (кратно 2) и… 6 + 3 + 6 = 15 (15 кратно 3) |
| 5,912 | Нет | Последняя цифра — 2 (кратно 2) , но … 5 + 9 + 1 + 2 = 17 (17 — это , а не , кратное 3) |
| 508 | Нет | Последняя цифра — 8 (это кратно 2) , но … 5 + 0 + 8 = 13 (13 — это , а не , кратное 3) |
Назад ко всем правилам делимости
Делится на 9?
Правило: Если сумма цифр кратна 9

| Число | Делимо? | Почему? |
| 7,686 | Да | 7 + 6 + 8 + 6 = 27 (27 кратно 9) |
| 252 | Да | 2 + 5 + 2 = 9 (9 кратно 9) |
| 883 | Нет | 8 + 8 + 3 = 19 (19 равно , а не , кратно 9) |
| 5,105 | Нет | 5 + 1 + 0 + 5 = 11 ( 11 — это , а не , кратное 9) |
| Помощник: Кратное 9 включает… |
| 9 18 27 36 45 54 63 72 81 90 99 108 117 126 135 |
Назад ко всем правилам делимости
Делимо на 10?
Правило: Если последняя цифра 0

| Число | Делимо? | Почему? |
| 880 | Да | Последняя цифра 0 |
| 9,560 | Да | Последняя цифра 0 |
| 312 | Нет | Последняя цифра 2 ( не a 0) |
| 7,897 | Нет | Последняя цифра — 7 (, а не a 0) |
Вернуться ко всем правилам делимости
Правила делимости
В этом уроке представлены правила делимости чисел 2, 3, 4, 5, 6, 7, 8, 9 и 10.
Правила делимости целых чисел очень полезны, потому что они помогают нам быстро определить, можно ли разделить число на 2, 3, 4, 5, 9 и 10 без деления в столбик.
Делимость означает, что вы можете разделить число поровну
Например, 8 можно разделить поровну на 4, потому что 8/4 = 2. Однако 8 не может делиться поровну на 3.
Чтобы проиллюстрировать концепцию, предположим, что у вас есть торт, и ваш торт состоит из 8 кусочков, вы можете равномерно разделить этот торт между собой и еще тремя людьми. Каждому дается по 2 ломтика.
Однако, если вы пытаетесь разделить эти 8 фрагментов между собой и еще двумя людьми, вы не сможете сделать это равномерно. Один человек получит меньше торта
В общем, целое число x делит другое целое число y тогда и только тогда, когда вы можете найти целое число n такое, что
x умножить на n = y
Например, 12 может быть делится на 3, потому что 3 раза по 4 = 12
Когда числа большие, используйте следующие правила делимости:
Правило № 1: делимость на 2
Число делится на 2, если его последняя цифра 0,2 , 4,6 или 8.
Например, 8596742 делится на 2, потому что последняя цифра — 2.
Правило № 2: делимость на 3:
Число делится на 3, если сумма его цифр делится на 3
Например, 3141 делится на 3, потому что 3 + 1 + 4 + 1 = 9, а 9 делится на 3.
Правило № 3: делимость на 4
Число делится на 4, если число, представленное его последние две цифры делятся на 4.
Например, 8920 делится на 4, потому что 20 делится на 4.
Правило № 4: делимость на 5
Число делится на 5, если его последняя цифра равна 0 или 5.
Например, 9564655 делится на 5, потому что последняя цифра равна 5.
Правило № 5: делимость на 6
Число делится на 6, если оно делится на 2 и 3. Будьте осторожны! это не то или другое. Число должно делиться как на 2, так и на 3, прежде чем вы сможете сделать вывод, что оно делится на 6.
Правило № 6: делимость на 7
Чтобы проверить правила делимости 7, внимательно изучите следующие два примера:
Делится ли 348 на 7?
Удалите последнюю цифру, равную 8.Число становится 34. Затем удвойте 8, чтобы получить 16 и вычтите 16 из 34.
34 — 16 = 18 и 18 не делится на 7. Следовательно, 348 не делится на 7
Делится ли 37961 на 7?
Удалите последнюю цифру, равную 1. Число становится 3796. Затем удвойте 1, чтобы получить 2, и вычтите 2 из 3796.
3796 — 2 = 3794, так что все равно слишком много? Таким образом повторите процесс.
Удалите последнюю цифру, которая равна 4. Число становится 379. Затем удвойте 4, чтобы получить 8, и вычтите 8 из 379.
379 — 8 = 371, так все еще слишком велик? Таким образом повторите процесс.
Удалите последнюю цифру, равную 1. Число становится 37. Затем удвойте 1, чтобы получить 2, и вычтите 2 из 37.
37 — 2 = 35 и 35 делится на 7. Следовательно, 37961 делится на 7 .
Правило № 7: делимость на 8
Число делится на 8, если число, представленное его последними тремя цифрами, делится на 8.
Например, 587320 делится на 8, потому что 320 делится на 8 .
Правило № 8: делимость на 9
Число делится на 9, если сумма его цифр делится на 9.
Например, 3141 делится на 9, потому что сумма его цифр делится на 9 .
Правило № 9: делимость на 10
Число делится на 10, если его последняя цифра или цифра в разряде единиц равна 0.
Например, 522480 делится на 10, потому что последняя цифра равна 0
Тест по правилам делимости
Пройдите тест ниже, чтобы увидеть, насколько хорошо вы усвоили урок на этой странице.
Новые уроки математики
Ваша электронная почта в безопасности. Мы будем использовать его только для информирования вас о новых уроках математики.
.правил делимости | Правила делимости чисел для 2, 3, 4, 5, 6, 7, 8, 9, 10 и 11
Концепция разделения связана с разбиением чего-либо на множество частей. Вы делитесь своими сладостями с товарищами. Вы делитесь кусочками своих любимых блюд за ужином с друзьями и семьей. Вы начинаете с одной суммы и заканчиваете маленькими кусочками.
Что касается слов, мы будем использовать три термина в этом сегменте. В каждой задаче деления у вас будет одно число, разделенное на другое.Число, которое вы нарушаете, называется дивидендом. Решения ваших проблем деления называются частными и остатками. Шесть, разделенная на два, дает остальные три.
Точно так же, как дроби
Этот сегмент переместится непосредственно в область дробей, поскольку дроби по сути являются альтернативным методом для составления задачи деления. Когда вы перейдете к более развитой математике, вы можете даже решить задачи деления, которые напоминают дроби.
Вы обнаружите, что дробь 1/4 имеет неделимый стимул от одного (1) деления на четыре (4).Работая с десятичными знаками, вы быстро обнаружите, что 1, деленная на 4, дает 0,25. Деление даже по ставкам обязательно. Десятичная дробь 0,25 эквивалентна 25 процентам. Четверть пирога — это 25% всего пирога.
Этот пример демонстрирует вам, что существует множество подходов к тому, чтобы выразить подобное в математике. Это похоже на язык. Большое количество терминов или слов обозначают одинаковые количества, но все они означают одно и то же. Синий, лазурный, голубой, синий и голубой — в значительной степени необычные слова, которые передают аналогичный оттенок синего.Вы можете начать с одного языка, а затем перейти к следующему с некоторой интерпретацией. Вы можете перейти от дробей к десятичным или ставкам с небольшими изменениями.
Предположим, вы находитесь в магазине канцелярских товаров и вам нужно выяснить, какая сделка лучше, используя правила делимости. Предположим, 2 карандаша стоят 6 рупий, а в другом магазине 4 карандаша стоят 8 рупий. Какая сделка лучше? В первом случае каждый карандаш стоит 3 рупии. Во втором случае каждый карандаш стоит 2 рупия. Мы понимаем, что магазин с 4 карандашами по цене 8 рупий является лучшим решением.
Метод длинного деления
Длинное деление — это метод решения проблем деления с действительными числами. Это проблемы разделения, которые вы не можете решить в уме.
Как это записать?
Для начала вам нужно записать проблему в длинной группе. Задача нормального деления выглядит следующим образом:
Дивиденд ÷ Делитель = Частное
Чтобы записать это в длинном месте, может показаться, что это:
Как насчет того, чтобы попытаться использовать действительно простой пример: 187 ÷ 11 =?
1.Первый шаг — поместить задачу в группу длинного деления:
11 ÷ 187
2. Второй шаг — определить наименьшее число в одну сторону от делимого, для этой ситуации 187, которое можно разделить на 11 Цифра 1 слишком мала, поэтому взглянем на первые две цифры «18». Поскольку 11 может поместиться в число 18, мы можем его использовать.
Таким образом, мы фиксируем, как часто 18 можно разделить на 11. В этой ситуации правильный ответ — 1. В случае, если мы попытались сделать 2, это будет 22, что больше 18.
Затем мы составляем 11 под 18 в свете того факта, что 1 × 11 = 11. В этот момент мы вычитаем 11 из 18. Это равно 7, которую мы записываем.
3. Поскольку у нас осталась цифра 7, проблема не решена. Сейчас мы перемещаем 7 вниз с конца 187.
4. Таким образом, мы решаем, как часто 11 попадет в 77. На самом деле это несколько раз. Мы записываем 7 на 1 в правой зоне срабатывания. Мы записываем 77 под 77 в свете того факта, что 7 × 11 = 77.
5. Теперь вычтем 77 из 77. Правильный ответ — ноль. Мы завершили задачу. 187 ÷ 11 = 17.
Несколько советов по длинному делению:
Напишите другую таблицу для делителя, прежде чем приступить к задаче. Например, если делитель 11, вы записываете 11, 22, 33, 44, 55, 66, 77, 88, 99 и т. Д. Это поможет вам избежать ошибок.
Поставьте 0 в левой части остатка, который вы не используете. Убедитесь, что вы упорядочили все свои числа.Правильное составление и правильное расположение чисел действительно помогут вам сделать меньше ошибок.
Еще раз проверьте проблему с проверкой. Когда у вас есть ответ, перемножьте задачу в обратном порядке, чтобы проверить правильность вашего решения.
Ниже приведены еще несколько примеров деления в столбик. Постарайтесь самостоятельно решить эти проблемы, чтобы проверить, получите ли вы аналогичные результаты.
Тесты на делимость
Вы приобрели 1235 шоколадных конфет, и вам необходимо распределить их по классу.Каким образом вы узнаете, с каким числом разделить их, не разыгрывая в действительности процесс деления?
Процедура определения того, делится ли данное число в точности на другое число без реальной разработки процесса деления, известна как проверка делимости. Точное деление означает, что при разделении не остается остатков. Чтобы понять правила делимости любого числа, мы должны знать его делимость с такими числами, как 2, 3, 4, 5, 9, 10 и 11.
Правила делимости
Тест делимости для 2
Если разряды единицы или разряда единицы числа равны 0, 2, 4, 6 или 8, то число считается делимым на 2 Другими словами, в случае, если последняя цифра числа четная, в этой точке она всегда делится на 2. Например, как насчет того, чтобы взять 24. Последняя цифра четная. 4 делится на 2, следовательно, число 24 делится на 2.
Проверка делимости на 4
Если число, образованное двумя последними цифрами, делится на 4, то считается, что число делится на 4.Например, как насчет того, чтобы взять 12343684. Вам не нужно подчеркивать каждое из чисел, просто проверьте последние 2 цифры чисел. Если последние две цифры, например, 84, отличаются на 4, тогда число делится на 4.
Тесты делимости для 3 и 9
Число делится на 3, если сумма его цифр делится на 3. Нам следует рассмотреть несколько примеров.
Подобные правила связаны с проверкой делимости числа 9. Число делится на 9, если сумма его цифр делится на 9.
Проверка делимости для 5
Число точно делится на 5 в том случае, если оно содержит цифры 0 или 5 в разрядах. Такие числа, как 15, 120, 205, 4405 и т. Д., В точности делятся на 5, поскольку в этих числах 0 или 5 стоят в разряде единиц. Как насчет того, чтобы взглянуть на пример.
Какой из чисел 21345650 и 459022 делится на 5? Из обоих чисел 21345650 и 459022 первое число, то есть 21345650, точно делится на 5, так как цифра единиц равна 0.
Проверка делимости для 6
Число делится на 6, если это число делится на 2 и 3 одновременно. Чтобы проверить делимость числа на 6, нам нужно применить тесты на делимость, которые мы проводим для делителей 2 и 3. Мы должны взглянуть на пример.
Проверьте, делится ли 12581 на 6.
В числе 12581 единичная цифра не имеет таких чисел, как 0, 2, 4, 6, 8. Таким образом, число не делится на 2. В дальнейшем число не делится на 6 на том основании, что для того, чтобы число делилось на 6, оно должно делиться и на 2, и на 3.
Тест на делимость для 8
Тест на делимость для 8 применяется в случае чисел, состоящих как минимум из трех цифр. Число делится на 8, если трехзначное число, образованное цифрами в точках единиц, десятков и сотен, делится на 8. В числе 5864 мы видим, что число, образованное цифрами в точках единиц, десятков и сотен, равно 864, которое делится на 8, поэтому число делится на 8.
Тест делимости для 10
Если цифра единиц числа равна 0, то оно делится на 10.
Тест делимости для 7
Тест 1:
Возьмите цифры числа в обратном порядке, справа налево, постепенно умножая их на цифры 1, 3, 2, 6, 4, 5, повторяя с этим шаблоном множителей столько, сколько необходимо. Если полученная сумма делится на 7, тогда число делится на 7.
Пример: делится ли число 1603 на 7?
Решение: (3 × 1) + (0 × 3) + (6 × 2) + (1 × 6) = 21. Это число делится на 7.
Тест 2:
Удвойте последнюю цифру и вычтите ее из оставшегося начального усеченного числа. Если результат делится на 7, то исходное число также делится на 7.
Пример: делится ли число 1603 на 7?
Решение: Применяя технику, 160 — 2 × 6 = 154. Это число отличается на 7.
Проверка делимости на 11
Если разница сумм альтернативных цифр числа равна 0 или кратна 11 , то само число делится на 11.Давайте посмотрим на пример.
Пример: проверьте, делится ли 19151 на 11 или нет.
Решение: (1 + 1 + 1) — (9 + 5) = 3-14 = -11, что делится на 11, поэтому 19151 делится на 11.
Решенные примеры
Вопрос: Что из следующего числа делится на 22?
Варианты:
(a) 4683
(b) 7106
(c) 3135
(d) 5682
Решение:
Чтобы число делилось на 22, оно должно делиться как на 2 и 11.Поскольку A и C нечетные числа, они не делятся на 22. В случае D (5 + 8) — (6 + 2) = 13-8 = 5, что не делится на 11, поэтому D равно не делится на 11, поэтому не делится на 22. Поскольку B — четное число, оно делится на 2. Кроме того, (7 + 0) — (1 + 6) = 7-7 = 0, следовательно, 7106 делится на 11. Итак, B делится на 22. Следовательно, ответ — B.
.