Числа косинус – Таблица косинусов | Онлайн калькуляторы, расчеты и формулы на GELEOT.RU

1.2.3 Синус, косинус, тангенс и котангенс числа

Итак, напоминаем, что при рассмотрении тригонометрических функций мы рассматриваем окружность, которая имеет единичный радиус. Данное упрощение используется для удобства. Все отношения справедливы для произвольных окружностей, с произвольным радиусом.

Пример. Давайте построим точки на единичной окружности, которые будут соответствовать повороту радиус-вектора на угол  

Решение. За начало отсчета принимаем точку Р₀. Угол, равный нулю радиан совпадает с данной точкой.

Мы знаем, что граничными считаются углы 0, π/2, π, 3π/2, 2π. Если использовать угол π/2 и разделить первую четверть на 3 равных части, то первое от начала отсчета разделение будет соответствовать углу π/6. На графике данная точка имеет место Р_π/6.

Чтобы получить угол

π/4, необходимо прямой угол разделить на две части. Если необходимо отметить угол с отрицательным аргументом, необходимо пойти по часовой стрелке от начальной точки. Например, точка — π/4 будет находиться симметрично относительно оси ОХ в 4 четверти.

Давайте теперь вспомним, каким образом исчисляются углы, выраженные в радианной мере. Чему, например, соответствует в радианах π/4? Чтобы это узнать, следует числовое значение числа π разделить на 4.

3,14 : 4 = 0,78, если углу π/2 соответствует 3,14 : 2 = 1,57. Следовательно, на окружности угол, равный единице будет лежать выше π/4, но ниже π/2. Отрицательное значение угла симметрично положительному относительно оси ОХ.

Таким же образом следует найти и местонахождение угла, равного 2. Так как граничному прямому углу соответствует значение 1,57, то угол, равный двум, будет находиться во второй четверти.

Можно убедиться, что каждому числу соответствует своя ордината и абсцисса на плоскости.

Отсюда можно сделать вывод, что: 

Синус некоторого числа — это значение ординаты на плоскости, которая соответствует точке этого числа на единичной окружности.

Косинус некоторого числа — это значение абсциссы на плоскости, которая соответствует точке этого числа на единичной окружности.

Тангенс некоторого числа — это значение, полученное в результате отношения синуса к косинусу, иначе говоря, отношение ординаты к абсциссе.

Котангенс некоторого числа — это значение, полученное в результате отношения косинуса к синусу, иначе говоря, отношение абсциссы к ординате.

Синус и косинус имеют период, равный 6,28. Тангенс и котангенс имеет период, равный 3,14.

cknow.ru

Косинус — число — Большая Энциклопедия Нефти и Газа, статья, страница 1

Косинус — число

Cтраница 1

Косинус числа t как абсцисса точки Pt положителен в первой и четвертой четвертях и отрицателен во второй и третьей.  [1]

А-абсцисса этой точки называется косинусом числа а и обозначается cos а. Если а 0, то поворот осуществляется против часовой стрелки, а если а 0, то по часовой стрелке.  [2]

Что называется синусом и косинусом числа.  [3]

А абсцисса этой точки называется косинусом числа а и обозначается cos а. Если а 0, то поворот осуществляется против часовой стрелки, а если а 0, то по часовой стрелке.  [4]

Синусом числа х называется число, равное синусу угла в к радиан, Косинусами числа х называется число, равное косинусу угла в х радиан. Аналогично определяются и другие тригонометрические функции числового аргумента.  [5]

Синусом числа х называется число, равное синусу угла в х радиан, Косинусом числа х называется число, равное косинусу угла в х радиан. Аналогично определяются и другие тригонометрические функции числового аргумента.  [6]

Таким образом, синус числа а равен синусу угла в а радиан, а косинус числа а — косинусу этого угла.  [7]

Ордината точки М ( х) называется синусом числа х и обозначается sinx, а абсцисса этой точки называется косинусом числа х и обозначается C.  [8]

Синусом числа х называется число, равное синусу угла в х радиан. Косинусом числа называется число, равное косинусу угла в х радиан. Аналогично определяются и другие тригонометрические функции числового аргумента.  [9]

Синусом числа х называется число, равное синусу угла в х радианов. Косинусом числа х называется число, равное косинусу угла в х радианов.  [10]

Устройство состоит из многофункциональной схемы ( см. рис. 2.37) и ДУ. Изменение выходного сигнала регулируется отношением R % / Ri, а косинус числа вычисляется для его изменения в первом квадранте.  [12]

Страницы:      1

www.ngpedia.ru

Косинус — это… Что такое Косинус?

Рис. 1
Графики тригонометрических функций: синуса, косинуса, тангенса, секанса, косеканса, котангенса

Тригонометрические функции — вид элементарных функций. Обычно к ним относят синус (

sin x), косинус (cos x), тангенс (tg x), котангенс (ctg x), секанс (sec x) и косеканс (cosec x), последняя пара функций в настоящее время сравнительно малоупотребительна (про ещё менее употребляемые функции см. здесь). В англоязычной литературе тангенс, котангенс и косеканс обозначаются tan x, cot x, csc x. Обычно тригонометрические функции определяются геометрически, но можно определить их аналитически через суммы рядов или как решения некоторых дифференциальных уравнений, что позволяет расширить область определения этих функций на комплексные числа.

Способы определения

Геометрическое определение

Рис. 2
Определение тригонометрических функций

Обычно тригонометрические функции определяются геометрически. Пусть дана декартова система координат на плоскости и построена окружность радиуса R с центром в начале координат O. Будем измерять углы как повороты от положительного направления оси абсцисс до луча OB. Направление против часовой стрелки считается положительным, по часовой стрелке отрицательным. Абсциссу точки

В обозначим x_B, ординату обозначим y_B (см. рисунок.)

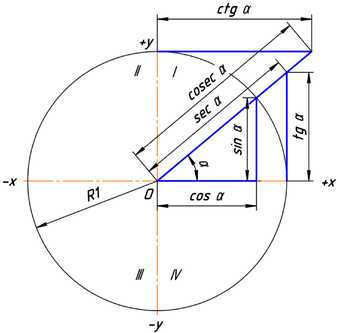
Рис. 3.
Тригонометрические функции угла α в тригонометрической окружности с радиусом, равным единице.

Ясно, что значения тригонометрических функций не зависят от величины радиуса окружности R в силу свойств подобных фигур. Часто этот радиус принимают равным величине единичного отрезка, тогда синус равен просто ординате y_B, а косинус — абсциссе x_B. На рисунке 3 показаны величины тригонометрических функций для единичной окружности.

Если α — действительное число, то синусом α в математическом анализе называется синус угла, радианная мера которого равна α, аналогично для прочих тригонометрических функций.

Определение тригонометрических функций для острых углов

Рис. 4.
Тригонометрические функции острого угла

Во многих учебниках элементарной геометрии до настоящего времени тригонометрические функции острого угла определяются как отношения сторон прямоугольного треугольника. Пусть OAB — треугольник с углом α. Тогда:

• Синусом α называется отношение AB/OB (противолежащего катета к гипотенузе)
• Косинусом α называется отношение ОА/OB (прилежащего катета к гипотенузе)
• Тангенсом α называется отношение AB/OA (отношение противолежащего катета к прилежащему)
• Котангенсом α называется отношение ОА/AB (отношение прилежащего катета к противолежащему)
• Секансом α называется отношение ОB/OA (гипотенузы к прилежащему катету)
• Косекансом α называется отношение ОB/AB (гипотенузы к противолежащему катету)

Построив систему координат с началом в точке O, направлением оси абсцисс вдоль OA и в случае необходимости изменив ориентацию (перевернув) треугольник так, чтобы он находился в первой четверти системы координат, и затем, построив окружность с радиусом, равным гипотенузе, сразу находим, что такое определение функций приводит к тому же результату, что и предыдущее. Данное определение имеет некоторое педагогическое преимущество, так как не требует введения понятия системы координат, но также и такой крупный недостаток, что невозможно определить тригонометрические функции даже для тупых углов, которые необходимо знать при решении элементарных задач про тупоугольные треугольники (см. Теорема синусов, Теорема косинусов).

Определение тригонометрических функций как решений дифференциальных уравнений

Функции косинус и синус можно определить как чётное (косинус) и нечётное (синус) решение дифференциального уравнения

с начальными условиями cos(0) = sin'(0) = 1, то есть как функций одной переменной, вторая производная которых равна самой функции, взятой со знаком минус:

Определение тригонометрических функций как решений функциональных уравнений

Функции косинус и синус можно определить как непрерывные решения (f и g соответственно) системы функциональных уравнений:

Определение тригонометрических функций через ряды

Используя геометрию и свойства пределов, можно доказать, что производная синуса равна косинусу и что производная косинуса равна минус синусу. Тогда можно воспользоваться теорией рядов Тейлора и представить синус и косинус в виде суммы степенны́х рядов:

Пользуясь этими формулами, а также уравнениями и можно найти разложения в ряд Тейлора и других тригонометрических функций:

где B_n — числа Бернулли.

где E_n — числа Эйлера.

Значения тригонометрических функций для некоторых углов

Значения синуса, косинуса, тангенса, котангенса, секанса и косеканса для некоторых углов приведены в таблице.

Значения косинуса и синуса на окружности.

Значения тригонометрических функций нестандартных углов

Свойства тригонометрических функций

Простейшие тождества

Так как синус и косинус являются соответственно ординатой и абсциссой точки, соответствующей на единичной окружности углу α то, согласно уравнению единичной окружности или теореме Пифагора, имеем:

Деля это уравнение на квадрат косинуса и синуса соответственно имеем далее:

Чётность

Косинус и секанс — чётные. Остальные четыре функции — нечётные, то есть:

Периодичность

Функции y = sin α, y = cos α, y = sec α, y = cosec α — периодические с периодом 2π. Функции: y = tg α, y = ctg α — c периодом π

Формулы приведения

Здесь f — любая тригонометрическая функция, g — соответствующая ей другая функция из пары (то есть косинус для синуса, синус для косинуса и аналогично для остальных функций). Нужный знак в правой части равенства определяется следующим образом: предположим что угол α находится в первой четверти, тогда определяем знаки значений функций в левой и правой части равенства и в случае их несовпадения перед правой частью пишем знак -, например:

Формулы сложения

Другие тригонометрические тождества.

Однопараметрическое представление

Все тригонометрические функции можно выразить через тангенс половинного угла.

Производные и интегралы

Все тригонометрические функции непрерывно дифференцируемы на всей области определения:

Интегралы тригонометрических функций на области определения выражаются через элементарные функции следующим образом:

См. также Список интегралов от тригонометрических функций

История

Линия синуса у индийских математиков первоначально называлась «арха-джива» («полутетива»), затем слово «арха» было отброшено и линию синуса стали называть просто «джива». Арабские переводчики не перевели слово «джива» арабским словом «ватар», обозначающим тетиву и хорду, а транскрибировали арабскими буквами и стали называть линию синуса «джиба». Так как в арабском языке краткие гласные не обозначаются, а долгое «и» в слове «джиба» обозначается так же, как полугласная «й», арабы стали произносить название линии синуса «джайб», что буквально обозначает «впадина», «пазуха». При переводе арабских сочинений на латынь европейские переводчики перевели слово «джайб» латинским словом sinus, имеющим то же значение.

Современное обозначение синуса sin и косинуса cos введено Леонардом Эйлером в XVIII веке.

Термины «тангенс» (от лат. tangens — касающийся) и «секанс» (лат. secans — секущий) были введены датским математиком Томасом Финке (1561—1656) в его книге «Геометрия круглого» (Geometria rotundi, 1583)

Сам термин тригонометрические функции введён Клюгелем в 1770.

См. также

Ссылки

Wikimedia Foundation. 2010.

muller.academic.ru

Косинус — это… Что такое Косинус?

Рис. 1
Графики тригонометрических функций: синуса, косинуса, тангенса, секанса, косеканса, котангенса

Тригонометрические функции — вид элементарных функций. Обычно к ним относят синус (sin x), косинус (cos x), тангенс (tg x), котангенс (ctg x), секанс (sec x) и косеканс (cosec x), последняя пара функций в настоящее время сравнительно малоупотребительна (про ещё менее употребляемые функции см. здесь). В англоязычной литературе тангенс, котангенс и косеканс обозначаются tan x, cot x, csc x. Обычно тригонометрические функции определяются геометрически, но можно определить их аналитически через суммы рядов или как решения некоторых дифференциальных уравнений, что позволяет расширить область определения этих функций на комплексные числа.

Способы определения

Геометрическое определение

Рис. 2
Определение тригонометрических функций

Обычно тригонометрические функции определяются геометрически. Пусть дана декартова система координат на плоскости и построена окружность радиуса R с центром в начале координат O. Будем измерять углы как повороты от положительного направления оси абсцисс до луча OB. Направление против часовой стрелки считается положительным, по часовой стрелке отрицательным. Абсциссу точки В обозначим x_B, ординату обозначим y_B (см. рисунок.)

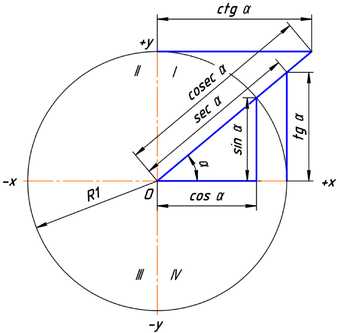
Рис. 3.
Тригонометрические функции угла α в тригонометрической окружности с радиусом, равным единице.

Ясно, что значения тригонометрических функций не зависят от величины радиуса окружности R в силу свойств подобных фигур. Часто этот радиус принимают равным величине единичного отрезка, тогда синус равен просто ординате y_B, а косинус — абсциссе x_B. На рисунке 3 показаны величины тригонометрических функций для единичной окружности.

Если α — действительное число, то синусом α в математическом анализе называется синус угла, радианная мера которого равна α, аналогично для прочих тригонометрических функций.

Определение тригонометрических функций для острых углов

Рис. 4.
Тригонометрические функции острого угла

Во многих учебниках элементарной геометрии до настоящего времени тригонометрические функции острого угла определяются как отношения сторон прямоугольного треугольника. Пусть OAB — треугольник с углом α. Тогда:

• Синусом α называется отношение AB/OB (противолежащего катета к гипотенузе)
• Косинусом α называется отношение ОА/OB (прилежащего катета к гипотенузе)
• Тангенсом α называется отношение AB/OA (отношение противолежащего катета к прилежащему)
• Котангенсом α называется отношение ОА/AB (отношение прилежащего катета к противолежащему)
• Секансом α называется отношение ОB/OA (гипотенузы к прилежащему катету)
• Косекансом α называется отношение ОB/AB (гипотенузы к противолежащему катету)

Построив систему координат с началом в точке O, направлением оси абсцисс вдоль OA и в случае необходимости изменив ориентацию (перевернув) треугольник так, чтобы он находился в первой четверти системы координат, и затем, построив окружность с радиусом, равным гипотенузе, сразу находим, что такое определение функций приводит к тому же результату, что и предыдущее. Данное определение имеет некоторое педагогическое преимущество, так как не требует введения понятия системы координат, но также и такой крупный недостаток, что невозможно определить тригонометрические функции даже для тупых углов, которые необходимо знать при решении элементарных задач про тупоугольные треугольники (см. Теорема синусов, Теорема косинусов).

Определение тригонометрических функций как решений дифференциальных уравнений

Функции косинус и синус можно определить как чётное (косинус) и нечётное (синус) решение дифференциального уравнения

с начальными условиями cos(0) = sin'(0) = 1, то есть как функций одной переменной, вторая производная которых равна самой функции, взятой со знаком минус:

Определение тригонометрических функций как решений функциональных уравнений

Функции косинус и синус можно определить как непрерывные решения (f и g соответственно) системы функциональных уравнений:

Определение тригонометрических функций через ряды

Используя геометрию и свойства пределов, можно доказать, что производная синуса равна косинусу и что производная косинуса равна минус синусу. Тогда можно воспользоваться теорией рядов Тейлора и представить синус и косинус в виде суммы степенны́х рядов:

Пользуясь этими формулами, а также уравнениями и можно найти разложения в ряд Тейлора и других тригонометрических функций:

где B_n — числа Бернулли.

где E_n — числа Эйлера.

Значения тригонометрических функций для некоторых углов

Значения синуса, косинуса, тангенса, котангенса, секанса и косеканса для некоторых углов приведены в таблице.

Значения косинуса и синуса на окружности.

Значения тригонометрических функций нестандартных углов

Свойства тригонометрических функций

Простейшие тождества

Так как синус и косинус являются соответственно ординатой и абсциссой точки, соответствующей на единичной окружности углу α то, согласно уравнению единичной окружности или теореме Пифагора, имеем:

Деля это уравнение на квадрат косинуса и синуса соответственно имеем далее:

Чётность

Косинус и секанс — чётные. Остальные четыре функции — нечётные, то есть:

Периодичность

Функции y = sin α, y = cos α, y = sec α, y = cosec α — периодические с периодом 2π. Функции: y = tg α, y = ctg α — c периодом π

Формулы приведения

Здесь f — любая тригонометрическая функция, g — соответствующая ей другая функция из пары (то есть косинус для синуса, синус для косинуса и аналогично для остальных функций). Нужный знак в правой части равенства определяется следующим образом: предположим что угол α находится в первой четверти, тогда определяем знаки значений функций в левой и правой части равенства и в случае их несовпадения перед правой частью пишем знак -, например:

Формулы сложения

Другие тригонометрические тождества.

Однопараметрическое представление

Все тригонометрические функции можно выразить через тангенс половинного угла.

Производные и интегралы

Все тригонометрические функции непрерывно дифференцируемы на всей области определения:

Интегралы тригонометрических функций на области определения выражаются через элементарные функции следующим образом:

См. также Список интегралов от тригонометрических функций

История

Линия синуса у индийских математиков первоначально называлась «арха-джива» («полутетива»), затем слово «арха» было отброшено и линию синуса стали называть просто «джива». Арабские переводчики не перевели слово «джива» арабским словом «ватар», обозначающим тетиву и хорду, а транскрибировали арабскими буквами и стали называть линию синуса «джиба». Так как в арабском языке краткие гласные не обозначаются, а долгое «и» в слове «джиба» обозначается так же, как полугласная «й», арабы стали произносить название линии синуса «джайб», что буквально обозначает «впадина», «пазуха». При переводе арабских сочинений на латынь европейские переводчики перевели слово «джайб» латинским словом sinus, имеющим то же значение.

Современное обозначение синуса sin и косинуса cos введено Леонардом Эйлером в XVIII веке.

Термины «тангенс» (от лат. tangens — касающийся) и «секанс» (лат. secans — секущий) были введены датским математиком Томасом Финке (1561—1656) в его книге «Геометрия круглого» (Geometria rotundi, 1583)

Сам термин тригонометрические функции введён Клюгелем в 1770.

См. также

Ссылки

Wikimedia Foundation. 2010.

xzsad.academic.ru

Косинус — это… Что такое Косинус?

Рис. 1
Графики тригонометрических функций: синуса, косинуса, тангенса, секанса, косеканса, котангенса

Тригонометрические функции — вид элементарных функций. Обычно к ним относят синус (sin x), косинус (cos x), тангенс (tg x), котангенс (ctg x), секанс (sec x) и косеканс (cosec x), последняя пара функций в настоящее время сравнительно малоупотребительна (про ещё менее употребляемые функции см. здесь). В англоязычной литературе тангенс, котангенс и косеканс обозначаются tan x, cot x, csc x. Обычно тригонометрические функции определяются геометрически, но можно определить их аналитически через суммы рядов или как решения некоторых дифференциальных уравнений, что позволяет расширить область определения этих функций на комплексные числа.

Способы определения

Геометрическое определение

Рис. 2
Определение тригонометрических функций

Обычно тригонометрические функции определяются геометрически. Пусть дана декартова система координат на плоскости и построена окружность радиуса R с центром в начале координат O. Будем измерять углы как повороты от положительного направления оси абсцисс до луча OB. Направление против часовой стрелки считается положительным, по часовой стрелке отрицательным. Абсциссу точки В обозначим x_B, ординату обозначим y_B (см. рисунок.)

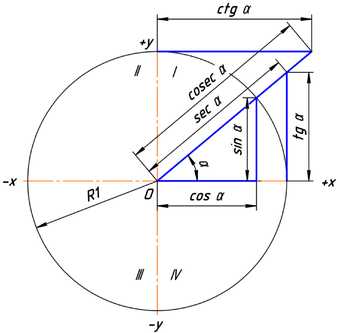
Рис. 3.
Тригонометрические функции угла α в тригонометрической окружности с радиусом, равным единице.

Ясно, что значения тригонометрических функций не зависят от величины радиуса окружности R в силу свойств подобных фигур. Часто этот радиус принимают равным величине единичного отрезка, тогда синус равен просто ординате y_B, а косинус — абсциссе x_B. На рисунке 3 показаны величины тригонометрических функций для единичной окружности.

Если α — действительное число, то синусом α в математическом анализе называется синус угла, радианная мера которого равна α, аналогично для прочих тригонометрических функций.

Определение тригонометрических функций для острых углов

Рис. 4.
Тригонометрические функции острого угла

Во многих учебниках элементарной геометрии до настоящего времени тригонометрические функции острого угла определяются как отношения сторон прямоугольного треугольника. Пусть OAB — треугольник с углом α. Тогда:

• Синусом α называется отношение AB/OB (противолежащего катета к гипотенузе)
• Косинусом α называется отношение ОА/OB (прилежащего катета к гипотенузе)
• Тангенсом α называется отношение AB/OA (отношение противолежащего катета к прилежащему)
• Котангенсом α называется отношение ОА/AB (отношение прилежащего катета к противолежащему)
• Секансом α называется отношение ОB/OA (гипотенузы к прилежащему катету)
• Косекансом α называется отношение ОB/AB (гипотенузы к противолежащему катету)

Построив систему координат с началом в точке O, направлением оси абсцисс вдоль OA и в случае необходимости изменив ориентацию (перевернув) треугольник так, чтобы он находился в первой четверти системы координат, и затем, построив окружность с радиусом, равным гипотенузе, сразу находим, что такое определение функций приводит к тому же результату, что и предыдущее. Данное определение имеет некоторое педагогическое преимущество, так как не требует введения понятия системы координат, но также и такой крупный недостаток, что невозможно определить тригонометрические функции даже для тупых углов, которые необходимо знать при решении элементарных задач про тупоугольные треугольники (см. Теорема синусов, Теорема косинусов).

Определение тригонометрических функций как решений дифференциальных уравнений

Функции косинус и синус можно определить как чётное (косинус) и нечётное (синус) решение дифференциального уравнения

с начальными условиями cos(0) = sin'(0) = 1, то есть как функций одной переменной, вторая производная которых равна самой функции, взятой со знаком минус:

Определение тригонометрических функций как решений функциональных уравнений

Функции косинус и синус можно определить как непрерывные решения (f и g соответственно) системы функциональных уравнений:

Определение тригонометрических функций через ряды

Используя геометрию и свойства пределов, можно доказать, что производная синуса равна косинусу и что производная косинуса равна минус синусу. Тогда можно воспользоваться теорией рядов Тейлора и представить синус и косинус в виде суммы степенны́х рядов:

Пользуясь этими формулами, а также уравнениями и можно найти разложения в ряд Тейлора и других тригонометрических функций:

где B_n — числа Бернулли.

где E_n — числа Эйлера.

Значения тригонометрических функций для некоторых углов

Значения синуса, косинуса, тангенса, котангенса, секанса и косеканса для некоторых углов приведены в таблице.

Значения косинуса и синуса на окружности.

Значения тригонометрических функций нестандартных углов

Свойства тригонометрических функций

Простейшие тождества

Так как синус и косинус являются соответственно ординатой и абсциссой точки, соответствующей на единичной окружности углу α то, согласно уравнению единичной окружности или теореме Пифагора, имеем:

Деля это уравнение на квадрат косинуса и синуса соответственно имеем далее:

Чётность

Косинус и секанс — чётные. Остальные четыре функции — нечётные, то есть:

Периодичность

Функции y = sin α, y = cos α, y = sec α, y = cosec α — периодические с периодом 2π. Функции: y = tg α, y = ctg α — c периодом π

Формулы приведения

Здесь f — любая тригонометрическая функция, g — соответствующая ей другая функция из пары (то есть косинус для синуса, синус для косинуса и аналогично для остальных функций). Нужный знак в правой части равенства определяется следующим образом: предположим что угол α находится в первой четверти, тогда определяем знаки значений функций в левой и правой части равенства и в случае их несовпадения перед правой частью пишем знак -, например:

Формулы сложения

Другие тригонометрические тождества.

Однопараметрическое представление

Все тригонометрические функции можно выразить через тангенс половинного угла.

Производные и интегралы

Все тригонометрические функции непрерывно дифференцируемы на всей области определения:

Интегралы тригонометрических функций на области определения выражаются через элементарные функции следующим образом:

См. также Список интегралов от тригонометрических функций

История

Линия синуса у индийских математиков первоначально называлась «арха-джива» («полутетива»), затем слово «арха» было отброшено и линию синуса стали называть просто «джива». Арабские переводчики не перевели слово «джива» арабским словом «ватар», обозначающим тетиву и хорду, а транскрибировали арабскими буквами и стали называть линию синуса «джиба». Так как в арабском языке краткие гласные не обозначаются, а долгое «и» в слове «джиба» обозначается так же, как полугласная «й», арабы стали произносить название линии синуса «джайб», что буквально обозначает «впадина», «пазуха». При переводе арабских сочинений на латынь европейские переводчики перевели слово «джайб» латинским словом sinus, имеющим то же значение.

Современное обозначение синуса sin и косинуса cos введено Леонардом Эйлером в XVIII веке.

Термины «тангенс» (от лат. tangens — касающийся) и «секанс» (лат. secans — секущий) были введены датским математиком Томасом Финке (1561—1656) в его книге «Геометрия круглого» (Geometria rotundi, 1583)

Сам термин тригонометрические функции введён Клюгелем в 1770.

См. также

Ссылки

Wikimedia Foundation. 2010.

dic.academic.ru