Правила площади и периметра: Как найти периметр и площадь?

Содержание

Периметры и площади . Магия математики [Как найти x и зачем это нужно]

Периметр полигона есть сумма длин его сторон. Так, периметр прямоугольника длиной b и шириной h будет равен 2b + 2h, потому что и b, и h суть размеры каждой из двух его сторон. А как насчет площади? Исходим из того соображения, что площадь квадрата размером 1 на 1 (так называемого единичного квадрата) равна 1. При положительных целых значениях b и h (как на рисунке) мы можем разбить всю площадь на bh единичных квадратов, а значит, она будет равна bh. В целом же, любой прямоугольник с длиной b и шириной h (где b и h суть положительные, но необязательно целые величины) имеет площадь bh.

Отступление

В этой главе мы уже не раз обращались к помощи алгебры, чтобы разрешить исключительно геометрические проблемы. Принцип этот прекрасно работает и в обратную сторону: порой геометрия значительно облегчает понимание алгебры.

Взгляните на типичную задачу. Насколько малым может быть значение где x есть любое положительное число? При x = 1 имеем 2, при x = 1,25 – 1,25 + 0,8 = 2,05, при x = 2 – 2,5. Логика подсказывает, что наименьшим ответом будет 2, и это на самом деле так, только вот как нам в этом удостовериться? Самый простой и эффективный метод расчета будет предложен в главе 11, пока же давайте ограничимся методом геометрическим.

Возьмем фигуру, состоящую из четырех костяшек домино, каждая из которых имеет размер x на 1/x. Расположены они так, чтобы в пространстве между ними получился квадрат. Какова будет общая площадь всей фигуры (включая этот внутренний квадрат)?

С одной стороны, поскольку фигура представляет собой квадрат x + 1/x на x + 1/x, ее площадь должна быть (x + 1/x)?. С другой стороны, площадь каждой костяшки домино равна 1, поэтому площадь фигуры в целом составит как минимум 4.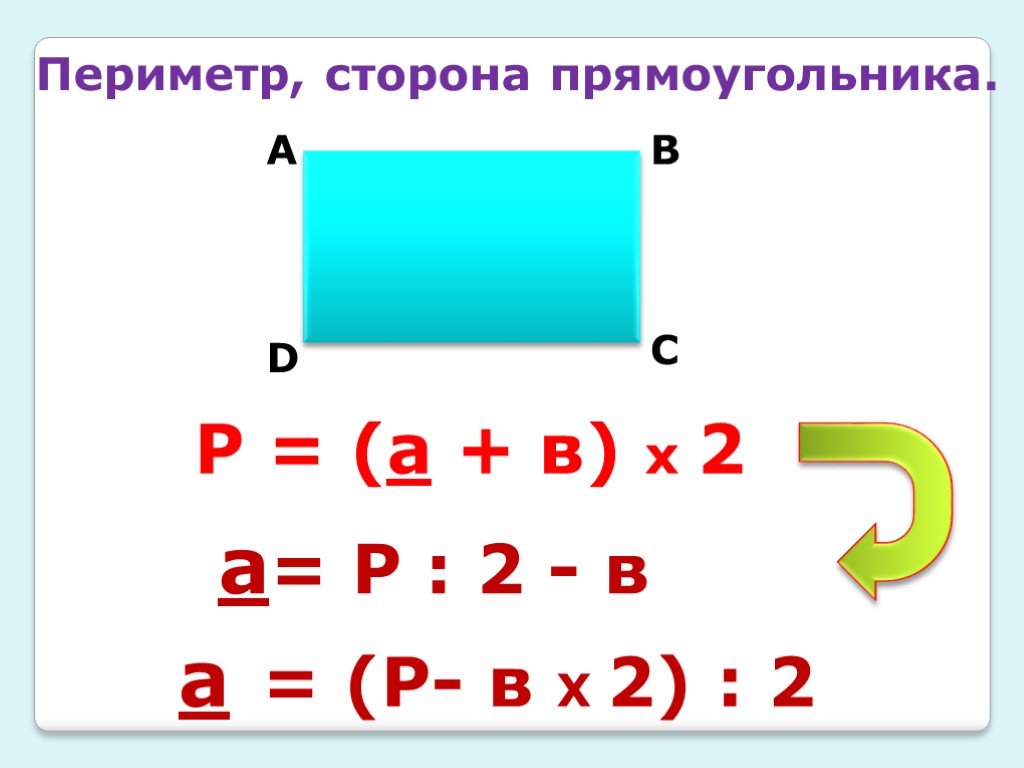

Следовательно,

(x + 1/x)? ? 4

или x + 1/x ? 2, что и требовалось доказать.?

Начав с площади прямоугольника, можно найти площадь практически любой другой геометрической фигуры, в первую очередь – треугольника.

Теорема: Площадь треугольника с длиной основания b и высотой h составляет

Для наглядности возьмем три конкретных треугольника, основание каждого из которых рана b, а высота – h, что значит, что их площадь также должна быть равна. Это, по сути, наш третий вопрос, ответ на который, готов поспорить, многих из вас удивил.

В зависимости от того, какие размеры имеют прилежащие к основанию AC углы ?

A и ?C, нам нужно рассмотреть три разных частных случая, а затем создать копию треугольника ABC и вписать его вместе с оригиналом в прямоугольник с площадью bh, как показано на рисунке.

Треугольник ABC займет ровно половину этой площади, а значит, его площадь составит как мы и предполагали.

Если углы ?A и ?C острые, остроумным будет и доказательство. Из точки B проведите линию длиной h так, чтобы она была перпендикулярна отрезку AC (она называется высотой треугольника ABC), пересекая его в точке X, как показано на рисунке:

AC, таким образом, состоит из отрезков AX и XC, длины которых составляют соответственно b₁ и b₂, где b₁ + b₂

= b. А так как треугольники BXA и BXC получились у нас прямоугольными, то, согласно предыдущему примеру, их площади будут равны соответственно. Следовательно, площадь большого треугольника ABC –

что и требовалось доказать.

В случае же, если ?A или ?C является тупым, чертеж будет выглядеть вот так:

В примере с остроугольным треугольником мы представляли ABC как сумму двух прямоугольных треугольников. Здесь же нам нужна их разность. Высота любом тупоугольном треугольнике выходит за его границы, образуя тем самым большой треугольник. В нашем случае это ABY, длина основания которого равна b + c, а площадь – Маленький же прямоугольный треугольник CBY имеет площадь Следовательно, площадь ABC может быть представлена как

что и требовалось доказать.

Памятка «Площадь и периметр квадрата и прямоугольника»

Главная / Начальные классы / Математика

Скачать

13.42 КБ, 1381536.docx Автор: Черненко Анна Анатольевна, 18 Янв 2016

Скачать

13.42 КБ, 1381538.docx Автор: Черненко Анна Анатольевна, 18 Янв 2016

Скачать

13. 42 КБ, 1381539.docx Автор: Черненко Анна Анатольевна, 18 Янв 2016

Памятка «Площадь и периметр квадрата и прямоугольника»

Автор: Черненко Анна Анатольевна

Тип	Название материала	Автор	Опубликован
документ	Памятка «Площадь и периметр квадрата и прямоугольника»	Черненко Анна Анатольевна	18 Янв 2016
документ	Проверочная работа по математике для 4 класса по теме «Площадь и периметр прямоугольника, квадрата»	Каминская Татьяна Юрьевна	7 Апр 2016
документ	периметр и площадь прямоугольника и квадрата	Цыганова-Рельгун Екатерина Тимофеевна	31 Мар 2015
документ	Технологическая карта урока Периметр и площадь прямоугольника и квадрата	Аглямова Райля Адгамовна	19 Мар 2016
разное	«Периметр и площадь прямоугольника»	Чаплоуская Любовь Геннадьевна	21 Мар 2015
презентация	Презентация к уроку: «Площадь и периметр прямоугольника»	Смирнова Валентина Ивановна	1 Апр 2015
презентация	Презентация по математике «Периметр и Площадь прямоугольника»	Мартыщенко Татьяна Михайловна	18 Мая 2015
презентация	Периметр квадрата и прямоугольника. Презентация.	Козик Ирина Валерьевна	30 Июн 2015
документ	Периметр квадрата и прямоугольника. Сценарий урока.	Козик Ирина Валерьевна	30 Июн 2015
разное	«Периметр квадрата»	Матвеева Нина Васильевна	31 Мар 2015
разное	Учебный материал по теме: «Площадь. Формула площади прямоугольника и квадрата»	Трофимова Елена Иозасовна	4 Апр 2015
разное	Интерактивный тест по геометрии на тему «Площадь квадрата и прямоугольника»	Скамейкина Ольга Романовна	6 Дек 2015
документ	Самостоятельная работа по теме «Площадь квадрата и прямоугольника. 8 класс»	Иванова Светлана Игоревна	27 Мар 2016
разное	Сценарий открытого урока «Обобщение и систематизация знаний по теме «Площадь и периметр прямоугольника».» в 5 классе ФГОС математика	Фатима Гучаева	21 Мар 2016
таблица	Интерактивный тренажёр «Стороны прямоугольника, его периметр и площадь» 2 вариант	Воронина Ольга Викторовна	30 Мар 2015
таблица	Интерактивный тренажёр «Стороны прямоугольника, его периметр и площадь» .Вариант 1	Воронина Ольга Викторовна	30 Мар 2015
презентация	Презентация к уроку математики в 5 классе «Площадь и периметр прямоугольника»	Елена Ивановна Кормилина	8 Фев 2016
документ	Рабочая программа по математике 5 класс. ФГОС прямоугольник, периметр, диагональ, площадь прямоугольника и треугольника, площадь фигуры, единица длины, равные фигуры, наложение фигур. прямоугольник, периметр, диагональ, площадь прямоугольника и	закирзянова фатима рахимзяновна	8 Апр 2015
документ	«Периметр и площадь»	Гриценко Галина Вячеславна	1 Апр 2015
документ	Проверочная работа «Периметр и площадь» 4 класс	Ванина Марина Анатольевна	23 Фев 2016
презентация	Презентация. Площадь и периметр прямоугольника.	Шумилина Татьяна Борисовна	21 Мар 2015
разное	Периметр и площадь прямоугольника. 3 класс.	Меликова Рима Надировна	30 Мар 2015
презентация, документ	Площадь и периметр прямоугольника. Решение задач.	Пaвловa Нaтaлья Ивaнoвна	31 Мар 2015
документ	Конспект занятия по формированию элементарных математических представлений «Сходство и различие прямоугольника и квадрата»	Морозова Татьяна Викторовна	31 Мар 2015
документ	Периметр треугольника и квадрата.	Филиппова Ирина Михайловна	14 Сен 2015
документ	Технологическая карта урока Площадь. Площадь прямоугольника и квадрата. Цели урока: самостоятельному нахождению способов сравнения площадей фигур, повторить	Аглямова Райля Адгамовна	19 Мар 2016
презентация	«Площадь прямоугольника, квадрата»	Акимова Алия Харисовна	20 Мар 2015
презентация	Презентация по теме: » Площадь квадрата, прямоугольника, параллелограмма»	Лялина Людмила Николаевна	21 Мар 2015
документ	Урок по теме :»Площадь прямоугольника, квадрата»	Русанова Галина Николаевна	8 Фев 2016
презентация	презентация к уроку на ему площадь прямоугольника и квадрата 5 класс	Бойкова Наталья Григорьевна	1 Апр 2015
документ	Проверочная работа по математике 4 класса по теме: «Площадь и периметр»	Муль Полина Владимировна	30 Мар 2015
документ	Дидактический материал по теме: «Периметр и площадь геометрических фигур».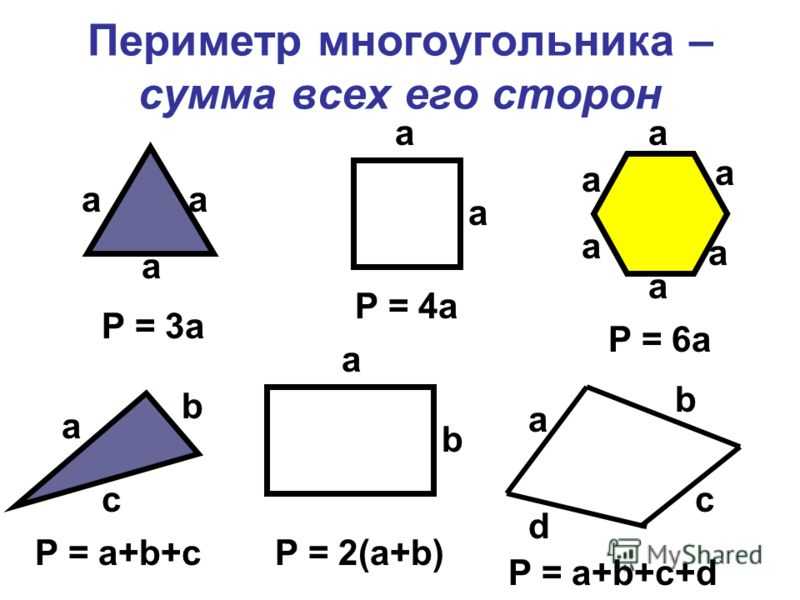 2 класс	Берлинова Екатерина Михайловна	30 Мар 2015
разное	Урок — проект по математике «Конструирование. Периметр и площадь многоугольника» 3 класс	Дерябина Наталья Викторовна	31 Мар 2015
документ	Конспект урока по математике 2 класс Тема урока: «Повторение и закрепление пройденного материала» (порядок действия в выражениях, площадь квадрата и прямоугольника, уравнения)	Хайрова Юлия Павловна	4 Апр 2015
документ	Урок математики «Свойства умножения и деления. Площадь прямоугольника.	Кабиева Гульфия Гелемхановна	31 Мар 2015
разное	Урок алгебры по теме «Формулы квадрата суммы и квадрата разности двух выражений»	Колташова Марина Александровна	28 Фев 2016
документ	урок в 7 классе по теме: «Разложение на множители с помощью формул квадрата суммы и квадрата разности»	Вельдясова Галина Михайловна	17 Фев 2016
документ	Формулы для вычисления площади и периметра квадрата и прямоугольника.	Виноходова Наталья Васильевна	21 Мар 2015
документ	Закрепление и обобщение знаний о площади прямоугольника и квадрата	Коробейникова Ольга Владимировна	14 Янв 2016
документ	Тема урока: Свойства диагоналей прямоугольника и квадрата. Проектная деятельность.	Черентаева Валентина Алексеевна	31 Мар 2015

Периметр и площадь Класс 7 Формулы

Понятие периметра и площади фигур широко используется в нашей повседневной жизни. Учащиеся обычно сталкиваются с проблемами при проведении различия между ними, если им не ясна основная логика и концепция измерения. Следовательно, эта статья была создана, чтобы помочь учащимся понять формулы периметра и площади 7 класса, а также дать некоторые практические советы по их запоминанию.

Список периметра и площади класса 7 Формулы

Вот список некоторых понятий и формул, связанных с периметром и площадью.

Периметром замкнутой фигуры является общая длина ее границы, а площадь — занимаемое ею пространство.
Периметр квадрата = 4 × сторона
Периметр прямоугольника = 2 × (длина + ширина)
Площадь квадрата = сторона × сторона
Площадь прямоугольника = Длина × Ширина
Площадь параллелограмма = Основание × Высота
Площадь треугольника = 1/2 × основание × высота
Расстояние вокруг круглой области называется ее окружностью.
Длина окружности = πd, d — диаметр, а π = 22/7 или 3,14
Площадь круга = πr ² , где «r» — радиус круга.

Применение формул периметра и площади Класс 7

Площадь и периметр фигур широко используются в нашей повседневной жизни. Несколько примеров приведены ниже.

Чтобы положить плитку на пол, нужно вычислить площадь пола и разделить ее на площадь одной плитки, чтобы узнать, сколько плиток потребуется, чтобы покрыть весь пол. Обычно плитка и пол комнаты имеют квадратную или прямоугольную форму, поэтому формулы площади квадрата и прямоугольника очень удобны.
Чтобы поставить забор вокруг поля, нам нужно рассчитать периметр поля. В зависимости от того, имеет ли поле квадратную, прямоугольную или круглую форму, мы можем использовать формулы, чтобы узнать длину периметра, а затем рассчитать необходимое количество ограждений.

Советы по запоминанию формул периметра и площади класса 7

Формулы периметра и площади класса 7 являются основными вводными формулами, которые используются для понимания понятий, связанных с измерением. Следующие советы помогут учащимся легко выучить эти формулы:

Один из лучших способов запомнить что-либо — записать это, так как мозг быстро обрабатывает это. Учащимся рекомендуется полностью записывать понятия и логику вместе с формулой, чтобы они имели для них смысл. Они должны прививать эту привычку каждый день, чтобы досконально понимать формулы.
После завершения письменной части учащиеся должны просмотреть все решенные примеры в своем учебнике, а затем попытаться решить их. Это познакомит их с различными вариантами использования формул. После решенных примеров они должны отработать как можно больше вопросов-упражнений. Это поможет им получить достаточную практику в использовании, а также в написании формул, что поможет им хорошо их запомнить.
Учащиеся также могут установить изображения формул в качестве обоев на своих ноутбуках и мобильных устройствах. Это обеспечит быстрый пересмотр в течение дня.

Периметр и площадь класса 7 Формулы Примеры

Пример 1: Лара хочет оградить свой сад с трех сторон забором длиной 15 м, 10 м и 11 м. Найдите стоимость ограждения сада с трех сторон, если цена ограждения 120 руб./м.

Решение: Общая стоимость ограждения = Скорость ограждения × общая длина требуемого ограждения

Требуемая общая длина ограждения = Периметр сада

Периметр сада = сумма трех сторон

= 15 + 10 +11

= 36 M

Общая стоимость ограждения = 120 × 36

= RS 4320

Пример 2: дверь с размерами 4 м × 2 м. с размерами 11 м × 11 м. Каковы будут общие трудозатраты на покраску стены, если затраты на покраску 1 м ² стены составляют рупий. 2.50.

Решение: Общие трудозатраты = Скорость покраски × Площадь стены, подлежащей покраске

Площадь стены, подлежащей окраске = Площадь стены — Площадь двери

Площадь стены = 11 × 11 = 121 кв. м

Площадь двери = 4 × 2 = 8 кв. м

Площадь, подлежащая окраске = 121 — 8 = 113 квадратных метров

Общая стоимость покраски стены = 2,5 × 113

= рупий. 282.5

Учащиеся могут загрузить лист Math Formulas Class 7 для распечатки ниже:

Часто задаваемые вопросы по формулам периметра и площади 7 класса

Каковы важные формулы периметра и площади класса 7?

Важные формулы Периметра и Площади приведены ниже:

Периметр замкнутой фигуры — это общая длина ее границы, а площадь — это занимаемое ею пространство.
Периметр квадрата = 4 × сторона
Периметр прямоугольника = 2 × (длина + ширина)
Площадь квадрата = сторона × сторона
Площадь прямоугольника = длина × ширина
Площадь параллелограмма = основание × высота
Площадь треугольника = 1/2 × основание × высота
Расстояние вокруг круглой области называется ее окружностью.
Длина окружности = πd, d — диаметр, а π = 22/7 или 3,14

Каковы основные формулы периметра и площади класса 7?

Основные формулы периметра и площади 7 класса помогают в вычислении площади и периметра квадратов, прямоугольников, кругов, треугольников, параллелограммов. Они обобщены в этой статье вместе с некоторыми практическими советами, чтобы запомнить их.

Сколько формул содержится в формулах периметра и площади класса 7?

В этой статье приведены десять формул, связанных с периметром и площадью, которые помогают решить основные вопросы измерения. Знание этих формул необходимо, так как понятие измерения встречается в повседневной жизни.

Как запомнить формулы периметра и площади для класса 7?

Учащиеся могут легко запомнить формулы периметра и площади 7 класса с помощью следующих пунктов:

Поскольку наш мозг легко обрабатывает рукописную информацию, запись формул является одним из лучших способов их запоминания.
Как только учащиеся поймут логику формул, они должны просмотреть все решенные примеры в своем учебнике и попытаться решить их самостоятельно. Это откроет для них широкий спектр применений формул. После этого они должны попрактиковаться в решении задач, чтобы получить достаточно практики в решении задач.
Учащиеся могут загружать изображения формул и устанавливать их в качестве обоев на своих ноутбуках и мобильных устройствах. Это даст им возможность быстрого пересмотра всякий раз, когда они используют свое устройство.

Скачать БЕСПЛАТНЫЕ учебные материалы

Математические формулы для 7 класса

Площадь и периметр круга

Введение

Всякий раз, когда мы видим круглый предмет, такой как кольцо, баскетбольный мяч или дыня, мы ассоциируем его с формой круг. Что делает эту форму особенной? Как мы можем измерить его, если, в отличие от большинства форм, форма, которую мы имеем, круглая?

В этой статье мы изучим основные понятия, начиная с определения формы, затем мы будем количественно определять свойства круга, определяя его периметр, а затем его площадь. При этом мы также попробуем несколько примеров, которые помогут нам в обучении.

Что такое круг?

Круг по определению является идеально круглой формой .

С точки зрения геометрии, окружность образована набором равноудаленных точек из фиксированной точки, называемой его центром .

Линия, соединяющая центр с любой точкой дуги окружности, имеет длину, равную радиусу окружности. Диаметром окружности называется любая линия, проходящая через две точки окружности и ее центр.

Что такое периметр?

Мы определяем периметр двумерной формы как меру границы, окружающей его .

При интуитивном подходе мы можем связать идею периметра с тем, как далеко мы пробегаем круг в парке. Если мы начнем измерять расстояние от начала круга, а затем проследим замкнутый путь, пока не вернемся к начальной точке, мы сможем измерить периметр парка через круг, который мы пробежали:

Таким образом, для любой замкнутой формы мы можем получить ее периметр, взяв длину ребер, охватывающих фигуру.

Что такое площадь?

С другой стороны, мы можем определить площадь двумерной формы как меру пространства, которое она занимает в двумерной плоскости .

Интуитивно мы можем думать о формах на плоскости как об объектах в комнате. Каждый объект занимает определенное место в комнате, в зависимости от типа объекта и его размера. В этом смысле мы можем измерить площадь фигуры через ее размеры.

Что такое Пи?

Прежде чем мы приступим к вычислению периметра и площади круга, мы также введем специальное число, которое окажется полезным для наших вычислений позже.

Математическая константа pi , обозначаемая как , представляет собой число, которое связывает диаметр круга с его окружностью. Если мы измерим периметр круга и разделим его на меру диаметра, то получим приблизительное значение числа пи:

π≈3,1415926…

Важно отметить, что эта константа является неконечным иррациональным числом . Это означает, что точное десятичное значение числа пи представляет собой бесконечный поток чисел! Однако в большинстве случаев нам нужно только округлить значение до сотых:

π≈3,14

Периметр круга

Из определений, данных ранее, мы можем теперь подробно обсудить формулу для решения периметра круга. Сначала мы выведем базовую формулу, обеспечим интуитивное понимание, а затем покажем, как мы применяем эту формулу на нескольких примерах.

Вывод формулы периметра окружности

Мы знаем, что периметр можно определить как сумму длин всех ребер, охватывающих фигуру. В большинстве многоугольников мы принимаем это как сумму длин его сторон. Однако что происходит в случае круга без сторон? Проведем простой эксперимент, чтобы показать, как измеряется периметр круга:

Предположим, мы вырезаем круг диаметром один фут и отмечаем одну точку на краю выреза, как показано:

Далее прокатываем круг по прямой линии, начиная с отметки, пока он не завершит один цикл:

Если мы измеряем длину прямой линии, мы также измеряем периметр вырезанного круга.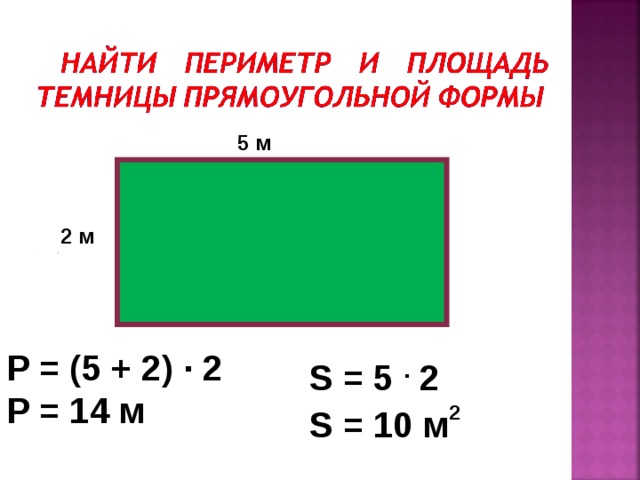 И в этом измерении мы получаем число, близкое к константе!

Теперь, если мы попробуем круги большего размера — для диаметра в два фута мы получим удвоенный периметр, для диаметра в три фута мы получим тройной периметр и так далее.

Таким образом, мы можем обобщить это наблюдение о периметре любого круга, диаметр которого задан:

Периметр=×Длина диаметра

Кроме того, мы можем описать диаметр круга как удвоенную длину его радиуса:

Длина диаметра=2×r

∴Длина диаметра=2r

Комбинируя эти выражения , тогда мы можем выразить периметр через радиус r:

Периметр=π×2r

Что такое формула периметра круга?

Из предыдущего вывода периметр P круга с известным радиусом r определяется как:

P=2πr

Если вместо радиуса задан диаметр d окружности, мы используем альтернативную формулу, которая выражается через диаметр:

P=πd

Отметим, что для обеих формул единица периметра выражается через тех же единиц , что и с данным радиусом/диаметром.

Как это используется?

Чтобы попрактиковаться в применении формулы, давайте вместе найдем периметр круга, показанного ниже:

Исходя из данного рисунка, радиус окружности равен 5 единицам. Следовательно, мы можем сказать, что:

r=5 единиц

Кроме того, поскольку радиус известен, мы можем использовать формулу периметра в терминах радиуса r:

P=2πr

Затем мы подставляем заданный радиус в по формуле вместе с приблизительным значением π≈3,14 получаем:

P=2×5 единиц×3,14

Затем, перемножая числа между собой, получаем периметр круга:

P=31,4 единицы

Тогда мы заключаем, что периметр круга равен 31,4 единицы. Эта величина выражается в тех же единицах, что и радиус.

Площадь круга

Следуя формуле периметра круга, мы также можем найти его площадь через заданный радиус или диаметр.

Что такое Формула площади круга?

Площадь A круга с известным радиусом r можно выразить по формуле:

A=πr ^{2 92$}

Это справедливо, поскольку длина радиуса окружности составляет половину длины диаметра окружности:

r=$\frac{d}{2}$

Заметим, что для обеих формул единиц измерения площадь выражается в виде квадратных единиц данного радиуса/диаметра.

Как это используется?

Опять же, мы применяем то, что мы узнали до сих пор, работая над тем же управляемым примером, что и раньше, но для нахождения площади круга:

Из данного рисунка нам дан радиус круга равный 5 единицам. Следовательно, мы можем сказать, что:

r=5 единиц

Кроме того, поскольку радиус известен, мы можем использовать формулу площади относительно радиуса r:

A=πr ²

заданный радиус в формулу вместе с приблизительным значением π≈3,14, чтобы получить:

A=3,14×(5 единиц) ²

После этого возьмем квадрат радиуса, чтобы получить:

A=3,14 ×25 шт. ²

Затем, перемножая числа вместе, мы получаем площадь круга:

A=78,5 единиц ²

Отсюда мы заключаем, что площадь круга составляет 78,5 единиц ² . Эта величина выражается в квадратах единиц радиуса.

Примеры решения задач

Теперь мы можем приступить к решению примеров задач, чтобы применить то, что мы уже узнали. Каждая проблема решает различные обсуждаемые формулы и ставит перед нами задачу решить ее с помощью предоставленной нам информации.

Периметр круга

Пример задачи 1:

Каков периметр круга, радиус которого равен 10 сантиметрам?

Решение:

Напомним, что периметр P окружности определяется формулой: значений в формулу:

P=2×3,14×10 см

Наконец, перемножая числа вместе, мы получаем значение периметра:

P=62,8 см

Отсюда делаем вывод, что периметр круга равен 62,8 см.

Пример задачи 2:

Предположим, у нас есть бублик, внешний диаметр которого составляет 6 дюймов, а отверстие имеет диаметр 1,5 дюйма. Решите следующее:

Каков внешний периметр пончика?
Каков его внутренний периметр?
Каков общий периметр пончика?

Решение:

Заметим, что вместо радиуса дан внешний диаметр бублика. Следовательно, мы можем использовать другую формулу для периметра P круга:

P _out =πd

. π=3,14:

P _out = 3,14×6 in

Наконец, мы умножаем два числа, чтобы получить значение периметра:

P _out = 18,84 in

Следовательно, внешний периметр пончика равен 18,84 дюйма.

Как и в части A, мы используем другую формулу для периметра P окружности:

P _in =πd

Подставляя заданный диаметр d=1,5 дюйма и приблизительное значение π=3,14, получаем :

P _в =3,14×1,5 в

Наконец, мы умножаем два числа, чтобы получить значение периметра:

P _в =4,71 в

Следовательно, внутренний периметр пончика равен 4,71. дюймы.

Мы получаем общий периметр PT пончика, складывая внешний и внутренний периметры пончика:

P _T =P _из +P _из

Подставляя вычисленные значения периметра из части A и часть B, мы имеем:

P _T = 18,84 дюйма + 4,71 дюйма

Наконец, сложив два числа, мы можем получить значение полного периметра:

P _T = 23,55 дюйма

Следовательно , общий периметр бублика составляет 23,55 дюйма.

Пример задачи 3:

Алекс хочет сделать подстаканник по индивидуальному заказу. Для этого ей нужно обернуть вокруг корпуса цилиндрической чашки пять колец из проволоки. Если чашка имеет диаметр 5,5 см, сколько проволоки ей нужно подготовить для подстаканника?

Решение:

Заметим, что радиус чашки равен r=5,5 см. Для заданного радиуса периметр P можно вычислить по формуле:

P=2πr

Следовательно, мы можем подставить данные значения с π≈3,14 в приведенное выше уравнение, чтобы получить:

P=2×3,14×5,5 см

Затем мы упростим уравнение, взяв произведение чисел вместе:

P =34,54 см

Таким образом, Алексу нужно 34,54 см на кольцо, чтобы обернуть чашку. Чтобы получить общую длину необходимой проволоки, умножаем вычисленный ранее периметр на количество необходимых ей колец:

P _T =34,54 см×5 колец=172,7 см

На общий периметр P _T составляет 172,7 см, тогда количество проволоки, необходимое Алексу для ее индивидуального подстаканника, также равно 172,7 см.

Площадь круга

Пример задачи 4:

Предположим, мы используем тот же круг из примера задачи 1, радиус которого равен 10 сантиметрам. Какова площадь круга?

Решение:

Напомним, что площадь круга A находится по формуле:

A=πr ²

При данном радиусе r=10 см и приблизительном значении π≈3,14 подставляем их в формулу, чтобы получить:

A=3,14×10 см ²

Получив квадрат радиуса, мы имеем:

A=3,14×100 см ²

Наконец, путем умножения трех чисел мы можем вычислить значение площади:

A=314 см ²

Следовательно, площадь круга 314 см ² .

Пример задачи 5:

Джули хочет заказать круглую 16-дюймовую овощную пиццу для своего соседа Кларка. Когда она пришла в пиццерию, ей предложили две 10-дюймовые пиццы по той же цене. Джулия хочет получить максимальную отдачу от своих денег. Получит ли она больше пиццы, если вместо этого воспользуется двумя пиццами меньшего размера?

Решение:

Сначала заметим, что нам задан диаметр обеих пицц. Для заданного диаметра d площадь круга A можно выразить по формуле:

92$

Затем находим площадь большей пиццы. Подставляя заданный диаметр d=16 дюймов и используя приблизительное значение π≈3,14, мы подставляем эти значения в формулу, чтобы получить:

A _{большой} =3,14×($\frac{16 in}{2}$ ) ²

Деля диаметр на два, упрощаем дробь внутри скобок. Заметим, что мы фактически получаем радиус окружности, используя заданный диаметр:

A _{большой} = 3,14×(8 дюймов) ²

Затем возьмем квадрат радиуса:

A _{большой} =3,14×64 дюйма ²

Таким образом, площадь большей пиццы можно получить, умножив числа:

A _{большая} = 200,96 дюйма ²

Далее мы приступаем к вычислению общей площади двух меньших пицц. Каждая 10-дюймовая пицца имеет площадь, равную:

A _{маленькая} =3,14×$(\frac{10 in}{2})$ ²

Повторяя те же шаги, что и для большей пиццы, мы упрощаем площадь каждой меньшей пиццы будет:

A _small =78.5 in ²

Taking the combined area of two pizzas, we add their areas together:

A _combined =78.5 in ² +78.5 in ²

∴A _вместе = 157 в ²

Наконец, мы сравним площадь большей пиццы и общую площадь пицц меньшего размера, предложенных Джули. Так как площадь большей пиццы составляет 200,96 дюймов ², а общая площадь меньших пицц составляет 157 дюймов ² , мы можем сказать, что объединенная площадь меньше, чем площадь большей пиццы:

A _вместе больше

Таким образом, мы заключаем, что Джули получит меньше пиццы , воспользовавшись двумя 10-дюймовые пиццы вместо одной 16-дюймовой пиццы.