2.1 Правила сложения — Информатика
Пример 3.16. Сложить двоичные числа 11012 и 110112. Запишем слагаемые в столбик и пронумеруем разряды, присвоив младшему разряду номер 1: номера разрядов: 5 4 3 2 1Процесс образования результата по разрядам описан ниже:
Таким образом: 1 1 0 1Проверим результат. Для этого определим полные значения слагаемых и результата: 11012 = 1*23 +1*22 + 0*21 + 1*20 = 8 + 4 + 1 = 13; 110112 = 1*24 + 1*23 + 0*22 + 1*21 + 1*20 = 16 + 8 + 2 + 1 = 27; 1010002 = 1*25 + 0*24 + 1*23 + 0*22 + 0*21 + 0*21 = 32 + 8 = 40. Поскольку 13 + 27 = 40, двоичное сложение выполнено верно. Пример 3.17. Сложить шестнадцатеричные числа 1С 16 и 7В16.
Таким образом:
1 СПроверим результат. Для этого определим полные значения слагаемых и результата: 1С16 = 1*161 + 12*160 = 16 + 12 = 28; 7В16 = 7*161 + 11*160 = 112 + 11 = 123; 9716 = 9*161 + 7*160 = 144 + 7 = 151. Поскольку 28 + 123 = 151, сложение выполнено верно. |
Правила сложения перемещений и скоростей при прямолинейном движении, абсолютная скорость при движении катера по реке
п.1. Правило сложения перемещений при прямолинейном движении
Рассмотрим движение катера по реке.
Можно говорить о движении катера как относительно реки, так и относительно берега.
При этом сама река также движется относительно берега.
Как было показано в §5 данного справочника, для описания движения необходимо указать тело отсчета и ввести связанную с ним систему отсчета.
Введем две системы отсчета.
Берег неподвижен. Назовем систему отсчета, связанную с берегом, неподвижной системой отсчета (НСО). Перемещение тела в НСО назовем абсолютным перемещением, \(\overrightarrow{r_a}.\)
Река подвижна. Назовем систему отсчета, связанную с рекой, подвижной системой отсчета (ПСО). Перемещение тела в ПСО назовем относительным перемещением, \(\overrightarrow{r_o}.\)
Перемещение реки относительно берега – это перемещение подвижной системы отсчета относительно неподвижной. Перемещение ПСО относительно НСО назовем переносным перемещением, \(\overrightarrow{r_п}.\)
Правило сложения перемещений
Абсолютное перемещение равно векторной сумме относительного и переносного перемещений: $$ \overrightarrow{r_a}=\overrightarrow{r_o}+ \overrightarrow{r_п} $$
Чтобы найти сумму двух векторов, нужно от конца первого вектора отложить второй вектор (см. §6 данного справочника).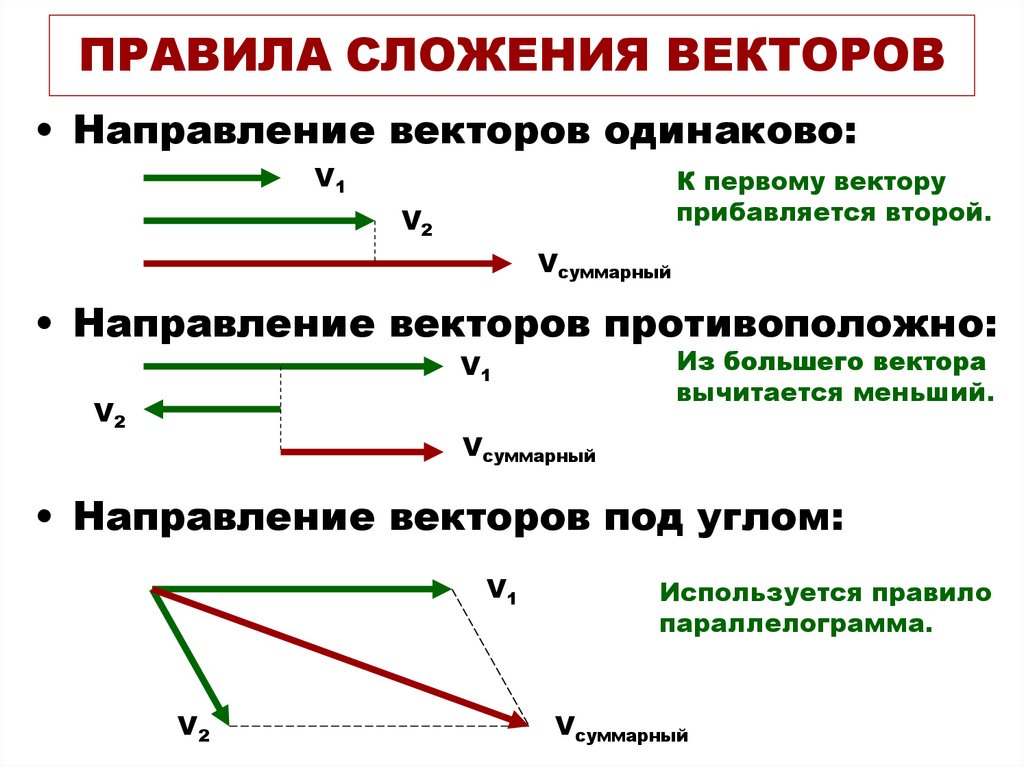
При прямолинейном движении все перемещения направлены вдоль одной прямой. В этом случае сумму векторов найти проще.
Пример: правило сложения перемещений при движении катера по реке
Пусть катер плывет по течению реки.
В этом случае векторы \(\overrightarrow{r_o}\) и \(\overrightarrow{r_п}\) направлены в одну сторону, и модуль абсолютного перемещения равен сумме модулей векторов-слагаемых:
$$ |\overrightarrow{r_a}|=|\overrightarrow{r_o}|+ |\overrightarrow{r_п}| $$
Теперь пусть катер плывет против течения.
В этом случае векторы \(\overrightarrow{r_o}\) и \(\overrightarrow{r_п}\) направлены в противоположные стороны, и модуль абсолютного перемещения равен разности модуля большего и модуля меньшего вектора:
$$ |\overrightarrow{r_a}|=|\overrightarrow{r_o}|- |\overrightarrow{r_п}| $$
п.2. Правило сложения скоростей при прямолинейном движении
Напомним, что:
Скорость – векторная величина, равная отношению перемещения ко времени, за которое это перемещение было совершено: $$ \overrightarrow{v}=\frac{\overrightarrow{r}}{t} $$
Тогда из закона сложения перемещений получаем: $$ \overrightarrow{r_a}=\overrightarrow{r_o} +\overrightarrow{r_п} \Rightarrow \frac{\overrightarrow{r_a}}{t}=\frac{\overrightarrow{r_o}}{t} +\frac{\overrightarrow{r_п}}{t}\Rightarrow \overrightarrow{v_a}=\overrightarrow{v_o} +\overrightarrow{v_п} $$
Правило сложения скоростей
Абсолютная скорость равна векторной сумме относительной и переносной скоростей: $$ \overrightarrow{v_a}=\overrightarrow{v_o} +\overrightarrow{v_п} $$
Если при описании движения выбрать направление координатной оси ОХ, то можно ввести проекции скоростей \(v_x\) (см.
§8 данного справочника) и получить еще одно очень полезное при решении задач правило сложения:
Правило сложения проекций скоростей при прямолинейном движении
Проекция абсолютной скорости на координатную ось ОХ равна сумме проекций относительной и переносной скоростей: $$ v_{ax}=v_{ox}+v_{пx} $$
п.3. Абсолютная скорость при движении катера по реке
Пусть собственная скорость катера (скорость относительно реки) равна \(v\), скорость течения (переносная скорость) равна \(u\).
Направим ось ОХ в направлении скорости катера, тогда её проекция будет положительной: \(v_{ox}=v\). Если катер плывет по течению, скорость течения также направлена по ОХ и её проекция положительна: \(v_{пx}=u\). Проекция абсолютной скорости равна сумме: $$ v_{ax}=v_{ox}+v_{пx}=v+u $$
Если катер плывет против течения, при сохранении направления оси OX скорость течения направлена противоположно и её проекция отрицательна: \(v_{пx}=-u\). Проекция абсолютной скорости равна разности $$ v_{ax}=v_{ox}+v_{пx}=v-u $$ Если \(v\gt u\), проекция абсолютной скорости положительна, \(v_{ax}\gt 0\), катер поднимается вверх по реке.
При недостаточной скорости катера \(v\lt u\), проекция абсолютной скорости отрицательна, \(v_{ax}\lt 0\). Катер не сможет подниматься вверх по реке, его будет сносить вниз.
Внимание!
При описании прямолинейного движения выбор направления оси ОХ, определение знаков проекций скоростей и перемещений важны для правильного хода решения задачи и объяснения полученных результатов.
Всегда помните: скорость и перемещение – это вектора, у которых есть не только величина, но и направление.
п.4. Задачи
Задача 1. По заданным векторам относительной и переносной скоростей найдите вектор абсолютной скорости. Какой путь пройдет тело в подвижной и неподвижной системе отсчета за 5 с?
a)
Вектор абсолютной скорости равен сумме векторов: \(\overrightarrow{v_a}=\overrightarrow{v_o} +\overrightarrow{v_п}\)
Находим сумму:
Пользуясь заданным масштабом, получаем:
\(\overrightarrow{v_o}=|\overrightarrow{v_o}|=4\ \text{м/с}\) — скорость тела в подвижной СО
\(\overrightarrow{v_a}=|\overrightarrow{v_a}|=3\ \text{м/с}\) — скорость тела в неподвижной СО
\(s_о=v_о t;\ \ s_о=4\cdot 5=20\ \text{м}\) — путь тела в подвижной СО
\(s_a=v_a t;\ \ s_a=3\cdot 5=15\ \text{м}\) — путь тела в неподвижной СО
Ответ: 20 м и 15 м
б)
Вектор абсолютной скорости равен сумме векторов: \(\overrightarrow{v_a}=\overrightarrow{v_o} +\overrightarrow{v_п}\)
Находим сумму:
Пользуясь заданным масштабом, получаем:
\(\overrightarrow{v_o}=|\overrightarrow{v_o}|=30\ \text{м/с}\) — скорость тела в подвижной СО
\(\overrightarrow{v_a}=|\overrightarrow{v_a}|=50\ \text{м/с}\) — скорость тела в неподвижной СО
Путь тела в разных СО:
\(s_о=v_о t;\ \ s_о=30\cdot 5=150\ \text{м}\) — путь тела в подвижной СО
\(s_a=v_a t;\ \ s_a=50\cdot 5=250\ \text{м}\) — путь тела в неподвижной СО
Ответ: 150 м и 250 м
Задача 2.
Между двумя катерами, которые движутся навстречу друг другу со скоростями 10 км/ч и 12 км/ч, летает альбатрос с постоянной скоростью 15 км/ч. Сколько километров он пролетит до момента встречи катеров, если первоначальное расстояние между ними равнялось 99 км.
Дано:
\(v_1=10\ \text{км/ч}\)
\(v_2=12\ \text{км/ч}\)
\(v=15\ \text{км/ч}\)
\(d=99\ \text{км}\)
_______________
\(s-?\)
Пусть первый катер – неподвижное тело отсчета. Тогда второй катер приближается к нему со скоростью, равной сумме скоростей \((v_1+v_2)\). Время, через которое катера встретятся: $$ t=\frac{d}{v_1+v_2} $$ За это время альбатрос пролетит расстояние: $$ s=vt=v\cdot\frac{d}{v_1+v_2}=\frac{v}{v_1+v_2}d $$ Подставляем: $$ s=\frac{15}{10+12}\cdot 99=67,5\ (\text{км}) $$ Ответ: 67,5 км
Задача 3. В подрывной технике используют бикфордов шнур, пламя по которому распространяется со скоростью 0,8 см/с. Какой длины шнур понадобится подрывнику, чтобы он успел отбежать на расстояние 300 м после того, как его подожжет?
Скорость бега равна 5 м/с.
Дано:
\(u=0,8\ \text{см/с}=0,008\ \text{м/с}\)
\(v=5\ \text{м/c}\)
\(s=300\ \text{м}\)
_______________
\(L-?\)
На чертеже объект, который нужно взорвать, находится в точке B. Подрывник находится в точке O и бежит в точку A, длина шнура L=OB, расстояние AB=s.
Скорости \(u\) и \(v\) направлены противоположно. Время, за которое шнур догорит и подрывник добежит, определяется суммой скоростей \((u+v)\): $$ t=\frac{s}{u+v} $$ Длина шнура определяется временем и скоростью сгорания: $$ L=tu=\frac{su}{u+v} $$ Подставляем: $$ L=\frac{300\cdot 0,008}{5+0,008}\approx 0,48\ (\text{м})=48\ (\text{см}) $$ Ответ: 48 см
Задача 4. Из городов A и B, расстояние между которыми d=9 км, одновременно навстречу друг другу выехало два велосипедиста. В направлении от 
Найдите скорость ветра \(v_0\) и скорость велосипедистов в безветренную погоду, если она у них одинакова.
Пусть \(v\) — скорость велосипедистов в тихую погоду.
Переведем время в часы: \begin{gather*} t_1=30\ \text{мин}=\frac{30}{60}\text{ч}=\frac12\text{ч}\\ t_2=45\ \text{мин}=\frac{45}{60}\text{ч}=\frac34\text{ч} \end{gather*} Составим таблицу:
| Скорость, км/ч | Время, ч | Расстояние, км | |
| 1й велосипедист, из А в Б | \(v+v_0\) | \(\frac12\) | \(\frac12(v+v_0)\) |
| 2й велосипедист, из Б в А | \(v-v_0\) | \(\frac34\) | \(\frac34(v-v_0)\) |
Расстояние: $$ d=\frac12(v+v_0)=\frac34(v-v_0)=9 $$ Получаем систему: $$ \begin{cases} \frac12(v+v_0)=9\\ \frac34(v-v_0)=9 \end{cases} \Rightarrow \begin{cases} v+v_0=9\cdot 2=18\\ v-v_0=9\cdot\frac43=12 \end{cases} \Rightarrow \begin{cases} 2v=18+12\\ 2v_0=18-12 \end{cases} \Rightarrow \begin{cases} v=\frac{30}{2}=15\\ v_0=\frac62=3 \end{cases} $$
Ответ:
Скорость ветра \(v_0=3\) км/ч
Скорость велосипедистов в тихую погоду \(v=15\) км/ч
Задача 5.
Катер проходит расстояние между двумя пристанями по течению реки за 2 ч, а против течения – за 4 ч. За какое время от одной пристани к другой проплывет плот?
Пусть \(v\) — скорость катера относительно реки (относительная скорость), \(u\) — скорость реки относительно берега (переносная скорость).
Составим таблицу:
| Скорость, км/ч | Время, ч | Расстояние, км | |
| Катер по течению | \(v+u\) | 2 | \(2(v+u)\) |
| Катер против течения | \(v-u\) | 4 | \(4(v-u)\) |
| Плот | \(u\) | \(t\) | \(s\) |
Расстояние во всех случаях одно и то же: $$ s=2(v+u)=4(v-u)\Rightarrow (v+u)=2(v-u)\Rightarrow u+2u=2v-v\Rightarrow 3u=v $$ Скорость катера в 3 раза больше скорости течения (скорости плота).
Тогда расстояние \(s=2(v+u)=2(3u+u)=8u\)
Время для плота: $$ t=\frac su=\frac{8u}{u}=8\ (\text{ч}) $$
Ответ: 8 ч
Задача 6*.
3}=\frac16\ \text{ч}=10\ \text{мин}\)
Второй корабль подбирает контейнеры каждые 10 мин.
Значит, в течение часа второй корабль подберет еще \(N=\frac{60\ \text{мин}}{10\ \text{мин}}=6\) контейнеров.
Ответ: 6 контейнеров
Задача 7*. Автомобиль, движущийся со скоростью 72 км/ч, был пробит пулей, летевшей перпендикулярно его движению. Отверстие в дальней стенке оказалось смещено относительно отверстия в ближней стенке на 4 см. Ширина салона 1,5 м. Считая, что пуля в салоне не изменила траекторию, определите её скорость.
Дано:
\(u=72\ \text{км/ч}=20\ \text{м/с}\)
\(d=4\ \text{cм}=0,04\ \text{м}\)
\(a=1,5\ \text{м}\)
_______________
\(v-?\)
Построим чертеж движения, вид сверху. Направим ось ОХ по движению автомобиля относительно земли, ось ОУ – по движению пули относительно земли.
Если перейти в систему отсчета, связанную с автомобилем, земля «побежит» в обратном направлении со скоростью \(–u\), и траектория пули в салоне сместится (пунктирная линия на чертеже).
Смещение на расстояние \(d\) за счет движения автомобиля происходит за время, в течение которого пуля пролетает от одной стенки салона к другой: $$ d=ut,\ \ t=\frac av $$ Откуда: $$ v=\frac ad u $$ Подставляем: $$ v=\frac{1,5}{0,04}\cdot 20=750\ (\text{м/с}) $$
Сложение целых чисел — правила, шаги
Сложение целых чисел — это процесс нахождения суммы двух или более целых чисел. Это может привести к увеличению или уменьшению значения, в зависимости от того, являются ли целые числа положительными или отрицательными или смесью. Сложение целых чисел — это арифметическая операция, выполняемая над целыми числами с одинаковым или разными знаками для нахождения суммы. Давайте узнаем больше о добавлении целых чисел в этой статье.
| 1. | Правила сложения целых чисел |
| 2. | Добавление целых чисел в числовую строку |
3. | Часто задаваемые вопросы о добавлении целых чисел |
Правила сложения целых чисел
Существуют определенные правила, которым необходимо следовать, чтобы сложить два или более целых числа. Целые числа — это полные числа, не имеющие дробных частей. Он включает в себя положительные целые числа, ноль и отрицательные целые числа. Правила сложения целых чисел приведены ниже:
- Сумма целого числа и его обратного сложения равна 0.
- Сложение двух положительных целых чисел всегда приводит к положительному значению, которое больше обоих целых чисел.
- Сложение двух отрицательных целых чисел всегда приводит к отрицательному числу, которое меньше заданных чисел.
- Сложение положительного числа с отрицательным выполняется путем нахождения разницы между абсолютным значением обоих чисел. Затем к сумме присоединяется знак с большим числом.
- Сложение целых чисел с 0 приводит к тому же числу.
Правила сложения целых чисел можно понять с помощью приведенной ниже таблицы.
Сложение целых чисел с одинаковым знаком
Когда мы складываем два целых числа с одинаковым знаком, мы складываем их абсолютные значения и присоединяем к сумме общий знак. Например, 2 + 3 = 5, (-2) + (-3) = — (2 + 3) = -5. Абсолютное значение числа — это положительное значение данного числа. Например, абсолютное значение 6 равно 6, абсолютное значение -6 равно 6 и так далее. Ниже приведены некоторые примеры сложения целых чисел с одинаковым знаком:
- (-1) + (-9) = — (1 + 9) = -10
- 3 + 8 = 11
- (-2) + (-17) = — (2 + 17) = -19
Воспользуйтесь онлайн-калькулятором Cuemath для сложения целых чисел, чтобы проверить эти ответы.
Сложение целых чисел с разными знаками
Сложение двух целых чисел с разными знаками выполняется путем вычитания абсолютных значений и последующего присоединения знака числа с большим абсолютным значением.
Например, если мы хотим сложить -2 и 3, сначала мы найдем абсолютные значения обоих. Абсолютное значение -2 равно 2, а 3 равно 3. Теперь найдите разницу между этими абсолютными значениями, которая равна 3 — 2 = 1. Поскольку 3 > 2, а 3 имеет положительный знак, знак результирующего числа будет положительным. Следовательно, — 2 + 3 = 1,
Добавление целых чисел в числовую строку
Сложение целых чисел в числовой строке основано на данных принципах:
- Добавление положительного числа осуществляется перемещением к правой стороне (или положительной стороне) числовой строки.
- Добавление отрицательного целого числа выполняется перемещением к левой стороне (или отрицательной стороне) числовой строки.
- Любое из заданных целых чисел принимается за исходную точку, с которой мы начинаем движение по числовой прямой.
Теперь давайте научимся складывать целые числа в числовой строке.
- Шаг 1: Первым шагом является выбор шкалы на числовой прямой. Например, хотим ли мы отображать числа, кратные 1, 5, 10, 50 и т. д., зависит от заданных целых чисел. Например, если нам нужно сложить 10 и -30, мы можем взять шкалу 10 на числовой прямой, чтобы упростить нашу работу.
- Шаг 2: Если нам нужно добавить -2 и 7, мы можем взять шкалу счета чисел, начиная с 1.
- Шаг 3: Следующим шагом является поиск любого целого числа в числовой строке, предпочтительно числа с большим абсолютным значением. Например, если нам нужно сложить 2 и 19, будет лучше, если мы сначала найдем 19 на линии, а затем сделаем 2 прыжка вправо, а не найдем 2, а затем сделаем 19 прыжков.
- Шаг 4: Последним шагом является прибавление второго целого числа к числу, расположенному на предыдущем шаге, с помощью прыжков либо влево, либо вправо, в зависимости от того, положительное это число или отрицательное.
Например, хотим ли мы отображать числа, кратные 1, 5, 10, 50 и т. д., зависит от заданных целых чисел. Например, если нам нужно сложить 10 и -30, мы можем взять шкалу 10 на числовой прямой, чтобы упростить нашу работу. Давайте рассмотрим пример, чтобы лучше понять сложение целых чисел в числовой строке.
Пример: Используйте числовую строку и добавьте следующие целые числа: 5 + (-10)
Решение: Поскольку нам нужно добавить отрицательное число (-10), мы будем двигаться влево по числу линия. Начиная с 5, мы сделаем 10 шагов влево, что приведет нас к -5.
☛ Похожие темы
- Целочисленные формулы
- Сложение и вычитание целых чисел
- Умножение и деление целых чисел
Сложение целых чисел Примеры
Пример 1: Сложите следующие целые числа, используя правила сложения целых чисел.
4 + (-6) + 13
Решение: Даны три целых числа. Итак, сначала давайте сложим оба положительных целых числа 4 и 13, что даст нам 17. Теперь у нас осталось следующее выражение 17 + (-6). Здесь мы должны применить правило сложения отрицательного и положительного целых чисел. Получаем 17 + (-6) = 11. Следовательно, 11 — это результат данных целых чисел.
Пример 2: Используя правила сложения целых чисел, найдите, какое число нужно вычесть из 13, чтобы получить -10 в качестве ответа?
Решение: Пусть x нужно вычесть из 13, чтобы получить -10. Итак, мы можем составить уравнение относительно х.
13 — х = -10
— х = -10 — 23
х = -23
х = 23
Следовательно, 23 нужно вычесть из 13, чтобы получить -10.
Пример 3: Сложите следующие целые числа: -2 и -9.
Решение: При сложении целых чисел с одинаковым знаком складываем их абсолютные значения и присоединяем к ответу общий знак слагаемых.
-2 + (-9) = — (2 + 9) = -11
Следовательно, сумма -2 и -9 равна -11.
перейти к слайдуперейти к слайдуперейти к слайду
Разбивайте сложные концепции с помощью простых визуальных средств.
Математика больше не будет сложным предметом, особенно когда вы понимаете концепции с помощью визуализаций.
Записаться на бесплатный пробный урок
Практические вопросы по сложению целых чисел
перейти к слайдуперейти к слайду
Часто задаваемые вопросы о добавлении целых чисел
Что такое сложение целых чисел?
Сложение целых чисел означает, что мы находим сумму целых чисел. Поскольку целые числа включают положительные числа, отрицательные числа и ноль, их добавление может привести к увеличению или уменьшению значения. Это зависит от того, являются ли целые числа положительными или отрицательными. Например, 5 + 6 = 11, и 5 + (-6) = -1, и -5 + 0 = -5
Каковы правила сложения целых чисел?
Ниже перечислены правила сложения целых чисел:
- Сумма целого числа и его обратной аддитивной величины равна 0. Например, 6 + (-6) = 0
- Сложение двух положительных целых чисел всегда приводит к положительному значению, которое больше обоих целых чисел. Например, 6 + 6 = 12 .
- Сложение двух отрицательных целых чисел всегда приводит к отрицательному числу, которое меньше заданных чисел. Например, -6 + (-6) = -12
- Сложение положительного числа с отрицательным выполняется путем нахождения разницы между абсолютным значением обоих чисел. Затем к сумме присоединяется знак с большим числом. Например, +6 — 2 = +4
- Сложение целых чисел с 0 приводит к тому же числу. Например, 6 + 0 = 6 или -6 + 0 = -6 .
Каково правило сложения целых чисел с разными знаками?
Для сложения целых чисел с разными знаками мы следуем шагам, указанным ниже. Складываем 5 и (-8)
- Шаг 1: Найдите абсолютные значения заданных целых чисел. Это означает, что это будет 5 и 8.
- Шаг 2: Найдите разницу между абсолютными значениями, найденными на шаге 1. Разница между 5 и 8 равна 3.
- Шаг 3: Прикрепите знак числа с большим абсолютным значением. Так как 8 имеет отрицательный знак, ответ также будет иметь отрицательный знак. Это означает, что 5 + (-8) = -3
Это означает, что 5 + (-8) = -3Каково правило сложения целых чисел с одинаковым знаком?
Чтобы сложить целые числа с одинаковым знаком, мы складываем абсолютные значения чисел, а затем присоединяем общий знак к окончательному ответу. Например, (-9) + (-3) = -12.
Как вычитание целых чисел связано со сложением целых чисел?
Вычитание целых чисел связано со сложением целых чисел, потому что, когда мы складываем два целых числа с разными знаками, мы находим их абсолютные значения, а затем находим их разницу. Это означает, что мы используем вычитание при сложении целых чисел с разными знаками. Кроме того, сложение и вычитание являются обратными операциями. Это означает, что каждое выражение сложения может быть выражено вычитанием и наоборот. Вычитание целых чисел связано со сложением целых чисел, потому что оба они могут быть выражены в форме друг друга. Например, мы можем написать 2 + (-9) как 2 — 9. Точно так же мы можем записать — 3 — 5 как -3 + (-5).
Каковы шаги для сложения целых чисел?
Шаги для сложения целых чисел приведены ниже:
- Найдите абсолютные значения заданных чисел.
- Если оба числа одного знака, то сложите значения. Присоедините общий знак к ответу.
- Если они имеют разные знаки, то вычтите их и найдите разницу между абсолютными значениями. Тогда к окончательному ответу будет присоединен знак целого числа с большим абсолютным значением.
Каков пример сложения целых чисел?
Ниже приведены некоторые примеры сложения целых чисел:
- 3 + 8 = 11
- (-9) + (-4) = -13
- -6 + 4 = -2
- 12 + (-8) = 4
Что такое элемент идентификации для сложения целых чисел?
Элемент идентификации для сложения целых чисел равен нулю (0). Это связано с тем, что при добавлении 0 к любому целому числу получается само число. Например, 0 + 56 = 56 или 0 + (-7) = -7
Скачать БЕСПЛАТНЫЕ учебные материалы
Сложение целых чисел.
Рабочие листы
Сложение и вычитание целых чисел
Сложение и вычитание целых чисел — это две операции, которые мы выполняем над целыми числами для увеличения или уменьшения их значений. Целые числа включают целые числа и отрицательные числа, такие как 4, 5, 0, -9, -18 и так далее. Каждое число, изображенное на числовой прямой, не имеющее дробной части, является целым числом. Давайте узнаем больше о сложении и вычитании целых чисел.
| 1. | Что такое сложение и вычитание целых чисел? |
| 2. | Правила сложения и вычитания целых чисел |
| 3. | Сложение целых чисел |
| 4. | Вычитание целых чисел |
| 5. | Часто задаваемые вопросы о сложении и вычитании целых чисел |
Что такое сложение и вычитание целых чисел?
Сложение и вычитание целых чисел означает выполнение операций сложения и вычитания над двумя или более целыми числами путем помещения между ними оператора сложения и вычитания.
Целые числа — это те числа, которые не имеют десятичной или дробной части. Они включают в себя положительные и отрицательные числа, а также ноль. Целое число является полным объектом. Как и целые числа, мы можем складывать или вычитать целые числа.
Прежде чем углубиться в концепцию, очень важно узнать, что такое абсолютное значение целого числа. На числовой прямой расстояние числа от 0 называется абсолютным значением целого числа. Сложение и вычитание целых чисел лучше всего можно продемонстрировать на числовой прямой, хотя работа с числовой строкой требует времени. Итак, лучше выучить все правила сложения и вычитания целых чисел.
Правила сложения и вычитания целых чисел
Правила сложения и вычитания целых чисел помогают нам легко решать математические задачи. Давайте узнаем об этих правилах в следующем разделе.
Правила сложения целых чисел
В следующей таблице показаны правила сложения целых чисел.
| Правило | Пояснение | Примеры | |
|---|---|---|---|
| Сложение двух положительных чисел | (+а)+(+б) = (а+б) | При сложении двух положительных чисел мы просто складываем оба числа и получаем ответ, который является положительным значением, как при сложении целых чисел. | 3+4=7
|
| Сложение положительного числа и отрицательного числа | (а+(-б)) = (а-б) | При сложении положительного и отрицательного числа мы берем разность абсолютных значений обоих чисел и присоединяем к ответу знак большего числа. | 4+(-5)=(-1)
|
| Сложение двух отрицательных чисел | (-а)+(-б) = -(а+б) | При сложении двух отрицательных чисел мы берем сумму обоих чисел и прикрепляем к ответу знак минус. | (-2)+(-4)=(-6)
|
Правила вычитания целых чисел
Мы знаем, что сложение и вычитание являются обратными операциями. Таким образом, факт вычитания можно записать как факт сложения. Например, 2-4 = 2 + (-4) и 6-3 = 6 + (-3) или -4-3 = -4 + (-3)
Другими словами, вычитание целых чисел — это осуществляется изменением знака вычитаемого. После этого шага мы можем просто применить правила сложения целых чисел.
Это означает, что если оба числа имеют один и тот же знак, то мы добавляем абсолютные значения и присоединяем общий знак. Если оба числа разного знака, то находим разность абсолютных чисел и подставляем в результат знак большего числа.
В следующей таблице показаны правила вычитания, чтобы облегчить наши вычисления при работе с целыми числами.
| Правило | Пояснение | Примеры | |
|---|---|---|---|
| Вычитание двух положительных чисел | (+а)-(+б)=а + (-б) | Факт вычитания может быть изменен на факт сложения, и знак вычитаемого должен быть изменен на противоположный. Затем мы можем использовать правила сложения целых чисел. Находим разность абсолютных значений обоих чисел и сохраняем при ответе знак большего числа. Например, +3 — (+4) = +3 + (-4) = -1 | 3-4=-1
|
| Вычитание положительного числа и отрицательного числа | a-(-b)=a + (+b) или -a-(+b) =-a + (-b)
| Факт вычитания может быть изменен на факт сложения, и знак вычитаемого должен быть изменен на противоположный. Тогда мы можем использовать правило сложения целых чисел. Например, 4-(-5) можно записать как 4 + (+5), а затем решить; аналогично, -6 — (+4) можно записать как -6 + (-4), и тогда его можно решить. | 4-(-5)=9
|
| Вычитание двух отрицательных чисел | (-а)-(-б)= -а + (+б) | Факт вычитания может быть записан как факт сложения, и знак вычитаемого необходимо поменять местами. Например, -2 — (-4) можно записать как -2 + (+4) и тогда можно применить правило сложения целых чисел. Это приведет к -2 + (+4) = 2. | (-2)-(-4)=2
|
Сложение целых чисел
Добавление обычно означает увеличение значения. Однако в случае целых чисел операция сложения может привести к увеличению или уменьшению значения данного числа. Давайте разберемся в этом на примере, используя приведенные выше правила.
Пример: У Салли было 3 шарика.
Она получила еще 4 от своего брата. Сколько шариков у нее сейчас?
Решение:
У Салли было 3 шарика, и еще 4 она получила от своего брата. Итак, теперь у нее (3 + 4 = 7) шариков.
Это означает, что количество шариков увеличилось, потому что нам пришлось складывать положительные числа.
Сложение целых чисел в числовой строке
Нам необходимо помнить следующие правила сложения целых чисел в числовой строке.
- Добавляя отрицательное число, мы движемся к левой стороне числовой строки.
- При добавлении положительного числа мы движемся к правой стороне числовой строки.
Теперь давайте рассмотрим пример, в котором нам нужно сложить отрицательные и положительные числа с помощью числовой строки.
Пример: Температура в городе была -4° С. Она увеличилась на 5 º С. Какая сейчас температура?
Решение: Температура в городе увеличилась на 5°, стало быть (-4 + 5 = 1°).
Обратите внимание на числовую строку, приведенную ниже, которая показывает, как мы добавили отрицательное и положительное число. Когда мы добавляем положительное число в числовую прямую, мы всегда движемся вправо, здесь мы переместились на 5 шагов вправо от -4 и получили 1. Это означает -4 + 5 = 1
Следует отметить, что когда мы добавляем отрицательное число, мы движемся к левой стороне числовой строки. Вспомним все правила сложения целых чисел, используя следующие числовые строки.
Вычитание целых чисел
Вычитание обычно означает уменьшение значения. Однако в случае целых чисел операция вычитания может привести к увеличению или уменьшению значения данного числа. При вычитании целых чисел необходимо помнить следующие правила.
- Каждый факт вычитания может быть записан как факт сложения.
- Затем нам нужно поменять знак второго числа, которое является вычитаемым. Например, -8 — (-2) = -8 + (+ 2) = -6
Вычитание целых чисел из числовой строки
Нам необходимо запомнить следующие правила вычитания целых чисел из числовой строки.
- После того, как мы изменим факт вычитания на факт сложения, операция изменится на сложение, поэтому мы можем следовать тем же правилам сложения целых чисел в числовой строке.
- Следует помнить, что при добавлении отрицательного числа мы движемся к левой стороне числовой строки, а при добавлении положительного числа — к правой стороне числовой строки.
Давайте разберемся в этом на примере с числовой линией.
Пример: Вычесть -7 — (-4)
Решение:
Обратите внимание на числовую строку, приведенную ниже, чтобы понять шаги.
- Поскольку каждый факт вычитания может быть записан как факт сложения, мы меняем знак вычитания на знак сложения и меняем знак вычитаемого. Здесь -7 — (-4) = -7 + 4
- При добавлении положительного числа мы движемся к правой стороне числовой строки. В этом случае мы будем двигаться вправо и дойдем до -3 .
- При сложении целых чисел, когда знаки совпадают, складываем целые числа и сохраняем тот же знак. Например, 4 + 5 = 9. Если знаки разные, вычтите целые числа и сохраните знак большего абсолютного значения. Например, 11 + (-2) = 9
- При вычитании целых чисел заменить знак вычитания на знак сложения и поменять знак второго числа на противоположный. Например, 6 — (- 9) = 6 + (+9) = 15.
- Если рядом с числом нет знака, мы считаем его положительным числом. Например, 2 можно переписать как +2.
- Каждый факт вычитания может быть переписан как факт сложения. Например, 9-10 можно переписать как 9+(-10).
- В выражении всегда пишите отрицательные числа в квадратных скобках.
- При добавлении отрицательного числа мы движемся к левой стороне числовой строки.
- При добавлении положительного числа мы движемся к правой стороне числовой строки.
Например, 4 + 5 = 9. Если знаки разные, вычтите целые числа и сохраните знак большего абсолютного значения. Например, 11 + (-2) = 9☛ Похожие темы
- Умножение и деление целых чисел
- Калькулятор целых чисел
- Калькулятор вычитания целых чисел
- Калькулятор умножения целых чисел
- Калькулятор вычитания целых чисел
Часто задаваемые вопросы о сложении и вычитании целых чисел
Каковы правила сложения положительных и отрицательных целых чисел?
Правило сложения положительных и отрицательных целых чисел гласит, что нам нужно найти разницу между абсолютным значением двух целых чисел, и тогда знак результата будет таким же, как у большего целого числа из двух.
Например, если нам нужно сложить 5 + (-9), мы найдем разницу между 5 и 9что 9 — 5 = 4, и мы сохраним знак большего числа. В этом случае большее число равно 9, что имеет отрицательный знак, поэтому наш результат также будет иметь отрицательный знак, и ответ будет 5 + (-9) = -4.
Каково правило сложения и вычитания отрицательных чисел?
- К прибавляем два отрицательных числа, берём сумму обоих чисел и к ответу присоединяем знак минус.
- Пока вычитает два отрицательных числа, нам просто нужно помнить, что факт вычитания может быть записан как факт сложения, и знак вычитаемого должен быть изменен на противоположный. Например, -8 — (-4) можно записать как -8 + (+4) и тогда можно применить правило сложения целых чисел. Это приведет к -8 + (+4) = -4.
Как складывать и вычитать целые числа?
Сложение и вычитание целых чисел можно выполнять, следуя приведенным ниже правилам.
- При сложении двух положительных чисел мы просто складываем оба числа и получаем ответ, который является положительным значением, как при сложении целых чисел. Например, (+3 + (+4) = 7
- При сложении положительного и отрицательного числа мы берем разность абсолютных значений обоих чисел и присоединяем к ответу знак большего числа. Например, 6 + (-2) = 4
- При сложении двух отрицательных чисел мы берем сумму обоих чисел и прикрепляем к ответу знак минус. Например, (-5) + (-3) = -8
- Для вычитания целых чисел мы можем изменить факт вычитания на факт сложения и поменять знак вычитаемого. После того, как выражение изменится на сложение, мы можем применить правила сложения целых чисел и решить выражение. Например, 9 — (+3) = 9 + (-3) = 6
Например, (+3 + (+4) = 7Как складывать и вычитать целые числа с разными знаками?
Чтобы складывать и вычитать целые числа с разными знаками, у нас есть определенный набор правил.
- При сложении положительного и отрицательного числа мы берем разность абсолютных значений обоих чисел и присоединяем к ответу знак большего числа. Например, 6 + (-7) = (-1)
- При вычитании положительного и отрицательного числа мы меняем факт вычитания на факт сложения, а затем меняем знак вычитаемого. После этого воспользуемся тем же правилом сложения целых чисел и решим выражение. Например, (-6)-8 = -6 -(+8) = -6 + (-8) = -14
После этого воспользуемся тем же правилом сложения целых чисел и решим выражение. Например, (-6)-8 = -6 -(+8) = -6 + (-8) = -14Как складывать и вычитать целые числа в числовой строке?
Чтобы складывать и вычитать целые числа на числовой прямой, у нас есть определенный набор правил.
- Если нам нужно прибавить положительное число к другому положительному числу, мы начинаем с первого числа и двигаемся вправо от числовой строки. Следует отметить, что когда мы добавляем отрицательное число, мы движемся к левой стороне числовой строки.
- Если нам нужно вычесть положительное число, мы можем изменить факт вычитания на факт сложения и поменять знак вычитаемого. После того, как выражение изменится на сложение, мы можем применить приведенные выше правила сложения.
Каковы применения целых чисел?
Применение положительных и отрицательных чисел в реальном мире отличается. Обычно они используются для обозначения двух противоречащих друг другу ситуаций.