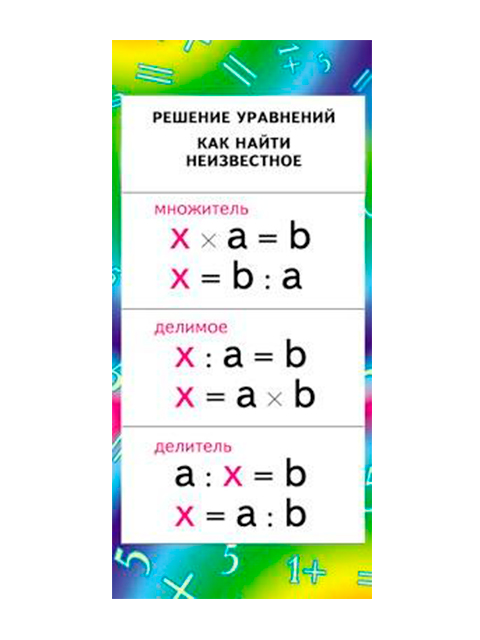
Корень уравнения. Правила решения уравнений
Похожие презентации:
Элементы комбинаторики ( 9-11 классы)
Применение производной в науке и в жизни
Проект по математике «Математика вокруг нас. Узоры и орнаменты на посуде»
Знакомство детей с математическими знаками и монетами
Тренажёр по математике «Собираем урожай». Счет в пределах 10
Методы обработки экспериментальных данных
Лекция 6. Корреляционный и регрессионный анализ
Решение задач обязательной части ОГЭ по геометрии
Дифференциальные уравнения
Подготовка к ЕГЭ по математике. Базовый уровень Сложные задачи
5 класс.
Шарабарина Галина Гавриловна – учитель математики
МОУ «Солоновская средняя общеобразовательная школа
имени Матренина А.П.
Ну-ка, проверь дружок,
Ты готов начать урок?
Всё ль на месте,
Всё ль в порядке,
Ручка, книжка и тетрадка?
Все ли правильно сидят?
Все ль внимательно глядят?
Каждый хочет получать
Только лишь оценку пять.
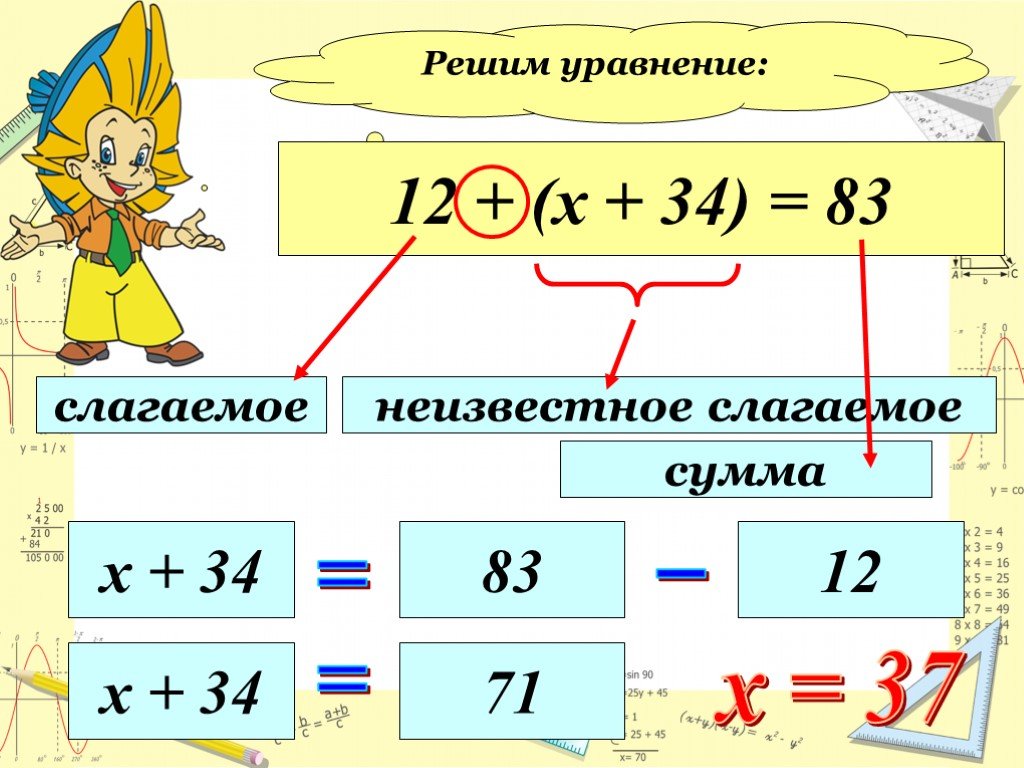
3. Вычислите :
4. Найдите корень уравнения
Задача.В корзине было несколько грибов.
После того как в неё положили ещё
27 грибов, их стало 75.
Сколько грибов было в корзине?
х = 48
Я приглашаю вас
Выполнить вместе со
мной следующие
упражнения
Раз, два — хлопок в ладоши,
А потом на каждый счет.
Раз, два, три, четыре –
Руки выше, плечи шире.
Раз, два, три, четыре, пять,
Надо нам присесть и встать.
Руки вытянуть пошире.
Раз, два, три, четыре, пять.
Наклониться — три, четыре,
И на месте поскакать.
На носки, затем на пятки.
Лень отбросить и опять.
Сесть за парту, взять тетрадку,
Уравнения решать.
10. Чтобы решать уравнения надо:
Заменять уравнениеравенством
Знать правила. Как найти
неизвестное слагаемое,
уменьшаемое,
вычитаемое.
Знать компоненты при
сложении и вычитании.
Надо помнить, что
уменьшаемое самое
большое число при
вычитании – значит
находить его –
сложением!
А вычитаемое – вычитай
и слагаемое – вычитай!
х+67 = 124
х = 124 – 67
у – 52 = 76
У = 76 +52
3+2=5
так как 3 = 5 – 2
5–2=3
так как 5 = 3 + 2
87 – р = 56
5–2=3
Р = 87 — 56
так как 2 = 5 — 3
Подумайте о своей работе на уроке и
попробуйте ее оценить.
солнышко –
старался, все получалось;
солнышко, прикрытое тучкой –
старался, но не все получалось;
тучка –
не старался.
12. Лист самоконтроля
Устный счетпримеры
правила
Решение
уравнений
Решение задач
№373 а
№373б
№373г
Составление
задач
Решение уравнений
№372 б
№372 д
№372 е
Самооценка на данном уроке:
№375
Автором рисунков к задаче является Савченко Е.М.
http://www.it-n.ru/profil.aspx?cat_no=692&d_no=9658&all=1
5,6 слайд из презентации Каратановой Марины Николаевны,
МОУ СОШ №256, г.Фокино.
Электронная физминутка для глаз. Галкина Инна Анатольевна, учитель
начальных классов
МОУ «Водоватовская СОШ» Арзамасского района,
Нижегородской области
English Русский Правила
Математика. Ее содержание, методы и значение. Том 1
Математика. Ее содержание, методы и значение. Том 1
ОглавлениеПРЕДИСЛОВИЕГлава I. ОБЩИЙ ВЗГЛЯД НА МАТЕМАТИКУ § 1. ОСОБЕННОСТИ МАТЕМАТИКИ § 2.  АРИФМЕТИКА§ 3. ГЕОМЕТРИЯ § 4. АРИФМЕТИКА И ГЕОМЕТРИЯ § 5. ЭПОХА ЭЛЕМЕНТАРНОЙ МАТЕМАТИКИ § 6. МАТЕМАТИКА ПЕРЕМЕННЫХ ВЕЛИЧИН § 7. СОВРЕМЕННАЯ МАТЕМАТИКА § 8. СУЩНОСТЬ МАТЕМАТИКИ § 9. ЗАКОНОМЕРНОСТИ РАЗВИТИЯ МАТЕМАТИКИ Глава II. АНАЛИЗ § 2. ФУНКЦИЯ Графики функций. § 3. ПРЕДЕЛ § 4 НЕПРЕРЫВНЫЕ ФУНКЦИИ § 5. ПРОИЗВОДНАЯ Примеры вычисления производных. § 6. ПРАВИЛА ДИФФЕРЕНЦИРОВАНИЯ Производная суммы. Производная произведения. Производная частного. Производная обратной функции. Таблица производных. Нахождение производной функции от функции. § 7. МАКСИМУМ И МИНИМУМ. ИССЛЕДОВАНИЕ ГРАФИКОВ ФУНКЦИЙ Отыскание наибольших и наименьших значений функции. Производные высших порядков. Смысл второй производной. Выпуклость и вогнутость. Признаки максимумов и минимумов. Исследование графиков функций. § 8. ПРИРАЩЕНИЕ И ДИФФЕРЕНЦИАЛ ФУНКЦИИ Теорема о среднем и примеры ее применения. § 9. ФОРМУЛА ТЕЙЛОРА Формула Тейлора.  Ряд Тейлора. § 10. ИНТЕГРАЛ Определенный интеграл. Связь дифференциального и интегрального исчисления. § 11. НЕОПРЕДЕЛЕННЫЕ ИНТЕГРАЛЫ. ТЕХНИКА ИНТЕГРИРОВАНИЯ § 12. ФУНКЦИИ МНОГИХ ПЕРЕМЕННЫХ Неявное задание функции. Геометрическое изображение. Частные производные и дифференциал. Дифференцирование неявных функций. Задачи на максимум и минимум. Формула Тейлора. Относительный максимум и минимум. § 13. ОБОБЩЕНИЯ ПОНЯТИЯ ИНТЕГРАЛА Контурные и поверхностные интегралы. Формула Остроградского. § 16. РЯДЫ Сходимость ряда. Ряды функций. Равномерно сходящиеся ряды. Глава III. АНАЛИТИЧЕСКАЯ ГЕОМЕТРИЯ § 2. ДВЕ ОСНОВНЫЕ ИДЕИ ДЕКАРТА Идея сопоставления уравнениям с двумя неизвестными линий на плоскости. Основные задачи, решаемые аналитической геометрией, и определение аналитической геометрии. § 3. ПРОСТЕЙШИЕ ЗАДАЧИ Площадь треугольника. Отыскание точек пересечения двух линий. § 4.  2.§ 6. ОБЩАЯ ТЕОРИЯ ДИАМЕТРОВ НЬЮТОНА § 7. ЭЛЛИПС, ГИПЕРБОЛА И ПАРАБОЛА Уравнение эллипса и его фокальное свойство. Законы движения планет. Эллипс инерции. Гипербола и ее фокальное свойство. Парабола и ее директрисса. Свойство касательной к параболе. Директриссы эллипса и гиперболы. Конические сечения. Парабола как график пропорциональности квадрату и гипербола как график обратной пропорциональности. § 8. ПРИВЕДЕНИЕ ОБЩЕГО УРАВНЕНИЯ 2-Й СТЕПЕНИ К КАНОНИЧЕСКОМУ ВИДУ Формулы преобразования координат. Приведение любого уравнения 2-й степени к одному из 9 канонических видов. § 9. ЗАДАНИЕ СИЛ, СКОРОСТЕЙ И УСКОРЕНИЙ ТРОЙКАМИ ЧИСЕЛ. ТЕОРИЯ ВЕКТОРОВ Арифметизация сил, скоростей и ускорений, введенная Лагранжей. Алгебра векторов. Скалярное произведение и его свойства. § 10. АНАЛИТИЧЕСКАЯ ГЕОМЕТРИЯ В ПРОСТРАНСТВЕ. УРАВНЕНИЕ ПОВЕРХНОСТИ В ПРОСТРАНСТВЕ И УРАВНЕНИЯ ЛИНИИ Уравнение плоскости и уравнения прямой. Общее уравнение 2-й степени с тремя переменными и 17 его канонических видов.  Эллипсоид. Гиперболоиды и конус 2-го порядка. Параболоиды. § 11. ПРЕОБРАЗОВАНИЯ АФФИННЫЕ И ОРТОГОНАЛЬНЫЕ Эллипс как результат «сжатия» окружности. Пример решения более сложной задачи. Важнейшие применения аффинных преобразований Формулы аффинных преобразований. Ортогональные преобразования. § 13. ПРОЕКТИВНАЯ ГЕОМЕТРИЯ Применение основной теоремы плоской перспективы в аэрофотосъемке. Проективная плоскость. Проективные отображения; основная теорема. Проективная геометрия. Запись проективных преобразований формулами. § 14. ПРЕОБРАЗОВАНИЯ ЛОРЕНЦА Проективные преобразования круга в себя. ЗАКЛЮЧЕНИЕ Глава IV. АЛГЕБРА (ТЕОРИЯ АЛГЕБРАИЧЕСКОГО УРАВНЕНИЯ) § 2. АЛГЕБРАИЧЕСКОЕ РЕШЕНИЕ УРАВНЕНИЯ Разложение многочлена на множители и формулы Виета. Теорема о симметрических многочленах. Работы Лагранжа. Открытие Абеля. Теория Галуа. Приложение теории Галуа к вопросу о разрешимости геометрической задачи циркулем и линейкой.  Две основные нерешенные задачи, связанные с теорией Галуа. § 3. ОСНОВНАЯ ТЕОРЕМА АЛГЕБРЫ Теория комплексных чисел. Поверхность модуля многочлена. О возрастании модуля многочлена при удалении от начала. Существование минимумов поверхности M. Лемма Даламбера. § 4. ИССЛЕДОВАНИЕ РАСПОЛОЖЕНИЯ КОРНЕЙ МНОГОЧЛЕНА НА КОМПЛЕКСНОЙ ПЛОСКОСТИ Простые и кратные корни многочлена. Теорема Ролля и некоторые ее следствия. Правило знаков Декарта. Теорема Штурма. Задача Гурвица. § 5. ПРИБЛИЖЕННОЕ ВЫЧИСЛЕНИЕ КОРНЕЙ |
записей в журнале | Пример, Уравнение, Правила дебета и кредита, Балансировка
Журнальные записи обычно являются первым этапом бухгалтерского цикла. Этот процесс включает в себя анализ бизнес-транзакций, чтобы определить, оказывает ли определенная транзакция экономическое влияние на бухгалтерские книги компании. Этот шаг начинается в начале цикла учета и продолжается в течение всего периода.
Определив, какие операции имеют экономический эффект, бухгалтер внесет эти записи в общий журнал. Общий журнал — это ежедневник или основной журнал, в котором записываются все операции компании, происходящие в течение цикла учета.
Пример цикла бухгалтерского учета
В этой серии статей, посвященных циклу бухгалтерского учета, мы рассмотрим пример компании Bob’s Donut Shoppe, Inc., чтобы лучше понять концепции каждой части цикла бухгалтерского учета. Ниже приведен полный список учебных пособий по бухгалтерскому циклу:
- Записи в журнале (вы здесь)
- Т-счета
- Нескорректированный пробный баланс
- Корректировка записей
- Скорректированный пробный баланс
- Подготовка финансовой отчетности
- Рабочий лист бухгалтерского учета
- Закрытие записей
- Суммарный счет доходов
- Пробный баланс после закрытия
- Сторнирование записей
У нас также есть сопроводительная таблица, в которой показан пример каждого шага.
Щелкните здесь, чтобы загрузить шаблон цикла бухгалтерского учета
Понимание уравнения бухгалтерского учета
Чтобы определить, имеет ли транзакция экономический эффект, ее следует проанализировать с помощью уравнения бухгалтерского учета.
Формула уравнения бухгалтерского учета
Уравнение бухгалтерского учета является основой системы бухгалтерского учета с двойной записью. Каждая бизнес-операция, зарегистрированная с помощью системы двойной записи, повлияет на уравнение бухгалтерского учета. Это простое уравнение, которое показывает взаимосвязь между несколькими статьями баланса компании. Активы представляют собой ценные ресурсы, которыми может владеть компания, и эти активы могут финансироваться либо за счет займа, либо за счет личного капитала/привлечения собственного капитала владельцем.
Для ведения точных записей каждая бизнес-операция, которая была зарегистрирована в журнале, будет использовать правила дебета и кредита для внесения изменений в уравнение бухгалтерского учета таким образом, чтобы оно всегда было в балансе.
Правила дебета и кредита
Система бухгалтерского учета с двойной записью гарантирует, что каждая операция регистрируется с использованием двух разных счетов. Для этого была разработана система дебета и кредита.
- Дебетовая запись увеличит актив или счет расходов и уменьшают обязательство или счет собственного капитала.
- Кредитовая запись увеличит обязательство или счет собственного капитала и уменьшит актив или счет расходов.
Всякий раз, когда происходит бизнес-транзакция, дебетовая запись для одной учетной записи и кредитовая запись для другой учетной записи влияют как минимум на два счета. Общие дебеты и кредиты должны быть равны друг другу, чтобы уравнение бухгалтерского учета всегда было сбалансированным.
Балансировка уравнения бухгалтерского учета
Давайте посмотрим, как правила дебета и кредита обеспечивают сохранение баланса уравнения бухгалтерского учета.
Предположим, что бизнес начинается со следующего бухгалтерского уравнения в начале бухгалтерского цикла:
В течение года регистрируются и анализируются следующие бизнес-операции:
- Приобретение оборудования на сумму 10 миллионов долларов за наличные.
- Приобретенный инвентарь на сумму 20 миллионов долларов в кредит.
Затем эти бизнес-операции будут регистрироваться в общем журнале с использованием правил дебета и кредита следующим образом: (оборудование) записывается как запись по дебету, а любое уменьшение актива (денежных средств) записывается как запись по кредиту. Обе записи повлияют на уравнение бухгалтерского учета, поскольку покупка оборудования увеличит часть активов, а оплата наличными уменьшит часть активов.
Активы останутся прежними на уровне 200 миллионов долларов:
Это означает, что уравнение бухгалтерского учета не изменится:
Запись в журнале 2
В соответствии с правилами системы дебета и кредита любое увеличение активов (запасов) отражается по дебету, а увеличение обязательств (кредиторской задолженности) – по кредиту.
Обе записи повлияют на уравнение бухгалтерского учета, поскольку покупка товарно-материальных запасов увеличит часть активов, а используемая кредитная линия увеличит часть обязательств.
После этой записи в журнале активы и пассивы увеличиваются:
Новое уравнение учета показано ниже:
Пример записей в журнале Bob’s Donut Shoppe, Inc. Следующие бизнес-операции имеют место в первый год деятельности:
Транзакции
- 1 января. Боб создает Donut Shoppe, Inc, приобретая 50 000 акций по цене 1 доллар за акцию.
- 2 января. Боб находит хорошее место для аренды на одной из самых оживленных улиц в своем районе и подписывает договор об аренде за 750 долларов в месяц.
- 3 января. Боб занимает в банке 25 000 долларов, чтобы оплатить расходы на ремонт и улучшение имущества. Он соглашается платить 1000 долларов в месяц в течение трех лет, чтобы погасить кредит.
- 5 января. Боб покупает инвентарь на сумму 20 000 долларов США в кредит у поставщиков и соглашается платить 1000 долларов США в месяц.
- 7 января. Боб покупает товары для магазина стоимостью 3000 долларов.
- 11 января. Боб впервые продает 20 коробок пончиков для вечеринки по случаю дня рождения соседа по цене 30 долларов за коробку. Изготовление стоило ему 10 долларов за коробку.
- 13 января. Боб продает еще 100 коробок пончиков для корпоратива по 30 долларов за коробку. Стоимость его изготовления составляет 10 долларов за коробку .
- 31 января. Боб оплачивает счет за электричество в размере 500 долларов.
- 31 января. Боб выплачивает зарплату своим сотрудникам в размере 2500 долларов.
- 31 янв. Пришел первый платеж Боба за инвентарь.
- 31 января. Первый платеж Боба по банковскому кредиту также должен быть погашен. В дополнение к погашению кредита в размере 1000 долларов США проценты по кредиту составляют 500 долларов США.
- 31 января. Боб платит арендную плату за первый месяц в размере 750 долларов США в установленный срок.
- 31 января. В конце месяца Боб получает прибыль и решает выплатить себе дивиденды в размере 500 долларов.
Записи в журнале
Ниже мы можем увидеть все транзакции, которые были добавлены в журнал.
Следующий шаг
Теперь, когда все бизнес-операции зарегистрированы в общем журнале с использованием правил дебета и кредита, следующим шагом будет их проводка по отдельным счетам бухгалтерской книги, которые обычно называют Т-счетами.
Часто задаваемые вопросы
1. Какие записи журнала?
Журнальные записи — это официальная запись финансовых транзакций, совершаемых предприятием. Операции сначала регистрируются в журнале, а затем размещаются на отдельных счетах бухгалтерской книги.
2. Что включается в запись в журнале?
Запись в журнале включает дату транзакции, имя затрагиваемой учетной записи и сумму транзакции.
3. Каковы основные типы журнальных записей?
Основными типами записей в журнале являются дебеты, кредиты, записи в журнале движения денежных средств, записи журнала отчета о прибылях и убытках и записи журнала баланса
4.
Какова цель записи журнала?Целью записи в журнале является документирование финансовых операций предприятия. Затем эта информация используется для составления финансовой отчетности.
5. Как начать запись в журнале?
Первая строка записи журнала начинается с даты транзакции. Вторая строка включает имя учетной записи, затронутой транзакцией. В третьей строке указана сумма транзакции.
Перекомпонуйте любое алгебраическое уравнение с помощью одного простого правила
Обновлено 4 февраля 2019 г.
Автор Lee Johnson больше всего отталкивает людей, это алгебра. Одного упоминания этого слова достаточно, чтобы поднять коллективный стон у каждого ученика седьмого класса и выше. Но если вы надеетесь поступить в хороший колледж или просто получить хорошие оценки, вам должны справиться с этим. Хорошая новость заключается в том, что на самом деле все не так плохо, как вы думаете. Как только вы привыкнете к тому, что вместо чисел вы используете буквы и символы, вам нужно усвоить одно важное правило: делать то же самое с обеими частями уравнения при перестановке.
Самое важное правило алгебры
Самое важное правило алгебры: I Если вы делаете что-то с одной частью уравнения, вы должны сделать это и с другой частью уравнения .
Уравнение, по сути, говорит: «Материал слева от знака равенства имеет ту же ценность, что и материал справа от него», как сбалансированный набор весов с одинаковым весом с обеих сторон. Если вы хотите, чтобы все было равным, все, что вы делаете, должно быть сделано для обеих сторон .
Глядя на простой пример с использованием чисел, вы действительно поймете это.
2 × 8 = 16
Это очевидно верно: две партии по восемь действительно равны 16. Если снова умножить обе части на два, получится:
2 × 2 × 8 = 2 × 16
Тогда обе стороны равны. Потому что 2 × 2 × 8 = 32 и 2 × 16 = 32. Если вы проделаете это только с одной стороны, например:
2 × 2 × 8 = 16
, вы на самом деле скажете, что 32 = 16, что явно неверно!
Заменив числа буквами, вы получите алгебраическую версию того же самого.
x × y = z
Или просто
xy = z
Неважно, что вы не знаете, что x , y или z среднее значение; на основании этого основного правила вы знаете, что все эти уравнения также верны:
2xy = 2z \\ xy / 4 = z/4 \\ xy + t = z + t
В каждом случае ровно то же самое было сделано с обеих сторон. Первый умножает обе части на два, второй делит обе части на четыре, а третий добавляет еще один неизвестный член, t , к обеим частям.
Обучение обратным операциям
Это основное правило — все, что вам нужно для перестановки уравнений, наряду с правилами, для которых операции отменяют какие другие. Это так называемые «обратные» операции. Например, обратным сложением является вычитание. Итак, если у вас x + 23 = 26, вы можете вычесть 23 с обеих сторон, чтобы удалить часть «+ 23» слева:
\begin{align} x + 23 −23 &= 26 − 23 \\ x &= 3 \end{aligned}
Точно так же вы можете отменить вычитание, используя сложение.
Вот список некоторых общих операций и их обратных операций (которые также применяются в обратном порядке):
- отменяется
by –
× отменяется
÷
- √ отменяется с помощью 2
- ∛ отменяется с помощью 3
Другие включают тот факт, что и могут быть вызваны с помощью наоборот
Попрактикуйтесь в перекомпоновке уравнений
Имея это в виду, вы можете перекомпоновывать почти любое уравнение, которое вам встретится. Целью перекомпоновки уравнения обычно является выделение определенного термина. Например, если у вас есть уравнение площади круга: 92}
Что (переворачивая) оставляет:
r=\sqrt{A \над{1pt} π}
Вот еще один пример, с которым вы можете попрактиковаться. Представьте, что у вас есть это уравнение:
v = u + at
И вам нужно уравнение для a .