Типы видеокассет
Существует несколько видов видеокассет, которые отличаются вместимостью, качеством записи и, конечно же, размером. Рассмотрим самые популярные варианты.
Формат VHS
• Вместимость: До 4-х часов записи, в режиме Long Play – до 8-ми часов.
• Размер кассеты: 19см×10см×2см.
Наиболее популярный и знакомый нам тип видеокассет. Именно его мы проигрывали на видеомагнитофоне, смотря фильмы или домашнее видео. Кассета была разработана фирмой JVC (Япония) в 1976 году. Благодаря простоте и надежности данного формата, JVC обошла своих конкурентов и прочно закрепилась на рынке.
Формат VHS-C
• Вместимость: стандарт 45 минут, а также 30, 45, 60, 90, 105 минут.
• Размер кассеты: 9,1×5,9×2см.
Видеокассета была выпущена в 1982 году фирмой Panasonic(Япония) для видеокамер Compact-VHS (легкие ручные камеры). Данный формат видеокассеты был в 2 раза меньше кассет VHS, для просмотра на обычном видеомагнитофоне, требовался специальный адаптер.
Формат Video8
• Вместимость: 120 минут записи.
• Размер кассеты: 9,5×6,2×1,5 см.
Аналоговый формат Video-8 был выпущен в 1985 фирмой Sony. Применялся также в бытовых видеокамерах. Отличался от VHS и VHS-C повышенным качеством видео и аудио.
Формат Hi8
• Вместимость: 120 минут записи.
• Размер кассеты: 9,5×6,2×1,5 см.
Был выпущен в 1989 году и стал усовершенствованным вариантом Video8. Достиг самого высокого качества среди аналоговых форматов и был популярен до конца 90-х годов.
Формат Digital8
• Вместимость: до 90 минут.
• Размер кассеты: 9,5×6,2×1,5 см.
Появился в 1999 году. Запись на данный формат велась уже в цифровом, а не в аналоговом виде, и это в разы повысило качество видеозаписи.
MiniDV
• Вместимость: 45, 60, 90 минут.
• Размер кассеты: 6,5х4,7х1,2 см.
Данный цифровой формат стал революцией в мире видеоиндустрии, так как позволил снимать профессиональные материалы в домашних условиях.
Отличием было полностью улучшенное качество видео, по сравнению с VHS, использовалось внутрикадровое сжатие DV. Данный формат стал популярен в производстве фильмов, именно на него было снято большое количество документальных фильмов, а часть телекомпаний снабдила сотрудников MiniDV-камерами.
Диски Mini DVD
• Вместимость: 20-40 минут.
• Размер диска: 8 см в диаметре.
Диски такого формата стали популярны в конце эпохи видеокассет, когда использовались компактные видеокамеры. Но у данного формата достаточно недостатков – малая вместимость и неудобный формат файла записи, которые часто не видел компьютер.
- Реставрация фотографий
- Фотопечать
- Ремонт видеокассет
- Типы видеокассет
- Формат вывода видео при оцифровке кассет
Статьи:
- Почему изображение на видеокассетах ухудшается с каждым годом?
Мобильная версия сайта
Главная Видеокассеты Фотопленка Слайды Фото Слайд-шоу Контакты Отзывы
Задачи 11 из ЕГЭ.
Совместная работаСначала рассмотрим простые задачи на совместную работу с двумя участниками. Далее указан год сборника заданий для подготовки к ЕГЭ, откуда взята задача. Начнём с подготовительной задачи.
Задача 1. Валя пропалывает грядку за 40 минут, а Галя — за 10 минут. За сколько минут Валя и Галя пропалывают грядку при совместной работе?
II способ. Предположим, что Валя и Галя работали совместно 40 минут. За это время Валя прополола 1 грядку.
1) 40: 10 = 4 (грядки) — прополола за 40 минут Галя,
2) 1 + 4 = 5 (грядок) — пропололи за 40 минут Валя и Галя при совместной работе,
3) 40: 5 = 8 (мин) — время прополки одной грядки при совместной работе Вали и Гали.
III способ. Предположим, грядка была длиной 40 м, тогда Валя пропалывает 40: 40 = 1 (м/мин), а Галя — 40: 10 = 4 (м/мин). Валя и Галя при совместной работе пропалывают 1 + 4 = 5 (м/мин). Вдвоём они прополют грядку за
40: 5 = 8 (мин).
Ответ. За 8 мин.
Замечание. I способ даёт нам полное решение, не зависящее от времени работы или длины грядки. II и III способы решения даны для частных случаев (можно было взять другое время работы или другую длину грядки). Полное решение получится, если мы докажем, что ответ не зависит от выбора дополнительного условия. Так как на экзамене нужно указать лишь правильный ответ, то II и III способы вполне можно применять. Чтобы обосновать III-й способ решения, можно обозначить объём работы (длину грядки) буквой и фактически повторить I-й способ решения.
Задача 2. (2018) Валя и Галя пропалывают грядку 8 минут, а одна Галя — за 10 минут. За сколько минут пропалывает грядку одна Валя?
II способ. Предположим, что Валя и Галя работали совместно 40 минут. За это время они вдвоём пропололи:
1) 40: 8 = 5 (грядок),
2) 40: 10 = 4 (грядки) — прополола за 40 минут Галя,
3) 5 — 4 = 1 (грядку) — прополола за 40 минут Валя.
Значит, одна Валя пропалывает грядку за 40 минут.
III способ. Предположим, грядка была длиной 40 м, тогда Валя и Галя при совместной работе пропалывали 40: 8 = 5 (м/мин), а одна Галя — 40: 10 = 4 (м/мин). Тогда одна Валя пропалывала 5 — 4 = 1 (м/мин). На всю грядку Вале требуется 40: 1 = 40 (мин).
Ответ. За 40 мин.
Задача 3. Через первый кран бассейн наполнится за 40 минут, через второй — за 60 минут, через третий — за 48 минут. За сколько минут три крана заполнят бассейн при совместной работе?
Решение. Примем всю работу за 1.
Есть ещё один способ решения, похожий на способ решения задачи про кадь кваса.
Пусть трубы могут одновременно наполнять несколько бассейнов. За 240 минут первая труба наполнит 6, вторая 4, третья 5 бассейнов, а вместе — 15 бассейнов. При совместной работе три трубы тратят на 1 бассейн
240: 15 = 16 (мин).
Задача 4. (2018) Каждый из двух рабочих одинаковой квалификации может выполнить заказ за 15 ч.
Через 5 ч после того, как один из них приступил к выполнению заказа, к нему присоединился второй рабочий, и работу над заказом они довели вместе. За сколько часов был выполнен весь заказ?
Решение. I способ. Примем всю работу за 1.
II способ. Пусть надо было обточить 30 деталей.
1) 30: 15 = 2 (дет.) — обтачивает один рабочий за 1 ч,
2) 2 + 2 = 4 (дет.) — обтачивают два рабочих за 1 ч совместной работы,
3) 2 ∙ 5 = 10 (дет.) — обточил один рабочий за 5 ч,
4) 30 — 10 = 20 (дет.) — обточили два рабочих при совместной работе,
5) 20: 4 = 5 (ч) — работали два рабочих вместе,
6) 5 + 5 = 10 (ч) — время выполнения всего заказа.
Ответ. За 10 ч.
Задача 5. (2018) Две бригады, состоящие из рабочих одинаковой квалификации, одновременно начали выполнять два одинаковых заказа. В первой бригаде было 12 рабочих, а во второй — 21 рабочий. Через 10 дней после начала работы в первую бригаду перешли 12 рабочих из второй бригады.
В итоге оба заказа выполнили одновременно. Найдите, сколько дней потребовалось на выполнение заказов.
Для решения задач, где все работники имеют одинаковую производительность труда, удобно применять единицу измерения объёма работы «человеко-день». Например, 10 чел. ∙ дней — это объём работы, который может выполнить 1 человек за 10 дней, или 5 человек за 2 дня, или 2 человека за 5 дней.
Решение. I способ. Примем всю работу за 1.
1) 12 ∙ 10 = 120 (человеко-дней) — объём работы, выполненной 12-ю рабочими первой бригады за 10 дней,
2) 21 ∙ 10 = 210 (человеко-дней) — объём работы, выполненной 21-им рабочим второй бригады за 10 дней,
3) 210 — 120 = 90 (человеко-дней) — объём работы второй бригады, который предстоит компенсировать первой бригаде после перехода 12 рабочих,
4) 12 + 12 — (21 — 12) = 15 (чел.) — на столько рабочих стало в первой бригаде больше, чем во второй,
5) 90: 15 = 6 (дней) — потребуется первой бригаде, чтобы наверстать отставание в объёме работы,
6) 10 + 6 = 16 (дней) — время выполнения двух заказов.
II способ. Пусть после перехода 12 рабочих бригады работали ещё x дней. Приравняем объёмы выполненной работы (в человеко-днях) двух бригад за всё время работы.
12 ∙ 10 + (12 + 12)x = 21 ∙ 10 + (21 — 12)x.
Это уравнение имеет единственный корень 6, поэтому время выполнения двух заказов равно 10 + 6 = 16 (дней).
Ответ. 16 дней.
Замечание. При решении этой задачи можно обойтись без человеко-дней, если считать, что каждый рабочий в час выполняет y единиц работы (обтачивает y деталей и т. п.). Тогда, рассуждая, как во втором способе решения, приравняем объемы работы двух бригад:
12 ∙ 10y + (12 + 12)xy = 21 ∙ 10y + (21 — 12)xy.
Разделив это уравнение на число y, отличное от нуля, получим то же уравнение, что и при II-м способе решения задачи.
Задача 6. (2018) Игорь и Паша красят забор за 12 часов. Паша и Володя красят тот же забор за 15 часов, а Володя и Игорь — за 20 часов.
За сколько часов мальчики покрасят забор, работая втроём?
II способ. Пусть было два Игоря, два Паши и два Володи. Мальчики с одинаковыми именами работали с одинаковой производительностью. Пусть они вшестером одновременно красят заборы 60 ч. За это время Игорь и Паша покрасят 60: 12 = 5 (заборов), Паша и Володя — 60: 15 = 4 (забора), а Володя и Игорь — 60: 20 = 3 (забора). Шесть мальчиков за 60 ч покрасят 5 + 4 + 3 = 12 (заборов), на 1 забор они тратят 60: 12 = 5 (ч), три мальчика тратят на забор в 2 раза больше времени — 10 ч.
Ответ. За 10 ч.
В следующей задаче нет совместной работы, но она решается похожим арифметическим способом.
Задача 7. (2018) Костя и Гриша выполняют одинаковый тест. Костя отвечает за час на 12 вопросов, а Гриша — на 20. Они одновременно начали отвечать на вопросы теста, и Костя закончил свой тест позже Гриши на 90 минут. Сколько вопросов содержит тест?
Решение. I способ.
1) 60: 12 = 5 (мин) — тратит на 1 вопрос Костя,
2) 60: 20 = 3 (мин) — тратит на 1 вопрос Гриша,
3) 5 — 3 = 2 (мин) — на каждый вопрос Костя тратит на 2 мин больше, чем Гриша, а всего он потратил на 90 мин больше,
4) 90: 2 = 45 (вопросов) — в тесте.
II способ. Пусть в тесте было x вопросов.
1) 60: 12 = 5 (мин) — Костя тратит на 1 вопрос, значит, 5x минут тратит на все вопросы,
2) 60: 20 = 3 (мин) — Гриша тратит на 1 вопрос, значит, 3x минут тратит на все вопросы.
Составим уравнение:
5x — 3x = 90,
x = 45.
В тесте 45 вопросов.
Ответ. 45.
Задача 8. (2009) Два плотника, работая вместе, могут выполнить задание за 36 ч. Производительности труда первого и второго плотников относятся как 3: 4. Плотники договорились работать поочерёдно. Какую часть этого задания должен выполнить второй плотник, чтобы всё задание было выполнено за 69,3 ч?
Решение. I способ. Примем всю работу за 1.
Пусть первый выполнил часть работы, выражаемую дробью x, тогда второй — часть работы, выражаемую дробью 1 — x, они затратили 84x ч и 63(1 — x) ч соответственно при поочерёдной работе, а всего — 69,3 ч. Составим уравнение:
84x + 63(1 — x) = 69,3.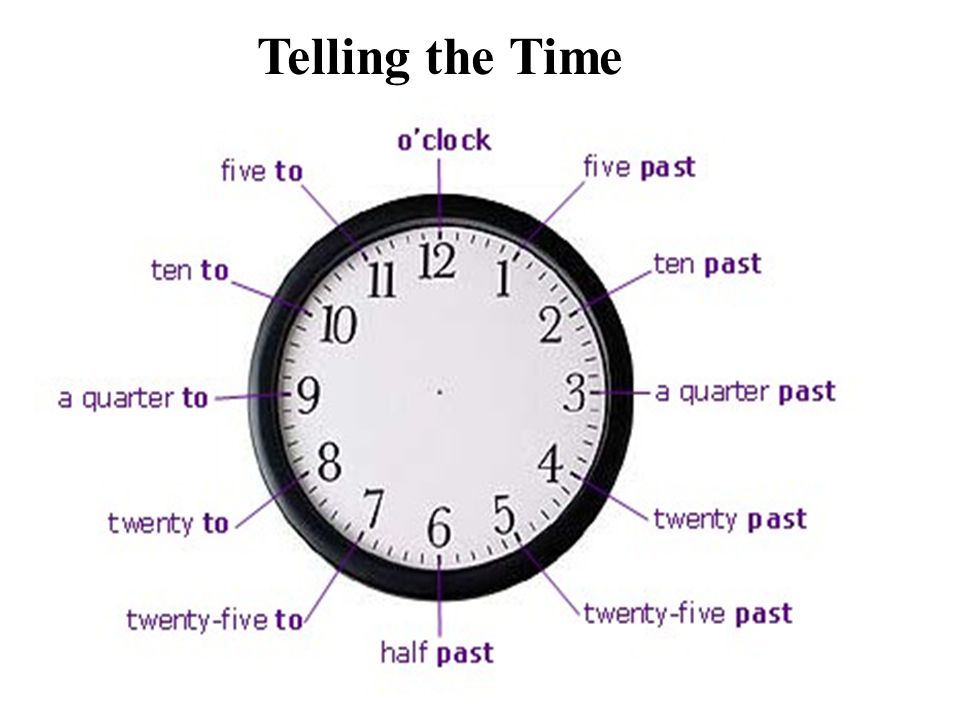
Это уравнение имеет единственный корень x = 0,3. Первый выполнил 0,3 работы, второй — 1 — x = 0,7.
Ответ. 0,7.
Для самостоятельного решения
9. Малыш может съесть все плюшки за 20 минут, а Карлсон — за 5 минут. За сколько минут они съедят все плюшки вместе?
10. Две бригады при совместной работе выполнят задание за 14 дней. Одна первая бригада могла бы выполнить это задание за 21 день. За сколько дней одна вторая бригада могла бы выполнить это задание?
11. Три трубы заполнили бассейн при совместной работе за 15 минут. Одна первая труба наполнит бассейн за 35 минут, а одна вторая — за 63 минуты. За сколько минут одна третья труба заполнит бассейн?
12. (2018) Коля и Митя выполняют одинаковый тест. Коля отвечает за час на 12 вопросов, а Митя — на 21. Они одновременно начали отвечать на вопросы теста, и Коля закончил свой тест позже Мити на 105 минут. Сколько вопросов содержит тест?
13.
(2009) Два каменщика, работая вместе, могут выполнить задание за 12 ч. Производительности труда первого и второго каменщиков относятся как 1: 3. Каменщики договорились работать поочерёдно. Сколько часов должен проработать первый, чтобы это задание было выполнено за 20 ч?
14. (2009) Отец с сыном должны вскопать огород. Производительность труда отца в 2 раза больше, чем у сына. Работая вместе, они могут вскопать огород за 4 ч. Однако вместе они проработали только 1 час, потом некоторое время работал один сын, а заканчивал работу уже один отец. Сколько часов в общей сложности проработал в огороде отец, если вся работа была выполнена за 7 часов?
15. (2019) Первый и второй насосы наполняют бассейн за 21 минуту, второй и третий — за 28 минут, первый и третий — за 36 минут. За сколько минут эти три насоса заполнят бассейн, работая вместе?
16. (2018) Игорь и Паша красят забор за 18 часов. Паша и Володя красят этот же забор за 24 часа, а Володя и Игорь — за 36 часов.
За сколько часов мальчики покрасят забор, работая втроём?
Ответы. 9. За 4 мин. 10. За 42 дня. 11. За 45 мин. 12. 49 ч. 13. 6 ч. 14. 4 ч. 15. За 18 мин. 16. За 16 ч.
Для работы с классом можно использовать презентацию:
Совместная работа. Задачи 11 из ЕГЭ
Преобразовать 105 минут в часы (105 минут в часы)
Из Столетия (c.) Дни (d) Десятилетия (dec) Часы (hr) Тысячелетия (mil.) Миллисекунды (ms) Минуты (min) Месяцы (mo) Наносекунды (ns) Секунды (s) Недели (wk) Рабочие недели (work) wk) Лет (год)
К Столетия (c.) Дни (d) Десятилетия (dec) Часы (hr) Тысячелетия (mil.) Миллисекунды (ms) Минуты (min) Месяцы (mo) Наносекунды (ns) Секунды (s) Недели (wk) Рабочие недели (work) нед) Лет (год)
Количество
Показать результат как DecimalScientific Notation
Результат
Вопрос: Что находится в или сколько ?
Ответ: равно .
Сколько времени по сравнению с другими единицами времени?
Эта таблица преобразования показывает, как длина по сравнению с другими единицами площади.
Таблица преобразования минут в часы
| мин | ч | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 105 | = | 1.75 | ||||||||||
| 105.01 | = | 1.750167 | ||||||||||
| 105.02 | = | 1.750333 | ||||||||||
| 105.03 | = | 1.7505 | ||||||||||
| 105.04 | = | 1,750667 | ||||||||||
| 105,05 | = | 1,750833 | ||||||||||
| 105.06 | = | 1.751 | ||||||||||
| 105.07 | = | 1.751167 | ||||||||||
| 105.08 | = | 1.751333 | ||||||||||
| 105.09 | 1.7515 | |||||||||||
| 105.1 | = | 1,751667 | ||||||||||
105. 11 | = | 1,751833 | ||||||||||
| 105.12 | = | 1,752 | 3339= | 1,752 | 33339= | 1,752 | 33339= | 1,752 | 333339.0024 | 105.13 | = | 1.752167 |
| 105.14 | = | 1.752333 | ||||||||||
| 105.15 | = | 1.7525 | ||||||||||
| 105.16 | = | 1.752667 | ||||||||||
| 105.17 | = | 1.752833 | ||||||||||
| 105.18 | = | 1.753 | ||||||||||
| 105.19 | = | 1.753167 |
| мин | ч | |
|---|---|---|
| 105.2 | = | 1.753333 |
| 105.21 | = | 1.7535 |
| 105.22 | = | 1.753667 |
| 105.23 | = | 1. 753833 |
| 105.24 | = | 1,754 |
| 105,25 | = | 1,754167 |
| 105.26 | = | 1.754333 |
| 105.27 | = | 1.7545 |
| 105.28 | = | 1.754667 |
| 105.29 | = | 1.754833 |
| 105.3 | = | 1.755 |
| 105.31 | = | 1.755167 |
| 105.32 | = | 1.755333 |
| 105.33 | = | 1.7555 |
| 105.34 | = | 1.755667 |
| 105.35 | = | 1.755833 |
| 105.36 | = | 1.756 |
| 105.37 | = | 1.756167 |
| 105.38 | = | 1,756333 |
| 105,39 | = | 1,7565 |
| 65 |
|---|
| 65 |
|---|
| 65 |
|---|
| 65 |
|---|
| 65 |
|---|
65. 0026 | ч | |
|---|---|---|
| 105.4 | = | 1.756667 |
| 105.41 | = | 1.756833 |
| 105.42 | = | 1.757 |
| 105.43 | = | 1.757167 |
| 105.44 | = | 1,757333 |
| 105,45 | = | 1,7575 |
| 105,46 | = | 1.757667 |
| 105.47 | = | 1.757833 |
| 105.48 | = | 1.758 |
| 105.49 | = | 1.758167 |
| 105.5 | = | 1.758333 |
| 105.51 | = | 1.7585 |
| 105.52 | = | 1.758667 |
| 105.53 | = | 1.758833 |
| 105.54 | = | 1.759 |
105. 55 | = | 1.759167 |
| 105.56 | = | 1.759333 |
| 105.57 | = | 1.7595 |
| 105,58 | = | 1,759667 |
| 105,59 | = | 1,759833 |
| мин. | ч | |||||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 105.6 | = | 1.76 | ||||||||||||||||||||||||
| 105.61 | = | 1.760167 | ||||||||||||||||||||||||
| 105.62 | = | 1.760333 | ||||||||||||||||||||||||
| 105.63 | = | 1.7605 | ||||||||||||||||||||||||
| 105.64 | = | 1,760667 | ||||||||||||||||||||||||
| 105,65 | = | 1,760833 | ||||||||||||||||||||||||
| 105,66 | 3 =3 | 1.761 | ||||||||||||||||||||||||
| 105.67 | = | 1.761167 | ||||||||||||||||||||||||
| 105.68 | = | 1.761333 | ||||||||||||||||||||||||
| 105.69 | = | 1.7615 | ||||||||||||||||||||||||
105. 7 | = | 1.761667 | ||||||||||||||||||||||||
| 105.71 | = | 1.761833 | ||||||||||||||||||||||||
| 105.72 | = | 1.762 | ||||||||||||||||||||||||
| 105.73 | = | 1.762167 | ||||||||||||||||||||||||
| 105.74 | = | 1.762333 | ||||||||||||||||||||||||
| 105.75 | = | 1.7625 | ||||||||||||||||||||||||
| 105.76 | = | 1.762667 | ||||||||||||||||||||||||
| 105.77 | = | 1.762833 | ||||||||||||||||||||||||
| 105.78 | Минчас | |||||||||||||||||||||||||
| 105.8 | = | 1.763333 | ||||||||||||||||||||||||
| 105.81 | = | 1.7635 | ||||||||||||||||||||||||
| 105.82 | = | 1.763667 | ||||||||||||||||||||||||
| 105.83 | = | 1.763833 | ||||||||||||||||||||||||
| 105.84 | = | 1,764 | ||||||||||||||||||||||||
| 105,85 | = | 1,764167 | ||||||||||||||||||||||||
| 105,86 | = | 1. | = | 1.764333 3 | = | 1,764333 3 | = | 1.764333 3 | = | 1,764333 3 | = | 1,764333 3 | .0030 | |||||||||||||
| 105.87 | = | 1.7645 | ||||||||||||||||||||||||
| 105.88 | = | 1.764667 | ||||||||||||||||||||||||
| 105.89 | = | 1.764833 | ||||||||||||||||||||||||
| 105.9 | = | 1.765 | ||||||||||||||||||||||||
| 105.91 | = | 1,765167 | ||||||||||||||||||||||||
| 105,92 | = | 1,765333 | ||||||||||||||||||||||||
| 105,93 | = | 1,7655 | = | 1,7655 | 1,7655 | 1,7655 | = | 1,7655 | = | 1,7655 | = | ,0032 105.94 | = | 1.765667 | ||||||||||||
| 105.95 | = | 1.765833 | ||||||||||||||||||||||||
105. 96 | = | 1.766 | ||||||||||||||||||||||||
| 105.97 | = | 1.766167 | ||||||||||||||||||||||||
| 105.98 | = | 1,766333 | ||||||||||||||||||||||||
| 105,99 | = | 1,7665 |
105 минут в часах | Сколько длится 105 минут?
105 минут равны 1 3 / 4 часов или 105 минут = 1 3 / 4 ч
В 105 минутах 1 3 / 4 часов. Чтобы преобразовать любое значение из минут в часы, просто умножьте минуты на коэффициент умножения, также известный как коэффициент преобразования, который в данном случае равен 0,0166667.
Таким образом, 105 минут умножить на 0,0166667 эквивалентно 1 3 / 4 часов.
Универсальный преобразователь единиц измерения
| ⇆ | ||
Пожалуйста, выберите физическую величину, две единицы, затем введите значение в любое из полей выше. | ||
Как перевести минуты в часы?
Чтобы преобразовать значение из минут в часы, просто умножьте количество минут на 0,0166667 (коэффициент преобразования). Используйте приведенную ниже формулу для преобразования минут в часы:
Значение в часах = значение в минутах × 0,0166667
Предположим, вы хотите преобразовать 105 минут в часы. В этом случае просто выполните «математику» ниже:
Значение в часах = 105 × 0,0166667 = 1 3 / 4 (часы)
Этот калькулятор отвечает на такие вопросы, как:
- Сколько часов составляет 105 минут. ?
- 105 минут равно количеству часов?
- Как преобразовать минуты в часы?
- На сколько следует умножить значение в минутах, чтобы получить соответствующее значение в часах? 909:40
- По какой формуле можно перевести минуты в часы? Среди прочих.
минут до часа.
917 hour| Minutes to hours conversion chart | ||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 105 minutes | = | 1 3 / 4 hours | ||||||||||||||
| 115 minutes | = | 1.92 hours | ||||||||||||||
| 125 minutes | = | 2 1 / 12 hours | ||||||||||||||
| 135 minutes | = | 2 1 / 4 hours | ||||||||||||||
| 145 minutes | = | 2. 42 hours | ||||||||||||||
| 155 minutes | = | 2,58 часа | ||||||||||||||
| 165 минут | = | 2 3 / 4 часы | ||||||||||||||
| 175 минуты | = | 2,92 часов | 333339= | 2,92 часа | 33333339= | 2,92 часа | 333333339= | 2,92 часа | 333333333339= | 2,92 часов | = | 2,92 часов | .0024 | 185 минут | = | 3 1 / 12 часы |
| 3 | = | 3 1 / | 4. 40373. . . | 1371391391391377. .3. .3. . . .|||||||||||||
