Правило де моргана онлайн: Онлайн-калькулятор по информатике

4. Метод резолюций в логике высказываний

Метод резолюций – это метод автоматического доказательства теорем – основы логического программирования. Это алгоритм, проверяющий отношение выводимости ├. В общем случае алгоритм автоматического доказательства теорем не существует, но для формальных теорий с несложной структурой (таких как исчисление высказываний, исчисление предикатов с одним одноместным предикатом) подобные алгоритмы известны.

Вообще говоря, в построенном в главе 3 исчислении высказываний (благодаря полноте исчисления) проверка выводимости формулы состоит в проверке того, является ли формула тавтологией или нет. Это можно легко установить по таблицам истинности. Но этот метод не обеспечивает построения вывода формулы.

Метод резолюций – классический алгоритм автоматического доказательства теорем. Для простоты изложения рассмотрим его для исчисления высказываний. Для любого множества формул и любой формулы метод дает утвердительный ответ, если ├, и дает отрицательный ответ, если неверно, что ├.

Теорема о доказательстве от противного. Если ,├, где – тождественно ложная формула, то ├.

Доказательство. Доказательство проведем для частного случая, когда представляет собой одну формулу. По теореме дедукции, ,├ – тавтология. Преобразуем правую часть равносильности, учитывая, что формула тождественно ложна.

– тавтология Û ├, что и требовалось доказать.

Как правило, в качестве формулы используют пустую формулу , которая не имеет никакого значения ни в какой интерпретации, и, по определению, является противоречием.

Метод резолюций использует специальную форму формул, которая называется предложением.

Определение. Предложением называется дизъюнкция формул вида или , где – атом (буква).

Любая формула исчисления высказываний может быть преобразована в предложение следующей последовательностью действий:

1. Замена импликации по формуле: (проверьте самостоятельно). В результате в формуле остаются связки: , , .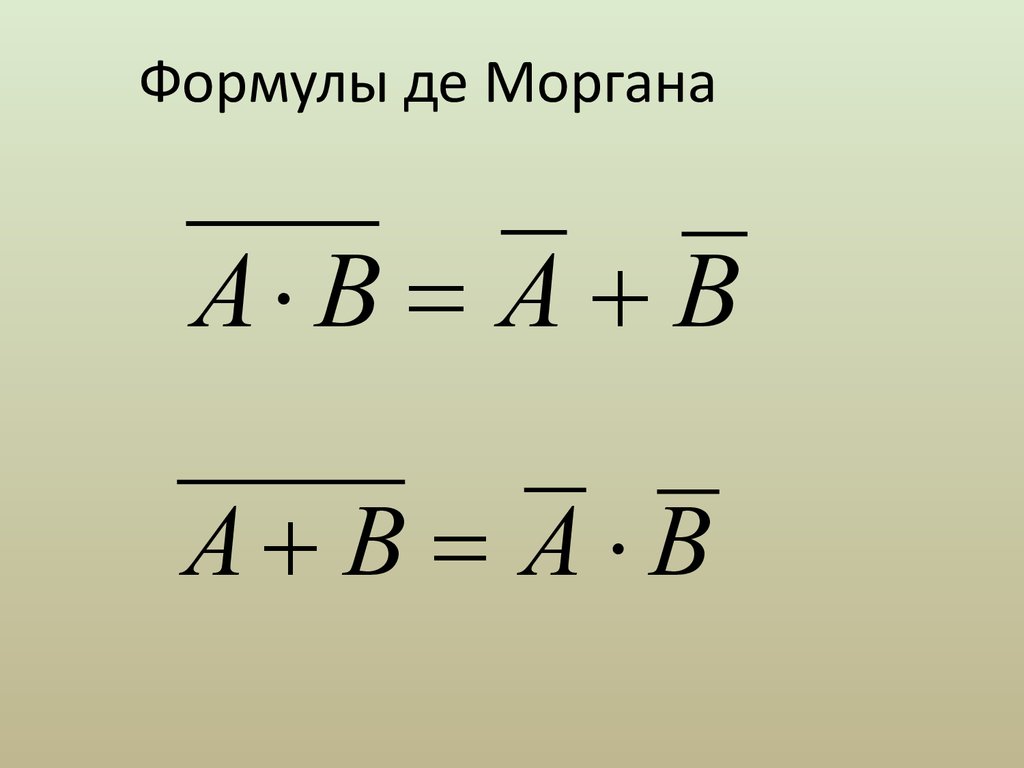

2. Преобразование выражений с инверсиями по закону двойного отрицания: , законам де Моргана: , . В результате инверсии остаются только перед буквами.

3. Приведение формулы к конъюнктивной нормальной форме с помощью дистрибутивных законов:

,

.

4. Преобразование конъюнктивной нормальной формы во множество предложений: .

Напомню, что связки , используются здесь для удобства записи.

Определение. Множество формул называется невыполнимым, если оно не имеет модели, то есть интерпретации, в которой все формулы истинны.

Без доказательства приведем следующую теорему.

Теорема. Если из формулы получено множество предложений, то формула тождественно ложна тогда и только тогда, когда множество невыполнимо.

До сих пор мы пользовались только одним правилом вывода – Modus ponens. В других исчислениях высказываний имеют место и другие правила вывода.

Правило резолюций. Даны предложения: , , где – пропозициональная буква, и – предложения (в частности, пустые или содержащие только одну букву или ее отрицание). Правило резолюций формулируется так: , ├.

, называются Резольвируемыми предложениями, а – Резольвентой.

Правило резолюций будем обозначать .

Теорема. Резольвента логически следует из резольвируемых предложений.

Доказательство. В вышеприведенных обозначениях, нам нужно доказать, что – тавтология (по теореме дедукции).

Предположим, что

Полученное противоречие доказывает утверждение теоремы.

Правило резолюций применяется в опровержении методом резолюций – алгоритме, устанавливающем выводимость ├.

Запишем . Каждая формула из множества и формула независимо преобразуются во множество предложений. В этом множестве нужно найти резольвируемые предложения и применить к ним правило резолюций. Резольвенты добавляются во множество предложений до тех пор, пока не будет получено пустое предложение. Возможны два случая:

· Среди множества предложений нет резольвируемых. Вывод: теорема опровергнута, и формула не выводима из множества формул .

· Получено пустое предложение. Теорема доказана. Имеет место выводимость ├.

Примеры. 1. Методом резолюций доказать теорему ├.

Доказательство. Запишем инверсию исходной формулы:

.

Заменим все импликации по соответствующей формуле:

.

Применим закон двойного отрицания и закон де Моргана:

.

Получаем предложения: , , . Резольвируем их:

1. – предложение.

2. – предложение.

3. – предложение.

4. . 1, 2.

2. Методом резолюций доказать теорему

├.

Доказательство. Запишем инверсию исходной формулы:

.

Заменим все импликации по соответствующей формуле:

.

Применим закон двойного отрицания и закон де Моргана:

.

Получаем предложения: , , .

1. – предложение.

2. – предложение.

3. – предложение.

4. . 1, 3.

5. . 2, 4.

< Предыдущая		Следующая >

Фильм Супруги Морган в бегах (США, 2009) смотреть онлайн – Афиша-Кино

• Абакан,
• Азов,
• Альметьевск,
• Ангарск,
• Арзамас,
• Армавир,
• Артем,
• Архангельск,
• Астрахань,
• Ачинск,
• Балаково,
• Балашиха,
• Балашов,
• Барнаул,
• Батайск,
• Белгород,
• Белорецк,
• Белореченск,
• Бердск,
• Березники,
• Бийск,
• Благовещенск,
• Братск,
• Брянск,
• Бугульма,
• Бугуруслан,
• Бузулук,
• Великий Новгород,
• Верхняя Пышма,
• Видное,
• Владивосток,
• Владикавказ,
• Владимир,
• Волгоград,
• Волгодонск,
• Волжский,
• Вологда,
• Вольск,
• Воронеж,
• Воскресенск,
• Всеволожск,
• Выборг,
• Гатчина,
• Геленджик,
• Горно-Алтайск,
• Грозный,
• Губкин,
• Гудермес,
• Дербент,
• Дзержинск,
• Димитровград,
• Дмитров,
• Долгопрудный,
• Домодедово,
• Дубна,
• Евпатория,
• Екатеринбург,
• Елец,
• Ессентуки,
• Железногорск (Красноярск),
• Жуковский,
• Зарайск,
• Заречный,
• Звенигород,
• Зеленогорск,
• Зеленоград,
• Златоуст,
• Иваново,
• Ивантеевка,
• Ижевск,
• Иркутск,
• Искитим,
• Истра,
• Йошкар-Ола,
• Казань,
• Калининград,
• Калуга,
• Каменск-Уральский,
• Камышин,
• Каспийск,
• Кемерово,
• Кингисепп,
• Кириши,
• Киров,
• Кисловодск,
• Клин,
• Клинцы,
• Ковров,
• Коломна,
• Колпино,
• Комсомольск-на-Амуре,
• Копейск,
• Королев,
• Коряжма,
• Кострома,
• Красногорск,
• Краснодар,
• Краснознаменск,
• Красноярск,
• Кронштадт,
• Кстово,
• Кубинка,
• Кузнецк,
• Курган,
• Курганинск,
• Курск,
• Лесной,
• Лесной Городок,
• Липецк,
• Лобня,
• Лодейное Поле,
• Ломоносов,
• Луховицы,
• Лысьва,
• Лыткарино,
• Люберцы,
• Магадан,
• Магнитогорск,
• Майкоп,
• Махачкала,
• Миасс,
• Можайск,
• Московский,
• Мурманск,
• Муром,
• Мценск,
• Мытищи,
• Набережные Челны,
• Назрань,
• Нальчик,
• Наро-Фоминск,
• Находка,
• Невинномысск,
• Нефтекамск,
• Нефтеюганск,
• Нижневартовск,
• Нижнекамск,
• Нижний Новгород,
• Нижний Тагил,
• Новоалтайск,
• Новокузнецк,
• Новокуйбышевск,
• Новомосковск,
• Новороссийск,
• Новосибирск,
• Новоуральск,
• Новочебоксарск,
• Новошахтинск,
• Новый Уренгой,
• Ногинск,
• Норильск,
• Ноябрьск,
• Нягань,
• Обнинск,
• Одинцово,
• Озерск,
• Озеры,
• Октябрьский,
• Омск,
• Орел,
• Оренбург,
• Орехово-Зуево,
• Орск,
• Павлово,
• Павловский Посад,
• Пенза,
• Первоуральск,
• Пермь,
• Петергоф,
• Петрозаводск,
• Петропавловск-Камчатский,
• Подольск,
• Прокопьевск,
• Псков,
• Пушкин,
• Пушкино,
• Пятигорск,
• Раменское,
• Ревда,
• Реутов,
• Ростов-на-Дону,
• Рубцовск,
• Руза,
• Рыбинск,
• Рязань,
• Салават,
• Салехард,
• Самара,
• Саранск,
• Саратов,
• Саров,
• Севастополь,
• Северодвинск,
• Североморск,
• Северск,
• Сергиев Посад,
• Серпухов,
• Сестрорецк,
• Симферополь,
• Смоленск,
• Сокол,
• Солнечногорск,
• Сосновый Бор,
• Сочи,
• Спасск-Дальний,
• Ставрополь,
• Старый Оскол,
• Стерлитамак,
• Ступино,
• Сургут,
• Сызрань,
• Сыктывкар,
• Таганрог,
• Тамбов,
• Тверь,
• Тихвин,
• Тольятти,
• Томск,
• Туапсе,
• Тула,
• Тюмень,
• Улан-Удэ,
• Ульяновск,
• Уссурийск,
• Усть-Илимск,
• Уфа,
• Феодосия,
• Фрязино,
• Хабаровск,
• Ханты-Мансийск,
• Химки,
• Чебоксары,
• Челябинск,
• Череповец,
• Черкесск,
• Чехов,
• Чита,
• Шахты,
• Щелково,
• Электросталь,
• Элиста,
• Энгельс,
• Южно-Сахалинск,
• Якутск,
• Ялта,
• Ярославль

Калькулятор законов ДеМорганса

Калькулятор законов ДеМорганса

---

Как работает калькулятор законов ДеМорганса?

Демонстрирует законы Де Моргана, включая доказательство
Этот калькулятор имеет 1 вход.

Какие 2 формулы используются в Калькуляторе законов ДеМорганса?

1. (A U B) ^C = A’ ∩ B’
2. (A ∩ B)’ = A’ U B’

Дополнительные математические формулы см. в нашем досье формул

Калькулятор законов ДеМорганса?

дополнение

Происходит противоположное событие
A ^C

законы Деморгана

элемент

элемент (или член) множества — это любой из отдельных объектов, принадлежащих этому множеству. В химии любое вещество, которое нельзя разложить на более простые вещества с помощью обычных химических процессов.

пересечение

множество, содержащее все элементы A, которые также принадлежат B, или, что то же самое, все элементы B, которые также принадлежат A.
A ∩ B

закон

математическое утверждение, которое всегда верно математическое утверждение, показывающее, что заявленные допущения логически гарантируют вывод

множество

совокупность различных вещей; набор содержит элементы или члены, которые могут быть математическими объектами любого вида 9C

Видео калькулятор законов ДеМорганса

• Электронная почта: [email protected]
• Тел.: 800-234-2933

• Математическая тревога
• судоку
• Раздор
• Информационный бюллетень о недобросовестном преимуществе
• Биографии математиков
• Подкаст цены за клик
• Математические Мемы
• Глоссарий по математике
• Предметы
• бейсбольная математика

• Друзья
• Спонсоры
• Связаться с нами
• Вакансии учителя математики
• Политика в отношении файлов cookie
• политика конфиденциальности
• Политика возврата

1.

3 Законы Де Моргана

Если $P$ — некоторое предложение или формула, то $\lnot P$ называется отрицание $P$. Способность манипулировать отрицание формулы точно имеет решающее значение для понимания математические рассуждения. Следующие тавтологии называются Законы де Моргана: $$\выравнивание{ \lnot (P\lor Q)&\iff (\lnot P\land \lnot Q)\cr \lnot (P\land Q)&\iff (\lnot P\lor \lnot Q)\cr} $$ Это легко проверить с помощью таблиц истинности, но с небольшим мысль, их нетрудно понять напрямую. Первый говорит что единственный способ, которым $P\lor Q$ может не быть истинным, состоит в том, что оба $P$ и $Q$ не соответствуют действительности. Например, высказывания «Я не люблю шоколад или ваниль» и «я не люблю шоколад и не люблю ваниль» четко выражают ту же мысль. Для более математического Пример второй тавтологии, рассмотрим «$x$ не находится между 2 и 3.» Символически это можно записать как $\lnot((2

Мы также можем использовать законы Де Моргана, чтобы упростить отрицание $P\implies Q$: $$\eqalign{\lnot (P\подразумевает Q) & \iff \lnot (\lnot P\lor Q)\cr & \iff (\lnot\lnot P)\land (\lnot Q)\cr & \iff P\land \lnot Q\cr} $$ так что отрицание $P\импульс Q$ есть $P\land \lnot Q$. Другими словами, это не тот случай, когда $P$ подразумевает $Q$ тогда и только тогда, когда $P$ истинно, а $Q$ ложно. Конечно, это согласуется с таблицей истинности для $P\имеет Q$, что мы уже видимый.

Существуют версии законов Де Моргана для кванторов: $$\выравнивание{ \lне \для всех x\,P(x) &\ тогда и только тогда, когда \существует x\,\lnot P(x)\cr \lне \существует x\,P(x) &\ тогда и только тогда, когда \для всех x\,\lnot P(x)\cr} $$ Вы можете быть в состоянии увидеть, что они верны немедленно. Если не, вот объяснение $\lnot \forall x\,P(x)\имплицитно \существует x\,\lnot P(x)$, что должно быть убедительным: если $\lnot \forall x\,P(x)$, тогда это не тот случай, когда $P(x)$ истинно для каждого $x$, т.е. говорят, что для некоторого значения $a$ $P(a)$ неверно. Это значит, что $\lnot P(a)$ истинно. Поскольку $\lnot P(a)$ истинно, случай, когда существует некоторое значение $x$, которое делает $\lnot P(x)$ истинным, что означает, что $\exists x\,\lnot P(x)$ истинно. Остальные три последствия могут быть объяснены аналогичным образом.

Вот еще один способ думать о кванторных версиях теории Де Моргана. законы. Оператор $\forall x\,P(x)$ очень похож на большой соединение. Если вселенная дискурса — это положительные целые числа, например, то это эквивалентно утверждению, что $$P(1)\земля P(2)\земля P(3)\земля \cdots $$ или, более кратко, мы могли бы написать $$\bigwedge_{x\in U} P(x), $$ с использованием обозначения, аналогичного «сигма-обозначению» для сумм. Конечно, это не совсем «заявление» в нашем официальном математическая логика, потому что мы не допускаем бесконечно длинных формул. Точно так же $\exists x\,P(x)$ можно рассматривать как $$\bigvee_{x\in U} P(x). $$ Теперь можно записать первый кванторный закон $$\lnot\bigwedge_{x\in U} P(x) \iff \bigvee_{x\in U} (\lnot P(x)), $$ очень похоже на закон $$\lnot (P\land Q)\iff (\lnot P\lor \lnot Q), $$ но с бесконечной конъюнкцией и дизъюнкцией. Обратите внимание, что мы также можем переписать законы де Моргана для $\land$ и $\lor$ как $$\выравнивание{ \lnot \bigwedge_{i=1}^2 (P_i(x)) &\iff \bigvee_{i=1}^2 (\lnot P_i(x))\cr \lnot \bigvee_{i=1}^2 (P_i(x)) &\iff \bigwedge_{i=1}^2 (\lnot P_i(x)). 2\ne -1$».

Легко спутать отрицание предложения с чем-то сильнее. Если вселенная есть совокупность всех людей, то отрицание предложение «Все люди высокие» не является предложением «Ни один человек не высокий.» Это можно было бы назвать напротив оригинальное предложение — оно говорит больше, чем просто «Все люди высокие’ не соответствует действительности». Правильное отрицание этого предложения «есть кто-то невысокого роста», что значительно слабее заявление. В символах отрицание $\forall x P(x)$ равно $\exists x\ \lnot P(x)$, а наоборот $\forall x \lnot P(x)$. («Отрицание» — широко используемый «официальный» термин; здесь широко не используется.)

Законы де Моргана можно использовать для упрощения отрицания «некоторых». форма и форма «все»; сами отрицания оказываются те же формы, но «обратные», то есть отрицание «всей» формы является «некоторой» формой, и наоборот. Предположим, что $P(x)$ и $Q(x)$ — формулы. Тогда у нас есть $$\lне \для всех x (P(x)\имеет Q(x)) \iff\ \существует x (P(x) \land \lnot Q(x)) $$ $$\lnot \exists x (P(x)\land Q(x)) \iff\ \для всех x (P(x)\имеет в виду \lnot Q(x)) $$ Отказ от предложения «все газонокосилки работают на бензин» — это фраза «какая-то газонокосилка делает не работать на бензине» (не «газонокосилки не работать на бензине,» наоборот). Проверим первое утверждение, а второе оставим для упражнения: $$\lне \для всех x (P(x)\имеет Q(x)) \ тогда и только тогда, когда \ существует x \lnot(P(x)\имплицитно Q (х)) \ тогда и только тогда, когда \ существует x (P(x) \land \lnot Q(x)) $$

Формула обычно проще, если $\lnot$ не стоит перед любое сложное выражение, то есть оно появляется только перед простым операторы, такие как $P(x)$. Ниже приведен пример упрощения отрицание формулы с использованием законов Де Моргана: $$ \eqalign{ \lnot \forall x (P(x)\lor \lnot Q(x))&\iff \существует x \lnot(P(x)\lor \lnot Q(x))\cr &\iff\exists x (\lnot P(x)\land \lnot \lnot Q(x))\cr &\iff\exists x (\lnot P(x)\land Q(x)) \cr} $$ Отрицание формул чрезвычайно полезно. В следующем разделе мы видим, что приемы, называемые доказательством от противного и доказательством путем контрапозитивные используют их широко. Отрицание также может быть полезным устройство для учебы. Когда вы читаете теорему или определение в математике часто бывает полезно сформировать отрицание этого предложения, чтобы увидеть что означает невыполнение условия. Чем больше способов вы думаете о понятии в математике, тем яснее оно должно стать. 92$.) Де Отец Моргана умер, когда ему было десять лет, после чего он был воспитан своей мать, набожный член англиканской церкви, которая хотела, чтобы он был министр. Далекий от того, чтобы стать министром, Де Морган развил выраженная антипатия к Церкви, которая глубоко повлиять на ход его карьеры.

Интерес де Моргана к математике и талант к математике не проявились. проявлялся до четырнадцати лет, но уже в шестнадцать он вступил Тринити-колледж в Кембридже, где он изучал алгебру у Джорджа Пикока. и логика под руководством Уильяма Уэвелла. Он также был превосходный флейтист, и стал известным в музыкальных клубах в Кембридж.

По окончании учебы Де Морган не смог получить должность в Оксфорде или Кембридж, так как он отказался подписать требуемый религиозный тест (тест не отменен до 1875 г.). Вместо этого в возрасте 22 лет он стал Профессор математики в Лондонском университете, новом учреждении основывается на принципе религиозного нейтралитета.

Де Морган много писал об алгебре и логике. Павлин и Григорий уже обратил внимание на фундаментальное значение для алгебры манипулирования символами; то есть, они установили, что основные операции алгебры не обязательно зависит от интерпретации переменных. Де Морган пошел один (большой) шаг вперед: он признал, что операции ($+$, $-$ и т. также не должны иметь фиксированного значения (хотя он сделал исключение для равенство). Несмотря на эту точку зрения, Де Морган, кажется, действительно думал, что единственные подходящие интерпретации алгебры были знакомы числовые области, прежде всего действительные и комплексные числа. Действительно, он считал, что комплексные числа образуют наиболее общие из возможных алгебре, потому что не мог заставить себя отказаться от привычного алгебраические свойства действительных и комплексных чисел, такие как коммутативность.

Одной из самых известных книг Де Моргана была «. Бюджет Парадоксы . Он использовал слово «парадокс» для обозначения всего, что выходит за рамки принятая мудрость предмета. Хотя это не нужно интерпретировать уничижительно, его примеры на самом деле были «математическим чудаком». разнообразие — математически наивные люди, которые настаивали на том, что могут например, разделить угол на три части или возвести в квадрат круг.

Сын де Моргана Джордж сам был выдающимся математиком. С друга, он основал Лондонское математическое общество и служил его первый секретарь; Де Морган был первым президентом.

В 1866 году Де Морган подал в отставку в знак протеста против назначения. это было сделано по религиозным мотивам, что, по мнению Де Моргана, злоупотребляло принцип религиозного нейтралитета, на котором основывался Лондонский университет. основан. Два года спустя умер его сын Джордж, а вскоре после этого дочь умерла. Возможно, эти события ускорили его собственную смерть. Морган умер в 1871 году от «нервного истощения».

Информация здесь взята из лекций о десяти британских Математики , Александр Макфарлейн, Нью-Йорк: John Wiley & Сыновья, 19 лет16.

Пример 1.3.1 Проверьте эти тавтологии с помощью таблиц истинности. $$\lnot (P\lor Q)\iff (\lnot P\land \lnot Q) $$ $$\lnot (P\land Q)\iff (\lnot P\lor \lnot Q) $$

Пример 1.3.2 Предположим, что $R(x)$ — это утверждение «$x$ — прямоугольник». а $S(x)$ — утверждение «$x$ — квадрат». Напишите следующее символически и решить, какие пары утверждений являются отрицаниями каждого другой:

а) Все прямоугольники являются квадратами.

б) Некоторые прямоугольники являются квадратами.

в) Некоторые квадраты не являются прямоугольниками.

d) Квадраты не являются прямоугольниками.

e) Никакие прямоугольники не являются квадратами.

f) Все квадраты являются прямоугольниками.

g) Некоторые квадраты являются прямоугольниками.

h) Некоторые прямоугольники не являются квадратами.

Пример 1.3.3 Запишите символически следующие отрицания определений относительно функции $f$:

Пример 1.

No related posts.