Правило углов: Угол — урок. Математика, 2 класс.

Первое правило эргономики: как создать «рабочий треугольник» на кухне

Об эргономике помещений задумались еще в прошлом веке немецкие ученые. Как сделать так, чтобы приготовление еды занимало меньше времени и хозяйка меньше уставала? Нужно оптимизировать перемещения по кухне, расположив рабочие зоны наиболее удобно. Для этого ученые анализировали передвижения женщин вдоль кухонного фронта, измеряли пройденные расстояния и засекали время. Их исследования выявили три центра активности, где хозяйки проводили больше всего времени: зона хранения, зона подготовки и зона приготовления еды. И немцы вывели принцип построения «рабочего треугольника», который и сейчас лежит в основе эргономики кухонных помещений.

Правило «рабочего треугольника» гласит: расположение основных рабочих зон – холодильника, раковины и плиты – должно укладываться в равносторонний треугольник со сторонами метр-полтора. При такой планировке человек во время приготовления еды будет двигаться по кратчайшей траектории и в итоге сэкономит силы и время.

Расположение рабочих зон относительно друг друга должно повторять ежедневные маршруты по кухне и не противоречить логике процессов: достал продукты, помыл, разделал, приготовил на плите. Важно учитывать и расстояние между вершинами треугольника – примерно два шага или полтора метра. Даже если у вас очень большая кухня, старайтесь располагать точки не дальше чем на 2,7 метра друг от друга.

Планируя кухню, мысленно прочертите линии между вершинами треугольника и убедитесь, что на пути между ними нет преград: стульев, тумб, выступающих углов. Ничто не должно мешать свободному передвижению между зонами. Угол кухонного острова не должен входить в пространство треугольника больше чем на 30 см.

Как оформить «рабочий треугольник» на кухнях разной планировки

В зависимости от планировки кухни эргономика будет отличаться. Если пользоваться математическими терминами, то треугольник не обязательно должен получиться равнобедренным или равносторонним. Тем не менее, при любой компоновке можно создать оптимальный маршрут, не слишком далеко отклоняясь от стандартов «рабочего треугольника».  

Линейная планировка

В рамках линейной планировки есть несколько вариантов создания «рабочего треугольника». 

• С точки зрения эргономики при однорядной компоновке лучше всего располагать мойку по центру, а холодильник и варочную поверхность – по бокам от нее. Во время готовки придется перемещаться по одной линии, поэтому важно соблюсти комфортное расстояние. Между раковиной и плитой должно быть 80–90 см, между зоной мойки и холодильником – 40–50 см.

 

• Можно вынести холодильник за пределы кухонного фронта, например, к соседней стене. При этом лучше расположить его ближе к раковине. При такой расстановке уже вырисовывается треугольник. 

 

• Если площадь кухни позволяет, разместите дополнительную рабочую поверхность – остров. Вынесите туда плиту или мойку – это решение позволяет сделать «рабочий треугольник» максимально приближенным к стандартам эргономики.

Параллельная планировка

При такой планировке кухонный фронт разбивается на два блока, расположенных параллельно друг другу. На одной стороне размещают плиту и мойку, разделенные рабочей поверхностью, напротив – зону хранения с холодильником и шкафами.

Угловая планировка

При угловой планировке кухонный фронт размещается вдоль двух смежных стен. Это один из самых эргономичных вариантов. Стандартное размещение по принципу «рабочего треугольника» – раковина в углу, а по обеим сторонам от нее холодильник и плита. 

П-образная планировка

Наиболее логичная и удобная с точки зрения эргономики пространства кухня – та, которая располагается по трем смежным стенам. П-образная планировка позволяет создать идеальный равнобедренный или равносторонний треугольник, в верхнем углу которого расположена раковина. 

Другие правила эргономичной кухни

С треугольника начинается планирование кухни, но им не заканчивается. Есть еще немало деталей, которые влияют на удобство пользования кухонным оборудованием. 

• Каждый кухонный элемент имеет свою «зону открывания». Учитывайте это на этапе планирования, чтобы в открытом виде холодильник, дверцы шкафов и духовки не блокировали проход.  

 

• По обе стороны от плиты оставьте как минимум 30 см чистой поверхности. Она очень пригодится, когда нужно будет срочно убрать горячую сковородку с плиты или разложить нарезанные ингредиенты. Минимальная поверхность по обе стороны мойки составляет 45 см.

• Стандартная высота столешницы составляет 85 см и подходит для людей ростом 160–170 см. Подбирайте высоту нижних шкафов под свой рост: правильная рабочая поверхность немного ниже пояса. Если быть точнее, на 15 см от согнутого локтя.

 

• Основную рабочую поверхность лучше всего расположить между раковиной и плитой. Это обосновано логикой действий: вы моете продукты, нарезаете и затем отправляете на плиту. 

 

• Навесные шкафы должны находиться на такой высоте, чтобы вы могли дотянуться до второй полки, не вставая на цыпочки.

 

• Не располагайте плиту и раковину ближе чем на 60 см друг от друга, чтобы брызги воды не летели в горячую сковороду.

 

• На эргономику кухни очень влияют различные приспособления для хранения кухонных принадлежностей: рейлинги, крючки, контейнеры, дополнительные полки. Благодаря этим помощникам каждой прихватке найдется свое место. 

 

• Для удобства передвижения и открывания дверей ширина между двумя рядами мебели при параллельной или п-образной планировке задается не менее 120 см и не больше 180 см.

Получайте вдохновение на почту

Подпишитесь на ежемесячную рассылку о свежих трендах в дизайне, обустройстве дома и наших специальных предложениях.

Углы Ганна — построение и применение. Как торговать по углам?

Содержание статьи:

(кликните, чтобы перейти к соответствующей части статьи):

• Базовый (балансовый) угол Ганна — 1х1 (45 градусов)
• Восходящий и нисходящий веера Ганна
• Оригинальные графики Углов Ганна, истинный масштаб (шкала)
• Расчет шкалы Углов Ганна по методу Джеймса Хьержика
• Построение Углов Ганна на графике
• Основные правила в применении Углов Ганна

---

Углы Ганна – один из эффективных инструментов для анализа и прогнозирования поведения цены. Метод основан на анализе изменения графика относительно линий, построенных от экстремумов под определенными углами.

 

Базовый (балансовый) угол Ганна — 1х1 (45 градусов)

Самый главный угол называется базовым или балансовым углом 1х1 и имеет наклон 45 градусов (на рисунке выше — красная линия). Линия балансового угла на графике является очень сильным уровнем сопротивления или поддержки.

 

Восходящий и нисходящий веера Ганна

Другие углы, образующие вместе с базовым углом так называемый веер Ганна, строятся на основе следующих величин:

• угол 2х1 – 63,75 градусов;
• угол 4х1 – 75 градусов;
• угол 8х1 – 85,5 градусов;
• угол 1х2 – 20,75 градусов;
• угол 1х4 – 15 градусов;
• угол 1х8 – 7,5 градусов.

Веер может быть как восходящим – с линиями, направленными вверх, так и нисходящим, являющимся зеркальным отражением первого.

 

Вышеприведенные веера являются стандартными. Существуют еще углы 16х1 и 1х16, но они являются дополнительными – с ними работают очень редко.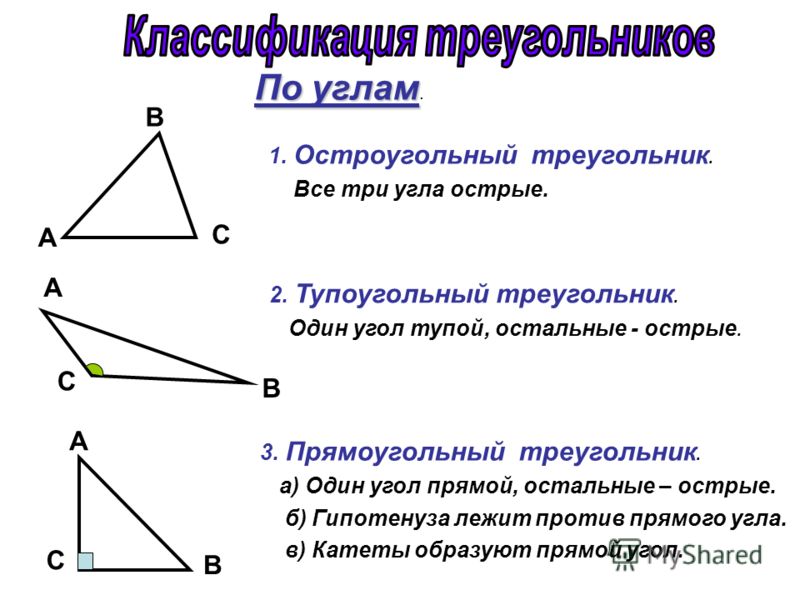

Помимо основных углов, стоит также отметить углы 90 и 0 градусов, которые не всегда упоминаются в учебной литературе по трейдингу. Тем не менее, они тоже имеют большое значение. При этом угол 0 градусов представляет собой горизонтальную линию.

 

Оригинальные графики Углов Ганна, истинный масштаб (шкала)

Ганн рисовал углы на графике, который был построен на миллиметровой бумаге при помощи транспортира. При нанесении углов на таком графике масштаб был уже учтен – то есть на единицу времени приходилось определенное количество пунктов изменения цены.

 

В настоящее же время мы не можем просто так нарисовать углы на графике в терминале, потому что в зависимости от масштаба самого графика линии будут располагаться по-разному.

Например, если в терминале построить простую трендовую линию под углом 45 градусов, получим такой результат:

 

Но, при изменении масштаба самого графика картина уже будет отличаться, так как ценообразование тоже изменилось.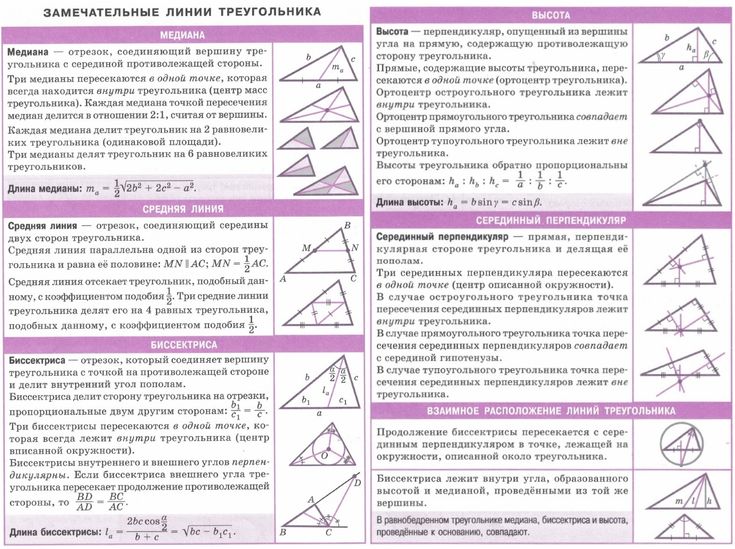 Сам угол визуально так и останется в 45 градусов, но по отношению к графику результат совершенно уже будет другим:

 

На бумаге же просто так изменить масштаб нельзя – определившись с ним заранее, для правильного построения графика, выбранному соотношению нужно придерживаться и далее. Как было упомянуто выше, на графике у Ганна на единицу цены приходится соответствующая единица времени. Если провести балансовый угол, разделяющий угол по диагонали, то есть под углом 45 градусов, то возникает вопрос: «А какая шкала у данного угла?» Все зависит от того, сколько пунктов приходится на один квадрат шкалы. Если на него приходится 30 пунктов, то говорят, что шкала балансового угла – 30 пунктов.

Когда Ганн рисовал свечи в виде скобок, шкала была уже в них учтена, то есть на одну ячейку приходилось определенное количество пунктов. Иначе говоря, Ганн вписывал шкалу именно в сами свечи (бары) на графике.

Учитывая, что 1 единица времени является баром, а значение бара зависит от типа графика, то, если рассматривается дневной график, где 1 бар равен 1 дню, то шкала в нашем примере будет равна 30 пунктам в день.

Ученики Ганна разработали таблицу различных шкал. Так, Джеймс Хьержик в своей книге приводит шкалы по разнообразным финансовым инструментам. При этом, рассматриваются только следующие таймфреймы: день, неделя, месяц, так как в то время не использовались таймфреймы менее 1 дня (Ганн даже считал дневной график слишком волатильным, с большим количеством шумов).

 

Вышеуказанные данные были высчитаны в 2000-х годах. Из таблицы видно, что дневная шкала Евродоллара составляла 2 пункта. При этом значение в центовом выражении не указано. Поэтому, исходя из этих данных, нельзя однозначно сказать, чему равняются те же 2 пункта в наше время.

Тогда каким же образом можно построить шкалу сейчас, если нет информации о масштабе графика? Ведь количество пунктов зависит еще и от количества знаков, используемых после запятой в котировке той или иной валютной пары. А их может быть четыре, пять, а в некоторых случаях и более.

Рассчитать шкалу можно по графику. Рассмотрим, как это можно сделать.

 

Расчет шкалы Углов Ганна по методу Джеймса Хьержика

Джеймсом Хьержиком был разработан простой метод расчета шкалы для рынка с неизвестными параметрами.

Для начала, нужно схематично расчертить на графике движение цены (от вершины к основанию, от основания к вершине). Затем рассчитывается разница в пунктах между одной вершиной и второй вершиной и результат делится на период времени между этими пунктами (на количество баров).

Затем точно такая же операция проделывается между одним основанием и вторым основанием. Затем между второй и третьей вершиной, затем между вторым и третьим основаниям и т.д.

После всех этих операций нужно рассчитать среднее значение получившихся результатов, для этого нужно сложить все результаты вместе и разделить на количество самих результатов. Получившееся среднее значение – это и будет значение шкалы для данного графика.

К примеру, если разница между одной вершиной и второй составила 50 пунктов, а период – 27 дней, то шкала будет равна 50/27= 1,85. Для получения средней величины нужно повторить такие же вычисления с другими вершинами и основаниями, посчитать среднее арифметическое значение и округлить полученный результат.

На представленном ниже графике для расчета шкалы были выбраны по три сформировавшихся вершины и основания (незаконченные вершины, такую как последнюю, в целях расчета использовать нельзя). Для каждой пары вершин (1-2, 2-3) и для каждой пары оснований (1-2, 2-3) необходимо посчитать разницу в пунктах и поделить результат на соответствующую величину времени — количество баров, которые разделяют данные вершины (основания). Для выведения среднего значения, полученные 4 числа нужно сложить и поделить на 4, а затем округлить.

 

Существуют и другие методы расчета шкалы, которые мы рассмотрим позже, в следующих статьях. Например, метод первого импульса, который задает основной темп движения тренда. Данный метод позволяет определить значение шкалы с точностью не менее 90%.

 

Построение Углов Ганна на графике

Теперь, после расчета шкалы, можно уже приступить непосредственно к построению самих Углов Ганна на графике. Для этого, в Метатрейдере нужно выбрать инструмент «Линия Ганна», открыть свойства этой линии, перейти на вкладку «Параметры» и в Масштабе прописать высчитанное ранее значение нашей шкалы:

 

Это мы построили базовый балансовый угол 1х1. Его нужно поставить на тот экстремум, от которого Вы будете строить сам веер Ганна.

Для того, чтобы построить остальные углы из веера, нужно просто то значение шкалы для основного угла 1х1, которое мы получили ранее, умножить на 2 или 4 или 8 (для углов, которые будут выше базового угла) или разделить на 2 или 4 или 8 (для углов, которые будут ниже базового угла).

Технически эти углы строим точно также, как и основной базовый угол, при помощи инструмента Gann Line в MetaTrader4.

 

Более подробно инструмент «Линия Ганна» (Gann Line) в MetaTrader4 (как эту линию использовать, настраивать и прочее) мы подробно рассмотрим в следующей статье.

 

Основные правила в применении Углов Ганна

После расчета шкалы и построения Углов Ганна можно приступить непосредственно к работе с углами и их анализу.

Анализ углов строится на принципе главного и основного правила — все движение цены происходит от одного угла к другому.

Так, пробив вниз линию одного восходящего угла, цена стремится к нижеследующему. Причем неважно, каким образом она будет идти к соответствующему углу – цена в принципе может не дойти до угла, она и не обязана, но, что очень важно, углы для цены являются магнитом и они так или иначе цену тянут к себе. Этот факт как раз и заложен в основное правило углов, что цена, пробив один угол будет стремиться к другому.

 

То же самое можно наблюдать и на нисходящем веере углов Ганна:

 

Но, внимание, правило углов Ганна (если цена пробила угол, то она будет стремиться к следующему углу), это еще далеко не торговая стратегия и просто так торговать, только основываясь на этом правиле ни в коем случае нельзя.

Данное правило не для торговли, данное правило нам очень сильно поможет в анализе графика цены. При помощи него мы можем для себя четко определить где сейчас цена и что нам точно делать, если цена пойдет в одну сторону, и что нам делать, если цена пойдет в другую сторону и так далее.

 

Понравилась статья? Делитесь данной статьей со своими знакомыми в социальных сетях, возможно, этот материал кому-то будет очень полезен.

 

Другие статьи по теме Методы Ганна Вы можете просмотреть в данном содержании уроков по методам Ганна.

 

Понравился материал статьи?
Добавьте эту статью в закладки Вашего браузера, чтобы вернуться к ней еще раз. Для этого, прямо сейчас нажмите на клавиатуре комбинацию клавиш Ctrl+D

 

Angle Facts — GCSE Maths — Руководство по геометрии

8 комментариев / GCSE Математика, Геометрия / Автор Лиам Магуайр

Факты об углах для GCSE

Чтобы хорошо сдать GCSE по математике, вам нужно хорошо разбираться в основных фактах об углах, лежащих в основе геометрии. К счастью, у нас есть для вас это удобное руководство, в котором изложены все основы, которые вам необходимо знать. Усвойте эти правила, и у вас все получится.

Вы также можете найти другие наши замечательные бесплатные руководства по пересмотру и практические вопросы на нашей странице ресурсов. Следите за изменениями с индивидуальной помощью наших опытных онлайн-репетиторов.

Сумма углов треугольника составляет 180 градусов Сумма внутренних углов любого треугольника составляет 180 градусов

Сумма углов четырехугольника составляет 360 градусов Сумма внутренних углов любого четырехугольника составляет 360 градусов

Углы на прямой в сумме дают 180 градусов a + b = 180 градусов

Противоположные углы равны При пересечении двух прямых противоположные углы равны.

Внешний угол треугольника равен сумме противолежащих внутренних углов x = y + z

Поскольку сумма углов на прямой составляет 180 градусов, а сумма трех внутренних углов треугольника также составляет 180 градусов, внешний угол треугольника равен сумме двух противоположных внутренних углы, как показано выше.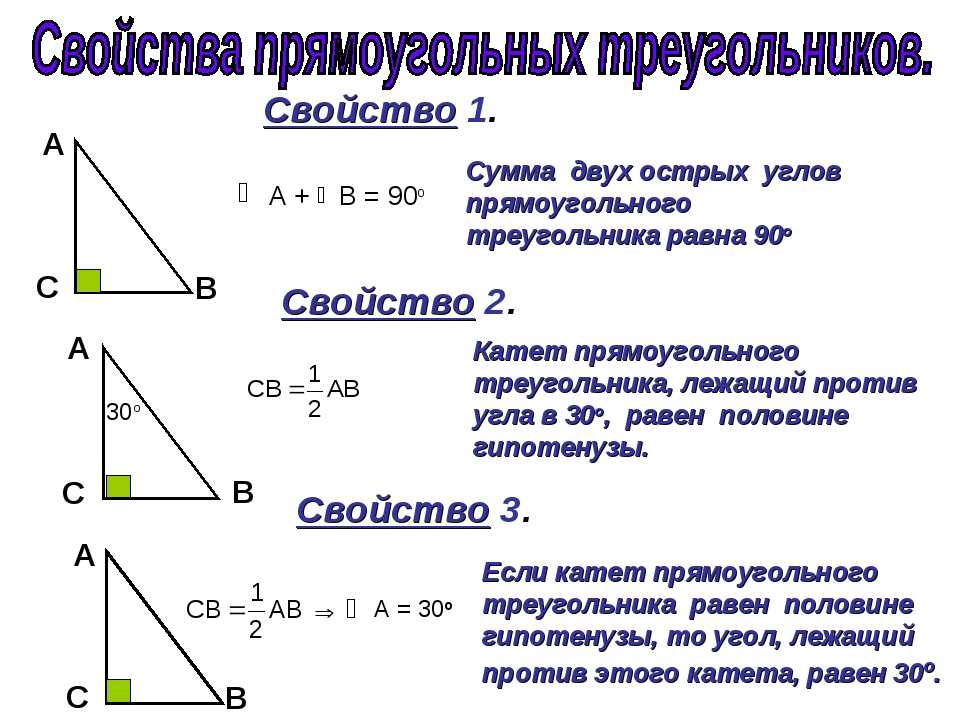

Вы также можете найти наше соответствующее руководство по площади и периметру, которое будет полезно для вашей доработки.

Работа с параллельными линиями

Соответствующие углы равны Соответствующие углы

Если у вас есть пара параллельных прямых, одна из которых пересекает их, соответствующие углы равны. В основном углы в одном и том же положении на каждой параллельной линии будут равны углу в этом положении на другой параллельной линии. Это правило иногда называют «F-углами», потому что углы образуют F-образную форму. Я знаю… проще всего увидеть это на схеме.

Альтернативные углы равны Альтернативные углы

Если у вас есть две параллельные линии, альтернативные углы (как показано выше) всегда равны. Это правило иногда называют «углы Z», потому что углы образуют Z-образную форму.

Внутренние совмещенные углы составляют 180 градусов Совмещенные внутренние углы составляют 180 градусов

Вот еще одно правило, где у вас есть две параллельные линии. На этот раз внутренние углы в сумме составляют 180 градусов. Это правило иногда называют «С-углами», потому что углы образуют форму буквы «С». Вы ищете углы на той же стороне линии, пересекающей параллельные линии, и на внутренней стороне параллельных линий.

Теперь попрактикуйтесь в том, что вы здесь откорректировали, ответив на наши практические вопросы.

Это основные сведения об углах, которые вам необходимо знать для сдачи GCSE по математике, поэтому обязательно выучите их. Посетите нашу страницу ресурсов, чтобы узнать больше вопросов по этой и другим темам. Вы также можете связаться с нами для любой конкретной поддержки или задать любые вопросы.

Правил углов — Математика GCSE

Здесь мы узнаем о правилах углов , в том числе о том, как решать задачи, связанные с углами на прямой линии, углами вокруг точки, вертикально противоположными углами, дополнительными углами и дополнительными углами.

Есть также рабочие листы угловых правил , основанные на экзаменационных вопросах Edexcel, AQA и OCR, а также дополнительные указания о том, что делать дальше, если вы все еще застряли.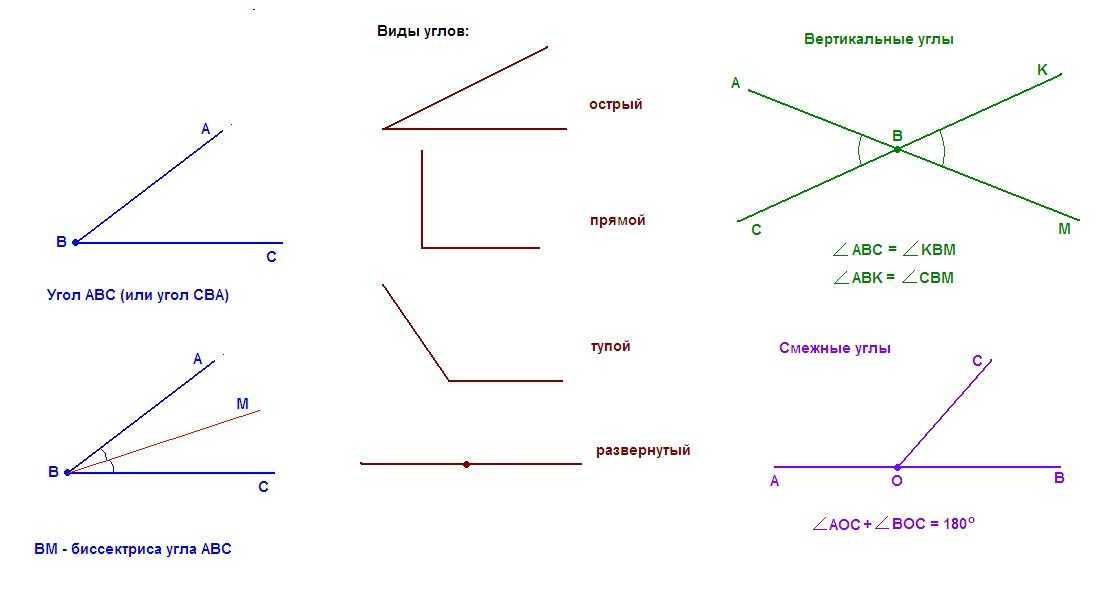

Что такое угловые правила?

Угловые правила позволяют нам вычислять неизвестные углы:

• Углы на прямой равны 180 º
  

Здесь два угла обозначены как 30° и 150° ^º . Сложенные вместе, они равны 180 ^º и, следовательно, лежат на прямой. Эти углы имеют общую вершину.

Однако ниже мы можем увидеть пример, где два угла не равны 180º:

Это потому, что они не имеют общей вершины и, следовательно, не лежат на одном и том же отрезке.

Примечание : вы можете проверить вышеприведенное правило, нарисовав приведенные выше диаграммы и измерив углы с помощью транспортира.

Пошаговое руководство: Углы на прямой линии

• Углы вокруг точки равны 360 ^o
  Углы вокруг точки всегда равны 360º.

Три приведенных выше угла имеют общую вершину и при суммировании равны 360 ^o .

Пошаговая инструкция: Углы вокруг точки

• Дополнительные углы
  Два угла дополнительные когда они в сумме дают 180º, они не должны быть рядом друг с другом.

Эти два угла являются дополнительными, так как в сумме они составляют 180°.

Пошаговое руководство: Дополнительные углы

• Дополнительные углы
  Два угла являются дополнительными , когда они в сумме составляют 90º , они не должны быть рядом друг с другом.

Эти два угла являются дополнительными, так как при сложении они равны 90º.

Пошаговое руководство : Дополнительные углы

• Вертикально противоположные углы
  Вертикально противоположные углы относятся к углам, которые противоположны друг другу в определенной вершине и образуются путем пересечения двух линий.

Здесь два угла, обозначенные буквой «а», равны друг другу, потому что они «вертикально противоположны» в одной и той же вершине.

То же самое относится к углам, помеченным буквой «b».

Пошаговое руководство: Вертикально противоположные углы

При решении задач, связанных с углами, иногда мы используем больше, чем приведенные выше правила. Ниже вы увидите ряд задач, связанных с углами, со ссылками на уроки, которые будут более подробно рассмотрены с более сложными вопросами.

Что такое угловые правила?

Ключевые слова

Важно, чтобы мы были знакомы с некоторыми ключевые слова , терминология и символы для этой темы:

• Угол : определяется как величина поворота вокруг общей вершины.

• Вершина : точка, созданная двумя отрезками (множественное число — вершины).

Обычно мы обозначаем углы двумя основными способами:

1Назначая углу «имя», которое обычно представляет собой строчную букву, такую ​​как a, x или y, или греческую букву θ (тета). См. пример ниже:

2 Ссылаясь на угол как три буквы, которые определяют угол. Средняя буква относится к вершине, в которой угол, например. см. ниже угол, который мы называем ABC:

Как использовать правила углов

Чтобы решить задачи, связанные с углами, вы должны выполнить следующие шаги:

1. Определите, какой угол вам нужно найти .
2. Определите, какое правило(я) угла применяется к контексту, и запишите их .
3. Решите задачу, используя приведенное выше правило(я) углов. Приведите причины, где это применимо .
4. Четко сформулируйте ответ, используя терминологию угла .

Как пользоваться угловыми линейками

Примеры правил углов

Пример 1: углы на прямой

Найдите углы a и b.

1. Определите, какой угол вам нужно найти (подпишите, если нужно) .

Вам нужно найти углы, обозначенные буквами a и b.

2 Определите, какие правила углов применяются к контексту, и запишите их (помните, что может потребоваться несколько правил) .

Углы на прямой в одной и той же вершине всегда составляют в сумме 180 ^o .

Обратите внимание, что углы a и b не имеют общей вершины.

3Решите задачу, используя приведенное выше правило(я) углов. Приведите причины, где это применимо.

\[\begin{выровнено} а+110&=180\\ а=&70 \end{выровнено}\]

\[\begin{выровнено} б+55&=180\\ б&=125 \end{aligned}\]

4Четко сформулируйте ответ, используя терминологию угла.

Угол a = 70°

Угол b = 125°

Пример 2: углы вокруг точки

Найдите размер θ:

Определите, какой угол вам нужно найти (обозначьте его, если нужно) .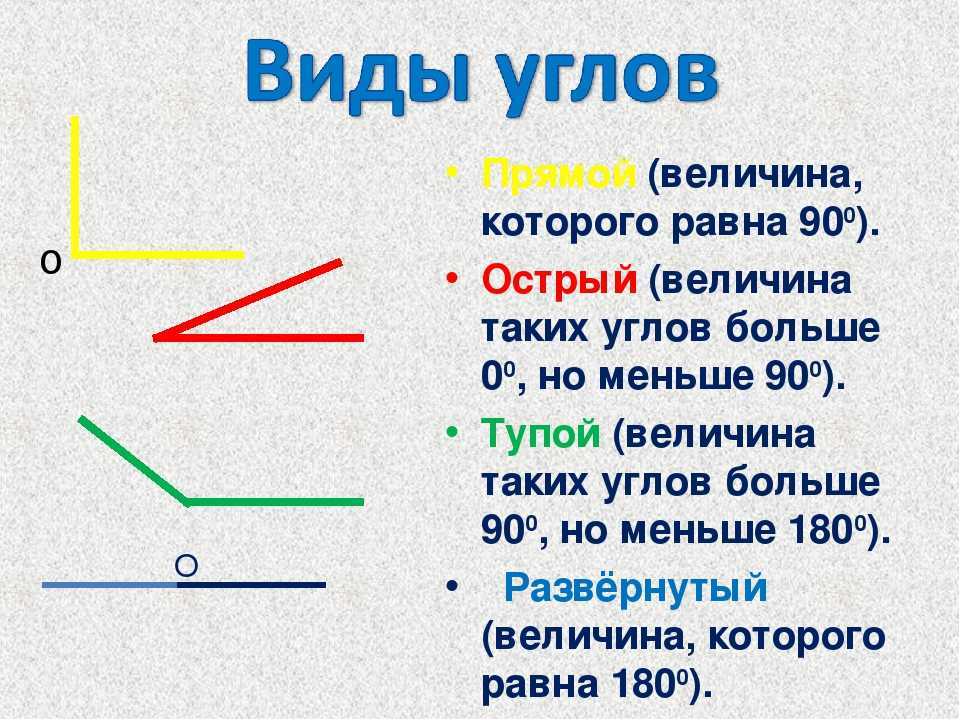

Вам нужно найти угол, обозначенный θ (тета) .

Определите, какие правила углов применяются к контексту, и запишите их (помните, что может потребоваться несколько правил) .

Все углы лежат вокруг одной вершины, и мы знаем, что углы вокруг точки равны 360 9{\circ}\]

Пример 3: использование дополнительных углов

Два угла являются дополнительными, и один из них равен 127°. Какова величина другого угла?

Определите, какой угол вам нужно найти (отметьте, если нужно) .

Вам нужно найти другой угол в паре дополнительных углов, один из которых равен 127°. Мы назовем этот угол «а».

Определите, какие правила угла применяются к контексту, и запишите их (помните, что может потребоваться несколько правил) .

Дополнительные углы в сумме составляют 180°.

Решите задачу, используя приведенное выше правило(я) углов. Приведите причины, где это применимо .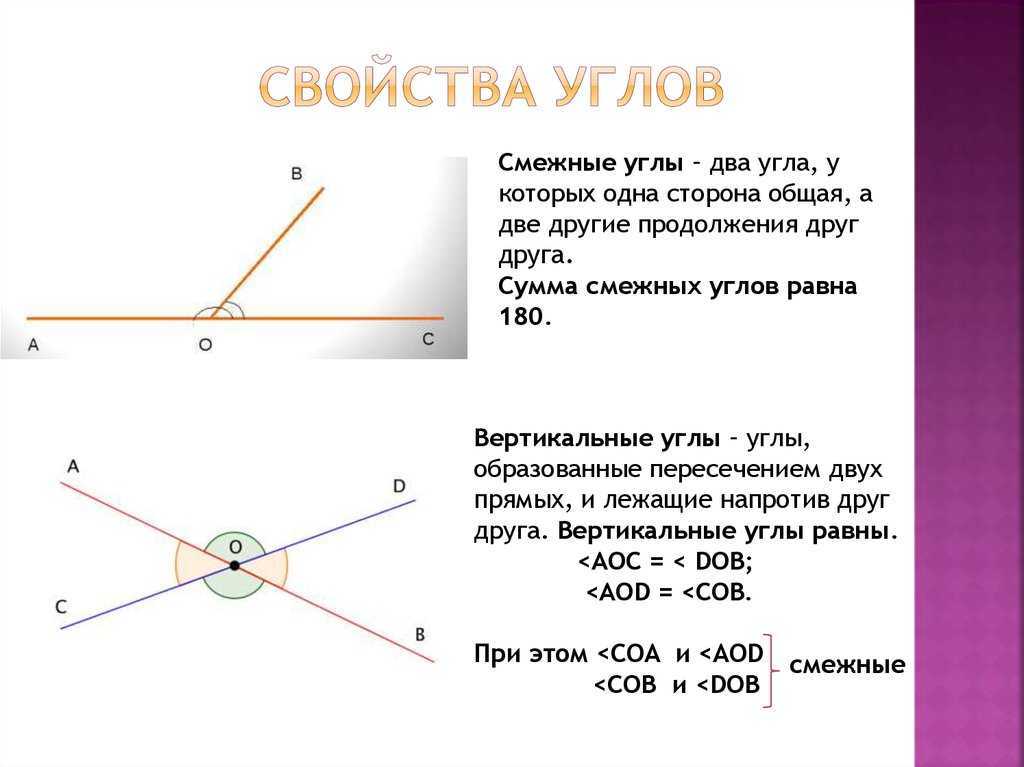

\[\begin{выровнено} 127 + а ​​&= 180\\ а&=53\\ \end{align}\]

Четко сформулируйте ответ, используя терминологию угла .

Другой угол равен 53°.

Пример 4: использование дополнительных углов

Если два угла являются дополнительными и один из них равен 34°, какова величина другого угла?

Определите, какой угол вам нужно найти (подпишите, если нужно) .

Вам нужно найти другой угол в паре дополнительных углов, один из которых равен 34°. Мы назовем этот угол ‘b’.

Определите, какие правила углов применяются к контексту, и запишите их (помните, что может потребоваться несколько правил) .

Дополнительные углы в сумме дают 90°.

Решите задачу, используя приведенное выше правило(я) углов. Приведите причины, где это применимо .

\[\begin{выровнено} 34 + б &=90\\ б &= 56\\ \end{align}\]

Четко сформулируйте ответ, используя терминологию угла .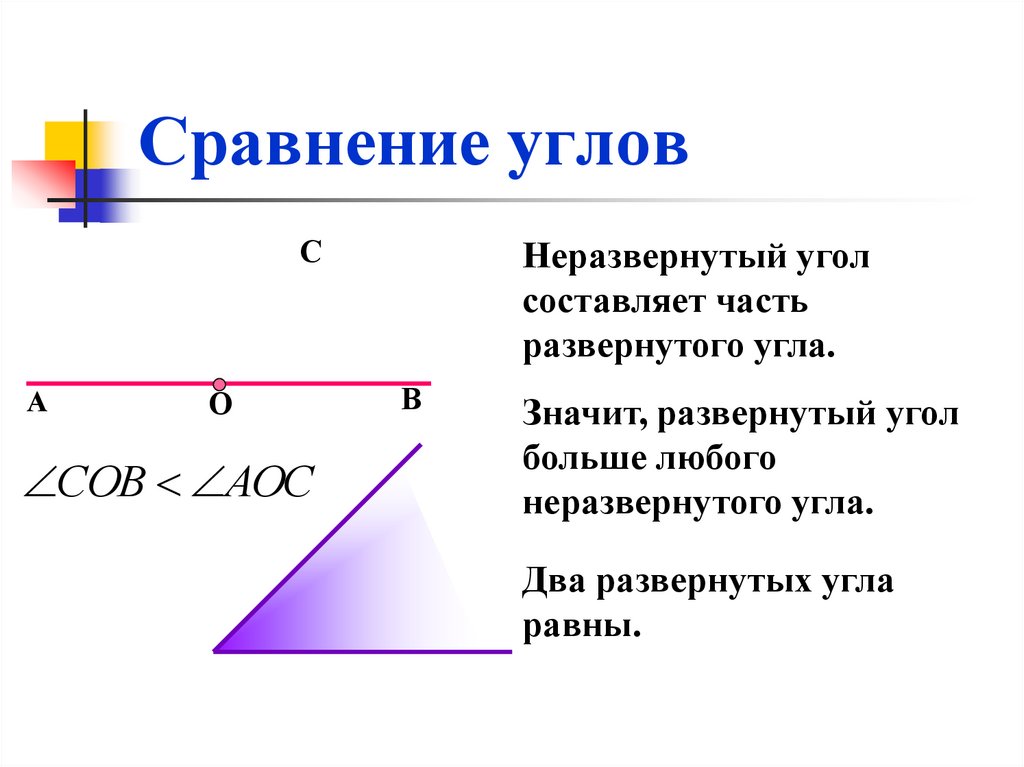

Другой угол равен 56°.

Пример 5: вертикально противоположные углы

Найдите угол BCD.

Определите, какой угол вам нужно найти (отметьте, если нужно) .

Найдите угол при вершине C, составленный из прямых CD и CB. На диаграмме он обозначен как x

Определите, какое правило(я) угла применяется к контексту, и запишите их (помните, что может потребоваться несколько правил) .

Угол x и 80 ^o  вертикально противоположны друг другу в вершине, образованной пересечением двух прямых.

Вертикально противоположные углы равны друг другу

Решите задачу, используя приведенное выше правило(я) углов. Приведите причины, где это применимо .

x = 80, потому что они вертикально противоположны

Четко сформулируйте ответ, используя угловую терминологию

Угол BCD = 80°

Пример 6: Применение нескольких правил для решения задачи

На рисунке ниже:

• Угол AOB прямой.

• AOE и EOD являются дополнительными углами.

• Угол AOE составляет 50 градусов.

Найти угол COD.

Определите, какой угол вам нужно найти (отметьте, если нужно) .

Начнем с обозначения диаграммы. Мы обозначили угол, который пытаемся найти, x.

Определите, какие правила угла применяются к контексту, и запишите их (помните, что может потребоваться несколько правил) .

Два угла являются дополнительными, если их сумма равна 90 ^o .

Углы вокруг точки всегда равны 360 ^o .

Углы на одной части прямой всегда составляют в сумме 180 ^o .

Вертикально противоположные углы равны.

Решите задачу, используя приведенное выше правило(я) углов. Приведите причины, где это применимо .

Примечание: есть несколько способов решить эту проблему. Ниже приведен только один метод.

Так как AOE и EOD являются дополнительными углами, они должны быть равны 90 градусам. Следовательно:

\[\begin{align} 50+Э О Д&=90 \\ Э О Д&=40 \end{aligned}\]

EOD и BOC вертикально противоположны. Следовательно:

\[\begin{align} В О С&=Е О D \\ Б О С&=40 \end{aligned}\]

Углы вокруг точки равны 360 градусам. Следовательно:

\[\begin{align} А О В+А О Е+Е О D+В О С+х=360 \\ 90+50+40+40+х=360\\ 220+х=360\\ х=140 \конец{выровнено}\]

Четко сформулируйте ответ, используя терминологию угла .

Angle COD = 140 °

Обычные заблуждения

• Неправильно ура маркировки
• Неправильное использование правила «Прямой линии», где углы не разделяют пособия для пособия на пособие и пособия на поставках.
•  Нахождение неправильного угла из-за непонимания терминологии 

9{\ круг}

(1)

Учебный контрольный список

Теперь вы научились:

•  Использовать общепринятые термины и обозначения для углов
• Применять свойства углов на прямой линии, вокруг точки и на вертикально противоположных углах
• Применение фактов и свойств углов (например, дополнительные и дополнительные углы) для решения задач 

Все еще застряли?

Подготовьте своих учеников KS4 к успешной сдаче выпускных экзаменов по математике с помощью программы Third Space Learning.