4.2. Умножение и деление графиков
Изучим правила перемножения и деления графиков функций. Рассмотрим как построить график суперпозиции двух функций. Приведем некоторые примеры.
Произведение. Пусть известны графики двух функций
и
.
Построим график функции .
Для этого изобразим на одном чертеже
графики функций, входящих в произведение.
Затем проведем ряд вертикальных прямых,
пересекающих графики этих функций, и
пометим на них точки, ординаты которых
равны произведению ординат перемножаемых
функций. При этом, если ордината одной
их функций, входящих в произведение
равна нулю, т.е. ее график пересекает
ось
,
то и ордината произведения будет равна
нулю, т.е. график
будет пересекать ось
при том же значении абсциссы. Если
ордината одной их функций
или
равна
,
то ордината произведения этих функций
будет раположена на графике другой
функции. Если перемножаются ординаты
одного знака (либо обе ординаты имеют
знак »
«,
либо обе ординаты имеют знак »
«),
то произведение будет положительно.
Например (см. рис. 21), при имеем , , значит .
Рис. 21. Графики функций , и .
Пример 10. Построить график функции .
Решение. График функций и нам известны. График — бисектрисса первого и третьего координатных углов, а график изображен на рис. 22. Заметим, что функция — нечётная и — нечётная, поэтому их произведение — чётная функция. Следовательно, достаточно построить график только для , а затем симметрично отобразить на полуплоскость . Заметим также, что поскольку , то произведение , т.е. график не выходит за пределы линий и .
Итак,
пусть
.
В точках ,
где произведение равно нулю, следовательно в этих точках
график
пересекает ось
.
Проведя вертикальные прямые через точки , …, и перемножая соответствующие ординаты функций и , получим график функции (см. рис. 22).
Рис. 22. Графики функций , и .
Частное. Теперь, зная графики функций и изобразим график функции . Если знаменатель дроби отличен от нуля: , то при делении графиков совершаются действия, аналогичные действиям при умножении графиков. А именно, изображаются графики и , проводится ряд вертикальных прямых, пересекающих эти графики, отмечаются точки, ординаты которых равны , полученные точки соединяются плавной линией (см. рис. 23).
Рис. 23. Графики функций , и .
Точки,
в которых заслуживают особого внимания, поскольку
в этих точках функция
не существует. В окрестнотях точек, в
которых знаменатель
функция
может вести себя по разному. Рассмотрим
возможные варианты.
В окрестнотях точек, в
которых знаменатель
функция
может вести себя по разному. Рассмотрим
возможные варианты.
Пусть при ( ). Возможны два случая: или .
При функция неограниченно возрастает или убывает в окрестности точки . В этом случае, нужно обратить внимание на знак частного при и при . Рассмотрим, например, правую окрестность, т.е. точки , которые больше : . Если при , достаточно близких к , таких, что частное , то график функции будет уходить вверх, прижимаясь справа к прямой , но не пересекая её. Если же , то график будет идти вниз, прижимаясь справа к прямой (см. рис. 23).
Аналогично поведет себя график и в левой окрестности, т.е. при (только прижиматься к прямой график будет слева) (см. рис. 23). Ситуацию
когда и
и
можно тщательно изучить только пользуясь
теорией пределов, однако в некоторых
случаях можно определить поведение
функции
исходя из графиков
и
и в этом случае.
Отметим также, что для построения частного можно перемножить графики и .
Замечание. При построении графиков произведения и частного двух функций полезно помнить, что если обе функции и чётные или обе нечётные, то и произведение и частное будет чётной функцией. Если же одна из функций или нечётная, а другая чётная, то их произведение и частное будет нечётной функцией.
Пример 11. 3 Построить график функции .
Решение. Используя рис. 2 и таблицу 1 изобразим графики функций и (см. рис. 24).
Функции определена и непрерывна во всех точках, за исключением нуля.
Заметим, что — четная функция, причем при , функция тоже четная, причем для всех . Поэтому функция график будет симметричен относительно оси и расположен выше оси .
Построим
график
при
.
Проведем вертикальные линии, проходящие
через точки
, , , и отметим на них значение частного
функций и . Так при
будем иметь ,
при
получим и т.д.
Так при
будем иметь ,
при
получим и т.д.
Замечая, что при знаменатель дроби обращаетя в нуль, а числитель отличен от нуля (равен единице), и учитывая, что для всех (значит, и в любой окрестности точки ) получим, что график рассматриваемой функции при будет уходить вверх, прижимаясь справа к оси .
Рис. 24. Графики функций , и .
Соединяя отмеченные точки и рисуя график функции в промежетке от до уходящим вверх и приближающимся справа к оси , получим график функции при . В силу четности рассматриваемой функции, слева от оси изображаем кривую, симметричную кривой справа от оси , получаем искомый график (см. рис. 24).
Операции c функциями — сложение, вычитание, умножение и деление
Операции c функциямиФункции можно складывать
Функции можно вычитать
Функции можно умножать
Функции можно делить
Функции могут быть составлены друг с другом
Давайте возьмем две функции
f(x) = x2 and g(x) = x
Сумма этих функций:
f(x) + g(x) = x2 + x
Сумма двух функций f и g определяется как f + g
Определение операций с функциями
(f + g)(x) = f(x) + g(x) Сложение
(f — g)(x) = f(x) — g(x) Вычитание
(f.

(f/g)(x) = f(x)/g(x) Деление
Для функции f + g, f — g, f.g, области определяются как пересечение областей f и g
Для f/g, область есть пересечение областей f и g кроме точек, где g(x) = 0
Пример
f(x) = 1 + √x — 2 and g(x) = x — 1
Тогда их сумма определяется как
(f + g)(x) = f(x) + g(x) = (1 + √x — 2) + (x — 1) = x + √x — 2
Теперь давайте сравним области первоначальных функций f и g с их суммой:
| Функция | Область |
| f(x) = 1 + √x — 2 | [2; +∞) |
| g(x) = x — 1 | (-∞ +∞) |
| (f + g)(x) = x + √x — 2 | [2; ∞)∩(-∞ +∞) = [2; ∞) |
Пример:
Рассмотрим две функции
f(x) = 3√x and g(x) = √x
Тогда их произведение определяется как
(f.
 g)(x) = f(x).g(x) = (3√x)(√x) = 3x
g)(x) = f(x).g(x) = (3√x)(√x) = 3xОбратите внимание, что
Натуральная область 3x есть (-∞; +∞)
Теперь сравним области первоначальных функций f и g, и их произведение:
| Функция | Область |
| f(x) = 3√x | [0; +∞) |
| g(x) = √x | [0; +∞) |
| (f.g)(x) = 3x, x ≥ 0 | [0; +∞) ∩ [0; +∞) = [0; +∞) |
Иногда произведение двух одинаковых функций записывается как
f2(x) = f(x).f(x)
В целом, если n есть положительным целым, тогда hen
f
Например,
sin(x).sin(x) = (sin(x))2 = sin2x
Допустим, что есть две функции
f(x) = x3 и g(x) = x + 4
Если мы заменим g(x) на x в формуле для f, мы получим новую функцию, определенную
(f o g)(x) = f(g(x)) = (g(x))3 = (x + 4)3
Чтобы вычислить f(g(x)) необходимо вычислить сначала g(x) для x из области g, а тогда необходимо g(x) в области f вычислить f(g(x))
Пример:
Есть
f(x) = x2 + 3 g(x) = √x
Тогда составная этих функций есть
(f o g)(x) = f(g(x)) = (g(x))2 + 3 = (√x)2 + 3 = x + 3
Теперь сравним областя оригинальных функций f и g, и их составную функцию
| Функция | Область |
| f(x) = x2 + 3 | (-∞; +∞) |
| g(x) = √x | [0; +∞) |
| (f o g)(x) = x + 3 | Все x в [0; +∞) такие, что g(x) лежит в (-∞; +∞) отсюда область is (-∞; +∞) |
Рассмотрим функцию
h(x) = (x + 1)2
мы можем разбить функцию h как
f(x) = x + 1
g(x) = x2
h(x) = g(f(x))
Примечание:
Обратите внимание, что мы можем выразить функцию как
(x2 + 1)10 = [(x2 + 1)2]5 = f(g(x))
g(x) = (x2 + 1)2
Также мы можем записать (x2 + 1) = [(x2 + 1)3]10/3 = f(g(x))
g(x) = (x2 + 1)3, f(x) = x10/3
Обратите внимание, что в целом мы не можем записать
(f o g) ≠ (g o f)
Область (f o g) состоит из всех x в области g для которых g(x) в области f
Как найти точки пересечения графиков функций — алгоритмы и примеры правила и методики » Kupuk.
 net
netСуществует определенный класс задач по дисциплине «Алгебра и начало анализа», в которых нужно найти точки пересечения графиков функций без их построения. Решать такие задания довольно просто, когда известна определенная методика нахождения координат по оси абсцисс и ординат. Однако для этого необходимо научиться правильно находить корни уравнений различных типов.
Общие сведения
Функция — некоторое выражение, описывающее зависимость между двумя величинами. Следует отметить, что последних может быть несколько. Параметр, который не зависит от других элементов, называется аргументом, а зависимое тождество — значением функции.
Точка пересечения графиков означает, что у системы уравнений существует общее решение. Следует отметить, что для их нахождения можно воспользоваться графическим и аналитическим методом. Первый подразумевает построение графического представления выражения с переменной.
Чтобы найти пересечение графиков функций аналитическим способом, необходимо решить уравнение, корни которого являются искомыми точками. 2+St+U=0).
2+St+U=0).
Равносильные тождества
При выполнении математических операций каждое выражение может быть заменено на эквивалентное, т. е. равносильное. Иными словами, равносильными называются уравнения, различные по составляющим их элементам, но имеющие одинаковые корни. Следует отметить, что ими являются также выражения, не имеющие решений. Математики выделяют три свойства: симметричность, транзитивность и разложение на множители.
Формулировка первого: когда I уравнение равносильно II, то значит, и II равносильно I. Суть транзитивности состоит в том, что если I равносильно II, а II — III, то значит I эквивалентно III. Второе свойство имеет такую формулировку: произведение двух элементов, содержащих переменные, равное нулевому значению, эквивалентно двум выражениям, которые можно приравнять к 0. Математическая запись утверждения имеет такой вид: R(t)*S(t)=0 {R(t)=0 и S(t)=0}.
Математические преобразования
Для решения уравнения необходимо выполнить некоторые математические преобразования. 2 -9 не заканчиваются, поскольку его можно представить в виде разности квадратов, т. е. (s+2-9)(s+2+9)=(s-7)(s+11). Кроме того, формулы сокращенного умножения рекомендуется применять при понижении степени.
2 -9 не заканчиваются, поскольку его можно представить в виде разности квадратов, т. е. (s+2-9)(s+2+9)=(s-7)(s+11). Кроме того, формулы сокращенного умножения рекомендуется применять при понижении степени.
Методики нахождения точек
Чтобы узнать, пересекаются ли графики функций, нужно приравнять соответствующие тождества, а затем решать уравнение. Однако при такой операции могут получиться различные равенства с неизвестными. В этом случае требуется обратить внимание на нижеописанные методики решения для каждого вида.
Первой и второй степени
Уравнение первой степени, или линейное, решается очень просто. Для этого необходимо перенести переменные величины в одну, а известные — в другую сторону. Методика решения имеет следующий вид:
 (1/2)]/2P, где t1 и t2 — точки пересечения с осью абсцисс.
(1/2)]/2P, где t1 и t2 — точки пересечения с осью абсцисс.Если коэффициент при второй степени (P) эквивалентен 1, то дискриминант можно не высчитывать, а воспользоваться сокращенным вариантом решения — теоремой Виета. Суть ее заключается в подборе корней по таким формулам: t1+t2=-S и t1*t2=U. Иногда для реализации этой методики нужно сократить обе части на коэффициент Р. Алгоритм решения квадратных уравнений имеет следующий вид:
Следует отметить, что распространенная ошибка новичков — отсутствие проверки. В результате неправильных действий образуются ложные корни, а оценка на контрольной, зачете или экзамене существенно снижается.
Кубические и биквадратные
Решение тождеств кубического и биквадратного типов с неизвестными осуществляется двумя способами. К ним относятся:
К ним относятся:
В первом случае необходимо выполнить преобразования, которые позволят применить одну из формул сокращенного умножения. Однако этот метод применяется довольно редко, поскольку математики отдают предпочтение второму способу. Для его реализации вводится дополнительная переменная, обладающая более низкой степенью и существенно упрощающая выражение. Алгоритм имеет такой вид:
Для проверки рекомендуется воспользоваться онлайн-приложениями, позволяющими вычислить корни, а также построить графики функций. 3 +km+l=0.
3 +km+l=0.
Следует отметить, что важным пунктом методики является правильный выбор выражения замены, а затем верное выполнение математических преобразований.
Пример решения
Для закрепления знаний необходимо перейти к практическому решению заданий.Одной из простых задач является следующая: найдите координаты точки пересечения графиков линейных функций z=2t+7 и z=t-1. Решается задача по такому алгоритму:
В четвертом пункте нужно подставить координату по оси абсцисс в любое из уравнений для получения второй составляющей, необходимой для точки. Следует отметить, что в этой задаче нет необходимости проводить математические преобразования. Однако существуют и более сложные задания, в которых необходимо решать квадратные уравнения, а также раскрывать скобки.
Следует отметить, что в этой задаче нет необходимости проводить математические преобразования. Однако существуют и более сложные задания, в которых необходимо решать квадратные уравнения, а также раскрывать скобки.
Таким образом, для определения точки пересечения графиков необходимо уметь находить корни уравнения, а также выполнять алгебраические преобразования.
Гипербола график. Гипербола график функции.
- Альфашкола
- Статьи
- Как построить график гиперболы?
График гиперболы имеет вид \(y =\frac{k}{x}\) , где k-вещественное число и x ≠ 0. Также данную функцию называют обратной пропорциональностью, где \(k-\)коэффициент обратной пропорциональности. Как выглядит сам график в зависимости стоит ли функция с минусом или без перед \(x \):
Как выглядит сам график в зависимости стоит ли функция с минусом или без перед \(x \):
Каковы особенности гиперболы?
График \(y =\frac{k}{x}\) приближается к оси \(x \) по мере увеличения значения \(x \), но никогда не встречается с осью \(X\). Это называют горизонтальной асимптотой графика.
Каждая часть графика также становится ближе к оси \(y\), поскольку \(x \) приближается к \(0\), но никогда не встречается с осью \(y\), потому что нет значения для \(y\), когда \(x = 0\). Это называется вертикальной асимптотой графика.
Пример 1.
Построим график \(y =\frac{5}{x}\) на промежутке от \(4\) до \(4\), за исключением точки когда \(x = 0\). Выберем призвольное значение \(x \) и посчитаем соответствующее значение \(y\):
По высчитанным точка из таблицы построим график:
Больше уроков и заданий по математике вместе с преподавателями нашей онлайн-школы «Альфа». Запишитесь на пробное занятие уже сейчас!
Запишитесь на бесплатное тестирование знаний!
Нажимая кнопку «Записаться» принимаю условия Пользовательского соглашения и Политики конфиденциальности
Наши преподаватели
Инна Ивановна Зименко
Репетитор по математике
Стаж (лет)
Образование:
Высший педагогический колледж
Проведенных занятий:
Форма обучения:
Дистанционно (Скайп)
Репетитор по русскому и английскому языку для 1-4 классов. Приглашаю вас на уроки. Здесь я помогу вам в решении любых грамматических, орфографических, лексических задач. Объясню вам легко и доступно почему мы произносим одно, а пишем во многих случаях по-другому, как узнать склонение и легко определить падеж. Вы поймете, что господин глагол не такой уж и жуткий, а необходимая и незаменимая часть речи, ровно как и мисс существительное и прилагательное. Жду вас в гости и вместе мы преодолеем любые трудности! Люблю детишек, терпелива и имею подход к детям, так как каждый ребенок индивидуален. И нет ребенка без таланта, главное выявить и направить его в нужное русло! Давайте дерзать!
Приглашаю вас на уроки. Здесь я помогу вам в решении любых грамматических, орфографических, лексических задач. Объясню вам легко и доступно почему мы произносим одно, а пишем во многих случаях по-другому, как узнать склонение и легко определить падеж. Вы поймете, что господин глагол не такой уж и жуткий, а необходимая и незаменимая часть речи, ровно как и мисс существительное и прилагательное. Жду вас в гости и вместе мы преодолеем любые трудности! Люблю детишек, терпелива и имею подход к детям, так как каждый ребенок индивидуален. И нет ребенка без таланта, главное выявить и направить его в нужное русло! Давайте дерзать!
Виктория Григорьевна Рагузина
Репетитор по математике
Стаж (лет)
Образование:
Самарская государственная академия. / Столичный учебный центр
/ Столичный учебный центр
Проведенных занятий:
Форма обучения:
Дистанционно (Скайп)
Репетитор по математике 2-9 классов, подготавливаю к ОГЭ. Математика есть прообраз красоты мира! Люблю математику и люблю учить так, чтобы был результат. С терпением отношусь к тем, кому математика дается не просто. Как репетитор использую новые методики, разные учебники и пособия, предлагаю дополнительные материалы и компьютерные технологии
Елена Анатольевна Фомина
Репетитор по математике
Стаж (лет)
Образование:
Орловский государственный университет
Проведенных занятий:
Форма обучения:
Дистанционно (Скайп)
Репетитор 5-9 классов. Мною разработана собственная методика повышения уровня грамотности. Использую только индивидуальный подход к каждому ученику. С радостью буду ждать на занятиях!
Мною разработана собственная методика повышения уровня грамотности. Использую только индивидуальный подход к каждому ученику. С радостью буду ждать на занятиях!
Похожие статьи
- Решение задач по геометрии синус и косинус угла
- Скалярное произведение векторов
- Возведение смешанных дробей в натуральную степень
- Признак делимости на 23
- Как строить графики функций с модулем из ОГЭ
- ЕГЭ по математике, базовый уровень. Простейшие уравнения (вариант 2)
- Летние хобби: 5 нестандартных способов рисования
- День матери: что подарить самому близкому человеку?
Нажимая кнопку «Записаться» принимаю условия Пользовательского соглашения и Политики конфиденциальности
Практика составления графика проекта в MS Project
Статья предоставлена редакцией информационно-аналитического журнала «Управление Проектами» в рамках совместного проекта с Финансовой академией “Актив”.
Современные методы и средства проектного управления, статьи по развитию навыков и компетенций в области управления проектами, программами и портфелями проектов доступны при приобретении выпуска журнала или при полугодовой и годовой подписке.
Читайте больше интересных статей в журнале «Управление Проектами»
Для кого эта статья
Существует масса пособий по работе в MS Project. Почти все они рассказывают о технике: как пользоваться приложением, какие сущности в нем существуют, какие связи между задачами используются и т.д. Однако когда доходит до практики, руководитель проекта сталкивается с необходимостью принимать решения другого характера – какие задачи должны входить в график, как найти золотую середину между детальностью графика и удобством работы с ним, какие приемы лучше использовать, чтобы минимизировать трудозатраты на планирование? Как, в конце концов, обеспечить выполнение сроков проекта?
Данная статья – для тех, кто не нуждается в детальных инструкциях по использованию MS Project. Статья предназначена для практиков, которым будет интересно познакомиться с опытом других руководителей проектов. Ниже изложены некоторые приемы и принципы, которые сформировались в результате многолетнего опыта работы, и которые позволяют сделать практичный график проекта.
Статья предназначена для практиков, которым будет интересно познакомиться с опытом других руководителей проектов. Ниже изложены некоторые приемы и принципы, которые сформировались в результате многолетнего опыта работы, и которые позволяют сделать практичный график проекта.
Планирование проекта
Хотя график проекта может служить разным целям, здесь мы сосредотачиваемся на задаче управления сроками. Как спланировать и обеспечить выполнение проекта в срок. При этом за скобками остаются задачи расчета полных трудозатрат и стоимости проекта. Решить обе задачи одновременно с помощью одного графика проекта возможно, но сложно, т.к. требования к детальности и полноте графика, в зависимости от поставленных целей, разные.
Если говорить об управлении сроками, то можно сформулировать следующие требования. Хороший график проекта:
- Приспособлен для информирования заказчика и проектной команды. Для этого он должен быть понятным, компактным, логичным, хорошо структурированным.

- Легко модифицируется в случае изменений сроков и состава задач. Его легко поддерживать в актуальном состоянии.
- Позволяет контролировать сроки, обнаруживать проблемы и принимать по этому поводу решения.
Для того, чтобы составить такой график предлагаем следующий план действий:
- Принять решение о способе планирования.
- Избавиться от всего лишнего и упростить план.
- Установить взаимосвязи между задачами.
- Оценить длительность задач
- Избавиться от распараллеливания задач
- Выровнять ресурсы.
- Установить ограничения по датам.
- Выявить критический путь.
- Добавить временные буферы в график.
- Проанализировать, как можно сократить сроки.
1. Принять решения о способе планирования
1.1. Планирование от начала
Более привычный для большинства способ. Удобен, если вы знаете начало проекта, но только приблизительно представляете, когда он закончится.
В свойства проекта устанавливаете дату начала. Все новые задачи автоматически сдвигаются в начало, т.к. по умолчанию для них устанавливается тип ограничения «Как можно раньше». После выстраивания последовательности задач с помощью связей, проект растягивается. Путем манипуляций с длительностью и последовательностью задач получаете желаемую дату окончания проекта.
Это более комфортный способ планирования с психологической точки зрения. Легче планировать сначала то, что ближе и понятнее, а затем на основе ближайших результатов, переходить к последующим задачам.
Минус в том, что задачи, которые могли бы быть сделаны позже, становятся в плане слишком близко к началу проекта. Некоторые считают, что это правильно, т.к. лучше делать все как можно быстрее. Наверняка возникнут осложнения, и раннее выполнение задач создает резервы времени. В некоторых случаях это справедливо. Но это также приводит и к негативным последствиям.
В начале проекта, как правило, нужно сосредоточиться на концептуальных и стратегических задачах, отложив все второстепенные, чтобы не распыляться, не терять фокус и не тратить понапрасну ресурсы. Во-вторых, сделанные заранее работы могут оказаться не нужны, или сделаны не так, как требуется из-за недостатка информации. Например, написанные в начале проекта документы придется переписывать, потому что изменились требования заказчика.
Во-вторых, сделанные заранее работы могут оказаться не нужны, или сделаны не так, как требуется из-за недостатка информации. Например, написанные в начале проекта документы придется переписывать, потому что изменились требования заказчика.
Чтобы избежать раннего начала задач и распределить задачи во времени, можно использовать ограничения на задачи типа «Не ранее чем», «Фиксированная дата начала».
Иногда используют задержки и сдвиги между задачами.
Рисунок 1
Однако пользоваться задержками лучше по возможности меньше.
Величина задержки выставляется произвольно, логики их применения и оценки не видна непосредственно из графика. Читать такой график сложнее. Впоследствии, при изменении графика, возможно, потребуется переоценка длительности и необходимости задержек. Вы вынуждены управлять ими вручную, трудоемкость поддержки графика увеличивается, вероятность ошибки возрастает.
Если задержка действительно необходима, то лучше добавить задачу ожидания явно. В приведенном примере, после Опытной эксплуатации, вместо задержки в 5 дней можно добавить задачу «Подготовка приемочных испытаний». Тогда будет понятно, для чего требуется 5 дней, кто должен это делать, и чем грозит изменение сроков по этой задаче.
В приведенном примере, после Опытной эксплуатации, вместо задержки в 5 дней можно добавить задачу «Подготовка приемочных испытаний». Тогда будет понятно, для чего требуется 5 дней, кто должен это делать, и чем грозит изменение сроков по этой задаче.
1.2. Планирование от конца
Если конечная дата проекта жестко определена, то правильнее планировать «от конца». Устанавливается дата окончания проекта, и во всех новых задачах автоматически устанавливается тип ограничения «Как можно позже».
Логика планирования в этом случае другая, но в некотором смысле более правильная. Вы задаете себе вопрос: «что необходимо, чтобы завершить проект?». Затем определяете, что необходимо, чтобы достичь этих промежуточных результатов, добавляете предшествующие задачи, к ним в свою очередь присоединяются предыдущие задачи и т.д. Выстраивается последовательная цепочка работ, которые ведут к результатам проекта.
Такой способ хорош тем, что выстраивается четкая логика цепочки работа-результат-работа. Последовательное выстраивание плана от конца позволяет осознать, для чего нужна каждая задача, и как будет использован ее результат. И задачи не начинаются раньше, чем необходимо.
Последовательное выстраивание плана от конца позволяет осознать, для чего нужна каждая задача, и как будет использован ее результат. И задачи не начинаются раньше, чем необходимо.
Многие скажут, что откладывать задачи на потом рискованно. Что если задача займет больше времени, чем запланировано, и результат опоздает? А она обязательно опоздает, и тогда следующая задача сдвинется и неизбежно сдвинется окончание проекта. Чтобы избежать этого, в график добавляются временные буферы. Подробнее об этом ниже.
2. Избавиться от лишнего и упростить план
Лишним считается все, что не помогает планировать сроки проекта.
2.1. Примеры задач, от которых можно избавиться
Рассмотрим группу задач «Управление проектом». Понятно, что задача управления проекта необходима, но она не определяет длительность проекта, а проект определяет ее длительность. Если мы сосредоточены на планировании сроков, можно ее убрать.
Рисунок 2
Задача «Поддержка». Как правило, это задача, которая начинается после запуска в эксплуатацию и имеет, как правило, фиксированную длительность (по договору), либо привязана к некоторым контрольным точкам. Можно включить ее в план проекта, но минимизировать ее детализацию. Эта задача может быть спокойно заменена в плане на две контрольные точки: Начало эксплуатации и Окончание поддержки.
Можно включить ее в план проекта, но минимизировать ее детализацию. Эта задача может быть спокойно заменена в плане на две контрольные точки: Начало эксплуатации и Окончание поддержки.
Рисунок 3
План, в конечном итоге, нужен чтобы ставить задачи и проверять факт и качество исполнения. Это очень хороший критерий, чтобы определить, с какой степенью детализации его делать. В план должны попадать только те задачи, которые РП собирается ставить и проверять их исполнения. Более мелкие задачи переносятся за пределы плана — в Excel, в JIRA или в связанный план рабочей группы в MS Project.
2.2. Пример излишней детализации
Расписать задачи до отдельных шагов и действий можно, но что это дает? С точки зрения оценки длительности — ничего. Скорее, приводит к ошибке, т.к. в каждой задаче заложена значительная погрешность.
Рисунок 4
- «Письмо Пятнициной» — «Ответ Пятнициной». Можно спокойно исключить из плана. Если какие-то задачи зависят от получения письма от Пятнициной, и это действительно шоу-стоппер, то вводим веху «Получение списка ключевых пользователей от Пятнициной».
 То, что для получения списка нам нужно связаться с Пятнициной, может остаться за кадром.
То, что для получения списка нам нужно связаться с Пятнициной, может остаться за кадром. - «Назначение встречи» — 1д. Скорее всего должно занять несколько минут. Вместо этого можно было бы вставить одну задачу по подготовке презентации и веху «Встреча с директорами обществ». Не нужна группировка задач. Вместо четырех строк — две.
- «Выпуск организационно-распорядительной документации» может быть одной задачей. В заметках по задаче, можно перечислить, кому нужно выслать письмо. Длительность задачи определяется суммарным временем подготовки всех документации. И эта информация будет точнее, растягивать эту задач на неделю нет никакой необходимости.
3. Установить взаимосвязи между задачами
Связи между задачам выстраивают логику плана. Связь от конца к началу, означает, что результаты предыдущей задачи, необходимы для начала следующей. По идее, в плане не должно быть задач, у которых нет последователей, кроме последней вехи завершения проекта или этапа.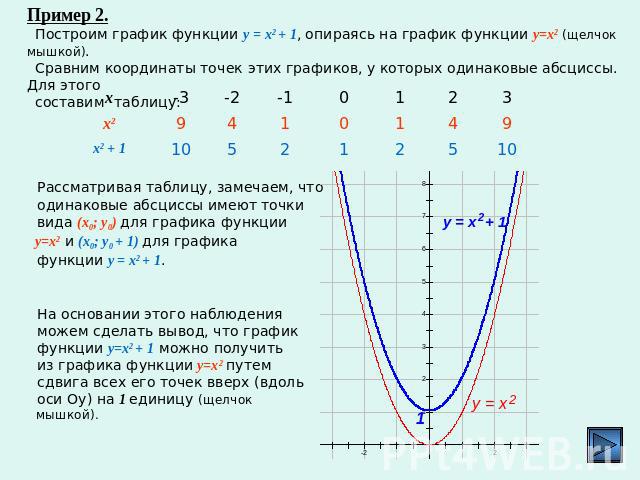 Каждая задача делается в плане для чего-то, ее результат всегда востребован.
Каждая задача делается в плане для чего-то, ее результат всегда востребован.
Можем дать следующие рекомендации для выстраивания графика.
3.1. Используйте минимум видов связей
В MS Project вы можете использовать разные виды связей между задачами «Окончание-начало», «Начало-начало» и т.д. По возможности, избегайте разнообразия использования разных типов связей. Читать график с разными видами связей сложно. Его поведение графика при модификации становится трудно предсказуемым. Чем проще, чем однообразнее — тем лучше.
3.2. Не используйте связи с суммарными задачами
Рассмотрим упрощенный пример проекта, состоящего из двух этапов. Иногда план выглядит так:
Рисунок 5
В результате мы имеем неоптимальный план. Иванов и Петров будут простаивать, ожидая завершения работы Сидорова по Этапу 1. Если у нас есть задача максимально сжать график проекта, мы начнем работы по Этапу 2, не дожидаясь завершения всех работ по Этапу 1. И тогда график будет выглядеть следующим образом. Связи между задачами, в данном случае отражают последовательность работ каждого из ресурсов.
Связи между задачами, в данном случае отражают последовательность работ каждого из ресурсов.
Рисунок 6
Если же действительно нужно закончить все работы по Этапу 1 и только после этого начинать Этап 2, то можно организовать план следующим образом, не прибегая к связям между суммарными задачами — вставить вехи завершения этапа 1 и начала этапа 2.
Рисунок 7
Такой способ организации графика имеет еще одно преимущество — он делает план очень легким для чтения. Это важно для выверки логики и наличия всех необходимых связей между задачами.
3.3. Используйте Сетевую диаграмму
Для выверки связей очень удобно пользоваться при этом не привычной диаграммой Гантта, а сетевой диаграммой.
Рисунок 8
Для этого типа диаграммы важно иметь хорошо организованную группировку связей на вехи. В противном случае очень легко запутаться в стрелках, которые идут из задач в одном углу диаграммы в другой.
Очень часто довольно сложный план на сетевой диаграмме выглядит проще и логичнее, что позволяет быстро проверить наличие и корректность связей между задачами. Смотрите пример реального графика проекта:
Смотрите пример реального графика проекта:
Рисунок 9
Рисунок 10
4. Оценить длительность задач
В литературе описано много специальных и общих методик (PERT, мозговые штурмы, Дельфи и проч.). В реальности вы либо делаете оценку из собственного опыта, либо запрашиваете у экспертов или непосредственных исполнителей.
При оценке исполнителями нужно делать поправку. Учитывайте следующие факторы:
- О достоверности оценки лучше судить, если известны предположения, их которых исходил оценщик.
- Учитывайте психологические особенность каждого исполнителя
- Сделать поправку длительности. Для некоторых исполнителей, исходя из опыта работы с ними, нужно делить оценку на два, для других — умножать на три.
Задачи не должны включать запас «на всякий случай». Добавление запаса в каждую задачу с целью повысить вероятность выполнения в срок каждой задачи, скажем до 90%, делает график длинным, и при этом вы все равно не уложитесь в срок. Реальность такова, что все опоздания накапливаются, а опережения съедаются. Почему так? Причины могут быть следующие:
Реальность такова, что все опоздания накапливаются, а опережения съедаются. Почему так? Причины могут быть следующие:
- «Студенческий синдром» — выучить курс в ночь перед экзаменом. И в проекте начинаем задачу когда до ее сдачи осталось минимум времени.
- Перфекционизм — если осталось время, надо работу довести до совершенства.
- Отсутствие доверия — «если сегодня я сделал быстрее, то в следующий раз моим оценкам не поверят, и урежут запрашиваемой мной время».
- Возможность работать менее интенсивно — «зачем напрягаться, если есть запас по времени?»
Поэтому придерживайтесь следующих правил при планировании работ:
- Вероятность выполнения в указанный срок установите в 50%. Это сократит оценку длительности по сравнению с 90% оценкой вероятности примерно вдвое. Сокращение времени позволит добавить в график временные буферы, которые вы будете расходовать из-за неизбежного опоздания по задачам. О добавлении буферов смотрите ниже.

- Ресурсы не должны быть перегружены. Люди не должны выполнять несколько задач одновременно. В этом случае их производительность будет максимально возможной.
5. Избавиться от распараллеливания задач
Часто можно увидеть в планах параллельные задачи, назначенные на одних и тех же исполнителей. Например,
Рисунок 11
Очевидно, РП отдает управление последовательностью и приоритетом задач консультантам. Тогда, с точки зрения планирования, достаточно было бы одной задачи «Функциональный блок Контроль», назначенной на Емельянову и Тену. Наличие пяти параллельных задач не имеет смысла. Все ресурсы перегружены, трудоемкость и длительность задачи не оценена, приоритеты не понятны.
Гораздо лучше было бы назначить одного исполнителя на каждую задачу, оценить каждую задачу по чистой трудоемкости с вероятностью выполнения ее в срок с 50% вероятностью, выстроить задачи в цепочку и добавить временно буфер в конце. Тогда это был бы реальный инструмент управления в руках РП.
6. Выровнять ресурсы
Часто руководители проекта не обращают внимание на то, что согласно составленному графику проекта ресурсы перегружены. Они просто не ставят задачу подгонки загрузки ресурсов под определенную планку. Действительно, если в плане ресурсы перегружены, то это не значит, что в реальной жизни они не смогут выполнить поставленные задачи. Проблема в том, что такой план нам об этом ничего не говорит, в нем нет информации о реализуемости плана. Многократная перегрузка ресурсов в плане равносильна отсутствию информации об их реальной загрузке.
Если мы хотим планировать загрузку ресурсов, нужно загрузку выравнивать. Можно это делать не для всех ресурсов, а только критических, которые мы действительно хотим планировать. Например, мы можем планировать своих сотрудников, но не планировать ресурсы заказчика, загрузка и возможности которых находятся за пределами нашего влияния.
В MS Project имеется функция выравнивания ресурсов. Эта функция расставляет задачи с учетом связей между задачами и ограничения по максимальной загрузке каждого ресурса и приоритета (поле «Приоритет»). Не всегда это приводит к нужному результату. План становится слишком длинным, а ресурсы недогружены. Задачи привязываются в плане к конкретным датам, что мешает их перепланировать. Можно добиться более адекватного плана в ходе автоматического выравнивания с помощью пересмотра зависимостей и расстановкой приоритетов, но это очень кропотливый и трудоемкий процесс.
Эта функция расставляет задачи с учетом связей между задачами и ограничения по максимальной загрузке каждого ресурса и приоритета (поле «Приоритет»). Не всегда это приводит к нужному результату. План становится слишком длинным, а ресурсы недогружены. Задачи привязываются в плане к конкретным датам, что мешает их перепланировать. Можно добиться более адекватного плана в ходе автоматического выравнивания с помощью пересмотра зависимостей и расстановкой приоритетов, но это очень кропотливый и трудоемкий процесс.
Альтернатива — это ручное выравнивание с помощью установки последовательности задач, выполняемых одним ресурсом. Это возможно, если план не очень сложный.
Например, модифицируем предыдущий пример:
Рисунок 12
В данном примере считается, что А.Тен участвует в доработке всех документов, и два документа пишет самостоятельно. Мы точно не знаем, как будет построена их совместная работа, но предполагаем в среднем он будет на 30% отвлечен на документы А.Емельянова. Поэтому собственные задачи, где он занят на 70% больше по длительности, и оцениваются в 5 рабочих дней. Кроме того, мы добавили буфер, предполагая, что часть задач могут занять больше времени, чем мы предполагаем.
Поэтому собственные задачи, где он занят на 70% больше по длительности, и оцениваются в 5 рабочих дней. Кроме того, мы добавили буфер, предполагая, что часть задач могут занять больше времени, чем мы предполагаем.
Было бы более правильно вообще разделить задачи между двумя участниками и избавиться от параллельного выполнения задач А.Теном, но в данном случае это сделать сложно. Поэтому приходится идти на нарушение правил, которые мы сами для себя установили выше. Тем не менее, такой план лучше, т.к. помогает контролировать выполнение задач не в конце 14 рабочих дней, которые мы отвели на проектирования функционального блока «Контроль», а уже через 3 дня после начала работы. Кроме того, это дисциплинирует исполнителя с первого дня, у которого нет 14 дней в запасе, а есть целевой срок 3 дня, когда нужно закончить первый документ.
7. Исключить жесткую привязку задач к датам
Следующий шаг – подгонка графика под необходимые даты. Не всегда удается это сделать естественными связями между задачами, возникает множество обстоятельств, диктующих необходимость начала или завершения задач в определенные периоды времени. Приходится привязывать задачи к датам.
Приходится привязывать задачи к датам.
Привязка к датам оправдана, если определяется внешними по отношению к плану условиями. Например, зафиксированная дата начала испытаний; контрольная точка, которая определяется внешним проектом; несдвигаемое событие. Во всех остальных случаях нужно избегать ограничений. Если их избежать не удается, то лучше использовать мягкие ограничения: «Начало не позднее», «Начало не ранее» и т.п. Это позволяет автоматически двигать задачи вслед за теми, от которых они зависят.
8. Выявить критический путь
Если задачи выстроены правильно, то MS Project покажет вам критический путь проекта — цепочку задач, которая определяет длительность. Изменение длительности или задержка начала выполнения любой задачи на критическом пути меняет дату окончания проекта.
Соответственно, чтобы уложиться в установленные сроки, нужно обеспечивать своевременное или опережающее выполнение именно задач критического пути. Для этого нужно:
- Уделять задачам критического пути ежедневное внимание, контролировать готовность всех необходимых ресурсов для их выполнения.

- Мотивировать участников на сокращение длительности выполнения задач критического пути, не допускать отвлечения на другие задачи.
- Использовать временные буферы, страхующие отклонение по срокам.
Например, заканчивается разработка функционального блока. Далее заказчик должен протестировать этот блок. Когда до окончания разработки остается 2 дня, необходимо предупредить ключевых пользователей о том, что через 2 дня они должны быть готовы принять разработку в тестирование. И зафиксировать это формально (электронным письмом, решением оперативного совещания, и т.п.). Разрыв между задачами критического пути приводит к увеличению срока проекта, поэтому управлять этим процессом нужно жестко.
При постановке задачи критического пути исполнителю нужно говорить о том, что эта задача является определяющей для проекта. Исполнитель должен полностью сосредоточиться на ней, не отвлекаться на второстепенные задачи. А в случае возникновения проблем и задержек, сразу оповестить об этом РП.
Но от осложнений никто не застрахован. Нет никаких гарантий, что задача будет выполнена в срок. Но это не означает, что нужно стремиться устанавливать такие сроки, которые гарантированно обеспечивают выполнение задачи в срок. Как известно, работа занимает ровно столько времени, сколько на нее отведено, об этом мы говорили ранее. Устанавливайте агрессивные сроки, но имейте запас для компенсации неизбежных опозданий. И лучше этот запас иметь консолидировано, в буфере, который добавляется в конец критического пути.
Рисунок 13
В приведенном примере красным выделены задачи критического пути, синие — другие задачи, зеленые — буферы. Обратите внимание, что некритические задачи тоже застрахованы буфером. Сроки по ним также с большой степенью вероятности будут нарушены. И чтобы не сорвать своевременное начало задачи критического пути, мы добавляем буфер на входе в цепочку.
Такой способ планирования хорошо сочетается с методикой планирования «от конца проекта».
9.
 Добавить временные буферы в график
Добавить временные буферы в графикДобавление буферов в план позволяет избежать нарушений конечной даты проекта или этапа при неизбежном изменении сроков по задачам.
Как правило, мы добавляем запас в каждую задачу, чтобы нас не наказывали за опоздания. Мы предпочитаем заложить запас на все риски, которые могут случиться — отвлечение на совещания, изменения требований заказчика, длительные согласования, технические проблемы и личные обстоятельства. Стараемся дать оценку необходимых сроков с вероятностью 90% их соблюдения. И несмотря на это, часто их срываем. Выше мы уже говорили о студенческом синдроме и прочих психологических моментах, которые приводят к нарушению сроков несмотря на все резервы, которые мы делаем в каждой задаче
В результате, опоздания всегда накапливаются, а опережения — практически никогда.
Выход следующий – избавиться от резервов в задаче и вынести их в общий буфер проекта. Установить целевую вероятность выполнения задачи в срок в 50% Это значительно сокращает оценку сроков по каждой задаче, согласно статистике – вдвое. В половине случаев он будет нарушен. И это может быт не вина исполнителя, а влияние обстоятельств и неправильной оценки. При таком подходе вы не будете наказывать исполнителей за нарушение сроков, а относиться к этому как к неизбежному.
В половине случаев он будет нарушен. И это может быт не вина исполнителя, а влияние обстоятельств и неправильной оценки. При таком подходе вы не будете наказывать исполнителей за нарушение сроков, а относиться к этому как к неизбежному.
При этом вы будете иметь запас, чтобы компенсировать отставание. Для этого в график добавляются буферы. Когда задачи опаздывают и сдвигают последующие, вы используете буфер. По скорости расходования буфера можно судить, насколько удачно вы спланировали проект, достаточно ли у вас ресурсов и правильно ли организованы работы. Если буфер расходуется слишком быстро, то необходимо принимать меры.
Рисунок 14
Различаются буферы проекта (этапа) — запас создаваемый в конце критической цепочки. И питающие буферы — временные резервы на входе в критическую цепочку, страхующие поток задач вне критического пути.
Размер буфера определяется длиной цепочки, которую он страхует, а также степенью неопределенности и рисков. Классики рекомендуют отводить на буферы около 50% длительности всей критической цепочки. Руководитель проекта должен исходить из собственной оценки рисков и возможностей графика проекта.
Руководитель проекта должен исходить из собственной оценки рисков и возможностей графика проекта.
Нужно понимать, что проект с маленьким запасом скорее всего опоздает. Проектов, в которых все идет, как запланировано, не бывает. Невозможность добавить буфер может быть либо в результате явной недооценки сроков проекта, либо из-за явной переоценки длительности проектных задач, что случается, когда мы закладываем запас в каждую задачу. Даже если запас есть, но он заложен в задачи, проект все равно опоздает, по перечисленным выше причинам.
Подробнее об этом методе построения графика проекта можно прочитать в книге Э.Голдратта «Критическая цепь», которая написана в форме бизнес-романа, легко читается и действует крайне вдохновляюще.
10. Проанализировать график
Далее мы переходим к тому, для чего, собственно мы проделывали все предыдущие шаги, непосредственно к работе с графиком.
Хороший график показывает, какие потенциальные проблемы есть в проекте; какие есть возможности для сокращения сроков; достаточно ли ресурсов для выполнения проекта.
10.1. Сокращение сроков
Рассмотрим пример:
Рисунок 15
Посмотрим, нельзя ли сократить этот график. Самые длинные задачи — номер 17 и 21. 18 и 15 дней — слишком длинные задачи для того, чтобы их можно было эффективно контролировать.
Нельзя ли детализировать и разделить эти задачи на части? Оказывается, это разработка отчетов, каждый из которых занимает в среднем по 1 дню. Не обязательно, чтобы их разработку вел один человек последовательно. Можно разделить их на порции и распределить между несколькими разработчиками. Добавили одного разработчика, разделили на неравные части и получили следующий график.
Рисунок 16
Таким образом, график наглядно показал, что необходим еще один человек в команду. Стало понятно, как нужно распределить задачи, чтобы сократить сроки и снизить риски зависимости от исполнителей, которые, например, могут в самый неподходящий момент заболеть.
10.2. Риски, связанные с графиком
Интересно посмотреть на график проекта с точки зрения управления рисками. Какие риски может обнаружить график проекта?
Какие риски может обнаружить график проекта?
- Параллельное выполнение множества блоков работ или функциональных направлений. Необходимо решить, влечет ли опоздание одного из них серьезные последствия для всего проекта? Сложные проекты включают в себя до десятка направлений. Внедряется одновременно финансы, бюджетирование, HR, логистика и т.д. Если не предусмотрены работы по интеграции и координации направлений, не заложены резервы на отклонения по каждому из направлений, нет этапа интеграционного тестирования, велика вероятность неуспеха проекта в целом, а не только срыва сроков.
- Отсутствие периода опытной эксплуатации. Если ОПЭ невозможна, то нужно рассматривать возможность поэтапного запуска, по функциональным областям или организационным единицам.
- Излишне агрессивный график, отсутствие или недостаточный размер резервов. Об этом уже говорили. Такой проект вероятнее всего опоздает.
- Этапы проекта или ключевые работы идут внахлест, с перекрытием.
 Во многих случаях это увеличивает риск переделки по уже выполненным задачам.
Во многих случаях это увеличивает риск переделки по уже выполненным задачам. - Если в графике отсутствуют работы и вехи, закрепленные за заказчиком, то возможно, мы плохо контролируем работы со стороны заказчика. Необходимо обратить внимание на то, что некоторые работы могут быть некорректно отнесены к зоне ответственности исполнителя.
- Отсутствие в графике вех, означающих формальную приемку работ, может означать, что мы не до конца понимаем, какие промежуточные результаты и в какой момент должны подтвердить. А это чревато проблемами при сдаче результатов в конце проекта.
Заключение
На практике часто бывает, что график проекта составляется, потому что так принято, так требуется, для галочки. Но реальное управление проектом идет без его использования, потому что это сложно, трудоемко, и жизнь значительно богаче.
График проекта становится реальным инструментом управления в руках руководителя проекта, если график составлен с умом и следуя определенным стандартам. Владение инструментом и методами позволяет управлять сроками проекта гораздо эффективнее, с меньшими трудозатратами времени.
Владение инструментом и методами позволяет управлять сроками проекта гораздо эффективнее, с меньшими трудозатратами времени.
Изложенные здесь принципы не являются исчерпывающими, единственно правильными и безусловными. Вы можете следовать другим правилам, если они доказали свою работоспособность.
Научитесь контролировать работу проекта в режиме реального времени с помощью дашбордов Power BI на курсе «ACPM: Бизнес-анализ данных в финансах». Зарегистрируйтесь и пройдите 1-й урок бесплатно!
Посмотреть занятие по бизнес-анализу
ГДЕ КУПИТЬ КНИГУ — 1(выбрать регион, магазин, узнать подробности и цены, купить или сделать заказ)⇓ Магазины В РОССИИ (регионы > магазины)Прямые ссылки на страницы СПРАВОЧНИКА в выбранном регионе и магазинеАНГАРСК • Книготорговая фирма «ПродаЛитЪ» — www.prodalit.ru АРХАНГЕЛЬСК • БУКВОЕД — www.bookvoed.ru БРАТСК • «ПродаЛитЪ» — www.prodalit.ru ВЕЛИКИЙ НОВГОРОД • БУКВОЕД — www.bookvoed.ru ВОЛГОГРАД • интернет-магазин uchebniki-vlg.ru ЕКАТЕРИНБУРГ • ЛЮМНА, торговая компания. Магазины «Живое слово» ИВАНОВО • ivanovo-shop.ru (Иваново | Кохма) ИРКУТСК • Книготорговая фирма «ПродаЛитЪ» — www.  prodalit.ru prodalit.ru КАЛИНИНГРАД • БУКВОЕД — www.bookvoed.ru КЛИН • «Ливре» — книжная лавка — book-stock.ru КОСТРОМА • «Ливре» — книжная лавка — book-stock.ru КРАСНОДАР • kogortashop.ru КРАСНОЯРСК • Книготорговая фирма «ПродаЛитЪ» — www.prodalit.ru МОСКВА • Московский Дом книги — www.mdk-arbat.ru (сеть магазинов: +7 (495) 789-35-91, интернет-магазин: +7 (495) 648-17-68) • ЧИТАЙ-ГОРОД — www.chitai-gorod.ru (57 магазинов в Москве, 200+ — в России) • Магазин «Книги на Бауманской» (б. ДОМ КНИГИ НА ЛАДОЖСКОЙ) — www.dom-knigi.ru • Дом Книги «Медведково» — www.bearbooks.ru • Дом Книги «Молодая Гвардия» — bookmg.ru • “Книжный Лабиринт” — сеть сеть специализированных книжных магазинов (Москва — 36 магазинов, Моск. область — 18 магазинов) Московская область+ • «Ливре» — книжная лавка — book-stock.ru (Розничные магазины и доставка: Дмитров, Дубна, Сергиев Посад, Ногинск, Клин, Ивантеевка, Иваново, Орехово-Зуево, Новочебоксарск, Пушкино, Солнечногорск, Королёв, Электросталь, Щелково, Кострома, Ярославль) Московская область, г.  Одинцово • «Свой Книжный» — www.svbooks.ru Одинцово • «Свой Книжный» — www.svbooks.ru МУРМАНСК • БУКВОЕД — www.bookvoed.ru НИЖНИЙ НОВГОРОД • Ккнижный магазин «Дом книги» — www.domkniginn.ru — новый сайт • Ккнижные магазины «Дирижабль» — dirigable-book.ru НОВОРОССИЙСК • kogortashop.ru ПЕТРОЗАВОДСК • www.bookvoed.ru ПСКОВ • www.bookvoed.ru РОСТОВ-на-ДОНУ • МАГИСТР — www.booka.ru (Батайск | Волгодонск | Новочеркасск | Ростов-на-Дону | Сальск | Таганрог | Шахты) РЯЗАНЬ • bookbars.ru — книжный магазин года в России по итогам конкурса в рамках Московской международной книжной выставки-ярмарки 2014 г. САМАРА • www.metida.ru (Бузулук | Отрадный | Пугачев | Самара | Сызрань | Тольятти ) • Чакона — www.chaconne.ru (Самара | Тольятти | Новокуйбышевск | Сызрань) САНКТ-ПЕТЕРБУРГ • БУКВОЕД — www.bookvoed.ru (25 магазинов во всех районах города. Выбор магазина по адресу, списку, карте).  • Дом книги — www.spbdk.ru (Невский пр.,28. СПРАВОЧНАЯ СЛУЖБА: (812) 448-23-55) САРАТОВ • moya-kniga.ru СЫЗРАНЬ • www.metida.ru ТАГАНРОГ • regionbook.ru ТОЛЬЯТТИ • www.metida.ru УЛАН -УДЭ • «ПродаЛитЪ» — www.prodalit.ru ЧИТА • Книготорговая фирма «ПродаЛитЪ» — www.prodalit.ru ЯРОСЛАВЛЬ • «Ливре» — книжная лавка — book-stock.ru • ЧИТАЙ-ГОРОД — www.chitai-gorod.ru (Информация с сайта: сеть современных универсальных книжных магазинов. Доставка в 224 магазина в 87 городах России, 1000 пунктов самовывоза) • БУКВОЕД — www.bookvoed.ru (С.-Петербург | Ленинградская область | Архангельск | Великие Луки | Великий Новгород | Вологда | Гатчина | Калининград | Кингисепп | Кириши | Мурманск | Петрозаводск | Псков | Североморск | Череповец ). 70 магазинов в Санкт-Петербурге и в Северо-Западном регионе.  250 пунктов самовывоза. 250 пунктов самовывоза. Книжные ИНТЕРНЕТ-МАГАЗИНЫ • БИБЛИО-ГЛОБУС — www.bgshop.ru • Библион — www.biblion.ru (открылся в 1999 году) • www.books.ru • www.combook.ru • ЛАБИРИНТ — www.labirint.ru (Информация с сайта: курьерская служба … в 323 городах и поселках России. 303 пункта самовывоза.) • my-shop.ru • ОЗОН — www.ozon.ru • Интернет-магазин «Время покупать» — shopping-time.ru • www.sprinter.ru • www.ukazka.ru (Информация с сайта: работает с 2007 года. Пункты самовывоза в 52 городах. Доставка … в 450 населенных пунктов на территории России.) ` ⇓ Магазины В ДРУГИХ СТРАНАХПрямые ссылки на страницы СПРАВОЧНИКА в выбранной стране и магазинеБЕЛАРУСЬ • Интернет-магазин www.oz.by (Работает 15 лет) • Книжный интернет-магазин uchitel.by • Книготорговое республиканское унитарное предприятие «Академическая книга» — www.akademkniga.  by (См. Новые аоступления. Предложение 16.10.2014 (Вильямс, БХВ, Компьютерная лит-ра) — скачать) by (См. Новые аоступления. Предложение 16.10.2014 (Вильямс, БХВ, Компьютерная лит-ра) — скачать) ГЕРМАНИЯ • Интернет-магазин www.sputnik2000.com КАЗАХСТАН • Интернет-магазин www.flip.kz • bestseller.kz КАНАДА • Сеть магазинов русской книги — www.knigomania.com (существует более 15 лет) ЛАТВИЯ • Компания «Janus» — www.janus.lv (основана в 1992 году) МОЛДОВА • ezotera.md УЗБЕКИСТАН • Интернет-магазин — www.bookstore.uz УКРАИНА • Интернет-магазин книг «Одиссей» — odissey.kiev.ua • Книжный интернет-магазин «Book Star» — bookstar.biz ФИНЛЯНДИИЯ • Книжный магазин Руслания — ruslania.com ЧЕХИЯ • www.ru-shop.cz ЭСТОНИЯ • Магазины Rahva Raamat — www.rahvaraamat.ee Spravochnik po matematicheskim formulam i grafikam funktsii by Starkov S. (Author). Russian Book. Publisher: BHV. Pages: 352.  Year: 2015. Cover: Softcover. Year: 2015. Cover: Softcover. Магазины В РАЗНЫХ СТРАНАХ • www.amazon.com (Australia Brazil Canada China France Germany India Italy Japan Mexico Netherlands Spain United Kingdom) • Электронный интернет-магазин www.biblio-globus.us (Информация с сайта: быстрая доставка во все страны мира…) • Онлайн-мегамаркет Ozonru.eu Предлагает доставку заказов в 27 странах Европейского Союза: Австрии, Бельгии, Болгарии, Великобритании, Венгрии, Германии, Греции, Дании, Ирландии, Испании, Италии, Кипре, Латвии, Литве, Мальте, Нидерландах, Польше, Португалии, Румынии, Словакии, Словении, Финляндии, Франции, Хорватии, Чехии, Швеции и Эстонии со склада OZON. • www.russian-books.com (Информация с сайта: Russian-books.com presents more then 130,000 russian books…) • vasha-kniga.com (Информация с сайта: Vasha Kniga Russian Books, more than 125,000 Russian Books…) Книга представляет собой универсальное пособие, состоящее из двух частей и содержащее 1200 формул и 1200 графиков.  Первая часть — справочник по математическим формулам по программам средней школы,
средних специальных и высших учебных заведений. Приводятся развернутые названия и пронумерованные
формулы и преобразования. Вторая часть — уникальный сборник графиков функций и изображений линий
на плоскости, систематизированных по виду функций, типу и уровню сложности преобразований
(элементарных и неэлементарных). Широта охвата материала позволяет использовать справочник
практически всем категориям читателей на разных ступенях обучения и в различных формах как для
самостоятельных, так и аудиторных занятий. Первая часть — справочник по математическим формулам по программам средней школы,
средних специальных и высших учебных заведений. Приводятся развернутые названия и пронумерованные
формулы и преобразования. Вторая часть — уникальный сборник графиков функций и изображений линий
на плоскости, систематизированных по виду функций, типу и уровню сложности преобразований
(элементарных и неэлементарных). Широта охвата материала позволяет использовать справочник
практически всем категориям читателей на разных ступенях обучения и в различных формах как для
самостоятельных, так и аудиторных занятий.СОДЕРЖАНИЕ Некоторые обозначения СПРАВОЧНИК имеется в БИБЛИОТЕКАХ • Воронеж. Библиотека Воронежского государственного архитектурно-строительного университета. edu.vgasu.vrn.ru. • Москва. Государственная публичная научно-техническая библиотека России (ГПНТБ России). www.gpntb.ru • Москва. Библиотека по естественным наукам Российской Академии наук (БЕН РАН). www.benran.ru • Москва. Библиотека Института астрономии Российской Академии наук (ИНАСАН РАН). www.inasan.rssi.ru • Новосибирск. Государственная публичная научно-техническая библиотека Сибирского отделения РАН. www.spsl.nsc.ru • Омск. Библиотека Сибирской автомобильно-дорожной академии.  lib.sibadi.org. lib.sibadi.org. • Санкт-Петербург. РОССИЙСКАЯ ГОСУДАРСТВЕННАЯ БИБЛИОТЕКА. www.rsl.ru • Саратов . Научно-техническая библиотека Саратовского государственного технического университета имени Гагарина Ю.А. lib.sstu.ru • Беларусь, Минск. Белорусский национальный технический университет (БНТУ). Научная библиотека. library.bntu.by/ www.bhv.ru — адрес сайта издательства «БХВ-Петербург» Интересные разделы: — Учебная литература для школ → Естественные науки — Учебная литература для вузов → Естественные науки — Естественные науки → Математика |
Правило умножения для расчета вероятностей
Правило умножения в вероятности позволяет вам вычислить вероятность нескольких событий, происходящих вместе, используя известные вероятности этих событий по отдельности. Есть две формы этого правила, специальные и общие правила умножения.
В этом посте вы узнаете, когда и как использовать как специальные, так и общие правила умножения. Кроме того, я буду использовать и объяснять стандартные обозначения вероятностей повсюду, помогая вам научиться их интерпретировать. Мы рассмотрим несколько примеров задач, чтобы вы могли увидеть их в действии. В конце есть даже проблема с бонусами!
Прежде чем мы перейдем к самим правилам, вам нужно знать определения независимых и зависимых событий:
- Независимые события : Возникновение одного события не влияет на вероятность другого события. Например, при подбрасывании монеты выпадение «орла» не влияет на вероятность выпадения «орла» при следующем подбрасывании монеты.
- Зависимые события : Возникновение одного события влияет на вероятность другого события. Например, если вы вытягиваете короля из колоды карт и не заменяете его, это снижает вероятность вытягивания другого короля.
Используя правило умножения, вы можете вычислить вероятность того, что события A и B произойдут вместе, если вы знаете вероятность того, что событие A и событие B произойдут по отдельности.
Обозначение совместной вероятности появления событий A и B следующее: P(A ∩ B).
Когда события независимы, вы можете использовать определенное правило умножения. Когда у вас есть зависимые события, вы должны использовать общее правило умножения.
Связанный пост : Основы вероятности
Специфическое правило умножения
Используйте конкретное правило умножения для расчета совместной вероятности независимых событий. Чтобы использовать это правило, умножьте вероятности независимых событий. Для независимых событий появление события A не влияет на вероятность события B. Это правило не действует для зависимых событий.
Используя обозначение вероятности, конкретное правило умножения выглядит следующим образом:
P(A ∩ B) = P(A) * P(B)
Или, совместная вероятность появления А и В равна вероятности появления А умножить на вероятность появления В.
Примеры специального правила умножения
Например, чтобы вычислить вероятность выпадения орла при двух последовательных подбрасываниях монеты, умножьте вероятность выпадения орла при первом подбрасывании монеты (0,5) на вероятность выпадения орла при второй монете. флип (0,5).
флип (0,5).
0,5 X 0,5 = 0,25
Совместная вероятность двух последовательных орлов равна 0,25.
Представьте, что вам особенно нравится носить коричневые брюки с синей рубашкой. Однако утром вы сонный и наугад берете штаны и рубашку из шкафа. Брюки находятся на одной стороне шкафа, а рубашки — на другой. Это независимые события, потому что получение пары брюк не влияет на вероятность получения рубашки.
У тебя десять пар штанов и три коричневые. Следовательно, вероятность выпадения коричневой пары (событие TP) равна 0,3.
У вас есть 16 футболок и четыре синие. Следовательно, вероятность получить синюю рубашку (событие BS) равна 0,25.
Это независимые события, потому что выбор пары брюк не влияет на вероятность получения синей рубашки и наоборот.
Используя специальное правило умножения для этих независимых событий:
P(TP ∩ BS)= P(TP) * P(BS)
0,3 X 0,25 = 0,075
Или, совместная вероятность случайного выбора пары светло-коричневых брюк и синей рубашки равна 0,075, то есть вероятность светло-коричневых брюк, умноженная на вероятность синей рубашки.
Вероятность выпадения желаемой комбинации низкая! Вы можете выпить кофе, чтобы увеличить свои шансы!
Общее правило умножения
Используйте общее правило умножения для расчета совместных вероятностей независимых или зависимых событий. Когда у вас есть зависимые события, вы должны использовать общее правило умножения, потому что оно позволяет учитывать, как появление события А влияет на вероятность события В.
Используя стандартные обозначения, общее правило умножения следующее:
P(A ∩ B) = P(A) * P(B|A)
Или, совместная вероятность появления A и B равна вероятности Произошло событие А, умноженное на условную вероятность наступления события В при условии, что произошло событие А.
Неудивительно, что разница между общими и специальными правилами заключается в том, что вы можете использовать общее правило в более широком смысле. Оно работает как для независимых, так и для зависимых событий, тогда как конкретное правило действует только для независимых событий.
Почему можно использовать общую форму как для независимых, так и для зависимых событий? В обозначениях сосредоточьтесь на P(B|A), которая представляет собой условную вероятность того, что событие B произойдет при условии, что произошло событие A.
В контексте независимых событий P(B|A) = P(B), поскольку событие A не влияет на вероятность события B. Это и есть определение независимых событий. Следовательно, это правило становится эквивалентным конкретному мультипликативному правилу для независимых событий.
Однако для зависимых событий P(B|A) ≠ P(B). Это просто еще один способ сказать, что событие А влияет на вероятность события Б (т. е. это зависимые события). Общее правило мультипликативности позволяет учитывать другое событие, как вы увидите в следующих двух примерах!
Связанный пост : Использование таблиц непредвиденных обстоятельств для расчета вероятностей
Примеры общего правила умножения
Классический пример зависимых событий — вытягивание карт из колоды карт без замены. Когда вы берете карты, это влияет на вероятность следующей карты, которую вы можете взять.
Когда вы берете карты, это влияет на вероятность следующей карты, которую вы можете взять.
Предположим, вас интересует вероятность выпадения червы в двух последовательных розыгрышах. Изначально в колоде 13 червей из 52 карт (13/52 = 0,25). Если вы рисуете сердце (событие h2), это меняет вероятность того, что выпадет еще одно сердце. Зависимая вероятность вытянуть вторую черву (событие h3) теперь равна 12/51 = 0,235.
В форме записи:
P(h2 ∩ h3) = P(h2) * P(h3|h2)
вторая черва, учитывая, что первая карта была червой.
0,25 * 0,235 = 0,059
Зависимые события: пример светло-коричневых брюк и синих рубашек
Вернемся к примеру со брюками и рубашкой. Представьте, что мы собираемся в короткую поездку и случайным образом выбираем две пары брюк и две пары рубашек, чтобы положить их в наш чемодан. Мы надеемся на две пары коричневых брюк и две синие рубашки.
Начнем с рассмотрения этого как двух наборов зависимых событий, один для брюк, а другой для рубашек.
Начнем с 10 пар штанов, три из которых коричневые. Следовательно, вероятность того, что первая пара брюк будет желто-коричневой (событие T1), равна 0,30. Вероятность того, что вторая пара будет желто-коричневой (T2), составляет 2/9 = 0,22. Отсюда:
P(T1 ∩ T2) = P(T1) * P(T2|T1)
0,30 * 0,22 = 0,066
Совместная вероятность вытянуть две пары светло-коричневых штанов равна 0,066, что равно вероятности первая пара коричневых штанов, умноженная на условную вероятность появления второй пары коричневых штанов при условии, что первая пара была коричневой.
Что касается футболок, мы начнем с четырех синих из 16. Используя тот же подход, мы получаем следующее:
P(B1 ∩ B2) = P(B1) * P(B2|B1)
0,25 * 0,20 = 0,05
У нас есть две совместные вероятности 0,066 для двух тангенсов. штаны и 0,05 за две синие рубашки.
Связанный пост : Использование перестановок для расчета вероятностей и использование комбинаций для расчета вероятностей
Бонус Пример задачи!
Наша конечная цель как случайного упаковщика состоит в том, что мы хотели бы иметь в нашем чемодане две коричневые штаны и две синие рубашки. Можете ли вы понять, как рассчитать эту вероятность, учитывая приведенную выше информацию?
Можете ли вы понять, как рассчитать эту вероятность, учитывая приведенную выше информацию?
Чтобы решить эту проблему, мы определим две коричневые штаны как событие 2TP и две синие рубашки как событие 2BS. Из наших предыдущих расчетов зависимых событий с использованием общего правила умножения мы знаем следующее:
P(2TP) = 0,066
P(2BS) = 0,05
Как рассчитать совместную вероятность P(2TP ∩ 2BS)?
Вспомните пример независимых мероприятий, где мы нарисовали одну пару брюк и одну рубашку. Выбор брюк не влияет на вероятность получения рубашки и наоборот. Следовательно, мы можем рассматривать события 2TP и 2BS как независимые события, хотя у нас были зависимые события при расчете вероятностей для нескольких штанов и нескольких рубашек. Другими словами, выбор нескольких брюк влияет на вероятность получения следующей пары брюк, но не влияет на рубашки.
Следовательно, мы можем использовать специальное правило умножения для независимых событий для этой части решения: двух пар коричневых брюк и двух синих рубашек составляет всего 0,0033 или 0,33%! Это вряд ли произойдет случайно. Если мы действительно хотим эту комбинацию, мы должны рассмотреть неслучайный подход к упаковке!
Если мы действительно хотим эту комбинацию, мы должны рассмотреть неслучайный подход к упаковке!
Вычисление совместных вероятностей с помощью правила умножения очень просто. Определите, являются ли ваши события независимыми или зависимыми, а затем используйте правильную форму правила!
Преобразования функций: сжатие и растяжение
Переводы, отражения, перемещение точек, работа в обратном направлении
Purplemath
Есть еще два преобразования, но их труднее «увидеть» с какой-либо степенью точности.
Первым из этих преобразований является умножение на всю функцию. Чтобы увидеть, как это выглядит, сравните графики 2 × f ( x ) = 2 x 2 , f ( x ) = x 2 , и ½ × F ( x ) = (½) x 2 , ниже:
График 2 × F (
Граф 2 (). 2 :
(это хуже, чем график обычной функции, в коробке ниже. )
)
Содержание Продолжается ниже
Mathhelp.com
Трансформации / переводы
График F ( x
график F (
график F (
график F (
график F (
график F (. ) = х 2 :
(это график регулярной функции.)
График ½ × F ( x ) = (½) x 2 :
x 2 : 999999999999999999999 ( x 2 : . толще, чем график регулярной функции, который был показан в предыдущей рамке.) Первая парабола, та, что для 2 x 2 , растет в два раза быстрее, чем x 2 (средняя график), поэтому его график высокий и худой. С другой стороны, третья парабола для функции (½) x 2 растет вдвое быстрее, чем x 2 , поэтому его график короткий и толстый.
Вы можете сказать, грубо говоря, что первый график, более тонкий, умножается на нечто большее, чем 1, поэтому он растет быстрее, чем обычно, и что третий график, более квадратный, умножается на что-то меньшее, чем 1, поэтому он растет медленнее, чем обычно. Но, как правило, довольно сложно точно сказать, на что был умножен график, просто взглянув на картинку.
Например, можете ли вы сказать, что на графике ниже показано, что 1,4 × f ( x ) = 1,4 x 2 ?
Маловероятно.
Другим более сложным типом преобразования является умножение на аргумент функции. Это часто очень похоже на умножение всей функции. Например, рассмотрим графики f (2 x ) = (2 x ) 2 , f ( x ) = x 2 , and f (½ x ) = (½ x) 2 , below:
graph of f (2 x ) = (2 x ) 2 :
(Этот график растет в два раза быстрее, чем график обычной функции, показанный в следующей рамке. (Это график обычной функции.) график f (½ x ) = (½ x ) 2 : (Этот график растет вдвое медленнее, чем график обычной функции, показанный в предыдущем блоке.)  )
)2 Как видите, умножение внутри функции (внутри аргумента функции) приводит к тому, что график становится тоньше или толще. Это очень похоже на другое преобразование умножения, но это преобразование является умножением вне всей функции или над ней. И обычно практически невозможно идентифицировать это преобразование по графику или отличить его от другого мультипликативного преобразования.
Иногда, однако, полезно посмотреть на нули графика (если их больше одного) или поворотные точки, так как они будут разбросаны дальше (если аргумент умножается на нечто большее, чем 1) или сгруппированы к оси y (если аргумент умножается на что-то меньшее, чем 1).
Например, глядя на y = x 2 − 4, вы можете видеть, что умножение вне функции не меняет положение нулей, но умножение внутри функции меняет:
график x 2 − 4:
(Это график f ( x ), с нулями на x = −2, 2) 9006 график f ( x ) = 2( x 2 − 4):
(Этот график выше, но нули совпадают с нулями исходной функции, показанной в предыдущей рамке. )
)
график (2 x ) 2 − 4:
(Этот график не только выше, но и нули сместились внутрь, до x = -1, 1.)
Напомним, что преобразования «влево», «вправо», «вверх», «вниз», «отразить» и «отразить» довольно просты, но » умножить», также называемые «растягиванием» и «сжатием», могут немного запутаться. Просто надеюсь, что они не часто требуется от вас.
В типичных домашних заданиях по этой теме вас просят изобразить преобразование функции с учетом исходной функции или вычислить преобразование с учетом сравнительных графиков.
График f ( x ) = x 4 выглядит следующим образом: будет перемещен вверх на одну единицу. И «-2» внутри аргумента говорит мне, что график будет сдвинут на две единицы ВПРАВО. (Помните, что смещение влево-вправо происходит в обратную сторону от ожидаемого.)
Обычно лучше работать изнутри наружу. Поэтому сначала я сдвину график вправо на две единицы. Затем я подниму результат на одну единицу вверх.
Затем я подниму результат на одну единицу вверх.
Тогда моя переведенная диаграмма выглядит так:
Когда они заставляют вас строить графики, перемещая другие графики, они не могут сильно критиковать ваш рисунок, так как вы не должны делать Т-диаграмму и вычисление точных точек. Но постарайтесь, чтобы ваш график выглядел разумным.
Кстати, вы всегда можете «обмануть», особенно если у вас есть графический калькулятор, быстро построив график y = ( x − 2) 4 + 1 и убедившись, что он соответствует тому, что вы нарисовали . Но вам нужно знать, как выполнять преобразования функций, потому что есть способы задавать вопросы, которые не позволяют вам обманывать, как мы увидим в следующем разделе.
URL: https://www.purplemath.com/modules/fcntrans3.htm
Страница 1Страница 2Страница 4Страница 5
Правила вероятности
вероятности других событий. В этом уроке рассматриваются некоторые важные правила
которые упрощают эти вычисления.
Примечание: Ваш браузер не поддерживает видео HTML5. Если вы просматриваете эту веб-страницу в другом браузере (например, последняя версия Edge, Chrome, Firefox или Opera), вы можете посмотреть видеообработку этого урока.
Определения и обозначения
Прежде чем обсуждать правила вероятности, мы сформулируем следующие определения:
- Два события взаимно эксклюзивный или непересекающийся если они не могут произойти одновременно.
- Вероятность того, что событие А произойдет при условии, что произошло событие В, называется условная вероятность . Условная вероятность события A при данном событии B обозначается символом P(A|B).
- дополнение события – это событие, которое не происходит. Вероятность того, что событие А произойдет 90 455, а не 90 456, обозначается P(A’).
- Вероятность того, что События A и B оба произойдут, равна
вероятность пересечения точек А и В.
 Вероятность пересечения Событий А и В обозначается
Р(А ∩ В). Если события А и В
взаимоисключающие, P(A ∩ B) = 0,
Вероятность пересечения Событий А и В обозначается
Р(А ∩ В). Если события А и В
взаимоисключающие, P(A ∩ B) = 0, - Вероятность того, что произойдут события A или B, равна вероятность союза А и Б. Вероятность объединения событий A и B обозначается Р(А ∪ В) .
- Если возникновение события А изменяет вероятность Событие B, затем события A и B зависят от . С другой стороны, если возникновение события А не меняется вероятность события B, то события A и B равны независимый .
Реклама
Правило вычитания
В предыдущий урок, мы узнали два важных свойства вероятности:
- Вероятность события находится в диапазоне от 0 до 1.
- Сумма вероятностей всех возможных событий равна 1.
Правило вычитания следует непосредственно из этих свойств.
Правило вычитания . Вероятность
что событие А произойдет, равно 1 минус вероятность того, что событие А произойдет , а не происходить.
P(A) = 1 — P(A’)
Предположим, например, что вероятность того, что Билл окончит колледж составляет 0,80. Какова вероятность того, что Билл не закончит колледж? По правилу вычитания вероятность того, что Билл не закончит учебу составляет 1,00 — 0,80 или 0,20.
Правило умножения
Правило умножения применимо к ситуации, когда мы хотим знать вероятность пересечения двух событий; то есть мы хотим знать вероятность того, что два события (событие А и событие В) произойдут одновременно.
Правило умножения Вероятность того, что произойдут события A и B, равна равна вероятности того, что событие А произойдет, умноженной на вероятность того, что Событие B происходит при условии, что произошло A.
P(A ∩ B) = P(A) P(B|A)
Пример
В урне 6 красных и 4 черных шарика. Два шарика вытащены без
замена из урн. Какова вероятность того, что оба
шарики черные?
Решение: Пусть A = событие, состоящее в том, что первый шарик черный; и пусть В =
случае, если второй шарик черный. Нам известно следующее:
Нам известно следующее:
- В начале в урне 10 шариков, 4 из которых черные. Следовательно, Р(А) = 4/10.
- После первого выбора в урне 9 шариков, 3 из которых черный. Следовательно, P(B|A) = 3/9.
Следовательно, по правилу умножения:
P(A ∩ B) = P(A) P(B|A)
P(A ∩ B) = (4/10) * (3/9) = 12/90 = 2/15 = 0,133
Правило сложения
Правило сложения применяется к следующей ситуации. У нас есть два события, и мы хотим знать вероятность того, что любое событие произойдет.
Правило сложения Вероятность того, что Событие A или событие B происходит равна вероятности того, что событие А произойдет, плюс вероятность того, что событие Произойдет B минус вероятность того, что произойдут оба События A и B.
P(A ∪ B) = P(A) + P(B) — P(A ∩ B)
Примечание: Ссылаясь на тот факт, что P(A ∩ B) = P(A)P( B | A ), Правило сложения можно также выразить следующим образом:
P(A ∪ B) = P(A) + P(B) — P(A)P( B | A ) В библиотеку. Вероятность того, что она проверит (а) работу
художественной литературы — 0,40, (b) научно-популярная работа — 0,30 и (c) обе художественные
а документальная литература — 0,20. Какова вероятность того, что студент проверит
художественное произведение, научно-популярная литература или и то, и другое?
Вероятность того, что она проверит (а) работу
художественной литературы — 0,40, (b) научно-популярная работа — 0,30 и (c) обе художественные
а документальная литература — 0,20. Какова вероятность того, что студент проверит
художественное произведение, научно-популярная литература или и то, и другое?
Решение: Пусть F = событие, когда учащийся проверяет художественную литературу; и разреши N = событие, когда учащийся проверяет научно-популярную литературу. Затем на основании правила сложения:
P(F ∪ N) = P(F) + P(N) — P(F ∩ N)
P(F ∪ N) = 0,40 + 0,30 — 0,20 = 0,50
Проверьте свое понимание
Задача 1
В урне 6 красных и 4 черных шарика. Два шарика нарисованы с заменой из урн. Какова вероятность того, что оба шарики черные?
(A) 0,16
(B) 0,32
(C) 0,36
(D) 0,40
(E) 0,60
Решение
; и пусть В = случае, если второй шарик черный. Нам известно следующее:
- В начале в урне 10 шариков, 4 из которых черные.
 Следовательно, Р(А) = 4/10.
Следовательно, Р(А) = 4/10. - После первого выбора заменяем выбранный мрамор; так что есть еще В урне 10 шариков, из них 4 черных. Следовательно, P(B|A) = 4/10.
Следовательно, по правилу умножения:
P(A ∩ B) = P(A) P(B|A)
P(A ∩ B) = (4/10)*(4/10) = 16/100 = 0,16
Калькулятор вероятности
Используйте калькулятор вероятности для вычисления вероятности событие из известных вероятностей других событий. Вероятность Калькулятор бесплатный и простой в использовании. Калькулятор вероятности можно найти в Stat Trek. Главное меню на вкладке Инструменты статистики. Или вы можете нажать кнопку ниже.
Калькулятор вероятностей
Задача 2
Из колоды обычных игральных карт случайным образом вытягивается карта. Вы выиграете 10 долларов, если карта пиковая или туз. Какова вероятность того, что вы выиграете игра?
(A) 1/13
(B) 13/52
(C) 4/13
(D) 17/52
(E) Ничего из вышеперечисленного.
Решение
Правильный ответ C. Пусть S = событие, состоящее в том, что карта пиковая; и пусть А = случае, если карта является тузом. Мы знаем следующее:
- В колоде 52 карты.
- Есть 13 пик, поэтому P(S) = 13/52.
- Тузов 4, поэтому P(A) = 4/52.
- Существует 1 туз, который также является пикой, поэтому P(S ∩ A) = 1/52.
Следовательно, по правилу сложения:
P(S ∪ A) = P(S) + P(A) — P(S ∩ A)
P(S ∪ A) = 13/52 + 4 /52 — 1/52 = 16/52 = 4/13
Последний урок Следующий урок
Умножение комплексных чисел
Комплексное число представляет собой комбинацию действительного числа и мнимого числа:
Вещественное число — это число, которое мы используем каждый день.
Примеры: 12.38, ½, 0, −2000
Мнимое число, при возведении в квадрат которого дается отрицательный результат:
«Единица» мнимого числа, возведенная в квадрат, равна −1
i 2 5 2 5
Examples: 5 i , −3. 6 i , i /2, 500 i
6 i , i /2, 500 i
Examples of Complex Numbers:
| 3.6 + 4 и | | (действительная часть 3,6, мнимая часть 4 i ) |
| −0,02 + 1,2 i | | (действительная часть −0,02, мнимая часть 1,2 i ) |
| 25 − 0,3 i | | (действительная часть равна 25, мнимая часть равна −0,3 i ) |
Любая часть может быть равна нулю:
| 0 + 2 и | | (нет реальной части, мнимая часть 2 i ) | | то же, что и 2 i |
| 4 + 0 i | | (действительная часть равна 4, мнимая часть отсутствует) | | то же, что и 4 |
Умножение
Чтобы умножить комплексные числа:
Каждая часть первого комплексного числа умножается на
каждая часть второго комплексного числа.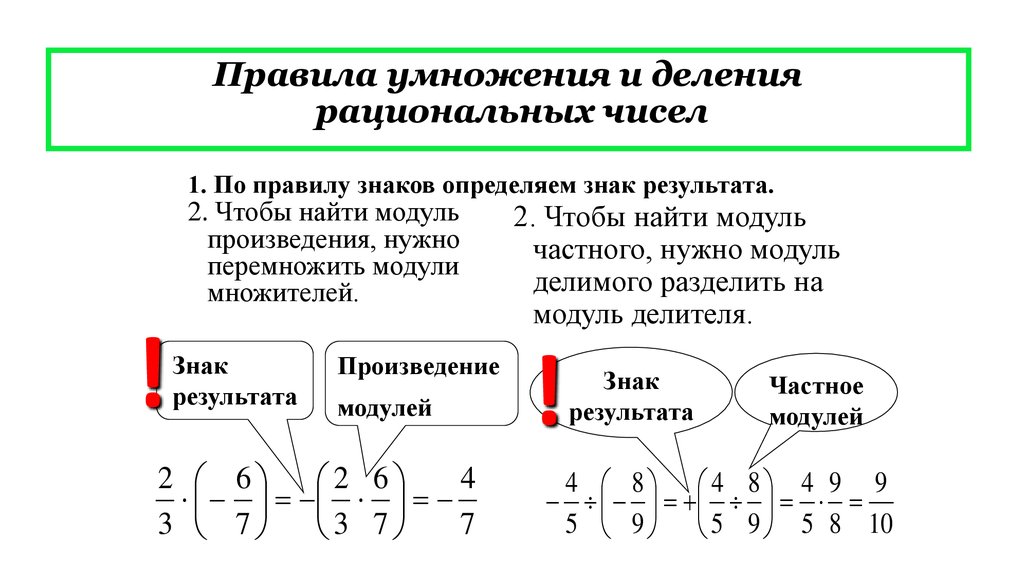 подробнее):
подробнее):
| |
(a+b i )(c+d i ) = ac + ad i + bc i + bd i 2 | |
Например:
Пример: (3 + 2
I ) (1 + 7 I )(3 + 2 I ) (1 + 7 I). 1 + 3×7 i + 2 i × 1+ 2 i × 7 i
= 3 + 21 i + 2 i + 14 i 2
= 3 + 21 i + 2 i − 14 (because i 2 = −1)
= −11 + 23 I
Вот еще один пример:
Пример: (1 +
I ) 2 (1 + I ) 2 6 (1 + I ) 2 6. = 1×1 + 1× i + 1× I + I 2 = 1 + 2 I — 1 (Потому что I 2 = −1) Используйте это правило: (a+b i )(c+d i ) = (ac−bd) + (ad+bc) i (3 + 902 900 i = −11 + 23 i Это просто метод «ФОЛЬГА» после небольшой работы: И вот вам шаблон (ac − bd) + (ad + bc) i . Это правило, безусловно, быстрее, но если вы его забудете, просто запомните метод FOIL. Теперь давайте посмотрим, как выглядит умножение на комплексной плоскости. Это самолет для сложных номеров ! Размещается Умножим на i : (3 + 4 i ) x i = 3 i + 4 i 2 Что упрощается до (потому что i 2 = −1): −4 + 3 i А вот и прикольная штука. Было ли это просто странным совпадением? Попробуем снова умножить на i : (-4 + 3 i ) x i = -4 i + 3 i 2 = -3 — 4 i и еще раз : (−3 − 4 i ) x i = −3 i − 4 i 2 = 4 − 3 и и еще раз : (4 − 3 i ) x i = 4 i − 3 i 2 = 3 + 4 i Разве это не потрясающе? Каждый раз он поворачивается на прямой угол, пока не окажется там, где начал. Попробуем на номер 1: Каждый раз под прямым углом. Выберите свой собственный комплексный номер и попробуйте сами, это хорошая практика. Давайте теперь более внимательно посмотрим на углы. Вот опять, но в полярной форме: Таким образом, комплексное число 3 + 4i также может быть представлено как расстояние (5) и угол (0,927 радиан). Как мы делаем преобразования? Мы можем сделать декартово преобразование в полярное: Мы также можем взять полярные координаты и преобразовать их в декартовы координаты: Обычно комплексное число записывается в полярной форме так: And «cos θ + i sin θ » is often shortened to «cis θ «, so: x + iy = r cis θ cis — это просто сокращение от , потому что θ + i sin θ Итак, мы можем написать: 3 + 4i = 5 цис 0,927 В некоторых предметах, таких как электроника, «цис» используется очень часто! Попробуем другое умножение: (1+ i ) (3+ i ) =1(3+ i ) + i 31 + I ) = 3 + I + 3 I + I 2 = 3 + 4 I — 1 )(1 + i )
)(1 + i )
)(1 + 7 i ) = (3×1 − 2×7) + (3×7 + 2×1) i 9999999999999999999999999999. Более быстрый способ!
Пример:
Почему это правило работает?
(a+b i )(c+d i ) = ac + ad i + bc i + bd i 2 Метод ФОЛЬГИ = акр + ад я + бк я — бд (потому что я 2 =-1) = (ac − bd) + (ad + bc) i (сбор одинаковых терминов) 
Сложный самолет
Это сложный самолет: Мы можем построить комплексное число, например 3 + 4i : Умножение на i
 .. она же поворот на прямой угол (90° или π/2)
.. она же поворот на прямой угол (90° или π/2) 1 × и = i я × я = -1 −1 × i = − i − i × i = 1 Вернуться к 1 снова! 
Полярная форма
Наш дружный комплексный номер 3+4i :
(расстояние и угол) Пример: число
3 + 4i  ..0 (достаточно близко)
..0 (достаточно близко) x + i y = r cos θ + i r sin θ = r(cos θ + i sin θ ) Теперь еще немного умножения
Пример: Умножьте 1+i на 3+i
 результат на комплексной плоскости:
результат на комплексной плоскости:Но более интересно увидеть эти числа в полярной форме:
Пример: (продолжение)
Преобразование 1 + I в полярный:
- R = √ (1 2 + 1 2 ) = √2 9049 + 1 2 ) = .
- θ = тангенс -1 (1/1) = 0,785 (до 3 десятичных знаков)
Преобразовать 3+i в полярную:
- r = √(3 2 + 1 2 ) =
0
- θ = тангенс -1 (1/3) = 0,322 (до 3 десятичных знаков)
Преобразовать 2+4i в полярную:
- r = √(2 2 + 4 2
Взгляните на значения r за минуту. Они как-то связаны?
А как насчет θ значений?
Вот это умножение в одну строку (используя «цис»):
(√2 цис 0,785) × (√10 цис 0,322) = √20 цис 1,107
Это самое интересное 0
Итак:
Величины умножаются.
И углы складываются.
При умножении в полярной форме: умножить величины, добавить углы.
И поэтому при умножении на i получается прямой угол:
i имеет величину 1 и образует прямой угол на комплексной плоскости
Квадрат сложного число, умножьте его само на себя:- умножьте величины: величина × величина = величина 2
- добавляем углы: угол + угол = 2 , поэтому мы удваиваем их.
Результат: квадрат величин, удвоение угла.
Пример: Let Us Square 1 +
2 I :(1 + 2 I ) (1 + 44444444949494949494949494949494949494949494944949494949494949494949494949494949494949494949494949494949494949н i + 4 i 2 = −3 + 4 i
На диаграмме угол выглядит (и есть!) удвоенным.
Также:
- Величина (1+2 i ) = √(1 2 + 2 2 ) = √5
- Величина (−3+4 i ) = √(3 2 + 4 2 ) = √25 = 5
Таким образом, величина тоже была возведена в квадрат.
В целом, комплексное число, такое как:
R (COS θ + I SIN θ )
Когда квадрат становится:
R 2 (Cos 2 40003 2 (COS 2 40002 2 (Cos 2 40002 R 2 (COS 2
R 2 (COS 2
R 2 (COS 2
R 2 (COS 2 . грех 2 θ )
(the magnitude r gets squared and the angle θ gets doubled.)
Or in the shorter «cis» notation:
(r cis θ ) 2 = r 2 CIS 2 θ
DE Moivre’s Formula
и математик Abraham de Moivre обнаружили, что он работает для любого интюгера n :
[Ros 1 SIN θ )] N = R N (COS N θ + I SIN N θ )
(MALDIUTY становится 904
4)(MALDIUTY становится 904
4) (MALDIUDA . )
)
или в более короткой «Цис» обозначения:
(R CIS θ ) N = R N CIS N θ
9003
88888888888888 гг. i
) 6Преобразовать 1+ i к полярному:
- r = √(1 2 + 1 2 ) = √2
- θ = тангенс -1 (1/1) = π/4
в «CIS» обозначениях: 1+ I = √2 CIS π/4
Сейчас с показателем 6, R становятся R 6 , θ становится 6 6666 , θ становятся 66666 6 , θ .
(√2 цис π/4) 6 = (√2) 6 цис 6π/4 = 8 цис 3π/2
Звездная величина теперь равна 8, а угол равен 3π/2 (=270°)
Что также равно 0−8 i (см. схему) умножать комплексные числа,
(a+b i )(c+d i ) = (ac−bd) + (ad+bc) i

[ r(cos θ + i sin θ ) ] n = r n (cos n θ + i sin n θ )
3.3 Два основных правила вероятности – статистика
При расчете вероятности необходимо учитывать два правила, когда вы определяете, являются ли два события независимыми или зависимыми, а также являются ли они взаимоисключающими или нет.
Правило умножения
, если A и B — два события, определенные в пространстве образца, затем P ( A и B ) = P ( B ) P (
A
 930330.930330.930330.930330.930330.930330.930330.930330.930330.930330.930330.930330.930330.930330.930330.930330.930330.930330.930330.930330.930330.930330. . . ).
930330.930330.930330.930330.930330.930330.930330.930330.930330.930330.930330.930330.930330.930330.930330.930330.930330.930330.930330.930330.930330.930330. . . ).Это уравнение можно переписать как P ( A И B ) = P ( B ) P ( A | B ), правило умножения.
Если A и B независимы, тогда P ( A | B ) = P ( A ). В этом специальном случае P ( A и B ) = P ( A | B ) P ( B ) становится P ( B ). ) = P ( A ) P ( B ).
) = P ( A ) P ( B ).
В мешке четыре зеленых, три красных и два желтых шарика. Марк достает из мешка два шарика без возврата. Вероятность того, что он вытащит сначала желтый, а затем зеленый шарик, равна 9.0003
P(желтый и зеленый)=P(желтый)⋅P(зеленый | желтый)=29⋅48=19P(желтый и зеленый)=P(желтый)⋅P(зеленый | желтый)=29⋅48=19
Обратите внимание, что P(зеленый | желтый)=48P(зеленый | желтый)=48. После извлечения желтого шарика в мешке остается четыре зеленых шарика и всего восемь шариков.
Правило сложения
Если A и B определены в пространстве выборки, то P ( A ИЛИ B ) = P ( A ) + P ( B ) − P ( A И B ).
Возьмите одну карту из стандартной колоды игральных карт. Пусть H = карта черва, а J = карта валет. Эти события не являются взаимоисключающими, поскольку карта может быть как червой, так и валетом.
P(H или J)=P(H)+P(J)−P(H и J)=1352+452−152=1652=413≈.3077P(H или J)=P(H)+P( J)−P(H и J)=1352+452−152=1652=413≈0,3077
Если А и B are mutually exclusive, then P ( A AND B ) = 0. Then P ( A OR B ) = P ( A ) + P ( B ) — P ( A и B ) становится
P ( A или B ) = P ( A ) +0. 0101010101010101010101010101010101010101010101010101010101010130.0. ).
0101010101010101010101010101010101010101010101010101010101010130.0. ).
Возьмите одну карту из стандартной колоды игральных карт. Пусть H = карта черва и S = карта пиковая. Эти события взаимоисключающие, потому что карта не может быть червой и пикой одновременно. Вероятность того, что карта червовая или пиковая, равна
.P(H или S)=P(H)+P(S)=1352+1352=2652=12=.5P(H или S)=P(H)+P(S)=1352+1352=2652= 12=0,5
Пример 3.14
Клаус пытается выбрать, куда поехать в отпуск. Два варианта: A = Новая Зеландия и B = Аляска.
- Клаус может позволить себе только один отпуск. Вероятность того, что он выберет A равно P ( A ) = 0,6, а вероятность того, что он выберет B , равна P ( B ) = 0,35.

- P ( A AND B ) = 0, потому что Клаус может позволить себе только один отпуск.
- Следовательно, вероятность того, что он выберет Новую Зеландию или Аляску, равна P ( A ИЛИ B ) = P ( A ) + P ( B + 90,560) = 0,3. = 0,95. Обратите внимание, что вероятность того, что он никуда не поедет в отпуск, должна быть 0,05.
Пример 3.15
Карлос играет в американский футбол. Он забивает гол в 65% случаев, когда бросает. Карлос собирается забить два гола подряд в следующем матче. A = событие Карлос успешен с первой попытки. Р ( А ) = 0,65. B = событие Карлос успешен со второй попытки. P ( B ) = 0,65. Карлос часто стреляет сериями. Вероятность того, что он забьет второй гол с учетом того, что он забил первый гол, равен 0,90.
B = событие Карлос успешен со второй попытки. P ( B ) = 0,65. Карлос часто стреляет сериями. Вероятность того, что он забьет второй гол с учетом того, что он забил первый гол, равен 0,90.
Проблема
а. Какова вероятность того, что он забьет оба гола?
Решение 1
а. Задача заключается в том, чтобы найти P ( A И B ) = P ( B И A ). Поскольку P ( B | A ) = 0,90: P ( B И A ) = P ( B | )1930 P ( A ) = (0,90)(0,65) = 0,585.
Карлос забьет первый и второй голы с вероятностью 0,585.
Проблема
б. Какова вероятность того, что Карлос забьет первый или второй гол?
Решение 2
б. Проблема заключается в том, чтобы найти P ( A ИЛИ B ).
P ( A ИЛИ B ) = P ( A ) + P ( B ) − P ( A И B ) = 0,65 + 0,65 − 0,585 = 0,715
Карлос забьет либо первый, либо второй гол с вероятностью 0,715.
Проблема
г. Являются ли A и B независимыми?
Решение 3
в. Нет, это не так, потому что P ( B И A ) = 0,585.
Нет, это не так, потому что P ( B И A ) = 0,585.
P ( B ) P ( A ) = (0,65)(0,65) = 0,423
.423 ≠ .585 = P ( B и A )
SO, P ( B и A ) — не , равного P ( ( ( ( ( ( ( ( ( ( ( ( ( ( ( ( ( ( и A ) — ( B и A ) — . Р ( А ).
Проблема
д. Являются ли A и B взаимоисключающими?
Являются ли A и B взаимоисключающими?
Решение 4
д. Нет, потому что P ( A и B ) = 0,585.
Взаимоисключающие, P ( A AND B ) должны быть равны нулю.
Пример 3.16
Общественная команда по плаванию насчитывает 150 членов. Семьдесят пять членов являются опытными пловцами. Сорок семь участников являются пловцами среднего уровня. Остальные — начинающие пловцы. Сорок опытных пловцов тренируются четыре раза в неделю. Тридцать пловцов среднего уровня тренируются четыре раза в неделю. Десять начинающих пловцов тренируются четыре раза в неделю. Предположим, случайным образом выбран один член команды по плаванию.
Предположим, случайным образом выбран один член команды по плаванию.
Проблема
а. Какова вероятность того, что участник — начинающий пловец?
Решение 1
а. Есть 150 членов; 75 из них продвинутые, а 47 пловцы среднего уровня. Итак, 150 − 75 − 47 = 28 начинающих пловцов. Вероятность того, что случайно выбранный пловец — новичок, равна 28150,28150.
Проблема
б. Какова вероятность того, что участник занимается четыре раза в неделю?
Решение 2
б. 40 + 30 + 10 150=8015040 + 30 + 10 150=80150
Проблема
г. Какова вероятность того, что участник хорошо плавает и занимается четыре раза в неделю?
Решение 3
в. Есть 40 продвинутых пловцов, которые тренируются четыре раза в неделю, поэтому вероятность равна 40150,40150.
Проблема
д. Какова вероятность того, что участник является продвинутым пловцом и пловцом среднего уровня? Являются ли продвинутый пловец и пловец среднего уровня взаимоисключающими? Почему или почему нет?
Решение 4
д. P (расширенный И промежуточный) = 0, поэтому это взаимоисключающие события. Пловец не может одновременно быть продвинутым пловцом и пловцом среднего уровня.
Проблема
эл. Вы начинающий пловец и практикуете четыре раза в неделю независимые соревнования? Почему или почему нет?
Решение 5
эл. Нет, это не самостоятельные события.
P (новичок И практикуется четыре раза в неделю) = 0,0667
P (новичок) P (занятия четыре раза в неделю) = 0,0996
0,0667 ≠ 0,0996
Пример 3.
 17
17Фелисити ходит в школу в Модесто, Калифорния. Вероятность того, что Фелисити запишется на урок математики, равна 0,2, а вероятность того, что она запишется на урок речи, равна 0,65. Вероятность того, что она запишется на урок математики, ПРИ УСЛОВИИ, что она запишется на урок речи, равна 0,25.
Пусть M = урок математики, S = урок речи и M | S = математика в речи.
Проблема
- Какова вероятность того, что Фелисити запишется на математику и речь?
Найти P ( M И S ) = P ( M | S ) P ( S ). - Какова вероятность того, что Фелисити запишется на уроки математики или речи?
Найти P ( M ИЛИ S ) = P ( M ) + P ( S ) − P ( S M И 9).
- Являются ли M и S независимыми? Является ли P ( M | S ) = P ( M )?
- Являются ли M и S взаимоисключающими? Является ли P ( M И S ) = 0?
Решение 1
а. P ( M И S ) = P ( M | S ) P ( S ) = 9,25 (0,005) P ( M или S ) = P ( M ) + P ( S ) — P ( M и S05.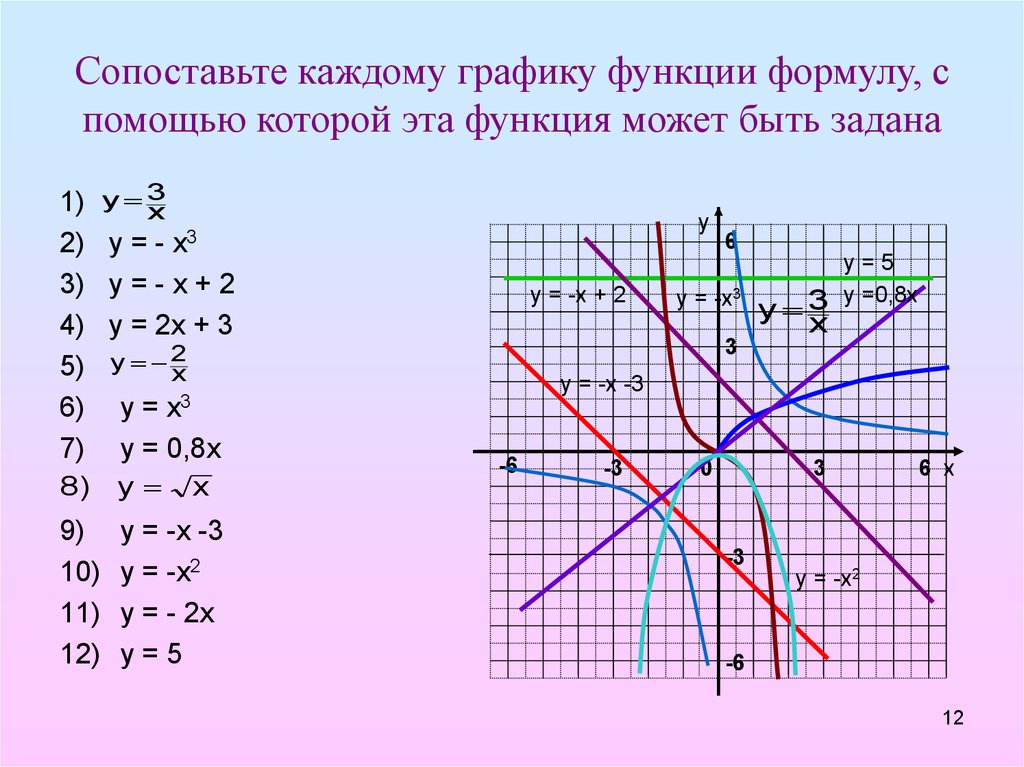 0,1625 = 0,6875
0,1625 = 0,6875
в. Нет, P ( M | S ) = 0,25 и P ( M ) = 0,2.
д. Нет, P ( M И S ) = 0,1625.
Пример 3.18
Исследователи изучают один конкретный тип заболевания, которым чаще страдают женщины, чем мужчины. Исследования показывают, что примерно у одной женщины из семи (примерно 14,3 процента), доживших до 90 лет, развивается заболевание. Предположим, что у тех женщин, у которых развивается это заболевание, тест отрицательный в 2 процентах случаев. Также предположим, что в общей популяции женщин тест на заболевание дает отрицательный результат примерно в 85% случаев. Пусть B = женщина заболевает и пусть N = тест отрицательный. Предположим, что наугад выбрана одна женщина.
Предположим, что наугад выбрана одна женщина.
Проблема
а. Какова вероятность того, что у женщины разовьется заболевание? Какова вероятность того, что тест женщины будет отрицательным?
Решение 1
а. P ( B ) = 0,143; Р ( Н ) = 0,85
Проблема
б. Учитывая, что у женщины развилось заболевание, какова вероятность того, что ее тест будет отрицательным?
Решение 2
б. Среди женщин, у которых развивается заболевание, тест отрицательный в 2% случаев, поэтому P ( N | B ) = 0,02
Проблема
г. Какова вероятность того, что у женщины есть заболевание И отрицательный результат?
Решение 3
в. P ( B И N ) = P ( B ) P ( N | B ) = (.143)(.022)
P ( B И N ) = P ( B ) P ( N | B ) = (.143)(.022)
Проблема
д. Какова вероятность того, что у женщины заболевание ИЛИ отрицательный результат?
Решение 4
д. P ( B или N ) = P ( B ) + P ( N ) — P ( B и 160160160160160160160160160160160160160160160.8. 0,0029 = 0,9901
Проблема
эл. Имеют ли заболевание и тестирование отрицательные независимые события?
Имеют ли заболевание и тестирование отрицательные независимые события?
Решение 5
эл. № P ( N ) = 0,85; P ( N | B ) = 0,02. Итак, P ( N | B ) не равно P ( N ).
Проблема
ф. Болезнь и отрицательный результат теста исключают друг друга?
Решение 6
ф. № P ( B И N ) = 0,0029. Чтобы B и N были взаимоисключающими, P ( B AND N ) должен быть равен нулю.
Пример 3.19
Проблема
См. информацию в примере 3.18. P = тест положительный.
- Учитывая, что у женщины развилось заболевание, какова вероятность того, что ее анализ окажется положительным? Найдите P ( P | B ) = 1 − P ( N | B ).
- Какова вероятность того, что у женщины разовьется заболевание и положительный результат теста? Найти Р ( Б И Р ) = Р ( Р | Б ) Р ( Б ).
- Какова вероятность того, что у женщины не разовьется заболевание? Найдите P ( B′ ) = 1 − P ( B ).

- Какова вероятность того, что женщина даст положительный результат на это заболевание? Найдите P ( P ) = 1 − P ( N ).
Решение 1
а. б. P ( B И P ) = P ( P | B ) P ( B ) = 0,98 (0,140) P ( B’ ) = 1 − P ( B ) = 1 − 0,143 = 0,857
d. P ( P ) = 1 − P ( N ) = 1 − 0,85 = 0,15
Исчисление II — Серия — Основы
Показать мобильное уведомление Показать все примечания Скрыть все примечания
Мобильное уведомление
Похоже, вы находитесь на устройстве с «узкой» шириной экрана ( т. \infty \) (обратите внимание, что \(n = 1\) для удобства, это может быть ничего) и определить следующее, 9\infty\). Также помните, что \(\Sigma\) используется для представления этой суммы и называется множеством имен. Наиболее распространенными именами являются: нотация серии , нотация суммирования и сигма нотация .
\infty \) (обратите внимание, что \(n = 1\) для удобства, это может быть ничего) и определить следующее, 9\infty\). Также помните, что \(\Sigma\) используется для представления этой суммы и называется множеством имен. Наиболее распространенными именами являются: нотация серии , нотация суммирования и сигма нотация .
Вы должны были хотя бы мельком увидеть это обозначение, когда увидели определение определенного интеграла в Исчислении I. Если вам нужно быстро освежить в памяти обозначения суммирования, см. обзор обозначений суммирования в Примечаниях к Исчислению I.
9\infty {{a_i}} = {a_1} + {a_2} + {a_3} + \cdots + {a_n} + \cdots \]Однако с этим нужно быть осторожным. Это означает, что бесконечный ряд — это просто бесконечная сумма членов, и, как мы увидим в следующем разделе, это не совсем верно для многих рядов.
В следующем разделе мы собираемся более подробно обсудить значение бесконечного ряда, если оно, конечно, есть, а также идеи сходимости и расхождения.
Этот раздел будет посвящен в основном проблемам с обозначениями, а также проверке того, что мы можем выполнять некоторые основные манипуляции с бесконечными рядами, чтобы мы были готовы к ним, когда нам понадобится иметь возможность иметь дело с ними в последующих разделах.
Во-первых, следует отметить, что в большей части этой главы мы будем называть бесконечные ряды просто рядами. Если нам когда-нибудь понадобится работать как с бесконечными, так и с конечными рядами, мы будем более осторожны с терминологией, но в большинстве разделов мы будем иметь дело исключительно с бесконечными рядами, поэтому будем называть их просто рядами. 92} + 1}}} \,\,\,\,\,\,и т.д.\]
Важно еще раз отметить, что индекс будет начинаться с любого значения, с которого начинается последовательность членов ряда, и это может быть буквально что угодно. До сих пор мы использовали \(n = 0\) и \(n = 1\), но индекс мог начинаться где угодно. На самом деле мы обычно будем использовать \(\sum {{a_n}} \) для представления бесконечного ряда, в котором начальная точка для индекса не важна. Когда мы удаляем начальное значение индекса, мы также удаляем бесконечность сверху, поэтому не забывайте, что технически она все еще существует.
Когда мы удаляем начальное значение индекса, мы также удаляем бесконечность сверху, поэтому не забывайте, что технически она все еще существует.
Мы будем отбрасывать начальное значение индекса во многих фактах и теоремах, с которыми мы встретимся в этой главе. В этих фактах/теоремах начальная точка ряда не повлияет на результат, поэтому для упрощения обозначений и во избежание создания впечатления, что начальная точка важна, мы опускаем индекс из обозначений. Не забывайте, однако, что есть отправная точка и что это будет бесконечный ряд.
Обратите внимание, однако, что если мы поместим начальное значение индекса в ряд в факте/теореме, оно будет там, потому что оно действительно должно быть там.
Теперь, когда некоторые проблемы с обозначениями устранены, нам нужно начать думать о различных способах манипулирования рядами.
Мы начнем с базовой арифметики с бесконечными рядами, так как нам нужно будет уметь делать это время от времени. У нас есть следующие свойства.
Свойства
Если \(\sum {{a_n}} \) и \(\sum {{b_n}} \) являются сходящимися рядами, то
- \(\displaystyle \sum {c{a_n}} \), где \(с\) — любое число, также сходится и \[\сумма {c{a_n}} = c\сумма {{a_n}} \] 9\infty {\left({{a_n} \pm {b_n}} \right)} \]
Первое свойство просто говорит нам, что мы всегда можем вынести мультипликативную константу из бесконечного ряда и снова вспомнить, что если мы не введем начальное значение индекса, то ряд может начаться с любого значения. Также напомним, что в этих случаях мы тоже не будем ставить бесконечность вверху.
Второе свойство говорит, что если мы добавляем/вычитаем ряды, все, что нам действительно нужно сделать, это добавить/вычесть члены ряда. Также обратите внимание, что для добавления/вычитания ряда нам нужно убедиться, что оба имеют одинаковое начальное значение индекса, и новый ряд также будет начинаться с этого значения. 93}\]
Да, это было просто умножение двух многочленов. Каждое из них является конечной суммой, и поэтому оно имеет значение. При выполнении умножения мы не просто умножали постоянные члены, затем члены \(x\), и т. д. . Вместо этого нам пришлось распределить 2 через второй многочлен, затем распределить \(x\) через второй многочлен и, наконец, объединить одинаковые члены.
Каждое из них является конечной суммой, и поэтому оно имеет значение. При выполнении умножения мы не просто умножали постоянные члены, затем члены \(x\), и т. д. . Вместо этого нам пришлось распределить 2 через второй многочлен, затем распределить \(x\) через второй многочлен и, наконец, объединить одинаковые члены.
Умножение бесконечных рядов (хотя мы сказали, что не можем думать о бесконечном ряду как о бесконечной сумме) нужно делать таким же образом. При умножении мы действительно просим нас сделать следующее: 9\infty {{b_n}} } \right) = \left( {{a_0} + {a_1} + {a_2} + {a_3} + \cdots } \right)\left( {{b_0} + {b_1} + {b_2} + {b_3} + \cdots } \right)\]
Чтобы сделать это умножение, мы должны распределить \({a_0}\) через второй член, распределить \({a_1}\) через, и т. д. , а затем объединить подобные члены. Это практически невозможно, поскольку оба ряда содержат бесконечное множество членов, однако для определения произведения двух рядов можно использовать следующую формулу. 9n {{a_i}{b_{n — i}}} \)
9n {{a_i}{b_{n — i}}} \)
Мы также не можем много сказать о сходимости продукта. Даже если оба исходных ряда сходятся, произведение может быть расходящимся. Реальность такова, что умножение рядов — довольно сложный процесс, и его обычно по возможности избегают. Мы кратко рассмотрим его ближе к концу главы, когда у нас будет больше работы за плечами, и мы столкнемся с ситуацией, когда это действительно может быть тем, что мы хотим сделать. До тех пор не беспокойтесь о умножении серий.
Следующая тема, которую нам нужно обсудить в этом разделе, — это сдвиг индекса . Честно говоря, это не та тема, которую мы будем часто видеть в этом курсе. На самом деле, мы будем использовать его один раз в следующем разделе, а затем, по всей вероятности, не будем использовать его снова. Несмотря на то, что мы не будем часто использовать его в этом курсе, это не означает, однако, что он не будет часто использоваться в других классах, где вы можете столкнуться с сериями.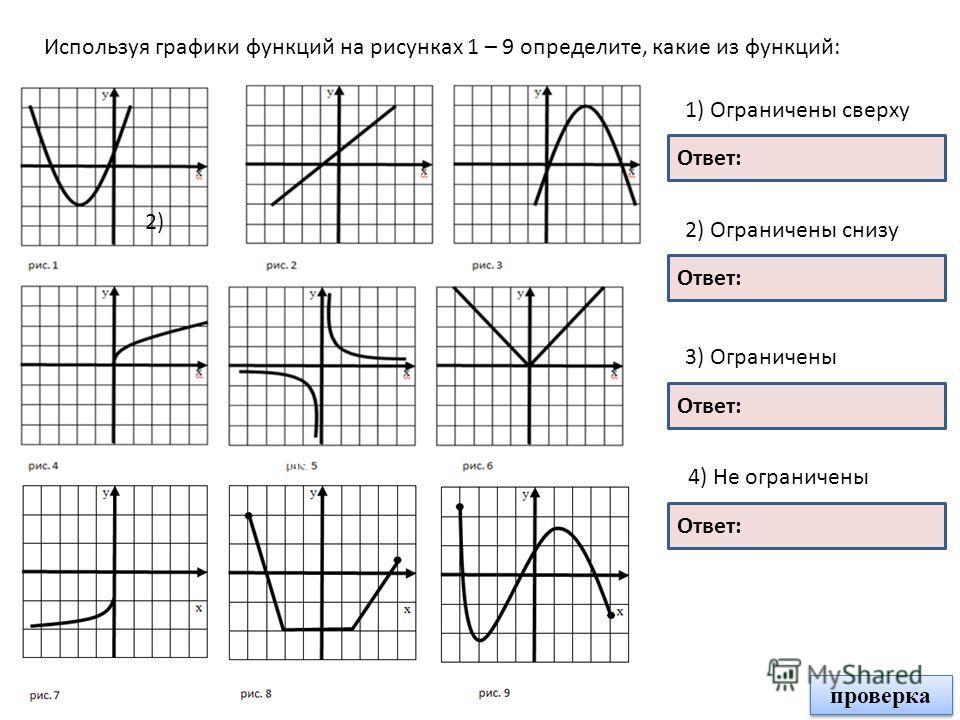 Итак, мы кратко расскажем об этом здесь, чтобы вы могли сказать, что видели это. 9п}}}} \]
Итак, мы кратко расскажем об этом здесь, чтобы вы могли сказать, что видели это. 9п}}}} \]
Предположим, что по какой-то причине мы хотели начать этот ряд с \(n = 0\), но не хотели менять значение ряда. Это означает, что мы не можем просто изменить \(n = 2\) на \(n = 0\), так как это добавит два новых члена к ряду и, таким образом, изменит его значение.
Сдвиг индекса — довольно простой процесс. Мы начнем с определения нового индекса, скажем, \(i\), следующим образом:
\[я = п — 2\]
Теперь, когда \(n = 2\), мы получим \(i = 0\). Обратите также внимание, что если \(n = \infty \), то \(i = \infty — 2 = \infty \), поэтому здесь изменится только нижний предел. Далее мы можем решить это для \(n\), чтобы получить
\[п = я + 2\]
Теперь мы можем полностью переписать ряд в терминах индекса \(i\) вместо индекса \(n\), просто подставив наше уравнение для \(n\) в терминах \(i\). {i + 2}}}}} \]
95}}} + \cdots \end{align*}\]
{i + 2}}}}} \]
95}}} + \cdots \end{align*}\]
Таким образом, обе серии имеют абсолютно одинаковые термины.
На самом деле есть более простой способ сделать сдвиг индекса. Приведенный выше метод является технически правильным способом выполнения сдвига индекса. Однако обратите внимание, что в приведенном выше примере мы уменьшили начальное значение индекса на 2, и все \(n\) в членах ряда также увеличились на 2.
Так будет всегда. Если мы уменьшим начальное значение индекса на заданную величину, то все остальные \(n\) в члене ряда увеличатся на ту же величину. Точно так же, если мы увеличим начальное значение индекса на заданную величину, то все \(n\) в члене ряда уменьшится на ту же величину. 9{п — 1}}}}} \]
Последняя тема в этом разделе снова является темой, которую мы не будем часто видеть в этом классе, хотя мы будем видеть ее чаще, чем сдвиги индекса. Эта последняя тема больше посвящена альтернативным способам написания сериалов, когда этого требует ситуация.


 То, что для получения списка нам нужно связаться с Пятнициной, может остаться за кадром.
То, что для получения списка нам нужно связаться с Пятнициной, может остаться за кадром.

 Во многих случаях это увеличивает риск переделки по уже выполненным задачам.
Во многих случаях это увеличивает риск переделки по уже выполненным задачам. см.
см.  Схема Горнера деления многочлена на двучлен. Теорема о подборе корней многочлена с целочисленными. коэффициентами. Разложение многочлена n — й степени на простейшие множители
Схема Горнера деления многочлена на двучлен. Теорема о подборе корней многочлена с целочисленными. коэффициентами. Разложение многочлена n — й степени на простейшие множители  Некоторые равносильные преобразования
Некоторые равносильные преобразования  Окружность и круг. Длина окружности и дуги окружности. Площадь круга и сектора круга. Вычисление объемов и площадей поверхности
Окружность и круг. Длина окружности и дуги окружности. Площадь круга и сектора круга. Вычисление объемов и площадей поверхности  ПРЯМАЯ НА ПЛОСКОСТИ
ПРЯМАЯ НА ПЛОСКОСТИ  Каноническое уравнение прямой в пространстве. Уравнение прямой в пространстве, проходящей через две различные точки. Угол между прямой плоскостью. Задание прямой в пространстве как линии пересечения двух плоскостей
Каноническое уравнение прямой в пространстве. Уравнение прямой в пространстве, проходящей через две различные точки. Угол между прямой плоскостью. Задание прямой в пространстве как линии пересечения двух плоскостей  МАТРИЦЫ
МАТРИЦЫ  Односторонние производные. Условие существования производной. Бесконечные производные. Таблица производных. Правила дифференцирования. Производная сложной функции. Производная обратной функции. Производная функции, заданной параметрически. Производная функции, заданной неявно. Производная показательно-степенной функции. Производные высших порядков. Формулы Тейлора и Маклорена. Теорема Ферма. Необходимое условие экстремума функции. Теорема Ролля. Теорема Лагранжа. Теорема Коши. Правило Лопиталя для раскрытия неопределенностей. Уравнения касательной и нормали к графику функции. Дифференциал функции. Приближенные вычисления с помощью дифференциала. Дифференциалы высших порядков
Односторонние производные. Условие существования производной. Бесконечные производные. Таблица производных. Правила дифференцирования. Производная сложной функции. Производная обратной функции. Производная функции, заданной параметрически. Производная функции, заданной неявно. Производная показательно-степенной функции. Производные высших порядков. Формулы Тейлора и Маклорена. Теорема Ферма. Необходимое условие экстремума функции. Теорема Ролля. Теорема Лагранжа. Теорема Коши. Правило Лопиталя для раскрытия неопределенностей. Уравнения касательной и нормали к графику функции. Дифференциал функции. Приближенные вычисления с помощью дифференциала. Дифференциалы высших порядков  ОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ
ОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ 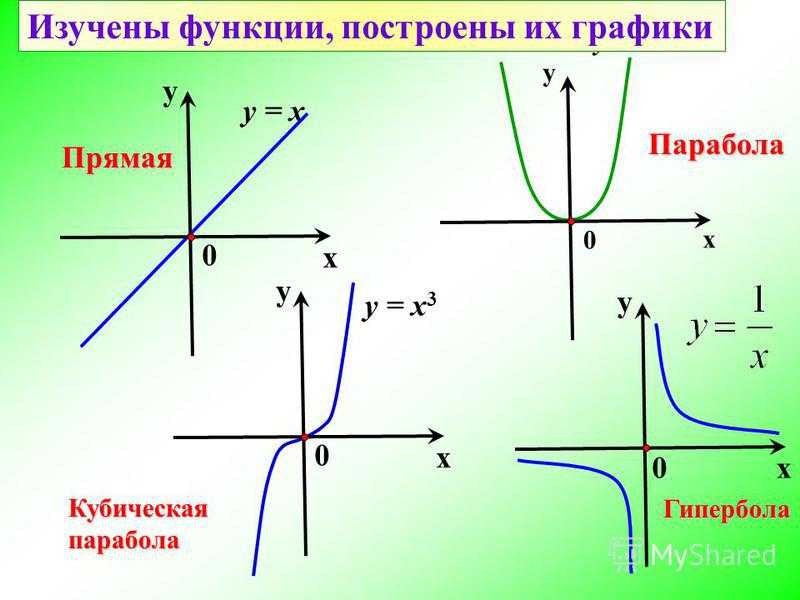 Свойства двойного и тройного интеграла. Вычисление двойного интеграла в полярных кординатах. Вычисление тройного интеграла в цилиндрических и сферических кординатах. Вычисление площадей и объемов
Свойства двойного и тройного интеграла. Вычисление двойного интеграла в полярных кординатах. Вычисление тройного интеграла в цилиндрических и сферических кординатах. Вычисление площадей и объемов 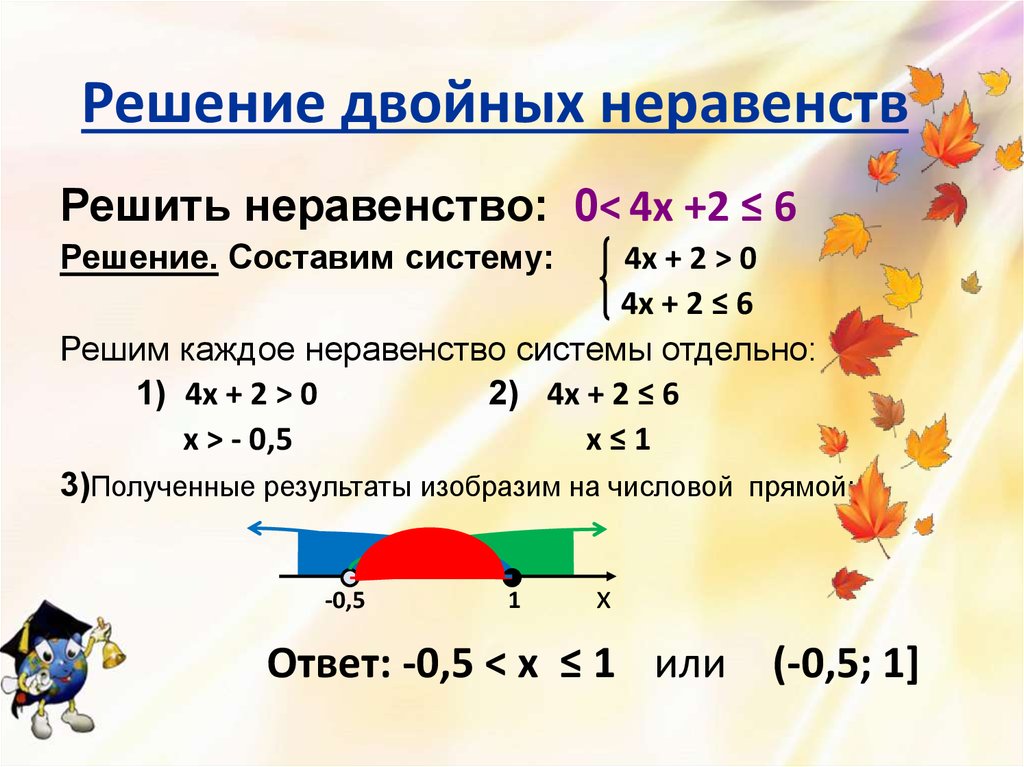 Разложения функций в степенные ряды. Значения сумм некоторых числовых рядов
Разложения функций в степенные ряды. Значения сумм некоторых числовых рядов  Комплексно сопряженное число. Модуль и аргумент комплексного числа. Тригонометрическая и показательная форма комплексного числа. Действия над комплексными числами в алгебраической, тригонометрической и показательной форме. Формула Муавра. Разложение многочлена на линейные множители. Основная теорема алгебры
Комплексно сопряженное число. Модуль и аргумент комплексного числа. Тригонометрическая и показательная форма комплексного числа. Действия над комплексными числами в алгебраической, тригонометрической и показательной форме. Формула Муавра. Разложение многочлена на линейные множители. Основная теорема алгебры  Законы распределения случайных величин: функция распределения, ряд распределения, плотность распределения. Числовые характеристики случайных величин: математическое ожидание, дисперсия, среднее квадратическое отклонение. Биномиальное распределение. Распределение Пуассона. Равномерное распределение. Нормальное распределение. Неравенство Чебышева
Законы распределения случайных величин: функция распределения, ряд распределения, плотность распределения. Числовые характеристики случайных величин: математическое ожидание, дисперсия, среднее квадратическое отклонение. Биномиальное распределение. Распределение Пуассона. Равномерное распределение. Нормальное распределение. Неравенство Чебышева  ИЗОБРАЖЕНИЯ ЗАВИСИМОСТЕЙ, ЗАДАННЫХ ПАРАМЕТРИЧЕСКИ
ИЗОБРАЖЕНИЯ ЗАВИСИМОСТЕЙ, ЗАДАННЫХ ПАРАМЕТРИЧЕСКИ  Вероятность пересечения Событий А и В обозначается
Р(А ∩ В). Если события А и В
взаимоисключающие, P(A ∩ B) = 0,
Вероятность пересечения Событий А и В обозначается
Р(А ∩ В). Если события А и В
взаимоисключающие, P(A ∩ B) = 0, Следовательно, Р(А) = 4/10.
Следовательно, Р(А) = 4/10.

