Предел функции 10 класс онлайн-подготовка на Ростелеком Лицей
Пример функции
Пусть задана функция и значение , значение аргумента. Что происходит с функцией, если ?
Рассмотрим функцию , за примем число 2, оно принадлежит области определения, т. е. , также известно, что .
Пусть , нам необходимо выяснить, что происходит с функцией и какова роль числа (рис. 1).
Рис. 1. График функции ,
Понятие предела функции, выделение
Начнем с выделения ε-окрестности в точке , – это произвольное малое число, например , тогда , , имеем -окрестность для . Имеем горизонтальную полосу шириной , получаем точки и .
Рис. 2. График функции , , ,
Значение достигается, когда , Значение достигается, когда .
меньше, чем , однако точка ближе к 2, значит, за мы выберем .
, так мы получили -окрестность для , получили точку (рис. 2).
– окрестность точки 2 выделяет такой кусок графика, который целиком расположен в горизонтальной полосе шириной .
Рис. 3. График функции ,
Кривая находится внутри горизонтальной полосы – это означает, что как только попадет в δ-окрестность точки 2, попадет в -окрестность точки .
То есть y и точность приближения зависит от . может быть сколько угодно малым числом, главное, чтобы положительным, но при заданном можно найти такое , что как только попадет в δ-окрестность точки 2, попадет в -окрестность точки , именно этим обстоятельством нам важна .
при . Для любой узкой горизонтальной полосы вокруг точки найдется подходящая вертикальная полоса вокруг точки такая, что выделяет такой кусок графика, который целиком находится в горизонтальной полосе (рис. 3).
Число называется пределом функции при , если сказанное справедливо для любого положительного .
Записывается это следующим образом:
Если находится вблизи точки 2, то находится вблизи своего предела, вблизи точки .
Предел функции в точке
Была функция , мы умножим числитель на , и разделим числитель на , ясно, что в точке 2 функция не существует, распишем эту функцию:
Наша новая функция совпадает со старой функцией везде, кроме одной точки, нарисуем новый чертеж (рис.
4):
Рис. 4. График
Важные отличия функций и
Важные отличия:
- .
- – предел равен .
- Непрерывна в точке .
- .
- – предел .
- Главное различие – это наличие разрыва в ОДЗ.
- Не является непрерывной в точке (рисунок 4).
Определения функции
Если первая функция существовала в точке 2, то вторая функция не существует в точке 2, а предел у них один и тот же. непрерывна потому, что предел этой функции при равен , т. е. значению функции в точке 2, чего нельзя сказать про функцию номер 2.
можно заменить на .
можно заменить другим числом из ОДЗ и получить важные определения:
- Функцию называют непрерывной в точке , если выполняется соотношение
- Функцию называют непрерывной на промежутке , если она непрерывна в каждой точке этого промежутка.
Утверждение непрерывности функции
Если выражение составлено из рациональных, иррациональных, тригонометрических выражений, то функция непрерывна в любой точке, в которой определено выражение , т. е.
Это утверждение позволяет определять, где данная функция непрерывна.
Теорема для вычисления пределов
Но каким образом вычислять пределы? Для этого существует теорема:
Если , , то:
- – предел суммы и при равен сумме пределов, т. е. .
- – предел произведения и g при равен произведению пределов, т. е..
- – предел частного при , есть частное от пределов, т. е. при .
- – предел произведения коэффициента на функцию равен умноженному на предел этой функции, т. е. постоянный множитель можно вынести за знак предела.
Пример 1, найти
Найти .
Во-первых, нужно взять предел от и отнять предел , во-вторых, в точке 1 функция непрерывна, значит, предел функции в этой точке равен значению функции при , т.
е. единицу подставляем, получаем:
Ответ: -1.
Пример 2, найти
Найти .
0 входит в область определения функции, значит, предел функции при равен значению функции в точке 0, функция непрерывна в точке 0, т. е. подставляем 0 и получаем:
Ответ: 0.
Вывод
Мы познакомились с важными понятиями предела функции в точке, непрерывности функции в точке, привели примеры.
Список литературы
- Алгебра и начала анализа, 10 класс (в двух частях). Учебник для общеобразовательных учреждений (профильный уровень) под ред. А. Г. Мордковича. – М.: Мнемозина, 2009.
- Алгебра и начала анализа, 10 класс (в двух частях). Задачник для общеобразовательных учреждений (профильный уровень) под ред. А. Г. Мордковича. – М.: Мнемозина, 2007.
- Виленкин Н.Я., Ивашев-Мусатов О.С., Шварцбурд С.И. Алгебра и математический анализ для 10 класса (учебное пособие для учащихся школ и классов с углубленным изучением математики). – М.: Просвещение, 1996.
- Галицкий М.Л., Мошкович М.М., Шварцбурд С.И. Углубленное изучение алгебры и математического анализа. – М.: Просвещение, 1997.
- Сборник задач по математике для поступающих во ВТУЗы (под ред. М.И. Сканави). – М.: Высшая школа, 1992.
- Мерзляк А.Г., Полонский В.Б., Якир М.С. Алгебраический тренажер. – К.: А.С.К., 1997.
- Саакян С.М., Гольдман А.М., Денисов Д.В. Задачи по алгебре и началам анализа (пособие для учащихся 10 –11 классов общеобразов. учреждений). – М.: Просвещение, 2003.
- Карп А.П. Сборник задач по алгебре и началам анализа : учеб. пособие для 10 –11 кл. с углубл. изуч. математики. – М.: Просвещение, 2006.
– М.: Просвещение, 1996.
Домашнее задание
- Найти .
- Вычислить .
- Вычислить .
Дополнительные рекомендованные ссылки на ресурсы сети Интернет
- Интернет-портал 5klass. net (Источник).
- Интернет-портал Mathematics-repetition.com (Источник).
- Интернет-портал Mathematics-tests.com (Источник).
net (Источник).
2. Предел функции, его свойства и геометрический смысл. Предел функции и бмф. Примеры
Пусть функция у=ƒ (х) определена в некоторой окрестности точки хо, кроме, быть может, самой точки хо.Сформулируем два, эквивалентных между собой, определения предела функции в точке.
Определение 1 (на «языке последовательностей», или по Гейне).
Число А называется пределом функции у=ƒ(х) в точке x0 (или при х хо), если для любой последовательности допустимых значений аргумента xn, n є N (xnx0), сходящейся к хо последовательность соответствующих значений функции ƒ(хn), n є N, сходится к числу А
В
этом случае пишут
или
ƒ(х)—>А при х→хо.
Геометрический смысл предела
функции:
означает,
что для всех точек х, достаточно близких
к точке хо,
соответствующие значения функции как
угодно мало отличаются от числа А.
Определение 2 (на «языке ε», или по Коши).
Число А называется пределом функции в точке хо (или при х→хо), если для любого положительного ε найдется такое положительное число δ, что для все ххо, удовлетворяющих неравенству |х-хо|<δ, выполняется неравенство |ƒ(х)-А|<ε.
Геометрический смысл предела функции:
если для любой ε-окрестности точки А найдется такая δ-окрестность точки хо, что для всех ххо из етой δ-окрестность соответствующие значения функции ƒ(х) лежат в ε-окрестности точки А. Иными словами, точки графика функции у=ƒ(х) лежат внутри полосы шириной 2ε, ограниченной прямыми у=А+ ε , у=А-ε (см. рис.) Очевидно, что величина δ зависит от выбора ε, поэтому пишут δ=δ(ε).
Функция f(x) называется бесконечно малой при ха, где а может быть числом или одной из величин , + или -, если.
Примеры:
1) Функция f(x) = tgx – бесконечно
малая при x→0.
2) f(x) = ln (1+x) – бесконечно малая при x→0.
Свойства пределов функции
1) Предел постоянной величины
Предел постоянной величины равен самой постоянной величине:
2) Предел суммы
Предел суммы двух функций равен сумме пределов этих функций:
Аналогично предел разности двух функций равен разности пределов этих функций.
Расширенное свойство предела суммы:
Предел суммы нескольких функций равен сумме пределов этих функций:
Аналогично предел разности нескольких функций равен разности пределов этих функций.
3) Предел произведения функции на постоянную величину
Постоянный коэффициэнт можно выносить за знак предела:
4) Предел произведения
Предел произведения двух функций равен произведению пределов этих функций:
Расширенное свойство предела произведения
Предел произведения нескольких функций равен произведению пределов этих функций:
5) Предел частного
Предел частного двух функций равен отношению пределов этих функций при условии, что предел знаменателя не равен нулю:
3.
Необходимый признак существования предела – ограниченность функции. Односторонние пределы функции в точке, их связь с пределом. Примеры.Ограниченность функции.
Функция f(x) называется ограниченной на данном промежутке (a,b), если существуют некоторые числа m и M такие, что
m ≤ f(x) ≤ M, при хє(a,b).
Число m o= inf {f(x)} [x є (a,b)] = max m называется нижней гранью функции ,
а число Mo= sup {f(x)} [x є (a,b)]=min M называется верхней гранью функции на данном промежутке (a,b).
Разность Mo— mo называется колебанием функции на промежутке (a,b).
Односторонние пределы.
Число A’ называется пределом слева функции f(x) в точке a:
если |A’
— f(x)| < ε при 0
< a — x < δ (ε).
Аналогично, число A» называется пределом справа функции f(x) в точке a:
если |A» — f(x) |< ε при 0 < x — a < δ (ε).
Для существования предела функции в точке необходимо и достаточно
Предел функции Примеры с ответами
О «пределе функции Примеры с ответами»
Предел функции Примеры с ответами :
Здесь мы увидим несколько примеров вопросов по оценке пределов.
Формулы можно найти на странице «Формулы для оценки пределов».
Вычисление пределов функции- Примеры
Вопрос 1 :
Оцените следующий предел
предел x -> 0 √ (x 2 + A 2 ) — A /√ (x 2 + B 2 ) — B
Решение:
= LIM x -> 00004 √(x 2 + a 2 ) — a / √(x 2 + b 2 ) — b
Мы можем распределить пределы для числителя и знаменателя.
= lim x -> 0 √(x 2 + a 2 ) — a / lim x -> 0 √(x 2 + b 2 ) — b
= lim x->0 [x 2 +a 2 -a 2 /√(x 2 +a 2 )2+a [04x]/) 2 +b 2 -b 2 /√(x 2 +b 2 )+b)]
= lim x->
0 [x 2 + /902(2 /902) a 2 )+a)]/[x 2 /√(x 2 +b 2 )+b)]= lim x->0 [x 2 /√04(x 902 2 +a 2 )+a)] ⋅ [√(x 2 +b 2 )+b)/x 2 ]
= lim x->0 [√(x 2 +b 2 )+b)/√(x 2 +a 2 )+a200 )]
= 2b/2a
= b/a
Отсюда значение lim x -> 0 √(x 2 + a 2 ) — 2 ) — б есть б/а.
Вопрос 2 :
Оцените следующий предел
lim x-> 0 (2 дуги sinx/3x)
Решение:
= lim x-> 0 (2 sin -1 x/3x)
= (2/3) lim x-> 0 90 2 (sin )
= 2/3
Следовательно, значение lim x -> 0 (2 arc sinx/3x) равно 2/3.
Вопрос 3:
Оцените следующий предел
LIM X-> 0 (1-COS X)/x 2
Решение:
= LIM x-> 0 (2 sin 2 (x/2)/(x 2 (4/4))
= lim x-> 0 (2/4) sin 2 (x /2)/(x/2) 2
= lim x-> 0 (2/4) (sin(x/2)/(x/2)) 2
= (1/ 2) lim x-> 0 (sin(x/2)/(x/2)) 2
= 1/2
Отсюда значение lim x-> 0 (1 – cos x )/x 2 равно 1/2
Вопрос 4 :
Вычислите следующий предел
lim x-> 0 (tan 2x/x)
Решение:
= lim x-> 7 = 0 (tan 2x/x(00/2/x) lim x-> 0 2 (tan 2x/2x)
= 2 lim x-> 0 (tan 2x/2x)
= 2
2x/x) равно 2.
Вопрос 5:
Оцените следующий предел
lim x-> 0 (2 x -3 x )/x
Решение:
= LIM x-> 0 (2 x -1 + 1-3 x ) /x
= lim x-> 0 [(2 x – 1) – (3 x — 1)]/x
= [lim x-> 0 (2 – 1)/x] – [lim x-> 0 (3 x — 1)/x]
= log 2 – log 3
= log (2/3)
Вопрос 6:
Оцените следующий предел
LIM X-> 0 (3 x -1)/√ (x+1)-1
Решение:
= LIM 22 x-> 0 ((3 x – 1)/√(x+1) – 1) (√(x+1) + 1 / √(x+1) + 1)
= lim x-> 0 ((3 x – 1)/((x+1) – 1) (√(x+1) + 1)
= lim x-> 0 ((3 x – 1)/x) (√(x+1) + 1)
= lim x-> 0 ((3 x – 1)/x) lim x-> 0 (√(x+1) + 1)
= log 3 (2)
= 2 log 3
= log 3 2
= 2 lim 9 x-
7 90 значение 0 (3 x – 1)/√(x+1) – 1 – это логарифм 9.
После того, как мы ознакомились с материалом, приведенным выше, мы надеемся, что учащиеся поняли, «Предел функции Примеры с Ответы»
Помимо материалов, приведенных в разделе «Предел функций, примеры с ответами», если вам нужны какие-либо другие материалы по математике, воспользуйтесь нашим пользовательским поиском Google здесь.
Пожалуйста, отправьте свой отзыв на [email protected]
Мы всегда ценим ваши отзывы.
©Все права защищены. onlinemath5all.com
2.2: Пределы функций — Mathematics LibreTexts
- Последнее обновление
- Сохранить как PDF
- Идентификатор страницы
- 10099
Концепция предела или предельного процесса, необходимая для понимания исчисления, существует уже тысячи лет.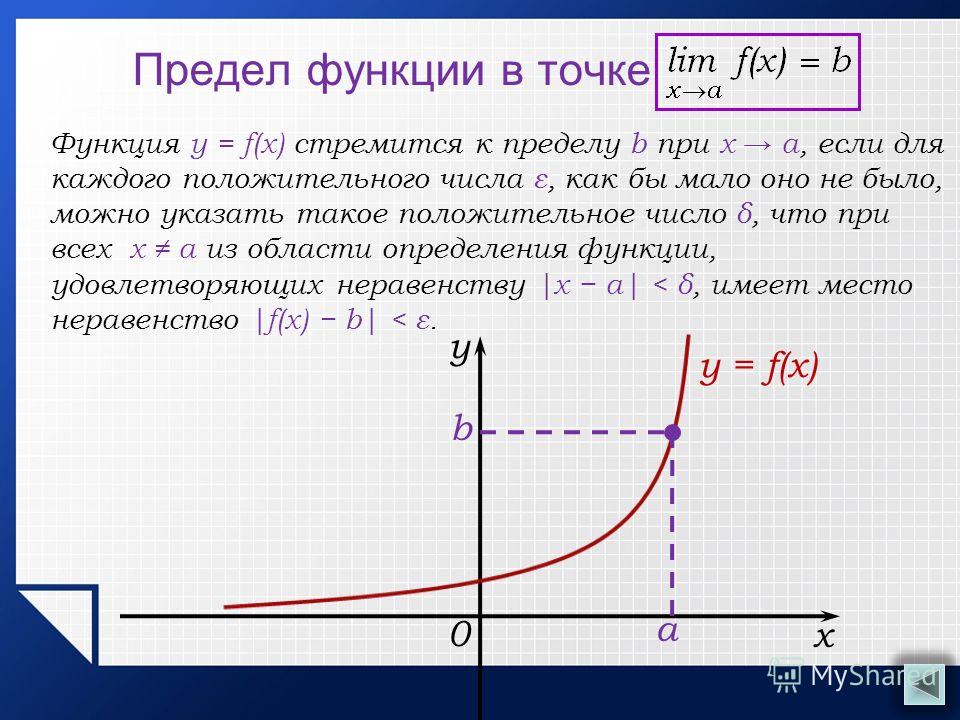
На самом деле ранние математики использовали ограничивающий процесс для получения все более и более точных приближений площадей кругов. Тем не менее, формальное определение предела — как мы его знаем и понимаем сегодня — появилось только в конце 19 века. Поэтому мы начинаем наши поиски понимания пределов, как это делали наши предки-математики, используя интуитивный подход. В конце этой главы, вооружившись концептуальным пониманием пределов, мы рассмотрим формальное определение предела. 92}\),
, которые показаны на рисунке \(\PageIndex{1}\). В частности, давайте сосредоточим наше внимание на поведении каждого графа при \(x=2\) и около него.
Рисунок \(\PageIndex{1}\): Эти графики показывают поведение трех различных функций вокруг \(x=2\).
Каждая из трех функций не определена в точке \(x=2\), но если мы делаем это утверждение и никакое другое, мы даем очень неполную картину того, как каждая функция ведет себя вблизи точки \(x=2\).
Чтобы более полно выразить поведение каждого графа вблизи 2, нам нужно ввести понятие предела. 92−4)/(x−2)\) ведет себя примерно так, как \(x=2\) на рисунке \(\PageIndex{1}\). Когда значения x приближаются к 2 по обе стороны от 2, значения \(y=f(x)\) приближаются к 4. Математически мы говорим, что предел \(f(x)\) при приближении x к 2 равен 4. Символически мы выражаем этот предел как
\(\displaystyle \lim_{x \to 2} f(x)=4\).
Из этого очень краткого неформального взгляда на один предел давайте начнем разрабатывать интуитивно понятное определение предела . Мы можем думать о пределе функции при числе а как об одном действительном числе \(L\), к которому функциональные значения приближаются по мере того, как значения x приближаются к а, при условии, что такое действительное число L существует. Сформулировав более тщательно, мы имеем следующее определение:
Определение (интуитивное): Предел
Пусть \(f(x)\) — функция, определенная для всех значений в открытом интервале, содержащем \(a\), за возможным исключением самого a, и пусть \(L \) быть действительным числом.
Если все значения функции \(f(x)\) приближаются к действительному числу \(L\), а значения \(x(≠a)\) приближаются к числу a, то мы говорим, что предел \( f(x)\) при приближении \(x\) к \(a\) есть \(L\). (Более кратко, поскольку \(x\) приближается к \(a\), \(f(x)\) приближается и остается близким к \(L\).) Символически мы выражаем эту идею как
\[\lim_{x \to a} f(x)=L.\]
Мы можем оценить пределы, составив таблицы функциональных значений и просмотрев их графики. Этот процесс описан в следующей стратегии решения проблем.
Стратегия решения проблем: оценка предела с использованием таблицы функциональных значений
1. Чтобы оценить \(\displaystyle \lim_{x \to a} f(x)\), мы начнем с заполнения таблицы функциональных значений . Мы должны выбрать два набора значений x: один набор значений, приближающихся к а и меньше а, и другой набор значений, приближающихся к а и превышающих \(а\). В таблице \(\PageIndex{1}\) показано, как могут выглядеть ваши таблицы.
| \(х\) | \(f(x)\) | \(х\) | \(f(x)\) |
|---|---|---|---|
| \(а-0,1\) | \(f(a-0. 1)\) | \(а+0,1\) | \(f(а+0,1)\) |
| \(а-0,01\) | \(ф(а-0,01)\) | \(а+0,001\) | \(f(а+0,001)\) |
| \(а-0,001\) | \(f(a-0,001)\) | \(а+0,0001\) | \(f(а+0,001)\) |
| \(а-0,0001\) | \(ф(а-0,0001)\) | \(а+0,00001\) | \(f(а+0,0001)\) |
| При необходимости используйте дополнительные значения. | При необходимости используйте дополнительные значения. | ||
2. Далее давайте посмотрим на значения в каждом из столбцов \(f(x)\) и определим, приближаются ли значения к одному значению по мере продвижения вниз по каждому столбцу. В наших столбцах мы смотрим на последовательность \(f(a-0,1)\), \(f(a-0,01)\), \(f(a-0,001)\), \(f(a-0,0001) \) и так далее, и \(f(a+0,1),f(a+0,01),f(a+0,001),f(a+0,0001)\) и так далее. (Примечание: хотя мы выбрали значения x \(a±0,1,a±0,01,a±0,001,a±0,0001\) и т. д., и эти значения, вероятно, будут работать почти каждый раз, в очень редких случаях мы возможно, потребуется изменить наш выбор.)
3. Если оба столбца приближаются к общему значению y L, мы указываем \(\displaystyle \lim_{x \to a}f(x)=L\). Мы можем использовать следующую стратегию для подтверждения результата, полученного из таблицы, или в качестве альтернативного метода оценки предела.
4. С помощью графического калькулятора или программного обеспечения, которое позволяет нам графически отображать функции, мы можем построить график функции \(f(x)\), убедившись, что функциональные значения \(f(x)\) для значений x близки в нашем окне.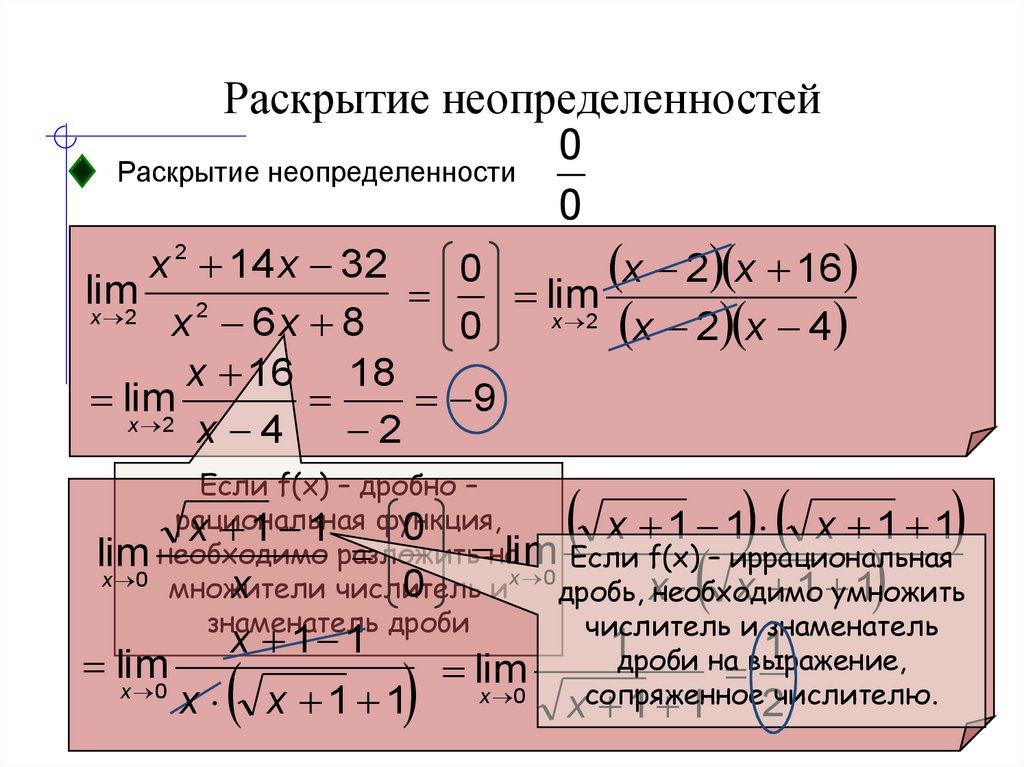
Мы можем использовать функцию трассировки, чтобы перемещаться по графику функции и наблюдать за показаниями значения y по мере того, как значения x приближаются к a. Если значения y приближаются к L, когда наши значения x приближаются к a с обоих направлений, тогда \(\displaystyle \lim_{x \to a}f(x)=L\). Возможно, нам придется увеличить наш график и повторить этот процесс несколько раз.
Мы применяем эту стратегию решения проблем для вычисления предела в примерах \(\PageIndex{1A}\) и \(\PageIndex{1B}\).
Пример \(\PageIndex{1A}\): оценка предела с помощью таблицы функциональных значений
Оценка \(\displaystyle \lim_{x \to 0}\frac{\sin x}{x}\) с использованием таблица функциональных значений.
Решение
Мы рассчитали значения \(f(x)=(\sin x)/x\) для значений \(x\), перечисленных в таблице \(\PageIndex{2}\) .
| \(х\) | \(\frac{\sin x}{x}\) | \(х\) | \(\frac{\sin x}{x}\) |
|---|---|---|---|
| -0,1 | 0,998334166468 | 0,1 | 0,998334166468 |
| -0,01 | 0,999983333417 | 0,01 | 0,999983333417 |
| -0,001 | 0,999999833333 | 0,001 | 0,999999833333 |
| -0,0001 | 0,999999998333 | 0,0001 | 0,999999998333 |
Примечание.
Значения в этой таблице были получены с помощью калькулятора и с использованием всех мест, указанных в выходных данных калькулятора.
Читая каждый столбец \(\frac{(\sin x)}{x}\), мы видим, что значения в каждом столбце приближаются к единице. Таким образом, вполне разумно заключить, что \(\displaystyle \lim_{x\to0}\frac{\sin x}{x}=1\). График \(f(x)=\frac{(sinx)}{x}\), построенный калькулятором или компьютером, будет аналогичен графику, показанному на рисунке \(\PageIndex{2}\), и подтверждает наши оценивать.
Рисунок \(\PageIndex{2}\): График \(f(x)=(\sin x)/x\) подтверждает оценку из табл.
Пример \(\PageIndex{1B}\): Оценка предела с помощью таблицы функциональных значений
Вычислить \(\displaystyle \lim_{x\to4}\frac{\sqrt{x}−2}{x −4}\) с помощью таблицы функциональных значений.
Решение
Как и прежде, мы используем таблицу — в данном случае Table \(\PageIndex{3}\) — для перечисления значений функции для заданных значений \(x\).
| \(х\) | \(\ гидроразрыва {\ sqrt {х}-2} {х-4} \) | \(х\) | \(\ гидроразрыва {\ sqrt {х}-2} {х-4} \) |
|---|---|---|---|
| 3,9 | 0,251582341869 | 4.1 | 0,248456731317 |
| 3,99 | 0,25015644562 | 4,01 | 0,24984394501 |
| 3,999 | 0,250015627 | 4. 001 | 0,249984377 |
| 3,9999 | 0,250001563 | 4.0001 | 0,249998438 |
| 3,99999 | 0,25000016 | 4.00001 | 0,24999984 |
Изучив эту таблицу, мы видим, что функциональные значения меньше 4 уменьшаются до 0,25, тогда как функциональные значения выше 4 увеличиваются до 0,25. Мы заключаем, что \(\displaystyle \lim_{x\to4}\frac{\sqrt{x}−2}{x−4}=0,25\). Мы подтверждаем эту оценку, используя график \(f(x)=\frac{\sqrt{x}−2}{x−4}\), показанный на рисунке \(\PageIndex{3}\).
Рисунок \(\PageIndex{3}\): График \(\frac{\sqrt{x}−2}{x−4}\) подтверждает оценку из таблицы
Упражнение \(\PageIndex{1}\)
Оценка \(\displaystyle \lim_{x \to 1} \frac{\frac{1}{x}−1}{x−1}\) с использованием таблица функциональных значений. Используйте график, чтобы подтвердить свою оценку.
- Подсказка
Используйте 0,9, 0,99, 0,999, 0,9999, 0,99999 и 1,1, 1,01, 1,001, 1,0001, 1,00001 в качестве табличных значений.
- Ответить
\[\lim_{x\to1}\frac{\frac{1}{x}−1}{x−1}=−1\]
На данный момент мы видим из примеров \(\PageIndex{1A}\) и \(\PageIndex{1b}\), что может быть так же просто, если не проще, оценить предел функции, исследуя его график, как он есть, для оценки предела с помощью таблицы функциональных значений. В примере \(\PageIndex{2}\) мы оцениваем ограничение исключительно по графику, а не по таблице функциональных значений.
Пример \(\PageIndex{2}\): оценка предела с помощью графика
Для \(g(x)\), показанного на рис. {х\к-1}г(х)\).
Рисунок \(\PageIndex{4}\): График \(g(x)\) включает одно значение не на гладкой кривой.
Решение :
Несмотря на то, что \(g(−1)=4\), когда значения x приближаются к −1 с любой стороны, значения \(g(x)\) приближаются к 3. Следовательно, \(\displaystyle \lim_{x\to-1}g(x)=3\). Заметим, что мы можем определить этот предел, даже не зная алгебраического выражения функции.
На основе примера \(\PageIndex{2A}\) мы делаем следующее наблюдение: возможно, что предел функции существует в точке, и функция может быть определена в этой точке, но предел функции и значение функции в точке могут быть разными.
Упражнение \(\PageIndex{2}\)
Используйте график \(h(x)\) на рисунке \(\PageIndex{5}\) для оценки \(\displaystyle \lim_{x \to 2 }h(x)\), если это возможно.
Рисунок \(\PageIndex{5}\):
- Подсказка
К какому значению y приближается функция, когда значения x приближаются к 2?
- Решение
\(\displaystyle \lim_{x \to 2}h(x)=−1.
\)
\)Глядя на таблицу функциональных значений или глядя на график функции, мы получаем полезную информацию о значении предела функции в данной точке. Однако эти методы слишком полагаются на догадки. Со временем нам потребуется разработать альтернативные методы оценки пределов. Эти новые методы носят более алгебраический характер, и мы рассмотрим их в следующем разделе; однако на этом этапе мы вводим два специальных ограничения, которые лежат в основе будущих методов.
Два важных ограничения
Пусть a — действительное число, а c — константа.
- \(\displaystyle \lim_{x \to a}x=a\)
- \(\displaystyle \lim_{x \to a}c=c\)
Мы можем сделать следующие замечания относительно этих двух пределов.
- Для первого предела заметим, что когда x приближается к a, то же самое происходит и с \(f(x)\), потому что \(f(x)=x\). Следовательно, \(\displaystyle \lim_{x \to a}x=a\).
- Для второго предела рассмотрим табл.
| \(х\) | \(f(x0=c\) | \(х\) | \(f(x)=c\) |
|---|---|---|---|
| \(а-0,1\) | с | \(а+0,1\) | с |
| \(а-0,01\) | с | \(а+0,01\) | с |
| \(а-0,001\) | с | \(а+0,001\) | с |
| \(а-0,0001\) | с | \(а+0,0001\) | с |
Обратите внимание, что для всех значений x (независимо от того, приближаются ли они к a), значения \(f(x)\) остаются постоянными в точке c.
У нас нет другого выбора, кроме как заключить \(\displaystyle \lim_{x \to a}c=c\).
Существование предела
Когда мы рассматриваем предел в следующем примере, имейте в виду, что для того, чтобы предел функции существовал в точке, функциональные значения должны приближаться к единственному вещественному значению в этой точке. Если функциональные значения не приближаются к единому значению, то предела не существует.
Пример \(\PageIndex{3}\): оценка несуществующего предела
Вычислить \(\displaystyle\lim_{x \to 0}\sin(1/x)\) с помощью таблицы значений.
Решение
В таблице \(\PageIndex{3}\) перечислены значения функции \(\sin(1/x)\) для заданных значений \(x\).
| \(х\) | \(\sin(1/x)\) | \(х\) | \(\sin(1/x)\) |
|---|---|---|---|
| -0,1 | 0,544021110889 | 0,1 | −0,544021110889 |
| -0,01 | 0,50636564111 | 0,01 | −0,50636564111 |
| -0,001 | −0,8268795405312 | 0,001 | 0,8268795405312 |
| -0,0001 | 0,305614388888 | 0,0001 | −0,305614388888 |
| -0,00001 | −0,035748797987 | 0,00001 | 0,035748797987 |
| -0,000001 | 0,349993504187 | 0,000001 | −0,349993504187 |
Изучив таблицу функциональных значений, мы видим, что значения y не приближаются ни к одному единственному значению.
Получается, что предела не существует. Прежде чем сделать такой вывод, давайте подойдем более системно. Возьмите следующую последовательность значений x, приближающихся к 0:
\[\frac{2}{π},\frac{2}{3π},\frac{2}{5π},\frac{2}{7π},\frac{2}{9π},\ frac{2}{11π},….\]
Соответствующие значения y равны
\[1,-1,1,-1,1,-1,….\]
В этой точке мы действительно можем заключить, что \(\displaystyle \lim_{x \to 0}sin(1/x)\) не существует. (Математики часто сокращают «не существует» до DNE. Таким образом, мы будем писать \(\displaystyle \lim_{x \to 0}\sin(1/x)\) DNE.) График \(f(x) =sin(1/x)\) показан на рисунке \(\PageIndex{6}\) и дает более четкое представление о поведении \(sin(1/x)\) при приближении x к 0. Вы можете видеть что \(sin(1/x)\) все более сильно колеблется между -1 и 1 по мере того, как \(x\) приближается к 0,92−4∣}{x−2}\) не существует.
Односторонние пределы
Иногда указание на то, что предел функции не существует в какой-то точке, не дает нам достаточно информации о поведении функции в этой конкретной точке.
Чтобы убедиться в этом, вернемся к функции \(g(x)=|x−2|/(x−2)\), представленной в начале раздела (см. рисунок (b)). Поскольку мы выбираем значения x, близкие к 2, \(g(x)\) не приближается к одному значению, поэтому предела при приближении x к 2 не существует, то есть \(\displaystyle \lim_{x \to 2 }g(x)\) ДНУ. Однако само по себе это утверждение не дает нам полной картины поведения функции вблизи значения x 2. Для более точного описания введем понятие 9+}g(x)=1.\]
Теперь мы можем дать неформальное определение односторонних пределов.
Определение: односторонние пределы
Мы определяем два типа односторонних пределов.
Предел слева:
Пусть \(f(x)\) — функция, определенная при всех значениях в открытом интервале вида \(z\), и пусть \(L\) — вещественная количество. Если значения функции \(f(x)\) приближаются к действительному числу \(L\), как значения \(x\) (где \(x