Предел функции тригонометрической: Как решать пределы с тригонометрическими функциями, примеры

Примеры решения пределов тригонометрических функций с ответами

Простое объяснение принципов решения пределов тригонометрических функций и 10 наглядных примеров. В каждом примере поэтапный ход решения и ответ.

Алгоритм решения пределов тригонометрических функций

Теорема

Для тригонометрических функций существует много разных пределов, но как правило, все они вычисляются, опираясь на первый замечательный предел и его следствия.

Первый замечательный предел выглядит следующим образом:

   

Следствия первого замечательного предела

Главным следствием первого замечательного предела считают:

   

Также следствиями являются:

   

   

   

Нужна помощь в написании работы?

Мы — биржа профессиональных авторов (преподавателей и доцентов вузов). Наша система гарантирует сдачу работы к сроку без плагиата. Правки вносим бесплатно.

Заказать работу

Примеры решения пределов тригонометрических функций

Пример 1

Задание

Найти предел функции:

   

Решение

Заменим значение х на число, к которому стремится функция:

   

Так как мы пришли на неопределённость вида 0/0, преобразуем синус так, чтобы он стал вида первого замечательного предела:

   

Мы знаем, что первый замечательный предел равен единице, следовательно

   

Таким образом найдём предел функции:

   

Пример 2

Задание

Найти предел функции:

   

Решение

При замене х на число, к которому он стремится, снова получаем неопределённость

   

Данную задачу можно решить, применив правило Лопиталя.

Найдём производные числителя и знаменателя функции и решим задачу:

   

Пример 3

Задание

Найти предел функции:

   

Решение

При подстановке нуля получим неопределённость типа 0/0:

   

Воспользуемся свойством

   

Преобразуем функцию и упростим её:

   

Вынесем константу ½ за лимит и, пользуюсь свойством первого замечательного предела, найдём передел данной функции:

   

Пример 4

Задание

Найти предел функции:

   

Решение

Если заменить x на число, придём к неопределённости 0/0:

   

Для решения данного примера применим правило Лопиталя и заменим х на число в производных:

   

Пример 5

Задание

Вычислить предел функции:

   

Решение

Для решения данного примера воспользуемся свойством разности косинусов:

   

и получим

   

Вынесем минус за лимит, дабы не потерять и продолжим решение. Для решения задачи приведём функцию к виду первого замечательного предела. Для этого нужно разделить дробь на множители и добавить в знаменатель коэффициент, равный коэффициенту в числителе. А потом упростим выражение:

   

Снова вынесем константы за лимит и получим вид первого замечательного предела, с помощью которого приходим к искомому решению:

   

Пример 6

Задание

Вычислить предел функции:

   

Решение

При подстановке х снова получаем неопределённость

   

Значит будем искать передел путём приведения к виду первого замечательного предела.

Представим тангенс в виде частного синуса х и косинуса х

   

Приведём к общему знаменателю и разделим выражение на множители следующим образом:

   

Мы видим первый замечательный предел, а значит, можем упростить до:

   

Далее снова приведём числитель к общему знаменателю:

   

Вновь разделим на множители и подставим значение х во второй косинус:

   

Таким образом нам остаётся разобраться с первым числителем. Поменяем местами 1 и косинус и вынесем минус за лимит.

Далее воспользуемся формулой понижения степени и найдём решение:

   

Пример 7

Задание

Вычислить предел функции:

   

Решение

При простом вычислении получаем неопределённость

   

Следовательно, будем вычислять предел, опираясь на правило первого замечательного предела. Приведём тангенс к виду частного синуса и косинуса:

   

Разделим пример на множители.

Приведём синусы к виду первого замечательного предела и получим ответ:

   

Пример 8

Задание

Найти предел функции:

   

Решение

При подставлении числа на место х приходим к неопределённости типа 0/0:

   

Преобразуем tg, приведем выражение к общему знаменателю cos x, вынесем общий множитель – sin x за скобку:

   

   

Используя следствие из первого замечательного предела, преобразим выражение и избавимся от тангенса.

Затем вновь приведем функцию к следствию первого замечательного предела и найдем ответ:

   

   

Пример 9

Задание

Найти предел функции:

   

Решение

При подстановке числа видим неопределённость.

   

Следовательно, искать предел будем, опираясь на правило первого замечательного предела. Для этого заменим переменную, которая будет стремиться к нулю:

   

   

Подставим в функцию:

   

Опираясь на свойства тригонометрии, заменим тангенс.

   

Зная, что предел косинуса нуля = 1, преобразуем пример и приведём к виду первого замечательного предела.

Найдём ответ.

   

Пример 10

Задание

Вычислить предел функции:

   

Решение

Здесь так же получим неопределённость:

   

Значит, введём новую переменную t:

   

   

   

Подставим получившиеся значения в пример и найдём предел:

   

Средняя оценка 2.

5 / 5. Количество оценок: 6

Поставьте вашу оценку

Сожалеем, что вы поставили низкую оценку!

Позвольте нам стать лучше!

Расскажите, как нам стать лучше?

29876

Закажите помощь с работой

Не отобразилась форма расчета стоимости? Переходи по ссылке

Не отобразилась форма расчета стоимости? Переходи по ссылке

Полезно

Непосредственное вычисление пределов, таблица пределов функций

Определение непрерывности функции  в точке  и передела функции на бесконечности  и на использовании свойств предела непрерывной функции способствует непосредственному вычислению пределов.

Определение 1

Значение предела в точке непрерывности определено значением функции в этой точке.

При опоре на свойства основные элементарные функции имеют предел в любой точке из области определения, вычисляется как значение соответствующей функции в этих точках.

Пример 1

Произвести вычисление предела функции limx→5arctg35·x

Решение

Функция арктангенса отличается непрерывностью на всей своей области определения.

Отсюда получим, что в точке x0=5 функция является непрерывной. Из определения имеем, что для нахождения предела является значением этой же функции. Тогда необходимо произвести подстановку. Получим, что

limx→5arctg35·x=arctg35·5=arctg3=π3

Ответ: π3.

Для вычисления односторонних пределов необходимо использовать значения точек границ предела. У акрксинуса и акрккосинуса  имеются такие значения x0=-1 или x0=1.

При x→+∞ или x→-∞ вычисляются пределы функции, заданные на бесконечностях.

Для упрощения выражений применяют свойства пределов:

Определение 2

1. limx→x0(k·f(x))=k·limx→x0f(x), k является коэффициентом.
2. limx→x0(f(x)·g(x))=limx→x0f(x)·limx→x0g(x), применяемое при получении неопределенности предела.
3. limx→x0(f(g(x)))=flimx→x0gx,используемое для непрерывных функций, где знак функции и предельного перехода можно менять местами.

Для того, чтобы научиться вычислять переделы, необходимо знать и разбираться в основных элементарных функциях. Ниже приведена таблица, в которой имеются переделы этих функций с приведенными разъяснениями и подробным решением. Для вычисления необходимо основываться на определении предела функции в точке и на бесконечности.

Таблица пределов функции

Для упрощения  и решения пределов используется данная таблица основных пределов.

Функция корень n-ой степени y=xn, где n=2, 4, 6 … limx→∞xn=+∞n=+∞ Для любых x0 из опрелеления  limx→x0xn=x0n	Функция корень n-ой степени y=xn, где n=3, 5, 7 …  limx→∞xn=+∞n=+∞limx→∞xn=-∞n=-∞ limx→x0xn=x0n
Степенная функция y=xa , a>0 Для любого положительного числа a limx→∞xa=+∞a=+∞ Если a=2, 4, 6 …, то limx→∞xa=-∞a=+∞ Если a=1, 3, 5, …, то limx→∞xa=-∞a=-∞ Для любых x0, из области определния limx→x0xa=(x0)a	Степенная функция y=xa, a<0 Для любого отрицательного числа a limx→∞xa=(+∞)a=+0limx→0+0=(0+0)a=+∞ Если a=-2, -4, -4, . .., то limx→∞xa=-∞a=+0limx→0-0xa=(0-0)a=+∞ Если a=-1, -3, -5, …, то limx→∞xa=-∞a=-0limx→0-0xa=(0-0)a=-∞ Для любых x0 из области определения limx→x0xa=(x0)a
Показательная функия y=ax, 0<a<1 limx→∞ax=a-∞=+∞limx→∞ax=a+∞=+0 Для любых x0 из области опреления limx→x0ax=ax0	Показательная функия y=ax, a>1limx→∞ax=a-∞=+0limx→x0ax=a+∞=+∞ Для любых знвчений x0 из област опредения limx→x0ax=ax0
Логарифмическая функция y=loga(x), 0<a<1 limx→0+0logax=loga(0+0)=+∞limx→∞logax=loga(+∞)=-∞ Для любых x0 из области опрелеленияlimx→x0logax=logax0	Логарифмическая функция y=loga(x), a>1 limx→0+0logax=loga(0+0)=-∞limx→∞logax=loga(+∞)=+∞ Для любых x0 из области опрелеления limx→x0logax=logax0
Тригонометрические функции Синус limx→∞ sin x не существует Для любых x0 из области опрелеления limx→x0sin x=sin x0 Тангненсlimx→π2-0+π·ktg x=tgπ2-0+π·k=+∞limx→π2+0+π·ktg x=tgπ2+0+π·k=-∞ limx→∞tg x не существует Для любых x0 из области опрелеления limx→x0tg x=tg x0	Тригонометрические функции Косинус limx→∞cos x не существует  Для любых x0 из области опрелеления limx→x0cos x=cos x0 Котангенсlimx→-0+π·kctg x=ctg(-0+π·k)=-∞limx→+0+π·kctg x=ctg(+0+π·k)=+∞ limx→∞ctg x не существует Для любых x0 из области опрелеления limx→x0сtg x=сtg x0
Обратные тригонометрические функции Арксинус limx→-1+0arcsin x=-π2limx→1-0arcsin x=π2 Для любых x0 из области опрелеления limx→x0arcsin x=arcsin x0 Арккосинус limx→-1+0arccos (x)=πlimx→1-0arccos (x)=0 Для любых x0 из области опрелеления limx→x0arccis x=arccos x0	Обратные тригонометрические функции Арктангес limx→-∞ arctg (x)=-π2limx→+∞ arctg (x)=π2 Для любых x0 из области опрелеления limx→x0arctg x=arctg x0 Арккотангенс limx→-∞arcctg (x)=πlimx→+∞arcctg (x)=0 Для любых x0 из области опрелеления limx→x0arcctg x=arcctg x0

Пример 2

Произвести вычисление предела limx→1×3+3x-1×5+3.

Решение

Для решения необходимо подставить значение х=1. Получаем, что

limx→1×3+3x-1×5+3=13+3·1-115+3=34=32

Ответ: limx→1×3+3x-1×5+3=32

Пример 3

Произвести вычисление предела функции limx→0(x2+2,5)1×2

Решение

Для того, чтобы раскрыть предел, необходимо подставить значение х, к которому стремится предел функции. В данном случае нужно произвести подстановку х=0. Подставляем числовое значение и получаем:

x2+2.5x=0=02+2.5=2.5

Предел записывается в виде limx→0(x2+2.5)1×2=limx→02.51×2. Далее необходимо заняться значением показателя. Он является степенной функцией 1×2=x-2. В таблице пределов, предоставленной выше, имеем, что limx→0+01×2=limx→0+0x-2=+∞ и limx→0+01×2=limx→0+0x-2=+∞, значит, имеем право записать как limx→01×2=limx→0x-2=+∞

Теперь вычислим предел. Получит вид limx→0(x2+2.5)1×2=limx→02.51×2=2.5+∞

По таблице пределов с показательными функциями, имеющими основание больше 1 получаем, что

limx→0(x2+2. 5)1×2=limx→02.51×22.5+∞=+∞

Ответ: limx→0(x2+2.5)1×2=+∞

Когда задан более сложный предел, то при помощи таблицы не всегда получится получать целое или конкретное значение. Чаще получаются разные виды неопределенностей, для разрешения которых необходимо применять правила.

Рассмотрим графическое разъяснение приведенной выше таблицы пределов основных элементарных функций.

Предел константы

 

Из рисунка видно, что функция у=С имеет предел на бесконечности. Такой же предел при аргументе, который стремится к х0. Он равняется числу C.

Предел функции корень n-ой степени

Четные показатели корня применимы для limx→+∞xn=+∞n=+∞, а нечетные, равные больше, чем значение 1, – для limx→+∞xn=+∞n=+∞, limx→-∞xn=-∞n=-∞.  Область определения может принимать абсолютно любое значение х предела заданной функции корня n-ой степени, равного значению функции  в заданной точке.

Предел степенной функции

Необходимо разделить все степенные функции по группам, где имеются одинаковые значения пределов, исходя из показателя степени.

1. Когда a является положительным числом, тогда limx→+∞xa=+∞a=+∞ и limx→-∞xa=-∞a=-∞. Когда x принимает любое значение, тогда предел степенной функции равняется значению функции в точке. Иначе это записывается как limx→∞xa=(∞)a=∞.

2. Когда a является положительным четным числом, тогда получаем limx→+∞xa=(+∞)a=+∞ и limx→-∞xa=(-∞)a=+∞, причем x из данной области определения  является пределом степенной функции и равняется значением функции в этой точке. Предел имеет вид limx→∞xa=∞a=+∞.

3. Когда a имеет другие значения, тогда limx→+∞xa=(+∞)a=+∞, а область определения x способствует определению предела функции в заданной точке.

4. Когда a имеет значение отрицательных чисел, тогда получаем limx→+∞xa=+∞a=+0, limx→-∞xa=(-∞)a=-0, limx→0-0xa=(0-0)a=-∞,limx→0+0xa=0+0a=+∞, а значения x может быть любым из заданной области определения и равняется функции в заданной точке. Получаем, что limx→∞xa=∞a=0 иlimx→0xa=0a=∞.

5. Когда a является отрицательным четным числом, тогда получаем limx→+∞xa=(+∞)a=+0, limx→-∞xa=-∞a=+0, limx→0-0(0-0)a=+∞, limx→0+0xa=(0+0)a=+∞, а любое значение x на области определения дает результат предела степенной функции равным значению функции в точке. Запишем как limx→∞xa=(∞)a=+0 и limx→0xa=(0)a=+∞.

6. Когда значение a имеет другие действительные отрицательные числа, тогда получим limx→+∞xa=+∞a=+0 и limx→0+0xa=0+0a=+∞, когда x принимает любое значение из своей области определения, тогда предел степенной функции равняется значению функции в этой точке.

Предел показательной функции

Когда 0<a<1, имеем, что limx→-∞ax=a-∞=+∞, limx→+∞ax=(a)+∞=+∞, любое значение x из области определения дает пределу показательной функции значению функции в точке.

Когда a>1, тогда limx→-∞ax=(a)-∞=+0, limx→+∞ax=(a)+∞=+∞, а любое значение x из области определения дает предел функции равный значению этой функции в точке.

Предел логарифмической функции

Когда имеем 0<a<1, тогда limx→0+0logax=loga(0+0)=+∞, limx→+∞logax=loga(+∞)=-∞ ,  для всех остальных значений x из заданной области определения предел показательной функции равняется значению заданной функции в точках.

Когда a>1, получаем limx→0+0logax=loga(0+0)=-∞, limx→+∞logax=loga(+∞)=+∞,остальные значения x в заданной области определения дают решение предела показательной функции равному ее значению в точках.

Предел тригонометрических функций

Предел бесконечности не существует для таких функций как y=sin x, y=cos x. Любое значение x, входящее в область определения, равняется значению функции в точке.

 

Функция тангенса имеет предел вида limx→π2-0+π·ktg(x)=+∞, limx→π2+π·ktg(x)=∞ или limx→π2+π·ktg(x)=∞, тогда остальные значения x, принадлежащие области определения тангенса, равняется значению функции в этих точках.

Для функции y=ctg x получаем limx→-0+π·kctg(x)=-∞, limx→+0+π·kctg(x)=+∞ или limx→π·kctg (x)=∞, тогда остальные значения x, принадлежащие области определения, дают предел котангенса, равный значению функции в этих точках.

Предел обратных тригонометрических функций

Функция арксинус имеет предел вида limx→-1+0arcsin(x)=-π2 и limx→1-0arcsin (x)=π2, остальные значения x из области определения равняются значению функции в заданной точке.

 

Функция арккосинус имеет предел вида limx→-1+0arccos(x)=π и limx→1-0arccos(x)=0, когда остальные значения x, принадлежащие области определения, имеют предел арккосинуса, равного значению функции в этой точке.

Функция арктангенс имеет предел вида limx→-∞arctg(x)=-π2 и limx→+∞arctg(x)=π2, причем другие значения x, входящие в область определения, равняется значению функции  в имеющихся точках.

 

Функция котангенса имеет предел вида limx→-∞arcctg(x)=π и limx→+∞arctg(x)=0, где x принимает любое значение из своей заданной области определения, где получаем предел арккотангенса, равного значению функции в имеющихся точках.

Все имеющееся значения пределов применяются в решении для нахождения предела любой из элементарных функций.

Объяснение урока: Пределы тригонометрических функций

В этом объяснителе мы узнаем, как вычислять пределы тригонометрических функций.

Пределы — полезный инструмент, помогающий нам понять форму функции вокруг значения; это один из фундаментальных строительных блоков исчисления. Мы можем найти предел любой тригонометрической функции, используя прямую замену.

Определение: оценка предела тригонометрических функций

Если 𝑎 находится в области определения тригонометрической функции, то мы можем вычислить ее предел в 𝑎 прямой подстановкой. В частности, для любого 𝑎∈ℝ

• limsinsin→𝑥=𝑎,
• limcoscos→𝑥=𝑎.

Для любого 𝑎 в области tan𝑥,

• limtantan→𝑥=𝑎.

Эти результаты позволяют оценить предел многих тригонометрических выражений. Однако есть примеры, которые мы не можем оценить. Например, рассмотрим limsin→𝑥𝑥, где 𝑥 измеряется в радианах. Если мы попытаемся вычислить этот предел с помощью прямой подстановки, sin00=00, мы обнаружим неопределенную форму, а это означает, что нам нужно вычислить этот предел другим способом. Один из способов сделать это — нарисовать график 𝑦=𝑥𝑥sin.

На схеме видно, что по мере того, как значения 𝑥 приближаются к 0 с любой стороны, выходы функции приближаются к 1. Следовательно, схема показывает, что limsin→𝑥𝑥=1. Мы также можем увидеть это, построив таблицу.

𝑥	−0,1	−0,01	−0,001	→	0	9 0031	0,001	0,01	0,1
sin𝑥𝑥	0,99833	0,99998	0,99999	→		←	0,99999	0,99998	0,99833

Один раз опять же, таблица предполагает, что по мере того, как значения 𝑥 приближаются к 0 с любой стороны, выходы функции приближаются к 1. Стоит отметив, что мы можем показать аналогичный результат, когда 𝑥 измеряется в градусах; однако при определении пределов мы почти всегда используем радианы. Итак, если не оговорено иное, будем считать, что предел любой тригонометрической функции включает в себя углы, измеряемые в радианах. Это дает нам следующий результат.

Теорема: предел тригонометрического выражения

Если 𝑥 измеряется в радианах, то limsin→𝑥𝑥=1.

Мы можем использовать этот результат, чтобы показать еще более общий результат. Пусть 𝑎∈ℝ−{0}. Подставляем 𝜃=𝑎𝑥 в предельный результат limsin→𝜃𝜃=1. Обратите внимание, что при 𝜃→0 и 𝑎𝑥→0, и 𝑥→0. Это дает нам 1 = 𝜃𝜃 = 𝑎𝑥𝑎𝑥.limsinlimsin→→

. Вынесение множителя 1𝑎 за пределы этого предела и перестановка дает нам limsin→𝑎𝑥𝑥=𝑎.

Стоит отметить, что этот результат справедлив и при 𝑎=0. Мы можем резюмировать это следующим образом.

Теорема: предел тригонометрического выражения

Если 𝑥 измеряется в радианах и 𝑎∈ℝ, то limsin→𝑎𝑥𝑥=𝑎.

Давайте рассмотрим пример использования этого результата для вычисления предела тригонометрического выражения.

Пример 1. Нахождение пределов с использованием тригонометрических функций

Оценить лимсинсин→𝑥.

Ответ

Поскольку этот предел включает частное тригонометрических функций, мы можем попытаться вычислить этот предел прямой подстановкой sin0=00. 

Это дает нам неопределенную форму, что означает, что мы не можем оценить этот предел прямой подстановкой. Вместо этого мы будем использовать тот факт, что если 𝑥 измеряется в радианах, а 𝑎 является вещественной константой, то limsin→𝑎𝑥𝑥=𝑎. Хотя в вопросе не говорится, что 𝑥 измеряется в радианах, при определении пределов мы почти всегда работаем в радианах, поэтому мы будем исходить из этого для вопроса. Мы можем переписать предел следующим образом:

Предполагая, что оба предела существуют, мы можем записать это как произведение двух пределов:  .

Возьмем обратное значение второго предела, используя правило степени для пределов, чтобы получить 𝑥𝑥 ×𝑥, если предел существует и не равен нулю. Затем мы можем оценить оба этих предела, используя наш предельный результат, limsin→𝑎𝑥𝑥=𝑎.

В первом пределе 𝑎=1, а во втором 𝑎=12. Следовательно, limsinlimsin→→𝑥𝑥×𝑥=1×12=2.

Есть еще два полезных предельных результата, связанных с тригонометрическими функциями, которые мы можем найти, исследуя их график или используя таблицу. Рассмотрим следующие наброски tan𝑥𝑥 и 1−𝑥𝑥cos, где 𝑥 измеряется в радианах.

На первой диаграмме мы видим, что по мере того, как значения 𝑥 приближаются к 0, выходы приближаются к 1. Итак, набросок предполагает limtan→𝑥𝑥=1. Точно так же на второй диаграмме, когда значения 𝑥 приближаются к 0, мы видим, что выходы приближаются к 0. Таким образом, набросок предполагает, что limcos→1−𝑥𝑥=0. Это дает нам следующие результаты.

Теорема: предел тригонометрического выражения

Если 𝑥 измеряется в радианах, тогда .

Как и в случае с предельным результатом, включающим синус, мы можем использовать подстановку, чтобы найти предельный результат, где аргумент является постоянным кратным. Если 𝑎∈ℝ, используя 𝜃=𝑎𝑥, мы имеем 1=𝜃𝜃=𝑎𝑥𝑎𝑥.limtanlimtan→→

Удаление постоянного множителя 1𝑎 и перестановка дает limtan→𝑎𝑥 𝑥=𝑎.

Аналогично, если 𝑎∈ℝ, используя 𝜃=𝑎𝑥, мы имеем 0=1−𝜃𝜃=1−𝑎𝑥𝑎𝑥.limcoslimcos→→

Убираем постоянный множитель 1𝑎 и переставляем ing дает limcos→1− 𝑎𝑥𝑥=0.

Мы можем подытожить это следующим образом.

Теорема: предел тригонометрического выражения. →1−𝑎𝑥𝑥=0.

Давайте рассмотрим пример того, как мы можем применить эти предельные результаты для вычисления предела тригонометрического выражения.

Пример 2. Нахождение пределов с использованием тригонометрических функций

Определить limcos→9−97𝑥3𝑥.

Ответ

Поскольку этот предел включает тригонометрическую функцию, мы можем попытаться вычислить этот предел путем прямой подстановки: 9−9(7×0)3(0)=00.cos

Это дает нам неопределенную форму, что означает, что мы не можем вычислить этот предел прямой подстановкой. Вместо этого мы будем использовать тот факт, что если 𝑥 измеряется в радианах и 𝑎∈ℝ, то limcos→1−𝑎𝑥𝑥=0.

Чтобы применить этот результат, мы упростим наш предел следующим образом: 1−7𝑥)𝑥=3×0=0.

Следовательно, limcos→9−97𝑥3𝑥=0.

В нашем следующем примере мы будем использовать предельный результат, включающий функции тангенса и синуса, для вычисления предела тригонометрической функции.

Пример 3. Нахождение пределов с использованием тригонометрических функций

Найти лимсинтан→7𝑥+33𝑥8𝑥.

Ответ

Поскольку это предел тригонометрического и алгебраического выражения, мы можем попытаться вычислить этот предел прямой подстановкой: sintan(7(0))+3(3(0))8(0) =00.

Поскольку это неопределенная форма, мы не можем определить значение этого предела из прямой подстановки. Вместо этого мы перепишем этот предел в терминах пределов, которые мы можем оценить. А именно, для любой реальной постоянной 𝑎 и 𝑥, измеряемой в радианах, limtanandlimsin→→𝑎𝑥𝑥=𝑎𝑎𝑥𝑥=𝑎.

Мы можем переписать предел в вопросе следующим образом: →→ →7𝑥+33𝑥8𝑥=7𝑥8𝑥+33𝑥8𝑥=7𝑥8𝑥+33𝑥8𝑥=187𝑥𝑥+383 𝑥𝑥=187𝑥𝑥+383𝑥𝑥.

Мы можем оценить каждый из этих пределов отдельно. Во-первых, напомним, что если 𝑥 измеряется в радианах и константа 𝑎∈ℝ, то limsin→𝑎𝑥𝑥=𝑎. Используя этот результат, мы имеем limsin→7𝑥𝑥=7.

Далее напомним, что если 𝑥 измеряется в радианах и 𝑎∈ℝ, то limtan→𝑎𝑥𝑥=𝑎.

Следовательно, лимтан→3𝑥𝑥=3.

Подстановка значений этих пределов в уравнение дает нам 3𝑥𝑥=18( 7)+38(3)=498+278=768=192.

Следовательно, лимсинтан→7𝑥+33𝑥8𝑥=192.

В нашем следующем примере мы объединим тригонометрическое тождество с предельными результатами тригонометрических функций для вычисления предела.

Пример 4. Нахождение пределов с использованием тригонометрических функций

Найти limsin→2−2𝑥4𝑥−2𝜋.

Ответ

Так как это предел тригонометрического и алгебраического выражения, мы можем попытаться вычислить этот предел прямой подстановкой: 2−24−2𝜋=00.sin является неопределенной формой, мы не можем определить значение этого предела из прямой подстановки. Вместо этого мы перепишем этот предел в терминах пределов, которые мы можем оценить. Перепишем предел следующим образом: 2 𝑥−.

Чтобы оценить этот предел, мы будем использовать замену 𝜃=𝑥−𝜋2. Когда 𝑥 приближается к 𝜋2, 𝜃 приближается к 0.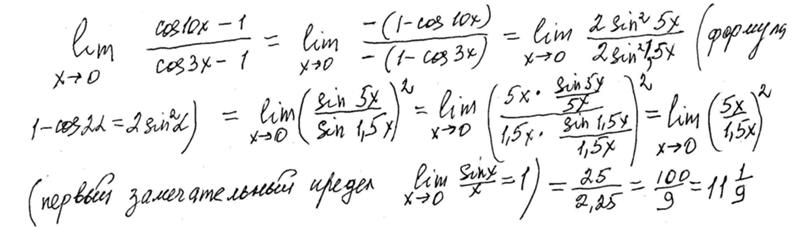 Это дает нам limsinlimsin→→1−𝑥2𝑥−=1−𝜃+2𝜃.

Напомним, что sincos𝜃+𝜋2≡𝜃. Мы можем использовать это, чтобы переписать предел следующим образом:

Наконец, напомним, что limcos→1−𝑎𝑥𝑥=0.

Следовательно, 121−𝜃𝜃=12×0=0.limcos→

Следовательно, limsin→2−2𝑥4𝑥−2𝜋=0.

В нашем последнем примере мы будем использовать эти предельные результаты для оценки предела обратного тригонометрического выражения.

Пример 5. Нахождение пределов с использованием тригонометрических функций

Найти limcotcsc→6𝑥4𝑥8𝑥.

Ответ

Поскольку это предел тригонометрического и алгебраического выражения, мы можем попытаться вычислить этот предел прямой подстановкой. Однако 0 не находится в области определения этой функции. Вместо этого мы перепишем предел, сначала используя взаимные тригонометрические тождества: 𝑥8𝑥4𝑥.tansin

Затем мы можем переписать это с точки зрения предельных результатов. Если 𝑥 измеряется в радианах и 𝑎∈ℝ, limsinlimtan→→𝑎𝑥𝑥=𝑎,𝑎𝑥𝑥=𝑎.

Таким образом, у нас есть →→6𝑥8𝑥4𝑥 =6𝑥8𝑥𝑥4𝑥=6𝑥4𝑥8𝑥𝑥=6𝑥4𝑥8𝑥𝑥=6𝑥4𝑥8𝑥 𝑥=64𝑥𝑥8𝑥𝑥.

Применяя предельные результаты, заключаем, что → 6𝑥4𝑥8𝑥=3.

Давайте закончим повторением некоторых важных моментов из этого объяснения.

Ключевые моменты

• Мы можем вычислить предел любой тригонометрической функции в точке 𝑥=𝑎 прямой подстановкой, если a находится в ее области определения.
• Если 𝑥 измеряется в радианах, мы имеем следующие тригонометрические предельные результаты: 1−𝑥𝑥=0.

Если 𝑥 измеряется в радианах и 𝑎∈ℝ, мы имеем следующие результаты тригонометрического предела: 𝑎𝑥𝑥=𝑎,

лимузин→1 −𝑎𝑥𝑥=0.

Мы можем использовать эти результаты для оценки предела тригонометрических функций.

Тригонометрические пределы Проблемы и решения

• Математические сомнения
• Проблемы
• Ограничения

Проблемы пределов, связанные с тригонометрическими функциями, появляются в исчислении.