404 — Страница не найдена
|
||||||||||||||||||||||||||||||||||||||||||||||||||
|
||||||||||||||||||||||||||||||||||||||||||||||||||
Квадратичная функция График квадратичного уравнения рабочего листа функции, формула функции, угол, текст, треугольник png
Квадратичная функция График квадратичного уравнения рабочего листа функции, формула функции, угол, текст, треугольник pngтеги
- угол,
- текст,
- треугольник,
- другие,
- график функции,
- учитель,
- параллель,
- парабола,
- квадратное уравнение,
- квадратичная функция,
- лист,
- алгебра,
- линия,
- диаграмма,
- уравнение,
- fx,
- f X 0,
- функция,
- формула функции,
- график,
- х 0,
- png,
- прозрачный,
- бесплатная загрузка
Об этом PNG
- Размер изображения
- 1700x689px
- Размер файла
- 43.
 6KB
6KB - MIME тип
- Image/png
изменить размер PNG
ширина(px) высота(px)Лицензия
Некоммерческое использование, DMCA Contact Us
- Квадратичное уравнение Квадратичная формула Квадратичная функция Математика, формула, угол, текст, прямоугольник png 1500x673px 7.22KB
- Квадратичное уравнение Квадратичная формула Алгебра Квадратичная функция, формула функции, угол, текст, прямоугольник png 1280x395px 13.9KB org/ImageObject»> Квадратичное уравнение Квадратичная функция График функции Ноль функции, OneNote, синий, угол, текст png 2000x1714px 101.53KB
- График функции Родительская функция Квадратичная функция Экспоненциальная функция, Математика, угол, текст, прямоугольник png 2000x2000px 75.49KB
- Квадратичное уравнение Квадратичная функция Квадратичная формула Завершая квадрат, формула, угол, текст, прямоугольник png 2000x617px 30.38KB
- Квадратичная функция Квадратичное уравнение Парабола Алгебра, Математика, угол, текст, симметрия png 700x750px 58.63KB
- Математика геометрия формула евклидово уравнение, математические заметки, угол, текст, треугольник png
6354x6354px
911.
 07KB
07KB - Квадратичная функциональная линия, Квадратичное уравнение, Степень, Полиномиальная функция, График функции, График, Парабола, Коэффициент, угол, площадь, круг png 1630x1553px 75.08KB
- Квадратичное уравнение Квадратичная формула Квадратичная функция Ноль функции, Математика, угол, белый, текст png 1705x586px 10.08KB
- математические уравнения, математические формулы, математические обозначения, cdr, угол, текст png 1080x763px 356.8KB
- Формула Математика Евклидова, математическая формула, угол, текст, монохромный png 3500x3313px 875.77KB
- Математика Геометрия Формула Тригонометрия Куб, Математика, угол, треугольник, монохромный png
1920x1308px
921.
 05KB
05KB - математические уравнения, математическое уравнение евклидовой формулы, математический набросок материала, угол, текст, цифровой png 918x670px 147.15KB
- Абсолютное значение Квадратичная функция Максимумы и минимумы Экспоненциальная функция, Математика, угол, текст, треугольник png 1200x1326px 37.18KB
- Математические уравнения, Формула Математика Функция Евклида, Оси математических функций, синий, угол, текст png 800x800px 366.32KB
- Система уравнений Математика Квадратичное уравнение Решение уравнений, рукописная математическая формула, угол, текст, число png 1920x2010px 152.49KB
- Квадрантная декартова система координат График функции Квадратичная функция Математика, 12 бис, угол, текст, прямоугольник png 907x907px 30.58KB
- Квадратичная функция Формула квадратичного уравнения Parabola, Mc logo, оранжевый, другие, число png 1412x1071px 332.1KB
- Декартова система координат График функции Диаграмма бумаги Плоскость, др., угол, прямоугольник, треугольник png 800x800px 30.81KB
- Математика евклидова геометрия формула, математика, угол, текст, треугольник png
4050x4050px
420.
 75KB
75KB - иллюстрация в черно-серой рамке, Диаграммная бумага, текстура, угол, белый png 1501x1501px 14.69KB
- График функции Экспоненциальная функция Обратная функция Экспоненциальный рост, Математика, угол, текст, треугольник png 617x617px 9.15KB
- Система линейных уравнений Математика, Математика, синий, угол, текст png 597x599px 16.58KB
- Математика, математика, евклидова формула Компьютерный файл, рукописная математическая формула, угол, текст, класс png
4520x3161px
338.
 87KB
87KB - Алгебра Математика Решение уравнений с переменными, угол, текст, логотип png 1050x1024px 68.67KB
- Квадратичное уравнение Квадратичная функция Математика Квадратичная формула, Математика, синий, угол, текст png 1500x1125px 39.77KB
- Квадратичное уравнение Квадратичная функция Квадратичная формула, формула, угол, текст, логотип png 2211x557px 27.73KB
- График функции Линия Парабола Вершина, линия, угол, текст, треугольник png 1024x1024px 37.52KB
- Линейная функция График функции Линейное уравнение, линейный график, угол, текст, треугольник png
700x446px
18.
 01KB
01KB - График функции Математическое производное уравнение, математическое уравнение, угол, белый, текст png 1600x625px 8.41KB
- Математическая формула Алгебра Евклидова, Математическая формула, угол, текст, монохромный png 2244x2244px 134.04KB
- Математика евклидова формула бумаги, математические различные формулы, угол, текст, монохромный png 4050x4050px 627.53KB
- Решение уравнений Математика Математическая запись Формула, администратор, текст, число, математик png 792x658px 240.21KB
- Сюжет Квадратичная функция Квадратичное уравнение параболы, круг, угол, текст, треугольник png
2000x1211px
57.
 78KB
78KB - красный х иллюстрация, красный х письмо компьютерные иконки, красный х, разное, угол, текст png 512x512px 10.3KB
- Квадратичная функция Квадратичное уравнение Квадратичная формула, Математика, угол, белый, текст png 1512x661px 8.6KB
- Теорема Пифагора Угол Числовая линия, Угол, угол, текст, прямоугольник png 2400x2384px 40.82KB
- гистограмма, гистограмма, график функции, шаблон альбома роста, разное, угол, текст png 1436x1111px 458.07KB
- Круг Коническое сечение Гипербола График функции Эллипс, круг, угол, текст, треугольник png
1572x1551px
140.
 41KB
41KB - Точка симметрии уравнения гиперболической функции, Математика, угол, текст, треугольник png 1333x1014px 18.66KB
- Parabola Normalparabel Математика Коническое сечение Функция, Математика, угол, текст, треугольник png 668x732px 21.69KB
- Квадратичное уравнение Квадратичная функция Квадратичная формула Ноль функции, топор, угол, белый, текст png 1600x565px 24.22KB
- Математика Число Точка Уравнение Геометрия, математическая формула, угол, текст, прямоугольник png 1546x646px 8.84KB
- Формула Математика Алгебраическое уравнение Число, управляющий, угол, текст, параллель png
1427x1096px
64.
 32KB
32KB - Квадратный корень n-й корень математика квадратное число ноль функции, математика, угол, текст, прямоугольник png 500x549px 9.46KB
- Гистограмма Компьютерные иконки График функции, другие, разное, угол, текст png 980x736px 14.39KB
- Квадратичная функция Математика Элемент финитарного отношения, Математика, угол, белый, текст png 1019x854px 74.57KB
Квадратичная функция
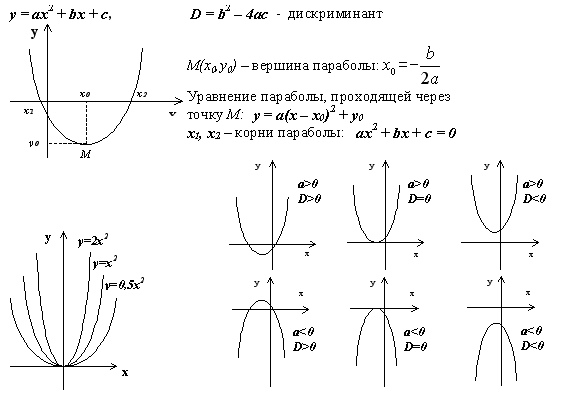
Общая форма квадратичной функции: ф ( Икс ) «=» а Икс 2 + б Икс + с . График квадратичной функции представляет собой парабола , тип 2 -мерная кривая.
«Основная» парабола, у «=» Икс 2 , выглядит так:
Функция коэффициента а в общем уравнении состоит в том, чтобы сделать параболу «шире» или «тоньше» или перевернуть ее вверх дном (если отрицательно):
Если коэффициент
Икс
2
положителен, парабола раскрывается; в противном случае он открывается вниз.
Вершина
вершина параболы – это точка в нижней части « U » форма (или вершина, если парабола направлена вниз).
Уравнение параболы также можно записать в «вершинной форме»:
у «=» а ( Икс − час ) 2 + к
В этом уравнении вершиной параболы является точка ( час , к ) .
Вы можете увидеть, как это соотносится со стандартным уравнением, перемножив его:
у «=» а ( Икс − час ) ( Икс − час ) + к
у «=» а Икс 2 − 2 а час Икс + а час 2 + к
Коэффициент
Икс
вот
−
2
а
час
.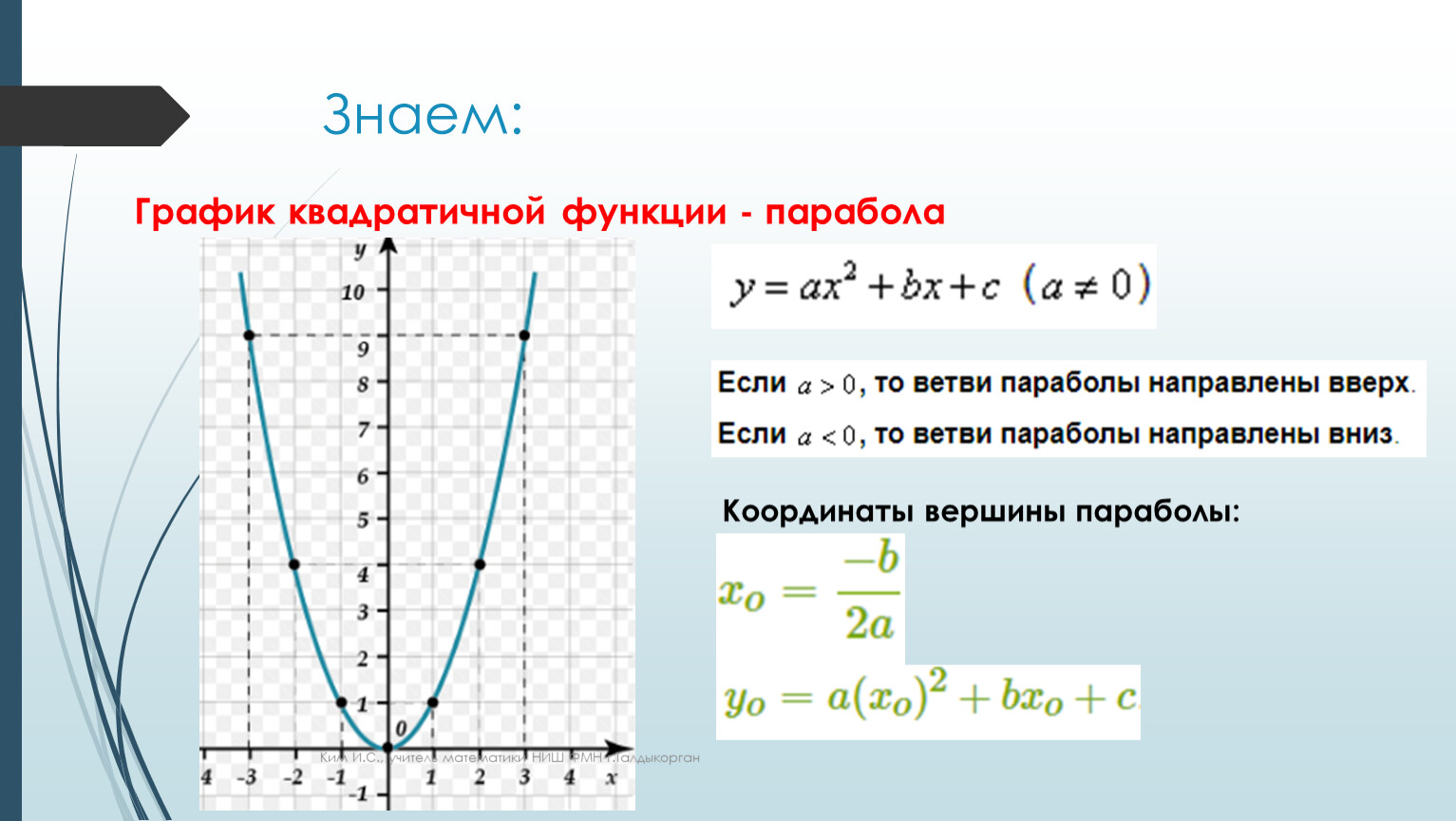 Это означает, что в стандартной форме
у
«=»
а
Икс
2
+
б
Икс
+
с
, выражение
Это означает, что в стандартной форме
у
«=»
а
Икс
2
+
б
Икс
+
с
, выражение
− б 2 а
дает Икс -координата вершины.
Пример:
Найдите вершину параболы.
у «=» 3 Икс 2 + 12 Икс − 12
Здесь, а «=» 3 и б «=» 12 . Итак Икс -координата вершины:
− 12 2 ( 3 ) «=» − 2
Подставив в исходное уравнение, чтобы получить у -координата, получаем:
у «=» 3 ( − 2 ) 2 + 12 ( − 2 ) − 12
«=» − 24
Итак, вершина параболы находится в точке
(
−
2
,
−
24
)
.
Ось симметрии
Ось симметрии параболы — это вертикальная линия, проходящая через вершину. Для параболы стандартной формы у «=» а Икс 2 + б Икс + с , ось симметрии имеет уравнение
Икс «=» − б 2 а
Обратите внимание, что − б 2 а также является Икс -координата вершины параболы.
Пример:
Найдите ось симметрии.
у «=» 2 Икс 2 + Икс − 1
Здесь, а «=» 2 и б «=» 1 . Итак, осью симметрии является вертикальная линия
Икс «=» − 1 4
Перехваты
Вы можете найти
у
-перехват параболы простым вводом
0
для
Икс
. Если уравнение находится в стандартной форме, то вы можете просто взять
с
как
у
-перехват. Например, в приведенном выше примере:
Если уравнение находится в стандартной форме, то вы можете просто взять
с
как
у
-перехват. Например, в приведенном выше примере:
у «=» 2 ( 0 ) 2 + ( 0 ) − 1 «=» − 1
Итак у -перехват − 1 .
Икс -перехваты немного сложнее. Вы можете использовать факторинг , или завершение квадрата , или квадратичная формула найти их (если они существуют!).
Домен и диапазон
Как и любая функция, домен квадратичной функции ф ( Икс ) это набор Икс -значения, для которых определена функция, и диапазон множество всех выходных значений (значений ф ).
Квадратичные функции обычно имеют областью определения всю действительную прямую: любая
Икс
является законным входом. Диапазон ограничен теми точками, которые больше или равны
у
-координата вершины (или меньше или равна, в зависимости от того, открывается парабола вверх или вниз).
Диапазон ограничен теми точками, которые больше или равны
у
-координата вершины (или меньше или равна, в зависимости от того, открывается парабола вверх или вниз).
Квадратичная функция — стандартная форма, формула, примеры
Квадратичные функции используются в различных областях техники и науки для получения значений различных параметров. Графически они изображаются параболой. В зависимости от коэффициента высшей степени решается направление кривой. Слово «Квадрат» происходит от слова «Квадрат», что означает квадрат. Другими словами, квадратичная функция — это «полиномиальная функция степени 2». Существует множество сценариев, в которых используются квадратичные функции. Знаете ли вы, что при запуске ракеты ее траектория описывается квадратичной функцией?
В этой статье мы исследуем мир квадратичных функций в математике. Вы узнаете о графиках квадратичных функций, формулах квадратичных функций и других интересных фактах по теме. Мы также будем решать примеры на основе концепции для лучшего понимания.
Мы также будем решать примеры на основе концепции для лучшего понимания.
| 1. | Что такое квадратичная функция? |
| 2. | Стандартная форма квадратичной функции |
| 3. | Формула квадратичных функций |
| 4. | Различные формы квадратичной функции |
| 5. | Область и диапазон квадратичной функции |
| 6. | График квадратичной функции |
| 7. | Максимумы и минимумы квадратичной функции |
| 8. | Часто задаваемые вопросы о квадратичной функции |
Что такое квадратичная функция?
Квадратичная функция — это полиномиальная функция с одной или несколькими переменными, в которой старший показатель переменной равен двум. Поскольку высший член квадратичной функции имеет вторую степень, поэтому его также называют многочленом степени 2. Квадратичная функция имеет минимум одного члена второй степени. Это алгебраическая функция.
Квадратичная функция имеет минимум одного члена второй степени. Это алгебраическая функция.
Родительская квадратичная функция имеет вид f(x) = x 2 и соединяет точки, координаты которых имеют вид (число, число 2 ). К этой функции можно применить преобразования, на которых она обычно имеет вид f(x) = a (x — h) 2 + k, а далее ее можно преобразовать в вид f(x) = ax 2 + бх + в. Давайте подробно изучим каждый из них в следующих разделах.
Стандартная форма квадратичной функции
Стандартная форма квадратичной функции имеет вид f(x) = ax 2 + bx + c, где a, b и c — действительные числа с a ≠ 0.
Примеры квадратичных функций
Уравнение квадратичной функции имеет вид f(x) = ax 2 + bx + c, где a ≠ 0. Рассмотрим несколько примеров квадратичных функций:
- f(x) = 2x 2 + 4x — 5; Здесь а = 2, Ь = 4, с = -5
- f(x) = 3x 2 — 9; Здесь а = 3, б = 0, с = -9
- f(x) = x 2 — x; Здесь а = 1, Ь = -1, с = 0
Теперь рассмотрим f(x) = 4x-11; Здесь a = 0, поэтому f(x) НЕ является квадратичной функцией.
Вершина квадратичной функции
Вершина квадратичной функции (в форме буквы U) находится там, где функция имеет максимальное или минимальное значение. Ось симметрии квадратичной функции пересекает функцию (параболу) в вершине.
Формула квадратичных функций
Квадратичную функцию всегда можно разложить на множители, но процесс факторизации может быть затруднен, если нули выражения являются нецелыми действительными числами или недействительными числами. В таких случаях мы можем использовать квадратную формулу для определения нулей выражения. Общая форма квадратичной функции задается следующим образом: f(x) = ax 2 + bx + c, где a, b и c — действительные числа с a ≠ 0. Корни квадратичной функции f(x) можно рассчитать по формуле квадратичной функции:
- х = [-b ± √(b 2 — 4ac)] / 2a
Различные формы квадратичной функции
Квадратичная функция может иметь различные формы: стандартную форму, форму вершины и форму пересечения. Вот общие формы каждого из них:
Вот общие формы каждого из них:
- Стандартная форма: f(x) = ax 2 + bx + c, где a ≠ 0,
- Форма вершины: f(x) = a(x — h) 2 + k, где a ≠ 0, а (h, k) — вершина параболы, представляющая квадратичную функцию.
- Форма точки пересечения: f(x) = a(x — p)(x — q), где a ≠ 0, а (p, 0) и (q, 0) — точки пересечения по оси x параболы, представляющей квадратичную функцию.
Парабола открывается вверх или вниз в зависимости от значения ‘a’ меняется:
- Если a > 0, то парабола открывается вверх.
- Если a < 0, то парабола направлена вниз.
Мы всегда можем преобразовать одну форму в другую. Мы можем легко преобразовать форму вершины или форму перехвата в стандартную форму, просто упростив алгебраические выражения. Давайте посмотрим, как преобразовать стандартную форму в форму каждой вершины и форму пересечения.
Преобразование стандартной формы квадратичной функции в вершинную форму
Квадратичная функция f(x) = ax 2 + bx + c может быть легко преобразована в вершинную форму f(x) = a (x — h) 2 + k, используя значения h = -b/2a и k = f(-b/2a). Вот пример.
Вот пример.
Пример: Преобразуйте квадратичную функцию f(x) = 2x 2 — 8x + 3 в вершинную форму.
- Шаг — 1: Сравнивая данную функцию с f(x) = ax 2 + bx + c, получаем a = 2, b = -8 и c = 3.
- Шаг — 2: Найдите ‘h’ по формуле: h = -b/2a = -(-8)/2(2) = 2.
- Шаг — 3: Найдите ‘k’ по формуле: k = f(-b/2a) = f(2) = 2(2) 2 — 8(2) + 3 = 8 — 16 + 3 = -5.
- Шаг — 4: Подставить значения в вершинную форму: f(x) = 2 (x — 2) 2 — 5.
Преобразование стандартной формы квадратичной функции в форму точки пересечения
Квадратичная функция f(x) = ax 2 + bx + c может быть легко преобразована в вершинную форму f(x) = a (x — p)(x — q), используя значения p и q (x-отрезки) путем решения квадратного уравнения ax 2 + bx + c = 0.
Пример: Преобразуйте квадратичную функцию f(x) = x 2 — 5x + 6 в форму пересечения.
- Шаг — 1: Сравнивая данную функцию с f(x) = ax 2 + bx + c, получаем a = 1,
- Шаг — 2: Решить квадратное уравнение: x 2 — 5x + 6 = 0
Разложив на множители левую часть, получим
. (х — 3) (х — 2) = 0
х = 3, х = 2 - Шаг – 3: Подставьте значения в форму вычленения: f(x) = 1 (x – 3)(x – 2).
Область и диапазон квадратичной функции
Область определения квадратичной функции — это множество всех значений x, определяющих функцию, а диапазон квадратичной функции — это множество всех значений y, которые функция получает путем замены различных значений x.
Область квадратичной функции
Квадратичная функция — это полиномиальная функция, определенная для всех действительных значений x. Итак, область определения квадратичной функции — это множество действительных чисел, то есть R. В интервальной записи областью определения любой квадратичной функции является (-∞, ∞).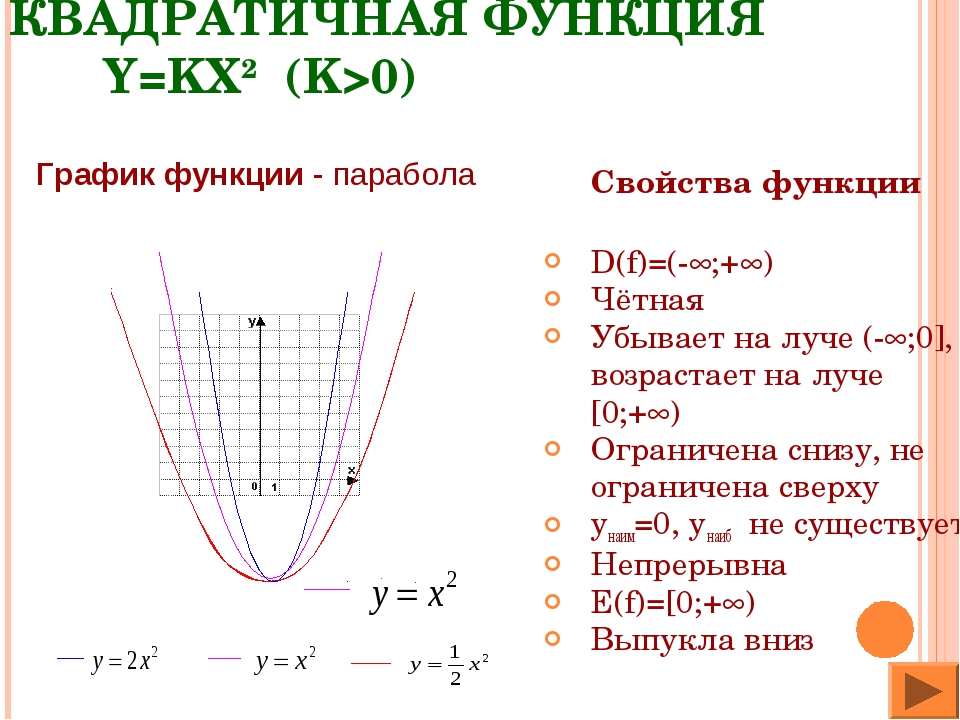
Диапазон квадратичной функции
Диапазон квадратичной функции зависит от открытой стороны и вершины графика. Итак, найдите самое нижнее и самое верхнее значения f(x) на графике функции, чтобы определить диапазон квадратичной функции. Область значений любой квадратичной функции с вершиной (h, k) и уравнением f(x) = a(x — h) 2 + k равно:
- y ≥ k (или) [k, ∞), когда a > 0 (поскольку парабола раскрывается, когда a > 0).
- y ≤ k (или) (-∞, k], когда a < 0 (поскольку парабола раскрывается вниз, когда a < 0).
График квадратичной функции
График квадратичной функции представляет собой параболу. т. е. открывается вверх или вниз в форме буквы U. Вот шаги для построения графика квадратичной функции.
- Шаг — 1: Найдите вершину.
- Шаг — 2: Вычислите таблицу квадратичных функций с двумя столбцами x и y с 5 строками (мы также можем взять больше строк) с вершиной в одной из точек и возьмите два случайных значения по обе стороны от нее.

- Шаг — 3: Найдите соответствующие значения y, подставив каждое значение x в заданную квадратичную функцию.
- Шаг — 4: Теперь у нас есть две точки по обе стороны от вершины, поэтому, нанеся их на координатную плоскость и соединив их кривой, мы можем получить идеальную форму. Кроме того, расширьте график с обеих сторон. Вот график квадратичной функции.
Пример: Нарисуйте график квадратичной функции f(x) = 2x 2 — 8x + 3.
Решение:
Сравнивая это с f(x) = ax 2 90 174 + бх + в, получаем a = 2, b = -8 и c = 3.
- Шаг — 1: Найдем вершину.
x-координата вершины = -b/2a = 8/4 = 2
y-координата вершины = f(-b/2a) = 2(2) 2 — 8(2) + 3 = 8 — 16 + 3 = -5.
Следовательно, вершина = (2, -5). - Шаг — 2: Создайте таблицу с вершиной, записанной в средней строке.
х и 2 -5 - Шаг — 3: Заполните первый столбец двумя случайными числами по обе стороны от 2.

х и 0 1 2 -5 3 4 - Шаг — 4: Найдите y, подставив каждое значение x в заданную квадратичную функцию. Например, когда x = 0, y = 2(0) 2 — 8(0) + 3 = 3.
х и 0 3 1 -3 2 -5 3 -3 4 3 - Шаг — 5: Просто нанесите указанные выше точки и соедините их плавной кривой.

Примечание: Мы можем построить точки пересечения по осям x и y квадратичной функции, чтобы получить более аккуратную форму графика.
График квадратичных функций также можно получить с помощью калькулятора квадратичных функций.
Максимумы и минимумы квадратичной функции
Максимумы или минимумы квадратичных функций находятся в его вершине. Его также можно найти с помощью дифференцирования. Чтобы лучше понять концепцию, давайте рассмотрим пример и решим его. Возьмем пример квадратичной функции f(x) = 3x 2 + 4x + 7.
Дифференцируя функцию,
⇒f'(x) = 6x + 4
Приравнивание к нулю,
⇒6x + 4 = 0
⇒ x = -2/3
Двойное дифференцирование функции,
9000 2 ⇒f»( x) = 6 > 0Поскольку двойная производная функции больше нуля, у нас будут минимумы при x = -2/3 (по тесту второй производной), а парабола направлена вверх.
Аналогично, если двойная производная в стационарной точке меньше нуля, то функция будет иметь максимумы.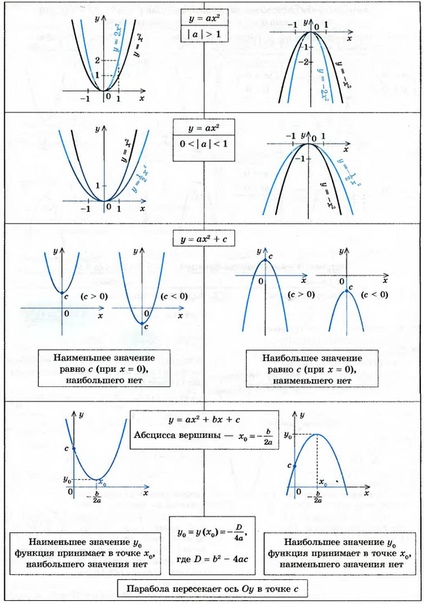 Следовательно, используя дифференцирование, мы можем найти минимум или максимум квадратичной функции.
Следовательно, используя дифференцирование, мы можем найти минимум или максимум квадратичной функции.
☛ Статьи по теме
- Калькулятор квадратных уравнений
- Калькулятор корней квадратного уравнения
Важные замечания по квадратичной функции:
- Стандартная форма квадратичной функции: f(x) = ax 2 +bx+c, где a ≠ 0,
- График квадратичной функции имеет форму параболы.
- Квадратная формула используется для решения квадратного уравнения ax 2 + bx + c = 0 и определяется как x = [-b ± √(b 2 — 4ac)] / 2a.
- Дискриминант квадратного уравнения ax 2 + bx + c = 0 равен b 2 -4ac. Это используется для определения характера нулей квадратичной функции.
Примеры квадратичной функции
Пример 1: Определить вершину квадратичной функции f(x) = 2(x+3) 2 — 2,
Решение: Имеем f(x) = 2(x+3) 2 — 2, что можно записать как f(x) = 2(x-(-3)) 2 + (-2 )
Сравнивая данную квадратичную функцию с вершинной формой квадратичной функции f(x) = a(x-h) 2 + k, где (h,k) вершина параболы, имеем
h = — 3, k = -2
Следовательно, вершина f(x) равна (-3,-2)
Ответ: Вершина = (-3,-2)
Пример 2: Найдите нули квадратичной функции f(x) = x 2 + 3x — 4, используя формулу квадратичной функции.

Решение: Квадратичная функция f(x) = x 2 + 3x — 4. Сравнивая f(x) с общей формой ax 2 + bx + c, получаем a = 1, b = 3, c = -4
Нули квадратичной функции получаются путем решения f(x) = 0.
Для этого используем квадратичную формулу: x = [ -b ± √(b 2 — 4ac) ] / 2а
х = [ -3 ± √{3 2 — 4(1)(-4)}] / 2(1) = [ -3 ± √(9 + 16) ] / 2 = [ -3 ± √25 ] / 2,
х = [ — 3 + 5 ] / 2, [ -3 — 5 ] / 2
= 1, -4
Ответ: Корни f(x) = x 2 + 3x — 4 равны 1 и -4
Пример 3: Запишите квадратичную функцию f(x) = (x-12)(x+3) в общем виде ax 2 + bx + c.
Решение: У нас есть квадратичная функция f(x) = (x-12)(x+3). Мы просто расширим (умножим биномы) его, чтобы записать в общем виде.
f(x) = (x-12)(x+3)
= x(x+3) — 12(x+3)
= x 2 + 3x — 12x — 36
= x 2 — 9x — 36
Ответ: x 2 — 9x — 36
перейти к слайдуперейти к слайдуперейти к слайду
Разбивайте сложные концепции с помощью простых визуальных средств.
Математика больше не будет сложным предметом, особенно когда вы понимаете концепции с помощью визуализаций.
Забронировать бесплатный пробный урок
Практические вопросы по квадратичной функции
перейти к слайдуперейти к слайду
Часто задаваемые вопросы о квадратичной функции
Что такое квадратичная функция в математике?
Квадратичная функция — это полиномиальная функция с одной или несколькими переменными, в которой старший показатель переменной равен двум. Другими словами, квадратичная функция — это «полиномиальная функция степени 2».
Почему название квадратичной функции?
Слово «quad» означает «квадрат». Следовательно, полиномиальная функция степени 2 называется квадратичной функцией.
Что такое квадратичное функциональное уравнение?
Квадратичная функция является многочленом степени 2, поэтому уравнение квадратичной функции имеет вид f(x) = ax 2 + bx + c, где «a» — ненулевое число; a, b и c — действительные числа.
Что такое вершина квадратичной функции?
Вершина квадратичной функции — это точка, в которой парабола меняет направление и пересекает ось симметрии. Это точка, в которой парабола меняется с возрастающей на убывающую или с убывающей на возрастающую. В этой точке производная квадратичной функции равна 0,
Что такое нули квадратичной функции?
Нули квадратичной функции — это точки, в которых график функции пересекает ось x. В нулях функции координата y равна 0, а координата x представляет собой нули квадратичной полиномиальной функции. Нули квадратичной функции также называют корнями функции.
Что такое таблица квадратичных функций?
Таблица квадратичных функций — это таблица, в которой мы определяем значения координат y, соответствующие каждой координате x, и наоборот. Таблица состоит из координат графика квадратичных функций. Мы обычно записываем вершину квадратичной функции в квадратичной функции в одной из строк таблицы.
Как рисовать квадратичный график?
График квадратичной функции представляет собой параболу. Его можно нарисовать, нанеся координаты на график. Мы подставляем значения x и получаем соответствующие значения y, таким образом получая координаты графика. После нанесения координат на график, свободной рукой соединяем точки, чтобы получить график квадратичных функций. Нахождение вершины помогает в построении квадратичного графа.
Его можно нарисовать, нанеся координаты на график. Мы подставляем значения x и получаем соответствующие значения y, таким образом получая координаты графика. После нанесения координат на график, свободной рукой соединяем точки, чтобы получить график квадратичных функций. Нахождение вершины помогает в построении квадратичного графа.
Как найти точку пересечения по оси x квадратичной функции?
X-пересечение квадратичной функции можно найти, рассматривая квадратичную функцию f(x) = 0 и затем определяя значение x. Другими словами, точка пересечения с осью x есть не что иное, как нуль квадратного уравнения.
Является ли парабола квадратичной функцией?
Парабола — это график квадратичной функции. Квадратичная функция имеет вид f(x) = ax 2 + bx + c, где a не равно 0. Парабола — это U-образный или перевернутый U-образный график квадратичной функции.
Как найти обратную квадратичную функцию?
Обратную квадратичную функцию f(x) можно найти, заменив f(x) на y.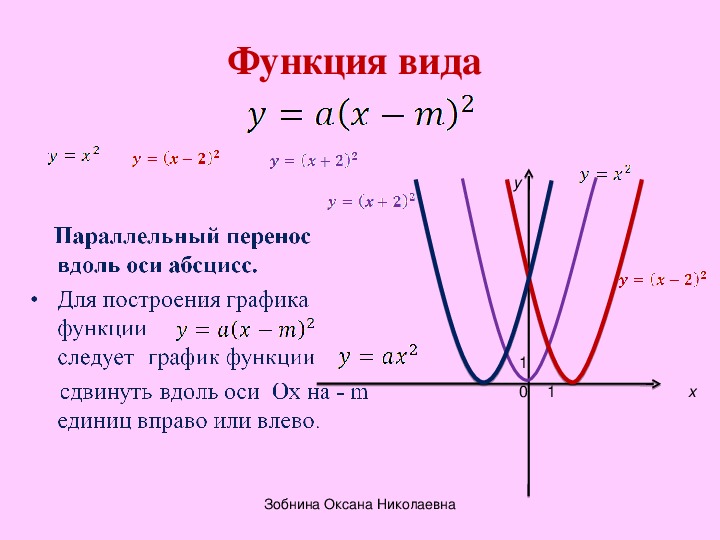

 by/algebra/funkcii/kvadratichnaja-funkcija] не найдена.
by/algebra/funkcii/kvadratichnaja-funkcija] не найдена.
 05.13
05.13  by 2013-2016
by 2013-2016 6KB
6KB 07KB
07KB 05KB
05KB 75KB
75KB 87KB
87KB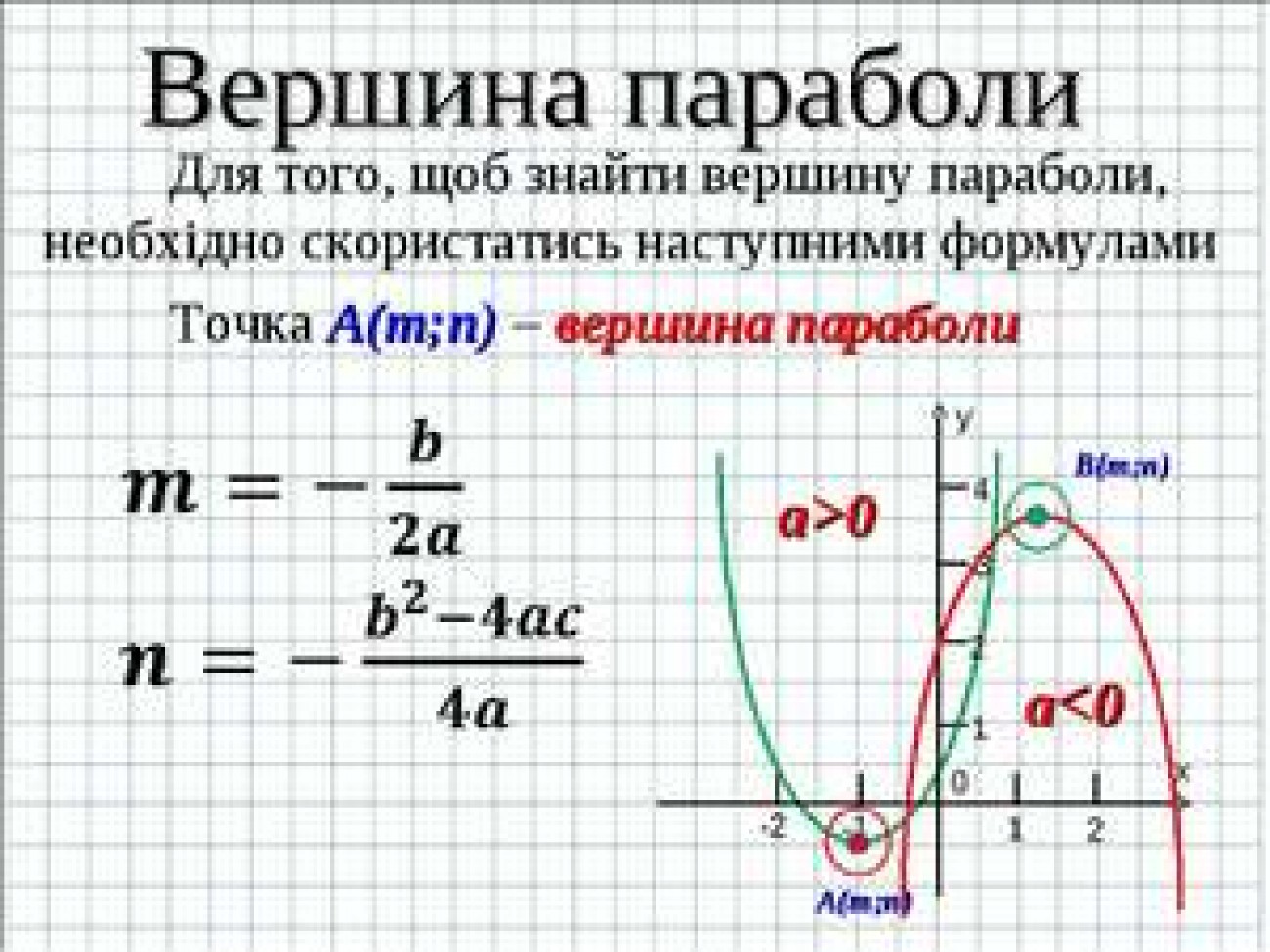 01KB
01KB 78KB
78KB 41KB
41KB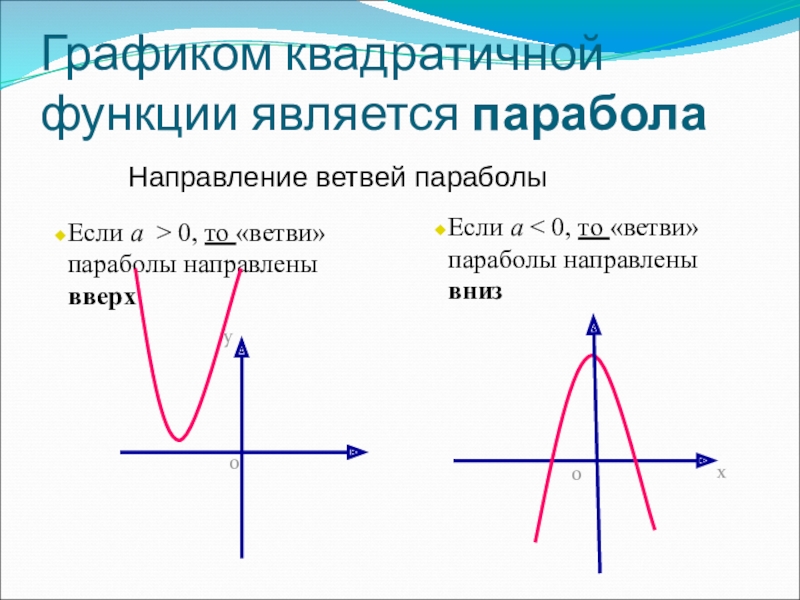 32KB
32KB